Multivariate Forecasting Evaluation: Nixtla-TimeGPT †
Abstract
1. Introduction
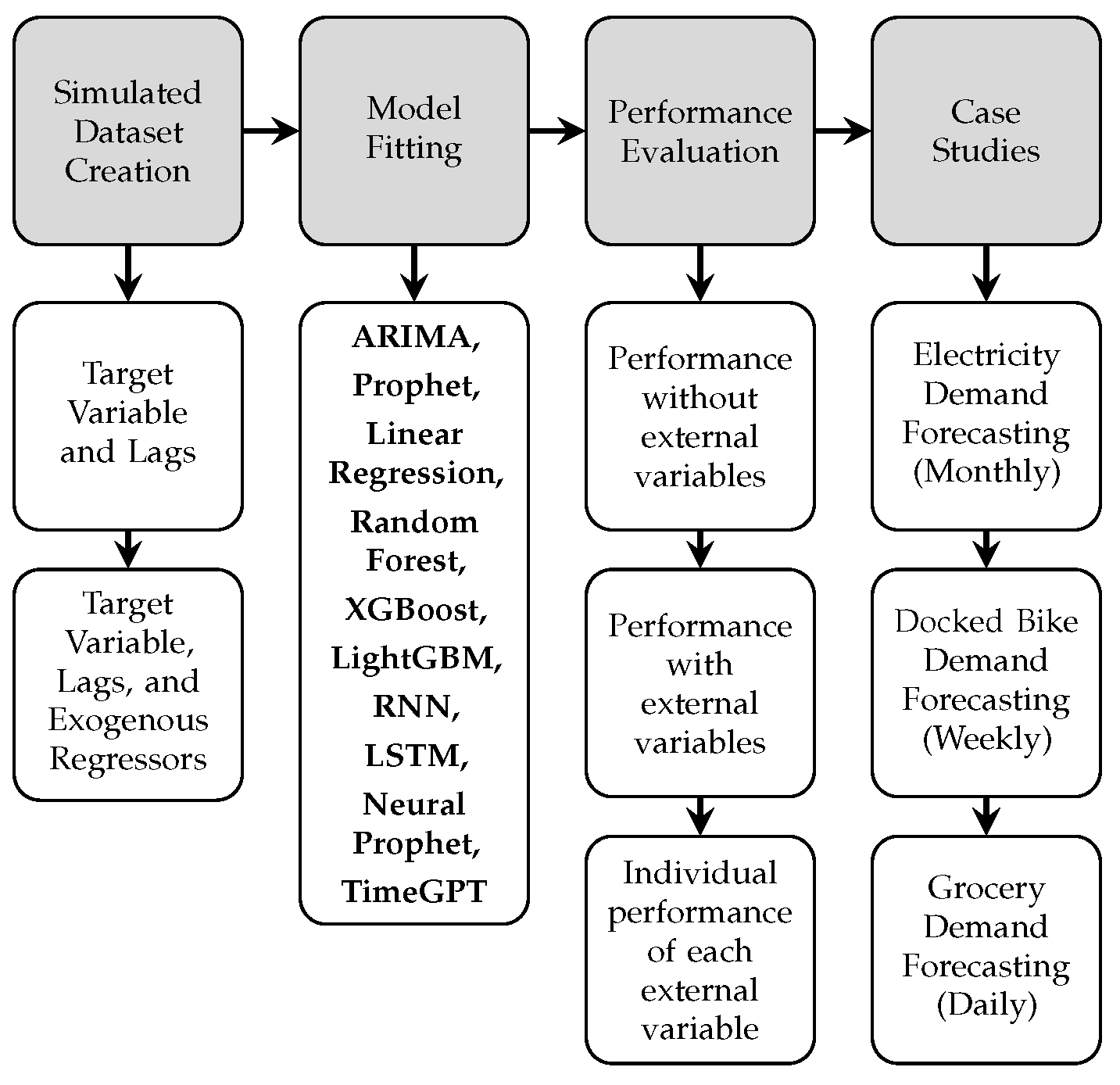
2. Materials and Methods
2.1. Dataset Creation and Evaluation
2.2. Simulated External Regressor Creation
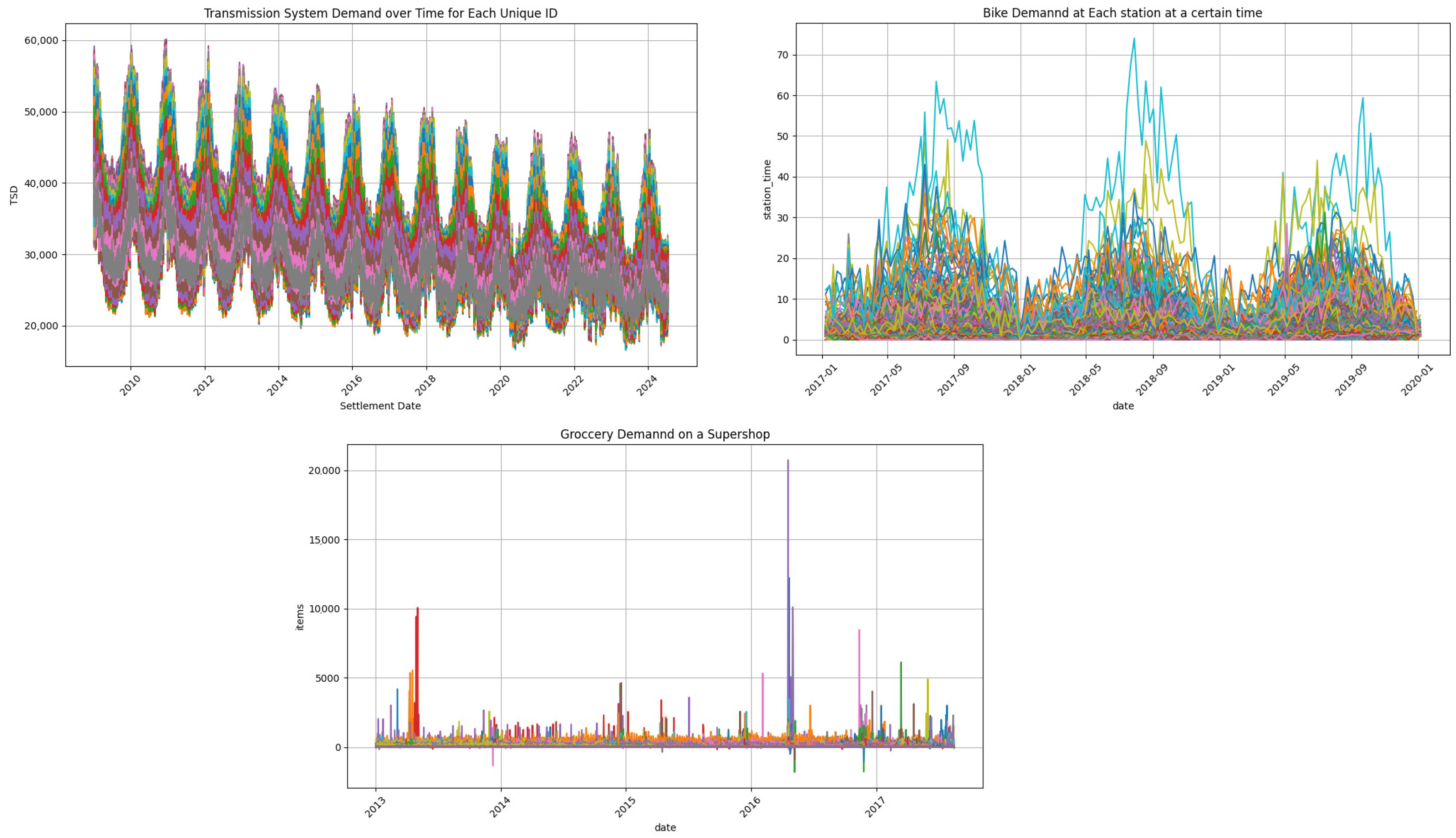
2.3. Case Studies
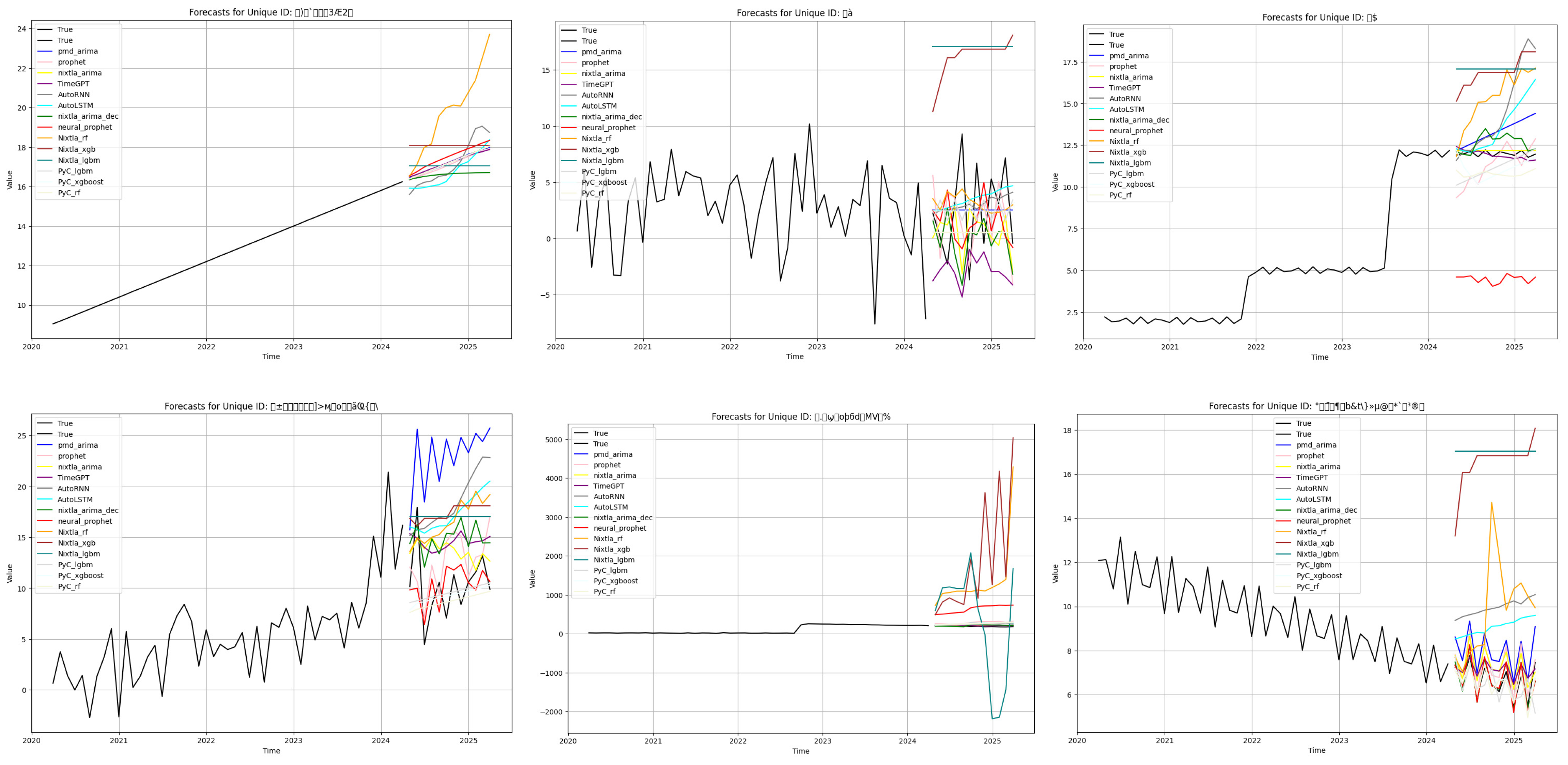
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ekambaram, V.; Jati, A.; Dayama, P.; Mukherjee, S.; Nguyen, N.H.; Gifford, W.M.; Reddy, C.; Kalagnanam, J. Tiny Time Mixers (TTMs): Fast Pre-trained Models for Enhanced Zero/Few-Shot Forecasting of Multivariate Time Series. arXiv 2024, arXiv:2401.03955. [Google Scholar]
- Rasul, K.; Ashok, A.; Williams, A.R.; Ghonia, H.; Bhagwatkar, R.; Khorasani, A.; Bayazi, M.J.D.; Adamopoulos, G.; Riachi, R.; Hassen, N.; et al. Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. arXiv 2024, arXiv:2310.08278. [Google Scholar] [CrossRef]
- Das, A.; Kong, W.; Sen, R.; Zhou, Y. A decoder-only foundation model for time-series forecasting. arXiv 2024, arXiv:2310.10688. [Google Scholar]
- Garza, A.; Challu, C.; Mergenthaler-Canseco, M. TimeGPT-1. arXiv 2024, arXiv:2310.03589. [Google Scholar]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural basis expansion analysis with exogenous variables: Forecasting electricity prices with NBEATSx. Int. J. Forecast. 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Kaggle. Electricity Consumption UK 2009–2024. 2024. Available online: https://www.kaggle.com/datasets/albertovidalrod/electricity-consumption-uk-20092022 (accessed on 1 July 2024).
- Kaggle. Divvy Station Dock Capacity Time Series Forecast. 2022. Available online: https://www.kaggle.com/datasets/leonidasliao/divvy-station-dock-capacity-time-series-forecast (accessed on 1 July 2024).
- Kaggle. Corporación Favorita Grocery Sales Forecasting. 2018. Available online: https://www.kaggle.com/competitions/favorita-grocery-sales-forecasting/overview (accessed on 1 July 2024).
- Ghiletki, D. Machine Learning-Based Demand Forecasting for Supply Chain Management. Master’s Thesis, Department of Technology, Management and Economics, DTU, Copenhagen, Denmark, 2023. [Google Scholar]
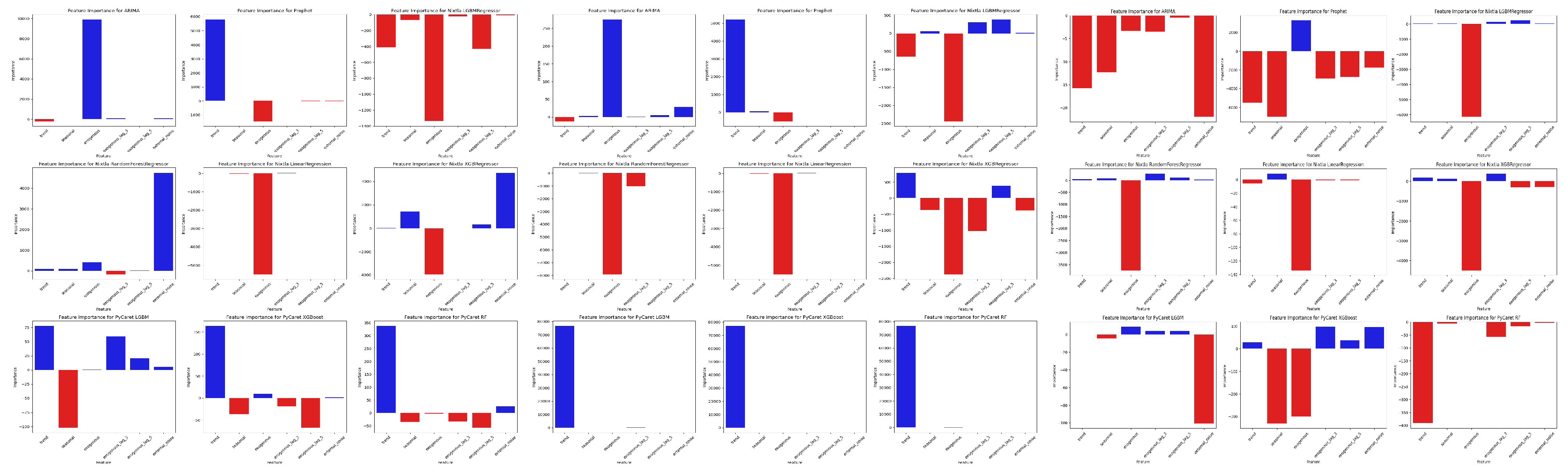
| X Feature | Daily | Weekly | Monthly |
|---|---|---|---|
| Static trend | 0.51 | 0.57 | 0.63 |
| Static seasonal | −0.07 | −0.07 | −0.04 |
| Exogenous | 0.31 | 0.36 | 0.43 |
| Exogenous_lag_3 | 0.27 | 0.35 | 0.4 |
| Exogenous_lag_5 | 0.27 | 0.35 | 0.44 |
| Noise | 0 | 0 | 0 |
| Model | Daily | Weekly | Monthly |
|---|---|---|---|
| AutoLSTM (neuralforecast) | 0.009652 | 0.002137 | 0.08955 |
| AutoRNN (neuralforecast) | 0.009892 | 0.002277 | 0.090511 |
| Neuralprophet | 0.009429 | 0.002662 | 0.104538 |
| TimeGPT(zeroshot) | 0.006097 | 0.001962 * | 0.090954 |
| LightGBM (Nixtla) | 0.00653 | 0.007487 | 0.158012 |
| Linear Regression (Nixtla) | 0.364913 | 0.123713 | 0.320041 |
| Random Forest (Nixtla) | 0.011217 | 0.003226 | 0.124173 |
| XGBoost (Nixtla) | 0.006377 | 0.004707 | 0.134841 |
| LightGBM (PyCaret) | 0.008808 | 0.00226 | 0.101377 |
| Linear Regression (PyCaret) | 0.728414 | 0.906034 | 0.783822 |
| XGBoost (PyCaret) | 0.008687 | 0.002192 | 0.100657 |
| Random Forest (PyCaret) | 0.008748 | 0.002243 | 0.100578 |
| ARIMA (Pmdarima) | 0.005902 | 0.002024 | 0.088495 |
| ARIMA (Nixtla) | 0.005812 * | 0.00234 | 0.077143 * |
| MSTL ARIMA (Nixtla) | 0.005834 | 0.002298 | 0.081126 |
| Prophet | 0.007215 | 0.001965 | 0.098457 |
| Title | Scenario | AutoLSTM | AutoRNN | NeuralProphet | TimeGPT | LGBM(Nixtla) | RF(Nixtla) | Xgb(Nixtla) | Lgbm(PyC) | Xgb(PyC) | Arima(Pmd) | MSTL Arima(Nixtla) | Prophet | Arima(Nixtla) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| trend- upward, linear | Weekly | 0.03 | 0.07 | 0.01 | 0.00 | 1.00 | 0.11 | 0.28 | 0.00 | 0.00 | 0.02 | 0.05 | 0.00 | 0.02 |
| Monthly | 0.10 | 0.12 | 0.06 | 0.01 | 0.59 | 0.50 | 0.63 | 0.00 | 0.00 | 0.01 | 0.12 | 0.02 | 0.00 | |
| Daily | 0.01 | 0.01 | 0.00 | 0.05 | 0.66 | 0.50 | 0.52 | 0.00 | 0.00 | 0.00 | 0.05 | 0.00 | 0.05 | |
| trend- upward with breaks, nonlinear | Weekly | 0.04 | 0.01 | 1.00 | 0.05 | 0.02 | 0.07 | 0.05 | 0.43 | 0.39 | 0.03 | 0.07 | 0.33 | 0.04 |
| Monthly | 0.02 | 0.01 | 0.18 | 0.02 | 0.57 | 0.63 | 1.00 | 0.07 | 0.09 | 0.11 | 0.01 | 0.07 | 0.01 | |
| Daily | 0.88 | 0.87 | 1.00 | 0.06 | 0.12 | 0.06 | 0.02 | 0.40 | 0.41 | 0.06 | 0.06 | 0.78 | 0.06 | |
| trend- upward with breaks, linear, Additive | Weekly | 0.03 | 0.05 | 0.17 | 0.01 | 1.00 | 0.00 | 0.44 | 0.02 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 |
| Monthly | 0.02 | 0.05 | 0.33 | 0.01 | 1.00 | 0.14 | 0.92 | 0.02 | 0.01 | 0.02 | 0.01 | 0.09 | 0.01 | |
| Daily | 0.28 | 0.34 | 0.42 | 0.01 | 1.00 | 0.01 | 0.84 | 0.10 | 0.07 | 0.01 | 0.01 | 0.00 | 0.01 | |
| trend- upward with breaks, linear | Weekly | 0.58 | 0.59 | 0.67 | 0.44 | 0.69 | 0.56 | 0.57 | 0.56 | 0.57 | 0.36 | 0.32 | 0.47 | 0.32 |
| Monthly | 0.34 | 0.34 | 0.39 | 0.33 | 0.77 | 0.64 | 0.46 | 0.38 | 0.38 | 0.30 | 0.26 | 0.37 | 0.19 | |
| Daily | 0.53 | 0.56 | 0.60 | 0.28 | 0.38 | 0.44 | 0.41 | 0.46 | 0.46 | 0.23 | 0.42 | 0.33 | 0.25 | |
| trend- upward with breaks | Weekly | 0.11 | 0.14 | 0.89 | 0.03 | 1.00 | 0.01 | 0.10 | 0.35 | 0.13 | 0.02 | 0.01 | 0.22 | 0.01 |
| Monthly | 0.01 | 0.01 | 0.13 | 0.01 | 0.96 | 0.21 | 1.00 | 0.01 | 0.01 | 0.00 | 0.01 | 0.02 | 0.00 | |
| Daily | 0.88 | 0.89 | 0.92 | 0.00 | 0.05 | 0.02 | 0.11 | 0.66 | 0.64 | 0.01 | 0.01 | 0.68 | 0.01 | |
| trend- stable with breaks, nonlinear | Weekly | 0.21 | 0.25 | 0.94 | 0.10 | 0.06 | 0.03 | 0.10 | 0.69 | 0.67 | 0.00 | 0.02 | 0.32 | 0.00 |
| Monthly | 0.04 | 0.05 | 0.12 | 0.01 | 1.00 | 0.49 | 0.59 | 0.08 | 0.08 | 0.07 | 0.01 | 0.06 | 0.00 | |
| Daily | 0.88 | 0.89 | 0.92 | 0.00 | 0.05 | 0.02 | 0.11 | 0.66 | 0.64 | 0.01 | 0.01 | 0.68 | 0.01 | |
| trend- stable with breaks, linear, Multiplicative | Weekly | 0.98 | 0.99 | 1.00 | 0.96 | 0.96 | 0.96 | 0.96 | 0.98 | 0.98 | 0.96 | 0.96 | 0.94 | 0.96 |
| Monthly | 0.99 | 1.00 | 1.00 | 0.96 | 0.76 | 0.68 | 0.66 | 0.98 | 0.98 | 0.92 | 0.95 | 0.97 | 0.96 | |
| Daily | 1.00 | 1.00 | 1.00 | 0.95 | 0.95 | 0.89 | 0.94 | 0.97 | 0.97 | 0.95 | 0.95 | 0.91 | 0.95 | |
| trend- stable with breaks, linear | Weekly | 0.23 | 0.28 | 0.95 | 0.19 | 0.29 | 0.21 | 0.29 | 0.40 | 0.40 | 0.13 | 0.14 | 0.34 | 0.12 |
| Monthly | 0.11 | 0.15 | 0.30 | 0.09 | 0.79 | 0.52 | 0.69 | 0.13 | 0.14 | 0.08 | 0.08 | 0.13 | 0.07 | |
| Daily | 0.74 | 0.72 | 0.41 | 0.12 | 0.28 | 0.19 | 0.20 | 0.19 | 0.19 | 0.07 | 0.08 | 0.24 | 0.06 | |
| trend- downward, linear | Weekly | 0.09 | 0.06 | 0.34 | 0.03 | 0.74 | 0.28 | 0.47 | 0.12 | 0.03 | 0.06 | 0.02 | 0.02 | 0.02 |
| Monthly | 0.26 | 0.35 | 0.33 | 0.08 | 0.84 | 0.16 | 0.72 | 0.06 | 0.03 | 0.10 | 0.05 | 0.07 | 0.00 | |
| Daily | 0.30 | 0.25 | 0.36 | 0.06 | 0.93 | 0.07 | 0.90 | 0.11 | 0.08 | 0.09 | 0.06 | 0.11 | 0.06 | |
| trend- downward with breaks, nonlinear | Weekly | 0.40 | 0.39 | 0.48 | 0.50 | 0.76 | 0.03 | 1.00 | 0.61 | 0.62 | 0.39 | 0.15 | 0.52 | 0.15 |
| Monthly | 0.03 | 0.03 | 0.36 | 0.42 | 1.00 | 0.87 | 0.63 | 0.51 | 0.51 | 0.38 | 0.12 | 0.48 | 0.04 | |
| Daily | 0.43 | 0.43 | 0.27 | 0.35 | 0.96 | 0.49 | 0.18 | 0.38 | 0.38 | 0.04 | 1.00 | 0.36 | 0.04 | |
| trend- downward with breaks, linear | Weekly | 0.35 | 0.38 | 0.83 | 0.32 | 0.64 | 0.39 | 0.61 | 0.61 | 0.60 | 0.28 | 0.24 | 0.43 | 0.24 |
| Monthly | 0.29 | 0.32 | 0.51 | 0.29 | 0.68 | 0.57 | 0.46 | 0.35 | 0.35 | 0.26 | 0.23 | 0.35 | 0.20 | |
| Daily | 0.60 | 0.49 | 0.70 | 0.22 | 0.39 | 0.45 | 0.30 | 0.40 | 0.42 | 0.21 | 0.32 | 0.35 | 0.21 | |
| trend- downward with breaks | Weekly | 0.22 | 0.26 | 1.00 | 0.02 | 0.06 | 0.05 | 0.19 | 0.32 | 0.33 | 0.04 | 0.01 | 0.42 | 0.03 |
| Monthly | 0.01 | 0.01 | 0.12 | 0.00 | 0.32 | 1.00 | 0.61 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | |
| Daily | 0.30 | 0.23 | 1.00 | 0.21 | 0.29 | 0.68 | 0.21 | 0.31 | 0.28 | 0.19 | 0.19 | 0.17 | 0.22 | |
| trend- downward | Weekly | 0.56 | 0.57 | 0.69 | 0.56 | 1.00 | 0.48 | 0.71 | 0.41 | 0.34 | 0.61 | 0.46 | 0.48 | 0.59 |
| Monthly | 0.54 | 0.79 | 0.56 | 0.46 | 1.00 | 0.54 | 0.95 | 0.50 | 0.61 | 0.51 | 0.49 | 0.60 | 0.50 | |
| Daily | 0.78 | 0.88 | 0.81 | 0.81 | 0.79 | 0.98 | 0.81 | 1.00 | 0.98 | 0.87 | 0.79 | 0.76 | 0.89 | |
| multiple seasonalities, upward, linear, Additive | Weekly | 0.29 | 0.30 | 0.58 | 0.24 | 0.54 | 0.29 | 1.00 | 0.26 | 0.49 | 0.39 | 0.21 | 0.16 | 0.23 |
| Monthly | 0.35 | 0.48 | 0.68 | 0.22 | 0.85 | 0.24 | 0.60 | 0.18 | 0.18 | 0.29 | 0.27 | 0.26 | 0.24 | |
| Daily | 0.43 | 0.58 | 0.57 | 0.15 | 1.00 | 0.40 | 0.91 | 0.25 | 0.24 | 0.21 | 0.15 | 0.28 | 0.15 | |
| multiple seasonalities, stable, linear, Multiplicative | Weekly | 0.79 | 0.77 | 1.00 | 0.82 | 0.75 | 0.83 | 0.81 | 0.87 | 0.91 | 0.83 | 0.81 | 0.76 | 0.81 |
| Monthly | 0.25 | 0.24 | 0.33 | 0.27 | 1.00 | 0.26 | 0.16 | 0.29 | 0.30 | 0.28 | 0.26 | 0.29 | 0.27 | |
| Daily | 0.75 | 0.76 | 1.00 | 0.82 | 0.79 | 0.44 | 0.69 | 0.87 | 0.87 | 0.82 | 0.82 | 0.67 | 0.82 | |
| multiple seasonalities, downward, linear, Multiplicative | Weekly | 0.91 | 0.90 | 1.00 | 0.95 | 0.77 | 0.89 | 0.30 | 0.94 | 0.96 | 0.93 | 0.94 | 0.92 | 0.94 |
| Monthly | 0.41 | 0.41 | 0.45 | 0.42 | 1.00 | 0.20 | 0.16 | 0.42 | 0.41 | 0.40 | 0.42 | 0.42 | 0.42 | |
| Daily | 0.76 | 0.77 | 1.00 | 0.91 | 0.84 | 0.91 | 0.77 | 0.92 | 0.90 | 0.95 | 0.92 | 0.86 | 0.92 | |
| cycles- upward, nonlinear, Additive | Weekly | 0.26 | 0.46 | 0.23 | 0.13 | 0.88 | 0.46 | 0.92 | 0.36 | 0.37 | 0.14 | 0.14 | 0.21 | 0.04 |
| Monthly | 0.30 | 0.35 | 0.37 | 0.15 | 0.84 | 0.63 | 0.65 | 0.34 | 0.31 | 0.22 | 0.25 | 0.12 | 0.09 | |
| Daily | 0.25 | 0.35 | 0.98 | 0.02 | 0.18 | 1.00 | 0.09 | 0.17 | 0.34 | 0.20 | 0.02 | 0.15 | 0.02 | |
| cycles- upward, linear, Multiplicative | Weekly | 0.07 | 0.04 | 1.00 | 0.11 | 0.74 | 0.03 | 0.15 | 0.14 | 0.13 | 0.16 | 0.02 | 0.15 | 0.03 |
| Monthly | 0.20 | 0.26 | 1.00 | 0.15 | 0.13 | 0.14 | 0.19 | 0.38 | 0.48 | 0.22 | 0.06 | 0.30 | 0.02 | |
| Daily | 0.25 | 0.35 | 0.98 | 0.02 | 0.18 | 1.00 | 0.09 | 0.17 | 0.34 | 0.20 | 0.02 | 0.15 | 0.02 | |
| cycles- upward, linear, Additive | Weekly | 0.00 | 0.05 | 0.35 | 0.01 | 1.00 | 0.22 | 0.31 | 0.08 | 0.01 | 0.00 | 0.01 | 0.01 | 0.00 |
| Monthly | 0.15 | 0.18 | 0.51 | 0.02 | 1.00 | 0.21 | 0.96 | 0.18 | 0.28 | 0.20 | 0.04 | 0.29 | 0.03 | |
| Daily | 1.00 | 0.97 | 0.31 | 0.06 | 0.43 | 0.49 | 0.34 | 0.31 | 0.23 | 0.03 | 0.04 | 0.17 | 0.04 | |
| cycles- upward with breaks, linear, Multiplicative | Weekly | 0.27 | 0.20 | 1.00 | 0.09 | 0.16 | 0.41 | 0.05 | 0.13 | 0.02 | 0.10 | 0.21 | 0.29 | 0.12 |
| Monthly | 0.09 | 0.11 | 0.31 | 0.05 | 0.23 | 0.69 | 0.55 | 0.05 | 0.10 | 0.08 | 0.07 | 0.12 | 0.07 | |
| Daily | 0.15 | 0.15 | 0.79 | 0.14 | 1.00 | 0.15 | 0.96 | 0.16 | 0.16 | 0.14 | 0.14 | 0.50 | 0.15 | |
| cycles- upward with breaks, linear, Additive | Weekly | 0.37 | 0.50 | 0.66 | 0.38 | 0.59 | 0.38 | 0.57 | 0.47 | 0.44 | 0.40 | 0.40 | 0.31 | 0.39 |
| Monthly | 0.34 | 0.48 | 0.57 | 0.27 | 0.49 | 0.64 | 0.34 | 0.35 | 0.37 | 0.36 | 0.32 | 0.27 | 0.26 | |
| Daily | 0.66 | 0.61 | 0.44 | 0.30 | 0.76 | 0.22 | 0.69 | 0.23 | 0.24 | 0.24 | 0.27 | 0.28 | 0.27 | |
| cycles- stable, linear, Additive | Weekly | 0.27 | 0.31 | 0.99 | 0.26 | 0.71 | 0.53 | 0.51 | 0.29 | 0.35 | 0.27 | 0.25 | 0.30 | 0.27 |
| Monthly | 0.44 | 0.51 | 1.00 | 0.23 | 0.37 | 0.30 | 0.38 | 0.35 | 0.38 | 0.34 | 0.30 | 0.37 | 0.28 | |
| Daily | 0.86 | 0.92 | 0.61 | 0.22 | 0.32 | 0.39 | 0.35 | 0.34 | 0.32 | 0.22 | 0.22 | 0.46 | 0.22 | |
| cycles- stable with breaks, linear, Additive | Weekly | 0.21 | 0.34 | 0.92 | 0.17 | 0.73 | 0.37 | 0.44 | 0.27 | 0.23 | 0.15 | 0.07 | 0.38 | 0.03 |
| Monthly | 0.34 | 0.45 | 0.90 | 0.22 | 0.53 | 0.46 | 0.34 | 0.32 | 0.28 | 0.43 | 0.20 | 0.42 | 0.08 | |
| Daily | 0.52 | 0.51 | 0.76 | 0.02 | 0.10 | 0.27 | 0.07 | 0.16 | 0.08 | 0.06 | 0.02 | 0.25 | 0.02 | |
| cycles- downward with breaks, linear, Multiplicative | Weekly | 0.20 | 0.25 | 1.00 | 0.10 | 0.19 | 0.52 | 0.39 | 0.29 | 0.25 | 0.12 | 0.11 | 0.47 | 0.14 |
| Monthly | 0.07 | 0.07 | 0.27 | 0.03 | 0.51 | 0.88 | 0.62 | 0.06 | 0.08 | 0.30 | 0.10 | 0.06 | 0.08 | |
| Daily | 0.53 | 0.55 | 0.89 | 0.28 | 0.17 | 0.30 | 0.29 | 0.20 | 0.21 | 0.12 | 0.24 | 1.00 | 0.26 | |
| cycle- upward, linear, Additive | Weekly | 0.86 | 1.00 | 0.46 | 0.91 | 0.40 | 0.91 | 0.94 | 0.82 | 0.98 | 0.77 | 0.07 | 0.70 | 0.20 |
| Monthly | 0.44 | 0.45 | 0.37 | 0.73 | 0.72 | 0.49 | 0.59 | 0.59 | 0.72 | 1 | 0.13 | 0.6 | 0.13 | |
| Daily | 0.53 | 0.55 | 0.89 | 0.28 | 0.17 | 0.3 | 0.29 | 0.2 | 0.21 | 0.12 | 0.24 | 1 | 0.26 |
| Model Name | Daily MAE | Weekly MAE | Monthly MAE | |||
|---|---|---|---|---|---|---|
| Without X | With X | Without X | With X | Without X | With X | |
| LightGBM (Nixtla) | 0.006865 | 0.013344 | 0.063523 | 0.063384 | 0.063523 | 0.07267 |
| Linear Regression (Nixtla) | 0.352763 | 0.081512 | 0.067139 | 0.095601 | 0.067139 | 0.171675 |
| Random Forest (Nixtla) | 0.011633 | 0.007133 | 0.062887 | 0.016148 | 0.062887 | 0.057416 |
| XGBoost (Nixtla) | 0.006671 | 0.006597 | 0.062794 | 0.04739 | 0.062794 | 0.060364 |
| LightGBM (PyCaret) | 0.009663 | 0.009685 | 0.068635 | 0.000482 | 0.068635 | 0.068837 |
| Linear Regression (PyCaret) | 0.731683 | inf | 0.36375 | 0.83549 | 0.36375 | 0.685998 |
| Random Forest (PyCaret) | 0.009592 | 0.009491 | 0.068217 | 0.000486 | 0.068217 | 0.068322 |
| XGBoost (PyCaret) | 0.009515 | 0.009698 | 0.068399 | 0.000486 | 0.068399 | 0.068336 |
| TimeGPT | 0.00645 | 0.064104 | 0.066995 | 0.000489 | 0.066995 | 0.064504 |
| ARIMA (pmdarima) | 0.006228 | 0.0066 | 0.069404 | 0.000519 | 0.069404 | 0.069404 |
| Neuralprophet | 0.010263 | 0.010255 | 0.070215 | 0.000676 | 0.070215 | 0.070183 |
| Prophet | 0.007307 | 0.008082 | 0.071083 | 0.000472 | 0.071083 | 0.067343 |
| Case Study | Best Model Used | Granularity | Forecast Horizon | MAE Univariate | MAE with All Corr. External Features | MAE TimeGPT |
|---|---|---|---|---|---|---|
| Electricity Demand Forecasting | XGBoost | Monthly | 35 months | 47,731.78 (MW) | 91,854.41 (MW) | 73,488.35 (MW) |
| Docked Bike Demand Forecasting | ARIMA | Weekly | 32 weeks | 1.112 | 1.7445 | 0.8898 |
| Perishable Goods Demand Forecasting | Prophet | Daily | 365 days | 6.56 | 6.729 | 42.098 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karim, S.M.A.; Zarrin, B.; Lassen, N.B. Multivariate Forecasting Evaluation: Nixtla-TimeGPT. Comput. Sci. Math. Forum 2025, 11, 29. https://doi.org/10.3390/cmsf2025011029
Karim SMA, Zarrin B, Lassen NB. Multivariate Forecasting Evaluation: Nixtla-TimeGPT. Computer Sciences & Mathematics Forum. 2025; 11(1):29. https://doi.org/10.3390/cmsf2025011029
Chicago/Turabian StyleKarim, S M Ahasanul, Bahram Zarrin, and Niels Buus Lassen. 2025. "Multivariate Forecasting Evaluation: Nixtla-TimeGPT" Computer Sciences & Mathematics Forum 11, no. 1: 29. https://doi.org/10.3390/cmsf2025011029
APA StyleKarim, S. M. A., Zarrin, B., & Lassen, N. B. (2025). Multivariate Forecasting Evaluation: Nixtla-TimeGPT. Computer Sciences & Mathematics Forum, 11(1), 29. https://doi.org/10.3390/cmsf2025011029





