Enhancing Public Health Insights and Interpretation Through AI-Driven Time-Series Analysis: Hierarchical Clustering, Hamming Distance, and Binary Tree Visualization of Infectious Disease Trends †
Abstract
1. Introduction
1.1. Contributions of This Study
- Hierarchical Clustering for Disease Classification
- –
- Automatically determines regional clusters of disease prevalence without requiring a predefined number of clusters.
- –
- Provides a dendrogram-based representation to capture hierarchical relationships among regions.
- Hamming Distance for Time-Series Similarity
- –
- Quantifies year-over-year variations in disease trajectories, allowing detection of significant shifts in prevalence.
- –
- Identifies epidemiologically similar regions based on shared trends over time.
- Binary Tree Visualization for Improved Interpretation
- –
- Introduces binary trees to represent disease clustering in a more interpretable structure.
- –
- Helps health professionals track regional transitions in disease prevalence and detect outlier patterns.
- Evaluation of Compactness and Variability
- –
- Incorporates compactness scores to measure intra-cluster consistency and inter-cluster distinctiveness.
- –
- Uses silhouette score analysis to validate cluster separations.
1.2. Case Study: Infectious Diseases in Uzbekistan
1.3. Organization of the Paper
- Section 2 provides a detailed description of the dataset, highlighting the key attributes analyzed.
- Section 3 presents the methodology, outlining the clustering techniques, Hamming Distance calculations, and visualization methods.
- Section 4 describes the case study findings, illustrating the application of the proposed methods in analyzing disease trends across regions.
- Section 5 discusses the implications of the results and suggests future improvements.
- Section 6 concludes the study, summarizing the key findings and future research directions.
2. Dataset Description
2.1. Data Attributes
- Region ID and Name: Unique identifier and administrative name for each region.
- Disease Type: The dataset includes seven infectious diseases—Brucellosis, Dysentery, Measles, Tuberculosis, Scarlet Fever, Typhoid Fever, and Meningococcal Infections.
- Yearly Incidence Rate: The number of reported cases per 100,000 people for each disease.
- Geographical Coordinates: Latitude and longitude values representing the central location of each region.
2.2. Data Preprocessing
- Data Cleaning: Duplicate and inconsistent entries were removed.
- Handling Missing Data: Missing incidence rates were imputed using the mean prevalence for the respective region and disease type.
- Standardization: Ensured consistency in temporal analysis across regions and disease types.
Time-Series Structuring
- Each row represents a unique region-disease combination with time-series values spanning 2010 to 2019.
- Disease trends are analyzed across multiple time scales (e.g., yearly aggregates and multi-year comparisons).
2.3. Regional Classification and Economic Zones
- Industrialized Zones: Highly urbanized regions with developed healthcare infrastructure (e.g., Tashkent City, Navoi).
- Agricultural Zones: Predominantly rural regions with agriculture as the primary economic activity (e.g., Andijan, Namangan).
- Emerging Zones: Regions undergoing rapid development but still facing healthcare accessibility challenges (e.g., Samarkand, Jizzakh).
- Less Developed Zones: Remote or historically underdeveloped regions with limited healthcare resources (e.g., Karakalpakstan, Khorezm).
2.4. Geographical Indicators
3. Literature Review
4. Methodology
4.1. Notation and Symbol Definitions
4.2. Hierarchical Clustering
- and are the clusters being merged;
- represents a data point in a cluster;
- , , and are the centroids of clusters , , and their merged cluster, respectively.
4.3. Cluster Selection for Region 1 and Region 2
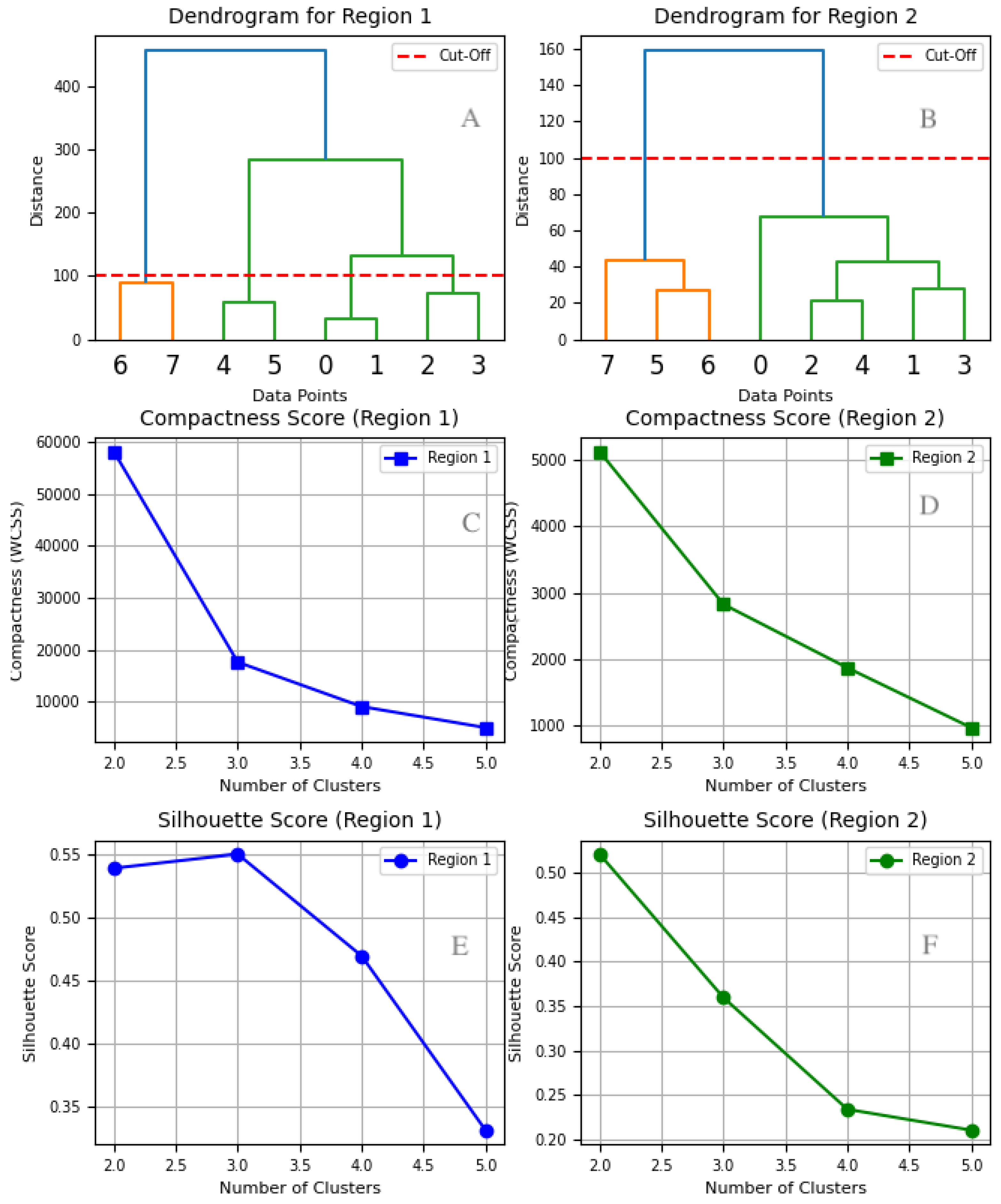
4.3.1. Dendrogram Analysis
4.3.2. Compactness Score (WCSS)
- For Region 1, the WCSS score drops significantly from two to three clusters, then continues declining at a slower rate beyond three. While additional clusters slightly improve compactness, the diminishing returns suggest that further separation offers limited benefit.
- For Region 2, the most notable drop occurs between one and two clusters, followed by a gradual decline. This indicates that two clusters provide the best balance between compactness and model simplicity.
4.3.3. Silhouette Score Analysis
- For Region 1, the highest silhouette score occurs at three clusters. While four and five clusters result in a steady decline in silhouette scores, three clusters maintain the best cluster cohesion and separation.
- For Region 2, the highest silhouette score is observed at two clusters, confirming that additional clusters reduce the clustering quality.
4.3.4. Final Cluster Selection
- Region 1 exhibits greater variability in disease prevalence. Although adding more clusters continues to reduce WCSS, the silhouette score decline suggests that three clusters strike the optimal balance between compactness and interpretability.
- Region 2 shows more stable patterns, making two clusters the best choice.
4.3.5. Findings from the Dendrograms
- Cluster 1: Diseases and show strong similarity and merge early in the clustering process, later joined by at a moderate distance.
- Cluster 2: Diseases and form a separate cluster, distinct from Cluster 1.
- Disease : Stands as an outlier, merging with the rest of the clusters only at a significantly high distance (∼500), indicating unique epidemiological patterns.
- Cluster 1: Diseases and exhibit highly similar trends and merge at a short distance.
- Cluster 2: Diseases and form a compact cluster, later joined by and at moderate distances.
4.3.6. Merging Distances: Key Differences Between Regions
- In Region 1, clusters merge at greater distances (e.g., ∼200 and ∼500), indicating higher disease pattern variability across regions.
- In Region 2, clusters merge at much lower distances (∼20–120), indicating more stable and predictable disease patterns.
4.3.7. Public Health Implications
- Region 1: Due to its high variability, Region 1 requires tailored strategies to address distinct epidemiological behaviors across clusters.
- Region 2: Demonstrates consistent patterns, making uniform public health interventions more feasible.
4.4. Hamming Distance Analysis
4.4.1. Mathematical Formulation
- and are the prevalence values of disease i in years t and , respectively;
- n represents the total number of diseases analyzed.
4.4.2. Cluster-Based Temporal Analysis Using Hamming Distance
4.4.3. Reformulated Hamming Distance for Disease Clusters
- and denote the aggregate prevalence of disease cluster i in years t and , respectively;
- n is the total number of disease clusters considered in the analysis.
4.5. Time-Series Structuring for Disease Analysis
4.5.1. Mathematical Representation of Time-Series Data
- Hamming Distance analysis to quantify year-over-year variability in disease prevalence;
- Hierarchical clustering to identify spatial similarities across disease prevalence patterns;
- Binary tree visualization to effectively represent disease clustering relationships over time.
4.5.2. Temporal Analysis via Hamming Distance
- represents the prevalence of disease i in year t;
- represents the prevalence of disease i in year ;
- n is the number of diseases analyzed.
4.5.3. Comparing Temporal and Spatial Clustering
- Stable disease trends (low Hamming Distance over time);
- Emerging disease patterns (high year-to-year variability within clusters).
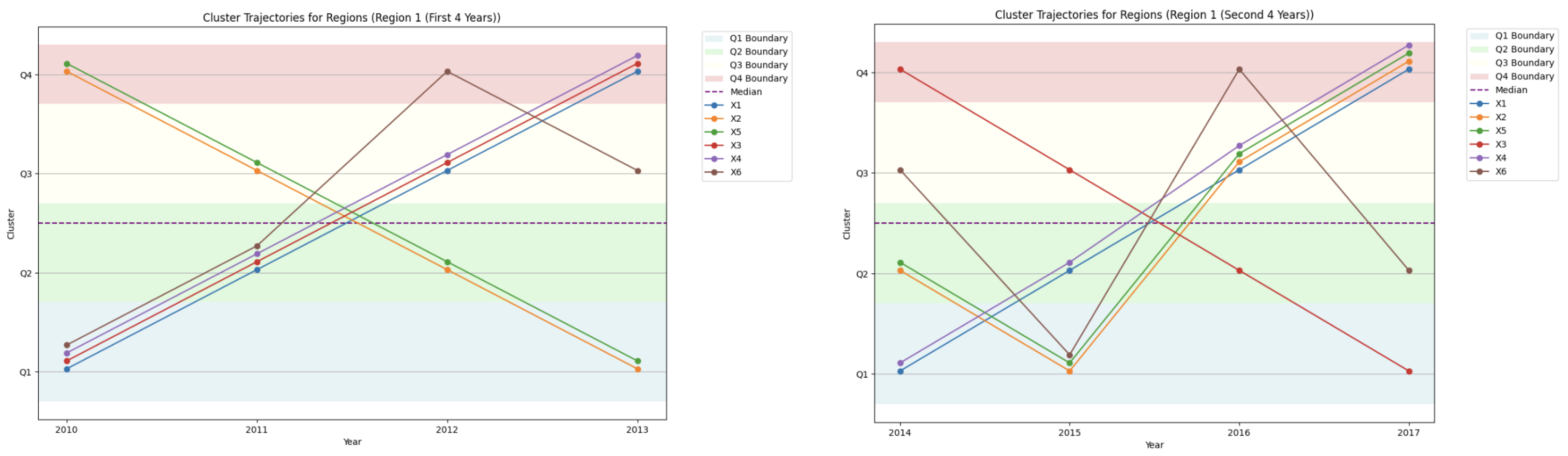
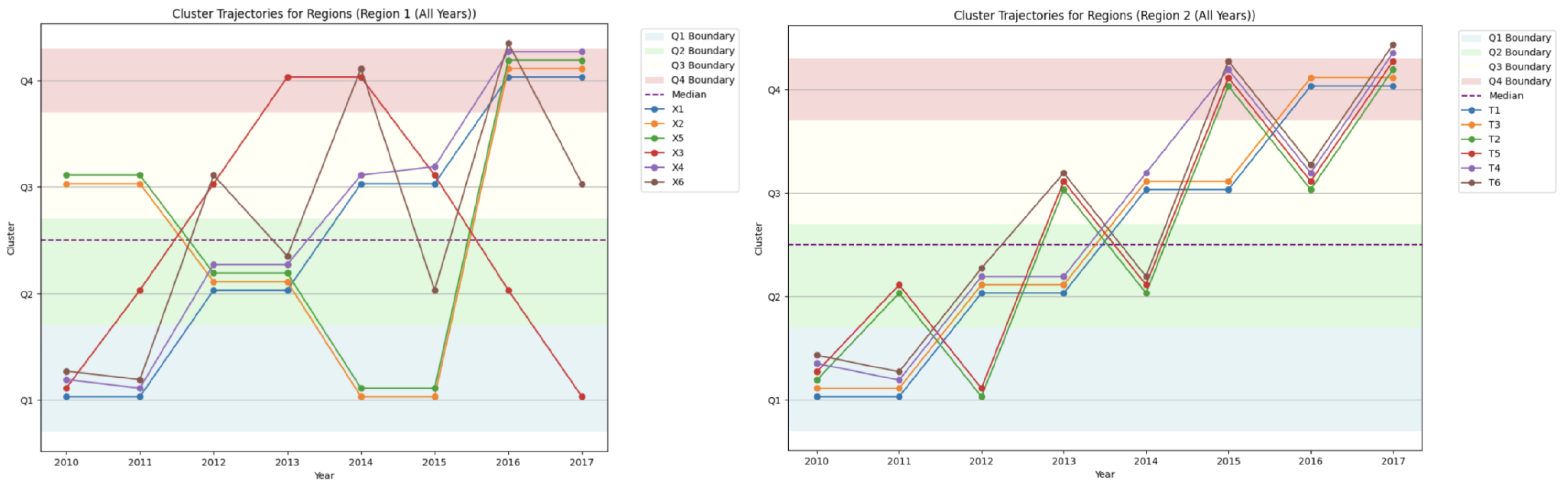
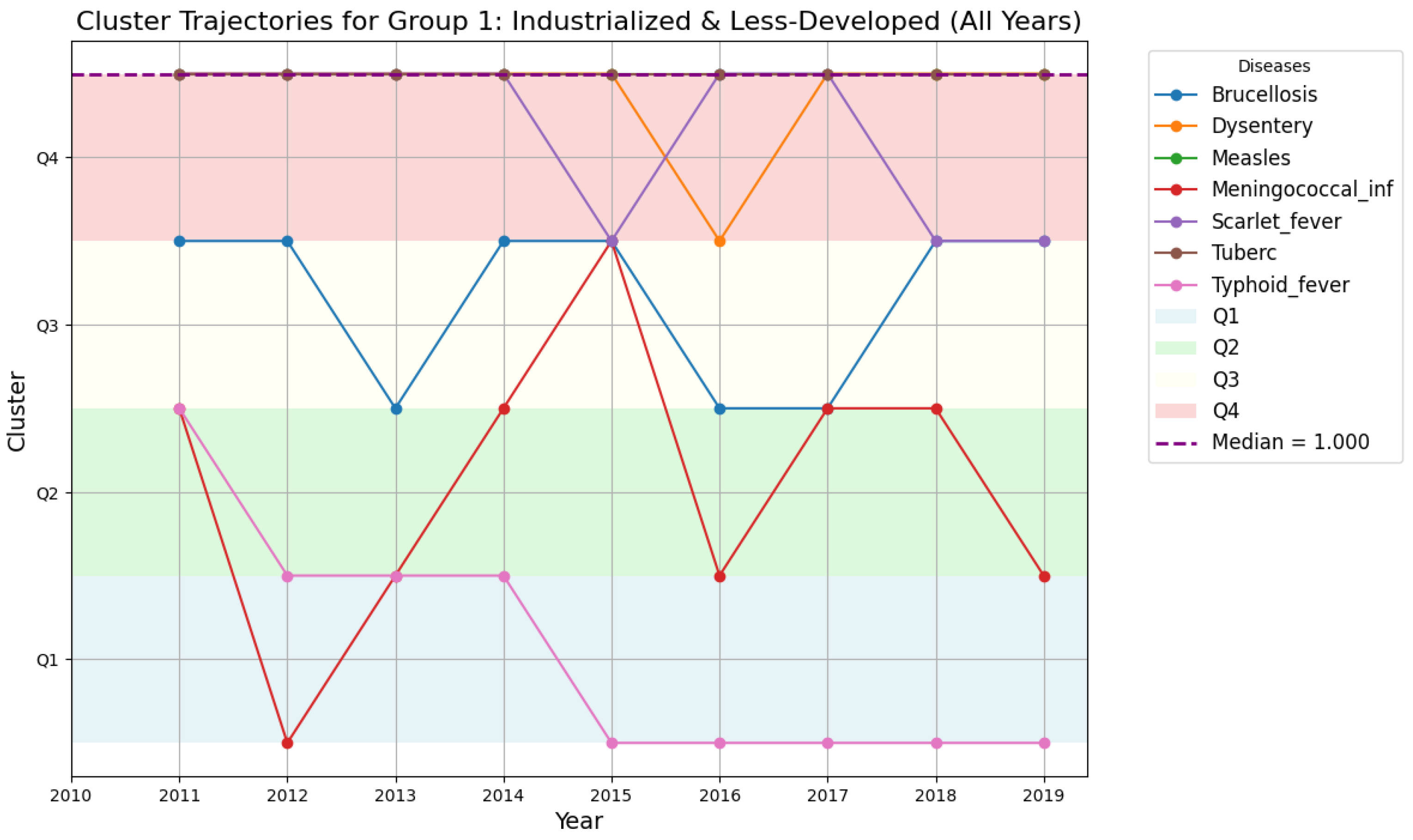
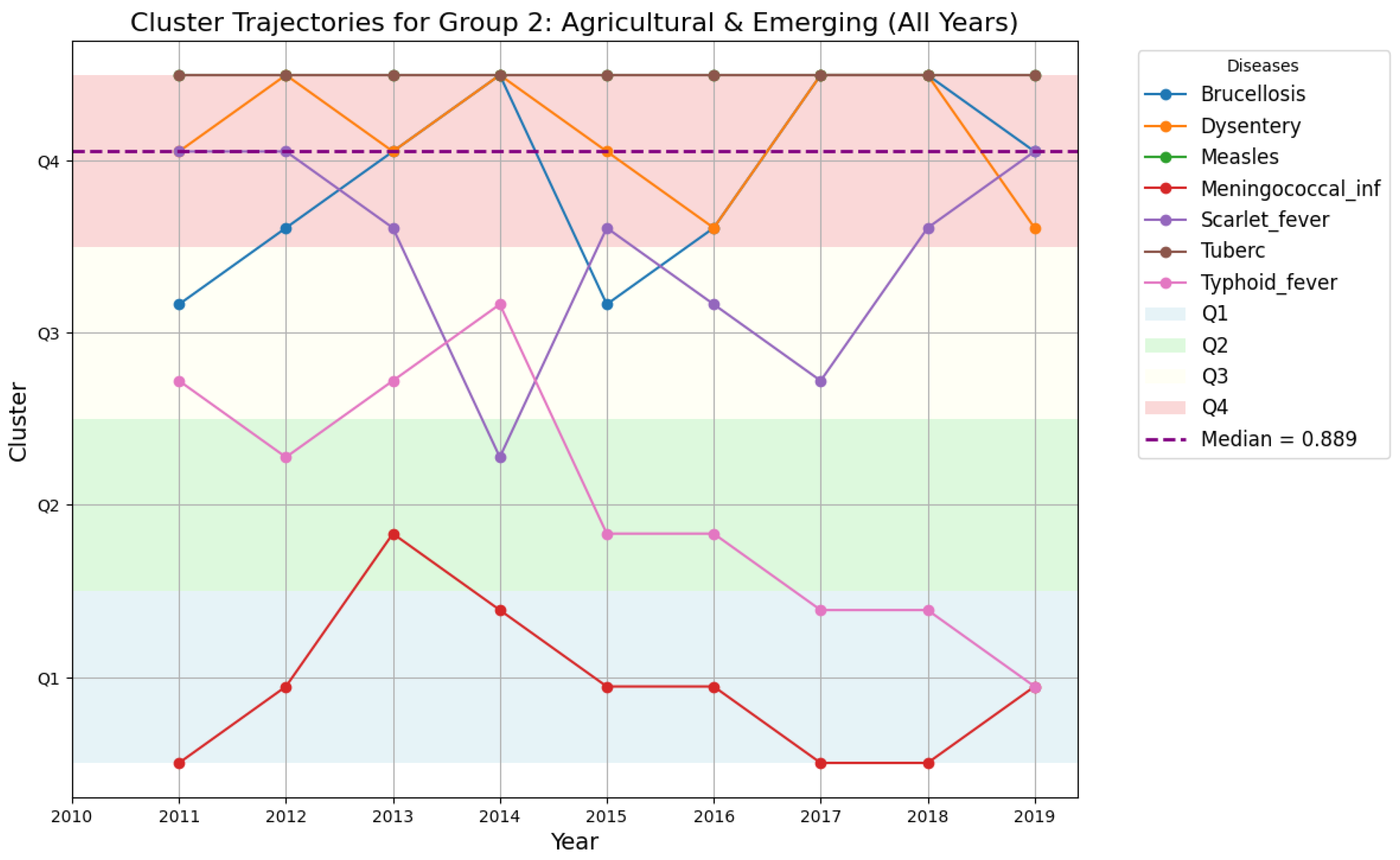
4.5.4. Cluster Trajectories for Region 1 and Region 2
- Disease drops from Quartile 4 to Quartile 1 in 2016, indicating a sharp decline in prevalence;
- Disease rises from Quartile 1 to Quartile 4, signaling a marked increase in prevalence.
4.5.5. Comparative Temporal Patterns: Region 1 vs. Region 2
- Region 1: Displays higher disease variability, with frequent transitions between quartiles.
- Region 2: Exhibits stable clustering patterns, suggesting more consistent epidemiological trends.
4.5.6. Hamming Distance Heatmap Analysis
4.5.7. Public Health Implications of Hamming Distance Trends
- Region 1: The high variability indicates the need for dynamic, region-specific interventions to address emerging disease patterns.
- Region 2: The stable clustering patterns suggest that standardized public health measures may suffice to maintain disease control.
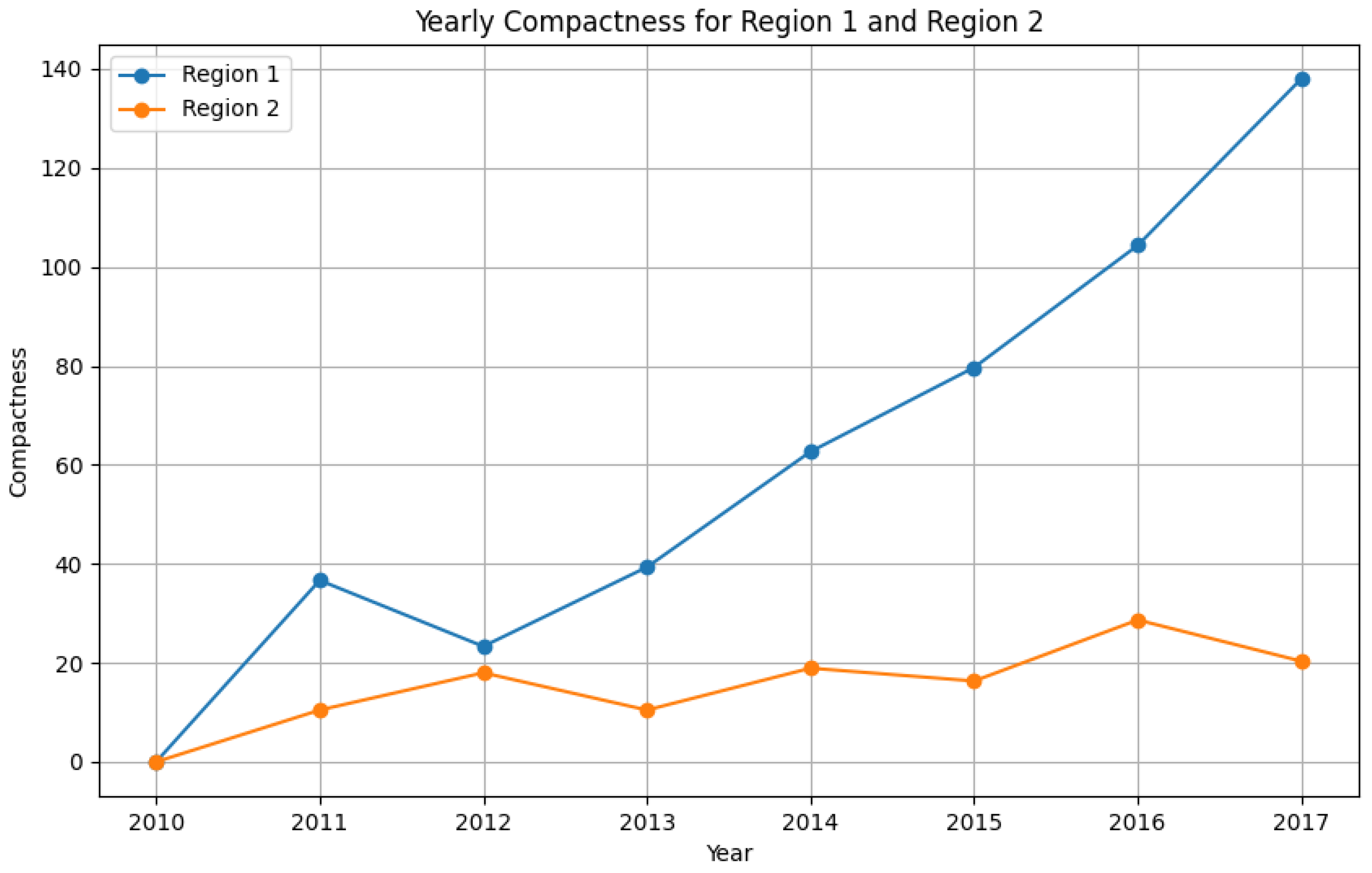
4.5.8. Compactness Trends as a Support Tool
- Region 1: Compactness scores decrease over time, indicating rising disease pattern variability.
- Region 2: Compactness scores remain relatively stable, reinforcing the consistency of disease trends.
4.6. Binary Tree Visualization
4.6.1. Structure and Interpretation of the Binary Tree
- Each node represents a cluster of regions grouped based on disease prevalence similarity;
- Each branch represents a merging event, with earlier merges indicating greater similarity;
- The depth of a node reflects disease variability, with deeper nodes indicating regions with distinct epidemiological patterns.
- A structured overview of regional clusters based on disease prevalence;
- A way to identify outliers with distinct disease trends;
- An intuitive representation of the progression of disease pattern similarity across regions.
4.6.2. Example of Binary Tree Visualization
4.6.3. Public Health Implications of Binary Tree Analysis
- Identification of High-Risk Regions: Deep nodes in the binary tree indicate regions where disease trends significantly deviate from others, signaling the need for specialized interventions.
- Hierarchical Similarity Among Regions: The tree structure highlights regions with closely aligned disease prevalence, allowing for shared intervention strategies.
- Outlier Detection: Isolated branches or late-merging nodes indicate regions with unique disease patterns, warranting further epidemiological investigation.
4.7. Compactness, Depth, and Variability Metrics
- Compactness (C): Compactness measures the overall tightness of clusters and is calculated aswhere represents the distance at which the i-th cluster merges, and n is the total number of clusters.
- Depth and Variability: Depth quantifies the position of cluster formation within the binary tree, with the root node having a depth of 0. Variability is evaluated using the standard deviation of depth values.
4.7.1. Example Calculation of Depth Metrics
- Depth Values:
- Mean Depth ():
- Standard Deviation ():
4.7.2. Comparative Depth and Compactness Analysis
4.7.3. Findings and Interpretation
- Dataset 1: A higher compactness score (233.61) and lower average depth (1.91) indicate greater variability in disease prevalence. The deeper nodes—such as Diseases and with a depth of 4—suggest that certain diseases follow distinct prevalence trends, requiring more targeted interventions.
- Dataset 2: A lower compactness score (52.06) and higher average depth (2.27) suggest more stable disease patterns across the region. The more balanced depth values across nodes—such as , , and —indicate that uniform public health measures may be more effective.
4.8. Summary of Methodology
- Identifies natural clusters of regions based on disease prevalence;
- Tracks year-over-year variability in disease patterns using Hamming Distance;
- Provides visual insights to aid in public health decision-making.
5. Case Study: Infectious Diseases—Analysis and Results
5.1. Introduction to Infectious Disease Trends
- Group 1: Industrialized and Less-Developed regions.
- Group 2: Agricultural and Emerging regions.
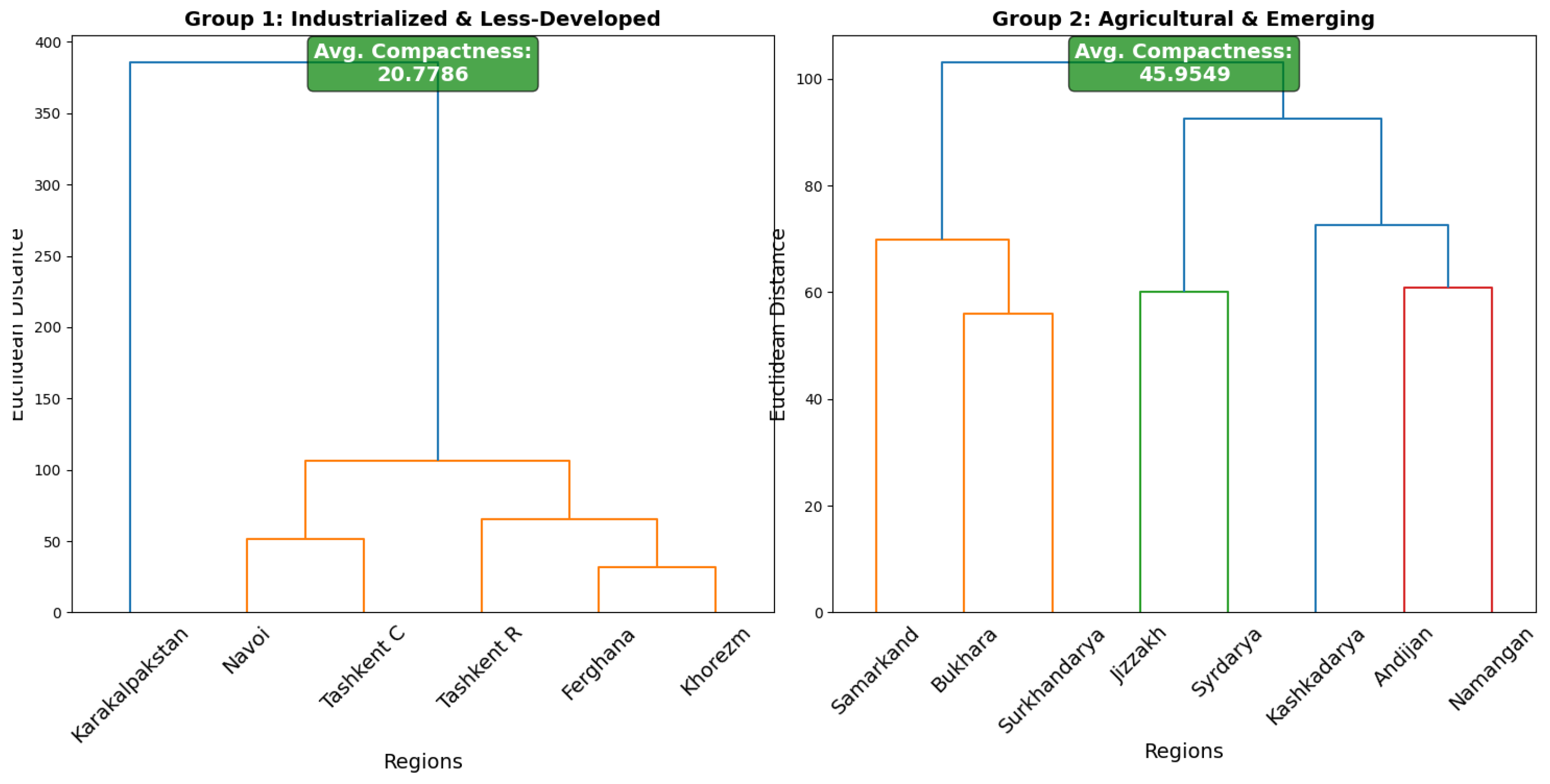
5.2. Clustering Insights from Dendrograms
5.2.1. Group 1: Industrialized and Less-Developed Regions
- Cluster 1: Navoi, Tashkent City, and Tashkent region exhibit similar patterns, likely due to shared socio-economic and healthcare factors.
- Cluster 2: Fergana and Khorezm form a tight subgroup with highly similar health profiles, suggesting shared public health interventions may be effective.
5.2.2. Group 2: Agricultural and Emerging Regions
- Cluster 1: Samarkand, Bukhara, and Surkhandarya merge at a moderate distance, indicating similar disease trends.
- Cluster 2: Andijan, Namangan, Kashkadarya, Jizzakh, and Syrdarya form a cohesive cluster. However, Jizzakh and Syrdarya join at a higher distance, suggesting the need for localized adjustments.
5.3. Binary Tree Representation: Simplifying Cluster Interpretation
| Group 1 | Group 2 | ||
|---|---|---|---|
| Node/Cluster | Depth | Node/Cluster | Depth |
| Karakalpakstan | 4 | Samarkand | 4 |
| Navoi | 3 | Bukhara | 3 |
| Tashkent City | 3 | Surkhandarya | 3 |
| Tashkent Region | 3 | Jizzakh | 3 |
| Fergana | 2 | Syrdarya | 2 |
| Khorezm | 2 | Kashkadarya | 2 |
| Cluster 1 | 3 | Andijan | 2 |
| Cluster 2 | 2 | Namangan | 2 |
| Cluster 3 | 2 | Cluster 1 | 3 |
| Cluster 4 | 1 | Cluster 2 | 2 |
| Cluster 5 (Root) | 0 | Cluster 3 | 2 |
| Average Depth | 2.55 | Average Depth | 2.33 |
| Standard Deviation | 1.13 | Standard Deviation | 1.07 |
| Compactness | 24 | Compactness | 21 |
5.4. Hamming Distance Analysis
- Group 1: Higher variability in disease patterns, with diseases like Tuberculosis and Dysentery showing consistent year-over-year changes. This suggests that outbreaks in these regions may be strongly influenced by environmental or socio-economic factors, requiring targeted control measures.
- Group 2: More stable disease patterns, although Measles showed significant fluctuations between 2012 and 2016, suggesting periodic outbreaks that may require vaccination-focused policies.
- Higher Variability in Industrialized Regions: Group 1 shows higher year-over-year variability, indicating the need for region-specific interventions.
- Stable Patterns in Agricultural Regions: Group 2 exhibits more consistent disease trends, suggesting uniform healthcare policies may be effective.
- Disease-Specific Trends: Tuberculosis, Dysentery, and Measles demonstrate the highest variability, requiring targeted public health measures.
6. Discussion of Results
- Regional Pattern Identification: Clustering similar regions based on disease progression allows for coordinated health interventions and resource allocation.
- Detection of Outlier Regions: Identifying regions with unique or irregular disease behaviors supports targeted intervention strategies.
- Scalability for Comparative Studies: The methodology can be applied to different epidemiological settings, supporting cross-regional and international comparisons of disease trends.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bamana, A.B.; Kamalabad, M.S.; Oberski, D.L. A systematic literature review of time series methods applied to epidemic prediction. IMU 2024, 50, 10571. [Google Scholar] [CrossRef]
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Verges, F.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A review. Sci. Total Environ. 2020, 739, 140033. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Fang, L.; Xie, M.; Tang, Z.; Zhang, Y.; Tian, F.; Wang, X.; Lin, X.; Liu, Q.; Xu, S.; et al. Revealing spatiotemporal inequalities, hotspots, and determinants in healthcare resource distribution: Insights from hospital beds panel data in 2308 Chinese counties. BMC Public Health 2024, 24, 423. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Qian, P.; Duan, Z.; Zhao, Z.; Pan, J.; Yang, M. Disparities in health system input between minority and non-minority counties and their effects on maternal mortality in Sichuan province of western China. BMC Public Health 2017, 17, 750. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K. Data Clustering: 50 Years Beyond K-Means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: San Francisco, CA, USA, 2012. [Google Scholar]
- Tan, P.N.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Addison-Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Porter, M.E. The Economic Performance of Regions. Reg. Stud. 2003, 37, 549–578. [Google Scholar] [CrossRef]
- Lai, S.; Farnham, A.; Ruktanonchai, N.W.; Tatem, A.J. Measuring mobility, disease connectivity and individual risk: A review of using mobile phone data and mHealth for travel medicine. J. Travel Med. 2019, 26, taz019. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. Thirty Years of Spatial Econometrics. Pap. Reg. Sci. 2010, 89, 3–25. [Google Scholar] [CrossRef]
- Sadeghi, B.; Cheung, R.C.Y.; Hanbury, M. Using hierarchical clustering analysis to evaluate COVID-19 pandemic preparedness and performance in 180 countries in 2020. BMJ Open 2021, 11, e049844. [Google Scholar] [CrossRef] [PubMed]
- Pattnaik, S.; Pinsky, E. Hamming Diversification Index: A New Clustering-Based Metric to Understand and Visualize Time Evolution of Patterns in Multi-Dimensional Datasets. Appl. Sci. 2025, 15, 7760. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Skiena, S.S. The Algorithm Design Manual, 2nd ed.; Springer: London, UK, 2012. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, revised ed.; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Aggarwal, C.C. Data Mining: The Textbook; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Hulten, G.; Spencer, L.; Domingos, P. Mining Time-Changing Data Streams. In Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 97–106. [Google Scholar] [CrossRef]
- Horne, E.; Tibbie, H.; Sheikh, A.; Tsanas, A. Challenges of Clustering Multimodal Clinical Data: Review of Asthma Subtyping Studies. JMIR Med. Inform. 2020, 8, e16452. [Google Scholar] [CrossRef]
- Lee, Y.-P.; Wen, T.-H. Understanding the Spread of Infectious Diseases in Edge Areas of Hotspots: A Spatial Analysis of COVID-19 Clusters in Taiwan. Int. J. Health Geogr. 2023, 22, 5. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Cummings, D.A.; Cauchemez, S.; Fraser, C.; Riley, S.; Meeyai, A.; Iamsirithaworn, S.; Burke, D.S. Strategies for Containing an Emerging Influenza Pandemic in Southeast Asia. Nature 2005, 437, 209–214. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, S.; Brown, G. On the Stability of Feature Selection Algorithms. J. Mach. Learn. Res. 2018, 18, 1–54. Available online: https://jmlr.csail.mit.edu/papers/volume18/17-514/17-514.pdf (accessed on 1 June 2025).
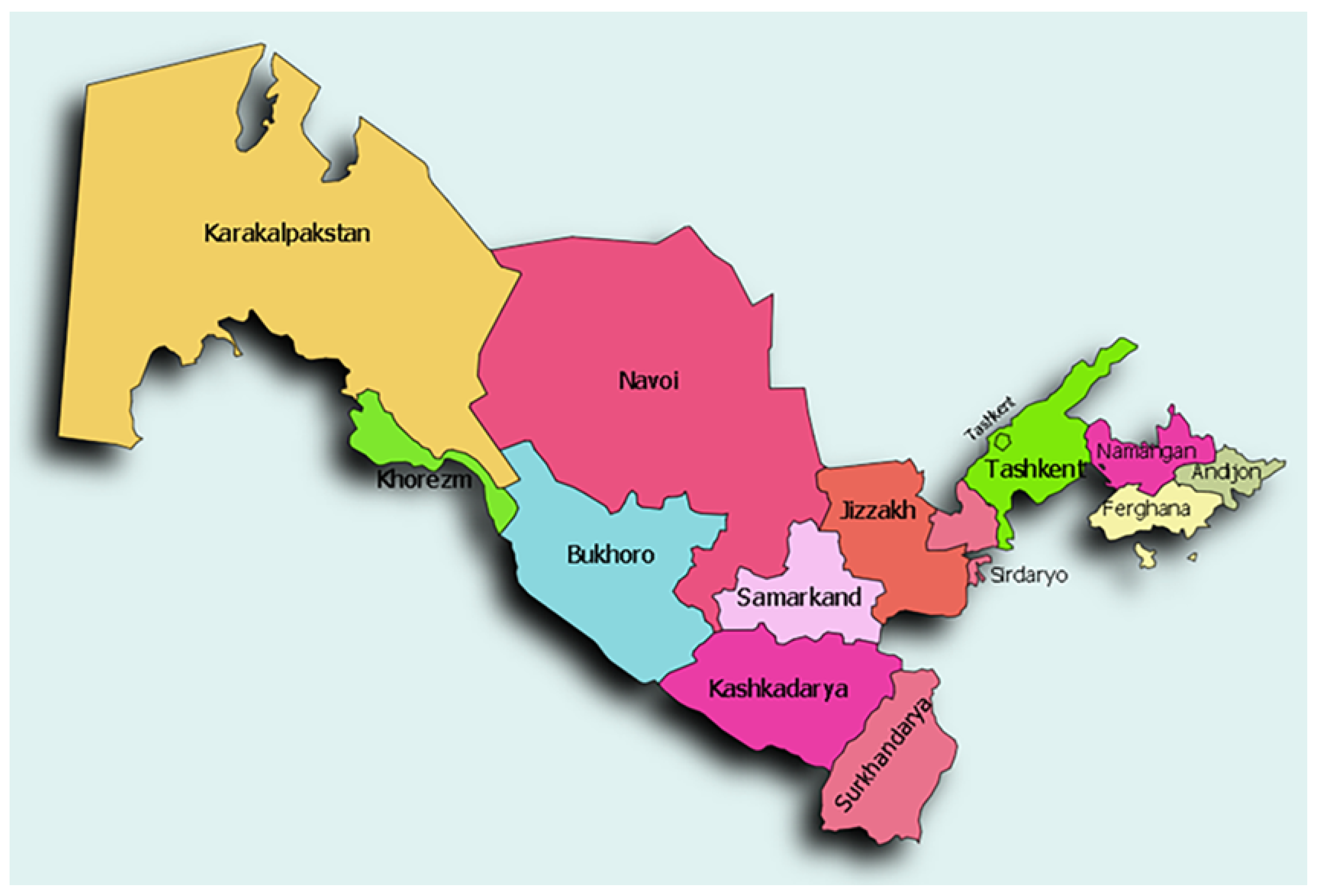




| Development Group | Economic Zone | Region |
|---|---|---|
| Group 1 | Less Developed | Karakalpakstan |
| Less Developed | Khorezm | |
| Industrialized | Navoi | |
| Industrialized | Tashkent R | |
| Industrialized | Fergana | |
| Industrialized | Tashkent C | |
| Group 2 | Agricultural | Andijan |
| Agricultural | Namangan | |
| Agricultural | Surkhandarya | |
| Agricultural | Syrdarya | |
| Emerging | Bukhara | |
| Emerging | Jizzakh | |
| Emerging | Kashkadarya | |
| Emerging | Samarkand |
| Symbol | Definition |
|---|---|
| Incidence rate of disease i in Region 1 | |
| Incidence rate of disease i in Region 2 | |
| Hamming Distance between two time-series X and Y | |
| Cluster k identified in hierarchical clustering | |
| Mean value of all points in cluster | |
| Within-Cluster Sum of Squares for cluster k | |
| Silhouette score for cluster k | |
| Dissimilarity between two regions i and j |
| Dataset 1 | Dataset 2 | ||
|---|---|---|---|
| Node/Cluster | Depth | Node/Cluster | Depth |
| 1 | 3 | ||
| 2 | 2 | ||
| 3 | 3 | ||
| 4 | 2 | ||
| 2 | 1 | ||
| 4 | 2 | ||
| Cluster 1 | 3 | Cluster 1 | 2 |
| Cluster 2 | 2 | Cluster 2 | 1 |
| Cluster 3 | 3 | Cluster 3 | 2 |
| Cluster 4 | 2 | Cluster 4 | 1 |
| Cluster 5 (Root) | 0 | Cluster 5 (Root) | 0 |
| Average Depth: 1.91 | Average Depth: 2.27 | ||
| Standard Deviation: 1.07 | Standard Deviation: 1.31 | ||
| Compactness: 233.61 | Compactness: 52.06 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arystambekova, A.; Pinsky, E. Enhancing Public Health Insights and Interpretation Through AI-Driven Time-Series Analysis: Hierarchical Clustering, Hamming Distance, and Binary Tree Visualization of Infectious Disease Trends. Comput. Sci. Math. Forum 2025, 11, 23. https://doi.org/10.3390/cmsf2025011023
Arystambekova A, Pinsky E. Enhancing Public Health Insights and Interpretation Through AI-Driven Time-Series Analysis: Hierarchical Clustering, Hamming Distance, and Binary Tree Visualization of Infectious Disease Trends. Computer Sciences & Mathematics Forum. 2025; 11(1):23. https://doi.org/10.3390/cmsf2025011023
Chicago/Turabian StyleArystambekova, Ayauzhan, and Eugene Pinsky. 2025. "Enhancing Public Health Insights and Interpretation Through AI-Driven Time-Series Analysis: Hierarchical Clustering, Hamming Distance, and Binary Tree Visualization of Infectious Disease Trends" Computer Sciences & Mathematics Forum 11, no. 1: 23. https://doi.org/10.3390/cmsf2025011023
APA StyleArystambekova, A., & Pinsky, E. (2025). Enhancing Public Health Insights and Interpretation Through AI-Driven Time-Series Analysis: Hierarchical Clustering, Hamming Distance, and Binary Tree Visualization of Infectious Disease Trends. Computer Sciences & Mathematics Forum, 11(1), 23. https://doi.org/10.3390/cmsf2025011023





