Abstract
Economic data is highly dependent on its arrangement within space and time. Perhaps the most obvious and important definition of space is geospatial configuration on the Earth’s surface. Consideration of geospatial effects produces a dramatic improvement in the prediction of median housing prices across 20,640 districts in California. Unconditional regression with engineered variables, two-stage least squares regression (2SLS), and iterative local regression approach r2 ≈ 0.8536, the goodness of fit attained in the original California study. Geospatial methods can be generalized to panel data analysis and time-series forecasting. Distance-sensitive analysis reveals the value of treating time-variant data as potentially discrete and discontinuous. This insight highlights the value of methodologies that suspend the assumption that data varies in a continuous or even linear fashion across space and time.
1. Introduction
Economic data is highly dependent on its arrangement within space and time. Whether proximity is expressed in geospatial, temporal, or sociological terms, economic observations often correlate to their nearest neighbors. Perhaps the most obvious distance metric is geospatial configuration on the surface of the Earth. Diversity in distance metrics—from Euclidean distance to Haversine distance on a spherical surface—raises the prospect that geospatial analysis might inform panel data analysis and time-series forecasting. In metaphorical if not mathematical terms, “time is the longest distance between two places” [1] (p. 96).
Part 2 presents materials and methods drawn from a canonical problem in geospatial econometrics: predicting housing prices in a spatially autocorrelated market. Part 3 summarizes results from the application of engineered variables, two-stage least squares evaluation of residuals, and iterative local regression based on the partitioning of the dataset through the k-nearest neighbors algorithm. Parts 4 and 5 discuss the methodological implications of these drift-and-diffusion approaches—first for geospatial analysis and then for extensions to panel data and time-series forecasting. Part 6 concludes that tools that separately evaluate deterministic drift and stochastic diffusion can inform a wide range of economic studies containing intertemporal, geospatial, and even sociopolitical elements that can be quantified by some distance metric.
2. Materials and Methods
This project examines median house prices in 20,640 California districts, as reported in the 1990 Census of the United States [2]. The California housing dataset includes hedonic features such as the average number of rooms, as well as the pivotal economic variable of median household income. Critically, the dataset also locates each of the 20,640 districts by latitude and longitude (Figure 1).
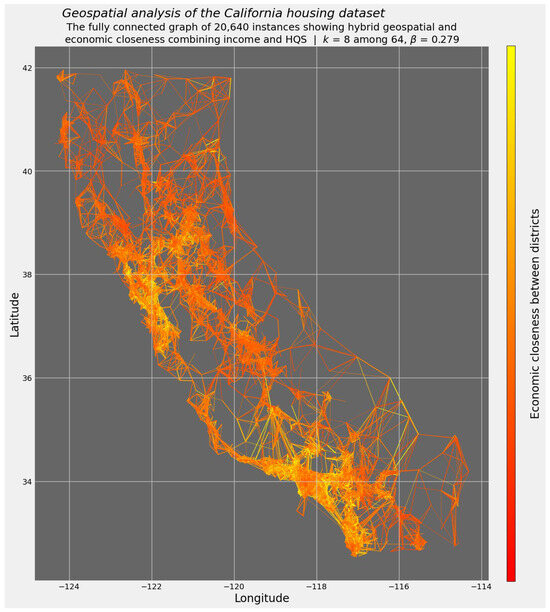
Figure 1.
A depiction of 20,640 districts in California and their k = 8 nearest neighbors. The red-to-yellow color gradient reflects nearby populations and their affluence.
This paper pursues three distinct strategies in order to extract, evaluate, and quantify the geospatial component of housing prices in the California dataset:
- Data engineering of predictive variables as a prelude to an escalating suite of predictive methods, from ordinary least squares (OLS) to machine learning ensembles such as random forests and extra trees;
- Two-stage least squares (2SLS) methodology [3];
- Iterative local regression of instances closest to each of the 20,640 observations.
All three of those strategies are generalizable beyond the strict confines of geospatial econometrics. This paper does not purport to explore the entire toolkit available to contemporary geospatial analysis. In the nearly half-century since Jean Paelinck and Leo Klaassen introduced the term “spatial econometrics” [4], the dramatically expanded field has added numerous methods [5,6]. “[B]y far the two most widely used” models in spatial econometrics are “the spatial error model and the spatial lag model, which exploit autoregression in the error or in the dependent variable respectively” [7] (p. 311). The difficulty in obtaining maximum likelihood estimators for spatial errors or lags has motivated alternative approaches [7] (pp. 311–312), including methods drawing on 2SLS [8,9,10].
Two further methodological observations deserve special notice. First, the k-nearest neighbors (KNN) algorithm is used in two different ways. KNN not only serves as a preprocessing step in 2SLS regression and iterative local regression [11] but also provides a method of supervised machine learning that relies exclusively on geospatial data [12]. This study uses both the supervised and unsupervised variants of KNN. To distinguish the variants, this study will designate them as sKNN and uKNN. As will become apparent in Section 4.3, both variants of KNN prove pivotal in implementing the spatial lag model.
Second, references to the term regression or even the least squares component of 2SLS by no means compel reliance on conventional OLS regression. Methods such as quadratic regression, regression incorporating an ℓ1 penalty [13], and Gaussian process regression [14] are deployed whenever they improve predictive accuracy at reasonable computational cost. Especially where an application emphasizes predictive accuracy over causal inference, methodological eclecticism embraces the full range of methods, from those based on traditional statistics to those based on machine-driven algorithms [15].
3. Results
Inasmuch as this paper is primarily methodological and theoretical in scope, this section will summarize empirical results as a prelude to a more extensive discussion of the methods underlying those results. Subsequent sections of this paper will also discuss theoretical implications beyond the specific context of geospatial analysis.
Explicit consideration of geospatial effects produces a dramatic improvement in predictive accuracy. The original evaluation of the California housing dataset improved goodness of fit from r2 ≈ 0.6078 using ordinary least squares (OLS) to r2 ≈ 0.8536 using sparse spatial autoregression [2] (p. 296). The methods used in this study set a lower baseline, with r2 as low as 0.47, and plateaued near r2 ≈ 0.83. This apparent ceiling on predictive accuracy governed all methods for evaluating the geospatial component of California housing price data: unconditional regression with engineered variables, 2SLS regression, and iterative local regression. This convergence is consistent with theorems of supervised learning positing the “unreasonable effectiveness of data” [16].
The publicly available version of the California housing dataset contains errors that may have been introduced upon its induction into a now deprecated data repository [17]. For instance, the variable for average number of rooms appears inconsistently coded, sometimes reporting the raw number of rooms instead of its natural logarithm. Four rooms per house is plausible; e4 ≈ 54.6 is absurd. Notwithstanding these obstacles, goodness of fit approaching r2 ≈ 0.83 with an imperfectly corrected version of SciKit-Learn’s California data vindicates this study’s empirical results.
Geospatial coordinates enable the visually compelling depiction of predictive outcomes. Figure 2a reports the best local regression model, which produced a test-set and overall r2 just shy of 0.83. After using unsupervised KNN to identify the k = 64 neighbors closest to each observation, this study regressed each local cohort according to diverse spatial weight matrices. The blue-white-red color gradient in Figure 2a (similar to the French national flag) is optimized for values in white. Underestimates of observed housing prices (along the blue gradient) and overestimates (along the red gradient) are rare.
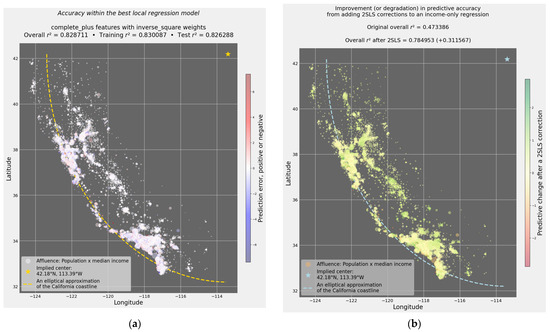
Figure 2.
Iterative local regression and 2SLS correction of residuals in the California housing dataset. (a) Accuracy within the best local regression model; test r2 = 0.826288. (b) 2SLS correction of residuals results in a gain of 0.311567 relative to an unconditional one-variable regression estimating housing prices according to each district’s median income.
For 2SLS, this study took a more minimalist approach. The depiction of 2SLS in Figure 2b, by contrast with Figure 2a’s stress on overall accuracy, uses a “traffic light” color gradient. The red-yellow-green progression, resembling the flag of Guinea, emphasizes improvements in predictive accuracy attributable to 2SLS. Relative to the neutral outcome indicated by yellow, the green gradient indicates improved accuracy. Rare instances in red indicate degradation in predictive accuracy arising from 2SLS.
The 2SLS strategy consisted of two concatenated exercises in univariable regression First, it estimated median house value on the basis of median income alone. The overall r2 for this baseline exercise was 0.473386. It then corrected residuals according to geospatial distance. A blend of second-stage results from Gaussian process and least angle regression (which implements the ℓ1 penalty [18]) raised r2 to 0.784953. This extraordinary +0.311567 improvement in accuracy combined (1) a minimalist baseline regression relying exclusively on median income with (2) exclusively geospatial 2SLS corrections.
For its part, data engineering also improved predictive outcomes. Table 1 reports test-set results based on methods not relying on iterative local regression or 2SLS correction of lagged errors. Notably, the application of XGBoost [19], a tree-boosting machine-learning method, to engineered geospatial features produced the highest test-set accuracy.

Table 1.
Test-set goodness of fit (r2) reported by methods not relying on iterative local regression or 2SLS correction of lagged errors.
This project therefore improved housing price predictions from a marginally credible r2 value near 0.6 (or below 0.5, in the case of an income-only baseline regression) to r2 exceeding 0.8. Notwithstanding those improvements in predictive accuracy, this paper aims primarily to clarify how specific methods of geospatial analysis can be generalized to panel data analysis and time-series forecasting. The next section therefore conducts a closer methodological examination in an effort to generalize methods used to extract, explain, and quantify geospatial effects and to apply them to other tasks.
4. Discussion: Geospatial Analysis
Each of the three analytical methods deployed in this paper—data engineering, two-stage least squares, and iterative local regression—merits closer examination. This paper examines each of those methods with specific attention to geospatial analysis. The paper then turns to a generalization of each strategy beyond geospatial econometrics, taking special care to describe the treatment of drift and diffusion terms under 2SLS and local regression in panel data analysis and time-series forecasting.
4.1. Data Engineering
Data engineering takes only indirect account of spatially variable conditions. Data engineering does have a prominent history. Before the emergence of modern geospatial analysis, numerous studies in urban economics coded attributes such as a district or plot’s proximity to a city center or to a desirable feature such as a riverfront or seashore. The California housing dataset includes five categorical descriptions—ocean, bay, island, one hour from salt water, and inland—intended to capture the hedonic value of proximity to California’s Pacific coast. Instead of adding five dummy variables through one-hot encoding, this study used target encoding for each of those geographical categories.
The engineering of new variables, especially if combined with more complex methods of supervised learning, can be computationally ruinous. The original motivation for estimating California housing prices was to reduce the computational cost of calculations on a dense 20,640 × 20,640 matrix [2] (pp. 294–295). Even using vastly faster and more sophisticated computer hardware, some of the data engineering and supervised machine learning routines in this evaluation of the California housing dataset exceeded the 1130 s that Pace and Barry needed to compute a sparse matrix determinant ten times [2] (p. 295).
As a method for geospatial analysis, data engineering relies heavily on subjective judgment—perhaps excessively so. Even the most astute observers might struggle to quantify interactive or polycentric effects. Modern metropolises contain multiple loci for employment or leisure beyond the historic city center. Road or bridge construction can change decades or even centuries of housing and commuting patterns.
4.2. Two-Stage Least Squares (2SLS)
Among the methods in this paper, 2SLS may be the most easily generalized. A second-stage regression explicitly exposes the diffusion term in geospatial analysis. Numerous models describe physical or social phenomena according to distinct terms of deterministic drift and stochastic diffusion:
- The deterministic drift term captures a system’s unconditional traits—namely, those that do not vary across time or space (however those dimensions might be defined);
- The stochastic diffusion term captures variability over time or space, perhaps most readily understood in the special instance of zero-drift Brownian motion [20].
The distinction between drift and diffusion pervades the analytical literature of many disciplines. Psychology, neuroscience, and behavioral economics have devised drift-and-diffusion models of decision-making [21,22]. Drift-and-diffusion approaches to time-series forecasting span traditional statistical methods [23] and generative deep learning approaches [24]. In hydrology, drift and diffusion hew closely to their original physical meaning [25].
Robin Dubin’s canonical 1992 study of housing quality in Baltimore provides a fruitful starting point for understanding drift and diffusion in geospatial econometrics [26]. Earlier studies in urban economics would engineer one or more variables designed to capture geospatial effects. For example, distance to a city’s central business district, a harbor, or the riverfront would be calculated and added to the design matrix [27].
By striking contrast, the Baltimore study ignored those attributes. It conspicuously omitted distance from Baltimore’s central business district. As Dubin later observed, “Rather than eliminating … spatial residual dependencies through the inclusion of many independent variables, spatial statistical methods typically keep fewer independent variables and augment these with a simple model of the spatial error dependence” [28] (p. 79).
In line with that preference for “a simple model” of spatial errors over a profusion of independent variables, the Baltimore study focused on the basic formulation of an unconditional OLS model [26] (p. 437):
Y = Xβ + u
Xβ is the design matrix times the coefficients on all predictive variables. It is equivalent to ŷ, the vector of fitted values. Isolating all non-geospatial features in Xβ treats this equation as the definition of the drift term.
If Xβ, as a deliberately underfit effort to find ŷ, contains only hedonic or other non-geospatial variables, then the error term, u, contains the information that presumably was not addressed in the design matrix. Isolating hedonic and other non-geospatial effects in the drift term redirects all geospatial effects to the error term.
u, in turn, is equivalent to the residuals, defined as u = y − ŷ. The error term u is the locus of diffusion for all geospatial effects. In the nomenclature adopted by Giuseppe Arbia, searching for dependencies within the error term u is the hallmark of a spatial error model [7] (p. 311). A second-stage regression can substitute û for u in the basic model. An improvement in predictive accuracy through a second-stage regression implies the analytical inadequacy of the unconditional first-stage regression of the drift term. The second-stage regression also requires a process for extracting û. In other words: u = û + v, where v is the error term in the second-order supervised learning process for estimating the residual.
This idea can be generalized to other elements. For data with a temporal element, û can be seen as a function of time. For strictly synchronic geospatial data, û is a function of distance from some reference point. If the reference point is defined according to the geospatial location of an observation, the relevant distance is zero, and the second-stage regression must rely on the intercept of an unenhanced linear model. Alternatively, we can find another geographic reference point, such as the geographic centroid that includes the neighbors as well as the original observation, and then measure distances from that centroid.
We then reconstruct the model by substituting fitted values of the residual back into the original specification of the model:
y = Xβ + û + v
This result follows from the original specification of the drift term, y = Xβ + u, and from the subsequent effort to extract spatial diffusion effects through the second-stage regression, u = û + v.
If fitted values for the residuals in û do not meaningfully improve the goodness of fit, then we can conclude that the data lacks effects defined by the second-stage regression’s predictive variables. But if the substitution of fitted residuals for the original error term improves the prediction, that improvement provides evidence that the second-stage regression has captured at least one omitted variable. In geospatial econometrics, that omitted variable is often one that exhibits autocorrelation across geographic space.
4.3. Iterative Local Regression
The third strategy, iterative local regression, assumes that the relationship between hedonic and socioeconomic predictors, on one hand, and the target variable of median house price is more likely to cohere within a geographically circumscribed subset of districts, at least relative to a spatially unconditional regression based on all of California. Prices in Marin County presumably reflect local conditions to a greater extent than more remote conditions in Malibu, Modesto, or Monterrey.
Within the literature of spatial econometrics, these instincts are typically expressed through spatial lag models. The basic specification of a spatial lag model is
where j indicates observations other than those in i but near them, W is a matrix of spatial weights, and ρ is an empirically estimated parameter [29] (pp. 97–101). Though the specification of W [30] and the estimation of ρ [31] command considerable attention in spatial econometrics, this paper and its larger goal of extending insights from spatial analysis to other economic domains will focus on the definition of j, the set of observations deemed close enough to influence estimates in i.
Yi = ρWYj + βXi + εi
Iterative local regression requires the identification of neighbors belonging to j. There are no fewer than three distinct strategies for identifying subsets of the data for iterative local regression. First, the original California housing study defined a minimum distance around a district, such that districts within d kilometers of a district would be given a weight of one, while all other districts would receive a weight of zero [2] (p. 293).
A second approach could use Haversine distance between the districts to conduct clustering analysis. Works beyond the strict definition of geospatial econometrics use clustering to identify subsets of a dataset upon which to conduct local regressions [32].
This study pursued a third approach. It used an unsupervised variant of k-nearest neighbors to perform the initial filtering. At k = 64, this study conducted 20,640 exercises in local regression, based on the assumption that the 64 closest districts (according to each district’s latitude and longitude to 0.01° precision) would provide more accurate exercises in OLS or ℓ1-regularized regression.
The k-nearest neighbors algorithm therefore holds the key to understanding spatial lag models. The unsupervised variant of the algorithm designates the observations that belong to the set of neighbors in j. This study’s implementation of supervised KNN directly reports the results of a degenerate variant of the spatial lag. The “location only” sKNN result of r2 = 0.781847 effectively sets the coefficient β in Equation (3) to zero. Under that assumption, the estimate of housing prices by district is equal to the spatially weighted and lagged values of nearby districts alone—namely, Yi = ρWYj + εi. This estimate proceeds wholly without regard to the hedonic and demographic variables in the term βXi.
By contrast, iterative local regression based on neighbors identified by unsupervised KNN—at least in the first instance—relies entirely on the identification of neighbors within set j and ignores the spatial lag term, ρWYj. In effect, each local regression estimate takes the form Yi = βXj + εj, inasmuch as the identification of neighbors in j dictates the observations used to estimate the target variable in i.
Notably, the value of k differs for supervised and unsupervised KNN. sKNN optimizes k at six neighbors. Iterative local regression based on uKNN proceeds on a uniform value of k = 64. Despite the differing values of k and the radically different assumptions underlying the separate application of supervised and unsupervised KNN, integrating sKNN results with predictions drawn from iterative local regression based on uKNN could produce a complete spatial lag model. Time-series forecasting models routinely incorporate temporally lagged values of the target variable into the vector of predictive variables. An sKNN model optimized at k = 6 implies that local regression could proceed by adding the target value of the six geographic nearest instances to each iteration’s vector of predictive variables. Alternatively, a machine learning environment enables the stacking generalization of predictions from sKNN, iterative local regression, and 2SLS [33]. Conceptually, nothing categorically excludes conventional regression results with geospatially engineered variables from meta-prediction through stacking generalization.
Relative to 2SLS, iterative local regression can be said to invert the treatment of drift and diffusion. Preprocessing through unsupervised KNN treats spatial proximity as an admittedly crude and deterministic first stage. Geospatial distance, whether defined by a fixed radius, by k neighbors, or a formal clustering analysis, circumscribes each exercise in local regression. A district elsewhere in California is either among the k = 64 closest neighbors or else adds nothing to the prediction. Local regression using a fuller vector of hedonic, socioeconomic, or even engineered variables then treats the relationship between those predictors and the target variable as the product of stochastic diffusion.
A second, “corrective” stage in local regression is theoretically possible. The identification of k nearest neighbors reports the Haversine distance for each of k = 64 districts. Following each instance of local regression with a further 2SLS correction remains an open option. An iterative and local implementation of the 2SLS methodology, however, should adhere to the conventions identified in [26,28]: the design matrix in local regression should eschew geospatial features, especially those based on data engineering, so that the second, spatially sensitive stage fits first-stage residuals as a function of distance.
5. Discussion: Panel Data Analysis and Time-Series Forecasting
Most time-series forecasting models can be readily understood according to treatment of drift and diffusion in the canonical 2SLS method in geospatial econometrics. Achieving stationarity by detrending and removing seasonal and cyclical effects reduces the forecasting problem to one akin to Brownian motion: stationarity as a zero-drift condition enables forecasting to focus exclusively on the diffusion term [20].
Walk-forward validation in time-series forecasting can also be seen as iterative local regression with very modest degrees of feature engineering [34,35]. Lagged terms are merely time-shifted observations of the target variable, cast anew as predictive variables for each forecast window. This is a direct analog of the spatial lag model defined in Equation (3). A fixed value of k, as in the KNN algorithm implemented in this study, is the geospatial equivalent of a fixed lookback period in time-series forecasting.
This definition of the drift term implies that the identification of neighbors, whether in space or time, according to distance by any metric, should be approached in a deterministic, invariable way. This implication flows from the very name of unsupervised KNN as a clustering method. The value of k directs the partitioning of the entire dataset into smaller subsets for local regression. A cutoff defined in kilometers, miles, or Haversine distance operates in a similarly categorical way: either a neighboring community imparts spatially variable impact on a prediction or it lies too far afield and therefore receives zero weight. Within that set of neighbors, of course, the spatial weighting matrix may be constant or variable.
The 2SLS approach to geospatial econometrics finds its parallel in simpler, static panel data models. Low-frequency panel data, with annual observations, is ubiquitous in economics. Inasmuch as panel datasets fitting this description are collections of geographically related time series, a 2SLS approach that corrects residuals according to time elapsed since the earliest observation should be well suited to panel data analysis. This insight suggests an alternative to the prevalent practice of using fixed effects to offset omitted variable bias in panel data [36] (pp. 871–872). The short, low-frequency time vectors in many panel studies invites the estimation of residuals by two-stage least squares.
Fixed-time-effects regression assigns a dummy variable for each separate year in the dataset. This method accordingly treats time as a discrete, categorical factor. Fixed-time-effects models cannot treat time as a continuous, autocorrelated variable. Correlation between the error term and the time of each observation in panel data, originally a troublesome defect, can fuel a powerful corrective tool. The second-stage regression generates a coefficient and (if desired) a p-value for the temporal variable.
Fixed-effects regression may also be treated as a species of data engineering. The motivation for fixed-effects regression is the suspicion that the dimensionality of a design matrix is too low and that the hypothesized vector of predictors underdetermines the target variable. Adding fixed effects adds a sparse submatrix of dummy variables. Like the use of data engineering to synthesize hedonic features that vary according to distance from a geographic point of interest, fixed effects reconfigure the design matrix outright rather than exploit the distinction between unconditional drift and stochastic diffusion. The effects of space and time, instead of being isolated within deterministic drift (through iterative local regression) or stochastic diffusion (through 2SLS regression of the baseline regression’s error term), are expressed in the coefficients on engineered dummy variables.
Discrete rather than continuous approaches to the temporal component of economic data pervade models positing the presence of critical periods or regime shifts. Jump-diffusion models in finance, which isolate a diffusion process within time [37], are merely special cases of a broader genre. Numerous economic studies acknowledge time-variant effects, with a mixture of continuous, even linear effects and discrete, punctuated periods of time where ordinary drift conditions no longer prevail and new cause-and-effect relationships take hold [38].
A slightly more complex but mathematically similar approach can address fixed entity effects in a panel dataset. Many datasets in European research are tagged according to the 27 member-states of the European Union. Though it may sound implausible, the GPS coordinates for each of the EU’s 27 member-states can supply a geospatial embedding that predicts numerous economic and sociopolitical phenomena as a function of distance from the historical center of the original six signatories of the Treaty of Rome [39]. Similarly, a 2SLS correction of residuals in American data might recognize the presence of multiple historical centers—estimated to be as many as eleven—throughout the United States [40].
The 2SLS methodology for extracting geospatial effects can be adapted to datasets whose fixed entity effects can be evaluated through other distance metrics. Gaussian distance from a particularly important threshold—such as a dataset centroid or a critical value—is a time-worn economic principle (as illustrated, for example, by the idea of “distance to default” [41]).
Even greater potential lies in further elaborations of the relationship between geospatial and time-series analysis. The original California housing study took a synchronic snapshot of that state’s housing market [2]. Both the original study and this effort at replication are “limited to the analysis of spatial data observed in a single moment of time,” leaving for future development “the case of dynamic spatial data” [42] (p. 146). A truly diachronic analysis of the state’s 20,640 Census districts would reveal the evolution of California’s real estate market across both space and time.
At levels of theoretical abstraction beyond the immediate task of predicting housing prices, distance-sensitive analytical approaches highlight the value of treating time-variant data as potentially discrete and discontinuous. This insight highlights the value of methodologies that suspend the assumption that data varies in a continuous (let alone linear) fashion across space and time.
6. Conclusions
Deterministic drift and stochastic diffusion decompose distinct elements of quantifiable phenomena and enable each element to be evaluated in isolation. Two-stage least squares and iterative local regression take distinct approaches toward isolating the spatial (or temporal or phenomenological) component of an economic system. 2SLS starts with a global, unconditional regression of hedonic and other nonspatial features. Spatial effects isolated in the residuals can then be evaluated as a diffusion process.
Iterative local regression adopts some structure of the dataset, distinct from treating the entire dataset as a unified whole, as an initial step in preprocessing. This step partitions the dataset into subsets suitable for local regression. In turn, local regression generates as many as n sets of Xβ, one for each data point representing the ground truth of median housing prices by district. Thanks to the iterative nature of this approach, each coefficient in β should be understood as a probability distribution in its own right, with its own mean and variance. The presence of µ and σ for each coefficient enables the entire apparatus of null hypothesis significance testing: a p-value, statistical significance at different levels of p, and confidence intervals.
Despite its deprecation in contemporary spatial analysis, data engineering still runs rampant elsewhere in econometrics. Data engineering often takes the form of fixed-effects tests. Unconditional regression with engineered features (including fixed effects) is another instance of zero-drift Brownian motion. Older studies express geospatial effects through the coefficient assigned to an engineered variable, such as distance from a central business district or the seashore. Fixed-effects tests operate even more simply. They ultimately report their impact through coefficients on dummy variables.
By contrast, the 2SLS and local regression methods deployed in this study correspond directly to methods for handling the temporal component of panel or time-series data. The correction of residuals through 2SLS not only improves predictive accuracy but also exposes spatial or temporal dependencies.
For its part, walk-forward validation in time-series forecasting performs a sort of iterative local regression across a sliding time window. Each regression generates a single instance of the stochastic distribution of each coefficient in β. The strategies for geospatial analysis examined in this article, despite data-specific differences in predictive performance, illuminate comparable strategies for quantifying the effects of time in panel analysis and time-series forecasting.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study relied upon the California housing dataset, which is available free of charge via the SciKit-Learn library at https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html. (accessed on 20 May 2025).
Acknowledgments
Charalampos Agiropoulos, Abdel Razzaq M. Al Rababa’A, and Juan Laborda provided helpful comments.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2SLS | Two-stage least squares |
| KNN | k-nearest neighbors. The prefatory letters “s” and “u,” respectively, indicate “supervised” and “unsupervised” k-nearest neighbors (sKNN and uKNN). |
| OLS | Ordinary least squares |
References
- Williams, T. The Glass Menagerie, 1st ed.; and introduction. 16th printing; Bray, R., Ed.; New Directions: New York, NY, USA; Random House: New York, NY, USA, 2011. [Google Scholar]
- Pace, R.K.; Barry, R. Sparse spatial autoregression. Stat. Prob. Lett. 1997, 33, 291–297. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Paelinck, J.H.P.; Klaassen, L.H. Spatial Econometrics; Saxon House: Farnborough, UK, 1979. [Google Scholar]
- Anselin, L. Thirty years of spatial econometrics. Pap. Reg. Sci. 2010, 89, 3–26. [Google Scholar] [CrossRef]
- Arbia, G. Spatial econometrics: A rapidly evolving discipline. Econometrics 2016, 4, 18. [Google Scholar] [CrossRef]
- Arbia, G.; Fingleton, B. New spatial econometric techniques and applications in regional science. Pap. Reg. Sci. 2008, 87, 311–317. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances. J. Real Estate Fin. Econ. 1998, 17, 99–121. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. 2SLS and OLS in a spatial autoregressive model with equal spatial weights. Reg. Sci. Urban Econ. 2002, 32, 691–707. [Google Scholar] [CrossRef]
- Lee, L.-F. GMM and 2SLS estimation of mixed regressive, spatial autoregressive models. J. Econom. 2007, 137, 489–514. [Google Scholar] [CrossRef]
- Lu, A.X.; Moses, A.M. An unsupervised kNN method to systematically detect changes in protein localization in high-throughput microscopy images. PLoS ONE 2016, 11, e0158712. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Liu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Chen, J.M. A practical introduction to regularized regression for panel data. Contrib. Stat. 2026; in press. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psych. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Halevy, A.; Norvig, P.; Pereira, F. The unreasonable effectiveness of data. IEEE Intell. Sys. 2009, 24, 8–12. [Google Scholar] [CrossRef]
- SciKit-Learn documentation. Fetch_California_Housing. 2025. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html (accessed on 11 May 2025).
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Annals Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the KDD ‘16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Pollak, M.; Siegmund, D. A diffusion process and its applications to detecting a change in the drift of Brownian motion. Biometrika 1985, 72, 267–280. [Google Scholar] [CrossRef]
- Fudenberg, D.; Newey, W.; Strack, P.; Strzalecki, T. Testing the drift-diffusion model. Proc. Natl. Acad. Scis. USA 2020, 117, 33141–33148. [Google Scholar] [CrossRef]
- Richter, T.; Ulrich, R.; Janczyk, M. Diffusion models with time-dependent parameters: An analysis computational effort and accuracy of different numerical methods. J. Math. Psych. 2023, 114, 102756. [Google Scholar] [CrossRef]
- Sura, P.; Barsugli, J. A note on estimating drift and diffusion parameters from timeseries. Phys. Lett. A 2002, 305, 304–311. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Li, R.; Li, X.; Gao, J. Diffusion models for time series applications: A survey. arXiv 2023, arXiv:2305.00624v1. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, Y.; Xu, G.; Liu, D. Simulation of red tide drift-diffusion process in the Pearl River estuary and its response to the environment. Front. Mar. Sci. 2023, 10, 1096896. [Google Scholar] [CrossRef]
- Dubin, R.A. Spatial autocorrelation and neighborhood quality. Reg. Sci. Urban Econ. 1992, 22, 433–452. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic housing prices and the demand for clean air. J. Environ. Econ. Mgmt. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Dubin, R.; Pace, K.; Thibodeau, T. Spatial autoregression techniques for real estate data. J. Real Estate Lit. 1999, 7, 79–95. [Google Scholar] [CrossRef]
- Darmofal, D. Spatial Analysis for the Social Sciences; Cambridge University Press: Cambridge, UK, 2015; ISBN 9781316395271. [Google Scholar]
- Lam, C.; Souza, P.C.L. Estimation and selection of spatial weight matrix in a spatial lag model. J. Bus. Econ. Stat. 2020, 38, 693–710. [Google Scholar] [CrossRef]
- Lambert, D.M.; Brown, J.P.; Florax, R.J.G.M. A two-step estimator for a spatial lag model of counts: Theory, small sample performance and an application. Reg. Sci. Urban Econ. 2010, 40, 241–252. [Google Scholar] [CrossRef]
- Tudor, S.; Cilan, T.F.; Năstase, L.L.; Ecobici, M.L.; Opran, E.R.; Cojocaru, A.V. Evolution of interdependencies between education and the labor market in the view of sustainable development and investment in the educational system. Sustainability 2023, 15, 3908. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Livieris, I.E.; Stavroyiannis, S.; Pintelas, E.; Pintelas, P. A novel validation framework to enhance deep learning models in time-series forecasting. Neural Comput. Appl. 2020, 32, 17149–17167. [Google Scholar] [CrossRef]
- Wahyuddin, E.P.; Caraka, R.E.; Kurniawan, R.; Caesarendra, W.; Gio, P.U.; Pardamean, B. Improved LSTM hyperparameters alongside sentiment walk-forward validation for time series prediction. J. Open Innov. Tech. Mark. Complex. 2025, 11, 100458. [Google Scholar] [CrossRef]
- Forbes, K.J. A reassessment of the relationship between inequality and growth. Am. Econ. Rev. 2000, 90, 869–887. [Google Scholar] [CrossRef]
- Christensen, H.L.; Murphy, J.; Godsill, S.J. Forecasting high-frequency futures returns using online Langevin dynamics. IEEE J. Sel. Top. Signal Process. 2012, 6, 366–380. [Google Scholar] [CrossRef]
- Ahmed, M.; Haider, G.; Zaman, A. Detecting structural change with heteroskedasticity. Commun. Stat.—Theory Methods 2016, 46, 10446–10455. [Google Scholar] [CrossRef]
- Chen, J.M.; Poufinas, T.; Panagopoulou, A. Drift and diffusion in panel data: Extracting geopolitical and temporal effects in a study of passenger rail traffic. Comput. Sci. Math. Forum, 2025; in press. [Google Scholar]
- Woodward, C. American Nations: A History of the Eleven Rival Regional Cultures of North America; Viking: New York, NY, USA, 2011. [Google Scholar]
- Merton, R.C. On the pricing of corporate debt: The risk structure of interest rates. J. Fin. 1974, 29, 449–470. [Google Scholar] [CrossRef]
- Arbia, G. Spatial econometrics: A broad view. Found. Trends Econom. 2016, 8, 145–265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).