Abstract
Anomaly detection in time series data is crucial across various domains. Traditional methods often struggle with continuously evolving time series requiring adjustment, whereas large language models (LLMs) and multi-modal LLMs (MLLMs) have emerged as promising zero-shot anomaly detectors by leveraging embedded knowledge. This study expands recent evaluations of MLLMs for zero-shot time series anomaly detection by exploring newer models, additional input representations, varying input sizes, and conducting further analyses. Our findings reveal that while MLLMs are effective for zero-shot detection, they still face limitations, such as effectively integrating both text and vision representations or handling longer input lengths. These challenges unveil diverse opportunities for future improvements.
1. Introduction
Time series data, consisting of chronologically ordered data points, is widely used in fields such as transportation, cybersecurity, healthcare, and industrial operations. Anomalies in time series often signal opportunities, such as stock prices’ drastic changes in finance, or issues such as traffic accidents in transportation or irregular vital signs in healthcare. As data grows especially with emerging scenarios, advanced techniques are increasingly needed for time series anomaly detection (TSAD) in evolving datasets.
Traditional TSAD methods, including the Z-score, exponential smoothing, and ARIMA [1], rely on rigid distributional assumptions, struggle with complex, non-linear relationships, and lack adaptability to changing data and the appearance of new patterns. Machine learning approaches like isolation forest [2] and neural networks [3] offer improvements but require extensive training and potential updates to remain effective, adding operational overhead.
The rapid development of large language models (LLMs) presents a promising shift in TSAD. With their embedded knowledge, LLMs can identify anomalies using vast pre-existing information from diverse sources without additional training, making them well-suited for dynamic time series data. Some studies have explored LLMs for TSAD using textual time series representations [4,5,6,7]. Recently, multi-modal LLMs (MLLMs) further extend this potential by introducing multiple data modalities, providing a richer understanding of complex time series [8,9,10]. Prior studies [8] found that vision representations outperformed textual representations, while refs. [9,10] focused solely on vision inputs, demonstrating MLLMs’ effectiveness in zero-shot and few-shot TSAD, respectively.
This study expands on these efforts by evaluating MLLMs’ zero-shot TSAD capabilities from multiple perspectives. The key differences between our study and recent zero-shot studies [8,9] are summarized in Table 1.

Table 1.
Comparison with related studies on zero-shot time series anomaly detection (TSAD) using multi-modal LLMs (MLLMs).
The main contributions of our study are summarized as follows:
- We conduct an extensive empirical evaluation of MLLMs for zero-shot TSAD, incorporating a wider range of models with newer versions, different model sizes, more time series representations, and varying input lengths.
- We analyze results at two levels, (i) assessing models’ ability to distinguish normal and anomalous time series and (ii) evaluating their precision in pinpointing anomalies.
- We extend analysis beyond detection accuracy and also assess response appropriateness to determine how well models follow instructions.
- Our findings highlight both MLLMs’ potential and limitations, such as their inability to effectively combine text and vision representations. These insights reveal new research directions for improving multimodal TSAD.
2. Methodology
This section outlines the experimental design, detailing the models, time series representations, prompting strategy, input lengths, dataset generation, and evaluation methods.
2.1. Evaluated MLLMs
For this study, we selected a diverse set of recent proprietary and open source MLLMs, including Gemini-2.0 [11], GPT-4o [12], LLama-3.2 [13], Ovis2 [14], Qwen2.5-VisionLanguage (Qwen2.5-VL) [15], and LLaVa-OneVision (LLaVa-OV) [16]. To analyze the impact of model size on performance, we evaluated both their large and lite versions, as detailed in Table 1.
To evaluate the capabilities of these models to detect anomalies, we defined a “Dummy” baseline, which considers that all time series are anomaly-free. We also included isolation forest, a classical anomaly detection algorithm, as used in [8], to serve as another baseline.
2.2. Time Series Representation
Unlike traditional LLMs, which process Text-only inputs, MLLMs integrate both language and vision capabilities, enabling them to handle text, images, or a combination of both. This multimodal flexibility has led to strong performance across various tasks. However, existing studies [8,9] on MLLMs for TSAD have primarily focused on a single representation type—either Text-only or Vision-only. Extending beyond these studies, we introduce a Text and Vision input type, where both textual and visual representations of the time series are provided simultaneously.
Our objective is to determine whether a particular input representation (Text-only, Vision-only, or Text and Vision) is optimal for time series anomaly detection.
2.3. Prompting Strategy
We base our prompting strategy on the template introduced by Zhou et al. [8], which instructs models to return a list of time step ranges corresponding to the positions of anomalies in the time series. However, we introduce the following key modifications to enhance instruction clarity and reduce ambiguity in model outputs: (i) Explicit indexing: We specify that time step indices range from 0 to [L − 1], where L is the time series length; (ii) exclusive end indices: the prompt clarifies that each anomaly range should follow an exclusive end index format; and (iii) strict format enforcement: we explicitly instruct models to adhere to the output template to prevent inconsistencies.
Our revised prompt is organized in two parts. The specific part varies depending on the input representation and describes how the time series is provided to the model. The common part remains consistent across all input representations and defines the task, ensuring the model understands the expected output format. Our template is shown below:
| Specific part |
| Text-only: [Time series text] This time series comprises [L] values. |
| Vision-only: [Image] This image depicts a time series comprising [L] values. |
| Text and Vision: [Time series text] [Image] This time series, illustrated by the accompanying image, comprises [L] values. |
| Common part |
| The indices range from 0 to [L − 1]. Assume there are up to [N] ranges of anomalies within this series. |
| Detect these anomaly ranges in the series. If there are no anomalies, answer with an empty list []. |
| Each range should be described by a start and an exclusive end index. List these ranges one by one in JSON format. |
| Use the following output template: [{“start”: …, “end”: …}, {“start”: …, “end”: …}, …]. Strictly follow this template. |
| Do not include any additional explanations, description, reasoning, or code. Only return the answer. |
In the specific part, the [Time series text] placeholder provides the time series as a plain text sequence, such as [0.23, −0.15, …]. The expected output is an empty list ([]) if the model detects that there are no anomalies. Otherwise, it follows a structured format, such as [{“start”: 0, “end”: 12}, {“start”: 72, “end”: 85}].
2.4. Time Series Length
We hypothesize that increasing the input length provides models with additional contextual information, such as periodic patterns, which may improve their ability to detect anomalies. However, longer inputs also require more tokens and computational resources, posing challenges for MLLMs in modeling long-term dependencies. This increased complexity could make anomaly detection more difficult and potentially reduce model efficiency.
For image-based inputs, larger time series may further introduce limitations, as compressing longer sequences into a fixed image resolution could reduce the level of detail available for analysis. Given these trade-offs, we aim to evaluate how input length affects MLLM performance and identify configurations where models either excel or struggle. To achieve this, we experiment with two primary input lengths: (short) and (long).
2.5. Synthetic Dataset
Following Zhou et al.’s work [8], we consider four types of anomalies observed in time series data. Our objective is to assess MLLMs’ ability to detect diverse anomaly patterns. The four anomaly types are defined as follows: (1) Trend anomalies—sudden shifts in the established trend, either accelerating or decelerating, as illustrated in Figure 1a. (2) Frequency Domain anomalies—abrupt increases or decreases in frequency components (Figure 1b). (3) Point anomalies—isolated data points that deviate significantly from the expected pattern, as illustrated in Figure 1c. (4) Range anomalies—a consecutive sequence of points where values exceed normal thresholds (Figure 1d).
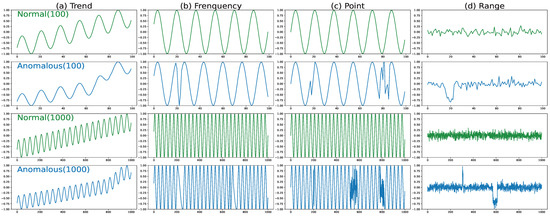
Figure 1.
Illustrations of the different anomaly types: (a) trend, (b) frequency, (c) point, and (d) range.
To ensure consistency with prior studies, we adopt the same parameters as Zhou et al. [8] for input sequences of length 1000. However, for input sequences of length 100, we increase the frequency and shorten anomaly ranges to better align with this shorter length. Figure 1 illustrates the differences between normal time series (green) and those containing anomalies (blue) across all anomaly types (columns) and both input lengths (rows). As expected, longer time series () tend to smooth out finer details, while shorter ones () appear more sparse, making anomalies visually distinct. For each anomaly type, we generate 400 synthetic time series following the methodology in a prior study. Table 2 details the distribution statistics of normal and anomalous time series.

Table 2.
Number of time series with and without anomalies over the 400 generated for each input length and each anomaly type (T = trend, F = frequency, P = point, and R = range).
2.6. Evaluation Methods and Metrics
We evaluate TSAD performance at two levels, namely series-level detection and step-level detection. Series-level detection assesses whether a model correctly classifies an entire time series as normal or anomalous. If the model outputs an empty list, the time series is considered normal; otherwise, it is classified as containing anomalies. Step-level, in contrast, evaluates whether the model can correctly identify the specific time steps that constitute anomalies. This distinction allows us to determine whether some models can detect the presence of anomalies but struggle to pinpoint their exact locations.
Both detection tasks are treated as binary classification problems, where normal instances belong to class 0 and anomalous ones to class 1. However, the generated dataset is imbalanced. As shown in Table 2, for series-level detection, approximately of the time series contains anomalies. The imbalance is even more pronounced in step-level detection, where as illustrated in Figure 1, the vast majority of time steps are normal. To account for these imbalances, we focus on precision, recall, and the F1-score for the anomaly class (). For these metrics, we also set the parameter to 0. In addition, we added the balanced accuracy (https://scikit-learn.org/stable/modules/generated/sklearn.metrics.balanced_accuracy_score.html (accessed on 31 March 2025)), which accounts for class distribution, with one being the optimal score. Given the numerous experimental settings, we report only results averaged across anomaly types, but full results are available in our GitHub repository (https://github.com/haoniukr/tsad (accessed on 31 March 2025)).
3. Cleaning Models’ Answers
Despite our revised prompt, the models did not always adhere to the instructed answer format in our experiment, necessitating output cleaning before evaluation.
Table 3 presents the percentage of answers that required cleaning, averaged across anomaly types and time series representations for each input length.

Table 3.
Percentage (%) of answer cleaned, average over anomaly and input types for experiments with input length 100 and 1000.
The results indicate that using longer time series tends to increase formatting issues, making it harder to maintain response appropriateness. Additionally, Gemini-2.0 models and GPT-4o produced a higher percentage of improperly formatted answers.
However, such a metric must be interpreted alongside the severity of the formatting issues. We classified them into five categories, each requiring a different cleaning process, as explained in the following:
- Unexpected character (UC): This comprises answers that contained extraneous characters (e.g., backticks, or JSON tags) preventing proper parsing but that did not affect anomaly detection results. Cleaning involved simply removing these characters.
- Low-impact issues (ERL): Answers that included unnecessary formatting elements (e.g., commas, double quotes, or leading zeros) that, while not altering results, required careful additional checks before removal to ensure proper processing.
- Moderate-impact issues (ERM): These answers hit the token limit due to listing every anomaly separately instead of using range-based notation. This issue led to missing portions of the answer, potentially affecting model performance. Cleaning involved discarding incomplete ranges while preserving the rest.
- High-impact issues (ERH): Answers that included indices exceeding the input length, indicating a failure to follow instructions. If both start and end indices were out of range, the range was removed; if only the end index was invalid, it was replaced with the maximum valid index.
- Formatting issues (FMT): Answers that did not follow the desired output format, requiring cleaning that might negatively impact the performance (however, this could also be interpreted as a penalty for not following the instructions). Some answers mixed explanations with properly formatted ranges, necessitating text removal. Others provided anomaly ranges only in textual descriptions, requiring conversion to the correct format. And, in two cases, the model failed to return a valid response (once outputting Python code and once stating that it lacked information to provide an answer). These were replaced with an empty list, meaning no anomalies were detected.
Figure 2 illustrates the distribution of cleaning operations using heatmaps across models and combinations of anomaly-type and time series representation for these categories (columns). The top row represents shorter time series (), while the bottom row represents longer ones ().
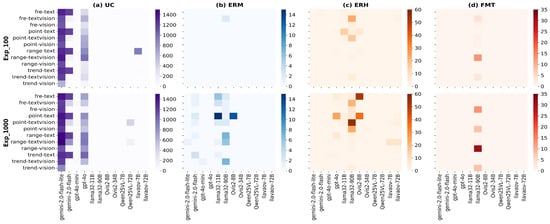
Figure 2.
Heatmaps of the total number of cleaning operations that was necessary per model, per anomaly type, per input type for each category: (a) UC, (b) ERM, (c) ERH, and (d) FMT.
In this figure, we omitted ERL, as they were rare and only occurred with a long input length. Some key observations can be drawn from this figure as follows: (i) UC issues appeared mostly with Gemini-2.0 (flash and flash-lite) and GPT-4o, with Gemini-2.0 Flash-lite producing them across all settings, while Flash had issues mainly with Text-only inputs; (ii) ERM issues occurred mainly in the experiment with using LLama-3.2 and Gemini-2.0 models; (iii) ERH issues primarily appeared in Frequency and Point anomaly types when using GPT-4o, both LLama-3.2 and Ovis2-8B; and (iv) FMT issues were exclusive to Llama32-90B.
Therefore, despite having a lower proportion of properly formatted answers, issues generated by Gemini-2.0 models are not severe. In contrast, errors from Llama-3.2-90B—and to a lesser extent GPT-4o—were more critical, which might impact their performance.
4. Experimental Results
4.1. Performance Evaluation
The tables in this subsection present the precision, recall, and F1-scores for the anomaly class, along with the balanced accuracy score, for various MLLMs (rows) and input representations (columns) and averaged across different anomaly types.
4.1.1. Series-Level Detection
Table 4 presents the series-level detection results for the short input length.

Table 4.
Performance comparison on 400 time series (). Gray cells indicate performance lower than [resp. equal to] the dummy baseline, and yellow indicates lower than isolation forest. Uncolored cells indicate models that outperform both baselines, for which the best and second-best performances are highlighted.
Based on both the F1-score and balanced accuracy, Qwen2.5-VL-72B achieves the highest overall performance with Vision-only input but struggles to further improve with multimodal data (Text and Vision), despite also excelling in that setting. In contrast, GPT-4o models can in most cases enhance their Text-only performance when using Text and Vision, highlighting their ability to benefit from both textual and visual information. However, Gemini-2.0 models exhibit a different behavior: they rank among the best in F1-score and balanced accuracy with Text-only and Vision-only inputs, respectively, but perform worse with Text and Vision, suggesting less affinity with both modalities.
Overall, except for LLama-3.2-11B and LLaVa-OV-7B, which mostly remain consistent across all inputs, the performance of other models appears to depend on the choice of input representation.
Table 5 presents results for the long input length. The highest F1-score of the anomaly class is achieved by Gemini-2.0-flash using Text-only input. However, the highest balanced accuracy is attained by Ovis2-34B using Vision-only input. This result is driven by this model’s high precision, indicating strong anomaly detection without an excessive misclassification of normal time series. Focusing on balanced accuracy, we observed that the results of GPT-4o and Gemini-2.0 models further improve when incorporating both modalities. On a separate note, we notice that Qwen2.5-VL-7B behaves similarly to the dummy baseline (i.e., assuming all time series contain no anomalies).

Table 5.
Performance comparison on 400 time series (). Red [resp. gray] cells indicate performance lower than [resp. equal to] the dummy baseline, and yellow indicates lower than isolation forest. Uncolored cells indicate models that outperform both baselines, for which the best and second-best performances are highlighted.
4.1.2. Step-Level Detection
Table 6 and Table 7 present the step-level detection results for the short and long input lengths, respectively. The results indicate that models struggle to accurately pinpoint the positions of anomalies, particularly with Text-only input and a long input length. Nevertheless, similar observations can be extracted from these results: overall, (i) most models do not benefit from combining both modalities and (ii) Vision-only achieves the best performance for both short and long input lengths. In addition, Gemini-2.0-flash-lite with Vision-only emerges as the top-performing model across both input lengths.

Table 6.
Performance comparison on time steps. Red [resp. gray] cells indicate performance lower than [resp. equal to] the dummy baseline, and yellow indicates lower than isolation forest. Uncolored cells indicate models that outperform both baselines, for which the best and second-best performances are highlighted.

Table 7.
Performance comparison on time steps. Red [resp. gray] cells indicate performance lower than [resp. equal to] the dummy baseline, and yellow indicates lower than isolation forest. Uncolored cells indicate models that outperform both baselines, for which the best and second-best performances are highlighted.
4.2. Overall Insights Derived from Our Study
Large vs. Lite Models: While larger models generally outperform their lite versions, the differences are sometimes subtle and exceptions exist. Notably, Gemini-2.0-flash-lite often surpasses Gemini-2.0-flash in step-level detection with Vision-based input, achieving the top performance.
Effect of Time Series Representation: Most MLLMs favor specific input representations, likely due to their training data and design. While Text and Vision is expected to provide the best performance as it integrates both modalities, the associated results often fall between or even behind those of Text-only and Vision-only approaches.
Impact of Input Length: Detection performance is significantly influenced by input length. Models are generally more effective at identifying anomalies in shorter time series.
Different Level of Detection: In both series- and step-level detections, Vision-only is the most effective representation for most MLLMs. However, GPT-4o and Gemini-2.0 exhibit distinct behaviors: they generally achieve the best performance in series-level detection with Text-only or Text and Vision input, whereas Vision-only or Text and Vision input is more effective for step-level detection, highlighting their varying strengths across detection levels.
5. Limitations and Opportunities
Our results demonstrate that MLLMs can be effective for TSAD, with some models outperforming the baselines for specific representations, input lengths, and detection levels. However, key limitations persist, requiring further research.
Limited Benefit from Multimodality: Most models fail to leverage both text and vision inputs effectively, likely due to training limitations or architectural constraints. Future research should explore improved fusion techniques, such as fine-tuning or dedicated alignment modules, to better leverage the presence of multiple time series representations.
Challenges with Long Input Length: Longer inputs not only decrease response appropriateness but also increase detection difficulty, as shown in our cleaning process and experimental results. Optimizing model performance for long inputs—e.g., a patching mechanism segmenting them using sliding windows—could be a valuable future direction.
Prompt Dependency: We used a uniform prompt to ensure transparency and consistency with the literature, but model-specific prompts might enhance performance. Moreover, for models being optimized for textual responses, requesting structured outputs like a list of ranges may not be optimal. Adapting prompts to each model could yield better results.
Response Quality and Performance Issues: Some MLLMs fail to generate the expected outputs, requiring cleaning processes that may affect their performance. While we used the cleaning rate to assess response appropriateness, a more comprehensive evaluation should consider factors such as hallucination rates and answer diversity and consistency.
Author Contributions
Conceptualization, H.N.; methodology, H.N., G.H., H.Q.U., R.L., Z.L., Y.W., D.Z., J.V. and M.T.; software, H.N. and G.H.; validation, H.N. and G.H.; formal analysis, H.N. and G.H.; investigation, H.N. and G.H.; resources, H.N., G.H., H.Q.U., R.L., Z.L., Y.W., D.Z., J.V. and M.T.; data curation, H.N. and G.H.; writing—original draft preparation, H.N. and G.H.; writing—review and editing, H.N., G.H., H.Q.U., R.L., Z.L., Y.W., D.Z., J.V. and M.T.; visualization, H.N. and G.H.; supervision, M.T.; project administration, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
In this work, we generated synthetic data based on Zhou et al.’s work [8], the code of which is available at https://github.com/Rose-STL-Lab/AnomLLM/ (accessed on 9 January 2025).
Conflicts of Interest
All authors were employed by the company KDDI CORPORATION or KDDI Research, Inc.
References
- Gujral, E. Survey: Anomaly Detection Methods. figshare 2023. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]
- Zamanzadeh Darban, Z.; Webb, G.I.; Pan, S.; Aggarwal, C.C.; Salehi, M. Deep Learning for Time Series Anomaly Detection: A Survey. ACM Comput. Surv. 2024, 57, 1–42. [Google Scholar] [CrossRef]
- Zhou, T.; Niu, P.; Wang, X.; Sun, L.; Jin, R. One Fits All: Power General Time Series Analysis by Pretrained Lm. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Dong, M.; Huang, H.; Cao, L. Can LLMs Serve As Time Series Anomaly Detectors? arXiv 2024, arXiv:2408.03475. [Google Scholar] [CrossRef]
- Liu, C.; He, S.; Zhou, Q.; Li, S.; Meng, W. Large Language Model Guided Knowledge Distillation for Time Series Anomaly Detection. arXiv 2024, arXiv:2401.15123. [Google Scholar] [CrossRef]
- Alnegheimish, S.; Nguyen, L.; Berti-Equille, L.; Veeramachaneni, K. Large Language Models Can Be Zero-shot Anomaly Detectors for Time Series? arXiv 2024, arXiv:2405.14755. [Google Scholar] [CrossRef]
- Zhou, Z.; Yu, R. Can LLMs Understand Time Series Anomalies? In Proceedings of the 13th International Conference on Learning Representations (ICLR 2025), Singapore, 24–28 April 2025. [Google Scholar]
- Xu, X.; Wang, H.; Liang, Y.; Yu, P.S.; Zhao, Y.; Shu, K. Can Multimodal LLMs Perform Time Series Anomaly Detection? arXiv 2025, arXiv:2502.17812. [Google Scholar]
- Zhuang, J.; Yan, L.; Zhang, Z.; Wang, R.; Zhang, J.; Gu, Y. See it, Think it, Sorted: Large Multimodal Models are Few-shot Time Series Anomaly Analyzers. arXiv 2024, arXiv:2411.02465. [Google Scholar] [CrossRef]
- Mallick, S.B.; Kilpatrick, L. Gemini 2.0: Flash, Flash-Lite and Pro. Available online: https://developers.googleblog.com/en/gemini-2-family-expands/ (accessed on 31 March 2025).
- OpenAI. GPT-4o System Card. arXiv 2024, arXiv:2410.21276. [Google Scholar] [CrossRef]
- Meta. Llama 3.2: Revolutionizing Edge AI and Vision with Open, Customizable Models. Available online: https://ai.meta.com/blog/llama-3-2-connect-2024-vision-edge-mobile-devices/ (accessed on 31 March 2025).
- Lu, S.; Li, Y.; Chen, Q.G.; Xu, Z.; Luo, W.; Zhang, K.; Ye, H.J. Ovis: Structural Embedding Alignment for Multimodal Large Language Model. arXiv 2024, arXiv:2405.20797. [Google Scholar] [CrossRef]
- Bai, S.; Chen, K.; Liu, X.; Wang, J.; Ge, W.; Song, S.; Dang, K.; Wang, P.; Wang, S.; Tang, J.; et al. Qwen2.5-VL Technical Report. arXiv 2025, arXiv:2502.13923. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Guo, D.; Zhang, R.; Li, F.; Zhang, H.; Zhang, K.; Zhang, P.; Li, Y.; Liu, Z.; et al. LLaVA-OneVision: Easy Visual Task Transfer. arXiv 2024, arXiv:2408.03326. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).