1. Introduction
As the most well-known cryptocurrency, Bitcoin has changed dramatically over the years for a variety of reasons, and as a result, it is a component of the new dynamics that are occurring in our financial ecosystem. Bitcoin began as a quirky technological experiment in 2009 when anonymous Satoshi Nakamoto created it [
1]. Since then, it has grown into one of the most successful financial assets ever, attracting the interest of regulators, investors, and tech experts alike. Decentralized and based on blockchain technology, it is a novel idea for a completely new kind of digital transaction that is upending traditional financial systems and introducing fresh concepts to economic interactions [
2,
3].
However, the volatility innate in Bitcoin and other cryptocurrencies remains a very contested and analyzed issue [
4]. Being in relatively uncharted territory, the market for cryptocurrency does not work according to established economic indicators of conventional financial markets or set regulatory frameworks. Market sentiment, regulatory news, technological advances, and macroeconomic trends may cause great fluctuations in a cryptocurrency’s price within a very short period [
5]. This volatility brings a symmetrical amount of opportunity and risk for investors; hence, studying price dynamics and predictive modeling becomes highly relevant to comprehending this emerging asset class.
Our goal in this paper is to explore the complexities of Bitcoin price fluctuations and create reliable models to forecast them. The effectiveness of several neural network models, such as Convolutional Neural Networks (CNNs), Recurrent Convolutional Neural Networks (RCNNs), and Long Short-Term Memory (LSTM) networks, in predicting Bitcoin prices will be specifically compared [
6,
7]. Through an extensive examination of various time-based price comparisons, including close-to-close, close-to-open, open-to-close, and day-to-day, we aim to spot patterns and trends that might help guide better investment tactics.
2. Overview of Neural Network Models
2.1. Convolutional Neural Networks (CNNs)
While CNNs are mostly known for their success with image processing, their application spans time series prediction [
8,
9]. CNNs are good at automatically learning hierarchical feature representations from raw data by using convolutional layers, which apply filters on the input data to capture local patterns [
10].
In a narrow context, the Convolutional Neural Network for price prediction in Bitcoin could be applied to detect the short-term trends and patterns that could change price data almost instantly. If the continuous time series data is convolved with filters, then CNN may pick up some informative features like sudden spikes or falls in prices, which might reflect the market movement. Being able to stack several convolutional layers, a CNN progressively grasps complicated patterns. Therefore, it is a mighty tool for analyzing such complex Bitcoin price movements.
The advantage of CNNs is that they can handle the underlying big data with efficiency [
9,
11]. They process their input data in parallel and are therefore appropriate for high-frequency trading applications, where one needs to make decisions very fast. Also, it is comparatively easier to train and tune the CNN compared to other models; hence, a robust framework for short-term price prediction using CNNs is established.
2.2. Recurrent Neural Networks (RNNs)
RNNs represent a class of neural networks that are very efficient in modeling sequential data due to their ability to maintain some sort of memory about the input entered previously in the sequence. Unlike other types of feed-forward neural networks, connections in RNNs bend backward and connect to the nodes in the preceding layer. This creates a feedback loop; hence, RNNs can maintain an internal state informed by previous time steps.
Since RNNs are specifically suitable for time series prediction tasks, they possess internal memory that may help them learn the temporal dependencies of data [
9,
12,
13]. In this regard, RNNs take in historical price sequences to predict the future prices of Bitcoin. They can effectively capture short-term dependencies and trends, but regarding long-term ones, they usually fail because of the vanishing gradient problem, which LSTMs are designed for.
That is, the plain RNN architecture possesses the input layers, hidden layers, and output layers, while feedback is made up of output that comes out from the hidden layer. This recurrence structure allows an RNN to process a sequence of any length; this makes the RNN applicable in time series analysis. They can be powerful but require very careful tuning and training to realize this performance in highly turbulent data like Bitcoin prices.
2.3. Long Short-Term Memory (LSTM) Networks
Long Short-Term Memory Networks are a kind of RNN that is specially designed to handle the shortcomings of traditional RNNs [
14]. The major reason it is used is most likely due to its potential for overcoming vanishing gradients when training deep networks. When the gradients diminish along with the depth of the network, the network becomes hard to train. In this regard, LSTMs will prevent this problem by keeping memory cells that can store information for a longer period.
Because LSTM networks can grasp long-term dependencies across the data and put them to use, they tend to behave well for any kind of time series prediction tasks. Regarding the price predictions of Bitcoin, LSTM network models will be able to learn from the historical patterns of price data across different time horizons. In such a manner, these models turn out to be proficient enough at making more accurate forecasts of subsequent fluctuations in price.
The LSTM architecture consists of three kinds of gates: input gate, forget gate, and output gate [
15]. These gates control the flow of information into and out of the memory cell, enabling the network to choose what information it forgets, retains, or uses in the prediction. Through this gating process, LSTMs will be able to model the temporal dynamics of the Bitcoin price very effectively, both for the short-term fluctuation and the long-term trend.
3. Methodology
3.1. Time Intervals Analyzed: Day, Overnight, and Close-to-Close
In this paper, we consider three important time factors explaining different aspects of Bitcoin price dynamics, namely day, overnight, and close-to-close. Each one captures unique price movements that help understand market behavior at different times of the trading cycle.
Open-to-Close Day Interval: The day interval describes the length between the opening price and the closing price of Bitcoin within one trading day. Because this interval encapsulates intra-day trades, it reflects price fluctuations from daily market events, trader sentiment, and economic announcements. Analysis of this interval brings to light daily volatility and an idea of how prices of Bitcoin respond to news and other influences during a trading day.
Close-to-Open Overnight Interval: The close-to-open overnight interval considers the change from the closing price of one trading day to the following day’s opening price. This is a very important period since it encompasses everything that has happened, including the activity in markets outside official trading hours. The study of this interval will help in understanding how global events, after-hours trading, and news released overnight influence Bitcoin prices. The overnight gap indeed gives a clue as to what risk happened overnight, along with the possible gaps in price created due to the after-hours market behavior.
Close-to-Close Interval: This precisely focuses on the differential price between the close price on any particular day and that of the following day in a close-to-close interval. On account of the day and night price movements, the interval has critical implications concerning the determination of the overall daily market behavior. It gives a full view of an entire trading cycle within 24 h and thus helps in evaluating aggregate daily volatility and trends.
3.2. Window Adaptations: 14-Day and 50-Day Windows
Here, in capturing the trends and patterns of Bitcoin prices, we considered two window adaptations comprising 14 and 50 days [
16]. These windows represent a rolling period during which several metrics are computed among other statistical features, such as moving averages and volatility.
The 14-day window is a relatively short-term window and can be used to capture recent and quick changes in the market. The window becomes more valuable in identifying recent short-term trends and patterns of Bitcoin prices. It has been quite useful in detecting recent spikes in volatility, price momentum, and other rapid changes in the market. Quite often, traders use short-term windows to make quick trading decisions and to respond to recent market movements.
We can now focus on the prices of Bitcoin, and using a 14-day window may allow for an analysis of the short-run behavior of Bitcoin prices, enabling analysts to spot patterns evident only in the shorter time frame. It also helps to assess what immediate impact recent news and events have on Bitcoin pricing, which is more in line with how the market acts.
The longer time frame is the 50-day window, which can smooth out short-term fluctuations and give a broader view of the market trends. This window can be very useful in catching medium- to long-term trends and understanding where the market is heading. It allows sustained price movements to be detected while filtering out noise from short-term volatility.
Therefore, the 50-day window will allow us to capture the stabilities and patterns of consistency within the Bitcoin prices well. Trends can occur in the long term, so showing long-term effects of fundamentals in markets as well as economic indicators and market sentiment is included. Traders as well as analysts have used longer windows to allow them to make more informed decisions based on the underlying trends rather than the short-term market noise.
4. Volatility Challenges
First, there was the inherent volatility of Bitcoin, which was a big challenge to analyze in this research [
17]. It is very complicated to accurately forecast, especially with both short-term and long-term windows. During the day interval, from open to close, high intra-day volatility causes erratic price fluctuations that are hard to predict. These swift movements, sometimes at the whims of market events or a sudden change in sentiment, overcomplicated our models because they could not fully capture how volatile the market would be within that 14-day window [
18,
19]. The overnight close-to-open gap was another issue in and of itself, due to price gaps from the market’s reaction to out-of-hours global events. These gaps usually resulted in huge differences between the closing price of one day and the opening price of the next. This, in turn, impacted our model’s ability to predict the price movements during the night exactly.
We used both 14- and 50-day rolling windows to smooth out volatility and catch the long-term trends in the market. However, even with this appropriateness, the adaptation of those models also required considerable feature engineering, such as adding measures of volatility like rolling standard deviations, to capture violent movements in the market. Even then, it was the challenging volatility that we kept tuning our models for in order to achieve good generalization on unseen data without overfitting to some short-term spike in prices.
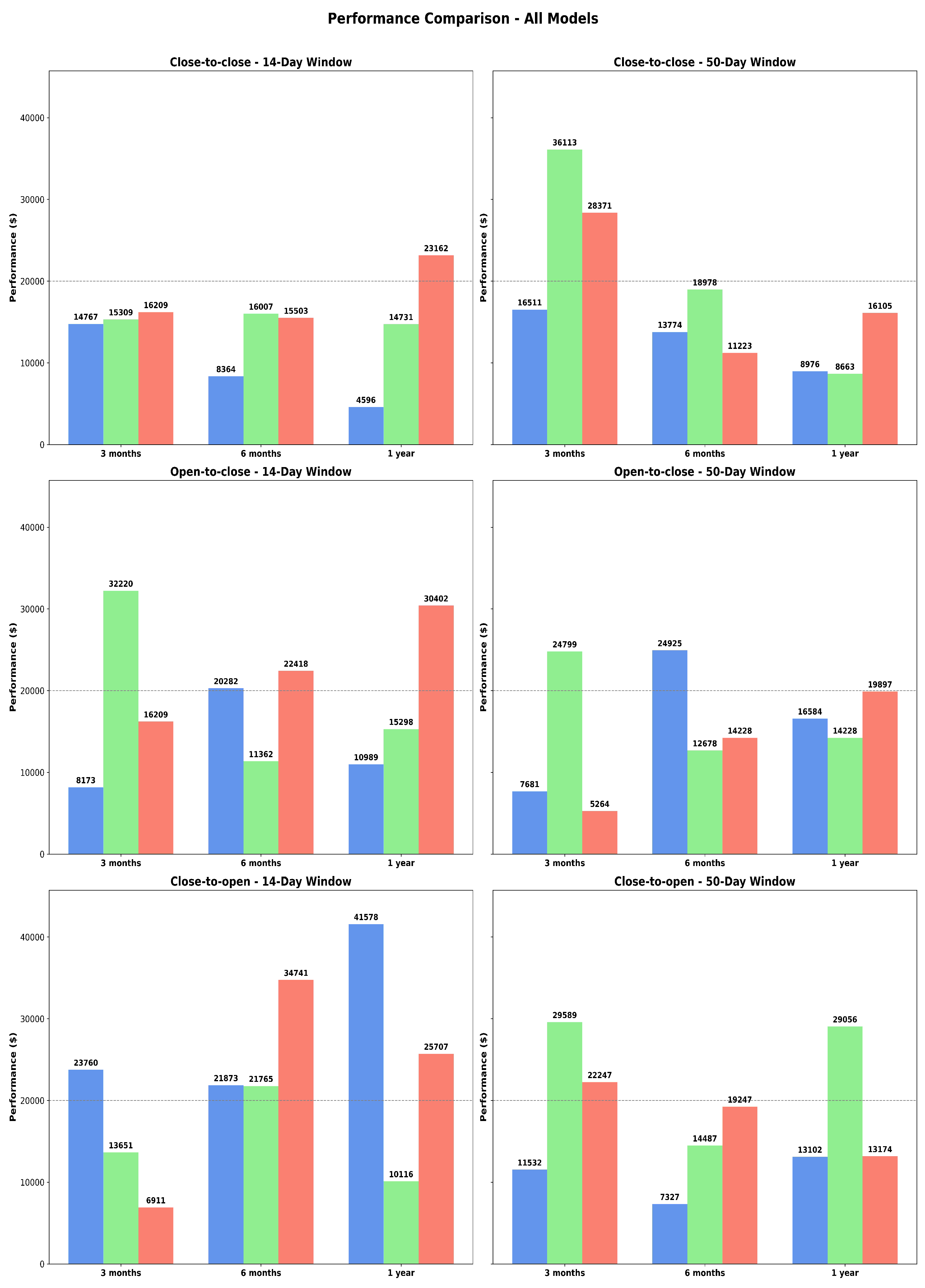
5. Observations
Let us now present some observations on the comparative performance of neural networks for different time periods and different sizes. This is illustrated in
Figure 1.
As we can see, for a shorter window
days, RNN provides the best performance for Close-to-Close time periods. For a larger window size
, CNN gives better results. The results change drastically when we restrict our holding times to either “overnight” (Close-to-Open) or “daytime” (Open-to-Close) only. For the daytime only, the best performer is CNN for both the 14-day and 50-day windows. For the overnight period, the clear winner is LSTM for
days and CNN for
. Comparing all the possibilities, the best performer is LSTM with
and 1 year of training. Detailed numerical comparisons for
days are presented in
Appendix A, and results for
days are presented in
Appendix B.
6. Results
We now present a more detailed discussion for different window sizes, volatility comparison, and risk management.
6.1. Fourteen-Day Window
The results for the 14-day window adaptation underline the crucial role of temporal patterns in predicting the movement of Bitcoin’s price. Among the tested neural network models, LSTM always performed better for each trading interval compared to CNN and RNN models and was able to generate the biggest returns, making it better suited for adapting to the volatile nature of the cryptocurrency market. The most promising results, especially for the LSTM model, were for the close-to-open interval, which captures overnight trading. This interval yielded the highest returns at relatively stable volatility. The fact that LSTM models sequential data with long-term dependencies greatly added to its performance and thus made it robust for any short-term strategy. Our analysis gives more credence to the focus on overnight trading using the 14-day rolling window. It is overnight market movements, caused by events around the world and after-hours trading, that provide lucrative opportunities, which are best captured by the sequential learning capabilities of the LSTM. This should be the interval of focus for traders seeking to maximize returns in a short-term framework with the use of LSTM models.
6.2. Fifty-Day Window
The results for the 50-day window analysis come out mainly for the same-day trading intervals. Again, the LSTM model demonstrated a distinct advantage. This window adaptation provided evidence that the close-to-open interval reaped higher returns than the intra-day open-to-close trade. With the LSTM being capable of predicting overnight price movements more accurately, it turned out to be the most effective model in this type of interval, thereby providing traders an edge to capture the fast changes in price. The results also provide further indication of the higher profit from trading within the overnight session compared to that of an intra-day trade. The inherent volatility during overnight sessions blends very well with LSTM’s capability for adaptation in quick market time alterations. This finding corroborates our belief that global events, together with pre- and after-market hours trading, present an opportunity for traders focused on these aspects by having a great bearing on the Bitcoin price.
6.3. Volatility and Risk Management
Volatility across all intervals exceeds 99 percent, emphasizing the need for careful risk management strategies such as stop-loss orders and portfolio diversification. Despite high volatility, LSTM effectively adapts to patterns, making it a viable model for traders focusing on overnight trading. Its consistent returns across intervals highlight its stability, while CNN and RNN may suit more aggressive strategies. Traders preferring lower volatility can optimize LSTM with risk management tools to balance risk and reward.
7. Why Does LSTM Outperform Other Models? Model Explanation
Although all three deep learning models utilized in this research—CNN, RNN, and LSTM—have been shown to possess time series forecasting abilities, their performances in Bitcoin price prediction were quite different. Among them, LSTM performed better than CNN and conventional RNN models in all time intervals considered, with particular dominance in overnight (close-to-open) and day-by-day intervals. Such superiority is based on both technical mechanisms and quirks of cryptocurrency markets.
7.1. Capturing Long-Term Dependencies
Bitcoin’s price movement is driven by a nonlinear and often unpredictable mix of macroeconomic variables—interest rates, inflation, and regulatory announcements—and shorter-term speculative waves. Traditional RNNs are unable to identify patterns that take place over longer periods because of the vanishing gradient problem. LSTM networks, on the other hand, were particularly built to resolve this problem using memory cells and gates. The architecture allows LSTMs to store and process information from very early events in the past. In Bitcoin prediction, this capability means greater potential for detecting momentum trends that accumulate over a series of trading periods. LSTMs are also capable of learning from responses delayed in time to news and events, a common occurrence in financial markets where large trades or regulatory announcements can influence prices with a lag. LSTMs can also detect and capture recurring temporal patterns, such as weekend effects or day-of-the-week-specific volatility patterns. These abilities render LSTMs highly suitable to pick up on the subtle, time-dependent patterns that are so frequently present in cryptocurrency price information.
7.2. Overnight Interval Sensitivity
One of the most robust results in this research was LSTM’s better performance in the close-to-open (overnight) prediction window for price. This window tends to reflect investor sentiment built up outside regular trading hours based on reactions to global events, policy releases, or after-market earnings releases. LSTM networks, by holding on to the sequential context of past sessions, are more capable of picking up these lagged but influential signals. They can, for instance, pick up on sentiment reversal after markets have closed, along with the carryover impact of past volatility on the opening activity the following day. On the other hand, Convolutional Neural Networks (CNNs) are architecturally limited to brief, local time windows. Although CNNs are very well suited to capture quick changes, e.g., abrupt volatility spikes or trend reversals, their inability to retain temporal memory makes them inefficient at processing price changes developing slowly over a sequence of sessions. As such, their capabilities in capturing the delayed and cumulative character of overnight changes are limited.
7.3. Real-World Implications
Practically, what is most critical to carry forward from this work as traders is that the most potent predictive signals for cryptocurrencies—and, indeed, especially for overnight trading strategies—are not always real-time changes. Instead, they build up cumulatively and need more substantive temporal modeling to identify. LSTM models, by virtue of learning from very long sequences and holding on to useful context, are especially well-suited to capitalize on such trends. Traders who depend on models that consider just the recent price movement, like CNNs, will miss these more subtle but extremely actionable signals and hence have inferior performance in the longer run. Moreover, LSTM’s architecture is also highly similar to how financial markets function in reality. Market dynamics are not just governed by real-time price action but by a complex web of nonlinear interdependencies, lagged responses, and extrinsic influences such as psychological effects, geopolitical events, and global economic trends. The ability of LSTMs to handle and learn from these diverse temporal signals is further evidence of their superiority to other architectures in this domain.
8. Conclusions
Our study shows that the LSTM model is better at predicting the price oscillations of Bitcoin, especially during the overnight trading situation, because this particular time frame comes with much higher volatility than during the daytime periods. Therefore, its ability to understand these patterns sequentially and relatedly provides a powerful ability to spot short-term trends and fluctuations in price-based competitive advantages for traders. Both profitability and maximum drawdown are best when overnight returns data is used and trading is performed overnight.
The LSTM model has shown good short-term forecasting ability by returning higher returns even with a difficult-to-predict market. Strong points of this model in processing time series bring out concealed patterns that enable traders to make data-driven decisions to exploit the market. More interestingly, an application to longer 50-day windows has the potential to smooth out market noise with consistent and stable returns through time. This makes it very versatile for both short-term trading and medium-term investment strategies.
To optimize performance, traders should incorporate risk management strategies such as stop-loss orders, diversification, and position sizing. These measures help to reduce losses while amplifying gains, thereby enhancing the model’s reliability in volatile markets.
The LSTM model, therefore, is balanced and reliable for making one’s way through the intricacies of cryptocurrency markets. It can handle short-term volatility and, at the same time, maintain stability over longer periods, thus proving as an ideal option for traders who are looking to combine profitability with risk management.
Author Contributions
E.P. conceptualization; P.T. and A.J. performed the experiments and analyzed data; P.T. and A.J. writing; E.P. writing and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted without external funding. All study aspects, including design, data collection, analysis, and interpretation, were carried out using the resources available within the authors’ institution.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Conflicts of Interest
We declare that there are no conflicts of interest regarding the publication of this paper.
Appendix A. Detailed
Results for 14-Day Window
Table A1.
CNN model results.
Table A1.
CNN model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 13,651 | 1.34 | 99.6 | −1.06 |
| Open-to-Close | 3 months | 32,220 | 1.28 | 99.4 | −5.80 |
| Close-to-Open | | 15,309 | 1.20 | 99.5 | −1.47 |
| Close-to-Close | | 21,765 | 1.15 | 99.4 | −5.64 |
| Open-to-Close | 6 months | 7362 | 26.27 | 100 | 0.92 |
| Close-to-Open | | 16,007 | 1.54 | 99.5 | −12.04 |
| Close-to-Close | | 10,116 | 1.42 | 99.4 | 0 |
| Open-to-Close | 1 year | 15,298 | 1.30 | 99.3 | 3.80 |
| Close-to-Open | | 14,731 | 17.03 | 100 | −5.24 |
Table A2.
LSTM model results.
Table A2.
LSTM model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 23,760 | 0.94 | 99.4 | 10.42 |
| Open-to-Close | 3 months | 8173 | 1.15 | 99.6 | 0.65 |
| Close-to-Open | | 14,767 | 0.94 | 99.2 | 1.01 |
| Close-to-Close | | 21,873 | 0.92 | 99.1 | −2.51 |
| Open-to-Close | 6 months | 20,282 | 0.88 | 98.9 | −1.62 |
| Close-to-Open | | 8364 | 1.06 | 99.4 | 4.69 |
| Close-to-Close | | 38,578 | 14.14 | 100.3 | 0 |
| Open-to-Close | 1 year | 10,989 | 0.92 | 99.3 | 2.20 |
| Close-to-Open | | 4596 | 6.83 | 99.8 | 8.64 |
Table A3.
RNN model results.
Table A3.
RNN model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 6911 | 19.59 | 99.7 | 6.06 |
| Open-to-Close | 3 months | 16,209 | 32.44 | 100 | 11.34 |
| Close-to-Open | | 23,162 | 21.20 | 99.7 | 15.84 |
| Close-to-Close | | 34,741 | 3.33 | 99.4 | 14.27 |
| Open-to-Close | 6 months | 22,418 | 3.85 | 99.3 | 18.63 |
| Close-to-Open | | 30,402 | 4.61 | 99.6 | 8.93 |
| Close-to-Close | | 25,707 | 6.06 | 100 | 0 |
| Open-to-Close | 1 year | 30,402 | 2.80 | 99.4 | 10.35 |
| Close-to-Open | | 23,162 | 3.03 | 99.1 | 12.48 |
Appendix B. Detailed Results for 50-Day Window
Table A4.
CNN model results.
Table A4.
CNN model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 29,589 | 1.04 | 99.3 | 3.46 |
| Open-to-Close | 3 months | 24,799 | 1.12 | 99.2 | −4.36 |
| Close-to-Open | | 32,113 | 1.08 | 99.1 | 0.73 |
| Close-to-Close | | 14,487 | 1.21 | 99.2 | −2.13 |
| Open-to-Close | 6 months | 12,678 | 1.31 | 99.5 | −10.36 |
| Close-to-Open | | 18,798 | 1.03 | 99.4 | −4.56 |
| Close-to-Close | | 29,056 | 3.63 | 100 | −9.53 |
| Open-to-Close | 1 year | 14,228 | 1.13 | 99 | −5.26 |
| Close-to-Open | | 8663 | 2.05 | 100.4 | −1.75 |
Table A5.
LSTM model results.
Table A5.
LSTM model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 11,532 | 1.36 | 99.2 | 1.59 |
| Open-to-Close | 3 months | 7681 | 1.50 | 99.7 | −3.15 |
| Close-to-Open | | 16,511 | 1.34 | 99.4 | 0.58 |
| Close-to-Close | | 7327 | 1.23 | 99.2 | 0.93 |
| Open-to-Close | 6 months | 24,925 | 1.18 | 99 | 3.87 |
| Close-to-Open | | 13,774 | 1.43 | 99.6 | −2.83 |
| Close-to-Close | | 13,102 | 1.88 | 99.7 | −3.61 |
| Open-to-Close | 1 year | 16,584 | 1.21 | 99.2 | −0.42 |
| Close-to-Open | | 8976 | 1.39 | 99.3 | 0.83 |
Table A6.
RNN model results.
Table A6.
RNN model results.
| Return Period | Interval | Med. Balance | Volatility (%) | MDD (%) | Comp R (%) |
|---|
| Close-to-Close | | 22,247 | 4.99 | 98.5 | 21.60 |
| Open-to-Close | 3 months | 5264 | 7.63 | 99.6 | 32.95 |
| Close-to-Open | | 28,371 | 4.41 | 99.4 | 10.87 |
| Close-to-Close | | 19,247 | 3.03 | 98.5 | 18.69 |
| Open-to-Close | 6 months | 14,228 | 8.82 | 99.3 | 7.40 |
| Close-to-Open | | 5223 | 16.41 | 99.1 | −16.05 |
| Close-to-Close | | 11,174 | 4.64 | 98.5 | 23.21 |
| Open-to-Close | 1 year | 15,897 | 5.74 | 99.2 | 5.06 |
| Close-to-Open | | 9105 | 4.32 | 99.4 | 12.32 |
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 July 2025).
- Yermack, D. Is Bitcoin a Real Currency? An Economic Appraisal. In Handbook of Digital Currency; Academic Press: San Diego, CA, USA, 2015; pp. 31–43. [Google Scholar] [CrossRef]
- Böhme, R.; Christin, N.; Edelman, B.; Moore, T. Bitcoin: Economics, Technology, and Governance. J. Econ. Perspect. 2015, 29, 213–238. [Google Scholar] [CrossRef]
- Dyhrberg, A.H. Hedging capabilities of bitcoin. Is it the virtual gold? Financ. Res. Lett. 2016, 16, 139–144. [Google Scholar] [CrossRef]
- Kristoufek, L. What are the main drivers of the Bitcoin price? Evidence from wavelet coherence analysis. PLoS ONE 2014, 10, e0123923. [Google Scholar] [CrossRef] [PubMed]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- McNally, S.; Roche, J.; Caton, S. Predicting the Price of Bitcoin Using Machine Learning. In Proceedings of the 2018 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, 21–23 March 2018; pp. 339–343. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Borovykh, A.; Bohté, S.M.; Oosterlee, C.W. Conditional Time Series Forecasting with Convolutional Neural Networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Connor, J.T.; Martin, R.D.; Atlas, L.E. Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Netw. 1994, 52, 240–254. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.C.; Sangiorgi, I.; Urquhart, A. Forecasting Bitcoin volatility using machine learning techniques. J. Int. Financ. Mark. Institutions Money 2024, 97, 102064. [Google Scholar] [CrossRef]
- Dyhrberg, A.H. Bitcoin, gold and the dollar—A GARCH volatility analysis. Financ. Res. Lett. 2016, 16, 85–92. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. Asymmetric volatility in cryptocurrencies. Econ. Lett. 2018, 173, 148–151. [Google Scholar] [CrossRef]
- D’Amato, V.; Levantesi, S.; Piscopo, G. Deep learning in predicting cryptocurrency volatility. Phys. A Stat. Mech. Its Appl. 2022, 596, 127158. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).