Leveraging Exogenous Regressors in Demand Forecasting †
Abstract
1. Introduction
2. Materials and Methods
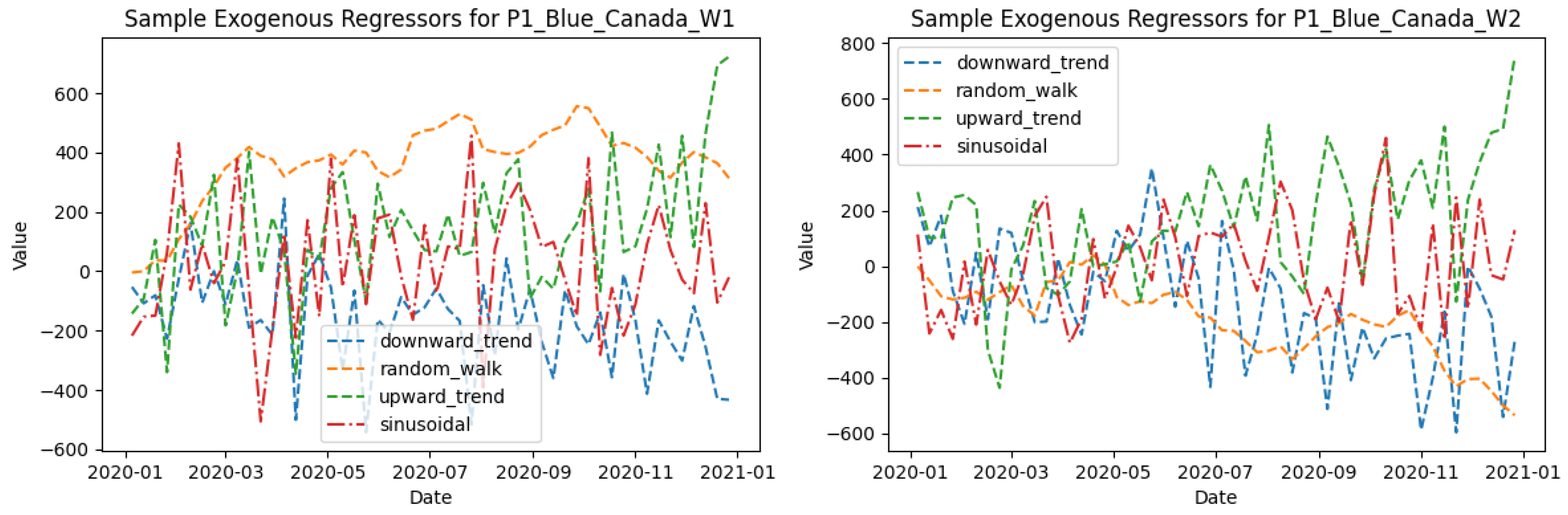
2.1. Dataset Creation
2.2. Dataset: Case Study
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swierczek, A. Investigating the role of demand planning as a higher-order construct in mitigating disruptions in the European supply chains. Int. J. Logist. Manag. 2020; ahead-of-print. [Google Scholar]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural basis expansion analysis with exogenous variables: Forecasting electricity prices with NBEATSx. Int. J. Forecast. 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Ekambaram, V.; Jati, A.; Dayama, P.; Mukherjee, S.; Nguyen, N.H.; Gifford, W.M.; Reddy, C.; Kalagnanam, J. Tiny time mixers (TTMs): Fast pre-trained models for enhanced zero/few-shot forecasting of multivariate time series. arXiv 2024, arXiv:2401.03955. [Google Scholar]
- Alhussein, M.; Aurangzeb, K.; Haider, S.I. Hybrid CNN-LSTM model for short-term individual household load forecasting. IEEE Access 2020, 8, 180544–180557. [Google Scholar] [CrossRef]
- Anggraeni, W.; Vinarti, R.A.; Kurniawati, Y.D. Performance comparisons between ARIMA and ARIMAX method in Moslem kids clothes demand forecasting: Case study. Procedia Comput. Sci. 2015, 72, 630–637. [Google Scholar] [CrossRef]
- Kim, T.Y.; Dekker, R.; Heij, C. Spare part demand forecasting for consumer goods using installed base information. Comput. Ind. Eng. 2017, 103, 201–215. [Google Scholar] [CrossRef]
- Gur Ali, O.; Pinar, E. Multi-period-ahead forecasting with residual extrapolation and information sharing—Utilizing a multitude of retail series. Int. J. Forecast. 2016, 32, 502–517. [Google Scholar] [CrossRef]
- Castilho, C.M. Time Series Forecasting with Exogenous Factors: Statistical vs. Machine Learning Approaches. Master’s Thesis, Universidade do Porto, Porto, Portugal, 2020. AAI30163992. [Google Scholar]
- Lim, B.; Arık, S.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Karim, S.M.A.; Zarrin, B.; Lassen, N. Multivariate Forecasting Evaluation: Nixtla-TimeGPT. In Proceedings of the International Conference on Time Series and Forecasting (ITISE 2025), Gran Canaria, Spain, 16–18 July 2025. (accepted). [Google Scholar]
- pmdarima: ARIMA Estimators for Python. 2017. Available online: http://www.alkaline-ml.com/pmdarima (accessed on 14 April 2025).
- Adhikari, R.; Agrawal, R.K. An introductory study on time series modeling and forecasting. J. Quant. Econ. 2013, 11, 1–15. [Google Scholar]
- Divvy Station Dock Capacity Time Series Forecast. 2022. Available online: https://www.kaggle.com/datasets/leonidasliao/divvy-station-dock-capacity-time-series-forecast (accessed on 1 July 2024).



| 1-Permutation Entropy | Sample Entropy | Autocorrelation | Hurst Exponent | Coefficient of Variation | Predictability Ratio | Dominant Frequency | ARIMA R² Score | |
|---|---|---|---|---|---|---|---|---|
| Sinusoidal | 0.01 | –1.21 | 0.08 | 0.17 | –31.2 | 0.13 | 0.34 | –0.02 |
| Upwards Trend | 0.01 | –0.31 | 0.85 | 0.44 | 0.39 | 0.90 | 0.19 | 0.87 |
| Random Walk | 0.08 | 0.53 | 0.89 | 0.53 | 1.80 | 0.98 | 0.25 | 0.98 |
| Downwards Trend | 0.01 | –0.26 | 0.85 | 0.42 | 1.62 | 0.90 | 0.07 | 0.88 |
| Permutation Entropy | Sample Entropy | Autocorrelation | Hurst Exponent | Coefficient of Variation | Predictability Ratio | Dominant Frequency | ARIMA R2 Score | |
|---|---|---|---|---|---|---|---|---|
| bus | 0.02 | –0.62 | 0.09 | 0.29 | 0.90 | 0.38 | 0.04 | –0.06 |
| bus_train_total_boarding | 0.02 | –0.32 | 0.15 | 0.34 | 0.90 | 0.42 | 0.04 | –0.00 |
| rail_boardings | 0.01 | –0.48 | 0.23 | 0.37 | 0.89 | 0.47 | 0.02 | 0.09 |
| cloudcover | 0.03 | –0.59 | 0.15 | 0.22 | 0.76 | 0.29 | 0.01 | 0.07 |
| dew | 0.02 | –0.29 | 0.61 | 0.37 | 0.54 | 0.88 | 0.02 | 0.78 |
| feelslike | 0.01 | 0.06 | 0.64 | 0.37 | 0.51 | 0.91 | 0.02 | 0.84 |
| sealevelpressure | 0.04 | –1.22 | 0.18 | 0.26 | 1.00 | 0.36 | 0.02 | 0.11 |
| snow | 0.55 | 0.84 | 0.09 | 0.40 | –2.20 | 0.34 | 0.04 | 0.15 |
| snowdepth | 0.56 | 0.90 | 0.08 | 0.41 | –2.70 | 0.34 | 0.04 | 0.23 |
| solarenergy | 0.04 | –0.29 | 0.62 | 0.34 | 0.47 | 0.85 | 0.01 | 0.74 |
| solarradiation | 0.04 | –0.37 | 0.62 | 0.34 | 0.47 | 0.85 | 0.01 | 0.74 |
| temp | 0.01 | 0.03 | 0.64 | 0.37 | 0.62 | 0.91 | 0.02 | 0.85 |
| total_holidays | 0.35 | 0.54 | 0.04 | 0.47 | 0.69 | 0.15 | 0.14 | –0.03 |
| uvindex | 0.04 | –0.23 | 0.62 | 0.34 | 0.46 | 0.86 | 0.01 | 0.75 |
| visibility | 0.01 | –0.22 | 0.16 | 0.30 | 0.90 | 0.39 | 0.98 | 0.06 |
| windgust | 0.01 | –0.80 | 0.21 | 0.17 | 0.43 | 0.36 | 0.01 | 0.13 |
| DATASETS (w. 16 Time Series Each) | Regressor Type | Coefficient | Correlation with Target | MAE After X Forecasted | MAE After X Provided |
|---|---|---|---|---|---|
| Set 1: DT RW UT SS Univariate MAE: 257 | Downward Trend | 1.00 | 0.49 | 414 | 173 |
| Random Walk | 0.75 | 0.85 | 368 | 181 | |
| Upward Trend | 0.50 | –0.37 | 263 | 247 | |
| Set 2: RW DT SS UT Univariate MAE: 409 | Random Walk | 1.00 | 0.94 | 758 | 178 |
| Downward Trend | 0.75 | 0.48 | 527 | 393 | |
| Upward Trend | 0.25 | –0.43 | 758 | 178 | |
| Set 3: SS UT RW DT Univariate MAE: 247 | Sinusoidal | 1.00 | 0.29 | 288 | 249 |
| Upward Trend | 0.75 | 0.23 | 309 | 249 | |
| Random Walk | 0.50 | 0.56 | 298 | 221 | |
| Set 4: UT SS DT RW Univariate MAE: 223 | Upward Trend | 1.00 | 0.97 | 336 | 160 |
| Sinusoidal | 0.75 | –0.92 | 251 | 194 | |
| Set 5: RW DT RW RW Univariate MAE: 409 | Random Walk | 1.00 | 0.84 | 758 | 178 |
| Random Walk | 0.75 | 0.69 | 758 | 178 | |
| Downward Trend | 0.50 | 0.84 | 527 | 393 | |
| Random Walk | 0.25 | 0.97 | 758 | 178 | |
| Set 6: RW RW SS DT Univariate MAE: 356 | Random Walk | 1.00 | 0.97 | 730 | 102 |
| Downward Trend | 0.25 | 0.45 | 409 | 381 | |
| Set 7: SS SS SS SS Univariate MAE: 383 | Sinusoidal | 1.00 | 1.00 | 540 | 16.5 |
| Sinusoidal | 0.75 | 1.00 | 540 | 16.5 | |
| Sinusoidal | 0.50 | 1.00 | 540 | 16.5 | |
| Sinusoidal | 0.25 | 1.00 | 540 | 16.5 | |
| Set 8: UT DT UT DT Univariate MAE: 277 | Upward Trend | 1.00 | 0.91 | 498 | 212 |
| Downward Trend | 0.75 | –0.71 | 346 | 333 | |
| Upward Trend | 0.50 | 0.91 | 498 | 213 | |
| Downward Trend | 0.25 | –0.71 | 346 | 333 | |
| Set 9: UT SS SS DT Univariate MAE: 276 | Sinusoidal | 1.00 | 0.96 | 328 | 202 |
| Sinusoidal | 0.75 | 0.23 | 328 | 193 | |
| Downward Trend | 0.50 | –0.23 | 275 | 193 | |
| Downward Trend | 0.25 | –0.92 | 328 | 206 | |
| Set 10: UT UT RW RW Univariate MAE: 301 | Upward Trend | 1.00 | 0.97 | 644 | 177 |
| Upward Trend | 1.00 | 0.97 | 644 | 177 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karim, S.M.A.; Zarrin, B.; Lassen, N.B. Leveraging Exogenous Regressors in Demand Forecasting. Comput. Sci. Math. Forum 2025, 11, 15. https://doi.org/10.3390/cmsf2025011015
Karim SMA, Zarrin B, Lassen NB. Leveraging Exogenous Regressors in Demand Forecasting. Computer Sciences & Mathematics Forum. 2025; 11(1):15. https://doi.org/10.3390/cmsf2025011015
Chicago/Turabian StyleKarim, S M Ahasanul, Bahram Zarrin, and Niels Buus Lassen. 2025. "Leveraging Exogenous Regressors in Demand Forecasting" Computer Sciences & Mathematics Forum 11, no. 1: 15. https://doi.org/10.3390/cmsf2025011015
APA StyleKarim, S. M. A., Zarrin, B., & Lassen, N. B. (2025). Leveraging Exogenous Regressors in Demand Forecasting. Computer Sciences & Mathematics Forum, 11(1), 15. https://doi.org/10.3390/cmsf2025011015





