A Smart Optimization Model for Reliable Signal Detection in Financial Markets Using ELM and Blockchain Technology
Abstract
1. Introduction
2. Related Works
Problem Description
3. Proposed Methodology
3.1. Data Description
Rationale for Indicator Selection
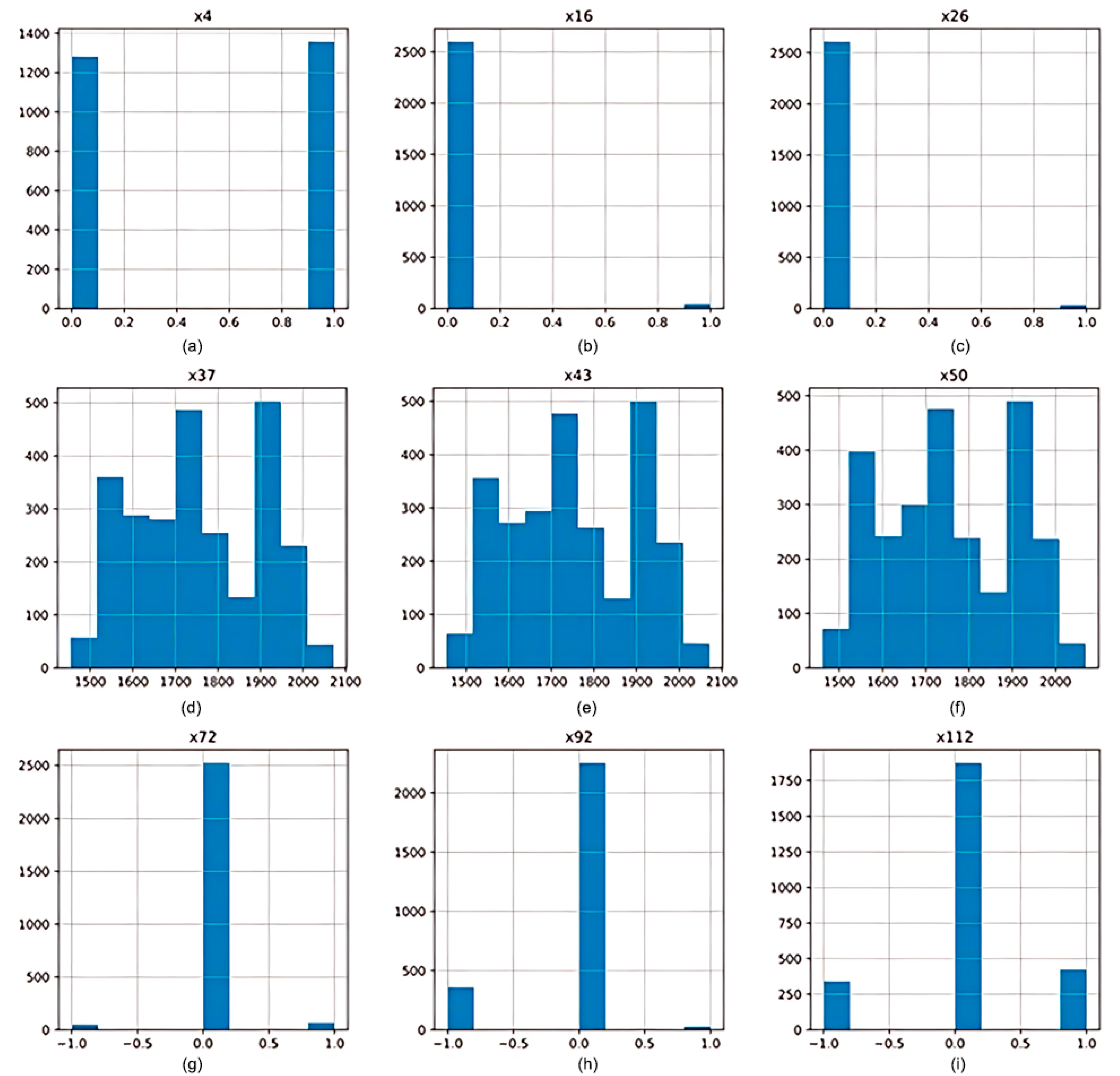
3.2. Data Preprocessing
3.3. Analysis of Indicators
3.3.1. Moving Average Convergence Divergence
3.3.2. Moving Average
3.3.3. Ichimoku
3.4. Classification: PSO-ELM
Blockchain Integration for Secure Signal Dissemination
3.5. Blockchain Registration with Machine Learning
3.6. Data Security for an Unreliable Environment
4. Results and Discussion
4.1. Implementation of Our Prediction Model
4.2. Experiment and Evaluation
4.3. Validation Analysis of Proposed Classifier
4.4. Practical Implications
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mintarya, L.N.; Halim, J.N.; Angie, C.; Achmad, S.; Kurniawan, A. Machine learning approaches in stock market prediction: A systematic literature review. Procedia Comput. Sci. 2023, 216, 96–102. [Google Scholar] [CrossRef]
- Han, C.; Fu, X. Challenge and opportunity: Deep learning-based stock price prediction by using Bi-directional LSTM model. Front. Bus. Econ. Manag. 2023, 8, 51–54. [Google Scholar] [CrossRef]
- Shobha Rani, B.R.; Bharathi, S.; Pareek, P.K.; Dipeeka. Fake Currency Identification System Using Convolutional Neural Network. In Proceedings of the International Conference on Emerging Research in Computing, Information, Communication and Applications, Bangalore, India, 24–25 February 2023; Springer Nature: Singapore, 2023; pp. 431–443. [Google Scholar]
- Sonkavde, G.; Dharrao, D.S.; Bongale, A.M.; Deokate, S.T.; Doreswamy, D.; Bhat, S.K. Forecasting stock market prices using machine learning and deep learning models: A systematic review, performance analysis and discussion of implications. Int. J. Financ. Stud. 2023, 11, 94. [Google Scholar] [CrossRef]
- Yun, K.K.; Yoon, S.W.; Won, D. Interpretable stock price forecasting model using genetic algorithm-machine learning regressions and best feature subset selection. Expert Syst. Appl. 2023, 213, 118803. [Google Scholar] [CrossRef]
- Zhang, E.; Zhang, X.; Pareek, P.K. Herd effect analysis of stock market based on big data intelligent algorithm. In Proceedings of the International Conference on Cyber Security Intelligence and Analytics, Shanghai, China, 30–31 March 2023; Springer Nature: Cham, Switzerland, 2023; pp. 129–139. [Google Scholar]
- Sheth, D.; Shah, M. Predicting stock market using machine learning: Best and accurate way to know future stock prices. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 1–18. [Google Scholar] [CrossRef]
- Habib, H.; Kashyap, G.S.; Tabassum, N.; Tabrez, N. Stock price prediction using artificial intelligence based on LSTM–deep learning model. In Artificial Intelligence & Blockchain in Cyber Physical Systems; CRC Press: Boca Raton, FL, USA, 2023; pp. 93–99. [Google Scholar]
- Zhao, Y.; Yang, G. Deep Learning-based Integrated Framework for stock price movement prediction. Appl. Soft Comput. 2023, 133, 109921. [Google Scholar] [CrossRef]
- Rao, S.S.; Pareek, P.K.; Vishwanatha, C.R.; Bhardwaj, A.K. Prediction of Technical Indicators for Stock Markets using HPO-CCOA Based Machine Learning Algorithm. In Proceedings of the 2023 International Conference on Evolutionary Algorithms and Soft Computing Techniques (EASCT), Bengaluru, India, 20–21 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Mukherjee, S.; Sadhukhan, B.; Sarkar, N.; Roy, D.; De, S. Stock market prediction using deep learning algorithms. CAAI Trans. Intell. Technol. 2023, 8, 82–94. [Google Scholar] [CrossRef]
- Aluvalu, R.; Sharma, T.; Viswanadhula, U.M.; Thirumalraj, A.D.; Prasad Kantipudi, M.V.V.; Mudrakola, S. Komodo Dragon Mlipir Algorithm-based CNN Model for Detection of Illegal Tree Cutting in Smart IoT Forest Area. Recent Adv. Comput. Sci. Commun. (Former. Recent Pat. Comput. Sci.) 2024, 17, 1–12. [Google Scholar] [CrossRef]
- Behera, J.; Pasayat, A.K.; Behera, H.; Kumar, P. Prediction based mean-value-at-risk portfolio optimization using machine learning regression algorithms for multi-national stock markets. Eng. Appl. Artif. Intell. 2023, 120, 105843. [Google Scholar] [CrossRef]
- Muhammad, T.; Aftab, A.B.; Ibrahim, M.; Ahsan, M.M.; Muhu, M.M.; Khan, S.I.; Alam, M.S. Transformer-based deep learning model for stock price prediction: A case study on Bangladesh stock market. Int. J. Comput. Intell. Appl. 2023, 22, 2350013. [Google Scholar] [CrossRef]
- Ashtiani, M.N.; Raahemi, B. News-based intelligent prediction of financial markets using text mining and machine learning: A systematic literature review. Expert Syst. Appl. 2023, 217, 119509. [Google Scholar] [CrossRef]
- Khan, R.H.; Miah, J.; Rahman, M.M.; Hasan, M.M.; Mamun, M. A study of forecasting stocks price by using deep Reinforcement Learning. In Proceedings of the 2023 IEEE World AI IoT Congress (AIIoT), Seattle, WA, USA, 7–10 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 0250–0255. [Google Scholar]
- Khattak, B.H.A.; Shafi, I.; Rashid, C.H.; Safran, M.; Alfarhood, S.; Ashraf, I. Profitability trend prediction in crypto financial markets using Fibonacci technical indicator and hybrid CNN model. J. Big Data 2024, 11, 58. [Google Scholar] [CrossRef]
- Fauzan, Z.T.; Barrelvi, I.P. The Impact Of Blockchain Technology On Capital Market Transparency And Security. J. Ekon. 2024, 13, 1241–1248. [Google Scholar]
- Li, Z.; Liang, X.; Wen, Q.; Wan, E. The Analysis of Financial Network Transaction Risk Control based on Blockchain and Edge Computing Technology. IEEE Trans. Eng. Manag. 2024, 71, 5669–5690. [Google Scholar] [CrossRef]
- Tong, Z.; Hu, Y.; Jiang, C.; Zhang, Y. User financial credit analysis for blockchain regulation. Comput. Electr. Eng. 2024, 113, 109008. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, J.; Zhang, G. Blockchain-driven operation strategy of financial supply chain under uncertain environment. Int. J. Prod. Res. 2024, 62, 2982–3002. [Google Scholar] [CrossRef]
- Nguyen, T.H. et al. GWO-Enhanced Hybrid Deep Learning with SHAP for Explainable. GWO-Enhanced Hybrid Deep Learning with SHAP for Explainable. 2024. Available online: https://jutif.if.unsoed.ac.id/index.php/jurnal/article/download/5205/949 (accessed on 1 September 2025).
- Chio, P.T. A comparative study of the MACD-base trading strategies: Evidence from the US stock market. arXiv 2022, arXiv:2206.12282. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, J.; Wang, Y. Optimizing MACD Trading Strategies A Dance of Finance, Wavelets, and Genetics. arXiv 2025, arXiv:2501.10808. [Google Scholar] [CrossRef]
- Gurrib, I.; Kamalov, F.; Elshareif, E. Can the leading US energy stock prices be predicted using the Ichimoku cloud? Int. J. Energy Econ. Policy 2020, 11, 41–51. [Google Scholar] [CrossRef]
- Mousapour Mamoudan, M.; Ostadi, A.; Pourkhodabakhsh, N.; Fathollahi-Fard, A.M.; Soleimani, F. Hybrid neural network-based metaheuristics for prediction of financial markets: A case study on global gold market. J. Comput. Des. Eng. 2023, 10, 1110–1125. [Google Scholar] [CrossRef]
- Agudelo Aguirre, A.A.; Duque Méndez, N.D.; Rojas Medina, R.A. Artificial intelligence applied to investment in variable income through the MACD (moving average convergence/divergence) indicator. J. Econ. Financ. Adm. Sci. 2021, 26, 268–281. [Google Scholar] [CrossRef]
- Deng, S.; Yu, H.; Wei, C.; Yang, T.; Tatsuro, S. The profitability of Ichimoku Kinkohyo based trading rules in stock markets and FX markets. Int. J. Financ. Econ. 2021, 26, 5321–5336. [Google Scholar] [CrossRef]
- Thirumalraj, A.; Chandrashekar, R.; Gunapriya, B.; Kavin Balasubramanian, P. NMRA-Facilitated Optimized Deep Learning Framework: A Case Study on IoT-Enabled Waste Management in Smart Cities. In Developments Towards Next Generation Intelligent Systems for Sustainable Development; IGI Global: Hershey, PA, USA, 2024; pp. 247–268. [Google Scholar]

| Indicator | Mean | Standard Deviation | Min | Max | Valid Signals (%) | False Signals (%) |
|---|---|---|---|---|---|---|
| MACD Histogram | 0.15 | 0.25 | −1.2 | 1.5 | 60 | 40 |
| Fast-Moving Average (EMA9) | 1.2 | 0.35 | 0.5 | 2 | 65 | 35 |
| Slow-Moving Average (EMA21) | 1.5 | 0.4 | 0.7 | 2.4 | 70 | 30 |
| Ichimoku Tenkan-sen | 1.1 | 0.3 | 0.8 | 1.7 | 55 | 45 |
| Ichimoku Kijun-sen | 1.2 | 0.25 | 0.9 | 1.8 | 60 | 40 |
| Ichimoku Span A | 1.05 | 0.3 | 0.7 | 2 | 62 | 38 |
| Ichimoku Span B | 1.3 | 0.32 | 0.9 | 2.1 | 58 | 42 |
| ELM | PSO | ||
|---|---|---|---|
| Parameters | Values | Parameters | Values |
| Output neurons | Class values | Best particle positions. | |
| Activation function | Sigmoid | Best site of all particles. | |
| P | Input weights in addition to biases | Population (particles) | Contains sites then velocities. |
| Β | Output weightiness | Positions | Produced at accidental initially, with input weights ranging within [−1, 1] and biases within [0, 1]. |
| Input weights | In the range of [−1, 1] | Velocity | Start with zero standards, limited to the range of [−2, 2] |
| Bias values | In the range of [0, 1] | Z | 50 |
| Input neuron quantities (n) | Input attributes | 0.7289, 1.496, 1.496 | |
| Hidden neuron number (L) | 100–600, with 50 augmentation steps | 100 | |
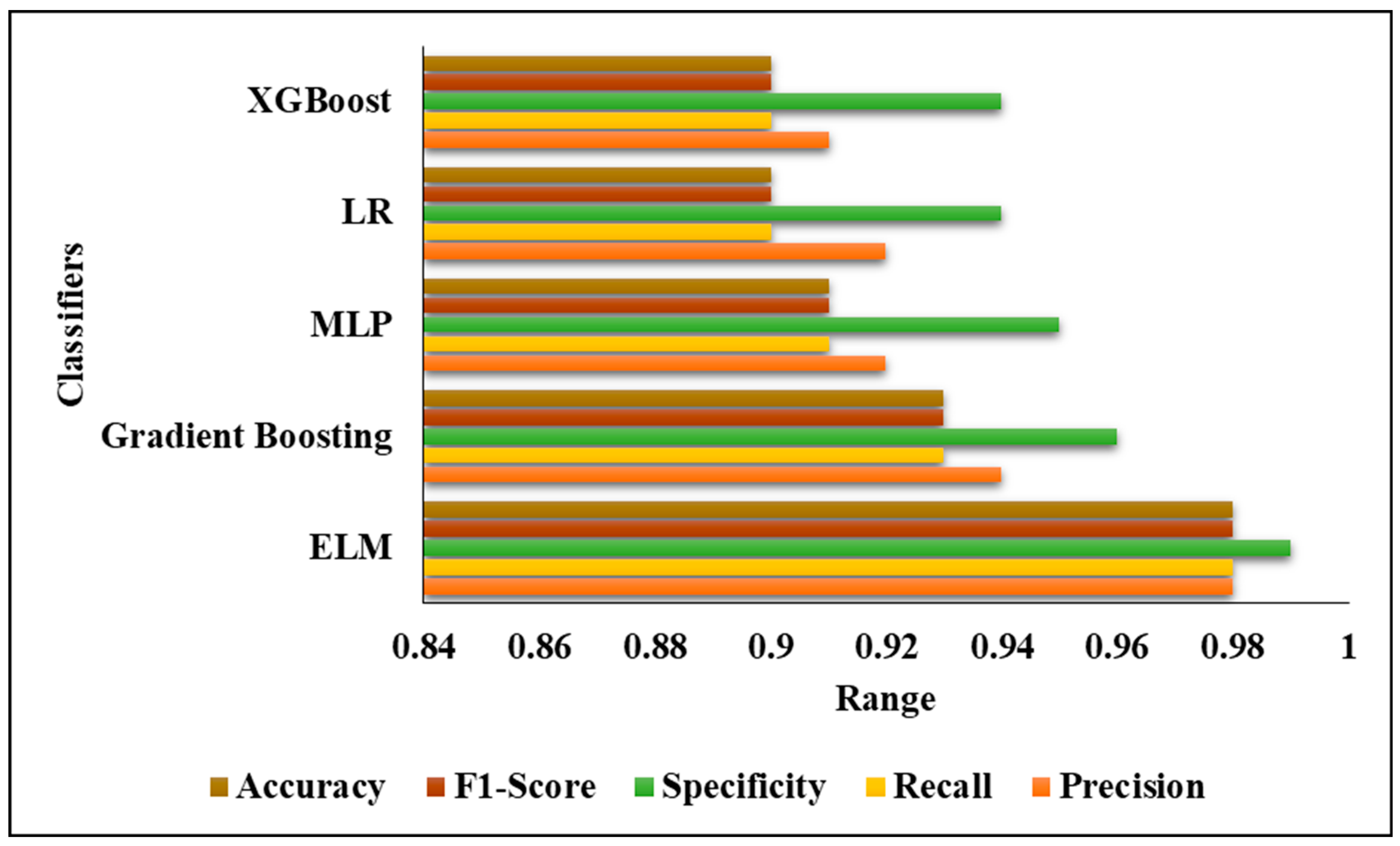
| Classifier | Precision | Recall | Specificity | F1-Score | Accuracy |
|---|---|---|---|---|---|
| ELM | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 |
| Gradient Boosting | 0.94 | 0.93 | 0.96 | 0.93 | 0.93 |
| MLP | 0.92 | 0.91 | 0.95 | 0.91 | 0.91 |
| LR | 0.92 | 0.90 | 0.94 | 0.90 | 0.90 |
| XGBoost | 0.91 | 0.90 | 0.94 | 0.90 | 0.90 |
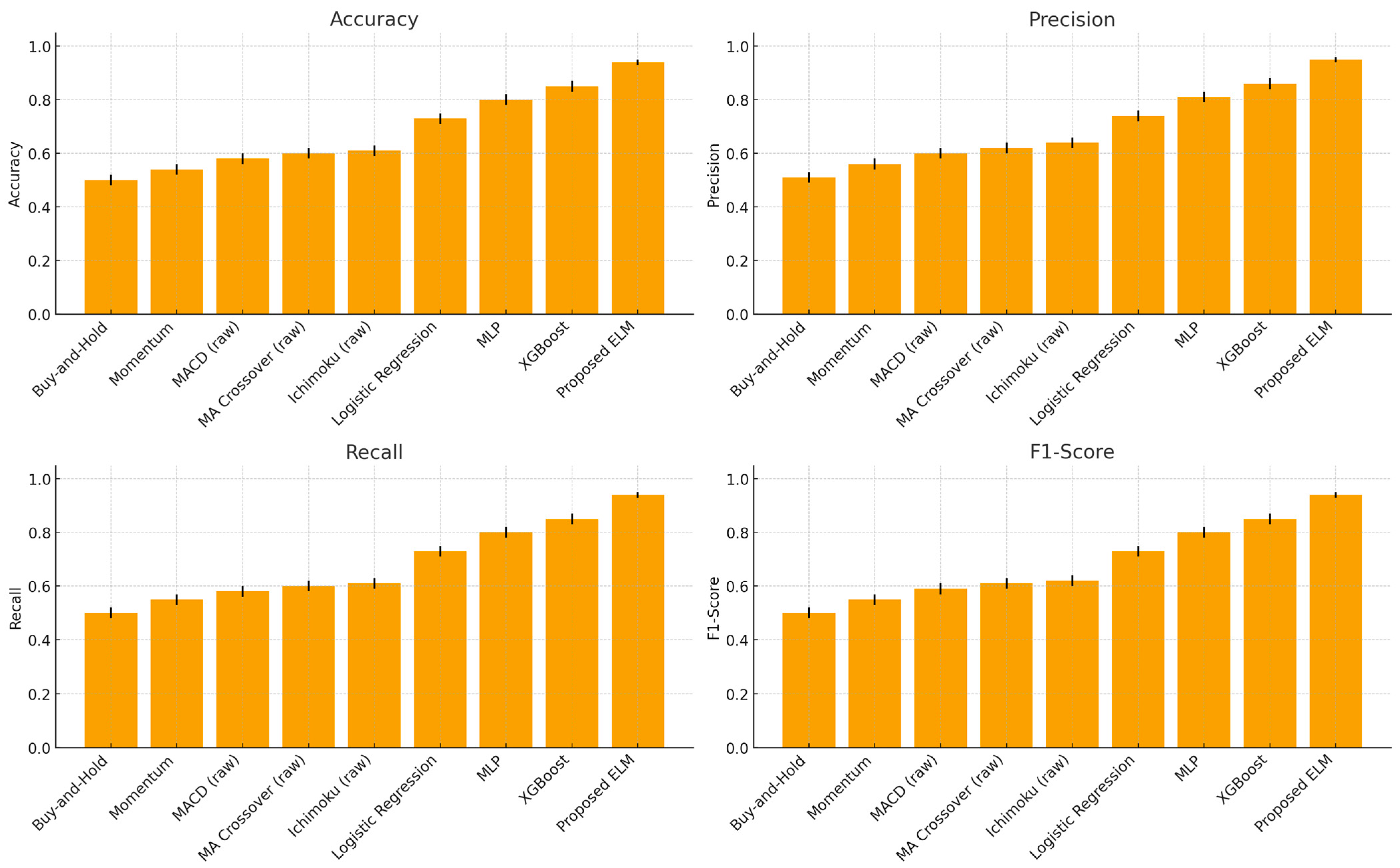
| Method | Precision | Recall | Specificity | F1-Score | Accuracy |
|---|---|---|---|---|---|
| Buy-and-Hold (naïve) | 0.51 | 0.50 | 0.50 | 0.50 | 0.50 |
| Momentum Rule | 0.56 | 0.55 | 0.52 | 0.55 | 0.54 |
| MACD Signal (raw) | 0.60 | 0.58 | 0.57 | 0.59 | 0.58 |
| MA Crossover (raw) | 0.62 | 0.60 | 0.58 | 0.61 | 0.60 |
| Ichimoku Cloud (raw) | 0.64 | 0.61 | 0.60 | 0.62 | 0.61 |
| Logistic Regression (LR) | 0.74 | 0.73 | 0.72 | 0.73 | 0.73 |
| Multilayer Perceptron (MLP) | 0.81 | 0.80 | 0.79 | 0.80 | 0.80 |
| XGBoost | 0.86 | 0.85 | 0.84 | 0.85 | 0.85 |
| Proposed Optimizer + ELM | 0.96 | 0.96 | 0.98 | 0.96 | 0.96 |
| Optimizer | Precision | Recall | Specificity | F1-Score | Accuracy |
|---|---|---|---|---|---|
| PSO | 0.96 | 0.96 | 0.98 | 0.96 | 0.96 |
| GWO | 0.95 | 0.95 | 0.97 | 0.95 | 0.95 |
| ACO | 0.93 | 0.92 | 0.95 | 0.92 | 0.93 |
| BOA | 0.91 | 0.91 | 0.96 | 0.91 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, D.; Pawar, P.P.; Addula, S.R.; Meesala, M.K.; Oni, O.; Cheema, Q.N.; Haq, A.U. A Smart Optimization Model for Reliable Signal Detection in Financial Markets Using ELM and Blockchain Technology. FinTech 2025, 4, 56. https://doi.org/10.3390/fintech4040056
Kumar D, Pawar PP, Addula SR, Meesala MK, Oni O, Cheema QN, Haq AU. A Smart Optimization Model for Reliable Signal Detection in Financial Markets Using ELM and Blockchain Technology. FinTech. 2025; 4(4):56. https://doi.org/10.3390/fintech4040056
Chicago/Turabian StyleKumar, Deepak, Priyanka Pramod Pawar, Santosh Reddy Addula, Mohan Kumar Meesala, Oludotun Oni, Qasim Naveed Cheema, and Anwar Ul Haq. 2025. "A Smart Optimization Model for Reliable Signal Detection in Financial Markets Using ELM and Blockchain Technology" FinTech 4, no. 4: 56. https://doi.org/10.3390/fintech4040056
APA StyleKumar, D., Pawar, P. P., Addula, S. R., Meesala, M. K., Oni, O., Cheema, Q. N., & Haq, A. U. (2025). A Smart Optimization Model for Reliable Signal Detection in Financial Markets Using ELM and Blockchain Technology. FinTech, 4(4), 56. https://doi.org/10.3390/fintech4040056







