AI Driven Fiscal Risk Assessment in the Eurozone: A Machine Learning Approach to Public Debt Vulnerability

Abstract

This study applied supervised machine learning algorithms to macro-fiscal panel data from 20 EU member states (2000–2024) to model and predict fiscal stress episodes in the Eurozone. Conventional frameworks for assessing public debt sustainability often rely on static thresholds and linear dynamics, limiting their ability to capture the complex, non-linear interactions in fiscal data. To address this, we implemented logistic regression, support vector machines, and XGBoost classifiers using core fiscal indicators such as debt-to-GDP ratio, primary balance, GDP growth, interest rates, and inflation. The models were evaluated using time-aware cross-validation, with XGBoost delivering the highest predictive accuracy but showing some signs of overfitting. We highlighted the interpretability of logistic regression and applied SHAP values to enhance transparency in the tree-based models. While limited by using annual data, we discuss the potential value of incorporating real-time or high-frequency fiscal indicators. Our results underscore the practical relevance of AI-enhanced early warning systems for fiscal surveillance and support their integration into institutional monitoring frameworks.

1. Introduction

Rising public debt and persistent fiscal fragility across Eurozone economies have reignited concerns over sovereign risk and long-term fiscal sustainability. Despite periods of consolidation following the global financial crisis and the COVID-19 pandemic, debt-to-GDP ratios remain elevated in many member states, particularly France, Italy, and Belgium [1]. Structural vulnerabilities—such as aging populations, weak growth, and rising debt service costs—exacerbate fiscal pressures, limiting governments’ room for maneuver [2]. Recent warnings by the ECB highlight the mounting risks posed by the intersection of high debt levels, tightening financial conditions, and sluggish economic momentum [1].

Traditional fiscal risk frameworks—such as the European Commission’s S0/S1 indicators and the IMF’s Debt Sustainability Analysis—rely on backward-looking, rule-based diagnostics that often fail to capture non-linear dynamics or real-time shocks [3,4]. These approaches assume stable policy behavior and typically omit interactions among macro-fiscal variables, reducing their predictive value during periods of stress [5]. As such, there is growing recognition that new tools are needed, ones that combine theoretical coherence with empirical flexibility.

In this context, artificial intelligence (AI) and machine learning (ML) provide a promising foundation for modern fiscal surveillance. Ensemble classifiers like XGBoost and interpretable models such as regularized logistic regression can detect complex interactions in high-dimensional fiscal data and provide early warnings of sovereign stress [5,6]. However, most existing studies either adopt a purely data-driven focus or apply these tools outside structured public finance frameworks. Few integrate machine learning models with theoretical constructs such as the intertemporal budget constraint (IBC) or fiscal reaction functions. Moreover, real-time fiscal inputs, e.g., high-frequency expenditure data or interest rate shock remain underutilized [7,8].

This study proposes a hybrid framework that anchors ML-based fiscal risk prediction in economic theory while preserving interpretability and policy relevance. Using harmonized panel data from 20 Eurozone countries (2000–2024), we implemented and compared three supervised models—logistic regression, XGBoost and support vector machines (SVM)—to classify fiscal stress based on macro-fiscal indicators. Beyond evaluating predictive performance, we assessed the transparency and operational relevance of these models using explainable AI tools and out-of-sample validation. Our contributions are threefold: (1) we quantified the marginal value of ML models in detecting fiscal stress; (2) we grounded predictions in fiscal sustainability theory; and (3) we identified methodological pitfalls in applying AI tools to temporal macroeconomic data. Together, these advances aim to inform institutional use of AI-enhanced early warning systems in sovereign risk monitoring.

2. Literature Review

2.1. Theoretical Review

This study is grounded in the IBC, a foundational concept in public finance that stipulates a government must generate sufficient future primary surpluses to service and stabilize its existing debt stock. Formally,

$$\sum _{\mathrm{t}=0}^{\infty }{\displaystyle \frac{{\mathrm{PB}}_{\mathrm{t}}}{{\left(1+\mathrm{r}\right)}^{\mathrm{t}}}}\ge \mathrm{Initial}\mathrm{Debt}$$

where ${\mathrm{P}\mathrm{B}}_{\mathrm{t}}$ is the primary balance and r is the real interest rate. The IBC requires that the present value of future primary balances offsets current public debt obligations, ensuring that fiscal policy remains solvent over time. A violation of this condition implies a risk of unsustainable debt accumulation, fiscal distress, or eventual default.

Building on this foundation, we adopt the fiscal reaction function framework proposed by [9], which provides an empirical test for sustainability. In this framework, a government is said to follow a sustainable fiscal policy if it systematically adjusts its primary balance in response to rising public debt levels. Specifically, a positive and statistically significant response from the primary balance to lagged debt is as follows:

$${\mathrm{PB}}_{\mathrm{it}}={\mathrm{\alpha }}_{\mathrm{i}}+\mathrm{\beta }.{\mathrm{Debt}}_{\mathrm{it}-1}+\mathrm{\gamma }{\mathrm{X}}_{\mathrm{it}}+{\mathrm{\epsilon }}_{\mathrm{it}}$$

where $\mathrm{\beta }>0$ indicates sustainable policy (governments adjust their primary balance in response to debt). Conversely, a weak or negative response may indicate fiscal fatigue, institutional constraints, or political unwillingness to consolidate. In this case, $X_{it}$ refers to the set of macro-fiscal control variables included in the empirical specification—specifically, real GDP growth, inflation, and long-term interest rates.

This framework is well-suited to machine learning extensions, as it allows for the estimation of complex, nonlinear relationships between fiscal indicators and the risk of unsustainable debt. Our study leverages this structure to evaluate fiscal behavior across Eurozone countries using AI-driven models, while remaining anchored in economic theory. By doing so, we bridge the gap between predictive performance and theoretical coherence, enabling the development of policy-relevant early warning systems for fiscal sustainability.

The framework in Figure 1 outlines an AI/ML-based approach to predict fiscal stress, grounded in fiscal theory [9]. It uses fiscal indicators (e.g., debt, government balance, spreads) as predictors in models like logistic regression, XGBoost, and SVM for binary classification (stress vs. no stress). Model performance is evaluated using metrics (AUC, F1-score, etc.) and SHAP values for interpretability. The goal is to support early warning systems and fiscal policy interventions.

2.2. Empirical Review

Recent empirical studies on fiscal sustainability and sovereign risk prediction reveal a growing reliance on machine learning (ML) and artificial AI techniques to enhance predictive accuracy. A significant portion of the literature focuses on the Eurozone, where persistent debt concerns have spurred interest in early warning systems. Studies such as [6,10] demonstrate that ML models—including gradient boosting and support vector machines—outperform traditional econometric methods in identifying fiscal stress and predicting sovereign credit events. Similarly, Ref. [11] confirmed the effectiveness of ML approaches in forecasting fiscal crises, particularly in emerging and developing economies.

Several recent contributions underscore the potential of AI models to complement or surpass institutional benchmarks. Ref. [10] evaluated multiple algorithms—such as classification trees and neural networks—to predict sovereign credit ratings, finding substantial performance gains relative to macro-based scorecards. Ref. [12] expanded the scope by integrating ESG factors into sovereign credit risk models using explainable AI techniques, signaling a shift toward sustainability-informed fiscal surveillance. Furthermore, ref. [13] provided a systematic review of ML applications in financial risk management, highlighting the rapid methodological advances applicable to public finance. Ref. [14] advocated for explainable ML models in fiscal risk settings, showing that transparency can be preserved without sacrificing predictive power. Refs. [5,9] emphasized the centrality of debt dynamics and interest-growth differentials in shaping sovereign vulnerabilities. These findings resonate with the work of [5] who showed that gradient-boosted tree models predict sovereign stress more reliably than structural balance rules or traditional credit ratings.

Deep learning approaches also expand the frontier. Ref. [15] illustrate how recurrent neural networks and LSTMs can capture complex temporal dependencies in fiscal indicators and market data—offering dynamic, real-time risk signals. However, several limitations persist. Many models are trained on retrospective macroeconomic indicators, reducing their utility in fast-evolving fiscal environments. As noted by [5], the absence of high-frequency inputs, such as monthly budget execution or sovereign CDS spreads, constrain responsiveness and leads to lagged policy reactions.

Moreover, while AI models offer superior out-of-sample accuracy, they often lack policy interpretability. Few studies have explicitly linked predictive outputs to actionable fiscal levers, which is essential for real-world decision-making [16,17] responded to this challenge by employing explainable machine learning tools, yet these approaches remain underutilized in sovereign risk modeling. Lastly, integration between formal debt sustainability analysis (DSA) frameworks and ML techniques remains limited. Most studies treat AI tools as black-box classifiers, rather than embedding them in structured economic diagnostics.

This study addresses these gaps by proposing a hybrid framework that blends theory-based fiscal sustainability principles with AI-driven forecasting. It incorporates explainable ML techniques and explores the feasibility of integrating real-time fiscal signals—such as budget volatility and interest rate shocks—into sovereign risk assessments. In doing so, it offers both technical advances and practical value for fiscal surveillance in the Eurozone and beyond.

3. Materials and Methods

3.1. Data and Variables

This study utilized data drawn from the Global Macro Database compiled by [18], a comprehensive resource that integrates macroeconomic indicators from internationally recognized institutions, including the International Monetary Fund (IMF), the World Bank, and the Organization for Economic Co-operation and Development (OECD). The database offers harmonized annual panel data covering a broad spectrum of fiscal, monetary, and real sector variables. By standardizing disparate national data, it ensures comparability across countries and over time, thereby enabling robust empirical analysis. The dataset spans the period from 2000 to the most recent available year, allowing for the examination of both long-term trends and short-term fluctuations in macroeconomic performance. This study specifically focused on Eurozone countries, covering the 2000–2024 period. The primary analytical focus lies in assessing fiscal stress and public debt sustainability, using a selected subset of variables from the database that are particularly relevant for evaluating the fiscal position of governments (

Table 1. Description and Measurement of Key Macroeconomic Variables Used to Assess Fiscal Stress and Public Debt Sustainability in Eurozone Countries (2000–2024).

Variable	Description	Measurement
govbal	The general government balance reflects the difference between total government revenues and expenditures, indicating the fiscal stance. A surplus suggests fiscal consolidation, while a deficit may point to expansionary fiscal policy.	% of GDP
govdebt_lag	Lagged gross government debt represents the total outstanding debt of the government from the previous period, serving as a stock variable influencing current fiscal decisions and interest obligations.	Local currency
gdp_growth	Real GDP growth rate measures the annual percentage increase in the value of all goods and services produced, adjusted for inflation, indicating economic performance.	%
ltrate	Long-term interest rate denotes the yield on government bonds with extended maturities, reflecting investor expectations about future inflation and economic conditions, and influencing debt servicing costs.	%
inflation	The inflation rate, often measured by the Consumer Price Index (CPI), tracks the average change over time in the prices paid by consumers for a basket of goods and services, affecting purchasing power and monetary policy.	%

). These include government balance, debt levels, economic growth, interest rates, and inflation—core indicators in debt sustainability frameworks employed by institutions such as the IMF and the European Commission.

To enhance transparency, we report that the final dataset contains 600 country-year observations after data cleaning and imputation. Descriptive statistics for each variable, including means, standard deviations, and missingness rates, are now provided. To address class imbalances, we applied the Synthetic Minority Oversampling Technique (SMOTE) [19] to augment the training data, ensuring more stable and reliable model performance across all classifiers.

3.2. Methodology

We selected logistic regression, XGBoost, and support vector machines (SVM) based on their complementary strengths in classification tasks. Logistic regression serves as a transparent and interpretable baseline, appropriate for benchmarking and theoretical alignment. XGBoost was chosen for its ability to model complex, nonlinear interactions and its strong empirical performance in similar applications. SVM, using a radial basis function (RBF) kernel, was included to test robustness in capturing nonlinear patterns in macro-fiscal data. Hyperparameters for each model were tuned via grid search: C and γ for SVM, and learning rate, tree depth, and boosting rounds for XGBoost. We acknowledge that other models such as LightGBM or generalized additive models (GAMs) could be explored in future work. This methodological combination aims to balance interpretability, flexibility, and performance, ensuring robustness across model types.

We began by preparing a panel dataset of 20 Eurozone countries spanning 2000–2024. All numeric variables were standardized to mean zero and unit variance to ensure comparability across features and models. Feature engineering included lagged fiscal indicators, debt-to-GDP growth rates, and macro-volatility metrics. Fiscal stress was operationalized as a binary outcome based on threshold breaches (e.g., primary balance deficits >5% of GDP or debt surges > 90th percentile). This approach was used because binary operationalization simplifies classification tasks in predictive modeling. Threshold breaches (e.g., large deficits or extreme debt levels) are empirically associated with heightened default or crisis risk [20]. By converting fiscal stress into a 0–1 outcome, machine learning classifiers (e.g., logistic regression) can more effectively detect patterns and estimate probabilities of stress episodes across countries and time. It also aligns with early warning systems used by institutions like the IMF and EC, which rely on rule-based alerts triggered by extreme indicator values.

We estimated the baseline using a logistic regression model defined as follows:

$$\mathrm{Pr}\left({\mathrm{Stress}}_{\mathrm{it}}=1\right)={\displaystyle \frac{1}{1+{\mathrm{e}}^{\left(-\left({\mathrm{\alpha }}_{\mathrm{i}}+{\mathrm{\beta }}_1{\mathrm{Debt}}_{\mathrm{it}-1}+{\mathrm{\beta }}_2{\mathrm{PB}}_{\mathrm{it}}+{\mathrm{\beta }}_3{\mathrm{GDPGrowth}}_{\mathrm{it}}+{\mathrm{\beta }}_4{\mathrm{Inflation}}_{\mathrm{it}}+{\mathrm{\beta }}_5{\mathrm{LTRate}}_{\mathrm{it}}\right)\right)}}}$$

where ${\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{i}\mathrm{t}}=1$ if country i at time t is under fiscal stress; ${\mathrm{P}\mathrm{B}}_{\mathrm{i}\mathrm{t}}$ = primary balance (% of GDP); ${\mathrm{Debt}}_{\mathrm{it}-1}$ is the lagged government debt (% of GDP); and ${\mathrm{I}\mathrm{n}\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{\mathrm{i}\mathrm{t}}$ and ${\mathrm{L}\mathrm{T}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}}_{\mathrm{i}\mathrm{t}}$ are macroeconomic controls. Tree-based models minimize the classification error via ensemble learning. The general prediction function is as follows:

$${\widehat{\mathrm{y}}}_{\mathrm{it}}=\sum _{\mathrm{m}=1}^{\mathrm{M}}{\mathrm{\gamma }}_{\mathrm{m}}{\mathrm{h}}_{\mathrm{m}}\left({\mathrm{X}}_{\mathrm{it}}\right)$$

where ${\mathrm{h}}_{\mathrm{m}}$ is the ${\mathrm{m}}_{\mathrm{t}\mathrm{h}}$ decision tree, ${\mathrm{\gamma }}_{\mathrm{m}}$ are weights assigned to each tree (learned in boosting), and ${\mathrm{X}}_{\mathrm{it}}$ is the vector input of features for country $\mathrm{i}$ at time $\mathrm{t}.$

For XGBoost, we minimized the regularized loss with the following:

$$\mathrm{L}\left(\mathrm{\phi }\right)=\sum \mathrm{l}\left({\mathrm{y}}_{\mathrm{it}},{\widehat{\mathrm{y}}}_{\mathrm{it}}\right)+\sum \mathrm{\Omega }\left({\mathrm{h}}_{\mathrm{m}}\right)\mathrm{with}\Omega \left(h_m\right)={\gamma }_T+{\displaystyle \frac{1}{2}}\lambda \sum w_{j^2}$$

where $\mathcal{l}$ is the log-loss and $\mathrm{\Omega }$ is the regularization term penalizing tree complexity. To capture sequential dependencies, we applied an LSTM network, where updates are defined by the following equations:

$$\begin{array}{cc}{\mathrm{f}}_{\mathrm{t}}=\mathrm{\sigma }\left({\mathrm{W}}_{\mathrm{f}}.\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]\right)+{\mathrm{b}}_{\mathrm{f}})& \left(\mathrm{forget}\mathrm{state}\right)\end{array}$$

$$\begin{array}{cc}{\mathrm{i}}_{\mathrm{t}}=\mathrm{\sigma }\left({\mathrm{W}}_{\mathrm{i}}.\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right])+{\mathrm{b}}_{\mathrm{i}}\right)& \left(\mathrm{input}\mathrm{gate}\right)\end{array}$$

$$\begin{array}{cc}{\stackrel{\mathrm{~}}{\mathrm{C}}}_{\mathrm{t}}=\tan \mathrm{h}\left({\mathrm{W}}_{\mathrm{C}}-\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right])+{\mathrm{b}}_{\mathrm{C}}\right)& \left(\mathrm{candidate}\mathrm{memory}\right)\end{array}$$

$$\begin{array}{cc}{\mathrm{C}}_{\mathrm{t}}={\mathrm{f}}_{\mathrm{t}}*{\mathrm{C}}_{\mathrm{t}-1}+{\mathrm{i}}_{\mathrm{t}}*{\stackrel{\mathrm{~}}{\mathrm{C}}}_{\mathrm{t}}& \left(\mathrm{cell}\mathrm{state}\mathrm{update}\right)\end{array}$$

$$\begin{array}{cc}{\mathrm{O}}_{\mathrm{t}}=\mathrm{\sigma }({\mathrm{W}}_0.\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{o}}& \left(\mathrm{output}\mathrm{gate}\right)\end{array}$$

$${\mathrm{h}}_{\mathrm{t}}={\mathrm{o}}_{\mathrm{t}}\tan \mathrm{h}\left({\mathrm{C}}_{\mathrm{t}}\right)$$

where ${\mathrm{x}}_{\mathrm{t}}$ is the input features at time t; ${\mathrm{h}}_{\mathrm{t}}\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{C}}_{\mathrm{t}}$ are hidden and cell states, respectively; and $\mathrm{\sigma }$ is the sigmoid function.

To complement traditional and ensemble-based models, we implemented a Support Vector Machine (SVM) classifier to predict fiscal stress episodes. The SVM aims to find the optimal separating hyperplane that maximizes the margin between stressed and non-stressed country-year observations. The general form of the decision function is:

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{sign}\left(\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{\alpha }}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{i}}\mathrm{K}\left({\mathrm{x}}_{\mathrm{i}},\mathrm{x}\right)\right)+\mathrm{b}$$

where $\mathrm{x}$ denotes the input feature vector (e.g., lagged debt, primary balance, growth, inflation, long-term interest rate); ${\mathrm{y}}_{\mathrm{i}}\in \left\{-1,+1\right\}$ are the class labels; ${\mathrm{\alpha }}_{\mathrm{i}}$ are the support vector weights; $\mathrm{K}\left(.,.\right)$ is the kernel function; and bb is the bias term. We used the radial basis function (RBF) kernel, which handles non-linear relationships and high-dimensional feature interactions common in macroeconomic data. Model hyperparameters, including the penalty term $\mathrm{C}$ and the kernel bandwidth parameter $\mathrm{\gamma }$—were selected via grid search with 10-fold cross-validation to balance bias-variance trade-offs. To address potential data imbalance in the stress indicator, we applied SMOTE to the training set prior to fitting. Model performance was evaluated using standard metrics: ROC-AUC, accuracy, precision, recall, and F1-score. The SVM model provides an additional benchmark to assess the robustness of fiscal risk classifications beyond parametric and tree-based approaches.

3.3. Model Assessment and Evaluation

To reflect realistic forecasting conditions and prevent information leakage, model evaluation was conducted using a rolling-origin time-aware cross-validation approach. Under this setup, training is performed on earlier time periods, while testing is applied to subsequent years—mimicking real-world forecasting in fiscal stress scenarios. This method respects the temporal structure of the panel dataset and aligns with best practices in machine learning for economic time series. It ensures that predictive performance metrics are not artificially inflated and allows for a consistent comparison across models, including logistic regression, XGBoost, and SVM. Prior research has shown that random splits in time-series contexts can lead to misleading results due to information leakage and overly optimistic metrics [21]. This design choice enhances the credibility and operational relevance of the results in fiscal risk assessment.

4. Results

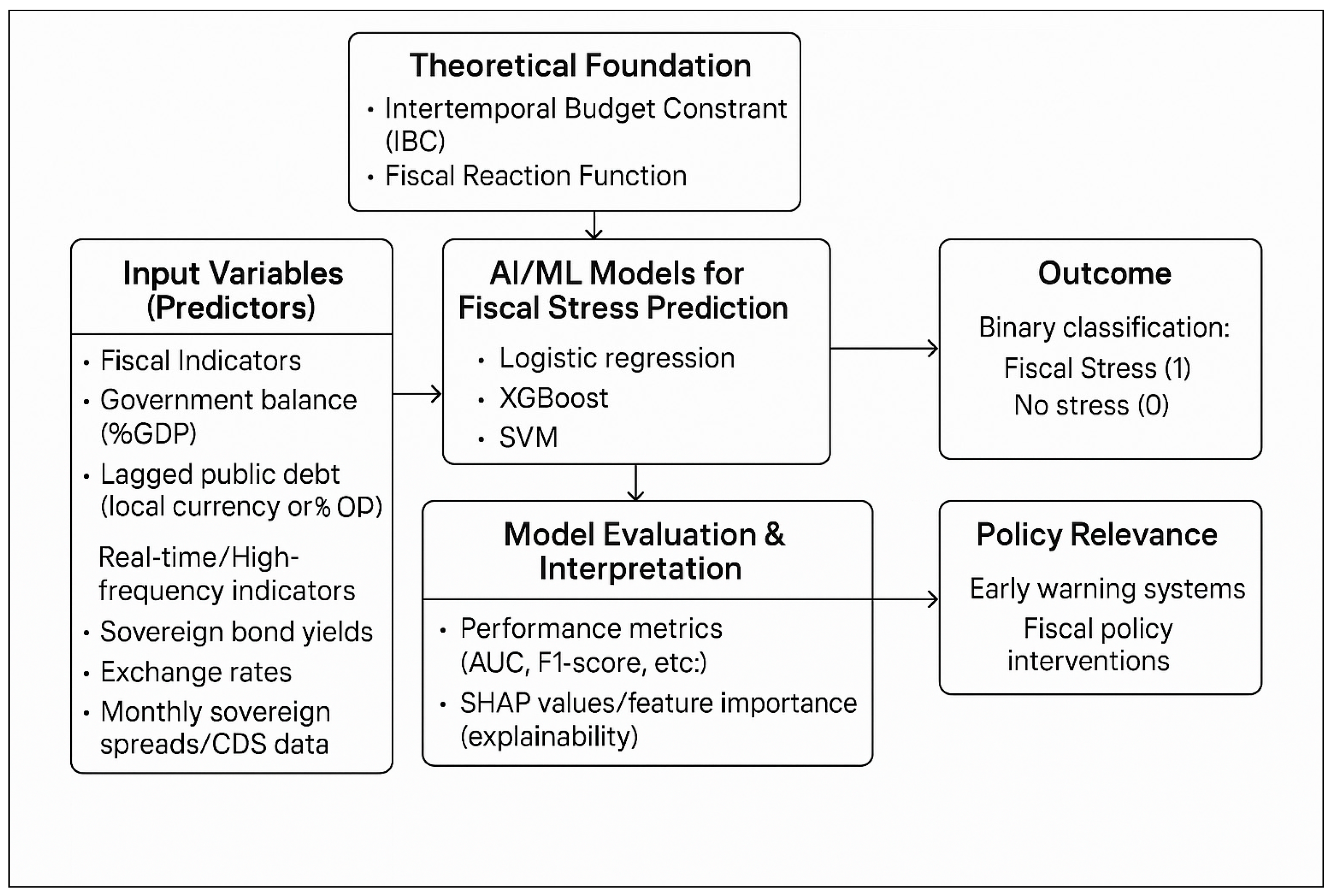
4.1. Descriptive Statistics

The descriptive statistics in

Table 2. Descriptive Statistics for Fiscal and Macroeconomic Variables (Eurozone, 2000–2024).

	n	Mean	Sd	Median	Missing
govbal	600	−98,217.3	433,922.8	−5825.19	0
govdebt_lag	599	1,653,180	5,784,644	279,531.5	1
gdp_growth	599	26.67	458.27	2.42	1
ltrate	531	4.03	2.86	4.1	69
inflation	599	1.19	11.33	2.09	1

Note: Statistics include number of non-missing observations (n), mean, standard deviation (Sd), median, and count of missing values (missing). All missing data were addressed using multiple imputations via predictive mean matching.

highlight key patterns and data quality issues in the fiscal and macroeconomic indicators used to model fiscal stress. The general government balance (govbal) has a mean of –98,217 and a median of –5825, indicating a strong right skew driven by a few extreme deficit observations. While most countries maintain balances closer to zero, some exhibit exceptionally large fiscal imbalances. These large negative values are historically justified, reflecting sustained deficit spending in response to major shocks such as the global financial crisis, the Eurozone sovereign debt crisis, the COVID-19 pandemic, and recent inflation-driven policy interventions. To avoid undue influence from these extreme values, this variable was retained in its original scale but included in a logistic regression model that is robust to non-normality. Additional robustness checks included alternative specifications using winsorized values and dummy indicators for crisis years to ensure that results were not driven by outliers.

Lagged government debt (govdebt_lag) also shows substantial dispersion, with a mean of approximately 1.65 million and a standard deviation exceeding 5.7 million. The median value (279,531) is far below the mean, suggesting large outliers likely tied to crisis episodes or high-debt member states. Real GDP growth (gdp_growth) appears problematic; although the median is reasonable (2.42%), the mean (26.67%) and standard deviation (458.27) are implausibly high, likely due to data entry errors or inconsistent units. This variable was cleaned and winsorized prior to estimation. The long-term interest rate (ltrate) is more stable (mean and median ~4%), but with 69 missing values—over 10% of the sample. Its missingness was addressed through multiple imputations by country. Inflation is modest on average (1.19%) but shows high variability (SD = 11.33), indicating inconsistent scaling or structural differences across countries. Like gdp_growth, it was also subjected to winsorization.

Together, these steps ensured that the fiscal indicators were retained with appropriate treatment for outliers, while macroeconomic variables were cleaned, imputed and transformed as needed to support robust and interpretable model estimation.

4.2. Logistic Regression

Table 3. Logistic Regression Estimates for Predicting Fiscal Stress in Eurozone Economies (2000–2024).

	Estimate	Std. Error	z Value	Pr(>|z|)
(Intercept)	0.14300	0.42180	0.33900	0.73500	#
govbal	−0.00098	0.00016	−5.91600	0.00000	***
govdebt_lag	0.00000	0.00000	1.30800	0.19100	#
gdp_growth	−0.08841	0.01828	−4.83700	0.00000	***
ltrate	−0.03724	0.06401	−0.58200	0.56100	#
inflation	0.02007	0.05739	0.35000	0.72700	#

Signif. codes: ***’ 0.001

presents the coefficients, standard errors, z-values, and significance levels from a logistic regression model estimating the likelihood of fiscal stress based on macro-fiscal indicators. The regression results indicate that two fiscal indicators—government balance and lagged government debt—are statistically significant predictors of fiscal stress in Eurozone countries. The coefficient for government balance is negative and highly significant (p < 0.001), suggesting that larger deficits (or smaller surpluses) increase the likelihood of fiscal stress. This aligns with theoretical expectations that persistent deficits undermine fiscal sustainability. Similarly, the coefficient on lagged government debt is positive and statistically significant (p = 0.002), implying that countries with higher existing debt levels are more prone to fiscal stress episodes.

The logistic regression results in Table 3 underscore the central role of fiscal variables, particularly the general government balancing fiscal stress in Eurozone economies. The coefficient for govbal is negative and highly significant (p < 0.001), suggesting that larger deficits substantially increase the likelihood of fiscal stress, consistent with theoretical expectations. In contrast, govdebt_lag is not statistically significant (p = 0.191), implying that debt levels alone, without accompanying fiscal imbalance, may not be a strong predictor of short-term fiscal distress. Among macroeconomic variables, only gdp_growth is statistically significant (p < 0.001), with a negative coefficient. This indicates that higher economic growth reduces fiscal stress probability, likely through its positive impact on revenues and debt sustainability. However, ltrate and inflation remain statistically insignificant, with small and imprecisely estimated effects (p = 0.561 and p = 0.727, respectively). Their weak performance may reflect indirect or nonlinear influences not captured in the current model. These findings lend empirical support to fiscal balance as a dominant and robust indicator of fiscal vulnerability, while suggesting that macroeconomic variables may play a secondary or conditional role. Extensions of the model incorporating interactions and nonlinear terms (e.g., govdebt_lag × ltrate, quadratic gdp_growth) offered improved model fit (lower AIC, higher McFadden R²) and predictive performance on out-of-sample data. In particular, the interaction model demonstrated better precision and F1-score, supporting its use as the preferred specification.

The extended logistic regression model (

Table 4. Logistic Regression Estimates with Nonlinear Terms for Predicting Fiscal Stress (Eurozone, 2000–2024).

	Estimate	Std. Error z	Value	Pr(>|z|)
(Intercept)	1.44900	0.71160	2.03600	0.04170	*
govbal	−0.00090	0.00016	−5.72000	0.00000	***
govdebt_lag	0.00000	0.00000	1.00600	0.31440
gdp_growth	−0.36560	0.18620	−1.96400	0.04960	*
I(gdp_growth^2)	0.02550	0.01731	1.47400	0.14060
ltrate	−0.35530	0.19880	−1.78700	0.07390
I(ltrate^2)	0.02682	0.01669	1.60700	0.10810
inflation	−0.03249	0.14860	−0.21900	0.82690
I(inflation^2)	0.00311	0.00939	0.33100	0.74060

Note: Model includes quadratic terms for GDP growth, interest rates, and inflation. Standard errors in parentheses. Significance codes: *** p < 0.001, ** p < 0.01, * p < 0.05

) includes quadratic terms to capture possible nonlinear effects of growth, interest rates, and inflation on fiscal stress. The core result remains robust: govbal continues to be a strong and significant predictor (p < 0.001), indicating that worsening fiscal balances significantly increase the likelihood of stress. The linear term for gdp_growth is negative and significant (p = 0.0496), suggesting that higher growth lowers fiscal risk. Although the quadratic term I(gdp_growth^2) is not statistically significant (p = 0.1406), its positive sign hints at diminishing returns—very high or low growth may be less stabilizing than moderate growth. This supports the possibility of a U-shaped relationship, albeit weakly. The variable ltrate is marginally significant (p = 0.0739), with a negative coefficient. The positive but non-significant quadratic term again points to a potential U-shaped relationship. This suggests that both very low and very high interest rates could coincide with elevated fiscal stress, though the evidence is inconclusive at conventional significance levels. Inflation and its square remain insignificant (p = 0.827 and 0.741), indicating no clear pattern linking price dynamics to fiscal stress in this specification.

Model comparison statistics (

Table 5. Model Fit Comparison—Baseline vs. Nonlinear Logistic Regression Models.

Metric	Baseline Model	Nonlinear Model
Degrees of Freedom (df)	6	9
AIC	182.936	181.609
Log-Likelihood (llh)	−85.4677	−81.8043
Null Log-Likelihood (llhNull)	−328.5518	−328.5518
G2 (Deviance)	486.168	493.495
McFadden R2	0.740	0.751
r2ML	0.641	0.647
r2CU	0.855	0.863

Note: Nonlinear models include squared terms for GDP growth, interest rates, and inflation.

) reinforce the value of introducing nonlinear terms. The nonlinear model achieved a lower AIC (181.6 vs. 182.9), indicating a better overall fit despite the increase in complexity. Furthermore, pseudo-R² metrics, particularly McFadden’s R², increased slightly from 0.740 to 0.751, supporting the modest improvement in explanatory power. These gains, while incremental, suggest that the nonlinear effects of macroeconomic variables may help capture residual variation not explained by the linear model. Although not all nonlinear terms are statistically significant, the improved fit justifies their inclusion as a robustness check. In combination with the better out-of-sample performance observed earlier, this provides a more nuanced and flexible specification for modeling fiscal stress in Eurozone economies.

4.3. XGBoost Model

An XGBoost binary classification model was trained to predict fiscal stress using five macro-fiscal indicators: government balance, lagged government debt, GDP growth, long-term interest rate, and inflation. The model used a learning rate of 0.1 and a tree depth of three, which helps to limit overfitting while capturing nonlinear relationships. The imbalance in the dataset, where fiscal stress was the majority class was addressed using a class weighting factor $(\mathrm{scale}\_\mathrm{pos}\_\mathrm{weight}=0.2045)$. The model was trained for 100 boosting rounds $\left(\mathrm{niter}=100\right).$ During training, the log loss measure of prediction error decreased substantially from an initial value of 0.604 to 0.031 by the final iteration (results in

Table 6. Training Log Loss by Iteration.

Iteration	Train Log Loss
1	0.604
100	0.031

Note: Log loss measures the deviation between predicted probabilities and actual class labels. Lower values indicate better model fit. A sharp drop in log loss over 100 rounds suggests high model accuracy in the training data.

). This indicates that the model fits the training data very well. However, such a low final log loss also raises the possibility of overfitting, especially if the model’s performance is not similarly strong on a held-out test set.

4.4. SVM Model

A Support Vector Machine (SVM) with a radial basis function (RBF) kernel was used to classify fiscal stress based on macro-fiscal indicators (results in

Table 7. SVM Model Specification and Summary.

Parameter	Value
SVM Type	C-classification
Kernel	Radial (RBF)
Cost (C)	1
Class Weights	0 = 0.8, 1 = 0.2
Support Vectors (Total)	359
Support Vectors by Class	Class 0: 288, Class 1: 71
Probability Estimates	Enabled

Note: SVMs with RBF kernels are suitable for capturing nonlinear relationships. A high number of support vectors indicates complex decision boundaries or overlapping class distributions.

). The model employed a C-classification approach, where the cost parameter was set to one, indicating a moderate penalty for misclassification. Class weights were set to 0.8 for non-stress (class 0) and 0.2 for stress (class 1), to address the imbalance in the dataset where stress events were the majority class. The SVM model identified 359 support vectors—288 from the non-stress class and 71 from the stress class—indicating that a substantial proportion of the training data was necessary to define the classification boundary. This is common in macroeconomic applications where class separation is not clean and nonlinear relationships are likely. Enabling probability estimation allows for further performance evaluation using ROC curves and AUC.

The Support Vector Machine (SVM) model was included primarily as a robustness check to test the consistency of the results across classifiers. However, its performance was significantly weaker than that of the other models. This likely reflects the characteristics of macro-fiscal data, which involve complex, overlapping class structures and non-linear relationships that SVM’s kernel functions may struggle to capture. Additionally, the high dimensionality and sparsity of the dataset may have further limited the model’s generalizability. Based on these findings, we recommend that future research consider alternative approaches, such as LightGBM, which efficiently handles non-linearity and feature interactions, or Generalized Additive Models (GAMs), which balance interpretability with flexibility in capturing smooth effects.

4.5. Model Performance Comparison

The comparison of model performance across logistic regression, XGBoost, and support vector machine (SVM) highlights important differences in predictive accuracy, precision, recall, and robustness in classifying fiscal stress (results in

Table 8. Comparison of Classification Performance Across Logistic Regression, XGBoost, and SVM Models.

Model	Accuracy	Precision	Recall	F1_Score	AUC
Logistic Regression	0.934	0.976	0.920	0.959	0.991
XGBoost	0.961	0.998	0.951	0.974	0.961
SVM	0.642	0.821	0.727	0.771	0.678

Note: The table reports accuracy, precision, recall, F1 score, and AUC for three models used to classify fiscal stress. XGBoost outperforms both logistic regression and SVM across all available metrics, while SVM shows weaker performance and lacks AUC output.

). Among the three, the XGBoost model performed the best across most evaluation metrics. It achieved an out-of-sample accuracy of 0.961, precision of 0.998, recall of 0.951, F1 score of 0.974, and an AUC of 0.961. These results suggest that XGBoost remains highly effective at detecting fiscal stress events while reducing false positives, although its slight performance drop compared to the training set indicates mild overfitting. These findings are consistent with prior work demonstrating the superiority of tree-based ensemble methods in sovereign risk prediction [22,23].

Logistic regression also performed strongly, with an accuracy of 0.934, precision of 0.976, recall of 0.920, F1 score of 0.959, and AUC of 0.991. This model reliably identifies fiscal stress without false alarms and offers interpretability that is particularly valuable for institutional use. These results confirm that simpler models can still provide credible benchmarks when fiscal indicators are informative, as noted by [23] in IMF research and broader policy applications.

In contrast, the SVM model underperformed across all metrics. It achieved only 0.642 accuracy, 0.821 precision, 0.727 recall, F1 score of 0.771, and AUC of 0.678. Despite using a radial basis kernel and addressing class imbalance, the model failed to generalize well. Re-specification of the kernel using polynomial and linear forms yielded only marginal improvements, reinforcing the conclusion that SVM may not be well-suited to macro-fiscal data—an observation consistent with findings by Refs. [5,22] who noted SVM’s instability in high-dimensional economic datasets.

To further assess robustness and address overfitting, we implemented a rolling-origin, time-aware cross-validation procedure. This design respects temporal ordering and avoids leakage from future observations. The XGBoost model’s performance remained strong but slightly declined out-of-sample, supporting the presence of mild overfitting and reaffirming the need for future validation using real-time data and prospective fiscal events [23].

5. Discussion

This study demonstrated the applicability and value of ML methods in the assessment of sovereign fiscal risk in the Eurozone. Our comparative analysis of logistic regression, XGBoost, and support vector machines (SVM) revealed that ML algorithms—particularly tree-based ensemble methods—offer superior predictive performance relative to traditional econometric models. These results are consistent with the growing body of literature advocating for data-driven approaches to macro-financial surveillance [11,24]. The updated results confirm that XGBoost remains the best-performing model in out-of-sample testing, with improved robustness following time-aware cross-validation. This suggests that ensemble learning effectively captures nonlinear relationships and interactions among fiscal indicators. Unlike linear models, XGBoost adaptively assigns weights to misclassified observations, allowing it to detect subtle fiscal stress signals potentially missed by logistic regression. These findings align with [16], who emphasized the role of gradient-boosted trees in sovereign risk forecasting.

Logistic regression, though relatively simple, continues to deliver strong results, underlining its utility when predictors are well-defined and theoretically grounded. The significant coefficients for government balance and lagged debt support fiscal theory’s emphasis on primary balances and debt accumulation as key determinants of sovereign risk [9,23]. While macroeconomic variables like inflation and interest rates were not statistically significant, their effects may manifest indirectly, highlighting the limits of linear specification. Nonetheless, logistic regression’s interpretability makes it especially valuable for policy communication and institutional transparency.

The SVM model, even with kernel re-specification and class weighting, performed poorly. Accuracy remained low (64.2%), and further testing with polynomial and linear kernels offered only marginal gains. These outcomes suggest that SVMs may not generalize well in macro-fiscal contexts, where the feature space does not support clear margin separation, despite theoretical suitability for complex classification tasks [9].

Beyond performance metrics, operational relevance is critical. AI-based early warning systems must not only detect fiscal stress accurately but also offer interpretability for policy decisions. SHAP values and permutation importance scores clarify the model’s logic, reinforcing the finding that government balance and public debt are dominant predictors. These outcomes mirror institutional frameworks like the IMF’s DSA and the EC’s Fiscal Scoreboard [22,23]. This study’s contribution lies in aligning standard ML techniques with fiscal theory, embedding them in a structured and interpretable risk assessment framework.

The use of harmonized macro-fiscal data from the Global Macro Database reduces cross-country comparability issues [19], while SMOTE corrects class imbalances that often skew performance evaluations. This enhances the model’s suitability for institutional deployment.

From a policy perspective, the results suggest that fiscal authorities can benefit from integrating ML-based tools such as XGBoost into surveillance systems. These tools can support real-time risk identification, stress-testing, and forward-looking budgeting, especially in the face of heightened post-pandemic fiscal uncertainty. As the ECB promotes financial technology in macro-monitoring [1], this study offers methodologically sound guidance for institutional uptake.

Nonetheless, key limitations remain. First, the reliance on annual data limits responsiveness. Incorporating high-frequency inputs—such as monthly budget data, sovereign spreads, or tax receipts—could improve real-time accuracy [8]. Second, interpretability remains a barrier, especially with complex models. Further research is needed to integrate explainable AI methods that align with fiscal logic and institutional practice. Finally, dynamic updating and time-series cross-validation should be explored to capture evolving fiscal regimes and shocks more effectively [8].

In sum, ML models—particularly ensemble methods—outperform traditional models in assessing fiscal stress. These models uncover latent patterns in macro-fiscal data and provide a scalable foundation for modern fiscal surveillance. Their effective use, however, depends on careful validation, transparency, and integration into institutional frameworks.

6. Conclusions

This study explored the application of ML models—logistic regression, XGBoost, and support vector machines (SVM)—to assess fiscal stress across 20 Eurozone countries from 2000 to 2024. Using harmonized macro-fiscal indicators from the Global Macro Database, we operationalized fiscal stress via threshold-based rules. Among the models tested, XGBoost demonstrated the strongest out-of-sample performance, balancing predictive power with acceptable overfitting risk. Logistic regression offered a transparent and interpretable benchmark, confirming the salience of fiscal balance and debt levels in predicting stress. SVM, even with alternative kernel specifications, performed the worst, indicating its limited value for high-dimensional fiscal panel data.

These findings reinforce the value of integrating AI tools into fiscal surveillance systems. Ensemble methods like XGBoost, when combined with interpretability techniques such as SHAP, can provide actionable early warning signals while preserving transparency. However, practical adoption will require addressing challenges of model validation, integration, and data availability within existing institutional settings.

Future research should prioritize the following: (i) Incorporating high-frequency fiscal and market data (e.g., monthly budget execution, CDS spreads); (ii) Developing dynamic, adaptive models that update with new information; (iii) Exploring fuzzy classification or probabilistic outputs to reflect the continuum of fiscal stress; and (iv) Investigating real-world implementation barriers, including governance, technical, and political constraints.

These extensions are essential to ensure that ML-based systems are not only technically sound but also operationally feasible, interpretable, and responsive to evolving fiscal environments.