Crypto Asset Portfolio Selection
Abstract
:1. Introduction
2. Methodology
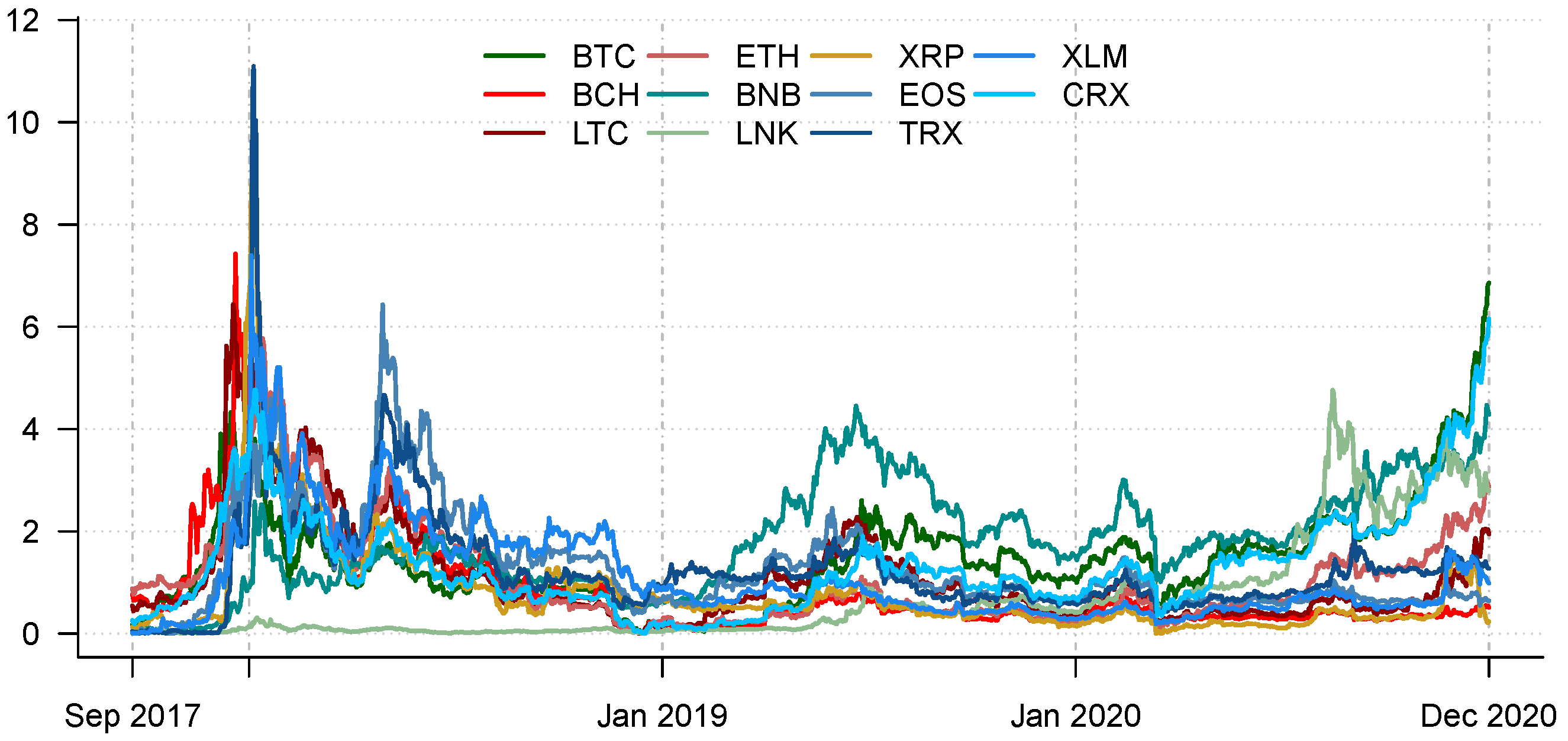
3. Empirical Findings
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markowitz, H. The Utility of Wealth. J. Political Econ. 1952, 60, 151–158. [Google Scholar] [CrossRef]
- Elton, E.J.; Gruber, M.J.; Spitzer, J. Improved Estimates of Correlation Coefficients and their Impact on Optimum Portfolios. Eur. Financ. Manag. 2006, 12, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Coherent Measures of Risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Bellini, F.; Di Bernardino, E. Risk Management with Expectiles. Eur. J. Financ. 2017, 23, 487–506. [Google Scholar] [CrossRef]
- Cesarone, F.; Tardella, F. Equal Risk Bounding Is Better than Risk Parity for Portfolio Selection. J. Glob. Optim. 2017, 68, 439–461. [Google Scholar] [CrossRef]
- DeMiguel, V.; Garlappi, L.; Uppal, R. Optimal Versus Naive Diversification: How Inefficient is the 1/N Portfolio Strategy? Rev. Financ. Stud. 2009, 22, 1915–1953. [Google Scholar] [CrossRef] [Green Version]
- Maillard, S.; Roncalli, T.; Teiletche, J. The Properties of Equally Weighted Risk Contribution Portfolios. J. Portf. Manag. 2010, 36, 60–70. [Google Scholar] [CrossRef]
- Castro, F.; Gago, J.; Hartillo, I.; Puerto, J.; Ucha, J. An Algebraic Approach to Integer Portfolio Problems. Eur. J. Oper. Res. 2011, 210, 647–659. [Google Scholar] [CrossRef] [Green Version]
- Kolm, P.N.; Tütüncü, R.; Fabozzi, F.J. 60 Years of Portfolio Optimization: Practical Challenges and Current Trends. Eur. J. Oper. Res. 2014, 234, 356–371. [Google Scholar] [CrossRef]
- Lynch, A.W.; Tan, S. Explaining the Magnitude of Liquidity Premia: The Roles of Return Predictability, Wealth Shocks, and State-Dependent Transaction Costs. J. Financ. 2011, 66, 1329–1368. [Google Scholar] [CrossRef] [Green Version]
- Mansini, R.; Ogryczak, W.; Speranza, M.G. Twenty Years of Linear Programming Based Portfolio Optimization. Eur. J. Oper. Res. 2014, 234, 518–535. [Google Scholar] [CrossRef]
- Mansini, R.; Ogryczak, W.; Speranza, M.G. Portfolio Optimization with Transaction Costs. In Linear and Mixed Integer Programming for Portfolio Optimization; Springer: Berlin/Heidelberg, Germany, 2015; pp. 47–62. [Google Scholar]
- Kadan, O.; Liu, F.; Liu, S. Generalized Systematic Risk. Am. Econ. J. Microecon. 2016, 8, 86–127. [Google Scholar] [CrossRef]
- Härdle, W.K.; Wang, W.; Yu, L. TENET: Tail-Event Driven NETwork Risk. J. Econom. 2016, 192, 499–513. [Google Scholar] [CrossRef]
- Battiston, S.; Gatti, D.D.; Gallegati, M.; Greenwald, B.; Stiglitz, J.E. Liaisons Dangereuses: Increasing Connectivity, Risk Sharing, and Systemic Risk. J. Econ. Dyn. Control 2012, 36, 1121–1141. [Google Scholar] [CrossRef] [Green Version]
- Ladley, D. Contagion and Risk Sharing on the Inter-bank Market. J. Econ. Dyn. Control 2013, 37, 1384–1400. [Google Scholar] [CrossRef] [Green Version]
- Elliott, M.; Golub, B.; Jackson, M.O. Financial Networks and Contagion. Am. Econ. Rev. 2014, 104, 3115–3153. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D.; Ozdaglar, A.; Tahbaz-Salehi, A. Systemic Risk and Stability in Financial Networks. Am. Econ. Rev. 2015, 105, 564–608. [Google Scholar] [CrossRef]
- Billio, M.; Getmansky, M.; Lo, A.W.; Pelizzon, L. Econometric Measures of Connectedness and Systemic Risk in the Finance and Insurance Sectors. J. Financ. Econ. 2012, 104, 535–559. [Google Scholar] [CrossRef]
- Diebold, F.; Yilmaz, K. On the Network Topology of Variance Decompositions: Measuring the Connectedness of Financial Firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Ahelegbey, D.F. The Econometrics of Bayesian Graphical Models: A Review With Financial Application. J. Netw. Theory Financ. 2016, 2, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Ahelegbey, D.F.; Billio, M.; Casarin, R. Bayesian Graphical Models for Structural Vector Autoregressive Processes. J. Appl. Econom. 2016, 31, 357–386. [Google Scholar] [CrossRef] [Green Version]
- Rietz, T.A. The Equity Risk Premium a Solution. J. Monet. Econ. 1988, 22, 117–131. [Google Scholar] [CrossRef]
- Barro, R.J. Rare Disasters and Asset Markets in the Twentieth Century. Q. J. Econ. 2006, 121, 823–866. [Google Scholar] [CrossRef]
- Gillman, M.; Kejak, M.; Pakoš, M. Learning about Rare Disasters: Implications for Consumptions and Asset Prices. Rev. Financ. 2015, 19, 1053–1104. [Google Scholar] [CrossRef] [Green Version]
- Gabaix, X. Variable Rare Disasters: An Exactly Solved Model for Ten Puzzles in Macro-Finance. Q. J. Econ. 2012, 127, 645–700. [Google Scholar] [CrossRef] [Green Version]
- Wachter, J.A. Can Time-Varying Risk of Rare Disasters Explain Aggregate Stock Market Volatility? J. Financ. 2013, 68, 987–1035. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.W.; Santa-Clara, P. Dynamic Portfolio Selection by Augmenting the Asset Space. J. Financ. 2006, 61, 2187–2217. [Google Scholar] [CrossRef]
- Cruz-Reyes, L.; Trejo, C.M.; Irrarragorri, F.L.; Santillán, C.G.G. A Decision Support System Framework for Public Project Portfolio Selection with Argumentation Theory. In Recent Advances on Hybrid Approaches for Designing Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 467–479. [Google Scholar]
- Harvey, C.R.; Liechty, J.C.; Liechty, M.W.; Müller, P. Portfolio Selection with Higher Moments. Quant. Financ. 2010, 10, 469–485. [Google Scholar] [CrossRef]
- Lwin, K.; Qu, R. A Hybrid Algorithm for Constrained Portfolio Selection Problems. Appl. Intell. 2013, 39, 251–266. [Google Scholar] [CrossRef] [Green Version]
- Perez, F.; Gomez, T. Multiobjective Project Portfolio Selection with Fuzzy Constraints. Ann. Oper. Res. 2016, 245, 7–29. [Google Scholar] [CrossRef]
- Ling, A.; Sun, J.; Wang, M. Robust Multi-period Portfolio Selection Based on Downside Risk with Asymmetrically Distributed Uncertainty Set. Eur. J. Oper. Res. 2020, 285, 81–95. [Google Scholar] [CrossRef]
- Jiang, C.; Ma, Y.; An, Y. Portfolio Selection with a Systematic Skewness Constraint. North Am. J. Econ. Financ. 2016, 37, 393–405. [Google Scholar] [CrossRef]
- Campbell, R.; Huisman, R.; Koedijk, K. Optimal Portfolio Selection in a Value-at-Risk Framework. J. Bank. Financ. 2001, 25, 1789–1804. [Google Scholar] [CrossRef]
- Li, Q.; Bai, Y.; Yan, X.; Zhang, W. Portfolio Selection with the Effect of Systematic Risk Diversification: Formulation and Accelerated Gradient Algorithm. Optim. Methods Softw. 2019, 34, 612–633. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, S.; Li, D.; Li, D. Active Allocation of Systematic Risk and Control of Risk Sensitivity in Portfolio Optimization. Eur. J. Oper. Res. 2013, 228, 556–570. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Sun, X. Portfolio Selection with Marginal Risk Control. J. Comput. Financ. 2010, 14, 3. [Google Scholar] [CrossRef]
- Grinold, R.C.; Kahn, R.N. Active Portfolio Management: A Quantitative Approach for Producing Superior Returns and Controlling Risk; McGraw Hill: New York, NY, USA, 1999. [Google Scholar]
- Ahelegbey, D.F.; Giudici, P.; Mojtahedi, F. Tail Risk Measurement in Crypto-Asset Markets. Int. Rev. Financ. Anal. 2021, 73, 101604. [Google Scholar] [CrossRef]
- Hardle, W.; Trimborn, S. CRIX an Index for Cryptocurrencies. J. Empir. Financ. 2018, 49, 107–122. [Google Scholar]
- Kwapien, J.; Watorek, M.; Drozd, S. Cryptocurrency market consolidation in 2020–2021. Entropy 2021, 12, 1674. [Google Scholar] [CrossRef]
- Huynh, T.L.D.; Nasir, M.A.; Vo, X.V.; Nguyen, T.T. Small things matter most: The spillover effects in the cryptocurrency market and gold as a silver bullet. N. Am. J. Econ. Financ. 2020, 54, 101277. [Google Scholar] [CrossRef]
- Iqbal, N.; Fareed, Z.; Wan, G.; Shahzad, F. Asymmetric nexus between COVID-19 outbreak in the world and cryptocurrency market. Int. Rev. Financ. Anal. 2021, 73, 101613. [Google Scholar] [CrossRef]

| Returns | Δ CVaR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Code | Name | Mean | Sd | Skew | Ex.Kurt | Mean | Sd | Skew | Ex.Kurt |
| BTC | Bitcoin | 0.17 | 4.15 | −1.08 | 15.61 | −0.00 | 1.63 | −3.56 | 213.77 |
| BCH | Bitcoin-Cash | −0.03 | 6.78 | 0.07 | 10.40 | 0.00 | 2.98 | 2.15 | 104.04 |
| LTC | Litecoin | 0.07 | 5.54 | 0.37 | 9.02 | 0.00 | 1.91 | −1.80 | 117.23 |
| ETH | Ethereum | 0.08 | 5.09 | −1.22 | 13.19 | 0.00 | 1.88 | −4.94 | 240.10 |
| BNB | Binance-Coin | 0.33 | 6.09 | 0.23 | 12.99 | −0.01 | 1.72 | −5.59 | 265.12 |
| LNK | Chain-Link | 0.34 | 7.76 | 0.18 | 6.93 | −0.01 | 2.06 | −0.13 | 224.65 |
| XRP | Ripple | 0.02 | 6.34 | 0.98 | 20.64 | 0.04 | 2.91 | 6.97 | 118.03 |
| EOS | EOS | 0.12 | 6.70 | 0.20 | 7.10 | 0.01 | 2.27 | −0.66 | 96.15 |
| TRX | Tron | 0.19 | 8.27 | 1.94 | 20.58 | −0.02 | 2.79 | 0.87 | 178.97 |
| XLM | Stellar | 0.20 | 6.89 | 1.41 | 13.12 | −0.02 | 2.21 | 3.75 | 117.72 |
| CRX | CRIX | 0.17 | 4.19 | −1.37 | 13.94 | 0.00 | 1.61 | −2.02 | 181.68 |
| BTC | BCH | LTC | ETH | BNB | LNK | XRP | EOS | TRX | XLM | CRX | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BTC | 1 | 0.63 | 0.74 | 0.76 | 0.63 | 0.46 | 0.51 | 0.64 | 0.54 | 0.53 | 0.11 |
| BCH | 0.63 | 1 | 0.66 | 0.72 | 0.49 | 0.41 | 0.54 | 0.67 | 0.44 | 0.49 | 0.05 |
| LTC | 0.74 | 0.66 | 1 | 0.82 | 0.59 | 0.45 | 0.60 | 0.69 | 0.51 | 0.55 | 0.03 |
| ETH | 0.76 | 0.72 | 0.82 | 1 | 0.62 | 0.56 | 0.66 | 0.73 | 0.58 | 0.61 | 0.03 |
| BNB | 0.63 | 0.49 | 0.59 | 0.62 | 1 | 0.44 | 0.44 | 0.55 | 0.44 | 0.47 | 0.04 |
| LNK | 0.46 | 0.41 | 0.45 | 0.56 | 0.44 | 1 | 0.43 | 0.46 | 0.40 | 0.46 | -0.01 |
| XRP | 0.51 | 0.54 | 0.60 | 0.66 | 0.44 | 0.43 | 1 | 0.61 | 0.52 | 0.64 | 0.04 |
| EOS | 0.64 | 0.67 | 0.69 | 0.73 | 0.55 | 0.46 | 0.61 | 1 | 0.56 | 0.56 | 0.04 |
| TRX | 0.54 | 0.44 | 0.51 | 0.58 | 0.44 | 0.40 | 0.52 | 0.56 | 1 | 0.44 | 0.08 |
| XLM | 0.53 | 0.49 | 0.55 | 0.61 | 0.47 | 0.46 | 0.64 | 0.56 | 0.44 | 1 | 0.06 |
| CRX | 0.11 | 0.05 | 0.03 | 0.03 | 0.04 | −0.01 | 0.04 | 0.04 | 0.08 | 0.06 | 1 |
| Year | BTC | BCH | LTC | ETH | BNB | LNK | XRP | EOS | TRX | XLM | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 | 0.5 | 0.05 | 0.06 | 0.10 | 0.11 | 0.11 | 0.06 | 0.14 | 0.13 | 0.06 | 0.17 | |
| 2018 | 5 | 0.05 | 0.06 | 0.10 | 0.11 | 0.11 | 0.06 | 0.14 | 0.13 | 0.06 | 0.17 | |
| 2019 | 0.5 | 0.13 | 0.14 | 0.08 | 0.09 | 0.07 | 0.08 | 0.10 | 0.10 | 0.11 | 0.10 | |
| 2019 | 5 | 0.13 | 0.14 | 0.09 | 0.09 | 0.07 | 0.08 | 0.10 | 0.10 | 0.11 | 0.10 | |
| 2020 | 0.5 | 0.19 | 0.03 | 0.11 | 0.03 | 0.09 | 0.06 | 0.19 | 0.09 | 0.07 | 0.13 | |
| 2020 | 5 | 0.19 | 0.02 | 0.12 | 0.04 | 0.10 | 0.07 | 0.19 | 0.07 | 0.06 | 0.13 |
| Year | BTC | BCH | LTC | ETH | BNB | LNK | XRP | EOS | TRX | XLM | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 | 0.5 | 0.80 | 0 | 0 | 0.15 | 0 | 0.02 | 0.02 | 0 | 0 | 0 | |
| 2018 | 5 | 0.80 | 0 | 0 | 0.17 | 0 | 0.01 | 0.01 | 0 | 0 | 0 | |
| 2019 | 0.5 | 0.77 | 0 | 0 | 0 | 0.12 | 0.03 | 0.08 | 0 | 0 | 0 | |
| 2019 | 5 | 0.76 | 0 | 0 | 0 | 0.11 | 0.01 | 0.12 | 0 | 0 | 0 | |
| 2020 | 0.5 | 0.57 | 0 | 0 | 0 | 0.04 | 0.02 | 0.36 | 0 | 0 | 0.01 | |
| 2020 | 5 | 0.53 | 0 | 0 | 0 | 0.04 | 0.01 | 0.40 | 0 | 0 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahelegbey, D.F.; Giudici, P.; Mojtahedi, F. Crypto Asset Portfolio Selection. FinTech 2022, 1, 63-71. https://doi.org/10.3390/fintech1010005
Ahelegbey DF, Giudici P, Mojtahedi F. Crypto Asset Portfolio Selection. FinTech. 2022; 1(1):63-71. https://doi.org/10.3390/fintech1010005
Chicago/Turabian StyleAhelegbey, Daniel Felix, Paolo Giudici, and Fatemeh Mojtahedi. 2022. "Crypto Asset Portfolio Selection" FinTech 1, no. 1: 63-71. https://doi.org/10.3390/fintech1010005
APA StyleAhelegbey, D. F., Giudici, P., & Mojtahedi, F. (2022). Crypto Asset Portfolio Selection. FinTech, 1(1), 63-71. https://doi.org/10.3390/fintech1010005








