The Quest for Efficient ASCON Implementations: A Comprehensive Review of Implementation Strategies and Challenges

Abstract

The rapid growth of the Internet of Things (IoT) has significantly expanded the deployment of resource-constrained devices, introducing new security and privacy challenges. To address these concerns, the National Institute of Standards and Technology (NIST) concluded a multi-year effort by announcing ASCON as the new lightweight cryptography standard in 2023. ASCON’s cipher suite includes both Authenticated Encryption with Associated Data (AEAD) and hashing functions, ensuring authenticity, confidentiality, and broad applicability. Since its standardization, there has been a significant research effort focused on enhancing ASCON’s performance under diverse application constraints as well as assessing its vulnerability to advanced side-channel attacks. This study offers a comprehensive overview of current ASCON hardware implementations on FPGA and ASIC platforms, examining key design trade-offs. Additionally, it examines the latest side-channel attacks on ASCON were examined. These attacks exploited weaknesses in the hardware implementations rather than in the algorithm itself. Being highly efficient, they could breach both unprotected and protected implementations. This survey also reviews the proposed countermeasures against these powerful attacks and analyzes how their associated overhead conflicts with the performance demands of real-world ASCON applications. The synthesis of these findings offers clear guidelines for designers seeking to implement ASCON. At the same time, areas requiring further investigation are identified. As ASCON sees ever more widespread deployment, this review serves as a reference for understanding the current state of research and guiding future developments toward efficient and secure implementations.

1. Introduction

The increasing demand for resource-constrained devices, prompted by the ever-growing deployment of IoT devices, introduces a range of new security and privacy challenges. Wearables, healthcare devices, wireless sensor networks (WSNs), and other resource-constrained devices require robust cryptographic modules with a minimal overhead impact. Cryptography standards such as AES-GCM (AES with Galois/Counter Mode) [1,2] and SHA-2 (Secure Hash Algorithm 2) [3] can be impractical in these constrained environments due to their computational and memory demands. To address this challenge, the National Institute of Standards and Technology (NIST) initiated research on lightweight cryptography (LWC), algorithms specifically designed to deliver essential security services with minimal hardware and software overhead. In 2015, NIST launched a public standardization process to select one or more schemes for Authenticated Encryption with Associated Data (AEAD) and optional hashing functionalities. The AEAD scheme ensures confidentiality, integrity, and authenticity, while the optional hashing component can be integrated to share many of the same resources, thereby reducing the overall implementation footprint.

NIST’s LWC competition evaluated candidate algorithms against four main criteria:

• Security. The algorithm had to demonstrate robust security properties through proofs and third-party analyses. Considerations such as nonce-misuse resistance, the effects of state recovery, and the release of unverified plaintext (RUP) were also taken into account.
• Efficient Implementation. The algorithm needed to be deployable within resource-constrained platforms, whether hardware- or software-oriented. It was expected to outperform existing standards such as AES-GCM and SHA-2 in both performance and cost and exhibit enough flexibility to meet application-specific needs.
• Ease of Protection. The design had to facilitate the incorporation of protections against side-channel and fault attacks. Countermeasures needed to impose minimal performance and cost overhead.
• Royalty-Free. The resulting standard needed to be freely implementable, without licensing fees.

Although not a primary criterion, post-quantum considerations also played a role. Symmetric-key ciphers are vulnerable to Grover’s algorithm [4], which speeds up key search and collision attacks quadratically. Therefore, some submissions included variants with increased key sizes or digest lengths to mitigate quantum threats. Nevertheless, it was not the primary focus since, if necessary, the AES-GCM scheme could serve as a fallback for post-quantum scenarios.

In February 2023, NIST selected the ASCON family as the winner of the LWC competition, establishing it as the new standard for lightweight cryptographic applications. ASCON includes both AEAD and hashing schemes, along with extendable-output functions, offering broad application versatility. ASCON’s design strikes a balance between throughput, area, and power efficiency. The benchmark results consistently place ASCON among the top performers for AEAD and hashing [5,6], outperforming older standards such as AES-GCM and SHA-2. Although it is neither the smallest nor the fastest design [7], its permutation-based architecture allows implementers to make trade-offs tailored to specific use cases. For instance, applications like closed-circuit television (CCTV) may require high-throughput implementations, as a significant volume of data must be encrypted in real-time. Conversely, IoT nodes such as smart street lighting must be compact, thereby demanding low-area accelerators, while, in battery-supplied applications like WSNs, it is essential to implement energy-efficient solutions.

From a side-channel resistance perspective, ASCON’s design employs a leveled implementation approach [8], which restricts the requirement for countermeasures to only the initialization and finalization phases. By narrowing down the portions of the cipher that require protection, the side-channel countermeasure overhead is significantly reduced. Furthermore, the non-linear low-degree layer in ASCON’s permutation block enables cost-effective implementations of masking [9] or threshold techniques [10]. To address quantum threats, ASCON offers variants with a 160 bit key, ensuring adequate security against quantum-capable adversaries.

Our Contribution

The primary goal of this review is to provide a comprehensive overview of existing solutions for implementing ASCON efficiently and securely. It serves as a practical guide for selecting the most suitable implementation strategies based on specific application requirements while also identifying gaps in current research that warrant further investigation. Although previous studies on ASCON exist [11,12], these primarily focus on providing an extensive bibliographic review without going into the details of the various solutions. In addition, they are outdated due to the significant research efforts driven by the selection of ASCON as the LWC standard. In contrast, this study takes a broader and more analytical approach by (i) identifying the critical operations of ASCON and exploring how they can be optimized for performance, (ii) pinpointing the most vulnerable aspects of the design and assessing how they can be protected, and (iii) examining the interplay between optimization techniques and security countermeasures and where they might conflict. This analysis is enriched by an examination of the most common ASCON applications and the performance constraints they impose. Ultimately, this study equips designers with the necessary parameters to develop an efficient and secure ASCON implementation tailored to their specific needs.

The rest of this study is structured as follows. Section 2 introduces the foundational concepts necessary for the rest of this paper. It provides an in-depth review of the ASCON cipher suite, covering its authenticated encryption and hashing modes, core permutation, and design rationale. In addition, it examines the nature of passive attacks on cryptographic implementations, explaining the fundamental mechanisms that attackers exploit. Section 3 summarizes the optimized ASCON architectures proposed in the literature and explores design trends influenced by application-specific constraints. Section 4 shifts the focus to implementation security, providing an overview of passive attacks targeting hardware implementations of ASCON, and discusses countermeasures designed to mitigate these threats. Finally, in Section 5, key insights derived from this study are presented and potential future research directions are highlighted.

2. Preliminaries

ASCON [8] is a family of permutation-based Authenticated Encryption with Associated Data (AEAD) and hashing schemes. The first version of the ASCON suite comprised seven algorithms [8]. It included three AEAD variants, two offering a 128 bit security level and one designed for 80 bit quantum security, along with two Hash variants and two Extendable Output Function (XOF) variants. The Hash and XOF algorithms provided 128 bit security against both collision and pre-image attacks. In a subsequent publication [13], the suite was expanded to also encompass two pseudorandom functions (PRFs) and a message authentication code (MAC) variant, all designed to provide a security level of 128 bits. On 7 February 2023, ASCON was selected by NIST as the new standard for lightweight cryptography. Previously, in 2019, it was also chosen as the primary candidate for lightweight authenticated encryption under the Competition for Authenticated Encryption: Security, Applicability, and Robustness (CAESAR) [14] (see Figure 1).

2.1. ASCON Design

The design rationale behind ASCON was to achieve an optimal balance between security, size, and speed in both software and hardware, with particular attention to minimizing size. All ASCON ciphers are built on the sponge design methodology [15] and exploit a 320 bit permutation function as the core component. This function employs an iterated substitution–permutation network (SPN) that ensures strong cryptographic properties and fast diffusion while maintaining low computational cost. In ASCON’s design, the permutation function has two variants: $p_a$, used for initialization and finalization, and $p_b$, used for data processing. The only difference between them is the number of iterations of the core round function, $ASCON-p$. The permutation-based approach offers several advantages [16], including a well-defined state size, the absence of additional key scheduling processes, and minimal decryption overhead since the same permutation is used for encryption and decryption. This simplicity, combined with the small state size and reusability of core components, can achieve a very low footprint area and support various trade-offs between cost and performance. Consequently, ASCON performs efficiently in both hardware and software.

The ASCON AEAD family is based on the duplex mode of operation, inspired by constructions like MonkeyDuplex [17]. In the duplex mode of operation, data are absorbed into the state and then squeezed out. Unlike block-cipher constructions, e.g., [18,19,20], the permutation-based design eliminates the need for a separate key-scheduling process, allowing for high-speed implementations and less memory requirements. To enhance the robustness of the scheme, the designers of ASCON introduced extra key additions during the initialization and finalization phases. This ensures that even if a single state is recovered, the key recovery attack is still unfeasible.

The design strategies adopted are reported in

Table 1. ASCON design strategies, effects, and optimizations.

Design Strategy	Effect	Optimization
Permutation-based design	→ No key schedule required	• No hidden setup costs when changing keys
	→ Online plaintext and ciphertext processing	• Supports real-time encryption and decryption
	→ Reuse of core component	• Same permutation used by encryption and decryption
Simple initialization and finalization	→ Low overhead	• Efficient for short messages
Small-state	→ Low memory footprint	• Fits in CPU registers, reducing cache reloads and attacks
	→ Efficient memory usage	• Faster and simpler HW implementation
	→ Platform adaptability	• Supports a wide range of architectures
Bit-sliced S-boxes	→ Prevents cache-timing attacks	• Low-cost side-channel countermeasures
Low algebraic degree of S-box	→ Compact implementation	• Easy first- and higher-order protection via masking
64 bit words, simple bitwise operations	→ Efficient linear and nonlinear layers	• SIMD acceleration and dedicated HW implementations

.

ASCON Permutation

The permutation function is the core element of all ASCON schemes. It operates on a 320 bit state S, which is bit-sliced into five 64 bit register words in big-endian order as

$$S=S_r\left|\right|S_c=x_0\left|\right|x_1\left|\right|x_2\left|\right|x_3\left|\right|x_4$$

where $\left|\right|$ represents concatenation.

• Outer part ($S_r$): Consists of r bits, known as the rate and is the maximum number of data bits that an invocation of permutation will process.
• Inner part ($S_c$): Consists of c bits ($c=320-r$), known as the capacity.

The values of r and c define the specific ASCON variant. All ASCON schemes utilize the same underlying permutation function, which is applied iteratively in a substitution-permutation network (SPN)-like structure. The main component of this permutation is the round transformation denoted as $ASCON-p$. The ASCON round transformation consists of three sequential layers: $p_c$, $p_s$, and $p_l$ and can be represented as

$$ASCON-p=p_c\circ p_s\circ p_l$$

where ∘ represents function composition. These layers are designed to use a minimal number of simple bitwise Boolean functions, enabling efficient hardware implementations and SIMD-based software optimizations. The ASCON permutation pseudo-algorithm is reported in Algorithm 1. Each layer is detailed below.

• Round Constant Addition $p_c$. In this layer, a 1-byte round constant is XORed with the least significant bits of register $x_2$. The round constant value depends on the round index and ensures differential and linear cryptanalysis resistance (

  Table 2. Constants and round mapping.

  Constant:	0xf0	0xe1	0xd2	0xc3	0xb4	0xa5	0x96	0x87	0x78	0x69	0x5a	0x4b
  p12	0	1	2	3	4	5	6	7	8	9	10	11
  p8	–	–	–	–	0	1	2	3	4	5	6	7
  p6	–	–	–	–	–	–	0	1	2	3	4	5

  ).
• Substitution Layer $p_s$. Updates ASCON state by applying in a column-wise fashion (Figure 2, down) a 5 bit S-Box (Figure 2, up). Each bit position in the five state words is updated simultaneously. This step introduces non-linearity and vertical diffusion across the state.
  The S-box design was inspired by the $\chi$ mapping used in Keccak [21]. This choice offers multiple advantages:
  • High efficiency on 64 bit processors, allowing parallel execution.
  • Avoidance of lookup tables, mitigating cache-timing attacks in software implementations.
  • Algebraic simplicity (degree 2), facilitating first- and higher-order side-channel protection using masking or sharing-based countermeasures.
• Linear diffusion layer $p_l$. The linear diffusion layer (Figure 3) enhances diffusion within each register by performing two bitwise rotations and XOR operations. The chosen rotation values are similar to the SHA-2 $\mathsf{\Sigma }$ function [3], ensuring strong diffusion properties.

Algorithm 1 ASCON Permutation over 320 bit State

Input: Five 64-bit registers $x_0,x_1,x_2,x_3,x_4$ (big-endian order) Output: The updated state after applying the permutation for $i\leftarrow 0$ to rounds do                                                                         ▹ Step 1: $p_c$ - Addition of Round Constant       $RC\leftarrow (0xF-i)\parallel (0x0+i)$       $x_2\leftarrow x_2\oplus RC$                                                                                                                                   ▹ Step 2: $p_s$ - Substitution Layer       if $S-box\_lut$ then                                                          ▹ Apply the ASCON S-Box transformation using LUT            for $col\leftarrow 0$ to 63 do                  $y[0:4]\left[col\right]\leftarrow LUT(x_0\left[col\right]\parallel x_1\left[col\right]\parallel x_2\left[col\right]\parallel x_3\left[col\right]\parallel x_4\left[col\right])$            end for       end if       if $S-box\_afn$ then                                                          ▹ Apply the ASCON S-Box transformation using AFN            for $col\leftarrow 0$ to 63 do                  $y\left[0\right]\left[col\right]\leftarrow x_4\left[col\right]\wedge x_1\left[col\right]\oplus x_3\left[col\right]\oplus x_2\left[col\right]\oplus x_1\left[col\right]\wedge x_0\left[col\right]\oplus x_1\left[col\right]\oplus x_0\left[col\right]$                  $y\left[1\right]\left[col\right]\leftarrow x_4\left[col\right]\oplus x_3\left[col\right]\oplus x_2\left[col\right]\oplus x_3\left[col\right]\wedge x_1\left[col\right]\oplus x_2\left[col\right]\wedge x_1\left[col\right]\oplus x_1\left[col\right]\oplus x_0\left[col\right]$                  $y\left[2\right]\left[col\right]\leftarrow x_4\left[col\right]\oplus x_3\left[col\right]\oplus x_4\left[col\right]\wedge x_2\left[col\right]\oplus x_1\left[col\right]\wedge x_0\left[col\right]\oplus 1$                  $y\left[3\right]\left[col\right]\leftarrow x_4\left[col\right]\wedge x_0\left[col\right]\oplus x_4\left[col\right]\oplus x_3\left[col\right]\wedge x_0\left[col\right]\oplus x_3\left[col\right]\oplus x_2\left[col\right]\oplus x_1\left[col\right]\oplus x_0\left[col\right]$                  $y\left[4\right]\left[col\right]\leftarrow x_4\left[col\right]\wedge x_1\left[col\right]\oplus x_4\left[col\right]\oplus x_3\left[col\right]\oplus x_1\left[col\right]\oplus x_0\left[col\right]$            end for       end if                                                                                                                              ▹ Step 3: $p_l$ - Linear Diffusion Layer       $x_0\leftarrow x_0\oplus (x_0⋙19)\oplus (x_0⋙28)$       $x_1\leftarrow x_1\oplus (x_1⋙61)\oplus (x_1⋙39)$       $x_2\leftarrow x_2\oplus (x_2⋙1)\oplus (x_2⋙6)$       $x_3\leftarrow x_3\oplus (x_3⋙10)\oplus (x_3⋙17)$       $x_4\leftarrow x_4\oplus (x_4⋙7)\oplus (x_4⋙41)$ end for

2.2. ASCON Suite

The ASCON cipher suite comprises a family of authenticated encryption schemes along with the ASCON-Hash function, which is derived from the extendable output function ASCON-XOF. Its permutation-based design enables straightforward extensions with minor modifications, allowing ASCON to be adapted for Message Authentication Codes (MACs) and Pseudorandom Functions (PRFs), similar to the approach used in KMAC [22]. The parameters for each variant of the ASCON suite are reported in

Table 3. Parameters of the ASCON cipher suite.

		Bit Size		Perm. Rounds
Variant	Algorithm	Key K	Rate r	${\mathit{p}}_{\mathit{a}}$	${\mathit{p}}_{\mathit{b}}$
AED	ASCON-128	128	64	12	6
	ASCON-128a	128	128	12	8
	ASCON-80pq	160	64	12	6
Hash	ASCON-HASH	-	64	12	12
	ASCON-HASHa	-	64	12	8
XOF	ASCON-XOF	-	64	12	12
	ASCON-XOFa	-	64	12	8
MAC	ASCON-MAC	128	256/128	12	-
PRF	ASCON-PRF	128	256/128	12	-
	ASCON-PRFshort	128	128	12	-

.

2.2.1. ASCON AEAD

ASCON has two main variants (

Table 4. Recommended parameters for ASCON.

Cipher Variants	Bit Size of						Rounds
	State ($\mathit{S}$)	Rate (${\mathit{S}}_{\mathit{r}}$)	Capacity (${\mathit{S}}_{\mathit{c}}$)	Key ($\mathit{K}$)	Nonce ($\mathit{N}$)	Tag ($\mathit{T}$)	$\mathit{a}$	$\mathit{b}$
ASCON-128	320	64	256	128	128	128	12	6
ASCON-128a	320	128	192	128	128	128	12	8

) designed for different message lengths: ASCON-128, which processes 64 bit message blocks, and ASCON-128a, which processes 128 bit blocks. The AEAD schemes are parameterized by four values: the key length k (≤160 bits), the rate r (block size), and the number of rounds a and b.

The authenticated encryption procedure ${\mathcal{E}}_{k,r,a,b}$ takes as input a secret key K of k bits, a 128 bit nonce N, an initialization vector (IV), and arbitrary-length associated data A and plaintext P. The output is the ciphertext C and a 128 bit authentication tag T.

The encryption function is defined as

$${\mathcal{E}}_{k,r,a,b}(K,N,A,P)=(C,T)$$

(1)

The decryption returns the plaintext P only if the computed tag matches the received tag; otherwise, decryption fails. The decryption function is expressed as

$$D_{k,r,a,b}(K,N,A,C,T)=\{P,\perp \}$$

(2)

The encryption process, depicted in Figure 4a and Algorithm 2, consists of four stages.

• Initialization phase. In this phase, the 320 bit state is split into five 64 bit registers $x_0$ to $x_4$, as shown in

  Table 5. State layout of IV, K, and N across registers $x0$:$x4$.

  	Byte7	Byte6	Byte5	Byte4	Byte3	Byte2	Byte1	Byte0
  x0	IV[7]	IV[6]	IV[5]	IV[4]	IV[3]	IV[2]	IV[1]	IV[0]
  x1	K[15]	K[14]	K[13]	K[12]	K[11]	K[10]	K[9]	K[8]
  x2	K[7]	K[6]	K[5]	K[4]	K[3]	K[2]	K[1]	K[0]
  x3	N[15]	N[14]	N[13]	N[12]	N[11]	N[10]	N[9]	N[8]
  x4	N[7]	N[6]	N[5]	N[4]	N[3]	N[2]	N[1]	N[0]

  . The IV encodes the key length, rate, and round numbers, ensuring separation between different primitives. The state undergoes the $p_a$ permutation, acting as a non-invertible key derivation function (KDF), followed by an XOR with the secret key.
• Processing Associate Data. The input A is padded if its length is not a multiple of r, using a single ‘1’ followed by ‘0’s as necessary. Each resulting block is XORed with the first r bits of the internal state $S_r$, followed by an invocation of the $p_b$ permutation. To ensure separation from the next phase, the resultant state is then XORed with ‘1’.
• Processing plaintext. The plaintext P is padded and split into r bit blocks using the same padding rule as for A. Each plaintext block is XORed with $S_r$ and the result is stored as a ciphertext block $C_i$. The state undergoes the $p_b$ permutation after each block. The final ciphertext block is truncated to match the length of the last unpadded plaintext block.
• Finalization. This phase ensures message authentication. The state is XORed with the key K and undergoes the $p_a$ permutation, acting as a Tag-Generating Function (TGF). The 128 bit authentication tag T is extracted from the resulting state, authenticating both the associated data and the encrypted message.

The decryption process is almost identical to encryption, with the roles of plaintext and ciphertext reversed (Figure 4b).

Algorithm 2 ASCON AEAD Encryption Algorithm

1: Input: Secret key K, Nonce N, Associated Data A, Plaintext P  2: Output: Ciphertext C and Authentication Tag T                                                                   ▹ Initialization  3: $IV\leftarrow K\left|\right|r\left|\right|a\left|\right|b\left|\right|0^{(160-|len(K))}$  4: $S\leftarrow IV\left|\right|K\left|\right|N$  5: $S\leftarrow p_a(S)\oplus (0^{(320-len(K))}\left|\right|K)$                                                                               ▹ Processing Associated Data  6: $A_{\mathrm{padded}}\leftarrow \mathrm{padding}(A)$  7: $A_1,\dots ,A_s\leftarrow \mathrm{split}(A_{\mathrm{padded}})$  8: for $i=1$ to s do  9:       $S_r\leftarrow S_r\oplus A_i$ 10:       $S\leftarrow p_b(S_r\left|\right|S_c)$ 11: end for 12: $S\leftarrow S\oplus 1$                                                                                                                       ▹ Processing Plaintext 13: $P_{\mathrm{padded}}\leftarrow \mathrm{padding}(P)$ 14: $P_1,\dots ,P_t\leftarrow \mathrm{split}(P_{\mathrm{padded}})$ 15: for $i=1$ to $t-1$ do 16:       $S_r\leftarrow S_r\oplus P_i$ 17:       $C_i\leftarrow S_r$ 18:       $S\leftarrow p_b(S)$ 19: end for 20: $S_r\leftarrow S_r\oplus P_t$ 21: $C_t\leftarrow \mathrm{truncate}(S_r)$                                                                                                                         ▹ Finalization 22: $S\leftarrow S\oplus (0^r|\left|K\right||0^{(c-|K|)})$ 23: $S\leftarrow p_b(S)$ 24: $T\leftarrow S[127:0]\oplus K$

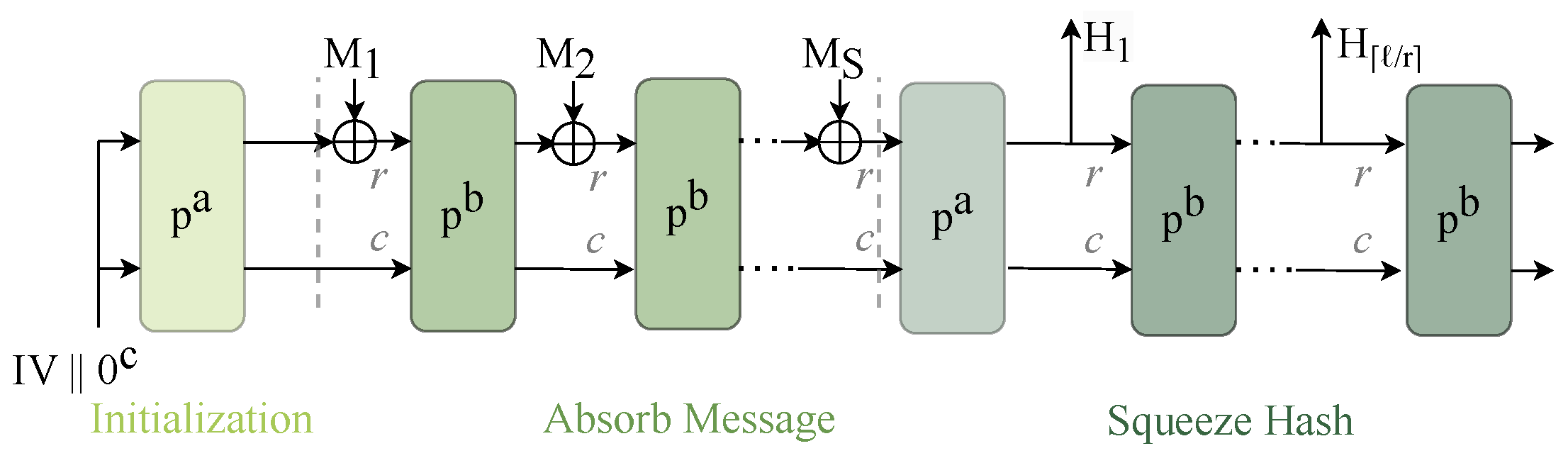
2.2.2. ASCON Hash and XOF

The sponge construction naturally extends to support hashing and extendable output functions (XOFs). Both ASCON-Hash (fixed output size) and ASCON-XOF (variable output size) use the same internal hashing function $X_{h,r,a}$, parameterized by the rate (data block size) r, round number a, and output length limit h. ASCON-Hash produces a fixed 256 bit Hash ($h=256$), while ASCON-XOF maps an input message M to an output H of arbitrary length ($h=0$ for unlimited output).

The hashing procedure (Figure 5) consists of three stages:

• Initialization: The 320 bit initial state is defined by r, a, and h. The permutation $p_a$ is applied to this state. Since the initial state is fixed, its transformation can be precomputed for efficiency.
• Message Absorption: ASCON-Hash and ASCON-XOF process the message M in r bit blocks. The same padding rule as ASCON-AEAD is used: a ‘1’ followed by the minimal number of ‘0’s to align the message length to a multiple of r. The padded message is split into blocks $M_1,\dots ,M_s$, each XORed with the first r bits of the state $S_r$, followed by a $p_a$ permutation.
• Squeezing: The Hash output is extracted in r bit blocks $H_i$ until the requested output length $\le h$ is reached. After each extraction, S undergoes another $p_a$ permutation.

Both ASCON-Hash and ASCON-XOF provide 128 bit security against collision attacks and (second) pre-image attacks.

2.3. Side Channel Attacks

Attempting to break cryptographic algorithms by looking for fundamental mathematical weaknesses is usually very complex and often unsuccessful. However, once these algorithms are implemented in hardware or software, operating in unprotected environments, they become vulnerable to a class of attacks known as side-channel attacks. By analyzing the runtime signatures of devices executing an algorithm, attackers can extract information about secret data, significantly reducing the difficulty of breaking the system. In a passive, non-invasive scenario, the attacker does not interfere with the device’s operation but instead infers secret information by observing its behavior. The device may leak information through execution time, power consumption, or electromagnetic (EM) emissions. Timing leaks are sometimes easier to detect and exploit but can often be mitigated by ensuring constant-time execution. In contrast, power or EM leakage is harder to suppress because it arises from switching activities within the device. Typically, an attacker will collect multiple power or EM traces while the device processes different inputs; for power analysis, the required equipment is relatively inexpensive [23]. A generic scheme depicting the setup for power and EM leakages analyses is depicted in Figure 6.

Regardless of whether the side channel measured is power or EM, the total observed signal can be expressed in the same way:

$$M(t)=M_{\mathrm{Sdata}}(t)+M_{\mathrm{Noise}}(t)+M_{\mathrm{algoNoise}}(t),$$

(3)

where $M_{\mathrm{Sdata}}(t)$ depends on the secret data being processed, $M_{\mathrm{Noise}}(t)$ includes noise introduced by the measurement setup, and $M_{\mathrm{algoNoise}}(t)$ captures other operations running on the device.

Before performing a side-channel attack, it is essential to verify whether the cryptographic implementation leaks sensitive information. The most common method is the test vector leakage assessment (TVLA) [24], which checks whether the side-channel measurements depend on sensitive data (e.g., the input). Two sets of traces are collected: one with fixed input $G_A$ and another with random input $G_B$. Welch’s t-test, Equation (4), is then applied.

$$t={\displaystyle \frac{{\mu }_A-{\mu }_B}{\sqrt{\frac{{\sigma }_A^2}{N_A}+\frac{{\sigma }_B^2}{N_B}}}}$$

(4)

${\mu }_A$ and ${\mu }_B$ are the sample means, ${\sigma }_A$ and ${\sigma }_B$ the sample standard deviations, and $N_A$ and $N_B$ are the numbers of traces in groups A and B, respectively. Since traces are vectors over time, t is computed point-wise. A $\left|t\right|>4.5$ strongly suggests the presence of leakage.

Once the cryptographic device leaks are established, a common method to exploit such a leakage is to guess part of the key (the sub-key) and compute the corresponding intermediate values for each known input. By applying a leakage model, for example, Hamming Weight or Hamming Distance, these intermediate values are translated into hypothetical leakage predictions. The recorded traces are then grouped according to these predictions, and a statistical test (such as correlation [25]) is performed to see which guessed sub-key produces the most distinguishable differences among the grouped mean traces. If the guess is incorrect, the mean traces appear very similar and differ only by noise. However, if the guess is correct, a clear divergence emerges around the point in time where the intermediate value is processed, indicating the correct sub-key. Two widely used metrics for evaluating attack effectiveness are the n-th order success rate (n-SR) and the guessing entropy ($GE$). The n-SR measures the fraction of trials in which the correct candidate ranks at or above a given threshold n. The $GE$ is the expected rank of the correct candidate, where a $GE$ of 1 implies that, on average, the correct key guess is ranked first. By iterating this process for each sub-key until all sub-keys have a $GE$ of 0, the full key can be successfully recovered.

A limitation of this standard approach is that it often requires a large number of traces collected directly from the target device. An alternative is to build a leakage model using a similar (ideally identical) device under controlled conditions. This is known as profile or template attacks: even a single trace from the actual target device can suffice to recover the key [26].

3. ASCON HW Accelerators

Many hardware implementations of ASCON have been proposed in the literature, with various architectures and integration methodologies. This variety of designs is due to an equally wide variety of applications. As already mentioned, lightweight cryptography is of primary importance in the IoT ecosystem, ensuring secure communication between the sensor nodes and the gateway device. A broad range of IoT nodes exists, each one dedicated to a specific application, thus requiring specific constraints. Smart street lighting, smart parking, and smart waste management solutions require strict area requirements, as the sensors for these applications must have a very small footprint. In addition to this, many of them rely on batteries. Consequently, power consumption and energy are fundamental. Conversely, throughput might be the main concern for other applications requiring the encryption of great amounts of data in real-time, such as video surveillance cameras or smart public transportation systems. Depending on the application, one design may be more suitable than another.

Concerning the architectures, a preliminary distinction can be made:

• Serialized Implementation. The aim of this approach is to obtain a compact accelerator. For this purpose, the S-Box implementation is reduced to process one bit per clock cycle. Obviously, registers are needed to store intermediate results.
• Unrolled Implementation. This implementation is used to obtain high throughput. The allocated hardware is repeated n times to increase throughput at the cost of area. In the fully unrolled version, the encryption and decryption are executed in one clock cycle. Since the updated state is directly fed to the next round, in this version, no registers are needed. Of course, for each unrolling degree, the critical path and, hence, the delay, will increase due to the additional combinational logic.
• Round-based Implementation. This approach offers the best trade-off between throughput and area. The hardware is re-utilized to execute m permutations (or rounds in one clock cycle). Therefore, differently from the previous technique, only the resources required by the permutation are repeated. Obviously, the higher m, the higher the area occupation and delay. In this case, the intermediate state must be stored.

Another classification of the accelerators can be made depending on the integration methodology within a larger system:

• Stand-alone IPs: The accelerator works independently, despite the system it is integrated in.
• Coprocessors: Although interfaced with the CPU, they exploit their own registers.
• Instruction Set Extensions (ISEs): The hardware is directly integrated within the CPU microarchitecture and has direct access to the internal registers.

The following sections provide a more detailed overview of the state of the art of the ASCON hardware implementations. Papers are categorized according to the type of application. When combined with the architectural and integration methodology distinctions discussed earlier, this classification can be useful in easily identifying the most suitable hardware implementation that meets the requirements of a specific user application. It is important to note that the focus is placed on works proposing novel techniques or insightful advancements on the topic. Other papers implementing well-known techniques but still obtaining competitive results are only included in the final comparison (Section 3.4), which thus features a broader selection of articles.

3.1. Low Area

Lightweight cryptography has the inherent constraint of occupying a small amount of the resources. Consequently, many works propose implementations aiming to occupy as little area as possible. Khan et al. [27] proposed a comparison between two implementations: an unrolled strategy and a recursive approach, analogous to the round-based one. The first architecture was used as a baseline to analyze how much area could be saved without compromising the throughput. The results for different FPGAs proved that the best $Throughput/Area$ was obtained when the hardware was optimized to perform two permutations per cycle, with a total of 24 cycles for encryption or decryption for ASCON-128 and ASCON-128a. In this configuration, the area could be reduced by up to 8 times with respect to the unrolled strategy.

A similar design space exploration was expanded upon in [28]. Along with unrolled and round-based implementations, a serial architecture was analyzed. Obviously, this last option was the most compact one, as a serial, scalable S-Box was employed. Starting from a one bit per clock cycle version, more options were explored to observe the impact of processing multiple bits per clock cycle. In this case, however, the area overhead given by the support circuits grew. The one-bit-per-cycle implementation occupied half the area of the round-based architecture (one permutation per cycle) and was almost 9 times smaller than the unrolled one. When four or more bits per cycle were used, the area advantages were almost completely lost.

Khan et al. [29] presented an analogous comparison with respect to [28], with the additional value of proposing an open-source design. Also in this case, three different architectures were examined: loop-folded, i.e., round-based; loop-unrolled; and fully unrolled. The difference between the last two implementations was in the number of permutations executed in a clock cycle: the fully unrolled was a loop-unrolled architecture where the maximum number of rounds per cycle was executed. In this case, the results were provided considering two ASIC technologies. For SAED 32 nm technology, the loop-folded version provided an 8x area reduction with respect to the fully unrolled one; the open-sourced 45 nm standard cell library yielded an enhancement of up to 10×.

An alternative design based on the ASCON permutation with the aim of obtaining a more lightweight AEAD scheme, Sycon, was proposed by Mandal et al. [30]. With respect to ASCON, Sycon was characterized by a lighter S-Box layer with the same cryptographic properties, demonstrating resistance to cryptanalitic attacks. Differently from ASCON, the key was not added to the capacity part of the internal state but to the rate part. This saved XOR gates but produced $\lceil key\_size/block\_size\rceil$ extra permutation calls. Overall, Sycon AEAD occupied approximately 85% of the ASCON AEAD footprint.

In [31], a design implementing ASCON-128 and ASCON-128a was evaluated on different AMD-Xilinx 7-series FPGA: Kintex-7, Virtex-7, Spartan-7, and Artix-7. The ASCON permutation block was implemented using an iterative approach, i.e., round-based, to minimize area and power consumption. The architecture also included input and output buffers to hold the initial values and results, respectively, for encryptions and decryptions. Their function was to replace instantiated and compiled memories, thus reducing access time for reading/writing data. The results showed that the minimum area was obtained on Kintex-7 and the maximum was obtained on Spartan-7. However, the variability range was approximately 300 LUTs.

Athanasiou et al. [32] proposed a complete ASCON coprocessor, able to perform not only ASCON-128 and ASCON-128a schemes but also the Hash, Hasha and MAC functionalities. The coprocessor relied on the ASCON IP, which included an input scheduler to arrange the inputs depending on the type of operation to perform, and all the peripherals for seamless integration in a SoC, such as two asynchronous FIFOs, a register file, an interrupt generator, and AMBA AHB, and APB interfaces. The design was implemented on both FPGAs (Artix-7, Virtex-7, Kintex-7) and synthesized in FD-SOI 22 nm technology. Considering the Artix-7 implementation, the ASCON IP occupied approximately 42% of the whole coprocessor.

Another ASCON loosely coupled accelerator was designed in [33]. The round-based architecture, supporting AEAD and Hash schemes, was integrated into a RISC-V SoC featuring a SERV core. Differently from most of the works in the literature, this design was both implemented on FPGA and physically implemented on a 180 nm CMOS chip. Although the on-chip measurements reported a core of 17.4 kGE, corresponding to 20% of the SoC area, the best area results were obtained for the FPGA case with 1277 LUTs and 366 FFs.

Steinegger and Primas [34] proposed an open-source RISC-V instruction extension to accelerate ASCON permutation. The accelerator was tightly coupled to the RI5CY core and exploited 10 out of the 32 available registers of the CPU register file. In this way, the load/store overhead were significantly reduced. Obviously, the decode unit was modified to be able to support the new custom instructions. The ASCON core occupied approximately 9% of the RI5CY base design.

3.2. Low Energy and Power

When talking about resource-constrained devices, the area is not the only metric to take into account. It is paramount that also the energy and power consumption are below a certain level to avoid faults and errors. This is especially critical for battery-powered IoT sensor nodes, which have limited energy availability and cannot sustain high power demands. Despite the importance of these metrics, many works in the literature provide incomplete or no information on energy and power results. This subsection tries to summarize the best achievements regarding these metrics in the state of the art.

Roussel et al. [35] proposed a CMOS/MRAM-based hardware implementation of the ASCON cipher to enhance the recovery of the accelerator from an unplanned power failure. The key idea was to replace the usual CMOS flip-flops with non volatile flip-flops (NVFF) based on CMOS/Spin Trasnfer Torque (STT) MRAM hybridization: in this way, the architecture was able to restore the previous state in case of power failure. To do so, the NVFF was designed and characterized to perform all the steps of the ASIC design flow. The Synopsys PrimePower tool results demonstrated that the hybrid implementation outperformed the CMOS one in terms of total power by 4%, at the cost of a 5% increase in area. Furthermore, by preventing loss information in the case of power failure, this architecture offered an energy saving of 11% to 48%.

Although focused on the Internet of Medical Things (IoMT), Raj and Bodapati [36] presented a low-power round-based ASCON design. A 5 bit S-box was implemented using two LUT6 and one LUT5 on Artix-7, producing a power consumption of 3 mW against the total power of the complete design, which was equal to 31 mW.

The ASCON coprocessor presented in [37] was not only a high-throughput, reconfigurable architecture but also demonstrated promising results in terms of power consumption and energy efficiency. Supporting ASCON-128, ASCON-128a, ASCON-Hash, and ASCON-Hasha modes, the ASCON core was composed of a round-based structure, along with the required logic to manage arbitrary round numbers, variable XOR operands, and block sizes. Besides the ASCON core, the coprocessor also included FIFOs and I/O interfaces to enable integration in more complex systems. The results with Synopsys’ 28/32 nm technology reported power consumption of 1.9 mW at 667 MHz and energy per bit ranging from 0.219 pJ/bit for the ASCON-128 scheme to 0.637 pJ/bit for the Hash.

Some of the works mentioned in the previous sections, particularly [28,29,31,33], not only proposed low-area designs but also low-power ones. This was quite expected, as the lower the resource occupation, the lower the total power consumption. Particularly, among all the implementations proposed in [28], the one consuming the least power was the 1-p round-based implementation (one permutation per clock cycle), close to the serialized architecture. However, the energy consumption of the latter was approximately two orders of magnitude higher than that of the former. The energy was indeed defined as $e=(Power·Latency)/Frequency$ and the serialized implementation provided a much longer latency with respect to the round-based one. The same power trend was obtained in [29]. In this case, the power–delay product was reported: as expected, the higher the unrolling factor, the higher both the critical path and the power, as the chip size became larger and larger.

As mentioned in the previous section, Alharbi et al. [31] implemented a round-based architecture on different FPGAs. This not only minimized the area occupation but also the power consumption. Even though the Kintex-7 implementation provided the smallest area, the best results in terms of power were achieved by the Spartan-7 device due to its reduced achieved frequency.

Finally, for the architecture presented in [33], the power remained below 1 μW, although these results referred to a low frequency of 32 kHz. The delta between the leakage power and the active state of the system was 0.8 μW.

3.3. High Throughput

As mentioned in [8], ASCON was designed to provide the best trade-off between security, size, and speed in both software and hardware. Consequently, although paramount, resource consumption optimization may not be of primary importance in a hardware implementation. As a matter of fact, for certain applications requiring the real-time encryption of data, such as video surveillance, throughput may be one of the main concerns. The main technique to obtain a high-throughput implementation is to employ an unrolled or high-degree round-based architecture, as widely proven in the literature.

The unrolled architecture presented in [28] computed a single encryption and decryption in a combinational circuit, achieving a throughput increase of almost 120 times with respect to the one-bit-per-cycle implementation for both the ASCON128 and ASCON128-a schemes and approximately 2 times with respect to the round-based design computing two rounds per clock cycle (2-p). However, the best throughput-area trade-off was obtained considering the 3-p round-based architecture. This configuration also allows one to find a balance between latency and critical path, which, for the unrolled implementation, increases excessively.

Although used only as a baseline for a comparison with respect to the round version, the unrolled architecture of [27] achieved more than 1.3 Gb/s of throughput on a Virtex-7 FPGA for the ASCON-128 scheme and more than 2.4 Gb/s for the ASCON-128a variant.

Different degrees of loop-unrolled architectures were analyzed in [29]. The throughput increased as the number of rounds executed in a clock cycle increased. However, beyond an unrolling of the third degree, the throughput started to decrease. This was due to the fact that the latency was not consistently decreased. Of course, the maximum throughput was obtained by a fully unrolled implementation. In both the analyzed technologies (SAED 32 nm and open-sourced 45 nm standard cell library), the fully unrolled implementation produced a speed-up of 2.5× with respect to the loop-folded architecture, for both the ASCON-128 and ASCON-128a schemes.

The same analysis was conducted in [38]. As mentioned in Section 3.1, four architectures were considered, implementing one, two, four, and six rounds, respectively. The throughput of ASCON-Hash obtained by the six-round design was approximately 2 times the one obtained by the 1-round implementation.

Tran et al. [39] also implement unrolling. During the initialization and finalization phases, the ASCON permutation was unrolled four times, whereas, in the associated data and processing plaintext/ciphertext phases, the unrolling factor was equal to 8. In this way, the system was able to process 128 bits in each clock cycle. The accelerator was also provided with a dedicated interface to effectively communicate with AXI4- and FIFO-based systems. The ASCON core was implemented on a Virtex-7 FPGA, resulting in a remarkable throuhgput of approximately 13 Gb/s.

Malal [40] presented a high-performance architecture, tailored for ASCON-128 and ASCON-128a. The hardware could be configured depending on the type of scheme. For ASCON-128, the architecture processed six rounds per cycle, as the number of permutations was a multiple of six. For the same reason, in the case of ASCON-128a, four rounds per cycle were processed. In this way, 128 bits were encrypted/decrypted in two cycles. The design was implemented on three different FPGAs: Artix-7, Kintex-7, and Spartan-7. For all the platforms, the implementation reached high values of throughput, ranging from 3.5 Gb/s (ASCON-128, Artix-7) to 10 Gb/s (ASCON-128a, Kintex-7). The best results were obtained on the Kintex-7 FPGA with regard to both throughput and throughput/area metrics.

Unrolling is not the only way to obtain high throughput. Pallavi et al. [41] proposed a different high-frequency architecture for ASCON encryption by modifying how the internal 320 bit state was processed: it was divided into two parts of 64 and 256 bits, respectively, which were then processed in parallel. The increase in hardware was rewarded by an increased frequency and throughput, as proven by the results obtained from four different FPGAs (Artix-7, Spartan-6, Virtex-7, and Zynq).

Albeit proposing a round-based architecture, Nguyen et al. [33] obtained high-throughput results for their Artix-7 implementation, with 2.233 Gb/s for the ASCON-128 scheme. Conversely, the ASIC results were less prominent due to the fact that, differently from other works, they were not obtained from simulations but from a physical chip.

The new, lighter, ASCON-based permutation proposed in [30], Sycon, obtained both a more compact design and higher performance. As mentioned in Section 3.1, in Sycon, the key was not added to the capacity part of the internal state but to the rate part. This implied a shorter critical path with respect to ASCON due to the removal of the message absorption module and various multiplexers in the critical path. Furthermore, the longer the message size, the more the additional $\lceil key\_size/block\_size\rceil$ extra permutation calls were amortized. At maximum frequency, Sycon-AEAD-64 throughput increased by 3 times, moving from a message size of 256 bits to a length of 4096 bits.

The tightly coupled accelerator designed by Steinegger and Primas [34] not only managed to achieve a low area but also a boosted throughput. The accelerated version of ASCON achieved a speed-up factor of 50 for the AEAD and 80 for the Hash.

Both the coprocessors presented in [32,37], mentioned in the previous sections, presented significant results in terms of throuhgput. Ref. [37] reached a maximum frequency of 213 MHz on Artix-7, with the ASCON-core achieving 244 MHz. The Synopsys’ 28/32 nm technology results demonstrated a maximum throuhgput of 9 Gb/s (ASCON-128a) and a minimum that was still higher than 3 Gb/s (Hash). Ref. [32], implementing a similar architecture, showed comparable performance, with throughput for the ASCON-128a scheme of 1.9 Gb/s and 10.2 Gb/s for FPGA (Artix-7) and ASIC (FD-SOI 22 nm), respectively.

3.4. Comparative Analysis

This subsection carries out a comparative analysis among the various works in the literature implementing ASCON accelerators. The focus is placed on the ASCON-128 scheme, as the implementations demonstrate similar trends in terms of PPA metrics for other ASCON variants.

A first direct comparison of the throughput-area trade-off is depicted in Figure 7 for both the FPGA and ASIC implementations. The power and energy results are not included in this first examination as too few papers reported these metrics. It is important to note that most of the previously mentioned works are included in this comparison. However, some of them did not report sufficient information for all the metrics; hence, they are not displayed. Others, such as [42,43,44], were not formerly cited, as they make use of well-known and already described techniques but still provide interesting results. These graphs confirm the points discussed in the preceding subsections. The unrolled implementations were obviously the most expensive in terms of area, although providing a high throughput. The most compact ones were [28] (FPGA) and [35] (ASIC). Ref. [28] proposed a serial implementation of the ASCON S-box, producing one bit per cycle. Consequently, the hardware resources were minimized at the cost of throughput. Nevertheless, ref. [42] presented an even lower result, approximately equal to 3.05 Mbps. In fact, the ISE proposed in [42] provided a minor level of acceleration with respect to the complete architecture presented in [28]. The best throughput–area trade-off was obtained by [32,33] among the various FPGA implementations and [30] among the ASIC ones.

In

Table 6. Best works for each specific constraint—ASCON-128.

	Device	Work	Freq [MHz]	Area	Thr. [Mbps]	Thr./Area	Power [mW]	Energy [nJ/bit]
Best area	FPGA	[28]—serial (one-bit-per-cycle version)	232.6	LUTs: 1030	6.5	0.006 Mbps/LUTs	57	10.25
	ASIC	[35]	100	5246.3 $\mathsf{\mu }{\mathrm{m}}^2$	66.7	0.0127 Mbps/$\mathsf{\mu }{\mathrm{m}}^2$	0.715	$6.69\times {10}^{-3}$
Best thr.	FPGA	[40]	92.59	LUTs: 2958, FFs: 595	5925.9	2.01	n.d	n.d
	ASIC	[37]	667	67,600 $\mathsf{\mu }{\mathrm{m}}^2$	5926	0.0877 Mbps/$\mathsf{\mu }{\mathrm{m}}^2$	1.9	$0.335\times {10}^{-3}$
Best power	FPGA	[36]	107	LUTs: 1330, FFs: 870	457	0.343 Mbps/LUTs	31	n.d.
	ASIC	[35]	100	5246.3 $\mathsf{\mu }{\mathrm{m}}^2$	66.7	0.0127 Mbps/$\mathsf{\mu }{\mathrm{m}}^2$	0.715	$6.69\times {10}^{-3}$
Best energy per bit	FPGA	[43]	100	LUTs: 1437, FFs: 366	884.1	0.615 Mbps/LUTs	n.d.	0.0385
	ASIC	[37]	667	67,600 $\mathsf{\mu }{\mathrm{m}}^2$	5926	0.0877 Mbps/$\mathsf{\mu }{\mathrm{m}}^2$	1.9	$0.335\times {10}^{-3}$

, the best implementations for each metric are reported. As already mentioned, refs. [28,35] provided the best area results. Ref. [35] also presented the most optimized design in terms of power: as a matter of fact, in contrast to other designs, Roussel et al. operated at the technological level, optimizing the architecture for this specific metric. Similarly, the high throughput achieved by [37] allowed this design to also obtain the best energy-per-bit result.

4. Protected ASCON Implementations

ASCON is designed with side-channel security in mind, thus avoiding conditional branches and lookup tables to mitigate timing attacks. Its nonlinear layer features a two-degree S-box, enabling low-overhead masking countermeasures. The leveled mode restricts the attack surface to only initialization and finalization [45]. Standardization analyses confirm these security strategies [6], contributing to ASCON’s selection as the new LWC standard. However, leakage evaluations [46] have identified vulnerabilities, particularly during the initialization phase, and recent attacks have successfully exploited these weaknesses, even breaking protected implementations.

4.1. Passive Attacks on ASCON

The initial state of ASCON consists of a 64 bit initialization value ($IV$), a 128 bit key (K), and a user-defined 128 bit nonce (N), which can be varied at each run. The nonlinear layer is vulnerable to power analysis. At initialization, two of the five input bits to the S-box correspond to secret key bits, with the remaining three being known. This dependency on a sub-key and a user-controlled nonce enables differential analysis attacks.

The ASCON state is stored in five 64 bit registers, shown in the Figure 5, denoted as $x_0:x_4$. The K’s upper half is stored in $x_1$, while lower half is stored in $x_2$. The user-defined N is stored in $x_3$ and $x_4$ and the IV is stored in $x_0$. The S-box output can be expressed in Algebraic Normal Form (ANF) as a Boolean polynomial over $GF(2)$. In power or electromagnetic (EM) analysis, all the bits contributing a constant amount to register activity, specifically $x_0$, $x_1$, $x_2$, and their combinations, can be disregarded. The equations obtaining the transformation are reported in

Table 7. S-box transformations in ASCON with updated notation.

	Algebraic Expression	Equivalent Expression
$S-box(x_0):y_0^{S-box}$	$x_4·x_1+x_3$	$m^{\prime }·k^{″}+m^{″}$
$S-box(x_1):y_1^{S-box}$	$x_3·(x_{1,2}+1)+x_4$	$m^{″}·(k^{\prime }+1)+m^{\prime }$
$S-box(x_2):y_2^{S-box}$	$x_4·(x_3+1)+1$	$m^{\prime }·(m^{″}+1)+1$
$S-box(x_3):y_3^{S-box}$	$(x_4+x_3)·(x_0+1)$	$(m^{\prime }+m^{″})·(iv+1)$
$S-box(x_4):y_4^{S-box}$	$x_4·(x_1+1)+x_3$	$m^{\prime }·(k^{\prime }+1)+m^{″}$

. In the attack, it is not possible to distinguish the XOR between $x_1$ and $x_2$, so their result is regarded as a single term, denoted as $x_{12}$. To simplify notation, the secret values $x_1$ and $x_{1,2}$ are represented as $k^{″}$ and $k^{\prime }$, respectively, while the values $x_3$ and $x_4$ are denoted as $m^{″}$ and $m^{\prime }$.

From the equations in Table 7, it can be observed that $y_2^{S-box}$ and $y_3^{S-box}$ cannot be attacked since they do not contain nonlinear terms combining both a key and a nonce. To recover the key, the first half of the key ($x_1$) can be retrieved by attacking $y_0^{S-box}$. The combined key term $x_{1,2}$ can then be extracted by analyzing the transformations affecting the $x_3$ or $x_4$ registers.

The first attack on ASCON was demonstrated by Niels et al. [47], who used differential power analysis (DPA) to perform key recovery attacks on hardware implementations of ASCON. The selection function, reported in Equation (5), extracts the key by correlating the register switching activity, known as the Hamming distance, of registers $x_0$ and $x_1$ with power consumption. In the linear diffusion layer, each register undergoes two rotations and is XOR’ed with itself ${\mathsf{\Sigma }}_i(x_i)$, meaning that guessing the output bit of $x_0$ and $x_1$ reveals three key bits. A full key recovery requires 30 CPA attacks to recover the first half of the key and 33 more for the second half. This method extracts the 128 bit key using 50 k power traces. However, the choice of column index output bits, which may impact attack efficiency, is not explained.

Output bit of first-round function:

$$\begin{array}{cc}\hfill S{0}_i(M,K)& =m_i^{\prime }·k_i^{″}+m_i^{″}+m_{i+45}^{\prime }·k_{i+45}^{″}+m_{i+45}^{″}+m_{i+36}^{\prime }·k_{i+36}^{″}+m_{i+36}^{″}\hfill \\ \hfill S{1}_i(M,K)& =m_i^{″}·(k_i^{\prime }+1)+m_i^{\prime }+m_{i+3}^{″}·(k_{i+3}^{\prime }+1)+m_{i+3}^{\prime }+m_{i+25}^{″}·(k_{i+25}^{\prime }+1)+m_{i+25}^{\prime }\hfill \end{array}$$

(5)

Using the same leakage model, Picek et al. [48] performed side-channel attacks on both unprotected and first-order protected software implementations of ASCON-128 v1.2 optimized for ARMv7-M microcontrollers [49]. The attack efficiency was improved by carrying out pre-processing on registers. The registers that leaked the most were identified by evaluating leakage through the signal-to-noise ratio (SNR). They found that register $y_4$ leaked nearly four times stronger than $y_1$, likely due to differences in ARM register usage. Correlation power analysis (CPA) was performed on the round function output, targeting 8 bit segments of the register. The full 128 bit key was successfully recovered with approximately 8000 traces and showed that the reference implementation was not side-channel secure. However, for the protected implementation, CPA failed even after 60 k traces due to noise amplification caused by the masking scheme. Since CPA was ineffective on the protected implementation, they applied a profiling attack using supervised deep learning (DL-SCA). The neural network trained to extract leakage information consisted of stacked convolutional layers followed by fully connected layers. Guessing entropy, accuracy, and loss were tracked on the validation set during training to evaluate performance. Two leakage models were considered: (i) The S-box Output Model, which targeted the nonlinear S-box output. This was highly effective for key recovery: for the unprotected implementation, it recovered a partial key after only 20 traces. Even on the protected dataset, the leakage remained significant, making this model a strong attack vector. (ii) The Output Register Model, which exploited the correlation between power consumption and the store operation of the S-box output register. Instead of attacking the full 32 bit register, the attack targeted 8 bit segments sequentially. In the unprotected implementation, key recovery required only 200 traces. However, in the protected version, the masking scheme effectively mitigated this leakage, preventing key extraction.

The results of the attacks using differential power analysis are reported in Table 8.

After training a model to recover partial keys, a multi-task learning approach was used to estimate multiple partial keys simultaneously. On the unprotected dataset, all partial keys converged to a guessing entropy (GE) of zero. However, some keys failed to generalize due to persistent prediction errors. The model ranked correct key candidates at fixed positions rather than randomly across traces, highlighting its limitations. While the multitask model recovered some partial keys, it failed to generalize across all of them.

Despite DLSCA’s strong performance, hyperparameter tuning remains a key challenge in optimizing models. One potential solution is the ensemble technique, in which multiple suboptimal neural networks are combined to improve overall performance. Following this approach, Rezaeezade et al. [50] applied an ensemble method to attack two publicly available datasets (https://zenodo.org/records/10229484 accessed on 29 March 2025) of 32 bit optimized ASCON-128 v1.2 implementations (one unprotected, one first-order protected). Using five neural networks, they tested two architectures: Multi-Layer Perceptron (MLP) and Convolutional Neural Networks (CNNs). Against the unprotected implementation, the CNN ensemble performed similarly to Picek et al.’s multi-task model, recovering the key with ∼1 k traces, while the MLP ensemble outperformed both, requiring only ∼100 traces. The authors attributed the CNN’s lower performance to inadequate hyperparameter tuning. The ensemble method’s success on the unprotected implementation matched that of a model selected via Bayesian optimization, confirming that an ensemble of weaker learners can rival advanced tuning techniques. The ensemble technique demonstrated its superiority over ASCON protection, where, unlike the multi-task model, the ensemble method was able to fully recover the key with fewer than 3000 traces. These results highlight the need for stronger countermeasures against DLSCA in future implementations.

The vulnerability of ASCON AEAD was further demonstrated in [51] through template attacks on ASCON-128 implementations (https://github.com/rweather/lwc-finalists/tree/5d2b22c9ff7744be429cabda0c078ea5b7b6f79e/src/individual accessed on 29 March 2025) running on an STM32F303 (ARM Cortex-M4). The attack began with a fragment template attack, using a modified Linear Discriminant Analysis (LDA) to extract side-channel leakage from the 32 bit device. Due to the inherent noise sensitivity of template attacks, the correct key candidate could sometimes rank below the top. Additional techniques were used to improve the attack. For instance, belief propagation (SASCA) refines likelihood tables by incorporating algorithmic dependencies between intermediate values; key enumeration, which is an optimized brute-force search to find key candidates beyond the top-ranked ones; and pre-processing, like interesting-point selection. The combination of these techniques made the attack more efficient and accurate than DLSCA. The method was tested on both unmasked and masked implementations, considering the impact of compiler optimizations on attack success rates. For the unmasked implementation, 64 k traces were used to build templates for two compiler settings: one optimized for space (U-0s) and another for time (U-03s). In U-0s, a single attack trace achieved nearly 100% success, with key enumeration costing less than $2^{20}$ steps. This high success rate was attributed to residual 8 bit instructions in a 32 bit adaptation of ASCON, making profiling alone sufficient. In contrast, U-O3 fully converted instructions to 32 bit, requiring belief propagation and key enumeration to recover the key. Even then, no more than 10 traces were needed. For the masked implementation, only the space-optimized version (M-0s) was attacked. Single-trace attacks failed, but, with at least five traces recorded using the same key, a $2^{36}$ key enumeration became successful.

Table 8. Statistical side-channel attacks on ASCON.

Work	ASCON Implementation	FPGA/MCU	Freq [MHz]	SCA Workstation		Attack Strategy	SR = 1
				Board	Oscilloscope
[47]	AEAD (ASCON-128) one-round-per-cycle HW implementation	Spartan-6 XC6SLX75	48	SAKURA-G	Lecroy Waverunner z610i (500 MSample/s)	DPA on Hamming weight of the S-box output	∼50 k traces
[48]	AEAD (ASCON-128) SW optimized for ARMv7-M	STM32F4 ARM Cortex-M4	7.37	ChipWhisperer Lite	Integrated 8 bit oscilloscope	CPA on S-box output (8 bit at a time)	∼8 k traces with unprotected, unsuccessful with first-order protected
[52]	AEAD of ASCON-128 (single S-box, 64 cycles/round)	Artix-7	n.d.	NewAE CW305 board	PicoScope 5000 (125 Samples/clk)	Self-supervised deep learning SCA on power traces	∼24 k traces

Table 8. Statistical side-channel attacks on ASCON.

Work	ASCON Implementation	FPGA/MCU	Freq [MHz]	SCA Workstation		Attack Strategy	SR = 1
				Board	Oscilloscope
[47]	AEAD (ASCON-128) one-round-per-cycle HW implementation	Spartan-6 XC6SLX75	48	SAKURA-G	Lecroy Waverunner z610i (500 MSample/s)	DPA on Hamming weight of the S-box output	∼50 k traces
[48]	AEAD (ASCON-128) SW optimized for ARMv7-M	STM32F4 ARM Cortex-M4	7.37	ChipWhisperer Lite	Integrated 8 bit oscilloscope	CPA on S-box output (8 bit at a time)	∼8 k traces with unprotected, unsuccessful with first-order protected
[52]	AEAD of ASCON-128 (single S-box, 64 cycles/round)	Artix-7	n.d.	NewAE CW305 board	PicoScope 5000 (125 Samples/clk)	Self-supervised deep learning SCA on power traces	∼24 k traces

ASCON’s vulnerability to profiling attacks can be traced to its leveled side-channel protection strategy, where the key is applied four times during AEAD mode. This strategy, which primarily targets CPA/DPA-style attacks, inadvertently increases key exposure, making full recovery feasible.

Template attacks and supervised learning-based SCA are highly effective but require a matching reference device to collect a proper training set. An alternative is unsupervised learning, which derives the leakage model directly from measurements without prior knowledge. In [52], Ramezanpour et al. introduced a novel method, SCARL (Side-Channel Analysis with Reinforcement Learning), to perform attacks without a predefined leakage model. SCARL assumes that all information about the secret key is embedded in power measurements, given access to the algorithm’s input and/or output. It combines an LSTM autoencoder with reinforcement learning. The autoencoder maps raw power traces into an intermediate representation that captures key-correlated features, estimating the leakage model. The reinforcement learning algorithm then divides (clusters) these intermedite states based on features that exhibit the highest inter-cluster difference, which corresponds to differing key hypotheses. The correct key is the one that maximizes this cluster, similarly to how a DPA attack distinguishes between key candidates. This method was tested on an ASCON RTL implementation, where the S-box operation was processed over 64 clock cycles. Using 24 k power traces from the initialization round, SCARL successfully recovered the 128 bit key. The results of attacks using profiling analysis are reported in the

Table 9. Template side-channel attacks on ASCON.

Work	ASCON Implementation	FPGA/MCU	Freq [MHz]	SCA Workstation		Attack Strategy	Template Dataset	SR = 1
				Board	Oscilloscope
[48]	AEAD (ASCON-128) SW optimized for ARMv7-M	STM32F4 ARM Cortex-M4	7.37	ChipWhisperer Lite	Integrated 8 bit oscilloscope	Deep learning SCA with a Bayesian-optimized neural network	60 k traces, 772 samples each	Unprotected: ∼1 k traces Protected: first-order, partial key recovery
[50]	AEAD (ASCON-128) SW optimized for ARMv7-M	STM32F4 ARM Cortex-M4	7.37	ChipWhisperer Lite	Integrated 8 bit oscilloscope	Ensemble deep learning SCA; tested MLP and CNN architectures	60 k traces unprotected, 772 samples protected: 1408 samples	Unprotected: ∼1 k traces with CNN ensemble ∼100 traces with MLP ensemble Protected: First-order, ∼3 k traces with MLP ensemble
[51]	Weatherley’s ASCON-128 on ARMv7-M	STM32F4 ARM Cortex-M4	7.37	ChipWhisperer Lite	PXIe-5160 (2.5 GHz, 500 PPC)	Pre-processing for highest leakage points; fragment template attack (modified LDA); SASCA + key enumeration	16 k cycles selected; 64 k traces for templates	Unprotected: Compiled with U-0s, single-trace with <220 key search Compiled with U-03s, ∼10 traces with <227 key search Protected: First-order compiled with M-0s, ∼5 traces with <236 key search

and, as it is shown, they surpass those of traditional techniques such as DPA or CPA.

These attacks demonstrated that ASCON’s design is susceptible to well-structured template attacks, even when first-order masking is applied. In ASCON implementations, robust countermeasures are required to ensure resilience against such threats.

4.2. ASCON Side-Channel Countermeasures

The side-channel attacks presented in Section 4.1 show how inexpensive and highly effective these attacks are in compromising the security of ASCON implementations. To mitigate these risks, countermeasures like masking [53], shuffling [54], and random delay insertion [55] can be implemented. Among these, researcher efforts have focused on masking due to its adjustable security levels and robust resistance to side-channel attacks.

Masking obfuscates the correlation between power consumption and intermediate states. The computations are performed on transformed shares of data and never on security. In order to achieve a masked implementation of order d, the standard techniques are Threshold Implementation (TI) [10] and Domain-Oriented Masking (DOM) [56]. In the TI scheme, a d-th-order secure implementation is realized by decomposing the function operating on sensitive data into $d+1$ independent sub-functions (shares). These sub-functions must adhere to three critical properties: correctness, non-completeness, and uniformity. Correctness implies that the sum (or XOR) of the individual output shares should yield the original function’s output applied directly to the summed input shares. Non-completeness ensures that each sub-function $f_i(·)$ does not simultaneously depend on all input shares, thereby preventing the leakage of sensitive information through individual sub-functions. Uniformity requires each sub-function to produce uniformly distributed outputs, a condition usually satisfied by ensuring that each sub-function is balanced or invertible. Applying TI masking to linear operations is straightforward. However, masking non-linear operations typically involves decomposing the non-linear function into an algebraically simpler form that must be constructed to ensure non-completeness and uniformity, often resulting in significant hardware overhead and increased numbers of required computations. In the DOM scheme, the circuit is partitioned into $d+1$ independent sub-circuits (domains), each handling one share per masked variable. Similar to TI, the implementation is trivial for linear operations. For non-linear operations, a cross-domain communication is required, along with re-sharing of the variables. This solution demands substantial randomness (per share: $d·(d+1)/2$ ), adds latency, and has a very high area overhead. The low-degree S-box of ASCON eases masking integration, and, additionally, ASCON’s substitution layer is affine-equivalent to Keccak’s $\chi$-mapping: existing and future findings on Keccak’s S-box can be applied to ASCON. Nevertheless, the overhead of the masking scheme may not meet application constraints. In the work by Bilgin et al. [57], a first-order protected Keccak $\chi$-S-box with minimal area overhead was designed. The efficiency of the design was due to an additional share that combined effectively with the other two, maintaining symmetry in the cross-domain communication. Another key insight presented in the work was that since slices of the state were independent and behaved as random bits, they could be used as fresh randomness. This approach resulted in a final masked implementation that required only four random bits per state.

This strategy was applied to ASCON in [58,59], where two first-order protected implementations were evaluated: ASCON-fast, able to execute a variable number of rounds per clock cycle, and ASCON-x-low, which performed a single S-box operation per cycle. As a result of the three-share masking scheme, the state size and the datapath logic triplicated. Furthermore, managing the shared S-boxes introduced additional overhead. ASCON-fast-TI exhibited a 4.0× area overhead compared to its unprotected counterpart, while ASCON-x-low-TI had an overhead factor of 3.1×, as a single S-box was instantiated. Despite offering minimal randomness requirements and a low area overhead, this otherwise optimal solution may not be suitable for security-critical applications because its first-order DPA resistance remains vulnerable to advanced attacks, as discussed in Section 4.1.

A general masking scheme with a reduced randomness requirement is the Unified Masking Approach (UMA) presented in [60]. The randomness consumption was reduced by adapting the Boolean masked multiplication of Belaïd et al. [61] to hardware and improving it with Barthe et al.’s algorithm [62]. For a single S-box design, the maximum randomness required per cycle ranged from 5 bits ($d=1$) to 320 bits ($d=15$) for the UMA scheme and from 5 bits to 600 bits for DOM. In the 64 parallel S-box design, UMA’s first-order protection required 320 bits per cycle, while, at $d=15$, the randomness demand increased to 20 k bits for UMA and 37.5 k bits for DOM. Although UMA reduced randomness consumption, it performed worse overall, with lower throughput, higher area usage, and increased latency, reaching up to five cycles for the UMA AND gate.

Several research efforts have tried to directly reduce the latency and randomness demands of the DOM scheme. In its basic form, in order to secure a circuit from combinatorial glitches, DOM adds a register stage and, hence, an extra clock cycle, whenever shares must be synchronized. In [63], a generic, low-latency masking scheme (GLM) based on DOM was presented. It eliminated the need for additional register stages, but, for consecutive non-linear layers, this approach exponentially increased the number of shares, randomness, and domains.

In [64], a general masking technique called SESYM scheme was proposed for single-cycle, glitch-resistant hardware. The synchronization of signals was obtained in a completely self-timed manner, i.e., without the need for a dedicated register. This was achieved by converting each operation to dual-rail logic with WDDL gates and Muller C-elements, enabling a continuous, glitch-free handshake from the generation of dual-rail signals to the final S-box output. The masked S-box was obtained by first structuring it following the DOM masking scheme and then replacing the XOR and AND with the SESYM gadgets. Additionally, other components like single to dual-rail converter were needed. The final implementation was a single-cycle ASCON masked implementation that required the same online randomness as DOM. Compared to GLM, the online randomness required was 6.4 times less. While this work optimized the latency and reduced the randomness requirements, the area overhead was still quite high.

The first low-latency, second-order, masked hardware design that eliminated the need for fresh randomness was presented in [65]. It achieved a two-cycle-per-round latency, relying only on $d+1$ shares. The masking scheme was based on DOM AND gate and extended the Changing of the Guards technique used in [57] to systematically reuse inputs of neighboring S-boxes as fresh random bits. One clock cycle of latency was saved by relocating the linear layer of the S-box after the $\chi$ mapping, which allowed for the removal of one register stage. The paper presented an implementation featuring 64 parallel S-boxes, each with five DOM AND gates, requiring five random bits per S-box. The fresh random bits were derived from existing S-box input. The bits were selected using a SAT solver, which primarly ensured that these were independent of their masked inputs and secondly selected neighboring bits that enhanced symmetry, reduced constraints, and minimized area overhead. As no additional randomness was needed, this approach offered a highly efficient and secure solution for resource-constrained IoT devices.

In

Table 10. Comparison of masking schemes for ASCON implementations.

Work	Masking Scheme	Technology	Architecture	Protection Order	Area	Randomness	Latency	Max Freq.	Throughput	T/A	Power	Energy
					[kGE]	[bit/cycle]	[cycles/round]	[MHz]	[Gbps]	[Gbps/GE]	[μW]	[μJ/B]
[58]	Unmasked implementation for comparison	90 nm UMC	ASCON with single S-box instance	unprotected	3.75	0	0	168	0.014	3.73	15	1397
			ASCON with 64 S-box instances	unprotected	7.95	0	0	1035	5.524	694.84	43	33
[58]	Threshold Implementation (TI)	90 nm UMC	ASCON-fast-TI 1-round unrolled	1-order	30.42	4	2	708	3.77	124	183	137.25
			ASCON-fast-TI 2-round unrolled	1-order	49.13	8	3	590	6.29	128	315	119.7
			ASCON-fast-TI 3-round unrolled	1-order	68.27	12	4	446	7.14	105	447	111.75
			ASCON-fast-TI 6-round unrolled	1-order	125.19	24	7	282	9.02	72	830	107.9
			ASCON-x-low-TI single S-box	1-order	9.19	4/64	128	180	0.015	1.6	45	17,280
[60]	Unified Masking Approach (UMA)	90 nm UMC	ASCON DOM with single S-box instance	1-order	10.8	5	192	864	0.048	4.4	n.d.	n.d.
				2-order	16.5	15	192	846	0.047	2.85	n.d.	n.d.
				5-order	32.0	75	192	828	0.046	1.44	n.d.	n.d.
			ASCON UMA with single S-box	1-order	10.8	5	192	864	0.048	4.44	n.d.	n.d.
				2-order	16.4	10	192	846	0.047	2.87	n.d.	n.d.
				5-order	33.0	55	448	1932	0.046	1.44	n.d.	n.d.
			ASCON DOM with 64 parallel S-box	1-order	28.89	320	3	632.8	2.25	77.88	n.d.	n.d.
				2-order	53.0	960	3	537.19	1.91	36.04	n.d.	n.d.
				5-order	161.87	4800	3	523.13	1.86	11.49	n.d.	n.d.
			ASCON UMA with 64 parallel S-box	1-order	27.18	320	3	632.81	2.25	82.78	n.d.	n.d.
				2-order	125.0	640	3	514.69	1.83	14.64	n.d.	n.d.
				5-order	220.01	3520	7	557.81	0.85	3.86	n.d.	n.d.
[64]	Self-synchronized masking	65 nm UMC	ASCON with 64 S-box instances	1-order	50.4	320	1	408.3	4.35	79.8	n.d.	n.d.
				2-order	102.39	960	1	377.1	4.02	39.3	n.d.	n.d.
				5-order	357.65	4800	1	312.9	3.34	9.3	n.d.	n.d.
[63]	Generic low-latency masking	90 nm UMC	ASCON with 64 S-box instances	1-order	42.75	2048	1	43.29	2.77	64.8	n.d.	n.d.
				2-order	90.94	4608	1	52.19	3.34	52.19	n.d.	n.d.
				5-order	339.82	18432	1	46.7	2.99	8.8	n.d.	n.d.
[65]	DOM AND gate with Changing of the Guards	lsi_10k library, node size undefined	ASCON permutation with 64 S-box	1-order	26.1	0	2	n.d.	n.d.	n.d.	n.d.	n.d.
				2-order	52.63	0	2	n.d.	n.d.	n.d.	n.d.	n.d.

, we report the metrics of various masking schemes discussed in this section. Many of the results are estimated as they were not explicitly provided in the original papers. Specifically, the latency was inferred when not directly stated, while the maximum frequency and throughput were calculated when only one of the two was reported using the following formula:

$$Throughput={\displaystyle \frac{f_{ck}·size(P_i)·unrolling}{latenc{y}_{round}·{\mathcal{E}}_{rounds}}}$$

where $size(P_i)$ is the plaintext block processed at each cycle, $f_{ck}$ represents the clock frequency, $unrolling$ denotes the degree of loop unrolling, $latenc{y}_{round}$ is the latency per round of the cryptographic operation, and ${\mathcal{E}}_{rounds}$ corresponds to the total number of rounds required for encryption. As observed in the table, the best trade-off between latency and area was achieved by the approach proposed in [65]. For first- and second-order masking, this method demonstrated the lowest resource consumption while requiring no randomness. However, it should be noted that the synthesis technology used in [65] was intended for educational purposes, and the reported results require validation with silicon-ready technology. Additionally, the maximum operating frequency and, consequently, the throughput of this design were not provided: this limits a comprehensive performance evaluation. For masking orders higher than two, it remains an open question how a SAT solver would behave in selecting state bits as random bits. If a single-cycle masking approach is required, the most suitable solution is presented in [64]. Although this design exhibited a higher area overhead compared to [63], its significantly reduced randomness requirements ultimately resulted in lower overall area consumption. Among general masking approaches, the standard DOM scheme achieved a well-balanced trade-off between randomness requirements, area overhead, and latency. However, if minimizing randomness is a critical constraint, the UMA scheme presents a more favorable alternative.

5. Takeaways for Designers and Conclusions

This study comprehensively reviewed various hardware implementations proposed for the NIST LWC winner ASCON and analyzed side-channel attacks on its authenticated encryption (AEAD) implementations, along with state-of-the-art solutions for their countermeasures. The literature demonstrates significant research effort for ASCON. However, many studies tend to focus on specific aspects, leaving several branches in need of further exploration. As ASCON becomes increasingly prevalent in securing resource-constrained embedded systems (e.g., implantable and wearable medical devices, smart homes, RFID tags), it is important to fully explore its design space. The current research trend particularly focuses on area reduction and performance improvements by means of round-based or unrolled architectures while neglecting other critical design metrics such as power and energy efficiency, key factors for battery-operated and resource constrained applications. This oversight highlights the need for further research to achieve a balanced trade-off between all the critical design metrics.

This review of hardware attacks on ASCON implementations shows that the initialization phase of the cipher with the secret key is vulnerable to passive side-channel attacks. Unprotected implementations can be compromised with online statistical analysis. The best attack leverages deep learning and is able to break the cipher and reveal the key using approximately 24,000 traces. Other attack techniques, such as template attacks, have demonstrated the possibility of successful key recovery on the unprotected implementation with even a single trace. These advanced attack techniques can even bypass defense systems, revealing the secret key with as few as 10 traces on protected ASCON implementations with first-order masking. The findings of this study underscore that for critical security applications, ASCON implementations should ideally be protected with at least second-order masking. However, integrating countermeasures introduces overhead that further complicates meeting application constraints and trade-offs between security, performance, and resource efficiency. In this study, state-of-the-art countermeasure proposals for ASCON were reviewed. To the best of our knowledge, countermeasure research has mainly focused on masking schemes, optimizing randomness requirements, and latency. Although optimizing the randomness requirement has the effect of reducing the area overhead of masking, there is a lack of research on masking schemes that address area optimization. Moreover, as previously mentioned, power consumption and energy efficiency are very often neglected in works proposing ASCON hardware implementations. This issue is further compounded when considering protected architectures, as the majority of proposed schemes demonstrate a lack of analysis with regard to these metrics, which are of paramount importance to embedded systems. In summary, while state-of-the-art ASCON countermeasures predominantly rely on masking to ensure security against side-channel attacks, their high implementation overhead necessitates exploring alternative schemes. Future research should investigate countermeasures that balance robust security with application-specific constraints, thereby broadening the considered trade-offs in the design of ASCON.