Automated R-DAC Layout Design with Parameterized Topology Written in SWA: SoftWare Analog

Abstract

Leading-edge analog/mixed-signal LSI designs are still hand-crafted using graphic editors. These graphic editors do not include functionality for parameterized topologies in variable designs. Instead of graphic editors, we have developed the SWA (SoftWare Analog) language, which can describe and display placements and routing for analog/mixed-signal LSI layouts with less or similar labor time. By using SWA, we have developed an R-DAC (resistive digital–analog converter) layout with a parameterized topology and various parameters, such as ~1 Gsps, 4~12-bit (upper segment type + lower R-2R type) R-DAC, and 1~3.3 V logic with 1~3.3 V_pp analog output.

1. Introduction

In advanced analog/mixed-signal LSI designs, the designer’s skills are directly linked to performance. In both circuit and layout designs, veteran designers typically conceive the topology, manually calculate element values, input circuit diagrams and layouts into graphic editors, and verify through simulation. As shown in Figure 1, high-level designers consider and represent multiple parameters (e.g., bin_bit, thermo_bit, ext_bit) as variables with dots ‘…’ for a single topology [1,2,3]. However, graphic circuit editors and graphic layout editors [4,5,6] cannot describe variables or variable topologies. Graphic ediItors for layout are equipped with parametric cells (p-cells) [7,8], which can be assigned dimensions via pull-down menus. A p-cell is essentially a collection of rectangle descriptions per layer of the photomask. Efforts to automate layout design using vendor-specific languages [8,9,10,11] that can describe the size calculation and the rectangles include constraint-based approaches [12,13,14,15,16] and module generators [17,18,19,20,21]. Because they describe using low-level rectangles, the program lines become lengthy [22], and the development takes time.

Instead of inputting layouts through a graphic editor, we developed and reported the SWA programming language to describe, display, and verify layout wiring with almost the same effort [22]. Using a prototype of SWA, we have created a layout design for RDAC, supporting various circuit topologies such as total bit number, upper segmented + lower R-2R-bit sharing, different maximum-voltage configurations for digital and analog parts, and making device parameters such as transistor size and resistance value variable, all within one program. As a result, we developed an automatic design program for RDAC that allows for the variation of bit numbers, DAC configurations, output resistance values, and transistor combinations based on the desired maximum analog output voltage. This report particularly focuses on the layout design of RDAC with parameterized and variable topologies.

2. Description of Parametric Topology for the R-DAC

2.1. Circuit Topology and Layout Topology

The well-known circuit topologies for RDAC include the R-2R type, segmented type (where the same resistance is added in parallel), and resistor string type. Considering high speeds of up to 1 Gsps for this design, we adopted the ‘upper segmented type + lower R-2R type’ shown in Figure 1. The bit numbers for each are given as variables, including zero. This implies that both the fully segmented type and the R-2R-only type are also options. Although not illustrated, logic-level shifter circuits were added to each DFF output to accommodate specifications where the logic input is 1 V and the output ranges from 0 to 3.3 V_pp, using different maximum-voltage transistors.

We proposed an equation-based circuit design to calculate the $L$ and $W$ of the resistors and transistors in Figure 1 from specifications such as DAC bit-width and either the unit resistance or output impedance [1,2,3]. The outline is as follows:

(1)

Using the process data “Pelgrom coefficient” of resistance $k_p$, and the variation range of $k_n\ast \sigma$ (e.g., $4\sigma$), the resistor variation range is given as:

$$k_n\ast k_p/\sqrt{L\ast W}$$

(1)

(2)

In a $b$-bit DAC, assuming the upper n-bits are segment-type (thermometer-type) and the lower (b − n) bits are R-2R-type (binary-type) (including $n=0$ and $n=b$), the allowable relative error of the MSB resistor in the R-2R type assigns the $m_1$ times of the LSB (e.g., $m_1=1/2$ or $1/4$; $2$ is also acceptable if calibration is installed).

$$2^{-(b-n)}\ast m_1$$

(2)

The segment type (thermometer type) guarantees a monotonic increase, allowing a similar level of variation as above.

(3)

From Equation (1) = Equation (2),

$$L\ast W={\left(k_n\ast k_p\ast 2^{b-n}/m_1\right)}^2$$

(3)

(4)

$R_u$, the unit resistance value of a silicide-blocked poly-resistor, is given as

$$R_u={\rho }_s\ast L/W$$

(4)

where ${\rho }_s$ is the sheet resistance.

(5)

From Equations (3) and (4), $L$ and $W$ can be calculated directly. If the result values are below the minimum process values, they should be replaced by the minimum process values.

(6)

The on-resistance of the transistor switches should be sufficiently small compared to the accuracy of the resistance in Equation (2) (e.g., $m_2$ times). $L$ is usually the minimum process value. Transistors’ $W$ can be calculated.

This calculation is straightforward and does not require simulation-based designs, iteration loops, or optimizations, unlike many other designs, such as [23]. As a result, our approach provides a quicker solution, taking less than one minute. The circuit simulations for the design are just for human error detection, not for design iterations. The above n-bit is any integer value between 0 and b. When n is small, a high relative accuracy of the big-size resistors is required, resulting in a large resistor area. When n is large, a large number 2ⁿ of slices will be laid, i.e., a wide area. The minimum point of the area lies somewhere in between. Although it is possible to show the calculation formula, we recommend executing the proposed software to create the layout per case of n. It takes less than a minute per case. Then, you can select the one with the smallest area, suitable aspect ratio, or lowest output capacitance using forward annotation.

The power consumption of the RDAC is primarily dominated by the unit resistance value or output impedance given as the specification.

Figure 2 shows a schematic and layout examples for a 7-bit R-DAC composed with a 4-bit segment type + 3-bit R-2R type.

We also proposed the most suitable layout structure, “sub-micron slices”, for the circuit shown in Figure 1, for fewer parasitics, excellent relative accuracy, a smaller area, higher speed, and lower power [1,2,3]. The sub-micron slice structure is shown in each red box in Figure 2, composed of 3 pieces of vertically stacked P- and N-type 4-finger MOS transistors, as shown in an orange box in Figure 2.

The built-in features of the “sub-micron slices” are as follows:

(1)

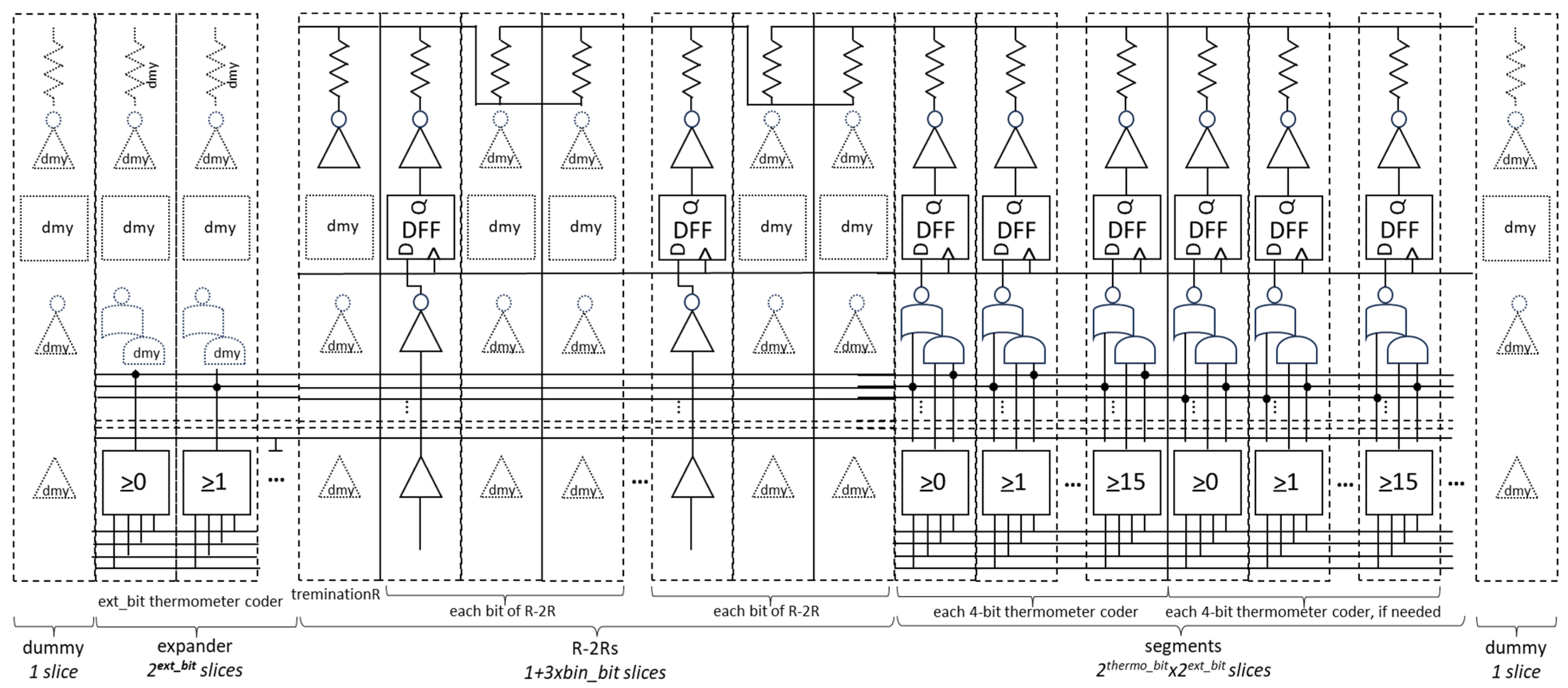
To fill a sea of the same slice bases in the same pitches on the entire RDAC. An example is the entirety of Figure 2.

--> All the slices lay the same way as their adjacent ones at the exposure point of view (except for the outermost dummies). This improves relative accuracy.

(2)

The slice consists of four-finger MOS transistors and resistors or capacitors with equal pitches.

--> Only the wirings of the digital section can be different from the adjacent ones.

--> The analog switch also has the same structure. (Deep N-well is possible.)

(3)

Both sides are assigned to sources and connected to VDD or GND planes located on the top layer(s) through stacked vias.

--> The wiring widths of the VDD or GND planes should be wider than or equal to the transistors’ W. The planes connect to the adjacent slices in a tile-like manner.

--> As a result, the parasitic wiring resistances of the VDD and GND are several orders smaller than the transistors’ on-resistance, allowing common impedances to be ignored.

(4)

Furthermore, (3) is shared with the adjacent slices.

--> The OD (Oxide Diffusion) is continuous in the horizontal direction (except for the outermost dummies), without isolation areas. This reduces the horizontal isolation area significantly. In many layouts, both automated and manually crafted by experts [24,25,26], the isolation areas are approximately the same size as the device area. This layout, therefore, occupies roughly half the space of previous automated layouts.

--> Moreover, there are no influences of OD edge distortion, improving relative accuracy.

(5)

Except for the digital input bit lines, clock lines, and analog output wiring, all connections are within a slice with an approximate width of 1 μm, thus requiring only a few μm and having a parasitic capacitance in the order of femto-farad (fF), which is almost negligible.

--> High-speed, low power consumption.

We proposed “a layout-driven schematic design”, i.e., designing all circuits on the sub-micron slice structure layout to realize fewer parasitics, excellent relative accuracy, a smaller area, higher speed, and lower power. In the design, optimization, and/or compaction processes are unnecessary.

2.2. Description of Parametric Topology Layout

The aforementioned SWA language was written with a general-purpose programming language that can use list commands such as SKILL in Virtuoso 6.1. Each element placement is represented in one line, such as list(“%pInst”, element name, various parameters, …), and multi-layer, single-stroke wiring is represented as list([terminal name], wiring layer 1, coordinate 1, coordinate 2, wiring layer 2, coordinate 3, …). The above wiring width and via specifications are set as defaults, and an origin shift command list(“%offset”, …) is also provided. To achieve the nesting of layout descriptions, we prepared the SWA_list() command, which combines the components and lists of elements and the above single list(), into a large list, i.e., list(list(), list(), …). Using variables substituted by the plural list()s described for components, and variables of coordinate, loops, and/or branches of general-purpose programming languages, the parametric and variable descriptions of the large list() are generated. Finally, we developed an interpreter function SWA_layout() that reads the completed large list and calls vendor-specific language functions to draw elements, wires, vias, etc.

In practical use, large lists of one or a few component placements and wirings are assigned into a variable, and this SWA_layout(variable name) is called to display on the drawing screen for visual confirmation. It can be followed by DRC or LVS as needed. This process requires less effort than inputting and displaying figures in conventional graphic editors by using variable component layouts, coordinates, and element values.

First, as shown in the orange box in Figure 2, the layout of the y-direction-stacked 4-finger N-type and P-type MOS transistors (named half_slice) is described using SWA in Figure 3a. Using the list(“%pInst”, …) commands in lines 4 and 5 in Listing 1, P-cells named “nch” or “pch” are placed at coordinates dx:dy. In a graphic editor, this corresponds to opening the transistor’s property box and specifying parameters such as L, W, and finger number. These parameters are then converted to a vendor-specific format using the SWA_trParam() function in lines 1 and 2, and substituted into the variables ParamsN and ParamsP. Here, the variable OD_xP_PN represents the minimum distance between the ODs of nch and pch as determined by the process design kit (PDK).

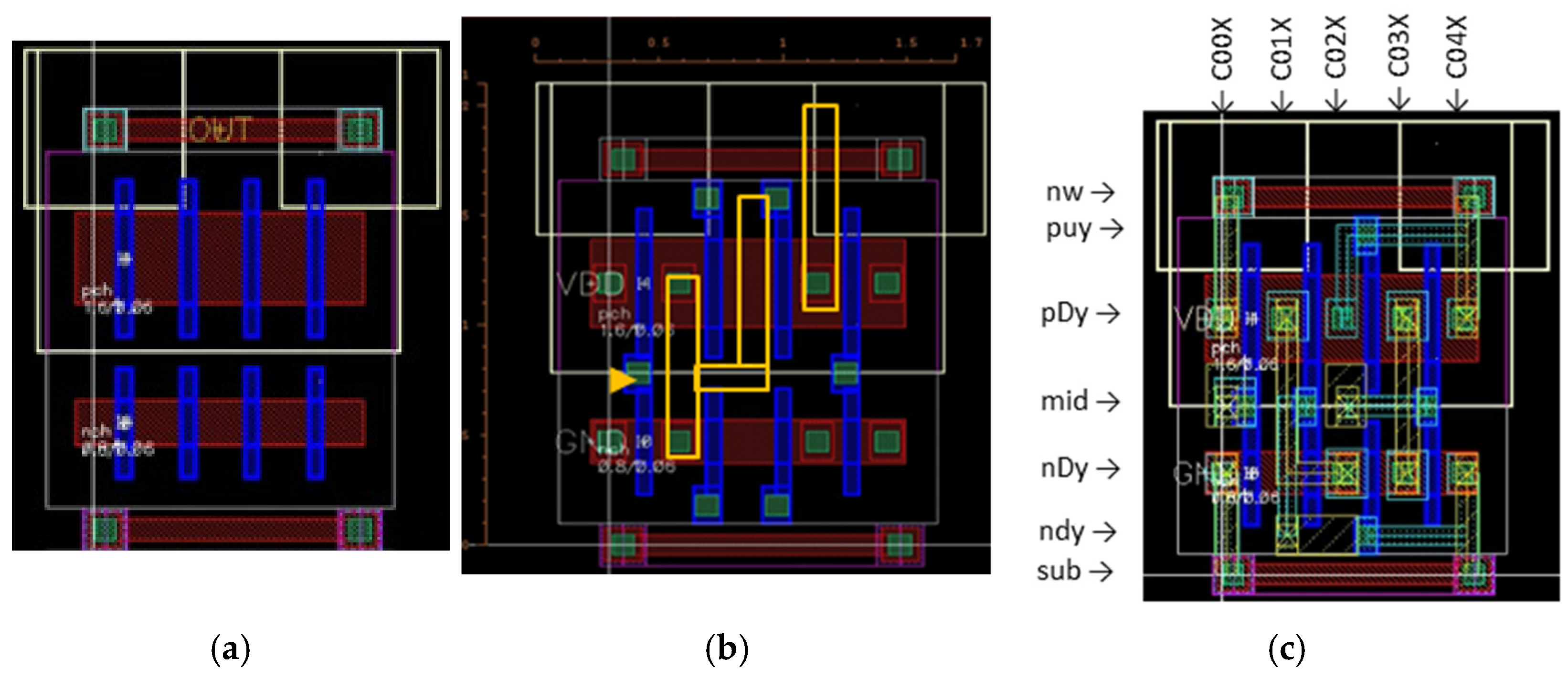
Listing 1. SWA description for layout of 4-finger, P/N MOS transistor pairs.

1  ParamsN = SWA_trParams( SWA_L SWA_Wn 4 0 “bare”)      ; finger=4, without NP, CO 2  ParamsP = SWA_trParams( SWA_L SWA_Wp 4 0 “bare”)       ; finger=4, without PW, PP, CO 3  half_slice = SWA_list( 4    list( “%pInst” SWA_techname nch “” dx:dy “R0” 1 ParamsN)   ; nch = “nch”, can be “nch_lvt”, “nch33”… 5    list( “%pInst” SWA_techname pch “” dx:dy+Wn+OD_xP_PN “R0” 1 ParamsP)    ; pch = “pch”, etc. 6    ) 7  ; SWA_layout( cv half_slice)                    ; drawing ( normally commented out)

In line 7, the layout of half_slice can be displayed by removing “;” from the comment line. Here, the output file pointer “cv” should be pre-opened, as cv = SWA_CheckOpen( libName cellName viewName _g_techname).

In many analog layouts, gate contacts are located at the center of the straight gate extension path. Conversely, in many digital standard-cell-based layouts, gate contacts’ x-axes are slightly shifted to the left, and metal wires are slightly shifted to the right to achieve better M1 wiring efficiency, as highlighted with orange paths in Figure 3b. We installed this automatic x-axis shift function for real coordination, using a shift value table per layer. Zero shift is, of course, available for typical analog layouts.

To minimize wiring grids at the x-axis to only C00X~C04X in Figure 3c, the shifted gate’s x-axis is calculated from the x-axis of the left source/drain contact C00X~C04X, using the function. Finally, users do not need to worry about slight shift values per layer in SWA descriptions.

Figure 3c shows a layout example of wiring 2NAND and INV on the base half_slice above. The wiring is performed using the aforementioned single-stroke wiring list command through multi-layers. As shown in Listing 2 and Figure 3b, the wiring coordinate matrix is pre-assigned to variables C00X~C04X for the x-axis direction and sub, ndy, nDy mid, pDy, puy, and nw for the y-axis direction. The gate contact positions specified by C00X to C04X are automatically placed at offset positions by the interpreter.

Listing 2. The SWA description for a layout of 2NAND+INV in a slice.

10 NAND2_INV = SWA_list( 11    half_slice                  ; “pch”+”nch” base layers in line 3 12    wire_VDD_GND_half             ; stacked vias from both end sources to top VDD/ GND layers 13    list( ““ “PO” C00X:mid “M2”)           ; from PO to M2 stacked vias for NAND input1 14    list( ““ “PO” C01X:mid “M1” C01X:ndy “M2”)  ; from PO to M1 via, M1 wire, via to M2 for NAND input2 15    list( ““ “PO” C03X:mid “M1” C02X:mid “M2”)  ; from PO to M1 via, M1 wire, via to M2 for INV input 16    list( ““ “pch” C01X:pDy “M2” C01X:nDy C02X:nDy “nch”) ; from CO to M2 vias, M2 wire, vias to CO for NAND output 17    list( ““ “nch” C03X:nDy “M2” C03X:pDy “pch”)  ; from CO to M2 vias, M2 wire, via to CO for INV output 18    list( ““ “pch” C02X:pDy “M1” C02X:puy C04X:puy)  ; VDD 19    list( ““ “PO” C02X:ndy “M1” C04X:ndy)    ; grounded gate for isolation 20     list( ““ “PO” C02X:puy “M1”)          ; pulled-up gate for isolation 21    ) 22 ; SWA_layout( cv NAND2_INV)             ; drawing ( normally commented out)

In line 22, the layout of NAND2_INV can be displayed by removing “;” from the comment line.

The SWA description of the entire R-DAC layout starts from the left to the right of the lower part of Figure 1, as shown in Figure 4, assigned to RDAC1. As shown in Listing 3, the left-end dummy, followed by an origin shift command to the right end of the dummy, is described in line 30 and is substituted into variable RDAC1. Here, p represents the slice width. The exp_bit thermometer encoder for the expander part is placed in lines 31–33 (nil if 0 bits), followed by the origin shift command to the right end of the expander slices.

In line 34, if the bin_bit R-2R part is not 0-bit, a dummy for the left-end termination resistor in line 35, followed by an origin shift to the right end by p, is added into RDAC1. In lines 36–40, BUFF logic for driving the 2R resistors and two dummies to space for the R resistor (which consists of two parallel 2R resistors), followed by the origin shift command by 3p, are added into RDAC1. These instructions are repeated bin_bits times.

In line 41, the seg_bit, such as 0~4-bit, thermometer encoder is selected as x. In lines 42–44, the thermometer encoder × selected above, followed by an origin shift command, is repeated to be added exp_bits times into RDAC1.

Finally, a right-end dummy is added into RDAC1 in line 46, followed by an origin shift command to reset the offset amount.

Similarly RDAC2 for the expander program logic array (PLA) matrix, RDAC3 for DFFs, RDAC4 for level shifters if needed, RDAC5 for analog switches similar to INV, and RDAC6 for resistors in Figure 1 are also described. Finally, they are combined as RDAC = SWA_list( RDAC1 RDAC2 RDAC3 RDAC4 RDAC5 RDAC6). To draw the entire RDAC, you can use SWA_layout( cv RDAC).

Listing 3. SWA layout description for bottom column of R-DAC.

30 RDAC1 = SWA_list( dummy list( “%offset” p:0.0) )         ; add left dummy and shift origin p(= width of slice) 31 case( exp_bit (0 x=nil) (1 x=thermo1) (2 x=thermo2) (3 x=thermo3) (4 x=thermo4) )        ; expander-bit selection 32 RDAC1 = SWA_list( RDAC1 x list( “%offset” p*exp_bit:0.0) )      ; add selected expander and origin shift into RDAC1 33 total_slice = 1 + exp_bit 34 if( bin_bit!=0 then 35  RDAC1 = SWA_list( RDAC1 dummy list( “%offset” p:0.0) )    ; add dummy and shift for space of left road of R-2R 36  for( i 1 bin_bit 37    RDAC1=SWA_list( RDAC1 BUF2 dummy dummy list( “%offset” p*3:0.0) )  ; add 3 logic slices for R-2R and shift 38  ) 39 total_slice = total_slice + 1 + 3*(bin_bit) 40 ) 41 case( thermo_bit (0 x=nil) (1 x=thermo1) (2 x=thermo2) (3 x=thermo3) (4 x=thermo4)  ; thermometer-bit selection 42 for( i 1 2**(exp_bit) 43   RDAC1 = SWA_list( RDAC1 x list( “%offset” p*2**seg_bit:0.0) )  ; add 4-bit expander and origin shift into RDAC1 44 ) 45 total_slice = total_slice + thermo_bit * exp_bit 46 RDAC1 = SWA_list( RDAC1 dummy list( “%offset” -p*total_slice:0.0) )       ; add dummy and reset shift

2.3. Standard Cell Wirings

Many digital standard cells generally use shifted-gate PO_contacts for better wiring. As shown in Figure 3b, the right edge of PO_contacts and the right edge of PO_gates are generally aligned. M1 may be shifted slightly to keep space between M1 and “M1 on adjacent gate PO_contact(s)”.

We installed 2 list()s of the shift values from each center of source/drain coordinate, such as C00X~C04X, per layer for both the x_axis and the y_axis. They automatically add each list()’s value to the actual coordinates in the interpreter function SWA_layout(). Of course, shift = 0.0 is available. This ensures that only 4 coordinates C00X~C04X are enough for the x_axis.

2.4. Multiple Voltage Transistor Handling

To earn higher-voltage output, RDAC often requires a combination of core transistors for the digital part and higher-voltage IO transistors for the analog part. The sizes of the transistors are quite different. We propose a method to accommodate transistors of varying sizes within the same pitch slice. Here, “pitch” refers to the center-to-center distance of sources at both ends in a 4-finger MOS transistor. As an example, we assumed that a 2.5 V transistor’s pitch was 2.0+ times the size of that of a 1.2 V core transistor in our target process. Therefore, the pitch of two 1.2 V core transistors with slightly fat source/drain lengths matched the pitch of one 2.5 V transistor. The 4th argument of function “SWA_trParams()” in Listing 1 is the increment length value of the fat source/drain than a normal one. In this case, two level shifters were laid out in a stack, consisting of 2.5 V transistors, and the lower one received the core transistor logic0, and the upper one logic1, as shown in Figure 5a. A 2-finger, 3.3 V transistor switch was utilized to match the core transistor pitch. Handling a 1.8 V transistor followed a similar approach to handling a 2.5 V transistor.

The pitch of a 3.3 V transistor was 3.0+ times that of a 1.2 V core transistor in our target process. Therefore, the pitch of three 1.2 V core transistors with slightly fat source/drain lengths could match the pitch of one 3.3 V transistor. We considered using two four-finger 1.2 V core transistors with four fat dummy fingers, as shown in Figure 5b. Here, a dummy finger refers to a finger of a core transistor with its gate shorted to its source. In general, an IO transistor pitch could be any multiple of a core transistor pitch in any process, allowing us to select two slightly fat core transistors with the appropriate number of dummy fingers.

2.5. SWA_layout(), Interpreter Function

Easy layout descriptions shown in Listings 1 through 3 were converted into a type X = list(list(), list(), …) with all known values. The proposed function SWA_layout(cv, X) converted our SWA description X into a vendor-specific layout description, which consisted of rectangles, paths, and p-cells. The output file cv was fully compatible with previous layout formats.

2.6. Schematic Netlist Creations

We proposed 2 types of schematic netlist creations, as follows:

The first one is “easy schematic description in SWA language”. We have also developed and reported SWA schematic commands without using a graphic editor with similar or fewer labor hours. The schematic commands are very similar to list(“%pInst”…) and list(“%wire”…) in the above layout commands. Therefore, the explanation is skipped in this paper. Please refer to [22]. We also described the parametric schematic of the R-DAC system in the SWA language.

An LVS tool can compare a schematic and a layout, both generated by the listings and explanations above per the same number of parametric topology cases, such as b-bit, n-bit, and output impedance.

The second type is “a netlist generated from the layout”. It was possible to perform circuit simulations using a netlist either with or without parasitics, extracted from the layout by LVS or LPE tools. The simulations guaranteed whole specifications when all passed. In this case, schematic description is unnecessary, so it takes less labor hours, and less developing time and cost.

Actually, we used this method, from small blocks to the entire R-DAC, to develop the R-parametric topology DAC layout description. We now use this way when a customer requests the simulated data.

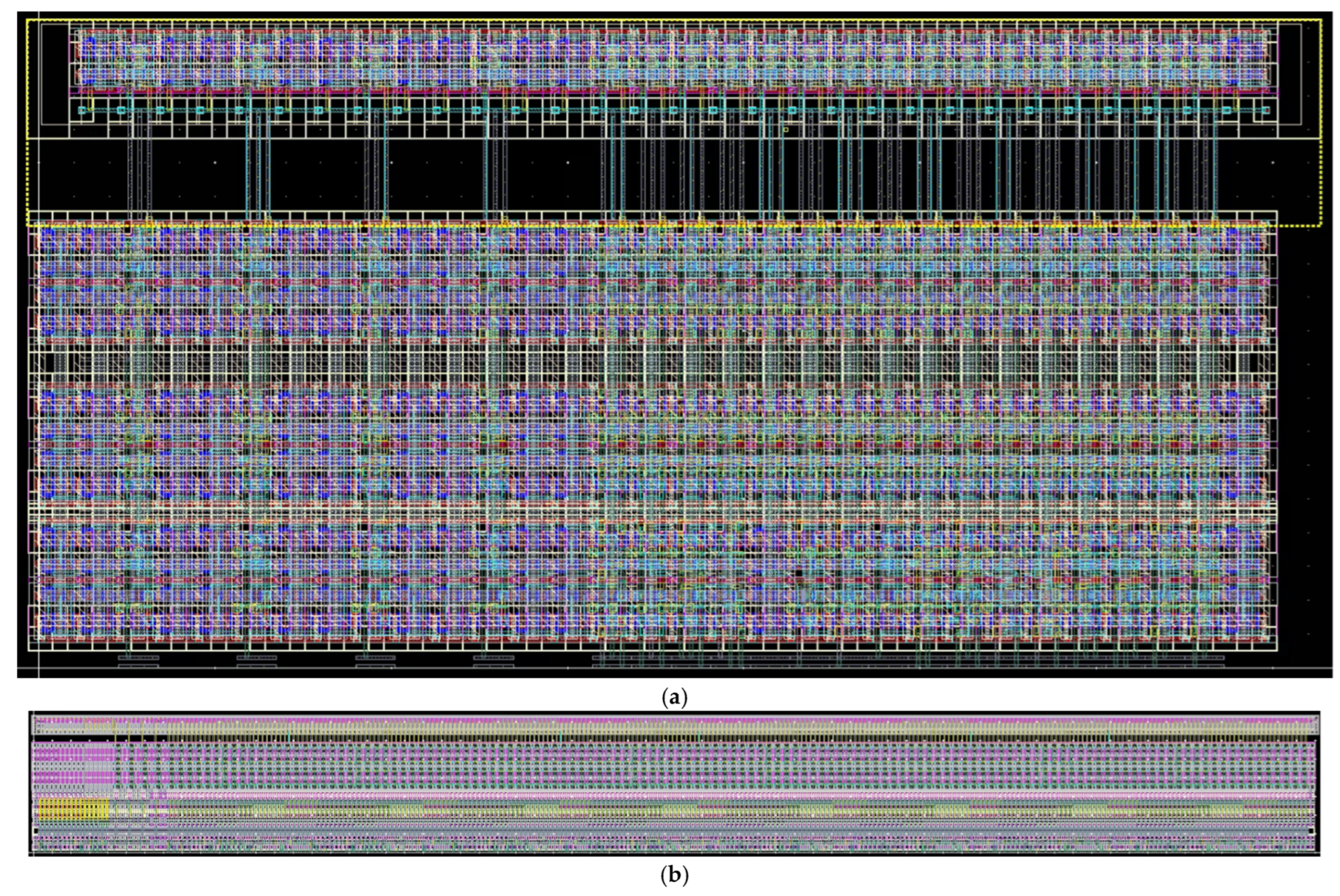
3. Experimental Results

We proposed the SWA layout description language. As a first step, we described a ~1 Gsps RDAC as a parameterized layout using the TSMC 65 nm CMOS process and the SKILL language on Cadence Virtuoso. The configurable parameters included the total number of bits (ranging from 4 to 12), R-2R bits (ranging from 0 to 12), various voltage transistor combinations, and the length (L) and width (W) dimensions of each transistor. The SWA-described RDAC layout allowed for automatic layout generation with different topologies, given different parameters. Simultaneously, we developed an interpreter function, SWA_layout(), to convert SWA descriptions into the Cadence layout database. This function was utilized for displaying and debugging the SWA descriptions of each component, and for outputting the final layout to the Cadence database.

Figure 6a–c show examples of RDAC layouts using only one RDAC description in the SWA language, by changing several input parameters.

Firstly, a layout for a ~1 Gbps, 8-bit RDAC (segmented part 4-bit, R-2R part 4-bit), 1.2 V logic, 1.2 V_pp analog output, was automatically generated as shown in Figure 6a. Its dimensions were 19.3 μm × 36.7 μm.

Secondly, another layout for a 12-bit RDAC (segmented part 4-bit × expander part 4-bit, R-2R part 4-bit), 1.2 V logic, 2.5 V_pp analog output, was automatically generated as shown in Figure 6b. Its dimensions were 36.7 μm × 347 μm.

Lastly, another 6-bit RDAC (segmented part 2-bit × expander part 2-bit, R-2R part 2-bit), 3.3 V logic, 3.3 V_pp analog output, was automatically generated as shown in Figure 6c. Its dimensions were 35.4 μm × 36.8 μm.

Each resistor part is located on the top side of each figure, with the same pitch for each slice, but not shown. Detailed reports on these will be provided in the near future.

4. Discussion

This report focuses on layout descriptions with outlines of equation-based R-DAC circuit design and schematic netlist creation. We are working on automated layout design with an equation-based circuit design for SAR-ADC with C-DAC using similar means, and will report it. We believe the proposed “Parameterized Topology layout written in SWA” can be applied to many other circuits.

Currently, the SWA description in Figure 3b causes minimum area errors in DRC, specifically with stacked vias. Therefore, in practice, patches adding list(“%rect” …) statements for minimum-area rectangles are applied in the SWA_list() in Figure 5b. This approach is similar to traditional methods used to address DRC errors during layout design with graphic editors. Appropriate rectangles have already been added in Figure 6a–c, and they are DRC/LVS-free. We anticipate that automated metal filling will be implemented in the near future.

For comparison, we developed a configurable RDAC layout generator with 8.3 K lines of code, which is 1/10th the size of a conventional layout dump description written in the SKILL language.

5. Conclusions

We have developed the SWA language to describe analog and mixed-signal (AMS) layouts as a program. Instead of using conventional graphic editors, descriptions with the SWA language allow for the conditional programming of variable topologies and parameters. Veteran designers’ SWA layout descriptions with variable topologies and parameters become automated layout generators for dedicated blocks, such as RDACs.

In addition, with SWA’s simple commands, users can program and display layouts in the same or even a shorter time than with conventional graphic editors.

We hope that SWA will encourage more designers to participate in design through programming.