Power Consumption Efficiency of Encryption Schemes for RFID

Abstract

This paper provides a comparative analysis of AES (Advanced Encryption Standard) and Salsa20 algorithm implementations, focusing on power consumption efficiency in passive RFID (radio-frequency identification) tags and ultra-low-power devices. The main objective of this work is to determine which of these algorithms is more suitable to operate in these types of devices. For this purpose, ASIC (application-specific integrated circuit) implementations of AES and Salsa20 based on low-power approaches were developed and their power consumption was evaluated. The results demonstrate that Salsa20 power consumption is lower than AES (about 17%), indicating that Salsa20 is a much better choice than AES for passive RFID tags.

1. Introduction

The range of applications for RFID (radio-frequency identification) systems is vast, spanning areas such as logistics, healthcare, access control, ubiquitous computing, and supply chain management, as well as applications in the context of IoT (Internet of Things) systems [1]. Among the different types of RFID tags, passive tags are the simplest, cheapest, and most ubiquitous [2]. Passive RFID tags operate without an internal power source, relying on energy received from the RFID reader for their operation. RFID systems are even being proposed for applications commonly covered by conventional battery-powered wireless sensor network (WSN) devices, through the emerging field of RFID sensors [3], which raise even more challenges for the severely energy-constrained passive RFID tags.

Driven by their increasing demand, the use of ultra-low-power RFID tags in commercial products has brought risks related to information security, industrial espionage and individual privacy. Inventory information or personal identification without cryptography can be easily monitored without a trace of the perpetrator. Therefore, most digital ID and tracking applications must have security and privacy addressed in their project architectures, just like credit card applications have.

To meet the growing demand for product tracking via RFID tags, there is a trend toward lowering the cost and power consumption of these devices. Consequently, their computational capabilities tend to be very low, which poses challenges in the implementation of encryption schemes for these devices.

The design of low-power devices should take into account three main fundamental aspects: chip area, power consumption, and latency (clock cycles). This work focuses primarily on the issue of power consumption, which may also contribute to improvements regarding other relevant aspects, such as chip area.

The power provided by the RFID reader over the air interface decreases linearly with the operating distance to UHF (ultra-high-frequency) tags. In order to allow cryptographic operations in the whole operating range of a tag, which, in the case of UHF tags, typically ranges up to seven meters, a limit on the power budget of approximately $20\mathsf{\mu }\mathrm{W}$ should not be exceeded [4].

In this paper, we present a comparative analysis of the power consumption efficiency of the AES (Advanced Encryption Standard) and Salsa20 ASIC implementations (both designed by us) optimized for use in passive RFID tags in order to determine which algorithm is more suitable to operate in low-power devices. In this sense, the main contributions of this work are the design, implementation, and evaluation of these algorithms with the goal to provide security to low-power devices for digital identification applications.

The remainder of this paper is organized as follows: Section 2 presents related work while Section 3 and Section 4 present the algorithm descriptions and implementations, respectively, and finally, Section 5 presents the results and discussions.

2. Background and Related Work

2.1. Security Level

A deep analysis of the security level of the AES and Salsa20 ciphers is out of the scope of this paper, but these two ciphers appear to have similar security levels, according to the related cryptanalytic studies presented below.

AES, also known by the name Rijndael, was announced as a standard by the U.S. National Institute of Standards and Technology (NIST) in 2001 [5]. Cryptanalytic papers in the next years culminated in attacks taking [6,7]:

• $2^{140}$ operations to break 7 rounds of 256-bit AES;
• $2^{204}$ operations to break 8 rounds of 256-bit AES.

Salsa20 was published in 2005 [8]. Refereed cryptanalytic papers by Fischer et al. [9] and Tsunoo et al. [10] reported attacks taking:

• $2^{151}$ operations to break 7 rounds of 256-bit Salsa20;
• $2^{251}$ operations to break 8 rounds of 256-bit Salsa20.

These results indicate that AES and Salsa20 present similar security performance for the same number of rounds.

2.2. AES and Salsa20 Implementations

Over the years, RFID tags have been designed with the goal of reducing their power consumption in order to meet the demand for passive chip applications and lower cost.

Experimental results from L. Fu et al. [11] show that an RFID-dedicated AES module can achieve low-power operation, down to $4.05\mathsf{\mu }\mathrm{W}$ @ $1.8\mathrm{V}$ and latency of 204 cycles.

The low cost demanded for RFID tags forces them to be very resource-limited. Typically, they can only store a few hundred bits, have 5–10 k logic gates, and offer a maximum communication range of a few meters. Within this gate count limitation, only between 250 and 3000 gates can be devoted to security functions [12].

Several papers have presented low-power implementations of the AES suitable for RFID tag applications in terms of power consumption and die size [4,13,14], where the best results are about $4.5\mathsf{\mu }\mathrm{W}$ on $0.35\mathsf{\mu }\mathrm{m}$ at 100 $\mathrm{kHz}$ [15].

There are several implementations of Salsa20 [16] for FPGA (field-programmable gate array) and ASIC (application-specific integrated circuit) simulations, all of them optimized for speed. However, these implementations are not concerned about low-power constraints.

Some software-based papers combine both ciphers by using Salsa20 for encryption and AES for authentication [17], but there is still a lack of hardware-based papers, as noted in a recent review that excludes a Salsa20 implementation on a chip for proper comparison [18].

2.3. Salsa20 vs. ChaCha8 for RFID Applications

Shortly after the publication of Salsa20, the same author published the variant known as ChaCha8, a 256-bit stream cipher based on the 8-round cipher Salsa20/8. The changes from Salsa20/8 to ChaCha8 are designed to improve the diffusion per round, conjecturally increasing resistance to cryptanalysis, while preserving—and often improving—time per round. In Ref. [19], they claim that ChaCha8 would provide better overall speed than Salsa20 for the same level of security.

Several recent works, such as Pfaul et al. [20], demonstrated the efficiency of the ChaCha8 algorithm implemented in FPGAs for encrypting high-speed communication channels. However, for RFID applications, the need for a smaller implementation area on chip is a more fundamental requirement than the operating speed, a fact that motivated the choice of the Salsa20 algorithm for this project, rather than its successor ChaCha8, due it smaller area and consequently smaller power consumption.

3. Algorithm Descriptions

3.1. The AES Algorithm

An official description of the AES is detailed in the NIST FIPS (Federal Information Processing Standards) PUB 197 [5]. For the sake of clarity, a brief outline of the AES’s structure is explained in this section. The AES algorithm is a block cipher that was published in the FIPS 197, in 2001. It was adopted by the U.S. government when the National Security Agency (NSA) approved AES as a cipher for top-secret information in 2002.

The AES is capable of using cryptographic keys of 128, 192, and 256 bits to encrypt or decrypt data in blocks of 128 bits (with a 128-bit message block). The data to be processed are usually expressed as an array of bytes organized as a 4 by 4 matrix and called the ‘State’.

The design principle is based on a substitution permutation network and it is specified to convert an input block into a final output block by a number of repetitive transformation rounds [5]. Each round consists of up to four processing steps, which are performed at the byte or bit level of the State. The transformations that describe a round of AES and the respective processing steps are:

• AddroundKey transformation: this is simply the XOR between each bit of the State to each bit of the round key. This is the operation that depends on the cryptography key.
• SubByte transformation: this is a non-linear byte substitution. It has two steps, of which the first one is a multiplicative inverse and the other is an affine transformation.
• ShiftRow transformation: this is a byte-wise operation. The first row of the State is not shifted, but the last three rows of the State are rotated over 1, 2, and 3 bytes, respectively. This operation adds linear diffusion.
• MixColumn transformation adds linear diffusion into the cryptography. Each column of the State is combined using an invertible linear transformation. Each column is treated as a polynomial over GF (Galois field) $\left(2^8\right)$ and it is then multiplied by a fixed polynomial $c\left(x\right)$ modulo $x^4+1$, given by

$$C\left(x\right)=03x^3+01x^2+01x+02$$

(1)

During the InvMixColumn operation, each column is treated as a polynomial over GF$\left(2^8\right)$, and then, multiplied by a fixed polynomial $C^{-1}\left(x\right)$ module $x^4+1$, given by

$$C^{-1}\left(x\right)=0b{x}^3+0d{x}^2+09x+0e$$

(2)

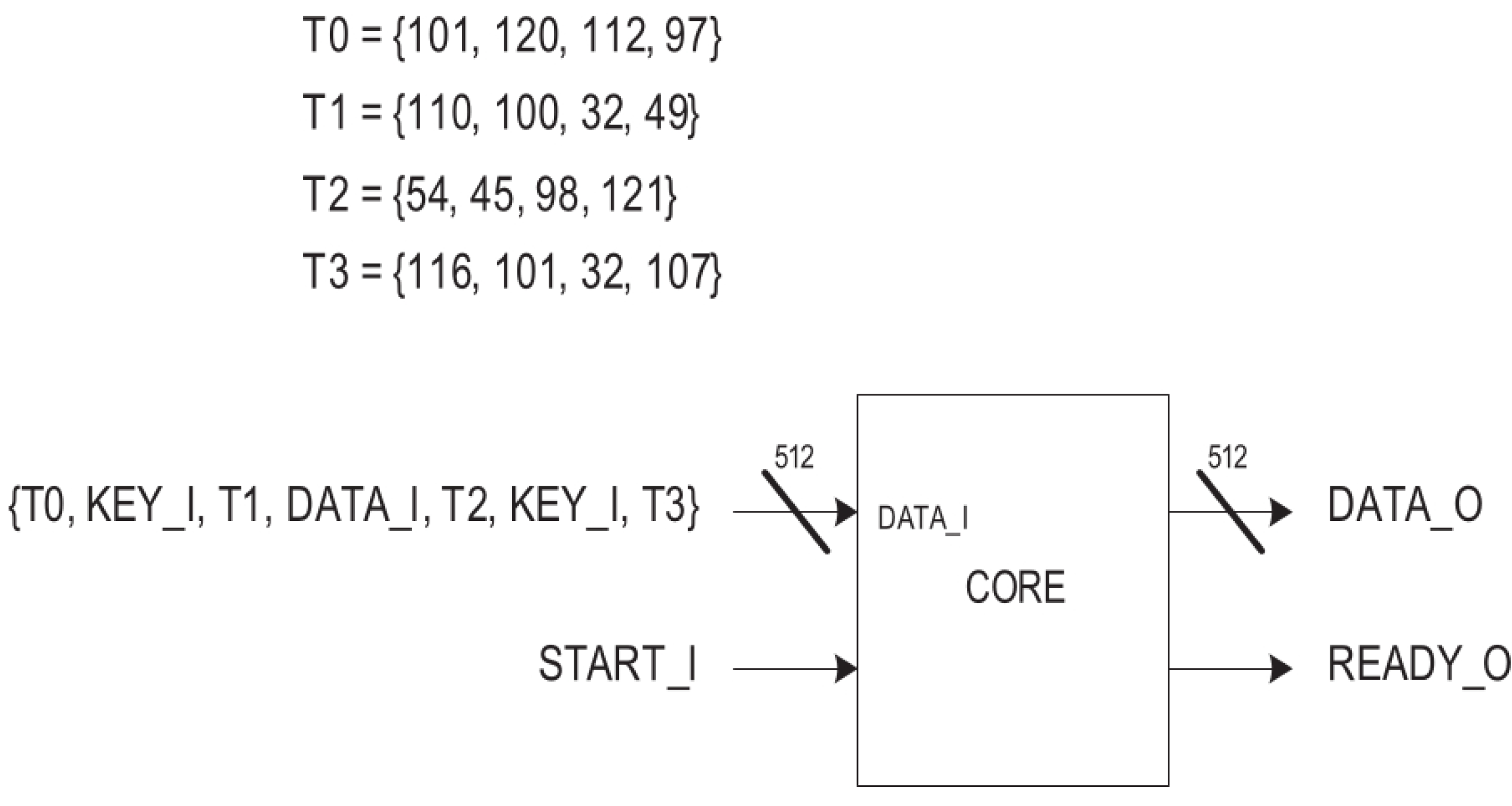
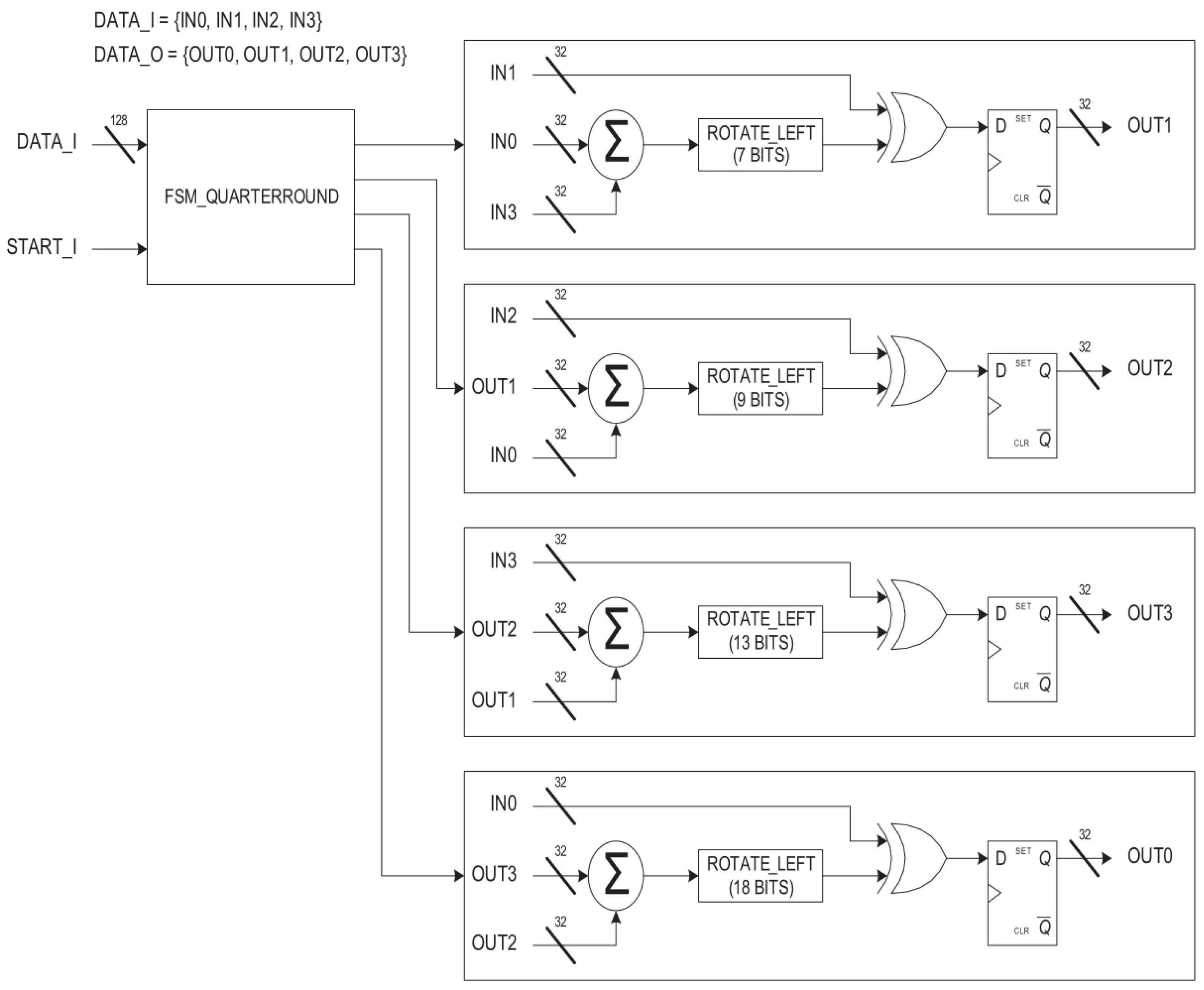
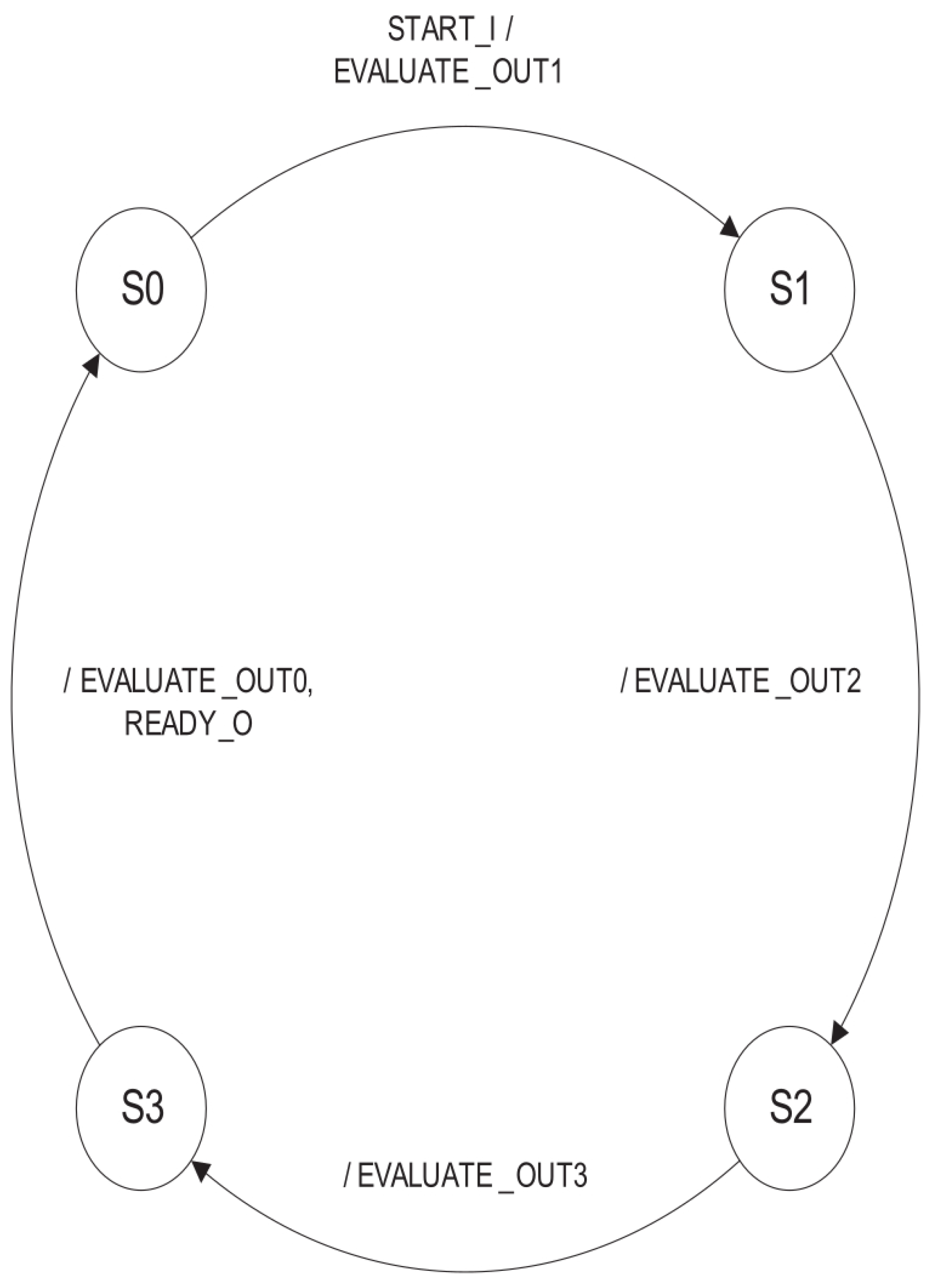
3.2. The Salsa20 Algorithm

Salsa20 is a stream cipher that works in counter mode. It generates a sequence of keystream blocks Z, which are then XORed with the input message (plaintext) to produce the encrypted message (ciphertext). The internal keystream generation function of Salsa20 takes as input a 256-bit secret key $k=\left(k_0,k_1,\dots ,k_7\right)$ and a 64-bit nonce $n=\left(n_0,n_1\right)$, i.e., a unique message number, to produce a sequence of 512-bit keystream blocks (as well a 512-bit message block). The inputs are configured as a 4 by 4 matrix of 32-bit words:

$$X=\left[\begin{array}{cccc}{x}_0& x_1& x_2& x_3\\ x_4& x_5& x_6& x_7\\ x_8& x_9& x_{10}& x_{11}\\ x_{12}& x_{13}& x_{14}& x_{15}\end{array}\right]=\left[\begin{array}{cccc}{\varphi }_0& k_0& k_1& k_2\\ k_3& {\varphi }_1& n_0& n_1\\ t_0& t_1& {\varphi }_2& k_4\\ k_5& k_6& k_7& {\varphi }_3\end{array}\right]$$

where the 64-bit counter $t=(t0,t1)$ corresponds to the message block index and ${\varphi }_i$ are predefined constants. The keystream block $Z$ is then defined as

$$Z=X+DR\left(X\right)$$

(3)

The double-round function $\mathit{DR}\left(\right)$ consists of the double computation of four QUARTERROUND functions $\mathit{QR}\left(\right)$ over the rotated columns and rows of X. $\mathit{DR}\left(\right)$ is divided into the column step, which applies four $\mathit{QR}\left(\right)$ functions on the columns of X, and the row step, for the rows of X:

$$\left\{\begin{array}{c}QR\left(x_0,x_4,x_8,x_{12}\right)\\ QR\left(x_5,x_9,x_{13},x_1\right)\\ QR\left(x_{10},x_{14},x_2,x_6\right)\\ QR\left(x_{15},x_3,x_7,x_{11}\right)\end{array};\left\{\begin{array}{c}QR\left(x_0,x_1,x_2,x_3\right)\\ QR\left(x_5,x_6,x_7,x_4\right)\\ QR\left(x_{10},x_{11},x_8,x_9\right)\\ QR\left(x_{15},x_{12},x_{13},x_{14}\right)\end{array}\right.\right.$$

The $QR(a,b,c,d)$ transformation updates four 32-bit words of the matrix $X$. It sequentially computes per line over the tuple $(a,b,c,d)$:

$$\begin{array}{c}b=b\oplus \left[\right(a+d)<<<7],\\ c=c\oplus \left[\right(b+a)<<<9],\\ d=d\oplus \left[\right(c+b)<<<13],\\ a=a\oplus \left[\right(d+c)<<<18]\end{array}$$

(4)

Considering Equation (4), r double-rounds are executed over the input matrix X. Finally, the updated matrix $X$ is added to the original input matrix. Salsa20 has been presented as an $r=10$-round stream cipher [16].

4. Algorithm Implementations

4.1. AES Implementation

Since the AES algorithm is iterative, a minimum set of processing blocks is used and a simple finite state machine controls the many rounds that repetitively reuse these processing blocks.

The current implementation has three main processing blocks, KeySchedule, MixColumn, and SubByte, where the latter includes also the ShiftRow operation, with both areas being executed by the same processing block. The encryption and decryption steps of the simple finite state machine are described in Figure 1.

In order to save any redundant processing during key expansion for decryption, the ten round keys are saved in registers before any data processing.

As you can see from the implementation flowchart, the first step during cryptography is to derive its ten round keys and to save each round key in a bank of registers. This approach provides a latency improvement of 135 cycles with the area addition of nine 128-bit registers.

Both SubByte and KeySchedule transformations use an S-box. Since the control unit does not request the SubByte and KeySchedule to operate at the same time, they can share the same S-box logic to minimize area. In this implementation, in order to speed up the S-box tasks, there are two identical instances that function in parallel, as shown in Figure 2.

The first step for the S-box comprises finding the multiplicative inverse of a byte from the AES’s state. The second step S-box comprises an affine transformation. The element of inversion is performed in $GF\left({\left(2^4\right)}^2\right)$ by means of mathematical manipulation.

The MixColumn controller sends a 32-bit input to a multiplier block Word_MixColumn. Each input stream sent from the MixColumn controller is a column of the AES State. Thus, the MixColumn operation is performed in four cycles (Figure 3), since each column of the State is processed per cycle. The 32-bit column is processed by four multiplier blocks. We reused common constant multipliers in the data path between the MixColumn and InvMixColumn operations to reduce the hardware area.

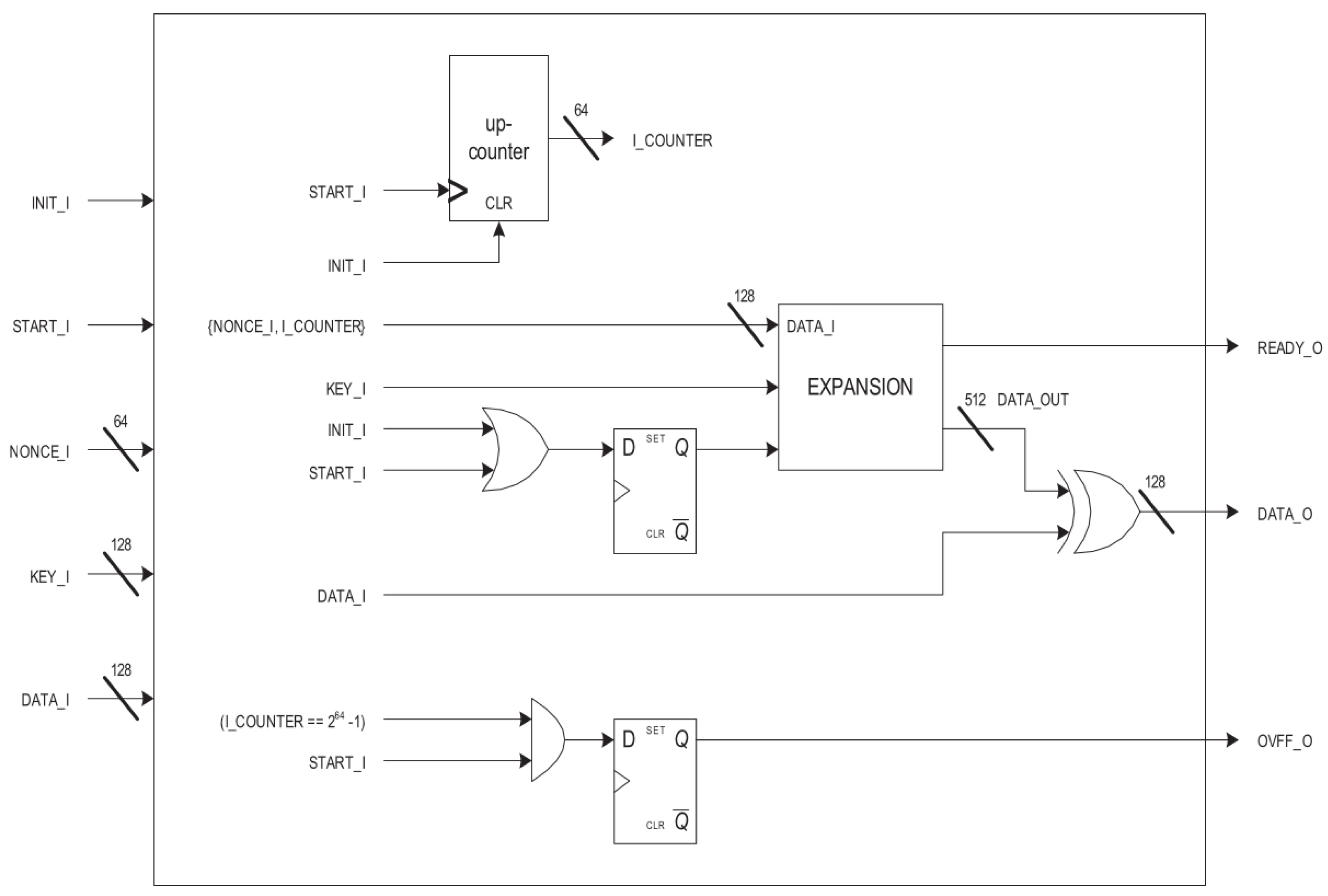
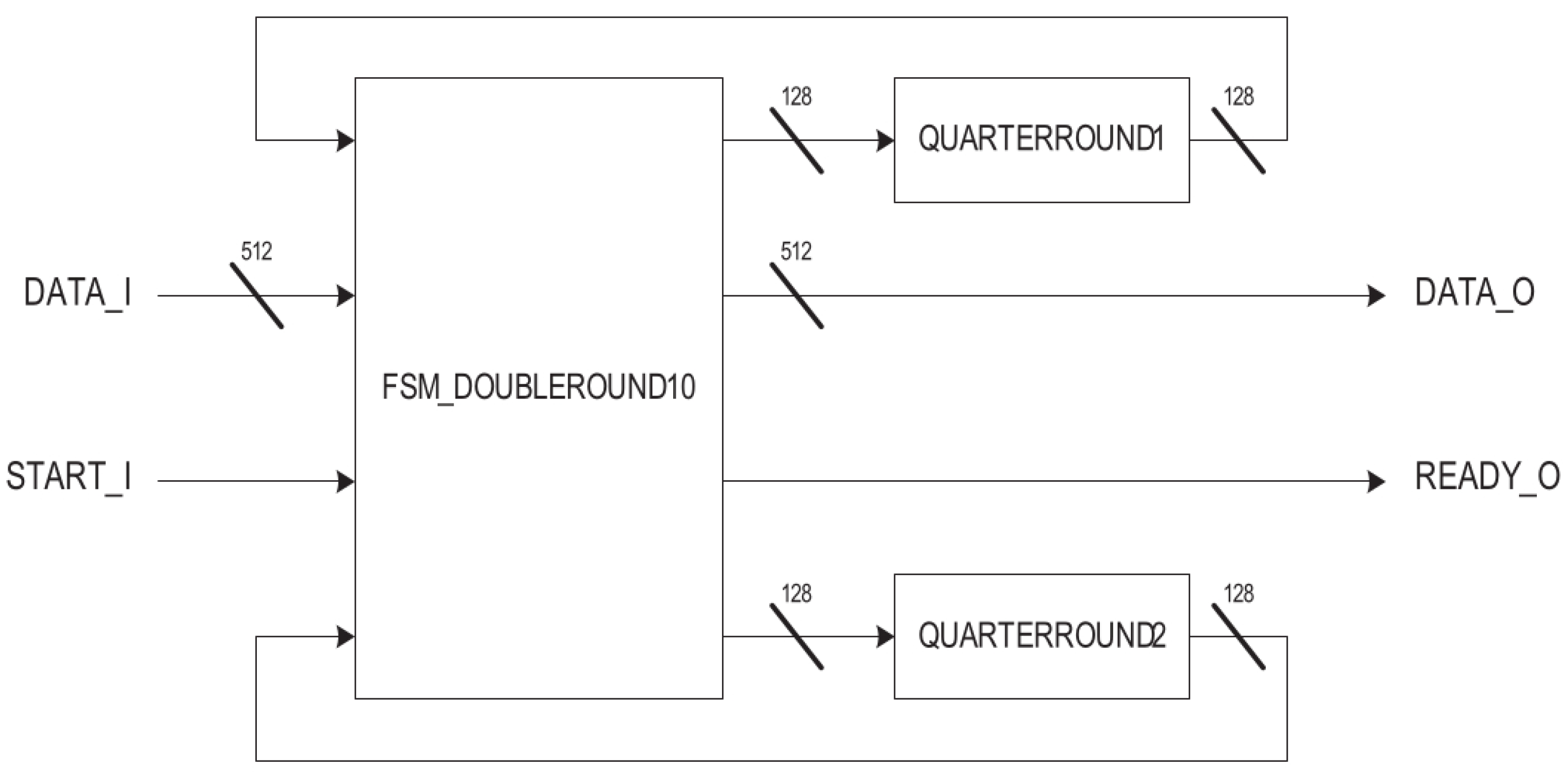
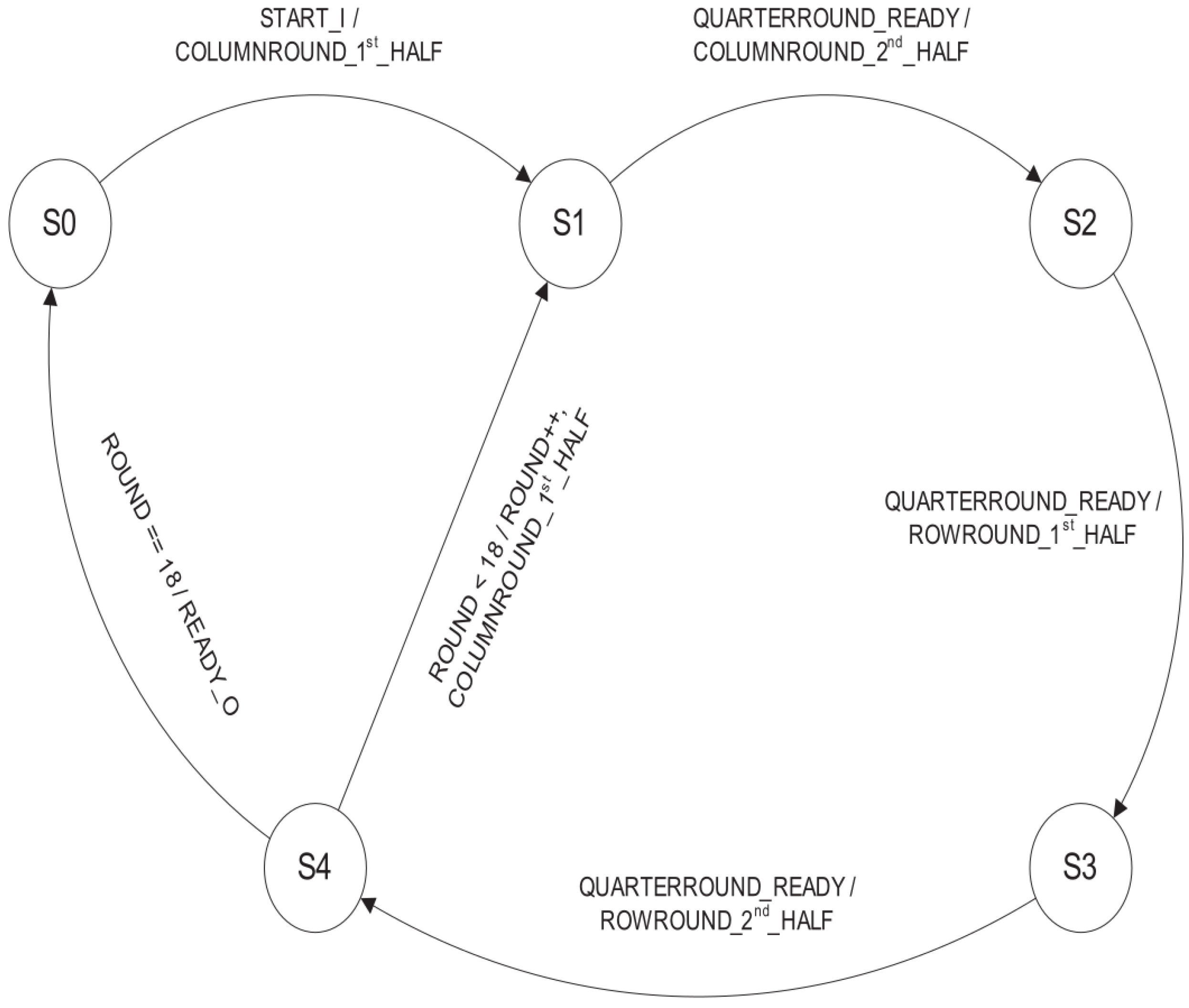
4.2. Salsa20 Implementation

The Salsa20 implementation prioritizes a low-power approach over execution time. Each step of the QUARTERROUND function is executed in a clock cycle for power-saving purposes. In this case, the QUARTERROUND function is executed in four clock cycles. For timing purposes, the double-round function control state machine uses two QUARTERROUND modules at the same time.

The basic operation of Salsa20 is the QUARTERROUND function. It is executed 80 times in the Salsa20 algorithm, so it is the most obvious choice for optimizing in terms of power. Figure 4 shows the Salsa20 encryption hardware implementation. It includes a 64-bit counter to generate the data input to the Salsa20 expansion module, as described in the Salsa20 specification [8]. It also evaluates the XOR for the encrypted output.

The ‘Salsa20 expansion’ module is a simple wire concatenation in the input of the Salsa20 core module as shown in Figure 5. The T0, T1, T2, and T3 constants are described in the Salsa20 specification [8].

The Salsa20 core module (Figure 6) is composed of the Salsa20 DOUBLEROUND10 module with LITTLE_ENDIAN functions at the input and output. The LITTLE_ENDIAN function changes the endianness, using a byte as the minimal block.

Figure 7 shows the Salsa20 DOUBLEROUND10 module implementation. It is composed of a control state machine and two QUARTERROUND modules. The double-round function is a column-round function followed by a row-round function.

The Salsa20 DOUBLEROUND10 control state machine (Figure 8) controls the data flow to and from the QUARTERROUND modules. This control state machine executes two QUARTERROUND functions at the same time for each half-round of the double-round (the first half of column-round, the second half of column-round, the first half of row-round and the second half of row-round).

Figure 9 shows the Salsa20 QUARTERROUND, where four words (32 bits each) are evaluated one at a time. The QUARTERROUND is optimized for power: each word takes a clock cycle in the QUARTERROUND execution, so each QUARTERROUND execution takes 4 cycles to complete.

The Salsa20 QUARTERROUND control state machine (Figure 10) controls the clock gating of the four-word evaluation sub-blocks.

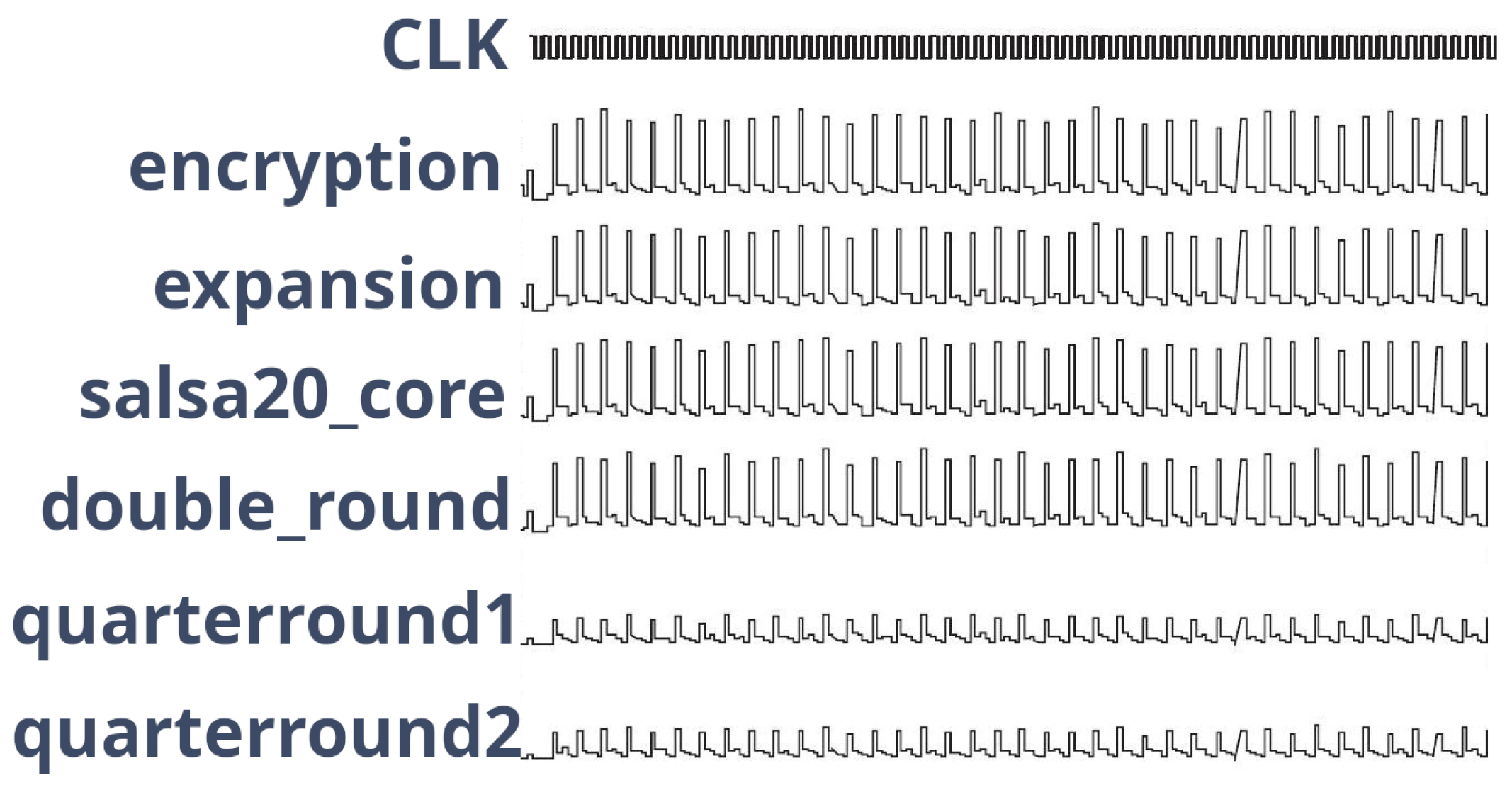
5. Results and Discussion

5.1. AES Design

The toggle count of each processing block during the simulation of an AES decryption can be observed in Figure 11. Since the technology node is $0.18\mathsf{\mu }\mathrm{m}$, dynamic power is the dominant factor in our power analysis. Based on the toggle counts of encryption and decryption simulations, one can conclude that the peak power consumption occurs during the MixColumn transformation. Therefore, the decision to add two S-boxes does not affect peak power. Moreover, the S-box implementation uses very little area, and the addition of a second S-box does not represent a considerable cost to the overall system.

Table 1. Summary of the AES results.

Average Power (μW)	Encryption/Decryption (# Cycles)	Block Size (# bits)	Cells (#)	Total Area (μm2)
4.01	180	128	4303	217,250

shows a summary of the main simulation results generated from the toggle waveform (that represents the number of transitions in a circuit in a given period, which is a good approximation for the power). The AES design has an average power consumption of $4.01\mathsf{\mu }\mathrm{W}$ with a clock of $100\mathrm{kHz}$. The encryption or decryption latency is 180 cycles and its critical path takes 19,045 ps (we basically achieved the same characteristics obtained by L. Fu et al. [11]). The reduced and balanced latency of both decryption and encryption is achieved at the cost of the nine 128-bit registers used by the KeySchedule block. These extra registers avoided redundant processing but had an impact on the overall area. This AES design has 4303 cells and a total area of 217,250 $\mathsf{\mu }{\mathrm{m}}^2$.

5.2. Salsa20 Design

The toggle count of each processing block of the Salsa20 simulation can be observed in Figure 12. As expected, the peaks of the toggle are concentrated in the QUARTERROUND function. Two QUARTERROUND blocks were used instead of only one to make the timing close to the AES implementation.

Table 2. Summary of the Salsa20 results.

Average Power (μW)	Encryption/Decryption (# Cycles)	Block Size (# bits)	Cells (#)	Total Area (μm2)
2.82	202	512	3468	135,150

shows the summary report generated by the simulation-based toggle waveform. Salsa20 has an average power consumption of $2.82\mathsf{\mu }\mathrm{W}$ with a clock of $100\mathrm{kHz}$ and a $0.18\mathsf{\mu }\mathrm{m},1.8\mathrm{V}$ cell library. The encryption and decryption latency is 202 clock cycles and its critical path takes 17,561 ps.

5.3. Layout Comparison

The layout of both designs used the X-FAB $0.18\mathsf{\mu }\mathrm{m}$ and $1.8\mathrm{V}$ library. The AES and Salsa20 modules have the same area utilization of $75\%$.

The AES layout, depicted in Figure 13, includes the AES module and a testing control logic. The layout of the AES module is colored in red and it is $395\mathsf{\mu }\mathrm{m}\times 550\mathsf{\mu }\mathrm{m}\left(\mathrm{217,250}\mathsf{\mu }{\mathrm{m}}^2\right)$ which is very close to the estimation from Table 1.

The Salsa20 layout (Figure 14) includes the Salsa20 module and the same testing control logic. The layout of the Salsa20 module is colored in red and it is $255\mathsf{\mu }\mathrm{m}\times 530\mathsf{\mu }\mathrm{m}$$\left(\mathrm{135,150}\mathsf{\mu }{\mathrm{m}}^2\right)$ which is also very close to the estimation from Table 2. The AES layout has two more filler pads than the Salsa20 layout because of its larger area.

6. Conclusions

In this paper, low-power implementations of the AES and Salsa20 were proposed and their results were compared. In order to fairly compare the cost and power consumption of those two cryptographic algorithms without any trade-off compromise, the same synthesis and simulation parameters, such as clock, test vectors and tech library, were used on both of them. In addition, both have been designed to have similar latencies.

Our work shows that Salsa20’s power consumption is considerably lower than the AES power consumption ($2.82\mathsf{\mu }\mathrm{W}/4.01\mathsf{\mu }\mathrm{W})\ast (128\mathrm{bits}/512\mathrm{bits})=0.176(17.6\%)$, since the block sizes are different, suggesting the former is a better choice for low-power devices. Moreover, the area of the Salsa20 implementation is also considerably lower than that of the AES one, presenting also a lower fabrication cost. Therefore, Salsa20 is a very attractive cryptographic algorithm for secure RFID applications.