Abstract
First-principles calculations were carried out to investigate the physical properties of the full-Heusler compound In2MnW. The WIEN2K code was utilized with various approximations, such as GGA and GGA+U, to analyze its structural, electronic, and magnetic properties. The unit cell was optimized to determine the ground-state energy. The calculated formation enthalpy (ΔH) of In2MnW is −0.189 eV, indicating its thermodynamic stability due to the negative value. Band structure analysis using both potentials confirms the compound’s metallic nature, which is further supported by total density of states calculations. The total magnetic moment is found to be 4.3 µB, which slightly increases to 4.4 µB when the U parameter is included. These findings suggest that In2MnW demonstrates metallic ferromagnetic behavior, highlighting its potential as a promising ferromagnetic material for mass storage applications.
1. Introduction
Heusler alloys, first discovered in 1903 [1], have gained considerable interest due to their remarkable properties, which have led to their broad use in a variety of technological fields. These materials are essential in applications such as energy harvesting systems, [2] magnetic random-access memory (MRAM), sensors, spintronic, actuators, thermoelectric devices, solar cells, semiconductor technologies [3,4,5], and thermoelectric materials [6,7,8,9,10,11]. Furthermore, Heusler alloys have proven to be valuable in storage technologies such as hard drives, optical discs, and magnetic disk drives [12]. Recent theoretical research on Heusler compounds has highlighted their potential for mass storage applications and ferromagnetic technologies, primarily due to their high magnetic moments [13,14,15]. Metals that conduct electricity via the spin-up channel, referred to as majority spin carriers, and those that exhibit conductivity in the spin-down channel, known as minority spin carriers, are classified as fully metallic materials. This characteristic results from an overlap between the valence and conduction bands at the Fermi level [16]. Structurally, Heusler alloys generally consist of two manganese atoms, along with copper and tin atoms. These materials follow the X2YZ formula, characterized by three interwoven face-centered cubic (FCC) sub lattices within the Fm3m space group. In some cases, symmetry breaking in the non-centrosymmetric F-43m space group leads to the division of one X2 sub lattice into two smaller sub lattices, with one remaining vacant, forming the XYZ composition found in half-Heusler phases [13,14].
The quest for new materials has advanced swiftly as scientists aim to drive technological progress for societal benefit. Heusler alloys, in particular, have attracted considerable scientific attention because of their distinct characteristics. Research by Dahal and Kaphle has highlighted their promising potential for a wide range of applications, encouraging further exploration in this area [15]. The physical properties of XYZ-type half-Heusler materials have been investigated, with results showing that various spin channels exhibit distinct band gaps (Eg), such as 0.38 eV for FeMnGe and 0.95 eV for CoMnSb. These results indicate that the studied Heusler alloys demonstrate half-metallic behavior. Additional studies by Fiedler and Kratzer provide further evidence for this conclusion [16,17]. First-principles calculations were carried out using the PBE and HSE06 exchange functionals to examine the structural, electronic, and phonon properties of ternary NiZrSn and CoZrBi semiconductors, both of which adopt the C1b crystal structure. Density functional theory (DFT) was applied to better understand their fundamental properties. In a similar vein, Wakeel et al. investigated the physical properties of Pd2AZ (where A = Cu, Hf, Mn, Ti, Zr and Z = Al, Ga, In, Sn) through DFT-based simulations. Their results showed that all these Heusler compounds exhibit metallic behavior, which is a result of the overlap between the valence and conduction bands [17]. In Kulkova et al. [18], first-principles calculations were carried out to investigate the electronic properties of both half-Heusler and full-Heusler alloys using the FLAPW method. The results revealed that the computed equilibrium lattice parameters and magnetic moments align well with existing experimental data. While metallic Heusler compounds are widely studied, half-metallic Heusler alloys have garnered significant attention due to their potential for various technological applications, particularly in spintronics, as highlighted by Munir [19].
The objective of this study is to conduct an in-depth analysis of the band gap, density of states, partial density of states, and magnetic moment values of In2MnW. Ferromagnetic (FM) Heusler alloys inherently exhibit distinct magnetic behavior, often responding sharply even in weak external magnetic fields. In Heusler alloys with the X2MnZ composition, the magnetic moment is mainly attributed to the Mn atoms, usually yielding values within a predicted range. While these compounds are metallic in nature, they preserve an optimal structural configuration and display localized magnetic properties [20,21]. The system is designed to examine the impact of changes in electron concentration on the magnetic properties in the presence of atomic disorder. To investigate the contribution of spin (Z) and 3d (X) elements in determining the magnetic behavior of Heusler alloys, comprehensive magnetic measurements and further analyses have been carried out. The results suggest that the concentration of electron spins is a key factor influencing these magnetic properties. During our study, we gathered important information about the physical properties of Heusler In2MnW. From its magnetic behavior to its electronic configuration, each discovery added to a more comprehensive understanding of the material. As the research advanced, the importance of In2MnW became clearer, motivating further investigation into its complex characteristics. This work not only deepens our understanding of its fundamental properties but, also underscores its potential for various technological uses. These findings lay the foundation for future research, bringing us closer to fully exploiting the capabilities of Heusler In2MnW and unlocking its broad range of possibilities.
Our study focused on the metallic cubic structure of the Heusler In2MnW compound as the foundation for analysis. Based on our calculations, the magnetic moment plays a critical role in making the In2MnW compound suitable for magnetic material applications. Prior to our research, the theoretical properties of In2MnW had not been extensively explored in the literature. The paper is organized into several sections: Section 2 outlines the computational methods used in the study, Section 3 delves into the structural, lattice, electronic, and magnetic properties of In2MnW, and Section 4 presents the conclusions drawn from the study.
2. Computational Method
First-principles calculations were carried out to examine the physical properties of the full-Heusler compound In2MnW using the WIEN2K code within the framework of density functional theory (DFT). The calculations utilized the full potential linearized augmented plane wave (FP-LAPW) method [18,19]. The Kohn–Sham equation was solved to analyze the ground-state properties, focusing particularly on the minority electrons required for calculating these characteristics. The study used the generalized gradient approximation (GGA) and GGA + U potentials. The GGA + U method, which includes a term for intramolecular Coulombic repulsion, was found to be the most effective for accurately addressing localized d and f electrons. For the In2MnW compound, a Ueff value of 7 eV was applied to treat the d and f states, helping to correct the self-interaction error, particularly in the partially filled d states of the In and Mn transition metals. The calculation procedure involved dividing the crystal into muffin-tin (MT) spheres with an interstitial region between them. Within the MT spheres, the basis set was expanded using spherical harmonic functions, while plane waves were employed in the interstitial region. The radius of the muffin-tin spheres (RMT) was calculated to be 2.5 atomic units (au) for Mn, W, and In. To avoid charge leakage from the MT spheres, a core-valence separation energy of −11 Rydberg (Ry) was applied. To achieve energy convergence, the wave function cutoff parameter was chosen as KmaxRMT = 5, where RMT refers to the smallest muffin-tin radius, and Kmax is the plane wave expansion parameter. A k-point mesh of 1000 was used to sample the Brillouin zone (BZ), ensuring precise results. The total energy convergence criterion was established with a threshold of less than 10−6 Ry.
3. Results and Discussion
3.1. Structural Properties
The Heusler compound In2MnW has a cubic crystal structure with the space group Fm-3m (No. 225) as described by Graf et al. (2009) [22]. In this crystal structure, In atoms are located at fractional coordinates (0.25, 0.25, 0.25) and (0.75, 0.75, 0.75), while Mn and W atoms occupy the positions (0, 0, 0) and (0.50, 0.50, 0.50), respectively, within the unit cell. The atomic arrangement within the primitive cell is depicted in Figure 1a. The compound exhibits a three-dimensional Heusler structure with an L21;-type configuration. In this ferromagnetic (FM) Heusler alloy, W forms bonds with four equivalent Mn atoms and ten In atoms in a distorted body-centered cubic structure. The W–Mn bond distances measure 2.86 Å and 2.88 Å, while the W–In bonds range from 2.86 Å to 3.33 Å. Additionally, Mn is coordinated to four equivalent W atoms and four equivalent In atoms, with Mn–In bond lengths varying between 2.86 Å and 2.87 Å. The structure features two distinct In sites. In the first site, In bonds to four W atoms and four In atoms, creating distorted edge-sharing InIn4W4 tetrahedral. At the second site, In adopts a 4-coordinate geometry, forming bonds with six W atoms, four Mn atoms, and four In atoms. Optimizing the crystal structure is essential for understanding the material’s stability, band gap characteristics, and carrier transport behavior. The lattice parameters were refined by minimizing the total energy within the Fm-3m symmetry space group [23,24]. The energy–volume optimization curve, shown in Figure 1, helps validate the stability of the compounds studied and confirms their suitability for the intended applications. Since density functional theory (DFT) provides precise ground-state calculations, structural optimization is necessary to obtain reliable results. To determine the structural parameters, we utilized the Birch–Murnaghan equation and analyzed atomic positions and unit cell dimensions to further investigate the compound’s structural properties. The Birch–Murnaghan equation is expressed as [25]:
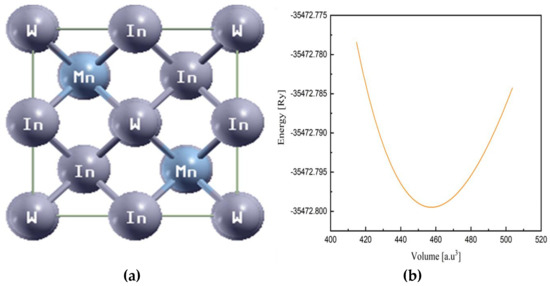
Figure 1.
Illustration of (a) compound structure and (b) volume optimization curve of In2MnW.
Our optimization results indicate that the ferromagnetic (FM) phase is the most favorable for In2MnW compared to the paramagnetic (PM) and antiferromagnetic (AFM) phases. The formation energy (ΔH) is calculated as the difference between the total energy (E0) of In2MnW and the sum of the individual energies of In, Mn, and W (EIn, EMn, and EW, respectively). It can be computed as [26,27]:
where EIn2MnW signifies the total energy of In2MnW, while EIn, EMn, and EW represent the optimized total energy of the respective atom. The value of ΔH was computed as −0.189 eV for In2MnW. The negative value of the ΔH indicates that it is thermodynamically stable [21].
3.2. Lattice Parameters
The structural refinement of In2MnW was carried out to explore its ground-state properties. By minimizing the total energy (Etot), the lattice constants were determined concerning the lattice parameter, ensuring the material’s stability and enabling precise calculation of its ground-state energy. The optimized lattice parameter was identified as 6.33 Å. Total energy computations were performed for various volumes near the experimentally observed value to further refine the unit cell and determine the ground-state energy. Figure 1b illustrates the optimization curve, depicting the correlation between total energy and volume. The Birch–Murnaghan equation was utilized to derive structural parameters, establishing the relationship between volume and pressure while determining the material’s energy as a function of volume. A detailed examination of atomic positions and unit cell dimensions provided additional insights into the compound’s structural characteristics [28,29]. For In2MnW, the ferromagnetic (FM) phase emerged as the most stable phase. Moreover, based on experimental findings and the existing literature, the ferromagnetic state is regarded as the most suitable phase for this material. The formation energy of the compound was found to be negative, signifying its thermodynamic stability. This formation energy was computed by subtracting the sum of the individual elemental energies (E(In2), E(Mn), and E(W)) from the total energy (E0) of the compound. The negative formation energy further substantiates the compound’s stability. The optimized parameters, including unit cell energy (E0), bulk modulus (B) in GPa, lattice constant (Å), and the pressure derivative of the bulk modulus (Bp), are presented in Table 1.

Table 1.
Optimized lattice parameters of ln2MnW compound.
3.3. Electronic Characteristics
To understand a material’s electronic properties, it is essential to examine its band structure, which provides key insights into its behavior. In this study, we compare the electronic characteristics of the In2MnW Heusler alloy using both GGA and GGA + U approximations. No comprehensive study has yet explored the electronic and magnetic properties of this compound. To address this, we computed spin-dependent band dispersions, total density of states (TDOS), and projected density of states (PDOS) to evaluate its potential for electronic applications. The band structure of In2MnW, presented in Figure 2 and Figure 3, reveals high-symmetry directions (Γ→M→K→Γ→A) within the first Brillouin zone. These findings confirm the metallic nature of the compound, as the electronic states cross the Fermi level in both spin channels [30,31]. The overlap between the valence band (VB) and conduction band (CB) further supports this metallic behavior. Specifically, in the majority spin channel, the VB and CB intersect near the Fermi level, indicating metallic characteristics. Similarly, in the minority spin channel, there is no gap between the valence band maximum and conduction band minimum, suggesting continuous electronic states at the Fermi level. Both the GGA and GGA + U approximations consistently show this metallic behavior. The presence of metallic characteristics in both spin channels indicates that In2MnW demonstrates full metallic ferromagnetism. To further support this, the TDOS was calculated for all applied potentials, as shown in Figure 4 and Figure 5. The TDOS analysis highlights the energy contributions from different electronic states and aligns with the band structure, reinforcing the metallic nature of the material. The TDOS plots confirm the absence of an energy gap in both the majority and minority spin channels under both GGA and GGA + U approximations. These results, in line with the band structure, support the compound’s metallic properties. This metallic behavior enhances the flow of spin-polarized current, leading to a high polarization ratio, which is advantageous for ferromagnetic materials [11,32]. Thus, the TDOS plots affirm the metallic nature of In2MnW, positioning it as a strong candidate for use in ferromagnetic technologies.
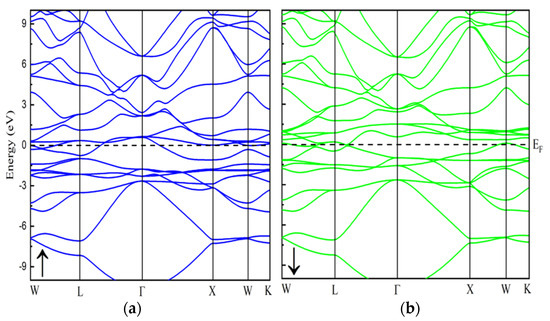
Figure 2.
The calculated band structure of In2MnW with spin-up and spin-down states by using PBE-GGA potential.
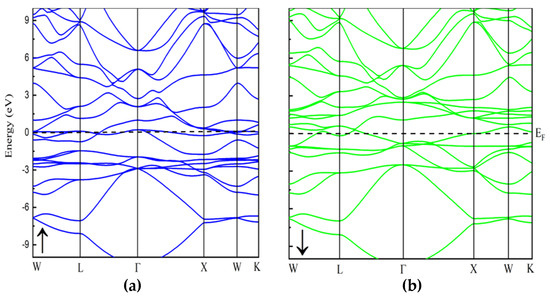
Figure 3.
The calculated band structure of In2MnW with spin-up and spin-down by using GGA + U potential.
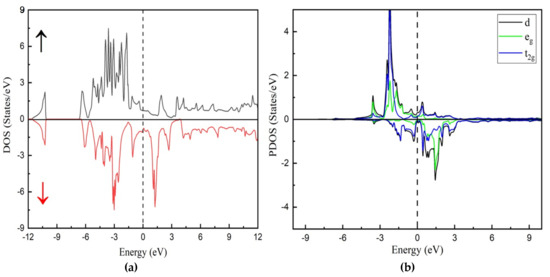
Figure 4.
Calculated (a) total density of state with spin-up and spin-down and (b) partial densities of states of In2Mn with GGA.
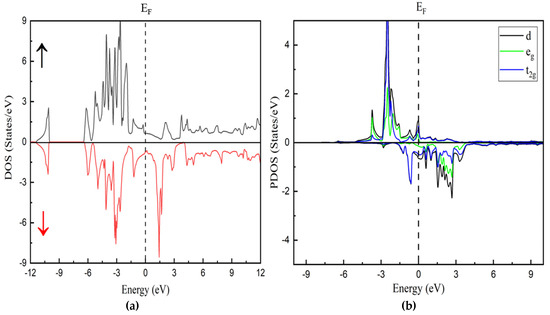
Figure 5.
Calculated (a) total density of state with spin-up and spin-down and (b) partial densities of states of calculated with GGA + U.
Additionally, the net magnetic moment (μB) of the In2MnW compound is influenced by contributions from interstitial regions and individual atoms, specifically Mn and In, while the W site counteracts this effect. This behavior is evident from the calculated μB values obtained through both computational approaches [33,34]. The repeated occurrence of Mn/In-d states plays a key role in this phenomenon. The projected density of states (PDOS) analysis reveals the significant contributions of Mn, W, and In, emphasizing their impact on the compound’s electronic structure. The In-p state crosses the Fermi level in the spin-up orientation, reinforcing the material’s metallic nature. The pronounced peaks near the Fermi level are primarily attributed to the Mn-d and W-d states. Therefore, the electronic properties of In2MnW are largely governed by the interactions between In-p and Mn-d states.
Figure 5a represents the spin-up states and spin-down states, showing good agreement with the previous results of band structure. A strong spin polarization is visible, indicating the ferromagnetic nature of the compound. Figure 5b shows the contributions from d orbitals of different elements. The blue and green curves correspond to t2g and eg states, respectively. The asymmetry between spin-up and spin-down states confirms strong exchange splitting and is significant, especially in the Mn d orbitals, which is expected for a ferromagnetic Heusler alloy.
Analyzing the partial density of states (PDOS) provides valuable insights into the magnetic properties of In2MnW. The asymmetry between spin-up and spin-down density of states confirms the compound’s magnetic nature. The PDOS reveals that Mn, In, and W orbitals play a dominant role in shaping the material’s electronic structure. Additionally, the spin-polarized electron density of In2MnW has been examined. Figure 6 illustrates a contour plot of the spin-up electron density, where the highest density regions (highlighted in red) correspond to Mn atoms, indicating their significant magnetic contribution. In contrast, In and W atoms exhibit considerably lower spin densities. The spin-down density is generally weaker, and the presence of opposite spin orientations in certain regions suggests antiparallel spin alignment, particularly for W, which exhibits a minor negative magnetic moment (−0.026 µB). These observations align with the computed magnetic moment values. To further explore atomic interactions, spin density contours have been plotted along the (110) plane, as shown in Figure 4. The spin-up states suggest a covalent bond between Mn and In atoms, whereas Mn and W exhibit an ionic interaction. In the spin-down channel, Mn–In bonds continue to display covalent character, while the Mn–W bond shows a reduction in ionic behavior due to atomic size variations. As the d-bands shift from nearly filled to partially filled, the Mn electron density transitions from a spherical to a dumbbell shape when moving from spin-up to spin-down states.
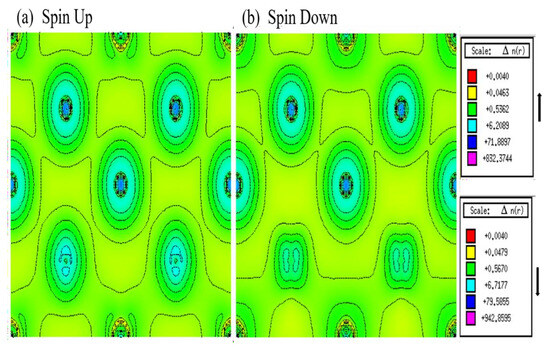
Figure 6.
Contour plot of electron density (spin-up and spin-down) of In2MnW.
3.4. Magnetic Properties
The magnetic properties of the In2MnW compound have been analyzed based on the asymmetry in spin-polarized electronic states, as observed in TDOS and PDOS plots. The magnetic moments (μB) of W, Mn, and In were calculated individually using both GGA and GGA + U methods. The obtained values confirm the magnetic nature of In2MnW, with total and interstitial contributions summarized in Table 2. The computed magnetic moments, approximately 4.30 μB and 4.40 μB for GGA and GGA + U, respectively, closely align with experimental measurements. In Heusler compounds, the alignment of μB arises from two competing effects: intra-atomic energy state splitting of d orbitals and covalent interactions between atoms. The proximity of In atoms influences the d-orbital correlation, leading to a strong interaction between the metallic elements. The presence of two X-type cations in Heusler materials introduces additional complexity to their physical properties. The PDOS analysis of In2MnW reveals strong hybridization between Mn and W atoms. This interaction leads to band restructuring, primarily influenced by the hybridized d orbitals of these transition metals. A well-established concept in magnetism suggests that a higher μB value enhances exchange coupling, which plays a crucial role in determining the material’s magnetic behavior [35]. Mn atoms exhibit a significantly stronger μB compared to ln and W atoms. The negative μB of ln atoms is responsible for their diamagnetic behavior, indicating an anti-parallel alignment that affects the overall ferromagnetic direction [36]. Consequently, W atoms influence the ferromagnetic nature of the ln2MnW compound. The opposite signs of the μB of the interstitial site, Mn, W, and ln atoms compared to the total μB of the ln2MnW, suggest that electrons VB interact in an anti-parallel manner with the total μB of the compound. The results show that ln2MnW exhibits FM behavior due to its strong magnetic features.

Table 2.
Total, interstitial, and localized magnetic moment values for ln2MnW.
4. Conclusions
This study employs density functional theory (DFT) calculations, with and without the inclusion of the Hubbard potential, to investigate the structural, electronic, and magnetic characteristics of the In2MnW compound. The results indicate that In2MnW forms a cubic structure within the Fm3m space group. The electronic behavior of the material was analyzed using both GGA and GGA + U approaches, revealing its metallic nature. The partial density of states was examined to assess the contributions of various atomic states. Notably, the material exhibits a strong magnetic response when subjected to an external magnetic field, which is attributed to its metallic properties and substantial magnetic moment (μB). The magnetic moments were calculated as 4.33 μB with GGA and 4.408 μB with GGA + U, supporting its ferromagnetic nature. These features position In2MnW as a promising candidate for future magnetic storage technologies.
Author Contributions
A.M.K.: conceptualization, data curation, formal analysis, investigation, methodology, writing-original draft, software; U.Z.: supervision, validation, writing-review & editing, visualization, project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research work did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Graf, T.; Felser, C.; Parkin, S.S.P. Heusler Compounds: Applications in Spintronics. In Handbook of Spintronics; Springer: Dordrecht, The Netherlands, 2016; pp. 335–364. [Google Scholar] [CrossRef]
- Bulman, G.; Cook, B. High-efficiency energy harvesting using TAGS-85/half-Heusler thermoelectric devices. Energy Harvest. Storage: Mater. Devices Appl. V 2014, 9115, 17–24. [Google Scholar] [CrossRef]
- Erkisi, A.; Surucu, G. The investigation of electronic, magnetic, mechanical, and lattice dynamical properties of Pd MX (M = Cr, Fe and X = Si and Ge) ferromagnetic half-Heusler metallics: An ab initio study. Mater. Res. Express. 2017, 4, 066504. [Google Scholar] [CrossRef]
- Wang, C.; Meyer, J.; Teichert, N.; Auge, A.; Rausch, E.; Balke, B.; Hütten, A.; Fecher, G.H.; Felser, C. Heusler nanoparticles for spintronics and ferromagnetic shape memory alloys. J. Vac. Sci. Technol. B 2014, 32, 020802. [Google Scholar] [CrossRef]
- Hirohata, A.; Sukegawa, H.; Yanagihara, H.; Zutic, I.; Seki, T.; Mizukami, S.; Swaminathan, R. Roadmap for Emerging Materials for Spintronic Device Applications. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miyazaki, Y. Contrasting role of bismuth doping on the thermoelectric performance of VFeSb half-Heusler. J. Alloys Compd. 2022, 908, 164623. [Google Scholar] [CrossRef]
- Agbaoye, R.O.; Adebambo, P.O.; Adetunji, B.I.; Osafile, O.; Adebayo, G.A. Thermoelectric properties, optimal doping levels and high figure of merit in Cobalt-based Half/Full Heusler alloys by First-Principles calculations. Mater. Sci. Eng. B 2019, 248, 114409. [Google Scholar] [CrossRef]
- Adebambo, P.O.; Osafile, O.E.; Laoye, J.A.; Idowu, M.A.; Adebayo, G.A. Electronic fitness function, effective mass and thermoelectric properties of Rh-based (-ScTe; -TiSb; -VSn) alloys for thermoelectric generator applications. Comput. Condens. Matter 2021, 26, e00523. [Google Scholar] [CrossRef]
- Graf, T.; Parkin, S.S.P.; Felser, C. Heusler Compounds—A Material Class With Exceptional Properties. IEEE Trans. Magn. 2011, 47, 367–373. [Google Scholar] [CrossRef]
- Xie, W.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T. Recent Advances in Nanostructured Thermoelectric Half-Heusler Compounds. Nanomaterials 2012, 2, 379–412. [Google Scholar] [CrossRef]
- Osafile, O.E.; Azi, J.O. Structural, electronic, elastic and mechanical properties of novel ZrMnAs half Heusler alloy from first principles. Phys. B Condens. Matter 2019, 571, 41–49. [Google Scholar] [CrossRef]
- Terris, B.D.; Thomson, T. Nanofabricated and self-assembled magnetic structures as data storage media. J. Phys. D Appl. Phys. 2005, 38, R199–R222. [Google Scholar] [CrossRef]
- Kervan, N.; Kervan, S. A first-principle study of half-metallic ferrimagnetism in the Ti2CoGa Heusler compound. J. Magn. Magn. Mater. 2012, 324, 645–648. [Google Scholar] [CrossRef]
- Berri, S.; Maouche, D.; Ibrir, M.; Zerarga, F. A first-principle study of half-metallic ferrimagnetism in the CoFeTiSb quaternary Heusler compound. J. Magn. Magn. Mater. 2014, 354, 65–69. [Google Scholar] [CrossRef]
- Lei, F.; Tang, C.; Wang, S.; He, W. Half-metallic full-Heusler compound Ti2NiAl: A first-principles study. J. Alloys Compd. 2011, 509, 5187–5189. [Google Scholar] [CrossRef]
- Birsan, A. Magnetism in the new full-Heusler compound, Zr2CoAl: A first-principles study. Curr. Appl. Phys. 2014, 14, 1434–1436. [Google Scholar] [CrossRef]
- Zada, Z.; Khan, A.A.; Reshak, A.H.; Khan, A.M.; Shakeel, S.; Ali, D.; Ismail, M.; Ramli, M.M. A first principles study of Palladium-based full Heusler ferromagnetic Pd2MnSb compound. Opt. Quant. Electron. 2024, 56, 248. [Google Scholar] [CrossRef]
- Kulkova, S.E.; Eremeev, S.V.; Kakeshita, T.; Kulkov, S.S.; Rudenski, G.E. The electronic structure and magnetic properties of full-and half-Heusler alloys. Mater. Trans. 2006, 47, 599–606. [Google Scholar] [CrossRef]
- Munir, J.; Jamil, M.; Jbara, A.S.; Fatima, K.; Ain, Q.; Ullah, H.; Yousaf, M. Spin-polarized electromagnetic and optical response of full-Heusler Co2VZ (Z = Al, Be) alloys for spintronic application. Eur. Phys. J. Plus 2021, 136, 1009. [Google Scholar] [CrossRef]
- Dahmane, F.; Mogulkoc, Y.; Doumi, B.; Tadjer, A.; Khenata, R.; Omran, S.B.; Rai, D.P.; Murtaza, G.; Varshney, D. Structural, electronic and magnetic properties of Fe2-based full Heusler alloys: A first principle study. J. Magn. Magn. Mater. 2016, 407, 167–174. [Google Scholar] [CrossRef]
- Page, A.; Uher, C.; Poudeu, P.F.; Van der Ven, A. Phase separation of full-Heusler nanostructures in half-Heusler thermoelectrics and vibrational properties from first-principles calculations. Phys. Rev. B 2015, 92, 174102. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Gürth, M.; Tavassoli, A.; Ebner, C.; Wünschek, A.; Puchegger, S.; Soprunyuk, V.; Schranz, W.; Bauer, E.; et al. Mechanical properties of half-Heusler alloys. Acta Mater. 2016, 107, 178–195. [Google Scholar] [CrossRef]
- Dahal, R.; Kaphle, G.C. Structural, electronic and magnetic properties of xyz type half-heusler alloys. J. Nepal Phys. Soc. 2019, 5, 97–102. [Google Scholar]
- Fiedler, G.; Kratzer, P. Ternary Semiconductors NiZrSn and CoZrBi with half-Heusler structure: A first-principles study. Phys. Rev. B 2016, 94, 075203. [Google Scholar] [CrossRef]
- Wakeel, M.; Murtaza, G.; Ullah, H.; Khan, S.; Laref, A.; Ameer, Z.; Khan, S.A. Structural, electronic, and magnetic properties of palladium based full Heusler compounds: DFT study. Phys. B Condens. Matter 2021, 608, 412716. [Google Scholar] [CrossRef]
- Schwarz, K.; Blaha, P.; Madsen, G.K.H. Electronic structure calculations of solids using the WIEN2k package for material sciences. Comput. Phys. Commun. 2002, 147, 71–76. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-potential, linearized augmented plane wave programs for crystalline systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Nasarullah; Yaseen, M.; Aldaghfag, S.A.; Zahid, M.; Misbah. Physical characteristics of X2NaMoBr6 (X = K, Rb): A DFT study. Mater. Sci. Semicond. Process. 2022, 147, 106760. [Google Scholar] [CrossRef]
- Graf, T.; Casper, F.; Winterlik, J.; Balke, B.; Fecher, G.H.; Felser, C. Crystal Structure of New Heusler Compounds. Z. Anorg. Allg. Chem. 2009, 635, 976–981. [Google Scholar] [CrossRef]
- Birch, F. The effect of pressure upon the elastic parameters of isotropic solids, according to Murnaghan’s theory of finite strain. J. Appl. Phys. 1938, 9, 279–288. [Google Scholar] [CrossRef]
- Rauf, S.; Arif, S.; Haneef, M.; Amin, B. The first principle study of magnetic properties of Mn2WSn, Fe2YSn (Y=Ti, V), Co2YSn (Y=Ti, Zr, Hf, V, Mn) and Ni2YSn (Y=Ti, Zr, Hf, V, Mn) heusler alloys. J. Phys. Chem. Solids 2015, 76, 153–169. [Google Scholar] [CrossRef]
- Nazar, M.; Nasarullah; Aldaghfag, S.A.; Yaseen, M.; Waqas, M.; Butt, M.K.; Boukhris, I. Electronic, Structural, Optical, and Magnetic Characteristics A2MgS4 of (A=Dy, Er) Spinel Sulfides: A Density Functional Theory Study. Phys. Status Solidi B Basic Res. 2023, 260, 2300003. [Google Scholar] [CrossRef]
- Nazar, M.; Nasarullah; Aldaghfag, M.I.S.A.; Yaseen, M.; Khera, S.N.R.A.; Abdellattif, M.H. First-principles calculations to investigate structural, magnetic, optical, electronic and thermoelectric properties of X2MgS4(X = Gd, Tm) spinel sulfides. J. Phys. Chem. Solids 2022, 166, 110719. [Google Scholar] [CrossRef]
- Gökoğlu, G. Ab initio electronic structure of NiCoCrGa half-metallic quaternary Heusler compound. Solid State Sci. 2012, 14, 1273–1276. [Google Scholar] [CrossRef]
- Hao, Z.; Liu, R.; Fan, Y.; Wang, L. First-principles calculations of a new half-metallic Heusler alloy FeCrAs. J. Alloys Compd. 2020, 820, 153118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).