Numerical Simulation and Experimental Study of the Thermal Wick-Debinding Used in Low-Pressure Powder Injection Molding
Abstract
1. Introduction
2. Methodology
2.1. Feedstock Preparation and Molding
2.2. Thermal Wick-Debinding Treatment
2.3. Numerical Modeling of Thermal Wick-Debinding Process
2.3.1. Problem Formulation and Governing Equations
2.3.2. Determination of Simulation Parameters
3. Results and Discussion
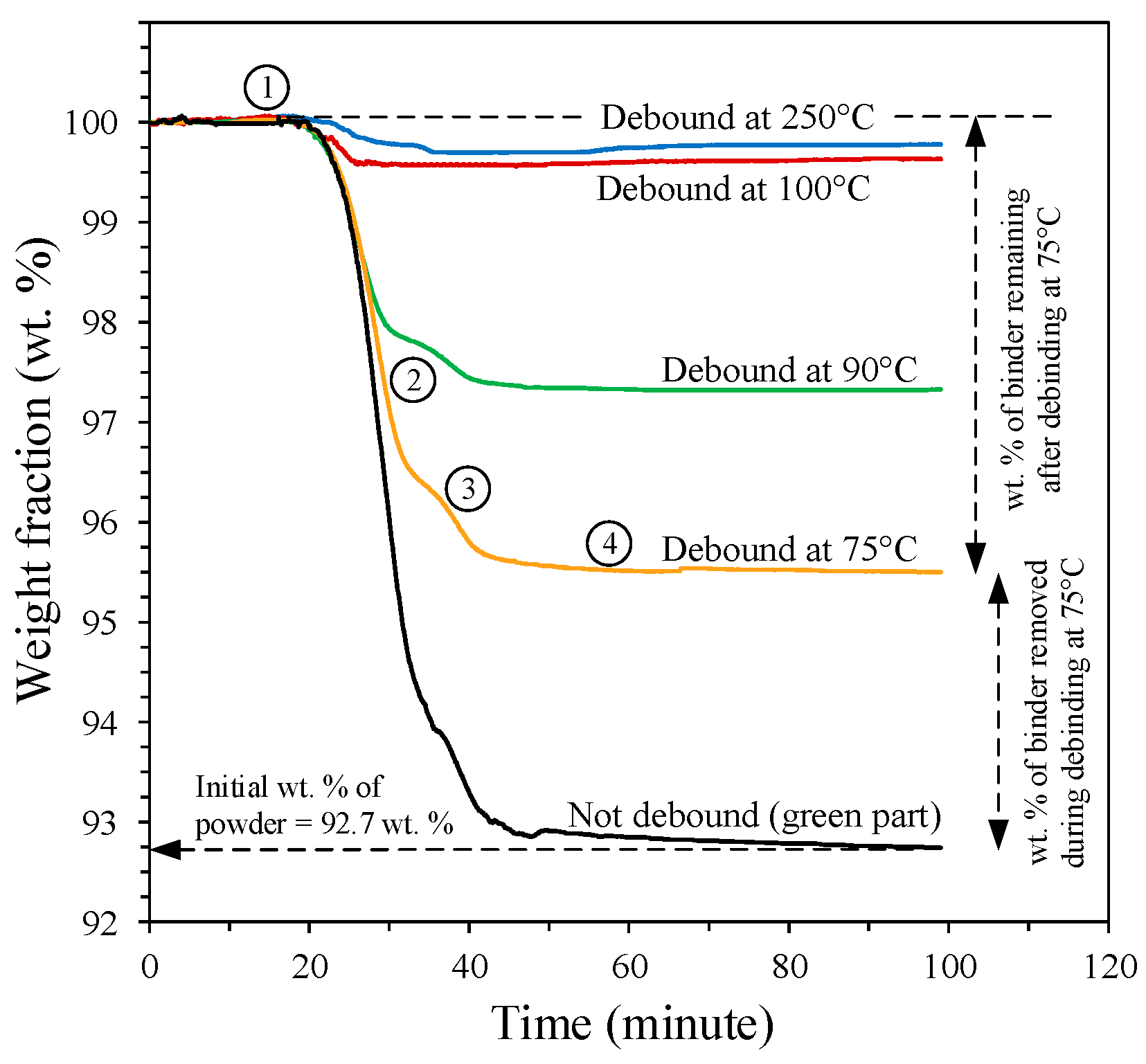
3.1. Calculation of the Binder Saturation
3.2. Validation of the Model
3.2.1. Comparison of the Binder Saturation
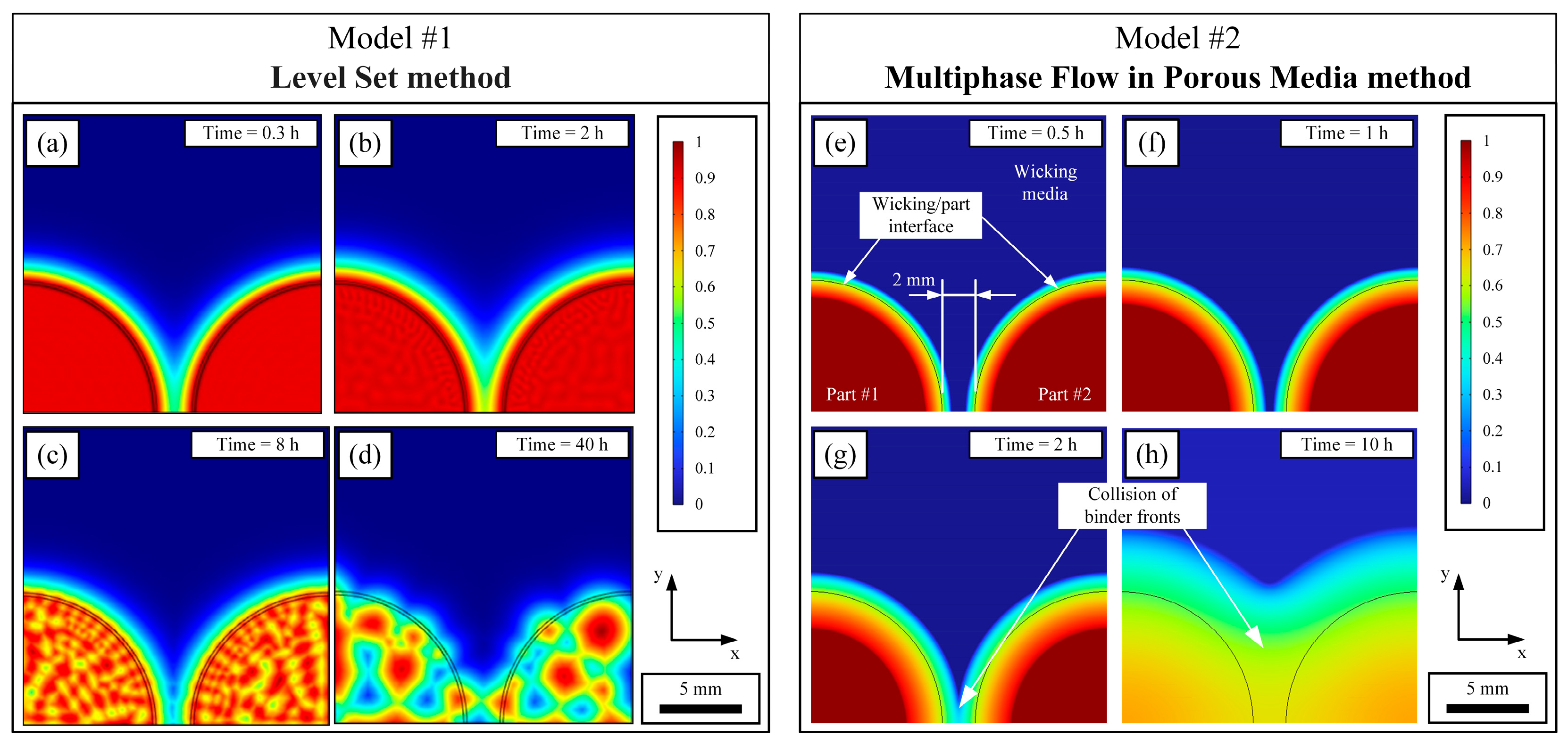
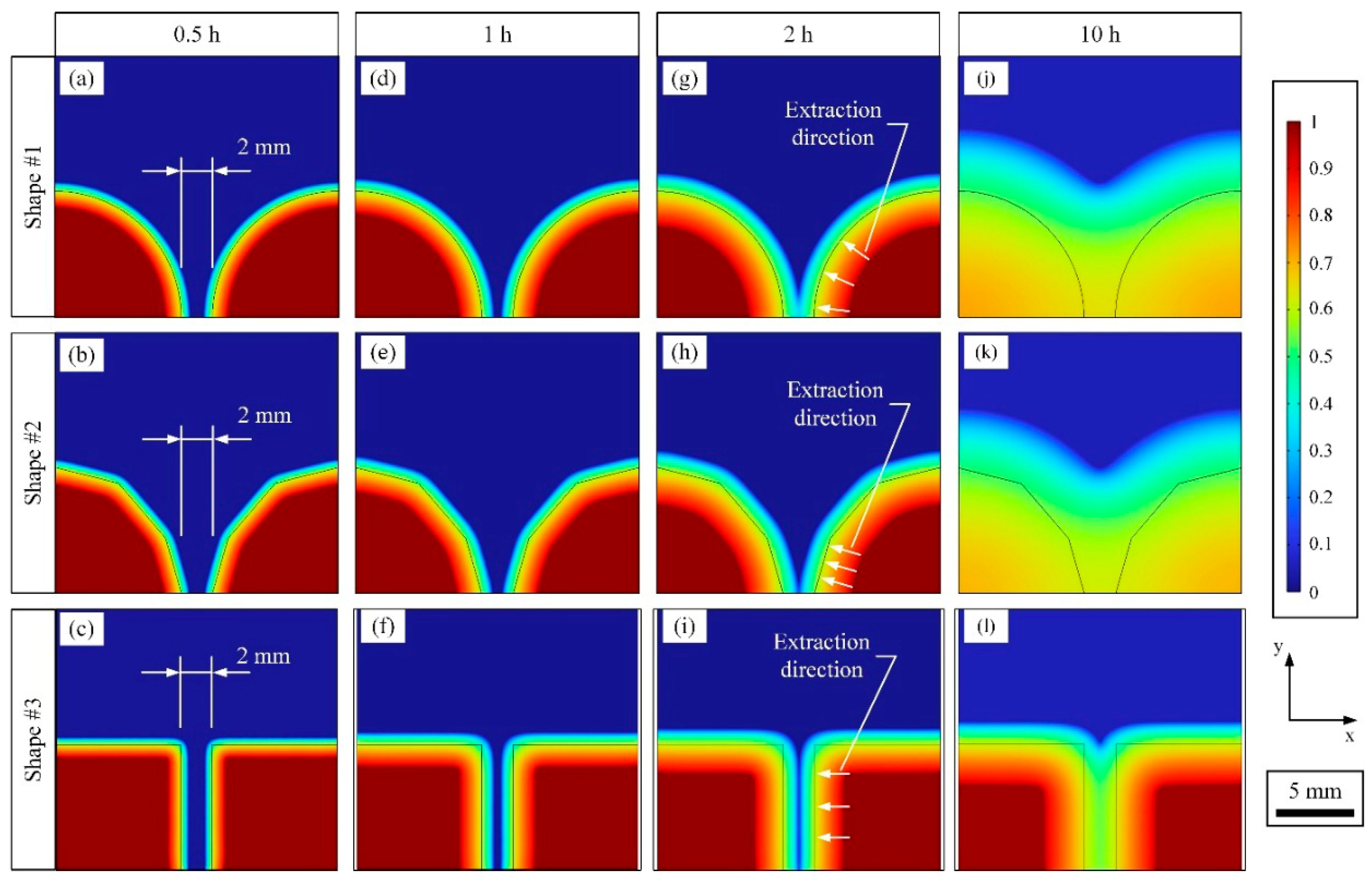
3.2.2. Visualization of the Binder Distribution
3.3. Study of the Influence of Process Parameters
4. Conclusions
- The Level Set method, previously used for LPIM of ceramic parts, produces a binder extraction pattern inconsistent with SEM observations.
- The Multiphase Flow in Porous Media method proposed in this work predicts a continuous binder extraction throughout the green part, in line with experimental evidence.
- The numerical model accurately captures the trend of decreasing binder saturation with increasing debinding temperature and time, as confirmed experimentally.
- Discrepancies between experimental and numerical results (ranging from 3 to 10 vol. %) are considered acceptable and are likely due to the mandatory brushing operation when handling the samples.
- The cylindrical 2-D model for LPIM metallic-based feedstock proposed in this work determined optimal debinding conditions at 100 °C with a gap distance of 5 mm, minimizing debinding time to approximately 7 h.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heaney, D.F. Handbook of Metal Injection Molding, 2nd ed.; Woodhead Publishing: Cambridge, UK, 2019; pp. 1–656. [Google Scholar]
- Vervoort, P.J.; Vetter, R.; Duszczyk, J. Overview of powder injection molding. Adv. Perform. Mater. 1996, 3, 121–151. [Google Scholar] [CrossRef]
- Randall, M.G.; Bose, A. Injection Molding of Metals and Ceramics, 1st ed.; Metal Powder Industry Federation: Princeton, NJ, USA, 1997; pp. 1–413. [Google Scholar]
- Wolff, M.; Schaper, G.J.; Suckert, M.R.; Dahms, M.; Feyerabend, F.; Ebel, T.; Willumeit-Römer, R.; Klassen, T. Metal injection molding (MIM) of Mg-alloys. In Proceedings of the TMS Annual Meeting, Phoenix, AZ, USA, 11–15 March 2018; Volume 6, pp. 1–12. [Google Scholar]
- Kupecki, J.; Kluczowski, R.; Papurello, D.; Lanzini, A.; Kawalec, M.; Krauz, M.; Santarelli, M. Characterization of a circular 80 mm anode supported solid oxide fuel cell (AS-SOFC) with anode support produced using high-pressure injection molding (HPIM). Int. J. Hydrogen Energy 2019, 44, 19405–19411. [Google Scholar] [CrossRef]
- Peltsman, M.I.; Peltsman, I.D. Low Pressure Hot Molding Machine. U.S. Patent 4416603, 22 November 1983. [Google Scholar]
- Mangels, J.A. Low-pressure injection molding. Am. Ceram. Soc. Bul. 1994, 73, 37–41. [Google Scholar]
- Medvedovski, E.; Peltsman, M. Low pressure injection molding of advanced ceramic components with complex shapes for mass production. In Proceedings of the 36th International Conference on Advanced Ceramics and Composites, Daytona Beach, FL, USA, 22–27 January 2012; pp. 35–51. [Google Scholar]
- Oliveira, R.V.B.; Soldi, V.; Fredel, M.C.; Pires, A.T.N. Ceramic injection moulding: Influence of specimen dimensions and temperature on solvent debinding kinetics. J. Mater. Process. Technol. 2005, 160, 213–220. [Google Scholar] [CrossRef]
- Hidalgo, J.; Abajo, C.; Jimenez-Morales, A.; Torralba, J.M. Effect of a binder system on the low-pressure powder injection moulding of water-soluble zircon feedstocks. J. Eur. Ceram. Soc. 2013, 33, 3185–3194. [Google Scholar] [CrossRef]
- Aslam, M.; Ahmad, F.; Bm-Yousoff, P.S.M.; Altaf, K.; Omar, M.A.; Raza, M.R. A study on the optimization of solvent debinding process for powder injection molded 316L stainless steel parts. Adv. Mater. Res. 2016, 1133, 324–328. [Google Scholar] [CrossRef]
- Bloemacher, M.; Weinand, D. CatamoldTM-a new direction for powder injection molding. J. Mater. Process. Technol. 1997, 63, 918–922. [Google Scholar] [CrossRef]
- Krug, S.; Evans, J.; Ter Maat, J.H.H. Transient effects during catalytic binder removal in ceramic injection moulding. J. Eur. Ceram. Soc. 2001, 21, 2275–2283. [Google Scholar] [CrossRef]
- Fu, G.; Loh, N.H.; Tor, S.B.; Tay, B.Y.; Murakoshi, Y.; Maeda, R. Injection molding, debinding and sintering of 316L stainless steel microstructures. Appl. Phys. A 2005, 81, 495–500. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Kim, Y.-H.; Lee, Y.-W.; Park, J.-K.; Lee, C.-H.; Lim, J.S. Supercritical carbon dioxide debinding in metal injection molding (MIM) process. Korean J. Chem. Eng. 2002, 19, 986–991. [Google Scholar] [CrossRef]
- Agne, A.; Barrière, T. Modelling and numerical simulation of Supercritical CO2 debinding of Inconel 718 components elaborated by Metal Injection Molding. Appl. Sci. 2017, 7, 1024. [Google Scholar] [CrossRef]
- Dugauguez, O.; Agne, A.; Jimenez-Morales, A.; Torralba, J.M.; Barriere, T. Experimental and numerical analysis of effects of supercritical carbon dioxide debinding on Inconel 718 MIM components. Powder Technol. 2019, 355, 57–66. [Google Scholar] [CrossRef]
- Zorzi, J.E.; Perottoni, C.A.; Da Jornada, J. A new partially isostatic method for fast debinding of low-pressure injection molded ceramic parts. Mater. Lett. 2003, 57, 3784–3788. [Google Scholar] [CrossRef]
- Tafti, A.A.; Demers, V.; Seyed, M.M.; Vachon, G.; Brailovski, V. Effect of thermal debinding conditions on the sintered density of low-pressure powder injection molded Iron parts. Metals 2021, 11, 264. [Google Scholar] [CrossRef]
- German, R.M. Theory of thermal debinding. Int. J. Powder Metall. 1987, 23, 237–245. [Google Scholar]
- Patterson, B.; Aria, C. Debinding injection molded materials by melt wicking. JOM 1989, 41, 22–25. [Google Scholar] [CrossRef]
- Vetter, R.; Sanders, M.J.; Majewska-Glabus, I.; Zhuang, L.; Duszczyk, J. Wick-debinding in powder injection molding. Int. J. Powder Metall. 1994, 30, 115–124. [Google Scholar]
- Vetter, R.; van den Brand Horninge, W.R.; Vervoort, P.J.; Majewska-Glabus, I.; Zhuang, Z.; Duszczyk, J. Square root wick debinding model for powder injection moulding. Powder Metall. 1994, 37, 265–271. [Google Scholar] [CrossRef]
- Chen, C.-C.; Hourng, L.-W. Basic permeability concepts related to wick debinding in metal injection moulding. Powder Metall. 2001, 44, 117–122. [Google Scholar] [CrossRef]
- Chen, C.-C.; Hourng, L.-W.; Liou, L.-M. Optimum analysis of wick debinding in MIM–laboratory experiment. Powder Metall. 2001, 44, 123–127. [Google Scholar] [CrossRef]
- Gorjan, L.; Dakskobler, A. Partial wick-debinding of low-pressure powder injection-moulded ceramic parts. J. Eur. Ceram. Soc. 2010, 30, 3013–3021. [Google Scholar] [CrossRef]
- Gorjan, L.; Dakskobler, A.; Kosmač, T. Strength evolution of injection-molded ceramic parts during wick-debinding. J. Am. Ceram. Soc. 2012, 95, 188–193. [Google Scholar] [CrossRef]
- Shih, M.-S.; Hourng, L.-W. Numerical simulation of capillary-induced flow in a powder-embedded porous matrix. Adv. Powder Technol. 2001, 12, 457–480. [Google Scholar] [CrossRef]
- Lin, T.-L.; Hourng, L.-W. Investigation of wick debinding in metal injection molding: Numerical simulations by the random walk approach and experiments. Adv. Powder Technol. 2005, 16, 495–515. [Google Scholar] [CrossRef]
- Somasundram, I.M.; Cendrowicz, A.; Wilson, D.I.; Johns, M.L. Phenomenological study and modelling of wick debinding. Chem. Eng. Sci. 2008, 63, 3802–3809. [Google Scholar] [CrossRef]
- Somasundram, I.M.; Johns, M.L.; Wilson, D.I. An Improved Model for Simulation of Wick Debinding of Moulded Parts. In Proceedings of the 17th Plansee Seminar, Reutte, Austria, 25–29 May 2009; Volume 3, pp. 1–10. [Google Scholar]
- Somasundram, I.M.; Cendrowicz, A.; Johns, M.L.; Prajapati, B.; Wilson, D.I. 2-D simulation of wick debinding for ceramic parts in close proximity. Chem. Eng. Sci. 2010, 65, 5990–6000. [Google Scholar] [CrossRef]
- B923–16; Standard Test Method for Metal Powder Skeletal Density by Helium or Nitrogen Pycnometry. ASTM International: West Conshohocken, PA, USA, 2016.
- Monzón, M.D.; Ortega, Z.; Martínez, A.; Ortega, F. Standardization in additive manufacturing: Activities carried out by international organizations and projects. Int. J. Adv. Manuf. Technol. 2015, 76, 1111–1121. [Google Scholar] [CrossRef]
- Gonçalves, A.C. Metallic powder injection molding using low pressure. J. Mater. Process. Technol. 2001, 118, 193–198. [Google Scholar] [CrossRef]
- Wen, G.; Cao, P.; Gabbitas, B.; Zhang, D.; Edmonds, N. Development and Design of Binder Systems for Titanium Metal Injection Molding: An Overview. Metall. Mater. Trans. A 2013, 44, 1530–1547. [Google Scholar] [CrossRef]
- Lin, D.; Sanetrnik, D.; Cho, H.; Chung, S.T.; Kwon, Y.S.; Kate, K.H.; Hausnerova, B.; Atre, S.V.; Park, S.J. Rheological and thermal debinding properties of blended elemental Ti-6Al-4V powder injection molding feedstock. Powder Technol. 2017, 311, 357–363. [Google Scholar] [CrossRef]
- Rei, M.; Milke, E.; Gomes, R.; Schaeffer, L.; Souza, J. Low-pressure injection molding processing of a 316-L stainless steel feedstock. Mater. Lett. 2002, 52, 360–365. [Google Scholar] [CrossRef]
- Hu, F.; Liu, W.; Xie, Z. Surface modification of alumina powder particles through stearic acid for the fabrication of translucent alumina ceramics by injection molding. Ceram. Int. 2016, 42, 16274–16280. [Google Scholar] [CrossRef]
- Standring, T.; Blackburn, S.; Wilson, P. Investigation into Paraffin Wax and Ethylene Vinyl Acetate Blends for Use as a Carrier Vehicle in Ceramic Injection Molding. Polym.-Plast. Technol. Eng. 2016, 55, 817–820. [Google Scholar] [CrossRef]
- Arès, F.; Delbergue, D.; Demers, V. Injection Flow Rate Threshold Preventing Atypical In-Cavity Pressure during Low-Pressure Powder Injection Molding. Powders 2023, 2, 709–726. [Google Scholar] [CrossRef]
- Majdi, S.M.; Tafti, A.A.; Demers, V.; Vachon, G.; Brailovski, V. Effect of powder particle shape and size distributions on the properties of low-viscosity iron-based feedstocks used in low-pressure powder injection moulding. Powder Metall. 2021, 65, 170–180. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous. Media Hydrol. Pap. 1964, 3, 1–27. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media, Rev ed.; Dover Publications: Garden City, NY, USA, 2013; pp. 1–800. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure, 2nd ed.; Academic Press: Cambridge, MA, USA, 2012; pp. 1–598. [Google Scholar]
- Argon—Density and Specific Weight. Available online: https://www.engineeringtoolbox.com/argon-density-specific-weight-temperature-pressure-d_2089.html (accessed on 7 May 2025).
- Gases—Dynamic Viscosities. Available online: https://www.engineeringtoolbox.com/gases-absolute-dynamic-viscosity-d_1888.html (accessed on 7 May 2025).









| Stainless Steel Powder | Paraffin Wax | Carnauba Wax | Stearic Acid | Ethylene Vinyl Acetate | |
|---|---|---|---|---|---|
| Density (g/cm3) | 7.8 | 0.9 | 1.0 | 1.0 | 0.9 |
| Melting point (°C) | >1404 | 55 | 84 | 62 | 86 |
| Volume fraction for feedstock (vol. %) | 60 | 30 | 7 | 2 | 1 |
| Description | Value | Technique |
|---|---|---|
| Density of binder (kg/m3) | = 920 | Experiment using a pycnometer |
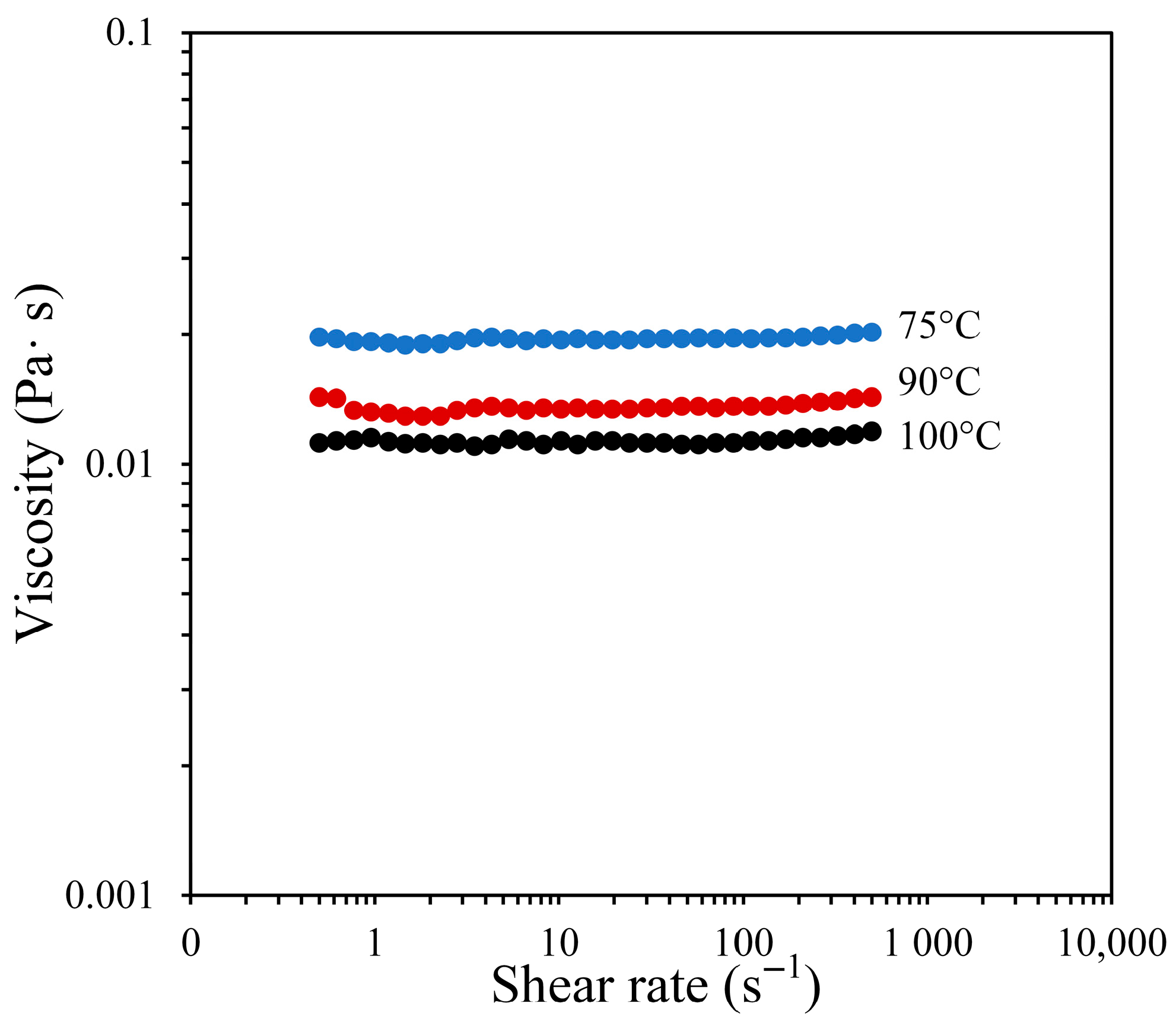
| Dynamics viscosity of binder (Pa·s) | = 0.011 | Experiment using a rotational rheometer |
| Density of Argon (kg/m3) | = 1.623 | Data from literature [48,49] |
| Dynamics viscosity of argon (Pa·s) | = 0.025 | Data from literature [48,49] |
| Porosity of green part (m3/m3) | = 0.40 | Directly calculated from the feedstock solid loading |
| Permeability of green part (m2) | = 1.2 × 10 − 10 | Simulation (see Figure 6a) |
| Porosity of wicking agent (m3/m3) | = 0.25 | Simulation using Equation (18) |
| Permeability of wicking agent (m2) | = 2.9 × 10 − 17 | Simulation (see Figure 6b) |
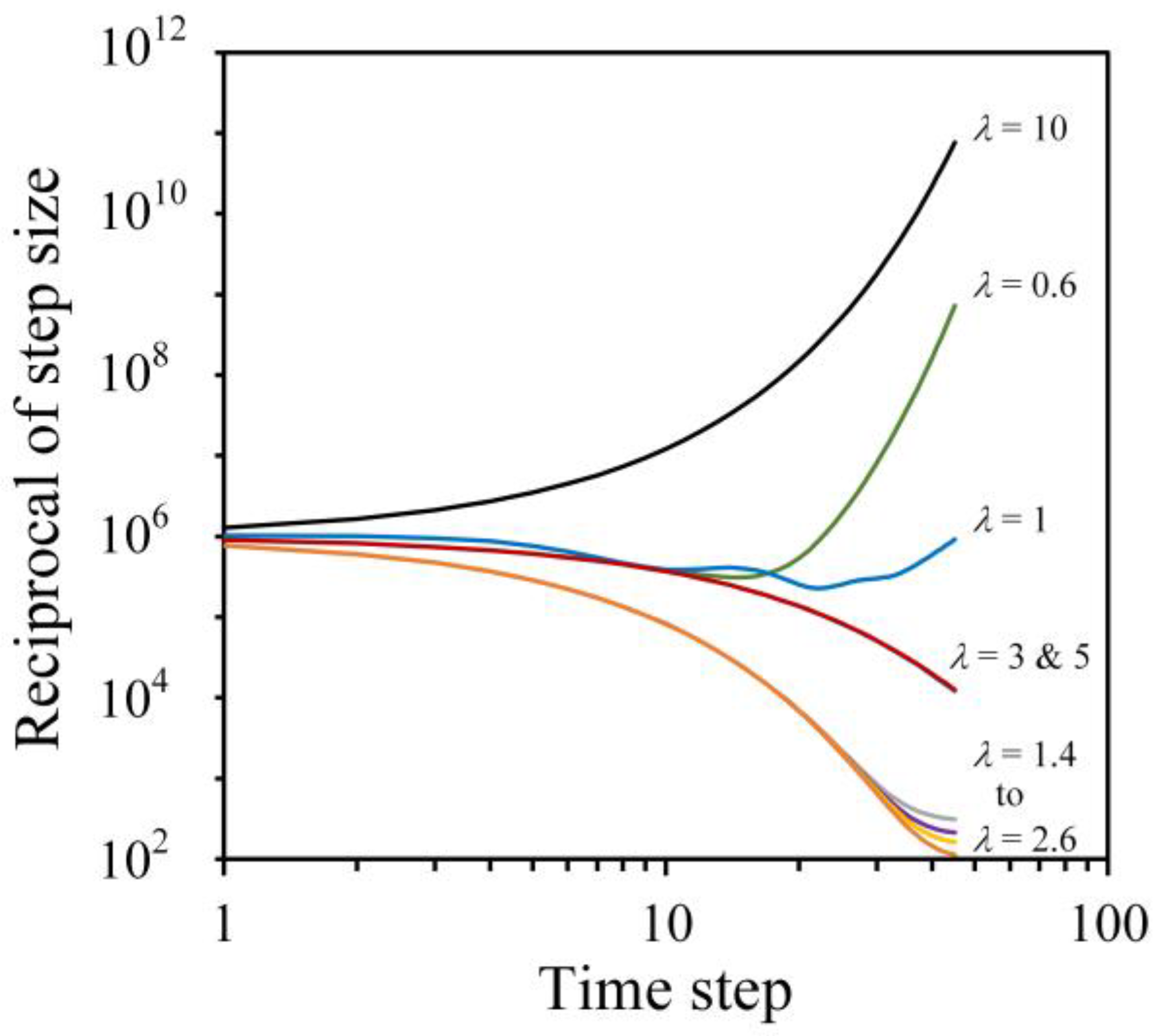
| Pore size distribution index in part | < 2.6 | Assessed in Figure 4 |
| Pore size distribution index in wicking medium | = 0.74 | Value from [32] |
| Minimum capillary pressure for part domain (Pa) | = 3.95 × 104 | By simulation (see Figure 7) |
| Minimum capillary pressure for wicking domain (Pa) | = 2.28 × 105 | By simulation (see Figure 7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turki, M.A.; Delbergue, D.; Marcil-St-Onge, G.; Demers, V. Numerical Simulation and Experimental Study of the Thermal Wick-Debinding Used in Low-Pressure Powder Injection Molding. Powders 2025, 4, 22. https://doi.org/10.3390/powders4030022
Turki MA, Delbergue D, Marcil-St-Onge G, Demers V. Numerical Simulation and Experimental Study of the Thermal Wick-Debinding Used in Low-Pressure Powder Injection Molding. Powders. 2025; 4(3):22. https://doi.org/10.3390/powders4030022
Chicago/Turabian StyleTurki, Mohamed Amine, Dorian Delbergue, Gabriel Marcil-St-Onge, and Vincent Demers. 2025. "Numerical Simulation and Experimental Study of the Thermal Wick-Debinding Used in Low-Pressure Powder Injection Molding" Powders 4, no. 3: 22. https://doi.org/10.3390/powders4030022
APA StyleTurki, M. A., Delbergue, D., Marcil-St-Onge, G., & Demers, V. (2025). Numerical Simulation and Experimental Study of the Thermal Wick-Debinding Used in Low-Pressure Powder Injection Molding. Powders, 4(3), 22. https://doi.org/10.3390/powders4030022







