Abstract
As part of the so-called interfacial separation techniques, selective particle agglomeration is one of the few options that are suitable for the separation of heterogeneous, multicomponent systems of particles smaller than 1 μm. In this regard, the component to be separated is exclusively transferred into a coarser size range, so that a material selective size separation by traditional mechanical methods can be achieved. In the presented study, this is demonstrated using heterogeneous suspensions of ceramic and organic particles, from which the separation of the inorganic material is pursued subsequent to the targeted control of the material-specific, electrostatic particle–particle interaction. Resulting from theoretical considerations on these interactions, favorable conditions for the selective agglomeration can be predicted. Experimental data reveal that for suitable parameters, resulting from variations in interfacial particle properties, particle size, and the composition of the dispersions, a separation efficiency of up to 97% can be obtained. Thereby, the importance of the particle-number fraction as an adjustable parameter needs to be clearly emphasized. Since a separation of the agglomerates can be achieved by simply using centrifugal forces, the shown technique is easy to apply and valuable for various industrial fields such as chemical and pharmaceutical engineering or recycling processes. In addition, no external additives are required for selective agglomeration, eliminating the risk of secondary contamination.
1. Introduction
The separation of multi-component particulate mixtures is a fundamental challenge in many areas of chemical, mechanical, or pharmaceutical engineering in order to generate high-purity products or to recycle costly/resource-scarce materials. Thereby, these mixtures can be targeted (e.g., ore processing, recycling) or they can be undesired in terms of contaminations (e.g., wear from mechanically intensive processes, by-products in chemical syntheses, fine particles in the environment). Especially for very small particles (<1 μm), interfacial particle properties and the resulting particle interactions become strongly relevant. For such materials, common mechanical technologies and the related physical separation principles face their limits and lose efficiency and selectivity. In this regard, the separation of both homogeneous particle systems and heterogeneous particle mixtures, respectively, including particles within the submicron range, requires the exploitation of certain particle characteristics in order to use them directly as separation attributes or to emphasize another attribute. These include, for example, magnetic, electrophoretic, and electrostatic particle properties, whose application belongs to the category of interfacial separation techniques [1].
If a binary particle mixture is considered, selective agglomeration refers to the exclusive coagulation of only one of the two present particle types (Figure 1). This allows one material component to be transferred to a coarser particle-size range while the other remains dispersed [2], enabling a material-selective separation through known mechanical principles. Unlike selective flocculation by bridging using polymeric flocculants [3,4,5] or by hydrophobic effects [6,7,8], successful selective agglomeration is induced by the targeted control of the electrostatic particle interactions and thus results mainly from the respective agglomeration kinetics between the different particles (for binary mixtures of 1 and 2: 1−1, 1−2, and 2−2). Compared to other approaches, one major advantage is that no organic flocculants are required for agglomeration and thus, at least in principle, a very clean separation is feasible without potential contamination by additional additives. Furthermore, selective agglomeration and separation steps can be carried out using simple process technology (common mixing and separation equipment) and therefore represents a readily scalable process.
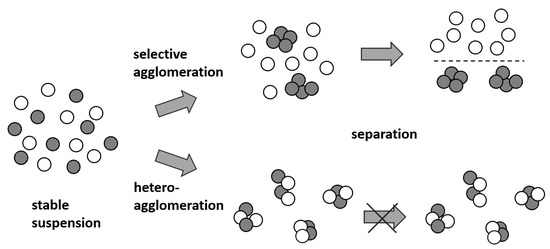
Figure 1.
Principle of selective agglomeration for separation.
With reference to Figure 1, it is obvious that the mutual interaction between the two particle species (heteroagglomeration) has to be completely prevented in order to achieve the highest possible level of separation. If, for example, the agglomeration and separation of particles 1 are pursued, the coagulation kinetic of 1−1 must be favored appropriately. According to theoretic considerations by Pugh and Kitchener, it is suggested that the rate of coagulation for selective agglomeration should be greater than a factor of 100 to allow for separation [9,10].
Despite the established knowledge of the theoretical conditions to achieve a selective agglomeration from these studies, there are only a few practical examples reported in the literature which are limited to a laboratory level. The reason lies in the complex task of precisely adjusting appropriate coagulation conditions with respect to the influencing parameters of particle interaction (e.g., particle size, pH or ionic strength) [11]. One known example can be found in the examination of rutile/quartz and hematite/quartz mixtures [12,13]. For suspensions with a total solids content of 2.2 wt.% and particle sizes of around 0.1 µm, narrow regions for selective agglomeration could be identified, wherein the rutile or hematite agglomerated while the quartz remained stabilized. However, most of the existing studies considered a similar type of particulates, i.e., selected inorganic mixtures and mineral clays [12,13,14,15,16]. From here, the question arises whether the fundamentals of a selective agglomeration and separation still apply to heterogeneous mixtures of truly different types of materials. This includes mixtures with distinct properties, such as hydrophilic inorganic oxides and hydrophobic organic crystals. Due to their characteristics, these substances need to be stabilized with different mechanisms. For hydrophobic, organic materials, colloidal stability in an aqueous environment is commonly achieved by implementing an electrosteric barrier on particle surfaces [17,18,19], while oxides often can be stabilized electrostatically [20,21,22]. On this matter, the presented study aims at investigating the selective agglomeration and following separation of zirconium dioxide ZrO2 (ZrO2) from submicron particle mixtures with hydrophobic anthraquinone C14H8O2 (AQ). In addition to a theoretical analysis, the agglomeration effects are investigated experimentally utilizing pure ZrO2 dispersions and the aforementioned binary system. Proceeding from complete particle stability, the study compares the state of agglomeration, corresponding separation efficiencies, and resulting agglomerate sizes for different conditions at the particle interface and volume ratios of the respective components. It is believed that such investigations can contribute to extending the applicability of interfacial separation techniques to highly heterogeneous particle systems. This would be beneficial in many industrial fields such as chemical and pharmaceutical engineering or waste management in order to achieve high-quality products and to reuse valuable materials.
2. Materials and Methods
2.1. Materials and Preparation of Suspensions
Prior to agglomeration experiments, suspensions of both the organic material AQ (Sigma Aldrich GmbH, Schnelldorf, Germany) and of the inorganic material ZrO2 (CC05, SAINT-GOBAIN ZirPro, Avignon, France) were obtained separately by wet fine grinding with a stirred media mill (PML2, Bühler AG, Uzwil, Switzerland). The mill was operated in circuit mode, utilizing the CentexTM S2 process unit (stirrer: polyurethane; grinding chamber: sintered silicon carbide) at a stirrer tip speed of 8 m/s and spherical grinding media made of yttrium-stabilized ZrO2 (ZY-E, Sigmund Lindner GmbH, Warmensteinach, Germany) with a median size of 243 or 315 µm. The solids content of AQ and ZrO2 was set to wAQ = 0.10 and wZrO2 = 0.20, respectively, applying deionized water as the suspension medium. Both materials were prepared at a pH of 11 using sodium hydroxide for the adjustment. As explained in more detail in the Section 3, this condition was deliberately chosen because it provides suitable electrostatic characteristics on the particle surfaces. According to previous studies, the colloidal stability of AQ particles was ensured by a polymer-surfactant complex that acts as an electrosteric barrier [23,24,25]. To achieve this, 25 wt.% of polymer Kollidon® VA64 (BASF SE, Germany, Ludwigshafen)) and 2.5 wt.% of surfactant sodium dodecyl sulfate (Sigma Aldrich GmbH, Germany) were added with regard to the solid mass of AQ. ZrO2 particles, on the other hand, were electrostatically stabilized at the chosen pH conditions [26,27]. The milling of materials was monitored by particle-size analysis and stopped after the desired size range was reached. Two characteristic samples of each material with different particle sizes were prepared for the investigation. Table 1 summarizes their median values, x50,0 and x50,3, obtained from differential centrifugal sedimentation analysis (DCS) and dynamic light scattering (DLS) measurements, respectively. Both methods and types of value are individually important, as explained in the Section 3.

Table 1.
Median particle sizes of characteristic samples.
2.2. Agglomeration
An agglomeration experiment was conducted with a total suspension mass of 25 g at 25 °C. In regard to investigations considering pure ZrO2 suspensions, the solid content of the inorganic material was kept constant at wZrO2,0 = 0.01. Experiments were performed by first diluting the corresponding amount of milled ZrO2 suspension with deionized water and by adjusting an ionic strength of I = 0.01 with 1 M NaCl solution. Subsequently, the pH was reset to 11 with sodium hydroxide, if necessary, and suspensions were sonicated for 15 s (SONOPLUS HD 2200, BANDELIN electronic GmbH & Co. KG, Berlin, Germany). In order to analyze the agglomeration behavior, the suspension pH was changed to a desired value between 5 and 11 by adding hydrochloric acid under magnetic stirring at 500 rpm. The pH was kept constant for an agglomeration time of 5 min.
In principle, the experimental procedure remained identical for the studies of the binary mixture. Within these experiments, however, the solid content of AQ was kept constant at wAQ,0 = 0.04 for all experiments, whilst the amount of ZrO2 was varied. Initially, the AQ suspension was diluted with deionized water, followed by pH adjustments to 11 (with sodium hydroxide). Subsequently, appropriate amounts of the ZrO2 suspension were added, resulting in relative volume ratios between ZrO2 and AQ of φs,ZrO2 = 0.20, 0.06, and 0.012, respectively.
2.3. Separation
To quantify the degree of agglomeration and to investigate the separability of the agglomerates, 7 mL of sample was transferred into three 15 mL tubes and gently centrifuged (UNIVERSAL 320, Andreas Hettich GmbH & Co.KG, Tuttlingen, Germany) in a horizontal position for 5 min at 1000 rpm (RCF = 169). Defined sample volumes of 4 mL were then carefully taken from the supernatants and dried at 600 °C for 15 min in a muffle furnace. Finally, the mass of ZrO2 was determined by weighing in order to calculate the remaining solids content wZrO2 and the recovery RZrO2 after separation. The mean value of three samples resulting from the individual tubes was used.
Analysis of samples with both materials required an additional drying step at 110 °C for 90 min in order to determine the total remaining mass msolid,110 °C of both materials prior to a second step at 600 °C for 15 min (identical to the analysis of the pure ZrO2 suspensions). In this case, the latter ensured complete combustion of the entire organic material, which enabled to obtain the remaining solids content wAQ by gravimetrical analysis after each heating step. Subsequently, the recovery RAQ can also be calculated according to Equation (2).
2.4. Particle-Size Characterization
In order to detect agglomeration phenomena, the vast majority of measurements were performed using DLS and laser diffraction (LD) analysis. For the former, a Nanophox instrument (Sympatec GmbH, Germany) was applied and all samples were diluted until reaching an appropriate measurement signal, i.e., 1000–1500 kcps, at a laser intensity of 50%. Subsequently, a fourfold analysis for 120 s each was conducted at 25 °C. If a significant disturbance of the autocorrelation function could be observed (e.g., due to the sedimentation of coarser, agglomerated particles as a result of suspension instability), LD analysis was used instead. These measurements were carried out with a Helos device (Sympatec GmbH, Clausthal-Zellerfeld, Germany) in a cuvette system under magnetic stirring at 1000 rpm. After diluting the samples to an optical concentration of 15–20%, all measurements were performed threefold for 20 s.
Initial samples of both materials were also characterized by DCS with a disk centrifuge DC24000 (CPS Instruments Inc., Prairieville, LA, USA) in order to obtain appropriate input values for the theoretical description. This method monitors particle sedimentation alongside a liquid-density gradient, and was chosen because it offers the highest accuracy and measurement resolution compared to other techniques [28,29]. The device mainly consists of a rotating disk equipped with an extinction detector (λ = 470 nm) to recognize sedimenting particles. Prior to the measurements, the disk speed was set to 15,000 rpm and the gradient fluid was built by injecting 9 different sucrose solutions ranging from 24 to 8 wt.% into the disk (each 1.6 mL). After passing an equilibrium time of 15 min, the device was calibrated using spherical reference particles made of polyvinylchloride with a modal value xm,3 of 359 nm according to the manufacturer (Quantum Design GmbH, Germany). All samples were measured three times.
During sample preparation, it was ensured that neither the pH nor the ionic strength was changed upon dilution.
2.5. Additional Methods
In order to estimate the electrostatic-charge properties on particle surfaces, zeta-potential measurements were performed using electroacoustic spectroscopy (DT1200, Dispersion Technology Inc., Bedford Hills, NY, USA) at different suspension conditions. The method was chosen because it allows for measurements at high particle concentrations, eliminating the consideration of potential dilution effects. Additionally, they take place in a stirred environment, enabling the analysis of highly unstable suspensions. Characterizations were conducted with pure AQ and ZrO2 suspensions (total mass of 50 g) containing solid contents of w = 0.05 and at an ionic strength of 0.01 mol·L−1 NaCl. Prior to the analysis, the sample pH was adjusted to a desired value between 3 and 11 with either hydrochloric acid or sodium hydroxide solutions, followed by subsequent sonication for 20 s. During measurements, the probe was arranged in an external set-up and immersed into the samples at constant stirring. Four values were recorded for each sample.
Microscopic images and elemental analyses of samples were obtained by scanning electron microscopy/energy dispersive X-ray spectroscopy (SEM/EDX). For sample preparation, suspensions were diluted, maintaining a constant pH, and small droplets were dried on a glass holder for at least 12 h at ambient conditions. Samples were sputtered with platinum prior to analyses. SEM images were taken using the microscope Helios G4 CX (FEI Deutschland GmbH, Dreieich, Germany), while applying a voltage of 5 kV. EDX mapping was conducted with the integrated sensor EDAX Octane Elite-70 (AMETEK Inc., Berwyn, PA, USA) at a voltage of 15 kV. Primarily, two elements were characterized, i.e., carbon, representing AQ, and zirconium for ZrO2.
Rheological behavior was investigated by viscosity measurements with a Bohlin Gemini 2 rheometer (Malvern Instruments Ltd., Worcestershire, UK) utilizing a Searle unit. Samples were tempered to 25 °C and were subjected to shear rates between 10 and 1000 s−1.
2.6. Description of Particle Interaction
Most of the widely used approaches to describe particle interactions in suspensions are based on the DLVO theory introduced by Derjaguin, Landau, Verwey, and Overbeek. With regard to the classical theory, total interaction energies VT are determined as a function of the particle distance H by summing attractive energies Va based on the van der Waals forces and repulsive energies Vr resulting from double-layer potentials [30,31].
Assuming spherical particles, the attractive interactions can be calculated analytically for binary particle systems of different sizes using Equation (4) [32].
Herein, a represents the radii of respective particle species and A132 the Hamaker constant between component 1 and 2 acting through medium 3. Within this study, it is specified by definition that 1 refers to ZrO2, 2 to AQ, and 3 to water. Hamaker constants are often unknown or not easy to determine for individual particle interactions. Other than A131, which can be found in the literature, unknown constants A232 and A132 were approximated, applying combing relations based on the known Hamaker constants A11, A22, and A33 in vacuum [32]. All relevant constants can be found in Table 2.

Table 2.
Non-retarded Hamaker constants in vacuum and across water.
In fact, Hamaker constants are not constant, but are subject to a retardation effect. According to Gregory, this influence can be taken into account using Equation (7) [34].
In this equation, A0 corresponds to the non-retarded Hamaker constant (see Table 2) and a value of 5.32 is suggested for the factor b as a result of empirical adjustments to the exact solutions of Clayfield et al. [35]. λc refers to the characteristic wavelength of the interaction, for which a magnitude of 100 nm is typically assumed [34,36,37].
Repulsive energies Vr principally result from existing charges on particle surfaces and the subsequent interactions of electrostatic double layers [11,20,38]. In case of stable suspensions, these energies are usually repulsive (positive value), but can also be attractive (negative value, opposite charge) when different particle species are considered. The latter might be severe to suspension stability, since heteroagglomeration is likely to happen [2]. The extent of a double layer, more precisely the diffuse part of it, is represented by the Debye–Hückel double-layer thickness λD. However, for calculations of double-layer interactions, its reciprocal value κ is often used (Equation (8)).
Practically, the determination of Vr is performed analytically by proximate equations, which differ in describing the decay of surface potentials with a growing distance of the particles. A good overview of the various approaches is given by Elimelech et al. [36]. Most of the commonly used formulas are based on solutions of the linearized Poisson–Boltzmann equation by applying the Debye–Hückel approximation [39]. Typically, particle approaches for a constant surface potential and constant surface charge, introduced by Hogg et al., Wiese, and Usui [40,41,42], are considered as theoretical limiting cases, whereas in practical situations the reality is often somewhere in between [9,43,44]. In this context, Gregory recommends a charge regulation according to the linear superposition approximation (LSA), as this model is regarded as a compromise between these boundary conditions. For dissimilar surfaces of unequal size, such an approach can be implemented to calculate Vr using Equation (9). Here, γi describes the dimensionless surface potential of particle component 1 or 2, which can be derived from Equation (10).
By plotting VT against H, qualitative statements can be derived about the stability of single- or multicomponent particle systems, for which a potential barrier of 15 kBT is typically applied as a stability criterion [2,21]. In such approaches, however, the kinetic aspect of stability is disregarded. In practical cases, the so-called stability factor Wij is frequently used for more profound analyses of the interactions between particles i and j, which compare the rate constant for the rapid coagulation kij,0 (only acting van der Waals forces) with the rate constant of a slow coagulation kij (existing potential barrier) [11,36]. This parameter can be theoretically derived from the interaction energy curves, applying Equation (11) [45,46,47,48]. βij represents the hydrodynamic correction factor through which a reduction in coagulation rates, due to viscous drag resulting from approaching particles, is taken into account. According to Hönig et al., such an effect can be included by employing the empirical correlation (12) [49].
Generally, investigations including Wij can contribute significantly to a better understanding of eventual agglomeration effects, since all existing combinations of particle interactions can be studied. For example, this allows us to compare tendencies towards hetero- or homoagglomeration under varying conditions. Thereby, values of Wij equal or close to 1 indicate rapid coagulation, as in this case kij,0 ≈ kij is given. On the other hand, increasing values of Wij result in a stronger stability for the considered particle interaction. Typically, it is assumed that an interaction is indefinitely stable for Wij ≥ 105 [2,9,11].
3. Results and Discussion
3.1. Zeta-Potential and Particle Interaction
In order to perform calculations of particle interactions, the zeta potential ζ was used instead of the surface potential ψ0, because this parameter can be measured comparatively easily. In addition, its applicability has been justified by many authors [36,47,50,51,52]. Values of ζ are shown in Figure 2 as a function of pH at a constant ionic strength of 0.01 for AQ and ZrO2.
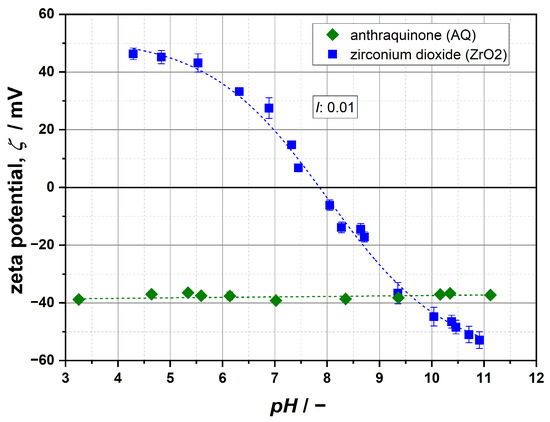
Figure 2.
Zeta-potential curves for AQ and ZrO2 (I = 0.01 NaCl). For an individual material, higher absolute values indicate stronger particle repulsion.
Considering the data, it can be seen that the surfaces of both materials are charged differently: AQ exhibits a negative potential that is largely independent of the pH value, while ZrO2 shows a much more pronounced curve, for which an isoelectric point (IEP) can be identified at a pH of 7.9. Thereby, high positive potentials are obtained in acidic regions and strongly negatively charged particle surfaces under basic conditions, which constitutes a typical dependence for oxides and is caused by their amphoteric surface properties in an aqueous environment [20,21,22,53].
Based on the determined zeta potentials, Figure 3 depicts the stability factors log(Wij) as a function of pH for all possible combinations of pair interactions (ZrO2- ZrO2, ZrO2-AQ and AQ-AQ). Number-weighted median particle sizes x50,0 obtained from DCS measurements were applied for the calculations (cf. Table 1). This was carried out because particle stability is mainly determined by collisions of individual particles, as well as the fact that DCS provides the highest accuracy and resolution compared to other methods [28,29]. The shown theoretical investigation considers both sizes of the ZrO2 particles for a constant AQ particle size of 184 nm. Commonly accepted stability limits of log(Wij) = 5 (stable suspension) and log(Wij) = 0 (rapid coagulation) are marked by dashed lines in the diagram [9,11]. As it can be seen, values for log(W12) fall below 0, which is typically the case for strong van der Waals interactions or oppositely charged particles [54].
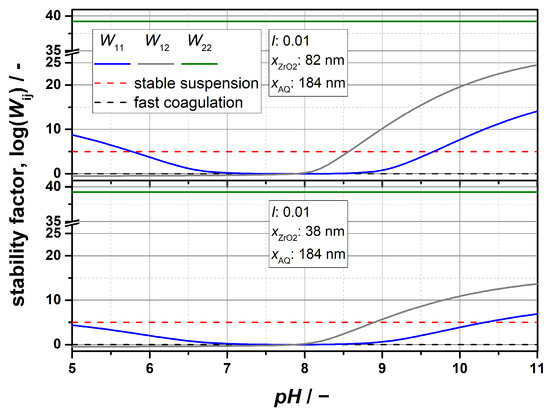
Figure 3.
Calculated stability factor log(Wij) in the dependence of pH for all combinations of pair interactions (ZrO2- ZrO2, ZrO2-AQ and AQ-AQ). (Top) Pair interactions for 82 nm ZrO2 particles; (bottom) pair interactions for 38 nm ZrO2 particles. A comparison of the curves allows for in-depth interpretations regarding the stability of the system and enables the identification of suitable regions for selective agglomeration.
In theory, a selective agglomeration is likely to occur if the agglomeration rates of the component to be agglomerated are comparatively fast and sufficiently different from all other rates of possible combinations within the multicomponent system. Considering Figure 3, favorable characteristics for a selective agglomeration can be estimated, as the stability factor Wij can be used as a measure to assess the tendency of a system to form agglomerates. Based on the already mentioned stability limits for log(Wij), the following conditions can be defined, under which a selective agglomeration of ZrO2 within a mixture of AQ is expected: A fundamental requirement is that the ZrO2 particles tend to agglomerate and that their agglomeration kinetics are rather fast (range of rapid agglomeration). By contrast, the colloidal stability of the AQ particles is ideally maintained indefinitely, from which the general conditions according to Equations (13) and (14) can be obtained.
In the simplest case, the formation of heteroagglomerates is also strictly excluded for the mutual interaction of the two components, which would generally apply to log(W12) > 5. However, this is not a necessary criterion. In fact, Pugh and Kitchener propose that useful separations could be achieved if the respective agglomeration kinetics differentiate by a factor of 100, which, in principle, would also allow for values of log(W12) ≤ 5 [9,10,13]. Taking this as a basis and considering Equation (13), a subsequent criterion can be defined by comparing the agglomeration-rate constants k11 and k12 (see Equation (15)). For unequal particles, the diffusion limited-rate constants for rapid agglomeration kij,0 can be thereby determined according to Equation (16) [36].
Figure 4 displays the logarithmic ratio of the considered rate constants as function of the pH value, from which the condition according Equation (15) can be examined.
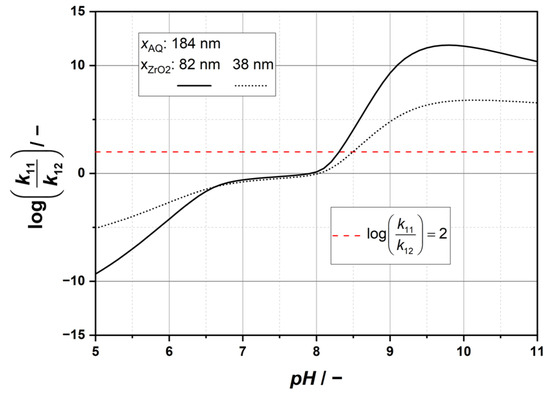
Figure 4.
Ratio of agglomeration-rate constants log(k11 · k12−1) in dependence of pH.
Depending on the size of ZrO2 particles, it is evident from the graphs that different pH values prove to be valid solutions. In this context, Table 3 summarizes all relevant pH ranges that match the respective criteria. Note that Figure 3 should be viewed to evaluate Equations (13) and (14). The intersection of the individual ranges in Table 3 allows for a good assessment of potential pH values at which the selective agglomeration of the ZrO2 particles is expected.

Table 3.
Relevant pH ranges satisfying the conditions according to Equations (13)–(15).
Assuming a ZrO2 particle size of 82 nm, a theoretical target pH range of 8.3 ≤ pH ≤ 9.6 can be determined, while for 38 nm 8.5 ≤ pH ≤ 10.3 appears to be a reasonable conjecture. This shift indicates an overall lower stability of the system with smaller ZrO2 particle size, which can be attributed to a relative increase in the van der Waals force. In theory, this means that the selective agglomeration should already occur at comparatively higher pH values by applying the 38 nm particles. However, in order to achieve a targeted agglomeration effect, it should further be advised that a fully stable suspension is initially required (no attractive particle interactions) [9,10]. Within the investigated framework, such conditions can be found for pH values ≥ 10.3 (cf. Figure 3), since W11 ∧ W12 ∧ W22 ≥ 105 is valid. Additionally, for values below the characteristic ranges in Table 3, the probability of a heteroagglomeration is high, since the attractive forces between both materials rise as the ratio of rate constants k11 and k12 declines. Corresponding experimental evaluations are shown in the following sections.
3.2. Agglomeration of Pure ZrO2 Suspensions
At first, the agglomeration of pure ZrO2 suspensions is considered. Figure 5 depicts the resulting particle size as well as the separated fraction of ZrO2 at different pH values. It is important to emphasize that the shown particle sizes were not determined using DCS, as this method is not suitable for detecting agglomeration phenomena, because it cannot be ruled out that the injection of the sample into the rotating disk may lead to desagglomeration effects. Further, and probably even more important, the fractal structure of any formed agglomerates is unknown and therefore cannot be implemented in the measurement routine, although it would affect the sedimentation properties of the particles. Instead, the given data are obtained from a combination of DLS and LD measurements. The median values x50,3 are used, because the separated material fraction 1 − RZrO2 also represents a mass-related parameter, and therefore these two variables can be directly linked to one another.
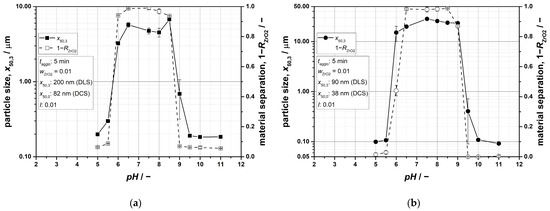
Figure 5.
Particle size and fraction of the separated material at different pH values for pure ZrO2 suspensions: (a) x50,3 = 200 nm (DLS); (b) x50,3 = 90 nm (DLS). The shown particle-size values should be viewed qualitatively, as no corrections for non-spherical particles were applied, and it cannot be completely ruled out that no further agglomeration effects occurred during the measurements.
As expected, it can be recognized that particle sizes increase significantly in the region of the IEP (pH ≈ 8), while the initial values can almost be determined in acidic and alkaline conditions. Exemplarily, such relations are also evidenced by SEM micrographs in Figure 6, as well as shown in the literature for alumina suspensions by Singh et al. [55]. It is further notable that significantly coarser agglomerates form when using the smaller particles of x50,3 = 90 nm, which is due to an increasing ratio of attractive force to inertia force with regard to the primary particles. Alongside a significant growth of agglomerates, the fraction of separated material also rises to reach full separation (Figure 5). The results clearly indicate that the agglomerates can be mechanically separated by centrifugation, and thus a removal of ZrO2 as a consequence of coagulation is feasible.

Figure 6.
SEM images of ZrO2 samples (x50,3 = 200 nm (DLS)) at different pH values for. (a) pH = 11; (b) pH = 8; (c) pH = 5. Images indicate colloidal stability at pH values of 5 and 11, while showing strong agglomeration at a pH of 8.
The analysis of the results for pure ZrO2 suspensions can be conducted with regard to the stability factor Wij by viewing the given pH ranges for Equation (15) in Table 3 and Figure 3 (blue curves). Especially for conditions of rapid agglomeration (log(W11) ≈ 0), which are given at a similar range of 6.8 ≤ pH ≤ 8.7 for both particle sizes, the experimental data are in good agreement with the theoretical expectation of a severe suspension instability. Within the transition regime of slow agglomeration (0 ≤ log(W11) ≤ 5), however, the data situation is less clear. Exemplarily, sufficient agglomeration cannot be achieved at a pH value of 9.5, although the stability factor would imply that this occurs. This shows that within the examined parameters, log(W11) values are assumingly required in order to achieve a significant separation success. This topic is also discussed in more detail in the following sections.
3.3. Selective Agglomeration in the Binary Mixture
Agglomeration effects within the mixture of AQ and ZrO2 particles are studied experimentally, aiming to achieve a selective separation of the ZrO2 particles subsequent to their exclusive agglomeration. Experiments were carried out for mixtures with particle sizes x50,0,ZrO2 = 82 nm and x50,0,AQ = 184 nm, in which the volume fraction of ZrO2 with regard to the total solids volume was set to φs,ZrO2 = 0.2. As mentioned earlier, the full stability of the mixed systems is an essential requirement at the beginning. Therefore, it was ensured that the particles were properly dispersed at a pH of 11, which marks the starting point prior to deliberately adjusting lower values.
In order to qualitatively monitor the change in suspension properties, Figure 7a,b show particle size density distributions q3 (xi) as well as viscosity curves at the characteristic pH values of 11, 8.5, and 5.5. However, with regard to the shown distributions, which were determined via LD using a simple lens system, it must be pointed out that these do not provide a representative view of the complete samples due to the applied measurement routine. This is caused by the fact that a lens with a focal length of 100 mm was used, allowing us to detect particle sizes in the range of 0.5–175 µm. Signals of smaller particles are not captured by the ring detector system since the diffraction angles of such particles are too large. Furthermore, Fraunhofer’s theory was chosen to evaluate the data, which is the only model suitable for characterizing particle mixtures, because no optical material constants are needed as measurement parameters. This approach leads to incorrect results for particles in the submicrometer range and below, as their material-dependent absorption can no longer be neglected. Therefore, the fine fractions of the samples in particular are not reflected accurately. The purpose of the measurements was rather to qualitatively identify the formation of coarser agglomerates and to roughly estimate their size.
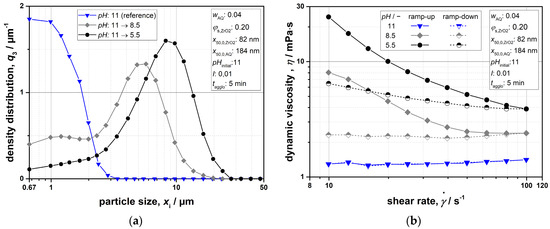
Figure 7.
(a) Particle-size density distributions q3 (xi) at different pH values (LD); (b) dynamic viscosity in the dependence of the shear rate at different pH values.
Referring to the aspects mentioned above, the distribution for a pH value of 11 can be employed as a reference for a stable suspension. If the pH value is changed, clear differences in the size properties can be observed. Not only in the target range for selective agglomeration but also below this region (cf. pH of 8.5 or 5.5 with Table 3), there is a considerable shift in the measured data towards higher particle sizes, generally indicating the agglomeration of particles (Figure 7a). The built structures exhibit a size range of 3 to 15 µm (pH = 8.5) and 4 to 25 µm (pH = 5.5). The change in microscopic properties that takes place along with the pH shift can also be determined using rheological studies (Figure 7b). Within the range of considered shear rates, Newtonian flow behavior can be observed for the initial condition at a pH of 11, supporting the assumption of colloidal stability. In contrast, a general increase in viscosity and shear thinning properties linked with a marked hysteresis is evident with decreasing pH values. These typical signs of instability result from an apparent increase in the effective volume of the disperse phase as well as a stronger deformation of the agglomerates with growing shear rate [39,56]. Thereby, the greater extent of these effects at pH = 5.5 is reasonable, considering that larger agglomerates are formed.
Although previous investigations have shown that the targeted pH shift caused a change in the particle structure in the binary system, the structural composition of the formed agglomerates is as yet unknown. A qualitative insight to elucidate the agglomerate composition can be provided by SEM/EDX analyses, which are shown in Figure 8. The organic material AQ is represented by the chemical element carbon (C, red), while ZrO2 can be identified by zirconium (Zr, green).
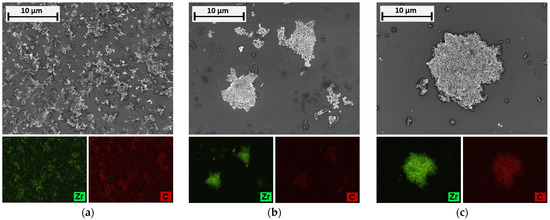
Figure 8.
SEM/EDX images for ZrO2/AQ mixtures (elements Zr and C are represented by colors green and red, respectively): (a) pH = 11; (b) pH = 8.5; (c) pH = 5. Results qualitatively confirm the selective agglomeration at a pH of 8.5, as agglomerates predominantly consist of ZrO2.
Expectedly, the micrograph for pH = 11 shows finely dispersed particles, which can be attributed to a good stability of the suspension. This finding is also confirmed by the homogeneous distribution of both element signals (Figure 8a). At pH values of 8.5 and 5.5, by contrast, coarse agglomerates can be observed, evidently matching the size range determined by the particle-size analysis (approx. 5–7 µm and 12 µm, respectively; cf. Figure 7a). However, a closer look at the EDX mappings reveals that these structures consist almost entirely of ZrO2 (only a weak signal of carbon) at a pH of 8.5, whereas the signal of carbon is significantly increased at 5.5 (Figure 8b,c). From this, it can be concluded that at pH = 8.5 a selective agglomeration of ZrO2 can be confirmed, whilst at pH = 5.5 the attractive, mutual particle interaction between both components promotes the formation of hetero structures. According to these results, the fundamental relationships obtained from Figure 3 can be validated experimentally.
From an engineering perspective, it is of further interest whether and to what degree a material separation of both components can be achieved based on the demonstrated particle agglomeration. In this context, Figure 9 shows a plot of the separated solids fractions for both materials as a function of the pH value. From these data, mass-related separation efficiency SPE can also be derived by multiplying the separated and remaining amounts of ZrO2 and AQ, respectively, according to Equation (17).
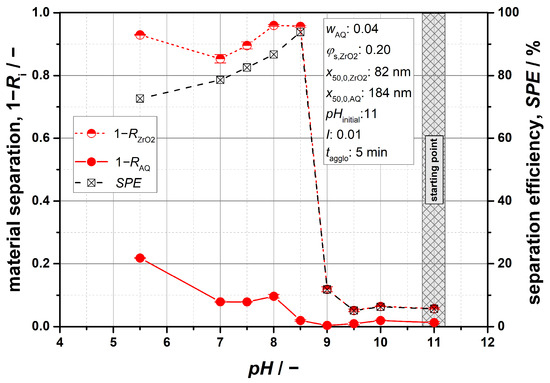
Figure 9.
Exemplary separation of a binary ZrO2/AQ suspension.
The results indicate optimal conditions at a pH value of 8.5, confirming a high level of selectivity. With an SPE value of about 95%, almost all ZrO2 particles were removed from the suspension, while nearly the entirety of the organic AQ was not affected. With regard to Figure 8, this finding is clearly associated with the selective agglomeration of the ceramic particles and also confirms the good separability of the formed agglomerates from the mixed-material system. The results are in good agreement with observations made from studies by Pugh and Kitchener, examining rutile/quartz and hematite/quartz mixtures [12,13]. Within their investigations, the best separation results were achieved near the IEP of the component to be agglomerated. The exact range was that at which the unstable particles still had a relatively low zeta potential but were of same sign compared to the stable particle species. This favors selective agglomeration, as some repulsive forces towards these particles remain present, ensuring that only the component to be agglomerated experiences strong attraction. A comparison with Figure 2 shows that similar conditions exist at the pH value of 8.5. At this point, the ZrO2 particles have a low negative potential of approximately −15 mV, while the AQ particles exhibit a potential of −38 mV. For lower pH values, on the other hand, the SPE value decreases, which is primarily caused by a higher separated fraction of organic particles. Considering a pH of 5.5, this could be expected, as heteroagglomeration takes place (cf. Figure 8c). But, Figure 9 further demonstrates that such effects already become significant at a pH value of 8. These findings can also be confirmed by Pugh and Kitchener. The reason for such behavior lies in the strong mutual attractive forces between the two types of particles, which primarily result from their oppositely charged potentials (cf. Figure 2).
Based on the available data, first conclusions can be drawn with regard to the theoretically predicted pH ranges for selective agglomeration (cf. Table 3). Overall, stability-factor trends align with experimental separation efficiencies, as most favorable separation results at the pH of 8.5 lie within the theoretical range of 8.3 ≤ pH ≤ 9.6. This proves that useful estimations are possible through the approach followed. Similarly to what has already been shown for pure ZrO2 suspensions, however, the upper limit of the target range is also overestimated by using Equation (13) as an agglomeration criterion. In this context, selective agglomeration of ZrO2 particles could additionally be expected for pH values around 9–9.6, which could not be observed experimentally. Nevertheless, the distinction between selective agglomeration and heteroagglomeration at the lower end of the range is in line with the experimental results. Theoretically, hetero effects were to be expected for pH ≤ 8.3, which could be practically confirmed at pH = 8 (Figure 9).
3.4. Impact of Particle Size and Composition
Previous results are essentially based on a single parameter set. Since, in practical separation tasks, the composition of the suspension can be subject to fluctuations, or certain parameters may even be unknown, it is advantageous to understand potential process limits regarding the selective agglomeration step. The evaluation of such limits can most effectively be carried out through studies with various, well-defined mixed suspensions.
Figure 10 demonstrates significant effects concerning the influence of particle size and particle quantities. For a constant particle size of x50,0,AQ = 184 nm, mixtures were prepared using both ZrO2 particle sizes and varying volume fractions φs,ZrO2. Depending on the pH, the separated solid fractions and their corresponding SPE values are presented in a comparative manner.
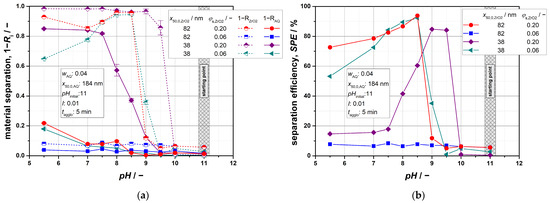
Figure 10.
(a) A material separation of binary mixtures for different particle sizes and compositions; (b) corresponding values for the separation efficiency SPE. Depending on the suspension composition, promising separation results can be found at pH values between 8.5 ≤ pH ≤ 9.5.
In general, it is noticeable that particle separation is significantly more pronounced when using the smaller ZrO2 particles (x50,0,ZrO2 = 38 nm) and extends over a broader pH range. Assuming agglomeration effects as the dominant cause, specifically the comparison for the volume fraction φs,ZrO2 = 0.20 shows that both selective agglomeration and heteroagglomeration occur at higher pH values, since the separation of ZrO2 particles begins at a pH of 9.5, and, simultaneously, a loss of AQ particles already occurs at pH ≤ 8.5. Consequently, the highest SPE for x50,0,ZrO2 = 38 nm is achieved within the pH range of 9 to 9.5 (Figure 10a). This trend supports the theoretical considerations regarding the influence of particle sizes, which have already been demonstrated through the calculation of the individual stability factors. The characteristic pH range that was identified for the smaller ZrO2 particles also tends towards higher pH values (cf. Table 3). Furthermore, it is evident that the impact of heteroagglomeration is considerably stronger. For instance, the separation efficiency falls below 20% at a pH of 7.5 due to the high amounts of separated organic material.
The effects of particle size on agglomeration are even more pronounced for the lower volume fraction of φs,ZrO2 = 0.06. In fact, when using ZrO2 particles with a characteristic size of 82 nm, no material separation from the suspension can be achieved, regardless of the pH value (Figure 10). This suggests that either no agglomeration occurred or that it was significantly slowed, making it undetectable under the applied agglomeration and separation conditions. Within the considered context, it appears that these parameters lead to a limitation of the agglomeration effects. In contrast, however, typical relations are again observable, if ZrO2 particles with 38 nm are used. In terms of practical application, it can be concluded from these results and with regard to a constant AQ particle size that the separation process is more sensitive towards smaller ZrO2 particles, allowing for the removal of lower ZrO2 material quantities.
By varying relative solid volume fractions and the particle sizes, the proportion of particle numbers between both materials is essentially altered. With reference to the component to be agglomerated, the relative particle-number fraction nZrO2 is calculated according to Equation (18). Ni represents the particle number of the respective material, which was estimated based on the median values x50,0.
Based on the present results, it is evident that this parameter has a significant impact on the agglomeration phenomena. Figure 11 shows multiple plots of the separation efficiency as a function of the particle-number fraction nZrO2 at characteristic pH values. An additional particle size of x50,0,AQ = 121 nm and the volume fraction φs,ZrO2 = 0.012 were additionally included in the analysis.
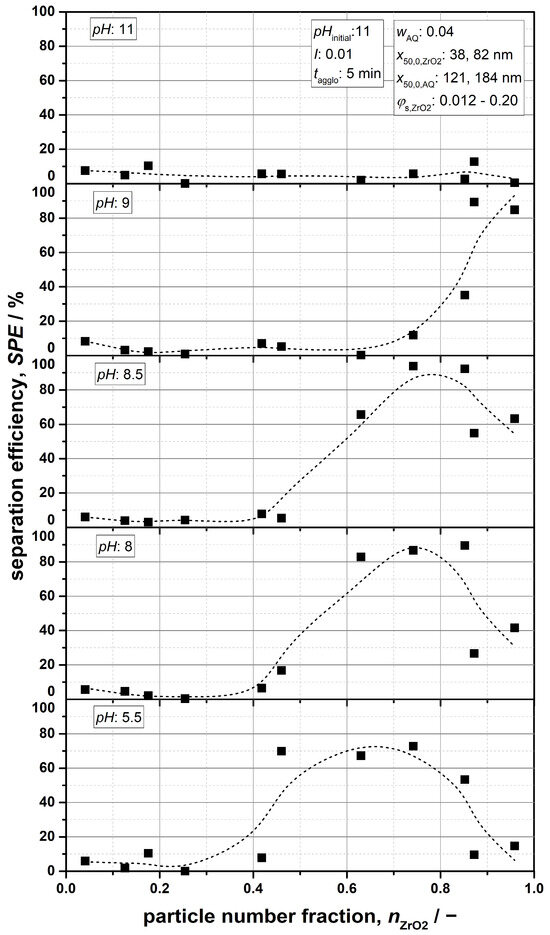
Figure 11.
Separation efficiency SPE as a function of the particle-number fraction nZrO2 at different pH values.
From the graphs, it can be observed that separation of the particle components is completely suppressed for nZrO2 < 0.4, regardless of the examined parameters. At a pH of 11, this applies as expected even for all number fractions due to the stable interaction properties. Regarding lower pH values, on the other hand, the formation of sufficiently large agglomerates also does not occur, which is likely caused by the low amounts of ZrO2 particles. Macroscopically, these suspensions can be regarded as stable. However, whether such stability is given at the micro level and whether it is suitable to even assume colloidal stability is challenging to assess and can therefore not be clearly evaluated because of the complex particle system.
For those conditions under which the SPE is clearly affected, two fundamental trends can be observed. At a pH of 9, a nearly steady increase in separation efficiency with increasing nZrO2 can be found. This seems reasonable, as the attraction between ZrO2 particles is still relatively weak due to conditions well above the IEP, and the effect of heteroagglomeration can be almost entirely excluded (see Figure 2 and Figure 3 for log(W12) ≥ 5). The latter, especially, suggests that the success of separation is primarily determined by the ZrO2- ZrO2 interaction. Consequently, the weaker attractive interaction is assumingly compensated by accelerated agglomeration kinetics at higher particle-number fractions, still enabling selective agglomeration and separation of the ceramic component.
As the pH decreases, the characteristics of the trends change, leading to the formation of various optima, which shift toward lower number fractions nZrO2 and reduced SPEs. The shape of the curves can be attributed to the increasing impact of heteroagglomeration in a more acidic environment, a phenomenon that has been demonstrated both theoretically and experimentally in previous sections. At pH values of 8.5 and 8, the electrostatic surface properties of the ZrO2 particles are close to their IEP, which suggests that, in addition to selective ZrO2 agglomeration, mutual attraction between both particle species intensifies, because the electrostatic repulsion is also reduced. This leads to a decrease in separation efficiency at high nZrO2, since an acceleration of heterokinetics makes it increasingly difficult to fully avoid the formation of mixed agglomerates. Such an effect is amplified as the conditions approach the IEP of the ZrO2 particles, and becomes most pronounced in the acidic pH range (e.g., pH = 5.5), at which heteroagglomeration essentially dominates particle stability. Consequently, it is plausible that under these conditions, SPE reaches its lowest values.
The data conclusively confirm that the particle-number fraction nZrO2 is a crucial parameter with regard to agglomeration and, consequently, particle separation. From an engineering perspective, effective separation can be achieved for 0.6 ≤ nZrO2 ≤ 0.8 at pH values of 8 to 8.5, allowing for separation efficiencies of up to 97%.
3.5. Limitation of the Theoretical Description
Previous investigations clearly show that the concept of selective agglomeration can be applied for material separation. Depending on the composition of the suspension and the conditions of the surrounding fluid, it is possible to nearly achieve complete removal of one component from the binary system. In this context, characteristic pH ranges based on the DLVO theory were predicted, in which the selective agglomeration is favored and thus the separation of agglomerated particles should be enabled. The experimental data show that these ranges provide effective guidance for estimating suitable conditions. Also, the impact of particle size was captured correctly in a qualitative manner (see Figure 9 and Figure 10).
However, the investigations also reveal that the observed effects, particularly for low quantities of ZrO2 particles, cannot be covered by the calculations. The absence of any separation results at small nZrO2 appears to contradict the calculated stability factors, as this is observed under theoretically favorable conditions and even within the range of heteroagglomeration. Therefore, it is reasonable to discuss the underlying causes in more detail, as the approach based solely on particle interactions is apparently limited in its descriptive range.
One key aspect is certainly that the stability factors Wij are derived from a pairwise evaluation of the interaction between two approaching particles, which does not take into account the composition of the colloidal system in terms of material quantities and contact probability. The experimental data in Figure 11 clearly show, however, that a significant influence of a parameter on the separation outcome, such as nZrO2, exists. Bearing this in mind, it may not be too surprising that the mentioned limitation applies. To be accurate, an often used approach according to Hogg et al. needs to be discussed at this point, which assesses the impact of suspension composition on the effective stability of a binary system through the so-called overall stability factor Wt. This approach is based on the statistical weighting of the individual stability factors Wij with the particle-number fraction ni, thereby accounting for the probability of an encounter between the respective types of particles [40,57]. In spite of that, a major drawback of this approach is that it does not allow for a differentiated analysis of homo- and heteroagglomeration. Therefore, it is generally recommended to use Wij if a distinction between the different types of agglomeration is required [39,40,58]. Thus, as previously described, the issue of not considering a parameter like ni remains.
The theoretical predictions presented in the studies are, undoubtedly, useful from an engineering perspective, but, given the discrepancy in descriptiveness, it is a valid question whether conclusions beyond a qualitative level are feasible. In this regard, it is important to note that the extent of a selective agglomeration and the separation efficiency can only be indirectly correlated, as in reality they are subject to different processes. For a more profound analysis, it would be beneficial to separate these processes and to perform individual descriptions. Referring to the agglomeration step, an ideal characterization would be the determination of the time-resolved changes in particle-number density distribution as a function of suspension properties, which could serve as input parameters for the separation process. To achieve this, however, the rates of agglomeration must be quantified accurately, which is challenging to assess experimentally. Although relatively easy-to-measure properties such as turbidity, viscosity, or the sedimented solids volume are often used for stability analysis of colloidal suspensions, such properties primarily reflect the formation of coarser agglomerates and offer only a qualitative indication of kinetic aspects [22]. Direct determination of agglomeration kinetics is possible through real-time measurements of particle sizes or through the immediate analysis of fluctuating light-scattering signals using specialized equipment [59,60,61,62]. Unfortunately, a restriction of these methods is their exclusive applicability to low particle concentrations, which significantly limits studies on technically relevant material systems. Furthermore, especially for colloidal multicomponent systems, common methods based on light scattering are technically not suitable due to the superposition of measurement signals and the physical dependence of light-scattering effects on optical material parameters.
In fact, computer-aided numerical approaches may be beneficial at this point, as they can provide insights into processes and phenomena that are difficult to measure directly. Promising results in this regard are shown by investigations of Rhein et al. on the separation of heterogeneous systems using magnetic seeded filtration, which relies on magnetic separation enabled through a selective heteroagglomeration between magnetic and non-magnetic particles [63,64]. In these studies, separation results were successfully modeled using a hybrid approach based on a serial arrangement of population balance equations and machine learning algorithms, as well as through Monte Carlo simulations. Primarily focusing on the agglomeration step, it is likely that such approaches can also be applied to the selective agglomeration and hold great potential for enabling a quantitative understanding of this process. However, implementing these kinds of methods was not the focus of this study and was therefore not further pursued. Since the characterization of particle interactions also plays a crucial role in these approaches, the presented theoretical investigations and experimental data can be viewed as important preliminary work for future studies in this field.
4. Conclusions
Selective agglomeration is a promising approach for enabling a material-specific separation from suspensions of heterogeneous particle mixtures, particularly effective for very fine particles < 1 µm. This technique could significantly improve beneficiation steps within the recycling of mixed industrial waste or increase the product qualities of mechanically manufactured dispersions for pharmaceutical or optical applications by separating process-related contaminations.
Through the specific control of particle interactions, the particle size is selectively emphasized as the favored separation criterion for one component of the system, ensuring its separation using conventional methods. In this study, such a principle was examined based on defined mixtures of inorganic zirconium dioxide (ZrO2) and organic anthraquinone (AQ) particles. Variations in the composition of the suspension and properties of the liquid-particle environment demonstrate that the selective agglomeration of ZrO2 particles provides an excellent separation of the two materials, revealing a separation efficiency of up to 97%. In particular, the number fraction of the respective particle component can be considered a suitable parameter for optimizing the agglomeration process. For example, appropriate conditions could be adjusted by intentionally adding small particles of the material to be separated, if a suspension does not show compatible properties in terms of composition. Within the investigations, particle-number fractions in the range of 0.6–0.8 proved beneficial. Furthermore, theoretical considerations of particle interactions contribute possibilities to confine the parameter range for the utilization of promising selective agglomeration results. They allow for predictive determinations of characteristic pH ranges in which the desired agglomeration effects predominantly occur and the highest separation efficiencies can be achieved. However, these studies also show that the dependence of the achieved separation on the particle-number fraction cannot be satisfactorily represented by the calculations. Even though they are highly useful from an engineering perspective, conclusions drawn from this approach are rather qualitative in nature. The reasons behind this findings and future integrations of more advanced computational models were discussed.
Author Contributions
Conceptualization, C.P. and S.B.-F.; methodology, C.P.; validation, A.K. and S.B.-F.; formal analysis, C.P.; investigation, C.P. and S.B.-F.; resources, A.K. and S.B.-F.; writing—original draft preparation, C.P.; writing—review and editing, C.P., A.K. and S.B.-F.; visualization, C.P.; supervision, A.K. and S.B.-F.; project administration, S.B.-F.; funding acquisition, C.P. and S.B.-F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG) and was part of the priority program 2045 “MehrDimPart—highly specific multidimensional fractionation of fine particles with technical relevance”, grant number 382120968.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon reasonable request from the corresponding author.
Acknowledgments
Special thanks are given to Clara Sangrós Giménez for proofreading the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, S.; Pugh, R.J.; Forssberg, E. Chapter 1 Introduction. In Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands; London, UK, 2005; pp. 1–7. ISBN 9780080495453. [Google Scholar]
- Lu, S.; Pugh, R.J.; Forssberg, E. Chapter 6 Coagulation, heterocoagulation and practical coagulation. In Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands; London, UK, 2005; pp. 290–353. ISBN 9780080495453. [Google Scholar]
- Lu, S.; Pugh, R.J.; Forssberg, E. Chapter 7 Flocculation with polymers. In Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands; London, UK, 2005; pp. 354–414. ISBN 9780080495453. [Google Scholar]
- Attia, Y.A. Fine Particle Separation by Selective Flocculation. Sep. Sci. Technol. 1982, 17, 485–493. [Google Scholar] [CrossRef]
- Attia, Y.A. Flocculation. In Colloid Chemistry in Mineral Processing; Elsevier: Amsterdam, The Netherlands, 1992; pp. 277–308. ISBN 9780444882844. [Google Scholar]
- Lu, S.; Pugh, R.J.; Forssberg, E. Chapter 8 Hydrophobic flocculation and hydrophobic aggregation separation (HAS). In Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands; London, UK, 2005; pp. 415–496. ISBN 9780080495453. [Google Scholar]
- Song, S.; Lu, S. Theory and applications of hydrophobic flocculation technology. In Developments in Mineral Processing; Elsevier: Amsterdam, The Netherlands, 2000; Volume 13, pp. C5-31–C5-38. [Google Scholar] [CrossRef]
- Song, S.; Lopez-Valdivieso, A. Parametric aspect of Hydrophobic flocculation technology. Miner. Process. Extr. Metall. Rev. 2002, 23, 101–127. [Google Scholar] [CrossRef]
- Pugh, R.J.; Kitchener, J.A. Theory of selective coagulation in mixed colloidal suspensions. J. Colloid Interface Sci. 1971, 35, 656–664. [Google Scholar] [CrossRef]
- Pugh, R.J. Selective coagulation of colloidal mineral particles. In Colloid Chemistry in Mineral Processing; Elsevier: Amsterdam, The Netherlands, 1992; pp. 243–276. ISBN 9780444882844. [Google Scholar]
- Lagaly, G.; Schulz, O.; Zimehl, R. Dispersionen und Emulsionen; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Pugh, R.J.; Kitchener, J.A. Experimental confirmation of selective coagulation in mixed colloidal suspensions. J. Colloid Interface Sci. 1972, 38, 656–657. [Google Scholar] [CrossRef]
- Pugh, R.J. Selective coagulation in quartz-hematite and quartz-rutile suspensions. Colloid Polym. Sci 1974, 252, 400–406. [Google Scholar] [CrossRef]
- Snoswell, D.R.E.; Duan, J.; Fornasiero, D.; Ralston, J. The selective aggregation and separation of titania from a mixed suspension of silica and titania. Int. J. Miner. Process. 2005, 78, 1–10. [Google Scholar] [CrossRef]
- Frey, E.; Lagaly, G. Selective coagulation in mixed colloidal suspensions. J. Colloid Interface Sci. 1979, 70, 46–55. [Google Scholar] [CrossRef]
- Laskowski, J. Interfacial Chemistry of Mineral Processing Separations. Surf. Colloid Sci. 1982, 35, 315–357. [Google Scholar] [CrossRef]
- Flach, F.; Konnerth, C.; Peppersack, C.; Schmidt, J.; Damm, C.; Breitung-Faes, S.; Peukert, W.; Kwade, A. Impact of formulation and operating parameters on particle size and grinding media wear in wet media milling of organic compounds—A case study for pyrene. Adv. Powder Technol. 2016, 27, 2507–2519. [Google Scholar] [CrossRef]
- Knieke, C.; Azad, M.A.; Davé, R.N.; Bilgili, E. A study of the physical stability of wet media-milled fenofibrate suspensions using dynamic equilibrium curves. Chem. Eng. Res. Des. 2013, 91, 1245–1258. [Google Scholar] [CrossRef]
- van Eerdenbrugh, B.; van den Mooter, G.; Augustijns, P. Top-down production of drug nanocrystals: Nanosuspension stabilization, miniaturization and transformation into solid products. Int. J. Pharm. 2008, 364, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Lyklema, J. Solid-Liquid Interfaces; Academic Press: London, UK, 2001; ISBN 978-0-12-460524-4. [Google Scholar]
- Hiemenz, P.C.; Rajagopalan, R. Principles of Colloid and Surface Chemistry, Revised and Expanded; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781315274287. [Google Scholar]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 2012; ISBN 9780521426008. [Google Scholar]
- Flach, F.; Breitung-Faes, S.; Kwade, A. Scaling Wet Fine Grinding Processes of Organic Particles Using Stirred Media Mills. Chem. Ing. Tech. 2017, 89, 1051–1059. [Google Scholar] [CrossRef]
- Flach, F.; Breitung-Faes, S.; Kwade, A. Tailoring product formulation properties to reduce grinding media wear. Chem. Eng. Sci. 2019, 207, 69–78. [Google Scholar] [CrossRef]
- Peppersack, C.; Kwade, A.; Breitung-Faes, S. Selective particle size analysis in binary submicron particle mixtures using density dependent differential sedimentation. Adv. Powder Technol. 2021, 32, 4049–4057. [Google Scholar] [CrossRef]
- Ogihara, T.; Mizutani, N.; Kato, M. Processing of monodispersed ZrO2 powders. Ceram. Int. 1987, 13, 35–40. [Google Scholar] [CrossRef]
- Wamkam, C.T.; Opoku, M.K.; Hong, H.; Smith, P. Effects of pH on heat transfer nanofluids containing ZrO2 and TiO2 nanoparticles. J. Appl. Phys. 2011, 109, 24305. [Google Scholar] [CrossRef]
- Anderson, W.; Kozak, D.; Coleman, V.A.; Jämting, Å.K.; Trau, M. A comparative study of submicron particle sizing platforms: Accuracy, precision and resolution analysis of polydisperse particle size distributions. J. Colloid Interface Sci. 2013, 405, 322–330. [Google Scholar] [CrossRef]
- Bell, N.C.; Minelli, C.; Tompkins, J.; Stevens, M.M.; Shard, A.G. Emerging techniques for submicrometer particle sizing applied to Stöber silica. Langmuir 2012, 28, 10860–10872. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1993, 43, 30–59. [Google Scholar] [CrossRef]
- Verwey, E.J.W. Theory of the stability of lyophobic colloids. J. Phys. Colloid Chem. 1947, 51, 631–636. [Google Scholar] [CrossRef]
- Israelachvili, N.J. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar] [CrossRef]
- Bergström, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar] [CrossRef]
- Gregory, J. Approximate expressions for retarded van der waals interaction. J. Colloid Interface Sci. 1981, 83, 138–145. [Google Scholar] [CrossRef]
- Clayfield, E.J.; Lumb, E.C.; Mackey, P.H. Retarded dispersion forces in colloidal particles—Exact integration of the casimir and polder equation. J. Colloid Interface Sci. 1971, 37, 382–389. [Google Scholar] [CrossRef]
- Elimelech, M.; Gregory, J.; Jia, X.; Williams, R.A. Particle Deposition & Aggregation; Butterworth-Heinemann: Oxford, UK, 1995. [Google Scholar] [CrossRef]
- Zhang, B.; Jin, J.; Wang, H.P. The calculation of retarded van der waals interaction for practical applications. J. Dispers. Sci. Technol. 1999, 20, 1485–1500. [Google Scholar] [CrossRef]
- Myers, D. Surfaces, Interfaces, and Colloids: Principles and Applications, 2nd ed.; Wiley-VCH: New York, NY, USA, 1999; ISBN 0471330604. [Google Scholar]
- Babick, F. Suspensions of Colloidal Particles and Aggregates; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-30661-2. [Google Scholar]
- Hogg, R.; Healy, T.W.; Fuerstenau, D.W. Mutual coagulation of colloidal dispersions. Trans. Faraday Soc. 1966, 62, 1638. [Google Scholar] [CrossRef]
- Wiese, G.R.; Healy, T.W. Effect of particle size on colloid stability. Trans. Faraday Soc. 1970, 66, 490. [Google Scholar] [CrossRef]
- Usui, S. Interaction of electrical double layers at constant surface charge. J. Colloid Interface Sci. 1973, 44, 107–113. [Google Scholar] [CrossRef]
- Lyklema, J. Particulate Colloids; Elsevier Academic Press: Amsterdam, The Netherlands, 2005; ISBN 978-0-12-460529-9. [Google Scholar]
- Carnie, S.L.; Chan, D.Y.C.; Gunning, J.S. Electrical Double Layer Interaction between Dissimilar Spherical Colloidal Particles and between a Sphere and a Plate: The Linearized Poisson-Boltzmann Theory. Langmuir 1994, 10, 2993–3009. [Google Scholar] [CrossRef]
- Fuchs, N. Über die Stabilitt und Aufladung der Aerosole. Z. Phys. 1934, 89, 736–743. [Google Scholar] [CrossRef]
- McGown, D.N.L.; Parfitt, G.D. Improved theoretical calculation of the stability ratio for colloidal systems. J. Phys. Chem. 1967, 71, 449–450. [Google Scholar] [CrossRef]
- Kihira, H.; Ryde, N.; Matijević, E. Kinetics of heterocoagulation. Part 2—The effect of the discreteness of surface charge. J. Chem. Soc. Faraday Trans. 1992, 88, 2379–2386. [Google Scholar] [CrossRef]
- Uricanu, V.; Eastman, J.R.; Vincent, B. Stability in Colloidal Mixtures Containing Particles with a Large Disparity in Size. J. Colloid Interface Sci. 2001, 233, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Honig, E.P.; Roebersen, G.J.; Wiersema, P.H. Effect of hydrodynamic interaction on the coagulation rate of hydrophobic colloids. J. Colloid Interface Sci. 1971, 36, 97–109. [Google Scholar] [CrossRef]
- Hunter, R.J. (Ed.) Zeta Potential in Colloid Science; Elsevier: Amsterdam, The Netherlands, 1981; ISBN 978-0-12-361961-7. [Google Scholar]
- Lyklema, J. Molecular interpretation of electrokinetic potentials. Curr. Opin. Colloid Interface Sci. 2010, 15, 125–130. [Google Scholar] [CrossRef]
- Sunkel, J.M.; Berg, J.C. The Stability Behavior of Sol-Emulsion Systems. J. Colloid Interface Sci. 1996, 179, 618–624. [Google Scholar] [CrossRef]
- Peppersack, C.; Wermbter, K.; Kwade, A.; Garnweitner, G.; Breitung-Faes, S. Top-Down Formulation of Goethite Nanosuspensions for the Production of Transparent, Inorganic Glass Coatings. Coatings 2022, 12, 330. [Google Scholar] [CrossRef]
- Kim, A.Y.; Berg, J.C. Fractal Aggregation: Scaling of Fractal Dimension with Stability Ratio. Langmuir 2000, 16, 2101–2104. [Google Scholar] [CrossRef]
- Singh, B.P.; Menchavez, R.; Takai, C.; Fuji, M.; Takahashi, M. Stability of dispersions of colloidal alumina particles in aqueous suspensions. J. Colloid Interface Sci. 2005, 291, 181–186. [Google Scholar] [CrossRef]
- Quemada, D.; Berli, C. Energy of interaction in colloids and its implications in rheological modeling. Adv. Colloid Interface Sci. 2002, 98, 51–85. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Pradip; Malghan, S.G. The stability of alumina-zirconia suspensions. Colloids Surf. A Physicochem. Eng. Asp. 1998, 133, 135–142. [Google Scholar] [CrossRef]
- Paciejewska, K.M. Untersuchung des Stabilitätsverhaltens von binären Kolloidalen Suspensionen. Ph.D. Dissertation, Technische Universität Dresden, Dresden, Germany, 2010. [Google Scholar]
- Gregory, J. Monitoring particle aggregation processes. Adv. Colloid Interface Sci. 2009, 147–148, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, M.; Juillerat, F.; Galletto, P.; Bowen, P.; Borkovec, M. Aggregation and charging of colloidal silica particles: Effect of particle size. Langmuir 2005, 21, 5761–5769. [Google Scholar] [CrossRef]
- Lichtenfeld, H.; Stechemesser, H.; Möhwald, H. Single particle light-scattering photometry—Some fields of application. J. Colloid Interface Sci. 2004, 276, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Ryde, N.; Matijević, E. Kinetics of heterocoagulation. Part 4.—Evaluation of absolute coagulation rate constants using a classical light scattering technique. J. Chem. Soc. Faraday Trans. 1994, 90, 167–171. [Google Scholar] [CrossRef]
- Rhein, F.; Hibbe, L.; Nirschl, H. Hybrid modeling of hetero-agglomeration processes: A framework for model selection and arrangement. Eng. Comput. 2024, 40, 583–604. [Google Scholar] [CrossRef]
- Rhein, F.; Ji, H.; Nirschl, H. Multidimensional Separation by Magnetic Seeded Filtration: Theoretical Study. Powders 2024, 3, 217–232. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).