Toward Multi-Dimensional Separation of Nanoparticles in Tubular Centrifuges
Abstract
1. Introduction
2. Materials and Methods
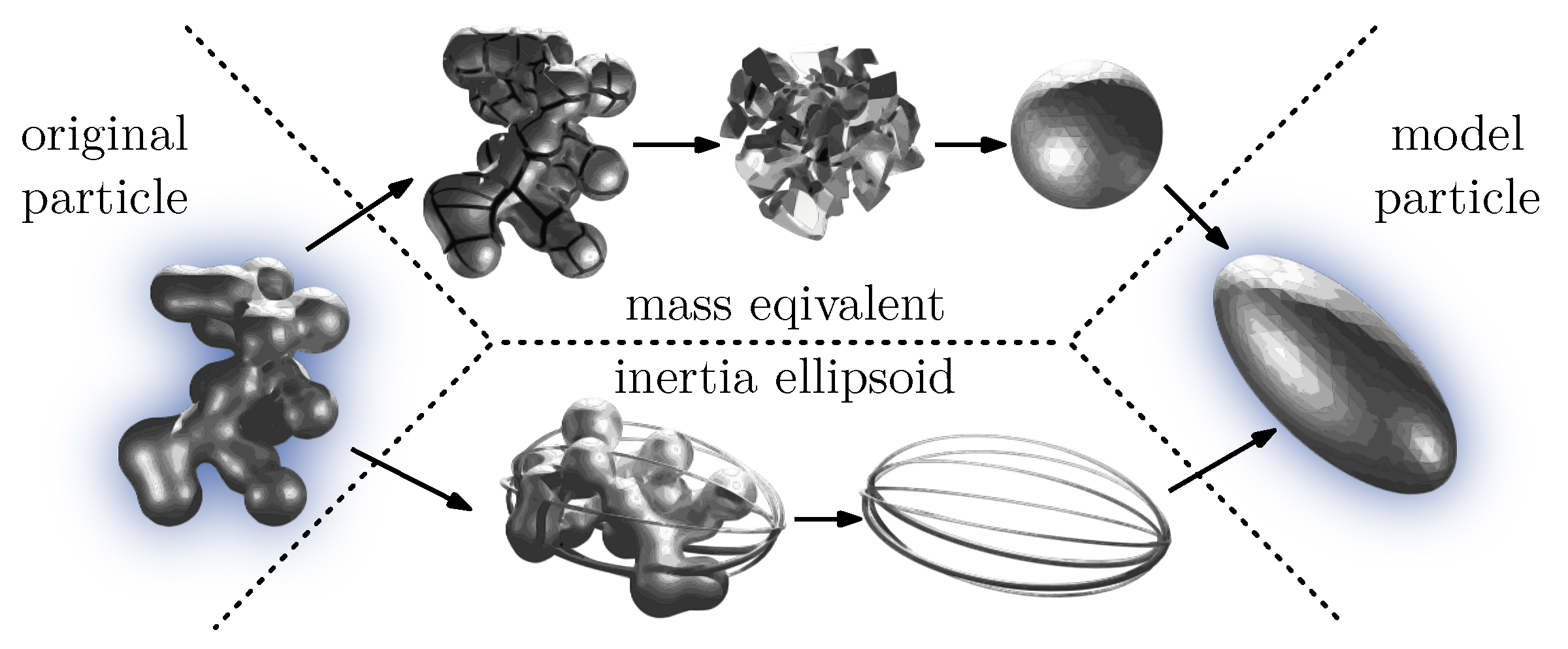
2.1. Mathematical Description of the Sedimentation Coefficient for Ellipsoids
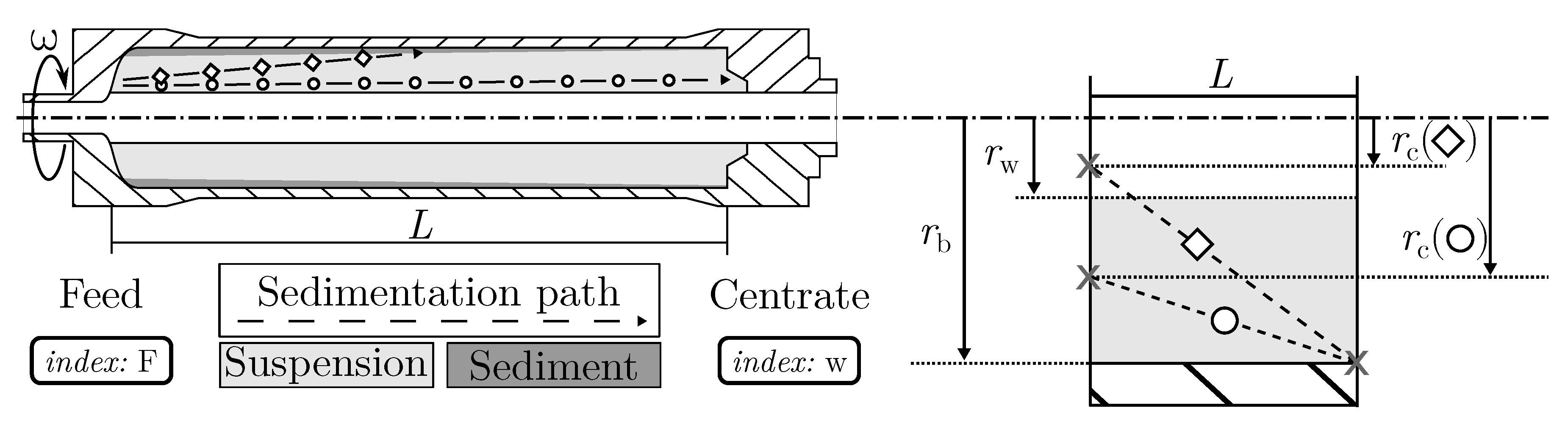
2.2. Tubular Centrifuge Separation Theory
2.3. Multi-Dimensional Grade Efficiency Definition
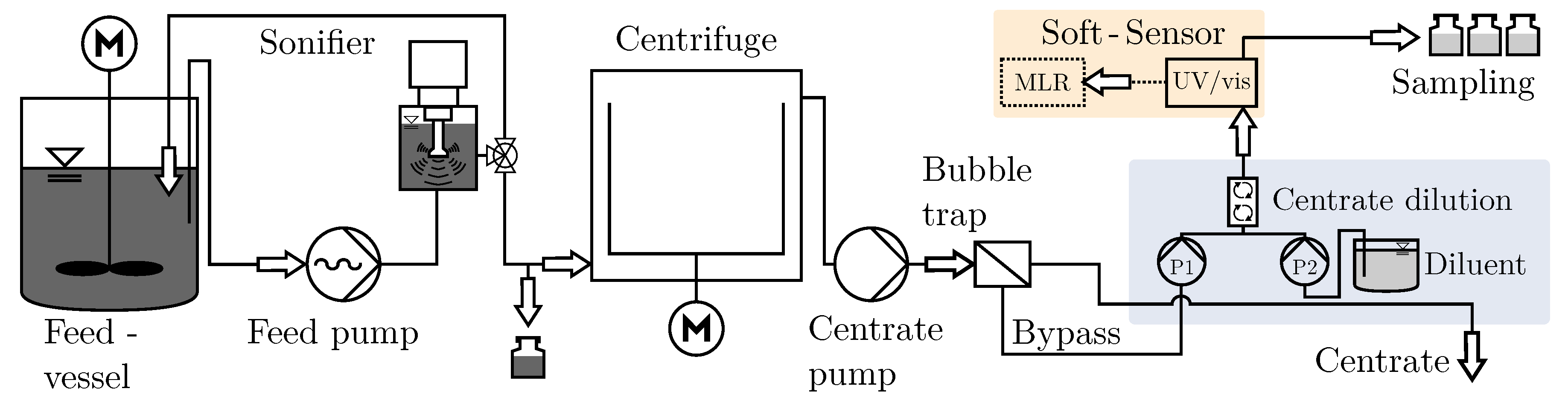
2.4. Experimental Setup and Procedure
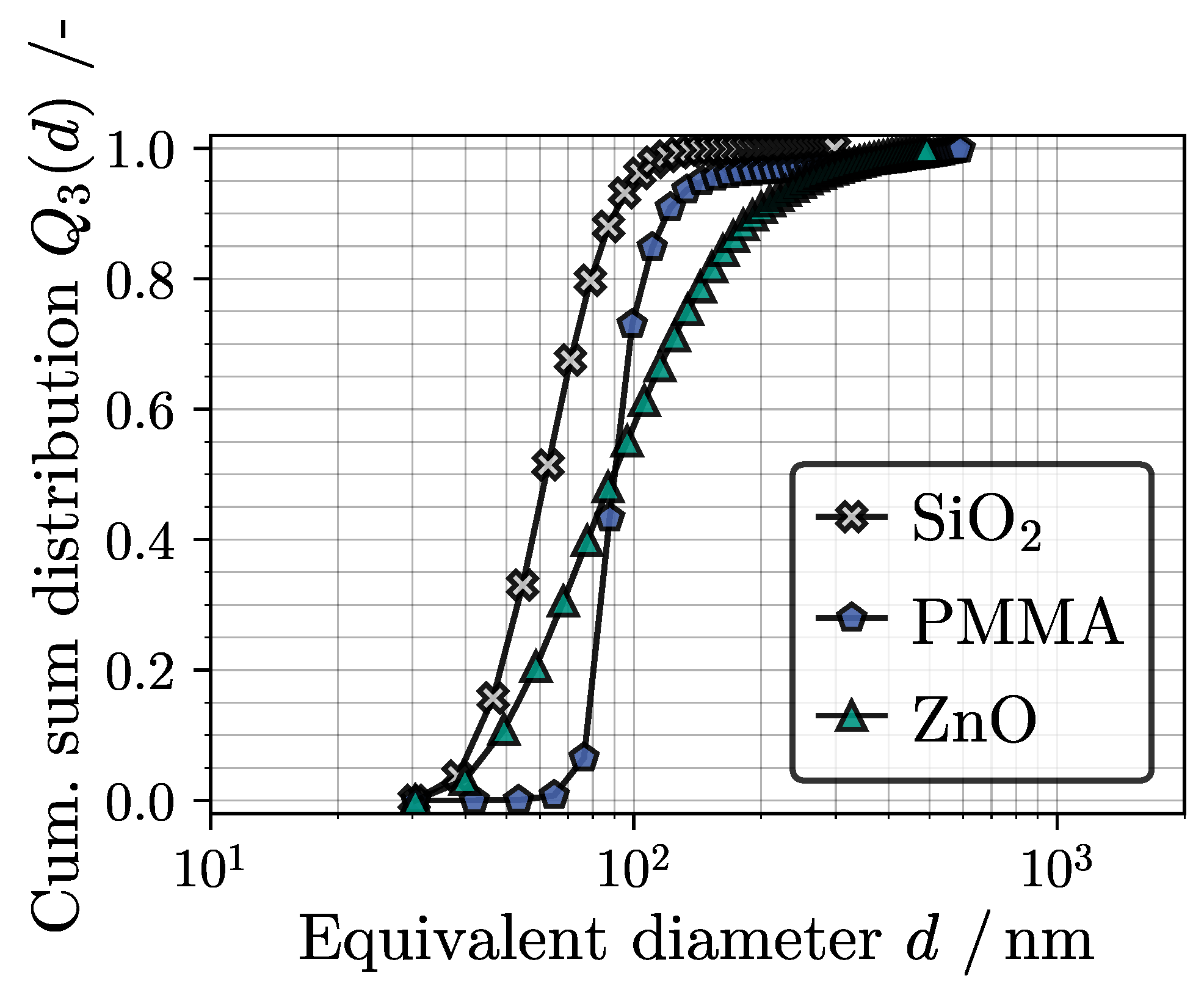
2.5. Particle Systems
2.6. Dynamic Separation Model Description
3. Results
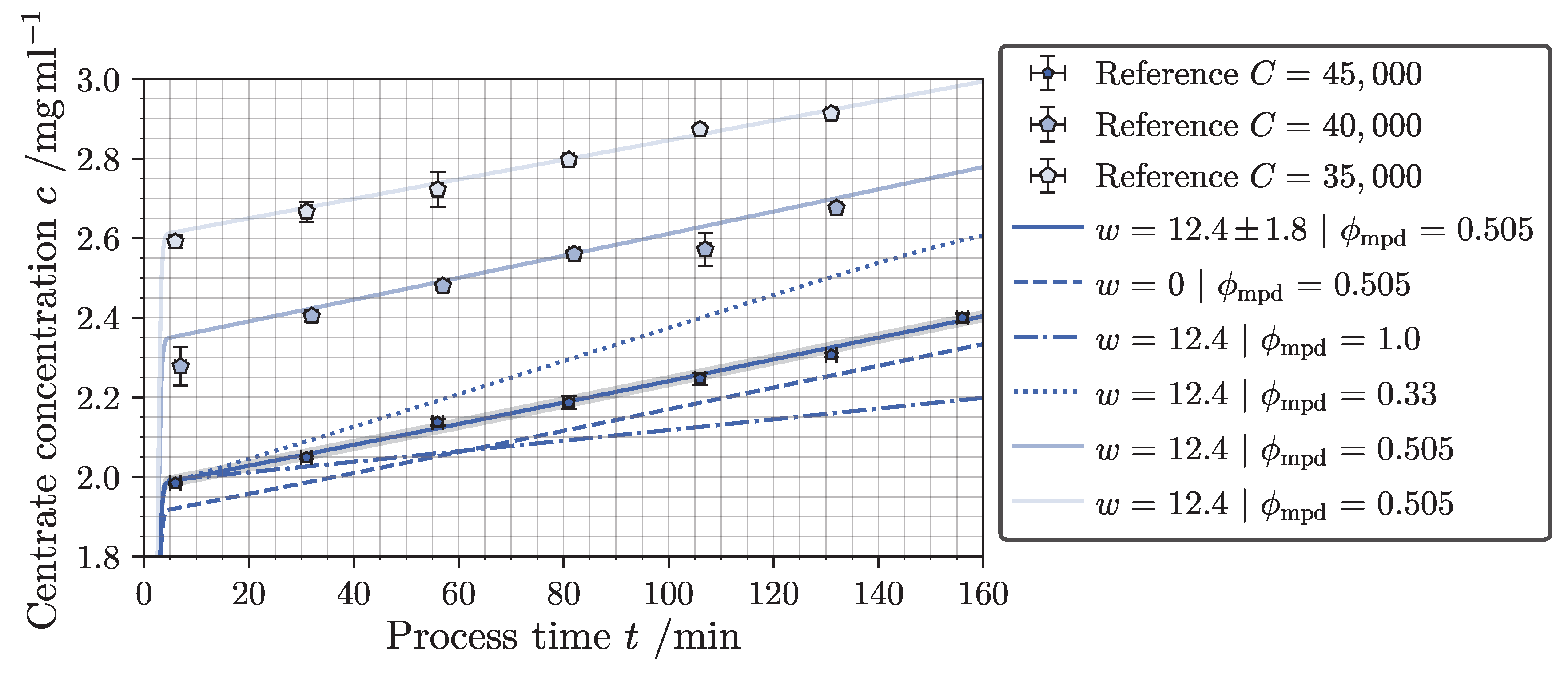
3.1. Long-Term Classification
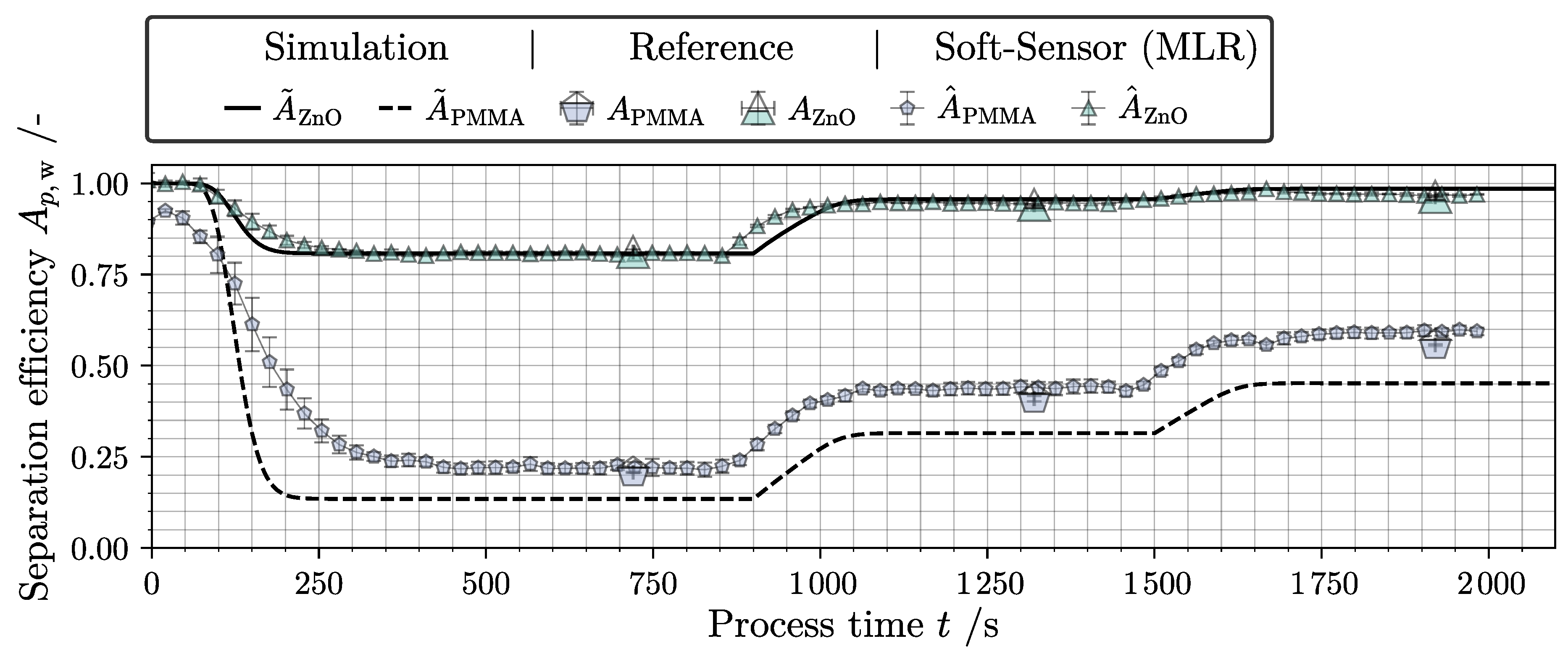
3.2. Short-Term Density Fractionation
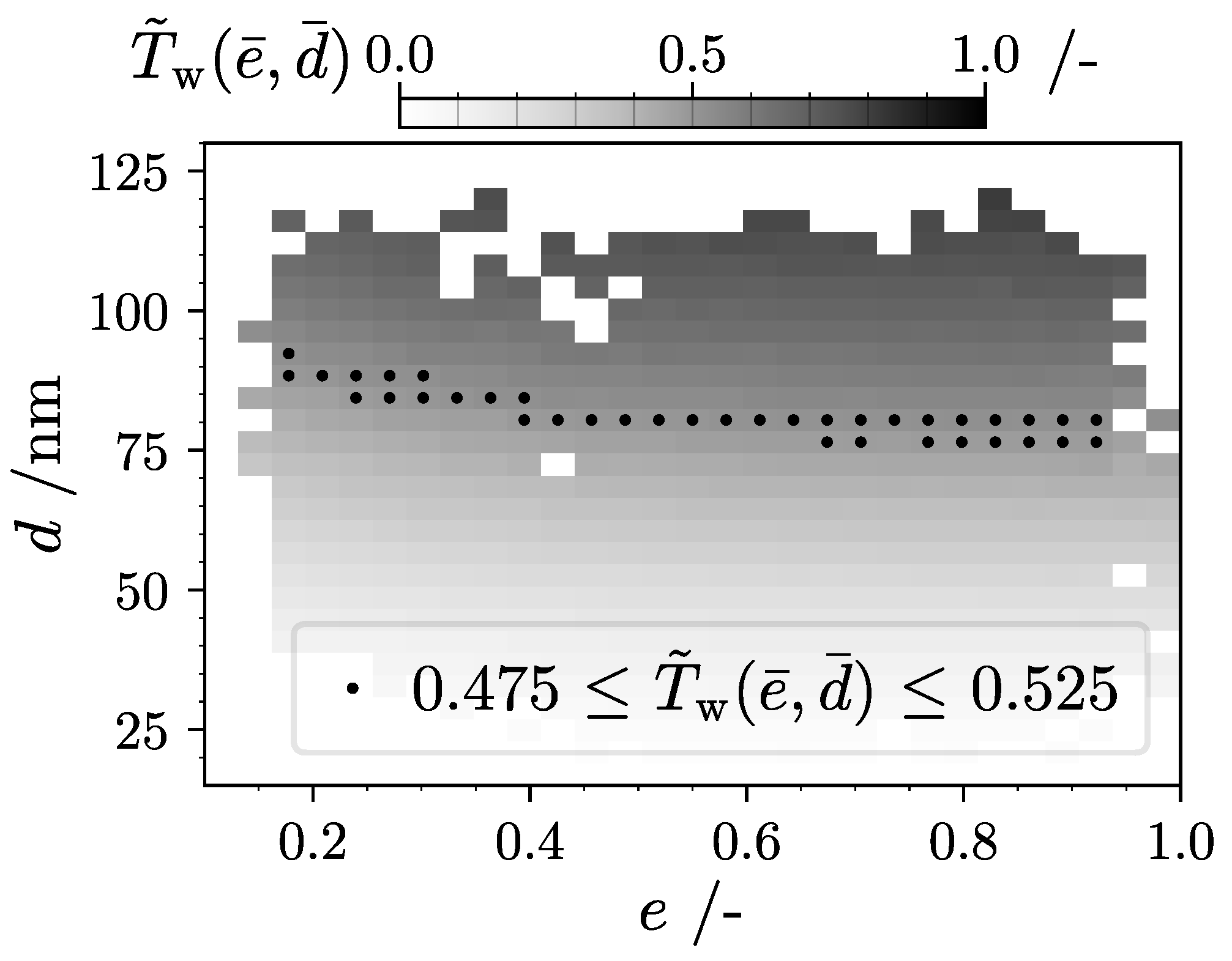
3.3. Short-Term Form Fractionation
3.4. Notes on Efficient Monitoring of Fractionation in Tubular Centrifuges
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| solid density | kg m−3 | |
| liquid density | kg m−3 | |
| angular velocity | rad s−1 | |
| dynamic viscosity | kg m−1 s−1 | |
| solid volume fraction | - | |
| partial particle volume | m3 | |
| local separation efficiency | - | |
| A | separation efficiency | - |
| A | particle projection surface | m2 |
| C | centrifugal number | - |
| drag coefficient | - | |
| c | particle concentration | kg m−3 |
| d | equivalent diameter | m |
| e | elongation | - |
| f | flatness | - |
| g | gravitational force | m s−2 |
| k | drag correction parameter | - |
| L | liquid pond length | m |
| q | probability density function | m−1 |
| r | radius | m |
| s | sedimentation coefficient | s |
| T | grade efficiency | - |
| t | time | s |
| terminal sedimentation velocity | m s−1 | |
| solid volume | m3 | |
| w | concentration coefficient | - |
| counter variables (subscripts) | - |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| I | Sedimentation zone |
| II | Sediment zone |
| AC | Analytical centrifugation |
| ADC | Analytical disk centrifuge |
| CFD | Computational fluid dynamics |
| CT | Computer tomography |
| EXP | Experiment |
| MLP | Multiple linear regression |
| NP | Nanoparticle |
| Probability density function | |
| PSD | Particle size distribution |
| PTD | Particle trait distribution |
| SC | Sedimentation coefficient |
| SEM | Scanning electron microscopy |
| TEM | Transmission electron microscopy |
| TCM | Tubular centrifuge model |
| UV/vis | Ultraviolet/visible |
Appendix A. Additional Simulation Parameters and Geometric Constants
| Parameter | Symbol | Value | SI Einheit |
|---|---|---|---|
| Weir radius (MGZ) | 0.0155 | ||
| Weir radius (Z11) | 0.0073 | ||
| Wall radius | 0.0215 | ||
| Pond length (MGZ) | L | 0.359 | |
| Pond length (Z11) | L | 0.175 | |
| Density liquid | 998.207 | ||
| Viscosity | |||
| Compartment count | J | 20 | − |
| Simulation time | case dependent | ||
| Time step size | 0.5 |
Appendix B. Marginalization of Higher Dimensional Particle Trait Distributions
References
- Hulla, J.; Sahu, S.; Hayes, A. Nanotechnology: History and future. Hum. Exp. Toxicol. 2015, 34, 1318–1321. [Google Scholar] [CrossRef] [PubMed]
- Nasrollahzadeh, M.; Sajadi, S.M.; Sajjadi, M.; Issaabadi, Z. An Introduction to Nanotechnology. In Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–27. [Google Scholar] [CrossRef]
- Wong, A.; Liu, Q.; Griffin, S.; Nicholls, A.; Regalbuto, J.R. Synthesis of ultrasmall, homogeneously alloyed, bimetallic nanoparticles on silica supports. Science 2017, 358, 1427–1430. [Google Scholar] [CrossRef] [PubMed]
- Adair, J.H.; Suvaci, E. Morphological control of particles. Curr. Opin. Colloid Interface Sci. 2000, 5, 160–167. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, S.; Chen, Z.; Yan, Y.; Zhao, J.; Li, J.; Jiang, Z. In Situ synthesis of SiC-graphene core-shell nanoparticles using wet ball milling. Ceram. Int. 2018, 44, 8283–8289. [Google Scholar] [CrossRef]
- Malamatari, M.; Taylor, K.M.; Malamataris, S.; Douroumis, D.; Kachrimanis, K. Pharmaceutical nanocrystals: Production by wet milling and applications. Drug Discov. Today 2018, 23, 534–547. [Google Scholar] [CrossRef]
- Ramos, A.P.; Cruz, M.A.E.; Tovani, C.B.; Ciancaglini, P. Biomedical applications of nanotechnology. Biophys. Rev. 2017, 9, 79–89. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Z.; Bi, S. Nanoparticles for organic electronics applications. Mater. Res. Express 2020, 7, 012004. [Google Scholar] [CrossRef]
- Plüisch, C.S.; Wittemann, A. Shape-Tailored Polymer Colloids on the Road to Become Structural Motifs for Hierarchically Organized Materials. Macromol. Rapid Commun. 2013, 34, 1798–1814. [Google Scholar] [CrossRef]
- Vogel, N.; Retsch, M.; Fustin, C.A.; del Campo, A.; Jonas, U. Advances in Colloidal Assembly: The Design of Structure and Hierarchy in Two and Three Dimensions. Chem. Rev. 2015, 115, 6265–6311. [Google Scholar] [CrossRef]
- Narayanan, R.; El-Sayed, M.A. Shape-Dependent Catalytic Activity of Platinum Nanoparticles in Colloidal Solution. Nano Lett. 2004, 4, 1343–1348. [Google Scholar] [CrossRef]
- Auffan, M.; Rose, J.; Bottero, J.Y.; Lowry, G.V.; Jolivet, J.P.; Wiesner, M.R. Towards a definition of inorganic nanoparticles from an environmental, health and safety perspective. Nat. Nanotechnol. 2009, 4, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Kutvonen, A.; Rossi, G.; Puisto, S.R.; Rostedt, N.K.J.; Ala-Nissila, T. Influence of nanoparticle size, loading, and shape on the mechanical properties of polymer nanocomposites. J. Chem. Phys. 2012, 137, 214901. [Google Scholar] [CrossRef] [PubMed]
- Truong, N.P.; Whittaker, M.R.; Mak, C.W.; Davis, T.P. The importance of nanoparticle shape in cancer drug delivery. Expert Opin. Drug Deliv. 2014, 12, 129–142. [Google Scholar] [CrossRef]
- Rodrigues, T.S.; da Silva, A.G.M.; Camargo, P.H.C. Nanocatalysis by noble metal nanoparticles: Controlled synthesis for the optimization and understanding of activities. J. Mater. Chem. A 2019, 7, 5857–5874. [Google Scholar] [CrossRef]
- Visalakshan, R.M.; García, L.E.G.; Benzigar, M.R.; Ghazaryan, A.; Simon, J.; Mierczynska-Vasilev, A.; Michl, T.D.; Vinu, A.; Mailänder, V.; Morsbach, S.; et al. The Influence of Nanoparticle Shape on Protein Corona Formation. Small 2020, 16, 2000285. [Google Scholar] [CrossRef]
- Rhein, F.; Zhai, O.; Schmid, E.; Nirschl, H. Multidimensional Separation by Magnetic Seeded Filtration: Experimental Studies. Powders 2023, 2, 588–606. [Google Scholar] [CrossRef]
- Wilhelm, T.; Sygusch, J.; Furat, O.; Bachmann, K.; Rudolph, M.; Schmidt, V. Parametric Stochastic Modeling of Particle Descriptor Vectors for Studying the Influence of Ultrafine Particle Wettability and Morphology on Flotation-Based Separation Behavior. Powders 2023, 2, 353–371. [Google Scholar] [CrossRef]
- Fagan, J.A.; Becker, M.L.; Chun, J.; Nie, P.; Bauer, B.J.; Simpson, J.R.; Hight-Walker, A.; Hobbie, E.K. Centrifugal Length Separation of Carbon Nanotubes. Langmuir 2008, 24, 13880–13889. [Google Scholar] [CrossRef]
- Sun, X.; Tabakman, S.; Seo, W.S.; Zhang, L.; Zhang, G.; Sherlock, S.; Bai, L.; Dai, H. Separation of Nanoparticles in a Density Gradient: FeCo@C and Gold Nanocrystals. Angew. Chem. Int. Ed. 2009, 48, 939–942. [Google Scholar] [CrossRef]
- Plüisch, C.S.; Bössenecker, B.; Dobler, L.; Wittemann, A. Zonal rotor centrifugation revisited: New horizons in sorting nanoparticles. RSC Adv. 2019, 9, 27549–27559. [Google Scholar] [CrossRef]
- Kohsakowski, S.; Seiser, F.; Wiederrecht, J.P.; Reichenberger, S.; Vinnay, T.; Barcikowski, S.; Marzun, G. Effective size separation of laser-generated, surfactant-free nanoparticles by continuous centrifugation. Nanotechnology 2019, 31, 095603. [Google Scholar] [CrossRef] [PubMed]
- Spelter, L.E.; Steiwand, A.; Nirschl, H. Processing of dispersions containing fine particles or biological products in tubular bowl centrifuges. Chem. Eng. Sci. 2010, 65, 4173–4181. [Google Scholar] [CrossRef]
- Konrath, M.; Brenner, A.K.; Dillner, E.; Nirschl, H. Centrifugal classification of ultrafine particles: Influence of suspension properties and operating parameters on classification sharpness. Sep. Purif. Technol. 2015, 156, 61–70. [Google Scholar] [CrossRef]
- Stahl, S.; Spelter, L.E.; Nirschl, H. Investigations on the Separation Efficiency of Tubular Bowl Centrifuges. Chem. Eng. Technol. 2008, 31, 1577–1583. [Google Scholar] [CrossRef]
- Konrath, M.; Hackbarth, M.; Nirschl, H. Process monitoring and control for constant separation conditions in centrifugal classification of fine particles. Adv. Powder Technol. 2014, 25, 991–998. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Souza, F.A.; Araújo, R.; Mendes, J. Review of soft sensor methods for regression applications. Chemom. Intell. Lab. Syst. 2016, 152, 69–79. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Haiss, W.; Thanh, N.T.K.; Aveyard, J.; Fernig, D.G. Determination of Size and Concentration of Gold Nanoparticles from UV-Vis Spectra. Anal. Chem. 2007, 79, 4215–4221. [Google Scholar] [CrossRef]
- Stone, K.A.; Shah, D.; Kim, M.H.; Roberts, N.R.M.; He, Q.P.; Wang, J. A novel soft sensor approach for estimating individual biomass in mixed cultures. Biotechnol. Prog. 2017, 33, 347–354. [Google Scholar] [CrossRef]
- Bartosiak, M.; Giersz, J.; Jankowski, K. Analytical monitoring of selenium nanoparticles green synthesis using photochemical vapor generation coupled with MIP-OES and UV–Vis spectrophotometry. Microchem. J. 2019, 145, 1169–1175. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Pan, R.; Roth, S.; Förster, S. Insights into Growth Kinetics of Colloidal Gold Nanoparticles: In Situ SAXS and UV–Vis Evaluation. J. Phys. Chem. C 2020, 125, 1087–1095. [Google Scholar] [CrossRef]
- Weirauch, L.; Giesler, J.; Pesch, G.R.; Baune, M.; Thöming, J. Highly Permeable, Electrically Switchable Filter for Multidimensional Sorting of Suspended Particles. Powders 2024, 3, 574–593. [Google Scholar] [CrossRef]
- Werther, J.; Heinrich, S.; Dosta, M.; Hartge, E.U. The ultimate goal of modeling—Simulation of system and plant performance. Particuology 2011, 9, 320–329. [Google Scholar] [CrossRef]
- Dosta, M.; Antonyuk, S.; Hartge, E.U.; Heinrich, S. Parameter Estimation for the Flowsheet Simulation of Solids Processes. Chem. Ing. Tech. 2014, 86, 1073–1079. [Google Scholar] [CrossRef]
- Menesklou, P.; Nirschl, H.; Gleiss, M. Dewatering of finely dispersed calcium carbonate-water slurries in decanter centrifuges: About modelling of a dynamic simulation tool. Sep. Purif. Technol. 2020, 251, 117287. [Google Scholar] [CrossRef]
- Menesklou, P.; Sinn, T.; Nirschl, H.; Gleiss, M. Scale-Up of Decanter Centrifuges for the Particle Separation and Mechanical Dewatering in the Minerals Processing Industry by Means of a Numerical Process Model. Minerals 2021, 11, 229. [Google Scholar] [CrossRef]
- Nirschl, H.; Winkler, M.; Sinn, T.; Menesklou, P. Autonomous Processes in Particle Technology. Chem. Ing. Tech. 2021, 94, 230–239. [Google Scholar] [CrossRef]
- Gleiss, M.; Nirschl, H. Dynamic Simulation of Mechanical Fluid Separation in Solid Bowl Centrifuges. In Dynamic Flowsheet Simulation of Solids Processes; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 237–268. [Google Scholar] [CrossRef]
- Schach, E.; Buchmann, M.; Tolosana-Delgado, R.; Leißner, T.; Kern, M.; van den Boogaart, K.G.; Rudolph, M.; Peuker, U.A. Multidimensional characterization of separation processes—Part 1: Introducing kernel methods and entropy in the context of mineral processing using SEM-based image analysis. Miner. Eng. 2019, 137, 78–86. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Leißner, T.; Kern, M.; Mütze, T.; Rudolph, M.; Peuker, U.A.; Tolosana-Delgado, R. Multidimensional characterization of separation processes—Part 2: Comparability of separation efficiency. Miner. Eng. 2020, 150, 106284. [Google Scholar] [CrossRef]
- Frank, U.; Wawra, S.E.; Pflug, L.; Peukert, W. Multidimensional Particle Size Distributions and Their Application to Nonspherical Particle Systems in Two Dimensions. Part. Part. Syst. Charact. 2019, 36, 1800554. [Google Scholar] [CrossRef]
- Furat, O.; Leißner, T.; Bachmann, K.; Gutzmer, J.; Peuker, U.; Schmidt, V. Stochastic Modeling of Multidimensional Particle Properties Using Parametric Copulas. Microsc. Microanal. 2019, 25, 720–734. [Google Scholar] [CrossRef] [PubMed]
- Furat, O.; Masuhr, M.; Kruis, F.E.; Schmidt, V. Stochastic modeling of classifying aerodynamic lenses for separation of airborne particles by material and size. Adv. Powder Technol. 2020, 31, 2215–2226. [Google Scholar] [CrossRef]
- Stokes, G. On the Effect of Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Philos. 1851, 9, 8–106. [Google Scholar]
- Leith, D. Drag on Nonspherical Objects. Aerosol Sci. Technol. 1987, 6, 153–161. [Google Scholar] [CrossRef]
- Trunk, R.; Bretl, C.; Thäter, G.; Nirschl, H.; Dorn, M.; Krause, M.J. A Study on Shape-Dependent Settling of Single Particles with Equal Volume Using Surface Resolved Simulations. Computation 2021, 9, 40. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Loth, E. Drag of non-spherical solid particles of regular and irregular shape. Powder Technol. 2008, 182, 342–353. [Google Scholar] [CrossRef]
- Oberbeck, A. Ueber stationäre Flüssigkeitsbewegungen mit Berücksichtigung der inneren Reibung. In Journal füR Die Reine und Angewandte Mathematik Band 81; De Gruyter: Berlin, Germany, 1876; pp. 62–80. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. On the drag of freely falling non-spherical particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef]
- Winkler, M.; Rhein, F.; Nirschl, H.; Gleiss, M. Real-Time Modeling of Volume and Form Dependent Nanoparticle Fractionation in Tubular Centrifuges. Nanomaterials 2022, 12, 3161. [Google Scholar] [CrossRef]
- Uttinger, M.J.; Walter, J.; Thajudeen, T.; Wawra, S.E.; Peukert, W. Brownian dynamics simulations of analytical ultracentrifugation experiments exhibiting hydrodynamic and thermodynamic non-ideality. Nanoscale 2017, 9, 17770–17780. [Google Scholar] [CrossRef] [PubMed]
- DIN ISO 9276-6:2012-01; Representation of Results of Particle Size Analysis—Part 6: Descriptive and Quantitative Representation of Particle Shape and Morphology. Technical Standard; DIN Deutsches Institut für Normung e. V.: Berlin, Germany, 2012.
- Batchelor, G.K. Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 1972, 52, 245–268. [Google Scholar] [CrossRef]
- Mächtle, W.; Börger, L. (Eds.) Analytical Ultracentrifugation of Polymers and Nanoparticles; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Spelter, L.E.; Nirschl, H.; Stickland, A.D.; Scales, P.J. Pseudo two-dimensional modeling of sediment build-up in centrifuges: A compartment approach using compressional rheology. AIChE J. 2013, 59, 3843–3855. [Google Scholar] [CrossRef]
- Winkler, M.; Gleiss, M.; Nirschl, H. Soft Sensor Development for Real-Time Process Monitoring of Multidimensional Fractionation in Tubular Centrifuges. Nanomaterials 2021, 11, 1114. [Google Scholar] [CrossRef]
- Green, M.D.; Eberl, M.; Landman, K.A. Compressive yield stress of flocculated suspensions: Determination via experiment. AIChE J. 1996, 42, 2308–2318. [Google Scholar] [CrossRef]
- Usher, S.P.; Studer, L.J.; Wall, R.C.; Scales, P.J. Characterisation of dewaterability from equilibrium and transient centrifugation test data. Chem. Eng. Sci. 2013, 93, 277–291. [Google Scholar] [CrossRef]
- Wasserman, L. All of Statistics; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Pitman, J. Probability; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Winkler, M.; Sonner, H.; Gleiss, M.; Nirschl, H. Fractionation of ultrafine particles: Evaluation of separation efficiency by UV–vis spectroscopy. Chem. Eng. Sci. 2020, 213, 115374. [Google Scholar] [CrossRef]
- Konrath, M.; Gorenflo, J.; Hübner, N.; Nirschl, H. Application of magnetic bearing technology in high-speed centrifugation. Chem. Eng. Sci. 2016, 147, 65–73. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: Amsterdam, The Netherlands; Heidelberg, Germany, 2011. [Google Scholar]
- Bohinc, K.; Kralj-Iglič, V.; Iglič, A. Thickness of electrical double layer. Effect of ion size. Electrochim. Acta 2001, 46, 3033–3040. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Steric Effects in Electrolytes: A Modified Poisson–Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef]
- Rhein, F. Mehrdimensionale Trennung Mit Hilfe Magnetischer Partikel. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2022. [Google Scholar] [CrossRef]
- Gleiß, M. Dynamische Simulation der Mechanischen Flüssigkeitsabtrennung in Vollmantelzentrifugen. Ph.D. Thesis, KIT Scientific, Karlsruhe, Germany, 2018. [Google Scholar] [CrossRef]
- Gleiss, M.; Hammerich, S.; Kespe, M.; Nirschl, H. Application of the dynamic flow sheet simulation concept to the solid–liquid separation: Separation of stabilized slurries in continuous centrifuges. Chem. Eng. Sci. 2017, 163, 167–178. [Google Scholar] [CrossRef]
- Zingg, T. Beitrag zur Schotteranalyse. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1935. [Google Scholar] [CrossRef]
- Ditscherlein, R.; Furat, O.; de Langlard, M.; de Souza e Silva, J.M.; Sygusch, J.; Rudolph, M.; Leißner, T.; Schmidt, V.; Peuker, U.A. Multiscale Tomographic Analysis for Micron-Sized Particulate Samples. Microsc. Microanal. 2020, 26, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Ditscherlein, R.; Furat, O.; Löwer, E.; Mehnert, R.; Trunk, R.; Leißner, T.; Krause, M.J.; Schmidt, V.; Peuker, U.A. PARROT: A Pilot Study on the Open Access Provision of Particle-Discrete Tomographic Datasets. Microsc. Microanal. 2022, 28, 350–360. [Google Scholar] [CrossRef]
- Neumann, S.; Menter, C.; Mahmoud, A.S.; Segets, D.; Rafaja, D. Microstructure characteristics of non-monodisperse quantum dots: On the potential of transmission electron microscopy combined with X-ray diffraction. CrystEngComm 2020, 22, 3644–3655. [Google Scholar] [CrossRef]
- He, P.; Mejia, A.F.; Cheng, Z.; Sun, D.; Sue, H.J.; Dinair, D.S.; Marquez, M. Hindrance function for sedimentation and creaming of colloidal disks. Phys. Rev. E 2010, 81, 026310. [Google Scholar] [CrossRef] [PubMed]
- Winkler, M. Prozesstechnische Fraktionierung von Nanoskaligen Partikeln in Röhrenzentrifugen. Ph.D. Thesis, Karlsruhe Institut of Technology (KIT), Karlsruhe, Germany, 2023. [Google Scholar] [CrossRef]







| Material | / | /mg mL−1 | C/- | /mL min−1 |
|---|---|---|---|---|
| Long-term classification (1D, ) | ||||
| PMMA | 1193 | 6.11 | 35,000 | 100 |
| 6.17 | 40,000 | |||
| 5.87 | 45,000 | |||
| Short-term density fractionation (1D, ) | ||||
| PMMA | 1193 | 1.663 | 30,000 | 100 |
| ZnO | 5610 | 0.619 | 10,000 | 100 |
| Short-term form fractionation (3D, ) | ||||
| SiO2 | 2200 | 18.37 | 47,000 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkler, M.; Gleiss, M.; Nirschl, H. Toward Multi-Dimensional Separation of Nanoparticles in Tubular Centrifuges. Powders 2025, 4, 4. https://doi.org/10.3390/powders4010004
Winkler M, Gleiss M, Nirschl H. Toward Multi-Dimensional Separation of Nanoparticles in Tubular Centrifuges. Powders. 2025; 4(1):4. https://doi.org/10.3390/powders4010004
Chicago/Turabian StyleWinkler, Marvin, Marco Gleiss, and Hermann Nirschl. 2025. "Toward Multi-Dimensional Separation of Nanoparticles in Tubular Centrifuges" Powders 4, no. 1: 4. https://doi.org/10.3390/powders4010004
APA StyleWinkler, M., Gleiss, M., & Nirschl, H. (2025). Toward Multi-Dimensional Separation of Nanoparticles in Tubular Centrifuges. Powders, 4(1), 4. https://doi.org/10.3390/powders4010004






