Application of Multivariate Tromp Functions for Evaluating the Joint Impact of Particle Size, Shape and Wettability on the Separation of Ultrafine Particles via Flotation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
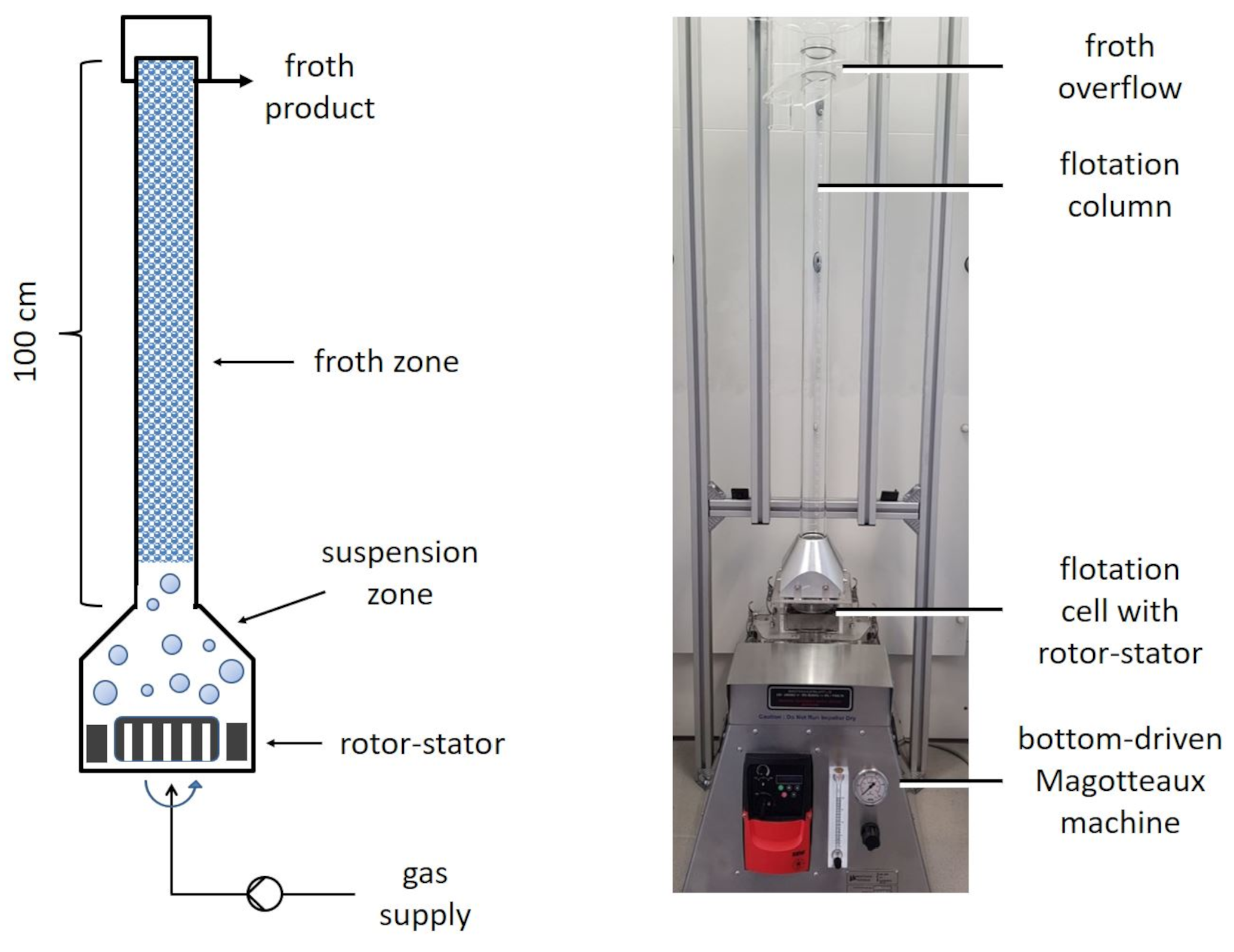
2.2. Flotation-Based Separation Experiments
2.3. Sample Preparation and SEM-Based Automated Mineralogy
2.4. Particle-Based Segmentation
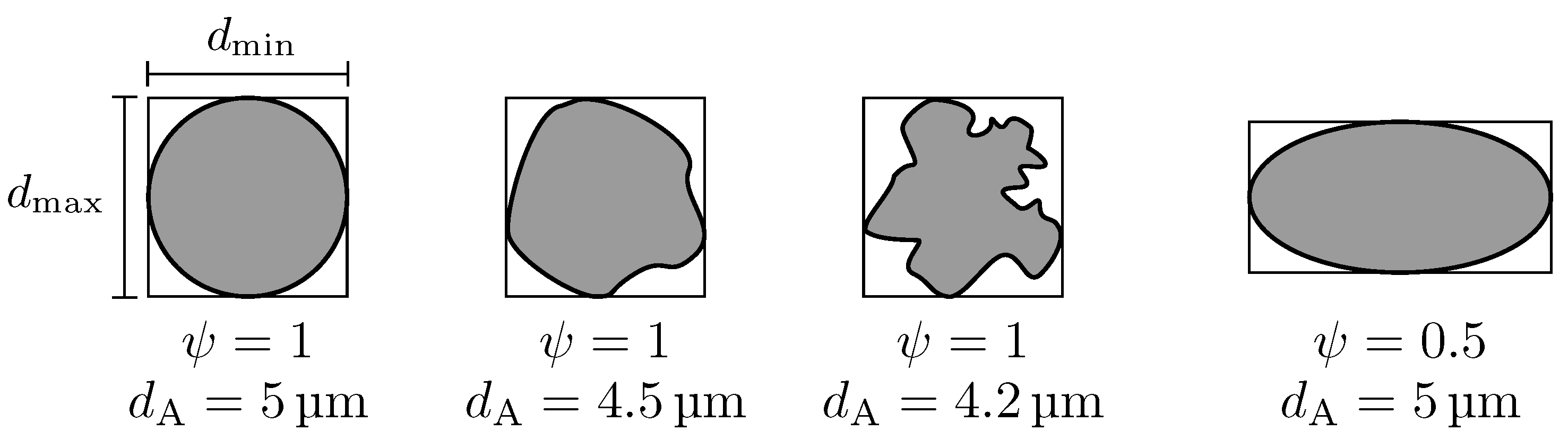
2.5. Characterization of Particles by Means of Size and Shape Descriptors
2.6. Stochastic Modeling of Particle Descriptor Vectors for the Computation of Multivariate Tromp Functions
2.6.1. Univariate Stochastic Modeling of Single Particle Descriptors
2.6.2. Bivariate Stochastic Modeling of Pairs of Particle Descriptors Using Archimedean Copulas
2.7. Computation of Yield
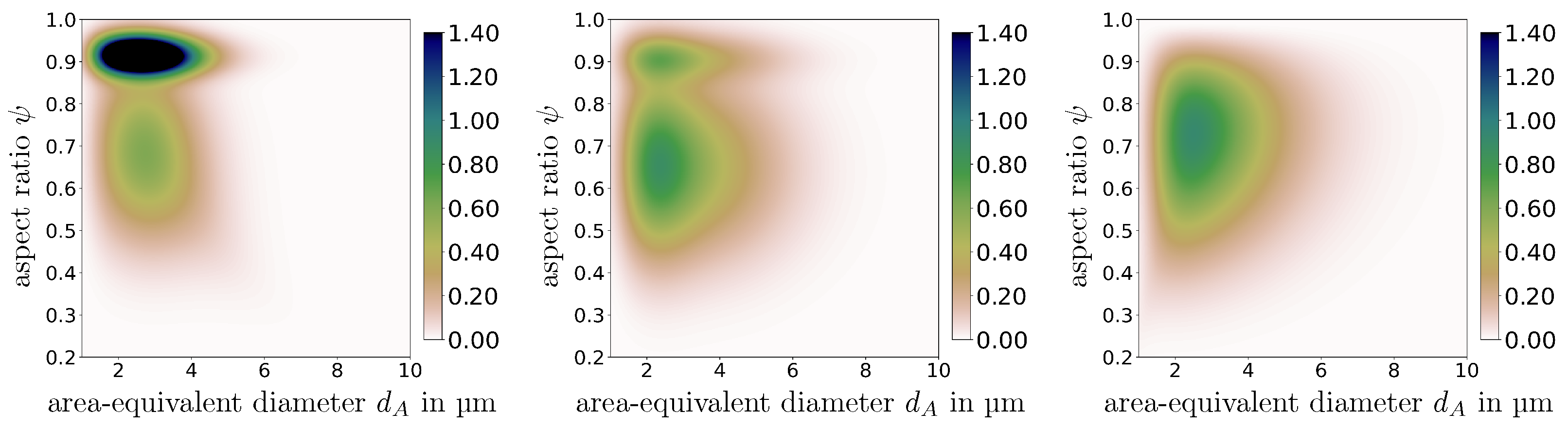
2.8. Probability Densities of Descriptor Vectors Associated with Particles in the Feed and Concentrate
2.9. Tromp Functions Conditioned on Particle Size and Shape Classes
2.9.1. Conditional Univariate Probability Densities
2.9.2. Conditional Univariate Tromp Functions
3. Results and Discussion
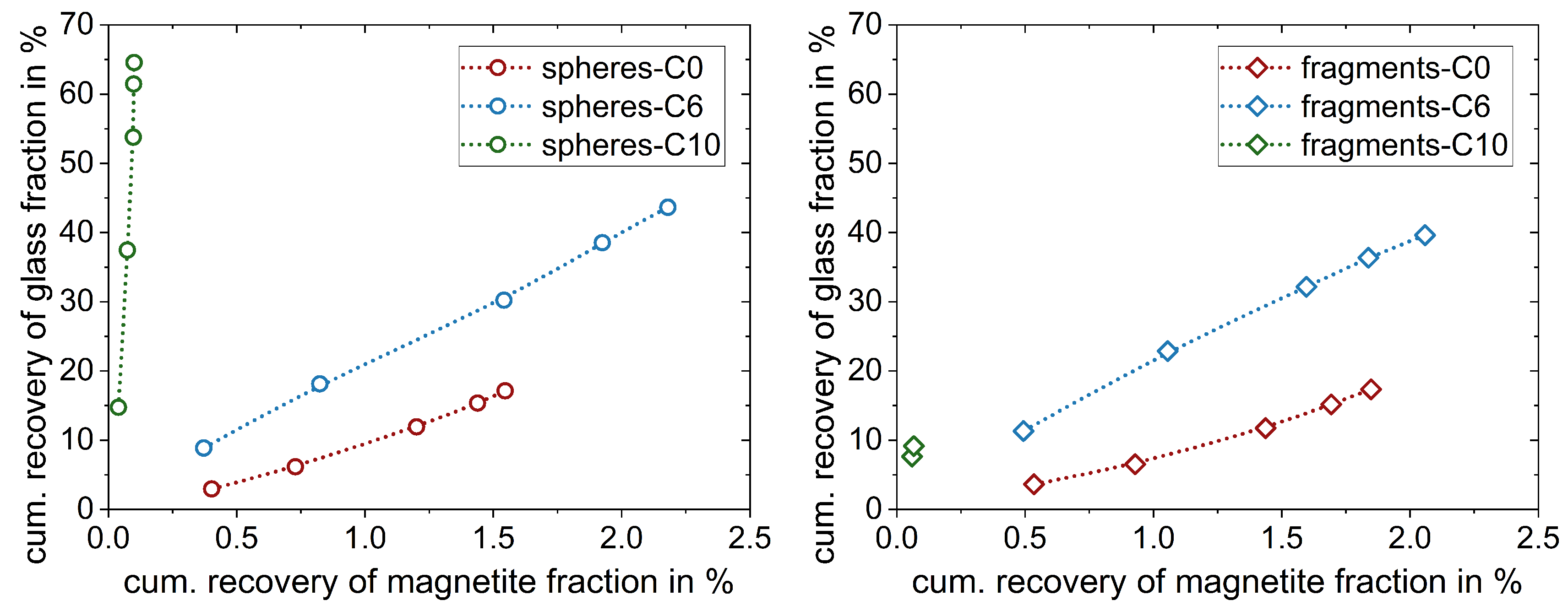
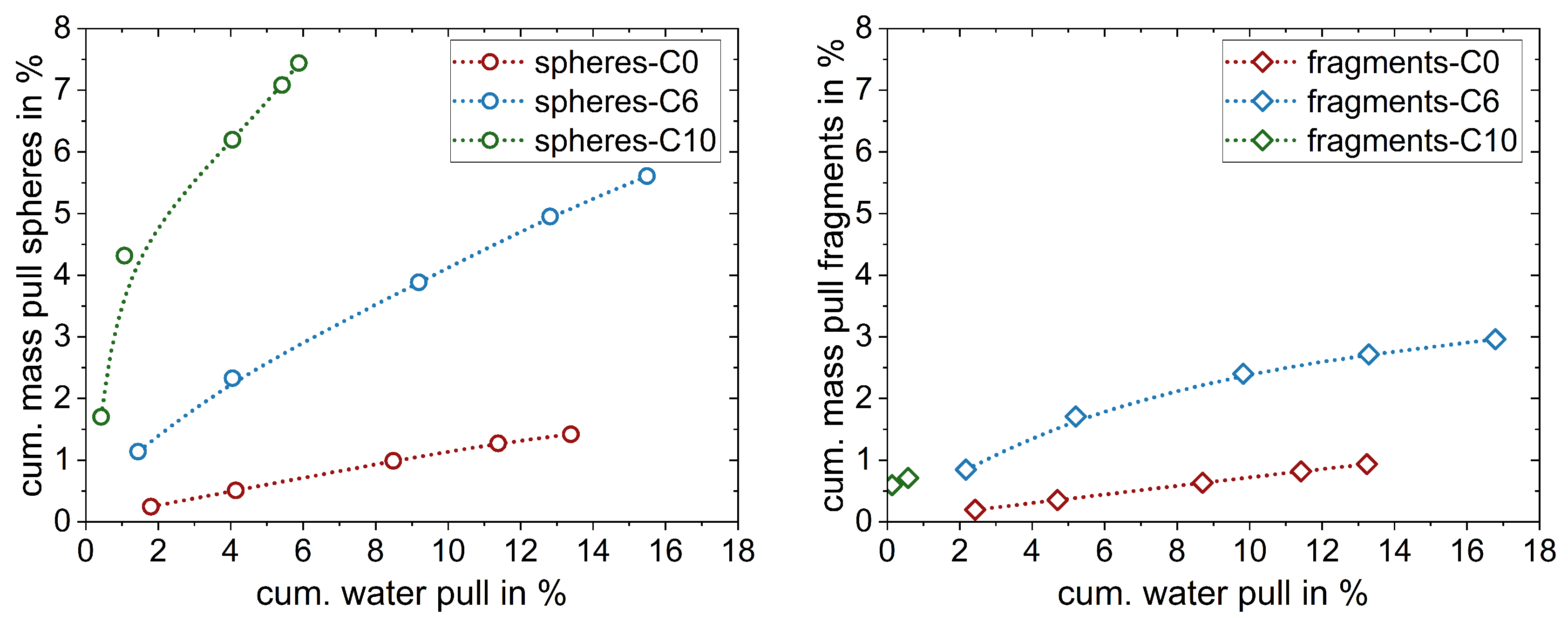
3.1. Classic Flotation Results
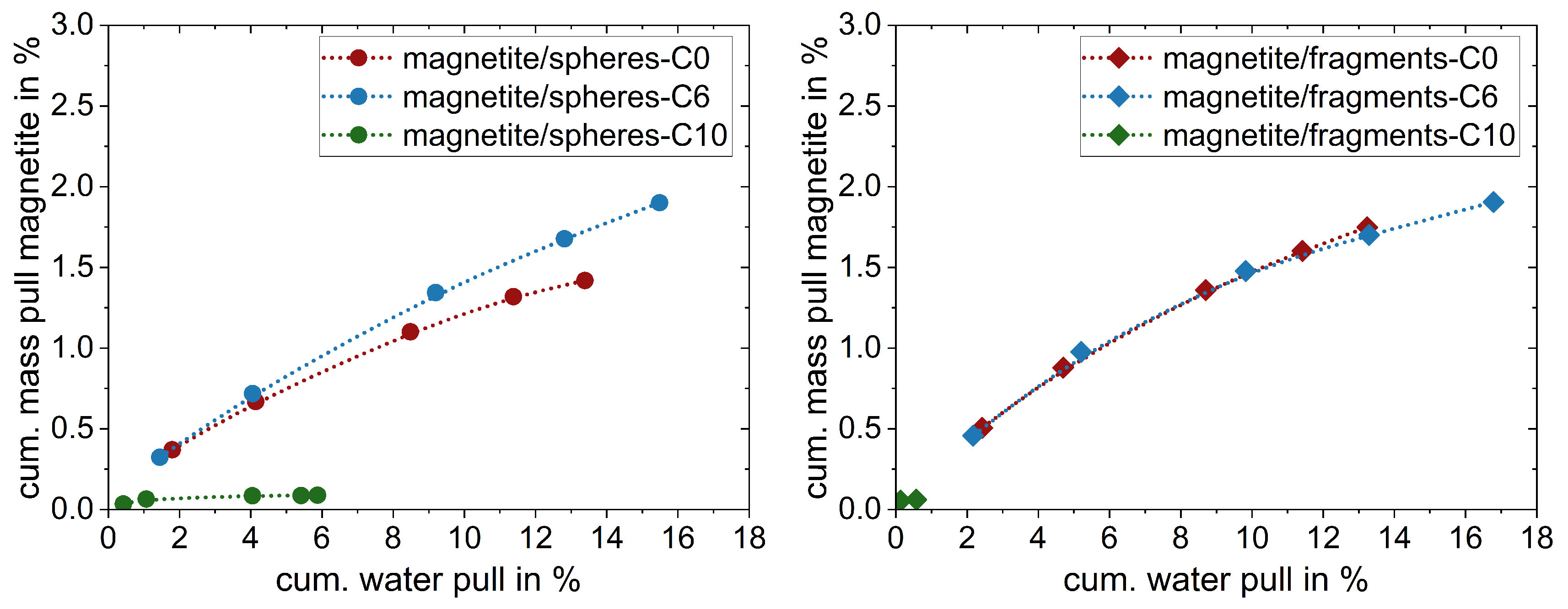
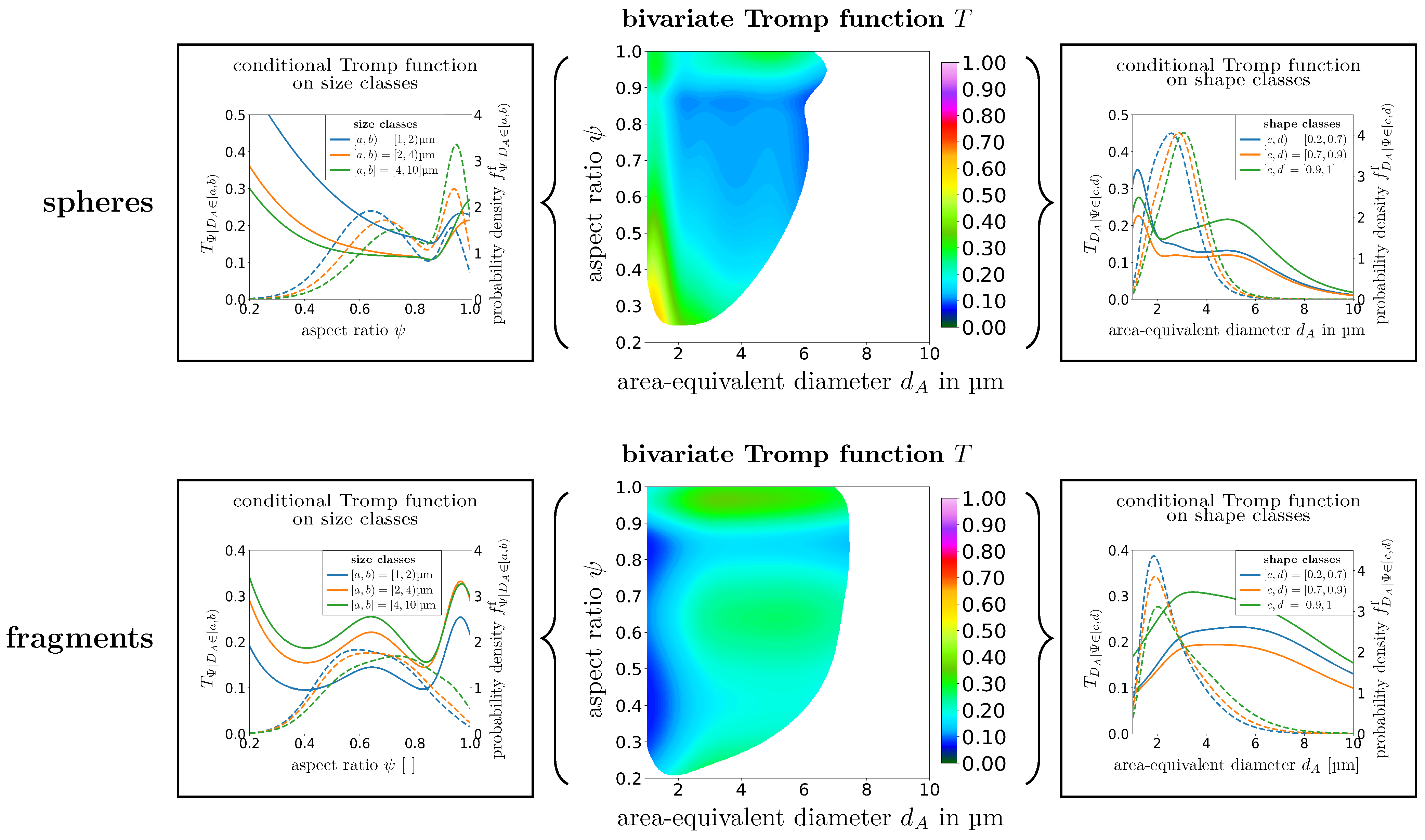
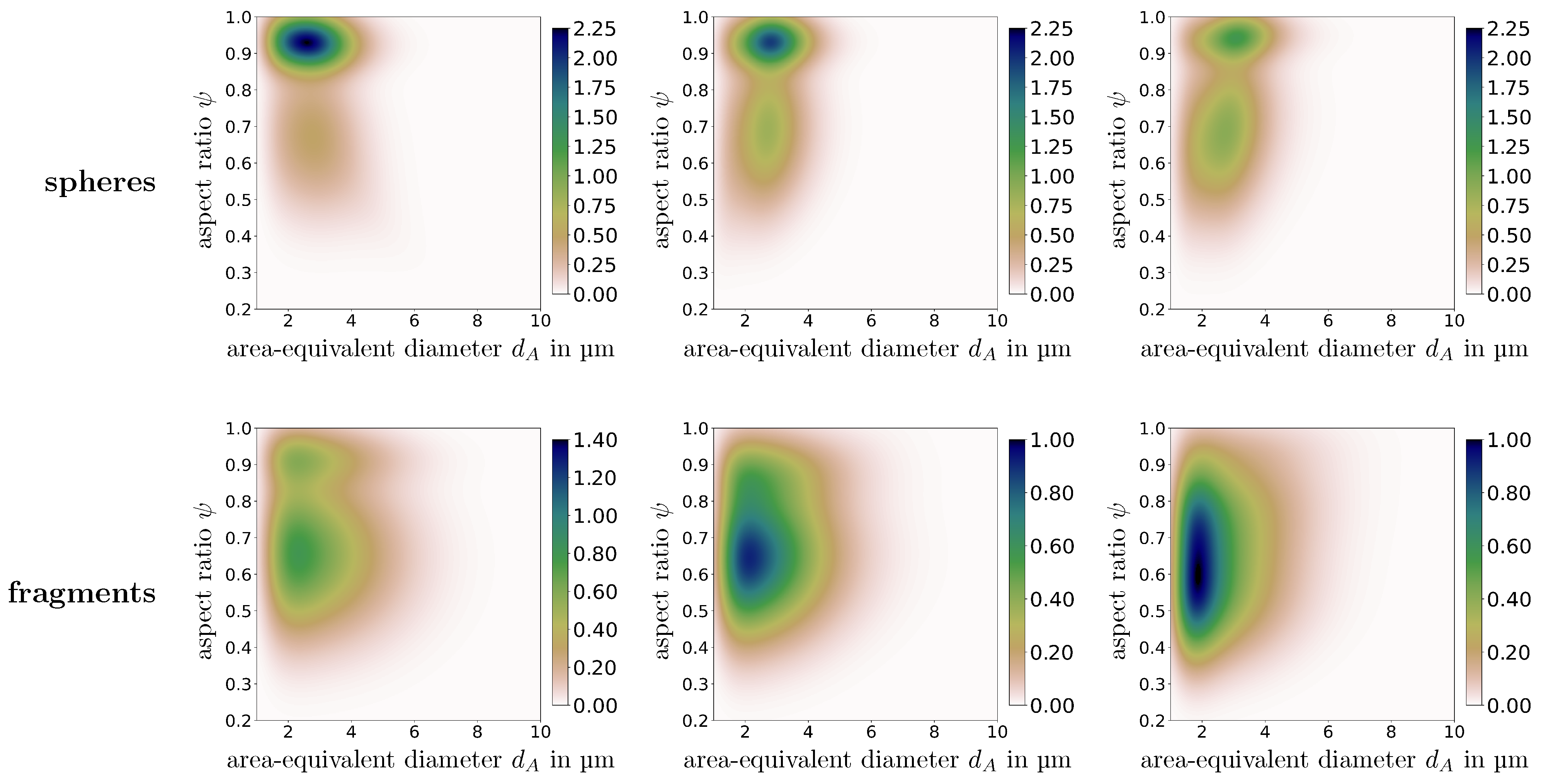
3.2. Influence of Particle Size and Shape on the Entrainment of Ultrafine Particles
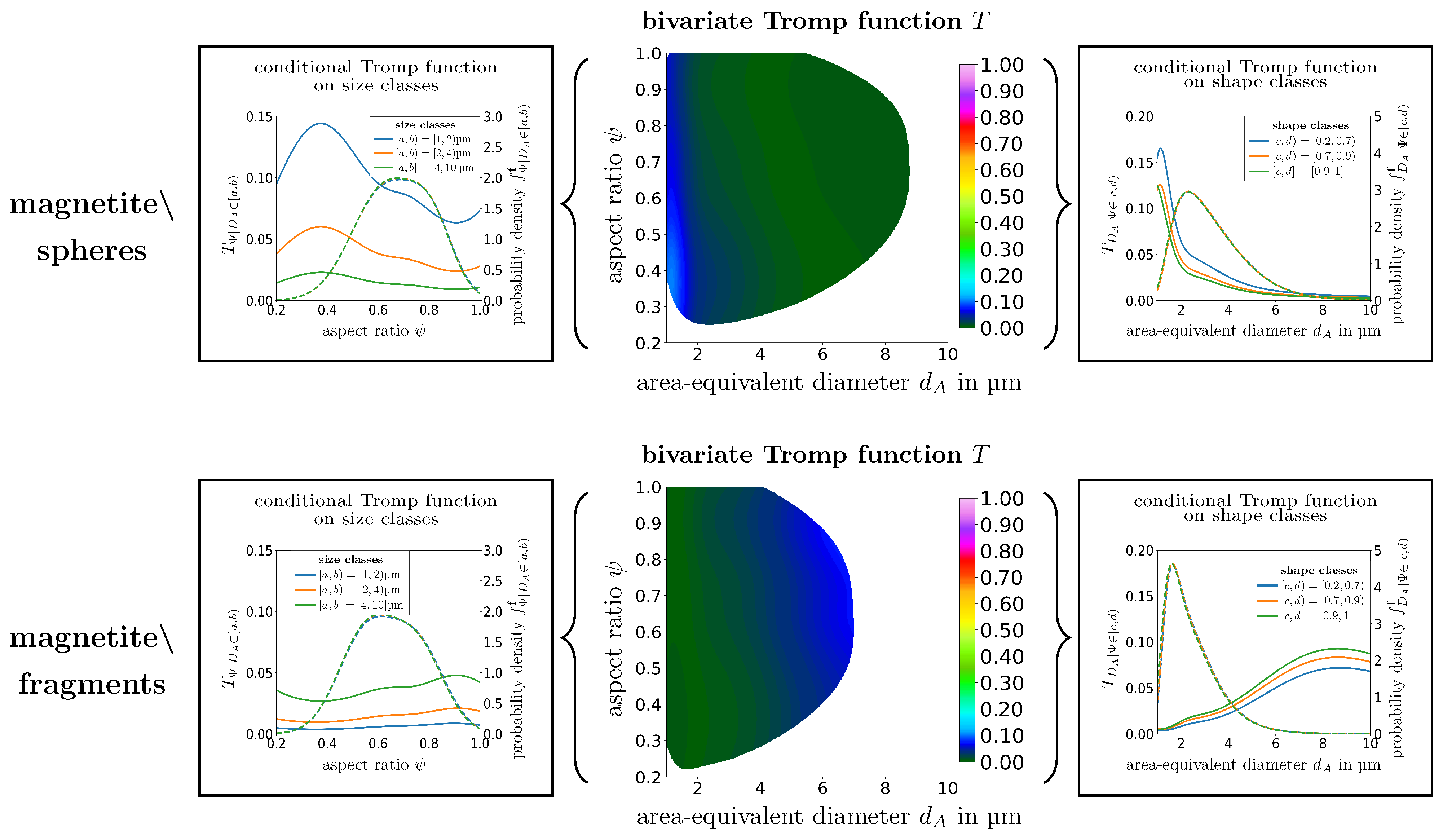
3.3. Influence of Particle Size, Shape and Wettability on the Separation Behavior of Ultrafine Particles
3.4. Usability of MLA Measurements to Determine Particle-Discrete Descriptor Vectors
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Pristine, unesterified hydrophilic particles | ||
| Hydrophobized particles using the primary alcohol 1-hexanol | ||
| Hydrophobized particles using the primary alcohol 1-decanol | ||
| m | Mass function | |
| /3 | Mass density of particles | |
| Expected volume of particles | ||
| n | Number of particles |
| W | Sampling window of image data | |
| P | Two-dimensional cross-section of a particle | |
| Area-equivalent particle diameter | ||
| Random area-equivalent particle diameter | ||
| Minimum Feret particle diameter | ||
| Maximum Feret particle diameter | ||
| A | Area | |
| B | Bounding box of a 2D particle cross-section | |
| Particle aspect ratio | ||
| Random particle aspect ratio | ||
| f | Number-weighted probability density function | |
| w | Mixing parameter of a bimodal probability density function | |
| F | Number-weighted cumulative distribution function of f | |
| Univariate number-weighted probability density function of | ||
| Univariate number-weighted probability density function of | ||
| Bivariate probability density function of and | ||
| Conditional probability density function of given | ||
| T | Tromp function | |
| Conditional Tromp function of given | ||
| Number of particles given that | ||
| Feed | ||
| Concentrate | ||
| Tailing |
Appendix A
Appendix A.1. Additional Information on Particle-Wise Segmentation
| Wettability Experiment | ||||
|---|---|---|---|---|
| Particle System | ||||
| spheres | concentrate: | 252,522 (3128) | 402,105 (3877) | 366,878 (3015) |
| tailing: | 18,223 (163) | 5715 (80) | 3114 (96) | |
| fragments | concentrate: | 299,724 (2131) | 463,711 (3017) | 139,505 (847) |
| tailing: | 12,677 (220) | 15,593 (158) | 22,623 (200) | |
| magnetite\spheres | concentrate: | 263,301 (11,831) | 137,235 (6756) | 20,252 (1102) |
| tailing: | 220,400 (3302) | 118,529 (4292) | 130,600 (4443) | |
| magnetite\fragments | concentrate: | 565,991 (8426) | 326,359 (7847) | 28,028 (896) |
| tailing: | 121,782 (4646) | 196,805 (2892) | 236,174 (3575) | |
Appendix A.2. Parametric Families of Probability Densities and Copulas Used for the Parametric Modeling Approach
| Parametric Family | Probability Density | |
|---|---|---|
| normal | ||
| log-normal | ||
| gamma | ||
| beta |
| Parametric Family | Copula Density | |
|---|---|---|
| Clayton | ||
| Frank | ||
| Gumbel | ||
| Joe |
Appendix A.3. Computation of Conditional Univariate Tromp Functions
References
- Trahar, W.J. A rational interpretation of the role of particle size in flotation. Int. J. Miner. Process. 1981, 8, 289–327. [Google Scholar] [CrossRef]
- Schubert, H. Aufbereitung fester Stoffe, Band II: Sortierprozesse; Deutscher Verlag für Grundstoffindustrie: Stuttgart, Germany, 1996. [Google Scholar]
- Wills, B.A.; Finch, J.A. Wills’ Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Butterworth-Heinemann: Boston, MA, USA, 2016. [Google Scholar]
- Trahar, W.J.; Warren, L.J. The flotability of very fine particles—A review. Int. J. Miner. Process. 1976, 3, 103–131. [Google Scholar] [CrossRef]
- Miettinen, T.; Ralston, J.; Fornasiero, D. The limits of fine particle flotation. Miner. Eng. 2010, 23, 420–437. [Google Scholar] [CrossRef]
- De Gontijo, C.F.; Fornasiero, D.; Ralston, J. The limits of fine and coarse particle flotation. J. Chem. Eng. 2007, 85, 739–747. [Google Scholar] [CrossRef]
- Konopacka, Z.; Drzymala, J. Types of particles recovery—Water recovery entrainment plots useful in flotation research. Adsorption 2010, 16, 313–320. [Google Scholar] [CrossRef]
- Leistner, T.; Peuker, U.A.; Rudolph, M. How gangue particle size can affect the recovery of ultrafine and fine particles during froth flotation. Miner. Eng. 2017, 109, 1–9. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle-bubble collision models—A review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Hao, F.P.; Smith, L.K.; Chau, T.T.; Bruckard, W.J. The effect of particle shape and hydrophobicity in flotation. Int. J. Miner. Process. 2009, 93, 128–134. [Google Scholar] [CrossRef]
- Vaziri Hassas, B.; Caliskan, H.; Guven, O.; Karakas, F.; Cinar, M.; Celik, M.S. Effect of roughness and shape factor on flotation characteristics of glass beads. Colloids Surfaces Physicochem. Eng. Asp. 2016, 492, 88–99. [Google Scholar] [CrossRef]
- Verrelli, D.I.; Bruckard, W.J.; Koh, P.T.L.; Schwarz, M.P.; Follink, B. Particle shape effects in flotation. Part 1: Microscale experimental observations. Miner. Eng. 2014, 58, 80–89. [Google Scholar] [CrossRef]
- Xia, W. Role of particle shape in the floatability of mineral particle: An overview of recent advances. Powder Technol. 2017, 317, 104–116. [Google Scholar] [CrossRef]
- Lu, S.; Pugh, R.J.; Forssberg, E. Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Chen, Y.; Zhuang, L.; Zhang, Z. Effect of particle shape on particle-bubble interaction behavior: A computational study using discrete element method. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 653, 13003. [Google Scholar] [CrossRef]
- Kursun, H.; Ulusoy, U. Influence of shape characteristics of talc mineral on the column flotation behavior. Int. J. Miner. Process. 2006, 78, 262–268. [Google Scholar] [CrossRef]
- Sygusch, J.; Stefenelli, N.; Rudolph, M. Ultrafine particle flotation in a concept flotation cell combining turbulent mixing zone and deep froth fractionation with a special focus on the property vector of particles. Minerals 2023, 13, 1099. [Google Scholar] [CrossRef]
- Little, L.; Wiese, J.; Becker, M.; Mainza, A.; Ross, V. Investigating the effects of particle shape on chromite entrainment at a platinum concentrator. Miner. Eng. 2016, 96–97, 46–52. [Google Scholar] [CrossRef]
- Kupka, N.; Tolosana-Delgado, R.; Schach, E.; Bachmann, K.; Heinig, T.; Rudolph, M. R as an environment for data mining of process mineralogy data: A case study of an industrial rougher flotation bank. Miner. Eng. 2020, 146, 106111. [Google Scholar] [CrossRef]
- Wiese, J.; Becker, M.; Yorath, G.; O’Connor, C. An investigation into the relationship between particle shape and entrainment. Miner. Eng. 2015, 83, 211–216. [Google Scholar] [CrossRef]
- Albijanic, B.; Ozdemir, O.; Nguyen, A.V.; Bradshaw, D. A review of induction and attachment times of wetting thin films between air bubbles and particles and its relevance in the separation of particles by flotation. Adv. Colloid Interface Sci. 2010, 159, 1–21. [Google Scholar] [CrossRef]
- Drelich, J.W.; Marmur, A. Meaningful contact angles in flotation systems: Critical analysis and recommendations. Surf. Innov. 2017, 6, 19–30. [Google Scholar] [CrossRef]
- Johansson, G.; Pugh, R.J. The influence of particle size and hydrophobicity on the stability of mineralized froths. Int. J. Miner. Process. 1992, 9, 1–21. [Google Scholar] [CrossRef]
- Ata, S.; Ahmed, N.; Jameson, G.J. A study of bubble coalescence in flotation froths. Int. J. Miner. Process. 2003, 72, 255–266. [Google Scholar] [CrossRef]
- Aveyard, R.; Binks, B.P.; Fletcher, P.D.I.; Peck, T.G.; Rutherford, C.E. Aspects of aqueous foam stability in the presence of hydrocarbon oils and solid particles. Adv. Colloid Interface Sci. 1994, 48, 93–120. [Google Scholar] [CrossRef]
- Dippenaar, A. The destabilization of froth by solids. I. The mechanism of film rupture. Int. J. Miner. Process. 1982, 9, 1–14. [Google Scholar] [CrossRef]
- Ata, S. Phenomena in the froth phase of flotation—A review. Int. J. Miner. Process. 2012, 102–103, 1–12. [Google Scholar] [CrossRef]
- Farrokhpay, S. The significance of froth stability in mineral flotation—A review. Adv. Colloid Interface Sci. 2011, 166, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kaptay, G. On the optimum contact angle of stability of foams by particles. Adv. Colloid Interface Sci. 2012, 170, 87–88. [Google Scholar] [CrossRef] [PubMed]
- Ata, S.; Ahmed, N.; Jameson, G.J. The effect of hydrophobicity on the drainage of gangue minerals in flotation froths. Miner. Eng. 2004, 17, 897–901. [Google Scholar] [CrossRef]
- Furat, O.; Leißner, T.; Bachmann, K.; Gutzmer, J.; Peuker, U.A.; Schmidt, V. Stochastic modeling of multidimensional particle characteristics using parametric copulas. Microsc. Microanal. 2019, 25, 720–734. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Sygusch, J.; Furat, O.; Bachmann, K.; Rudolph, M.; Schmidt, V. Parametric stochastic modeling of particle descriptor vectors for studying the influence of ultrafine particle wettability and morphology on flotation-based separation behavior. Powders 2023, 2, 353–371. [Google Scholar] [CrossRef]
- Schach, E.; Buchmann, M.; Tolosana-Delgado, R.; Leißner, T.; Kern, M.; van den Boogaart, K.G.; Rudolph, M.; Peuker, U.A. Multidimensional characterization of separation processes–Part 1: Introducing kernel methods and entropy in the context of mineral processing using SEM-based image analysis. Miner. Eng. 2019, 137, 78–86. [Google Scholar] [CrossRef]
- Leißner, T.; Bachmann, K.; Gutzmer, J.; Peuker, U.A. MLA-based partition curves for magnetic separation. Miner. Eng. 2016, 94, 94–103. [Google Scholar] [CrossRef]
- Pereira, L.; Frenzel, M.; Hoang, D.H.; Tolosana-Delgado, R.; Rudolph, M.; Gutzmer, J. Computing single-particle flotation kinetics using automated mineralogy data and machine learning. Miner. Eng. 2021, 170, 107054. [Google Scholar] [CrossRef]
- Pereira, L.; Frenzel, M.; Khodadadzadeh, M.; Tolosana-Delgado, R.; Gutzmer, J. A self-adaptive particle-tracking method for minerals processing. J. Clean. Prod. 2021, 279, 123711. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; J. Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Schubert, H. Aufbereitung Fester Mineralischer Rohstoffe, Band I; Deutscher Verlag für Grundstoffindustrie: Stuttgart, Germany, 1989. [Google Scholar]
- Sygusch, J.; Rudolph, M. A contribution to wettability and wetting characterisation of ultrafine particles with varying shape and degree of hydrophobization. Appl. Surf. Sci. 2021, 566, 150725. [Google Scholar] [CrossRef]
- Heinig, T.; Bachmann, K.; Tolosana-Delgado, R.; van den Boogaart, K.; Gutzmer, J. Monitoring gravitational and particle shape settling effects on MLA sample preparation. In Proceedings of the 17th annual conference of the International Association of Mathematical Geosciences, Freiberg, Germany, 5–13 September 2015; pp. 200–206. [Google Scholar]
- Fandrich, R.; Gu, Y.; Burrows, D.; Moeller, K. Modern SEM-based mineral liberation analysis. Int. J. Miner. Process. 2007, 84, 310–320. [Google Scholar] [CrossRef]
- Schulz, B.; Sandmann, D.; Gilbricht, S. SEM-based automated mineralogy and its application in geo- and material sciences. Minerals 2020, 10, 1004. [Google Scholar] [CrossRef]
- Bachmann, K.; Frenzel, M.; Krause, J.; Gutzmer, J. Advanced identification and quantification of in-bearing minerals by scanning electron microscope-based image analysis. Microsc. Microanal. 2017, 23, 527–537. [Google Scholar] [CrossRef]
- Roerdink, J.B.T.M.; Meijster, A. The watershed transform: Definitions, algorithms and parallelization strategies. Fundam. Informaticae 2001, 41, 187–228. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Chiu, S.N.; Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and its Applications; J. Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Furat, O.; Leissner, T.; Ditscherlein, R.; Ondřej, S.; Weber, M.; Bachmann, K.; Gutzmer, J.; Peuker, U.A.; Schmidt, V. Description of ore particles from X-Ray microtomography (XMT) images, supported by scanning electron microscope (SEM)-based image analysis. Microsc. Microanal. 2018, 24, 461–470. [Google Scholar] [CrossRef]
- VolkerH/feret_diameter.py. Available online: https://gist.github.com/VolkerH/0d07d05d5cb189b56362e8ee41882abf (accessed on 16 August 2022).
- Held, L.; Bové, D.S. Applied Statistical Inference: Likelihood and Bayes; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: Berlin/Heidelberg, Germany, 1998; pp. 199–213. [Google Scholar]
- Nelsen, R. An Introduction to Copulas; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Joe, H. Dependence Modeling with Copulas; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ditscherlein, R.; Furat, O.; de Langlard, M.; de Souza e Silva, J.M.; Sygusch, J.; Rudolph, M.; Leißner, T.; Schmidt, V.; Peuker, U.A. Multi-scale tomographic analysis for micron-sized particulate samples. Microsc. Microanal. 2020, 26, 676–688. [Google Scholar] [CrossRef]
- Frank, U.; Wawra, S.E.; Pflug, L.; Peukert, W. Multidimensional particle size distributions and their application to nonspherical particle systems in two dimensions. Part. Part. Syst. Charact. 2019, 36, 1800554. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Tolosana-Delgado, R.; Leißner, T.; Astoveza, J.; Möckel, R.; Ebert, D.; Rudolph, M.; van de Boogaart, K.G.; Peuker, U.A. Evaluation of magnetic separation efficiency on a Cassiterite-Bearing Skarn ore by means of integrative SEM-based image and XRF–XRD data analysis. Minerals 2018, 8, 390. [Google Scholar] [CrossRef]
- Kun, P., II. Fundamentals of Probability and Stochastic Processes with Applications to Communications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Szczerkowska, S.; Wiertel-Pochopien, A.; Zawala, J.; Larsen, E.; Kowalczuk, P.B. Kinetics of froth flotation of naturally hydrophobic solids with different shapes. Miner. Eng. 2018, 121, 90–99. [Google Scholar] [CrossRef]
- Rahimi, M.; Dehghani, F.; Rezai, B.; Aslani, M.R. Influence of the roughness and shape of quartz particles on their flotation kinetics. Int. J. Miner. Process. 2012, 19, 284–289. [Google Scholar] [CrossRef]
- Schwarz, S.; Grano, S. Effect of particle hydrophobicity on particle and water transport across a flotation froth. Colloids Surfaces A Physicochem. Eng. Asp. 2005, 256, 157–164. [Google Scholar] [CrossRef]
- Xu, R. Particle Characterization: Light Scattering Methods; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Merkus, H.G. Particle Size Measurements: Fundamentals, Practice, Quality; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zheng, J.; Hryciw, R. Traditional soil particle sphericity, roundness and surface roughness by computational geometry. Geotechnique 2015, 65, 494–506. [Google Scholar] [CrossRef]
- Tafesse, S.; Fernlund, J.M.R.; Sun, W.; Bergholm, F. Evaluation of image analysis methods used for quantification of particle angularity. Sedimentology 2013, 60, 1100–1110. [Google Scholar] [CrossRef]
- Stachowiak, G.W. Particle angularity and its relationship to abrasive and erosive wear. Wear 2000, 241, 214–219. [Google Scholar] [CrossRef]
- Kench, S.; Cooper, S.J. Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion. Nat. Mach. Intell. 2021, 3, 299–305. [Google Scholar] [CrossRef]
- Fuchs, L.; Kirstein, T.; Mahr, C.; Furat, O.; Baric, V.; Rosenauer, A.; Maedler, L.; Schmidt, V. Using convolutional neural networks for stereological characterization of 3D hetero-aggregates based on synthetic STEM data. arXiv 2023, arXiv:2310.18523. [Google Scholar] [CrossRef]






| Wettability Experiment | Contact Angle in ° |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sygusch, J.; Wilhelm, T.; Furat, O.; Bachmann, K.; Schmidt, V.; Rudolph, M. Application of Multivariate Tromp Functions for Evaluating the Joint Impact of Particle Size, Shape and Wettability on the Separation of Ultrafine Particles via Flotation. Powders 2024, 3, 338-366. https://doi.org/10.3390/powders3030020
Sygusch J, Wilhelm T, Furat O, Bachmann K, Schmidt V, Rudolph M. Application of Multivariate Tromp Functions for Evaluating the Joint Impact of Particle Size, Shape and Wettability on the Separation of Ultrafine Particles via Flotation. Powders. 2024; 3(3):338-366. https://doi.org/10.3390/powders3030020
Chicago/Turabian StyleSygusch, Johanna, Thomas Wilhelm, Orkun Furat, Kai Bachmann, Volker Schmidt, and Martin Rudolph. 2024. "Application of Multivariate Tromp Functions for Evaluating the Joint Impact of Particle Size, Shape and Wettability on the Separation of Ultrafine Particles via Flotation" Powders 3, no. 3: 338-366. https://doi.org/10.3390/powders3030020
APA StyleSygusch, J., Wilhelm, T., Furat, O., Bachmann, K., Schmidt, V., & Rudolph, M. (2024). Application of Multivariate Tromp Functions for Evaluating the Joint Impact of Particle Size, Shape and Wettability on the Separation of Ultrafine Particles via Flotation. Powders, 3(3), 338-366. https://doi.org/10.3390/powders3030020





