Hygroscopicity in Epoxy Powder Composites
Abstract
1. Introduction
2. Materials and Methodology
2.1. Materials
2.2. Experimental
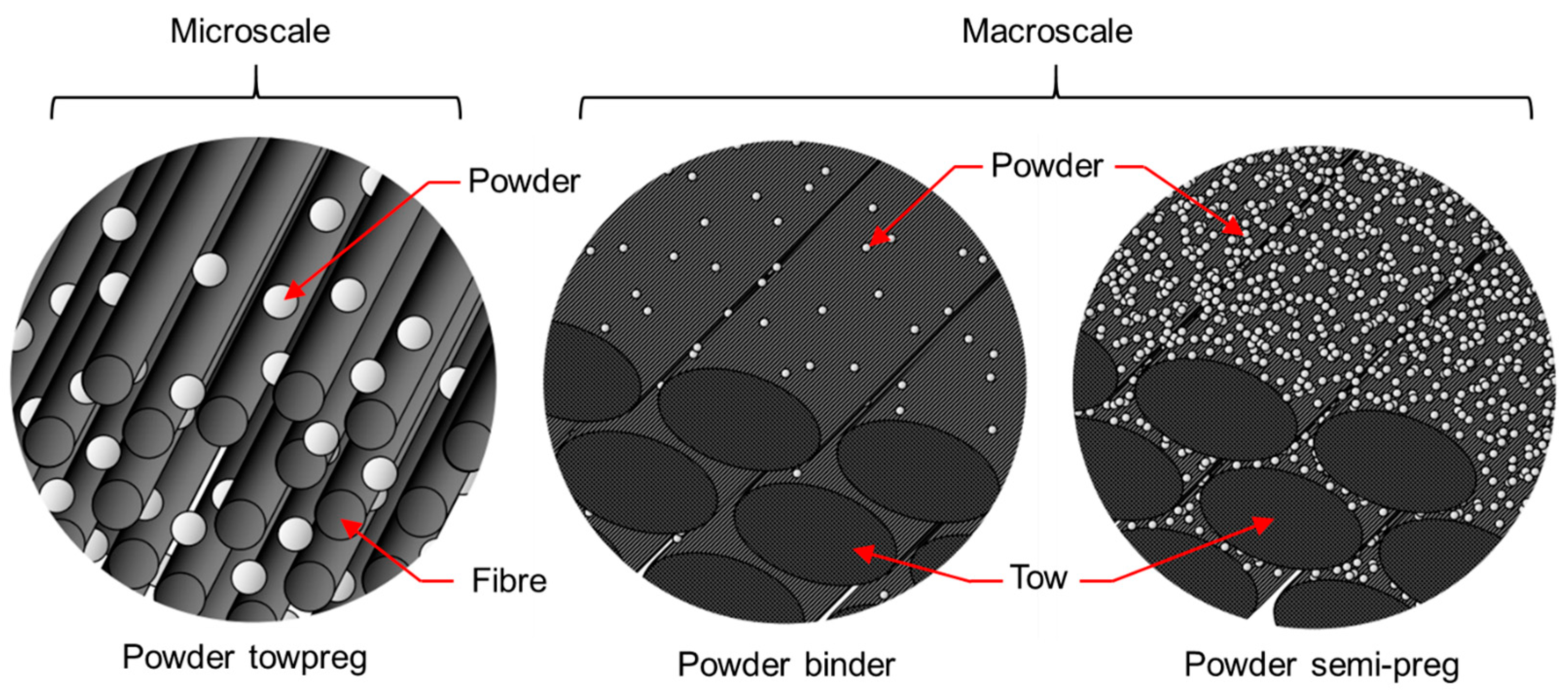
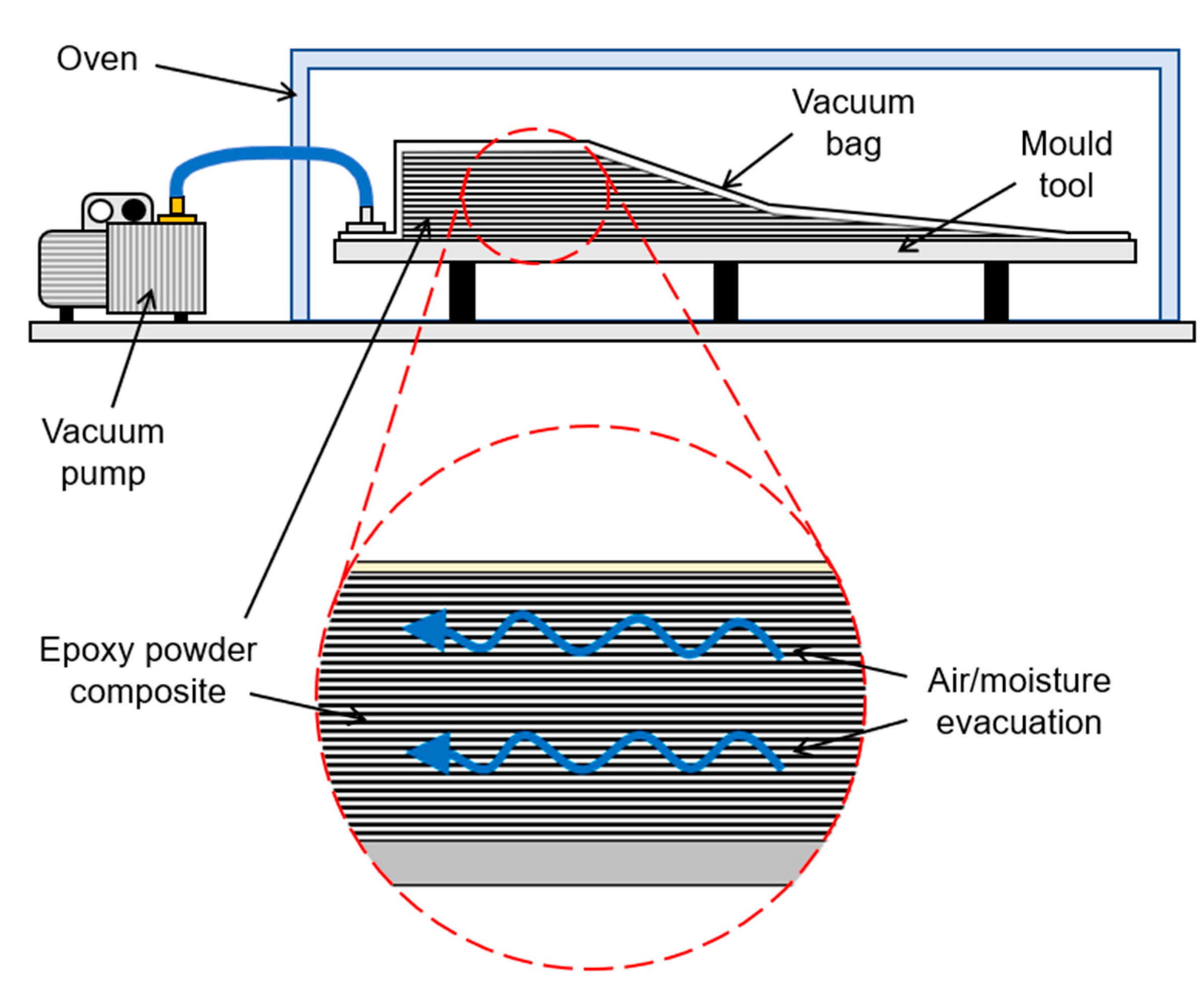
2.2.1. Composite Manufacturing
- -
- Ramp to 120 °C at 1.5 °C/min
- -
- Soak at 120 °C for 30 min
- -
- Ramp to 180 °C at 1.5 °C/min
- -
- Soak at 180 °C for 60 min.
2.2.2. Mechanical Testing
2.2.3. Void Content
2.2.4. Dynamic Vapour Sorption
- -
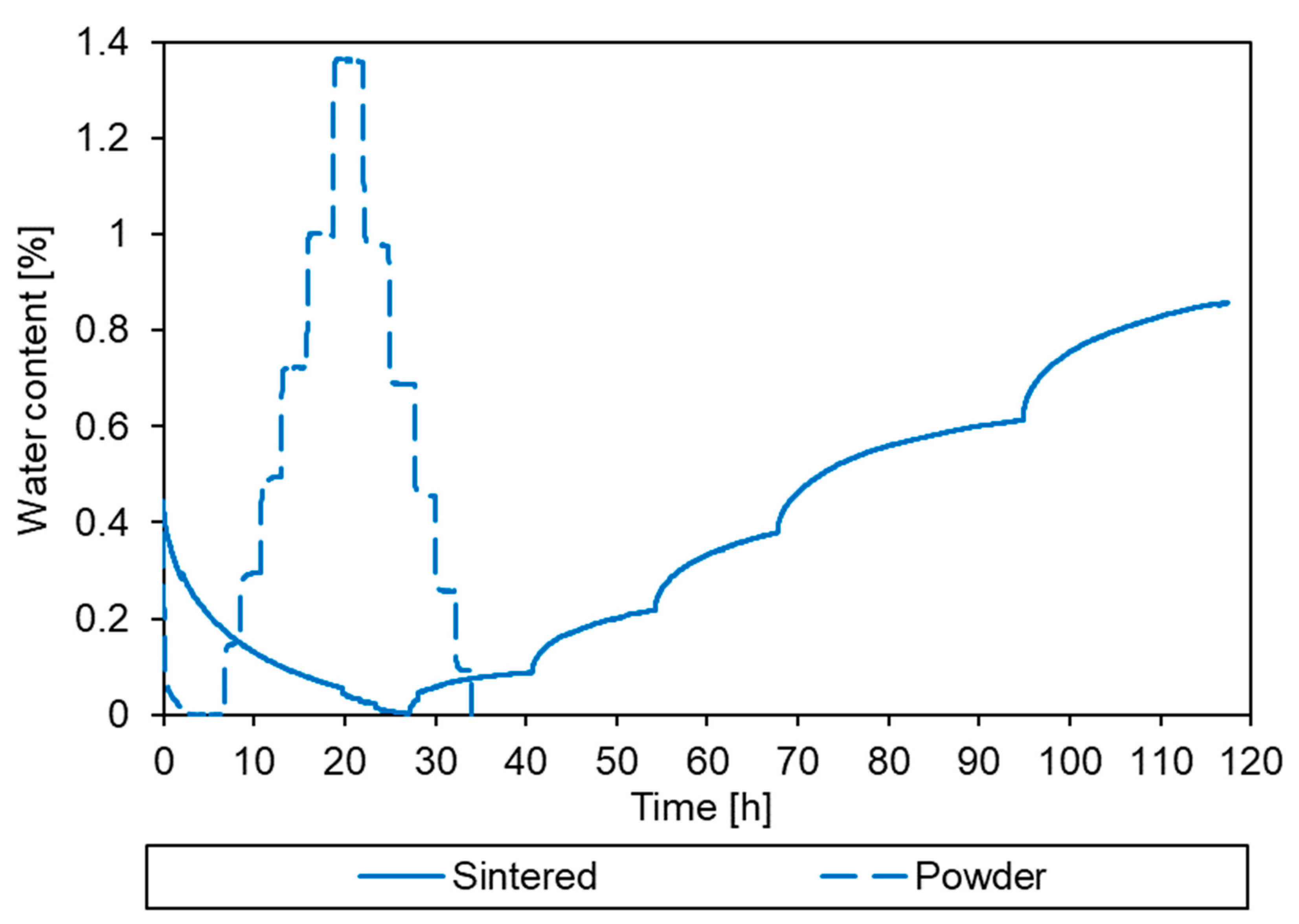
- Sintered samples—tested at 35 °C using the above procedure.
- -
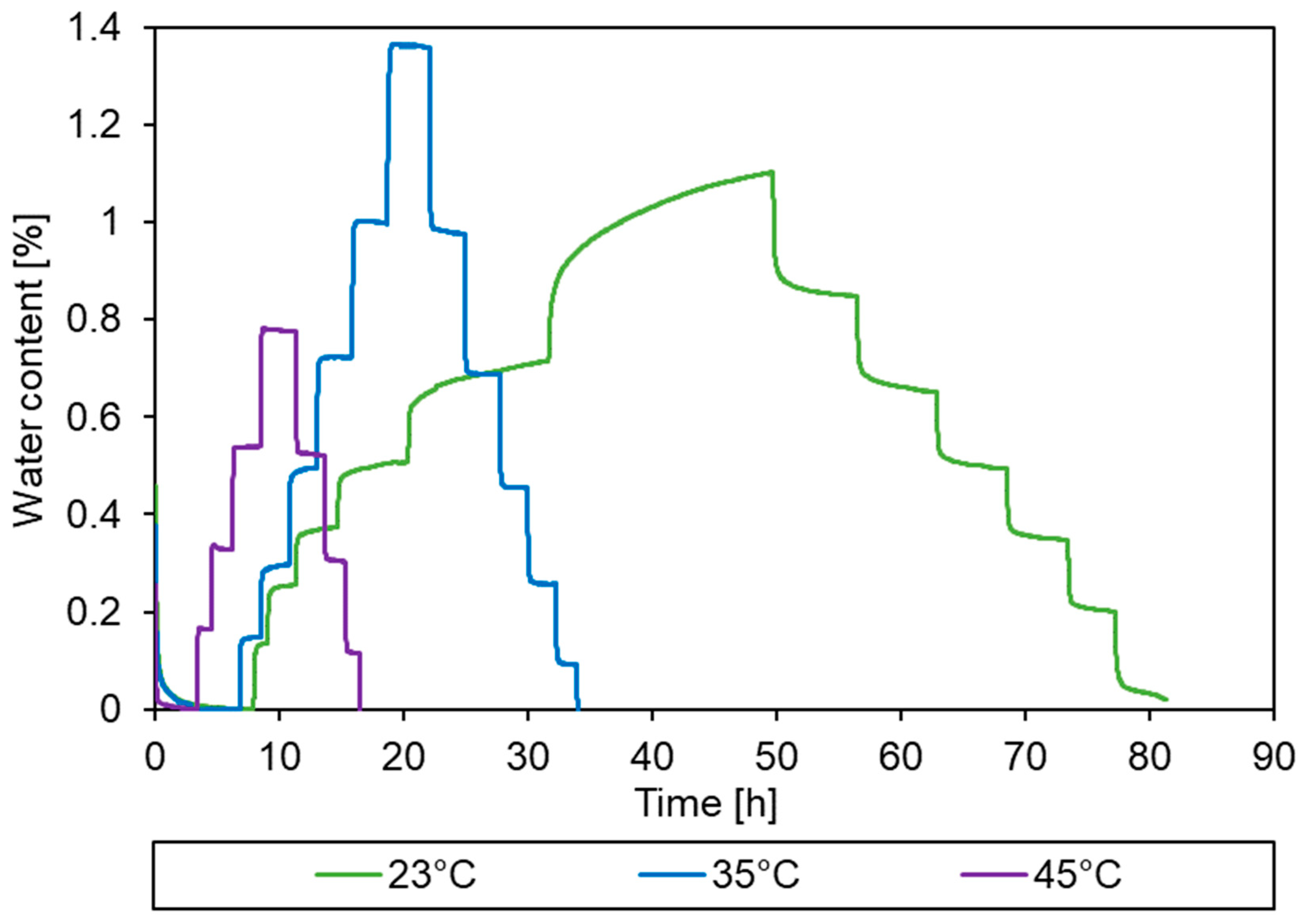
- Powder samples—tested at 45 °C and 50 °C, with the RH increasing from 1–2% to 90% in increments of approx. 1% RH every 6 min, then decreasing at the same rate.
2.3. Modelling
2.3.1. Sorption Kinetics
- Effect of temperature and isotherm non-linearity:
- If the experiment is not isothermal (e.g., due to the endothermic enthalpy of desorption), the desorption kinetics will appear to be slower due to the combined effect of shifted equilibrium and slower diffusion at lower temperatures.
- The diffusivity also depends on the shape of isotherm. If the experiment is performed over the linear part of the isotherm, the diffusivity can be assumed to be constant. Otherwise, more careful treatment is required and the Darken correction factor can be used to account for the isotherm non-linearity [45].
- is the equilibrium loading with RH at a given time. The derivation from Equation (3) to Equation (4) assumes that RH drops instantaneously to almost 0, which is not the case for DVS experiments. As described in [45], solutions have been derived for constant pressure/constant volume experiments (for an initial step change in pressure in an infinite medium/finite medium, respectively). However, a more complex analysis would be required to take into account the varying RH.
2.3.2. Process Simulations
3. Results and Discussion
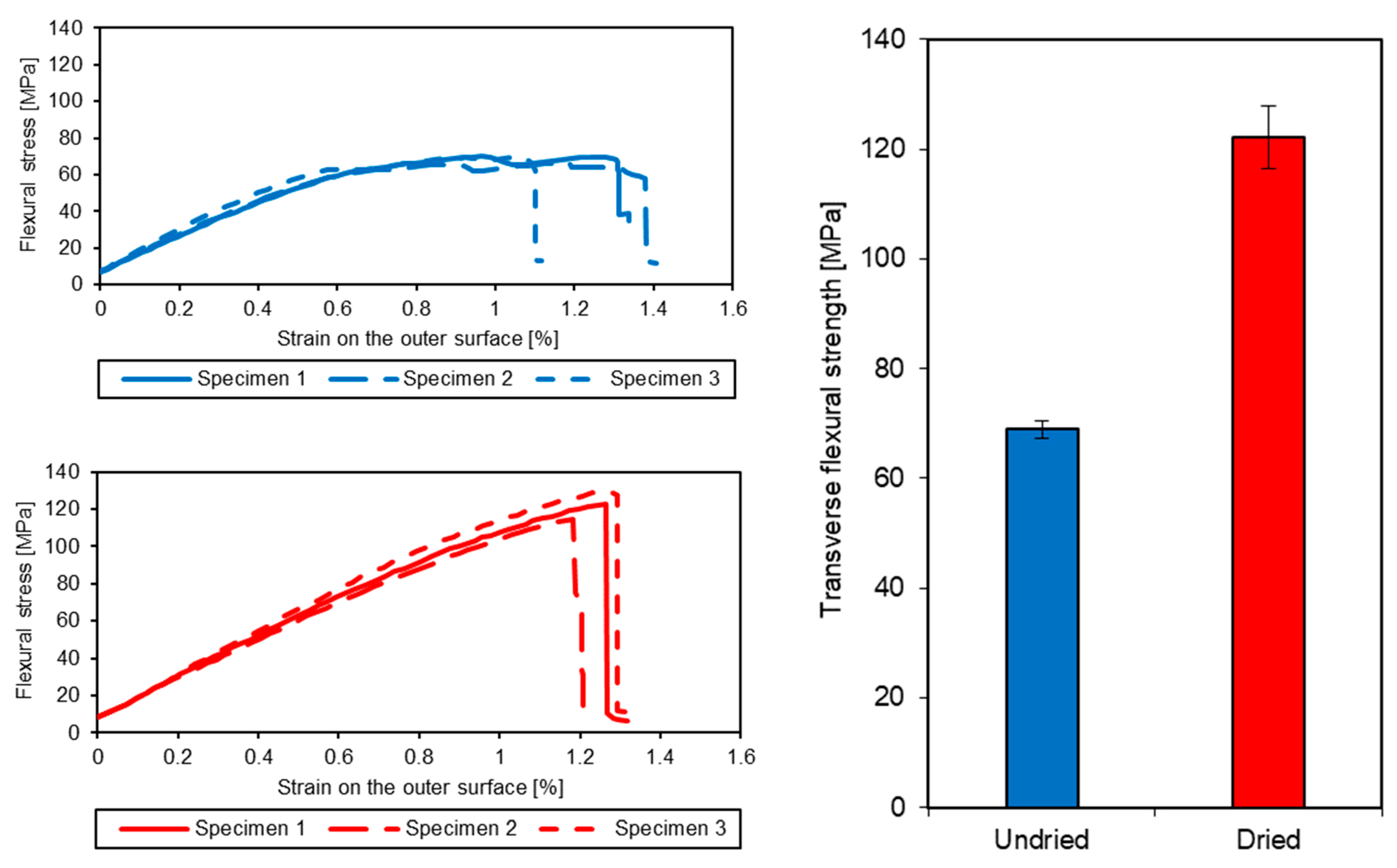
3.1. Effect of Entrapped Moisture on Epoxy Powder Composite Properties
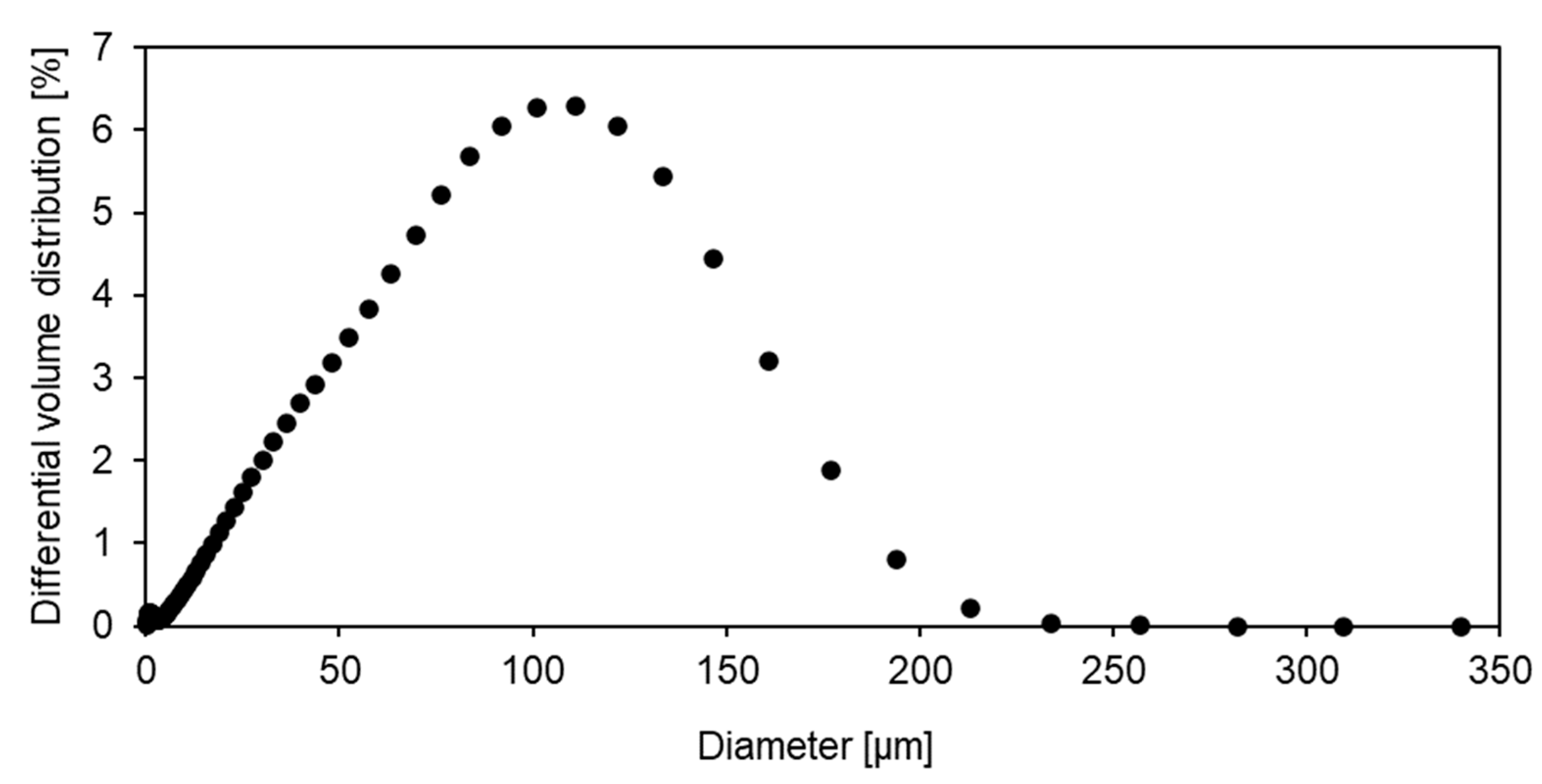
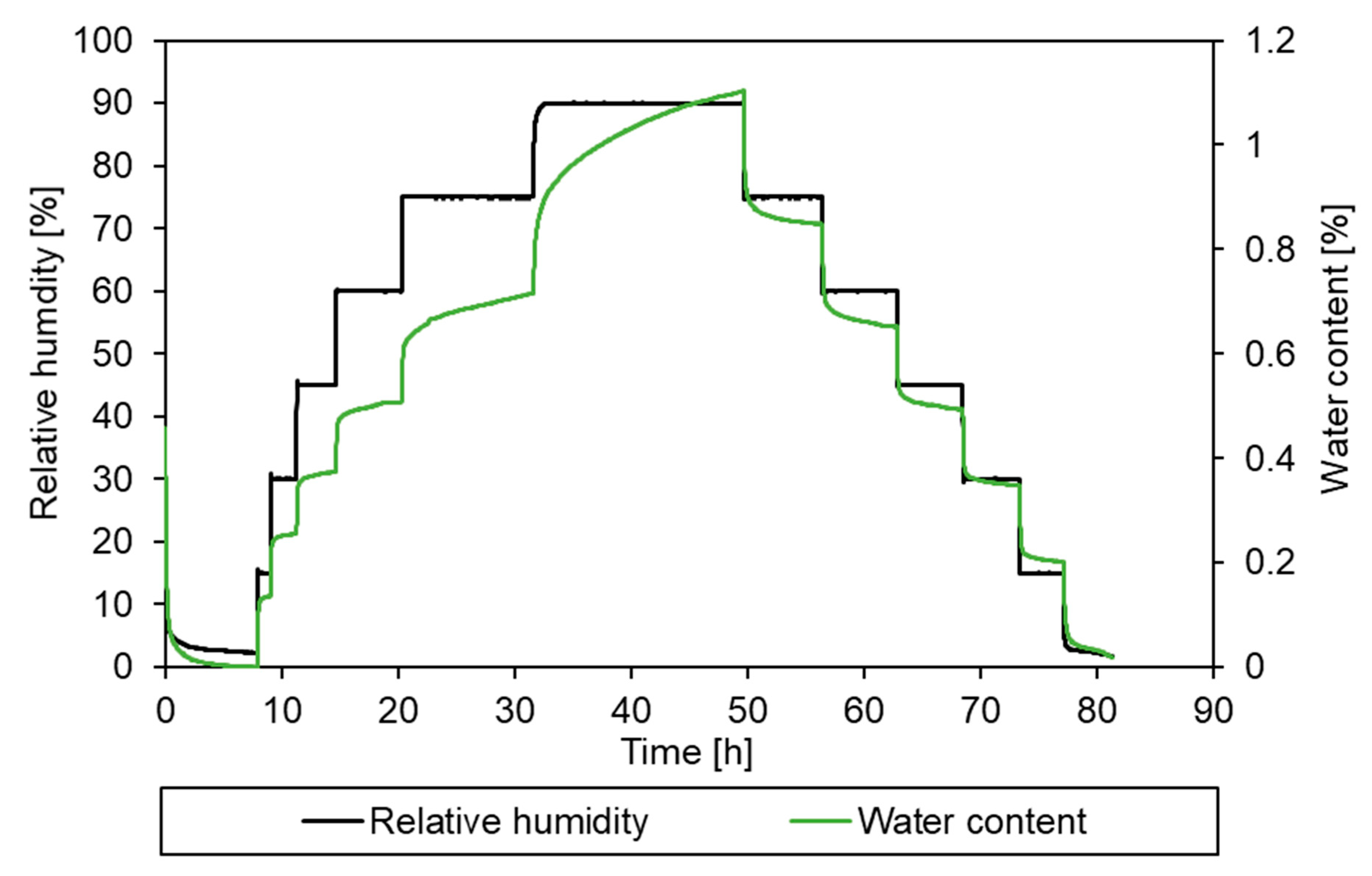
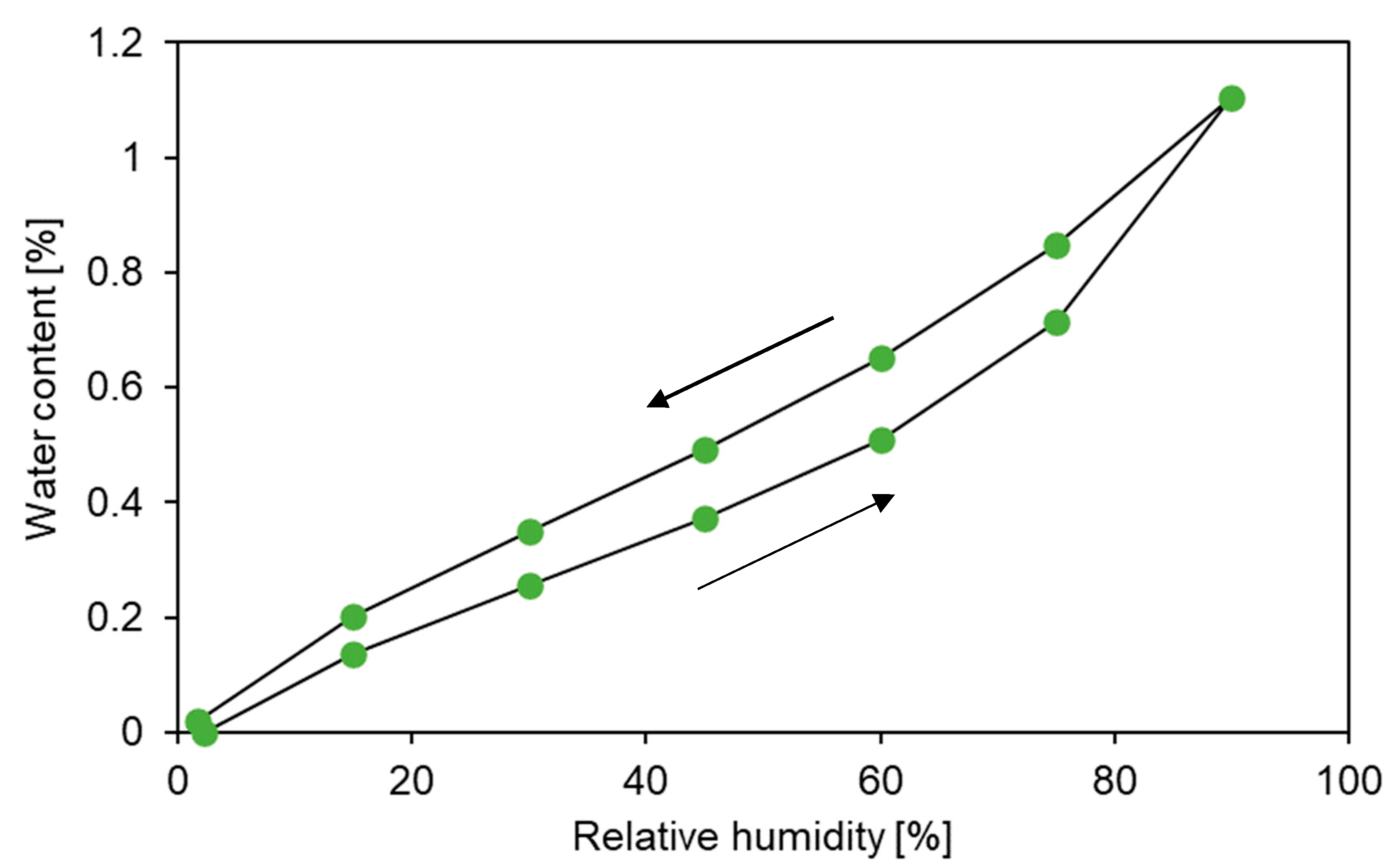
3.2. Sorption Behaviour of Epoxy Powder
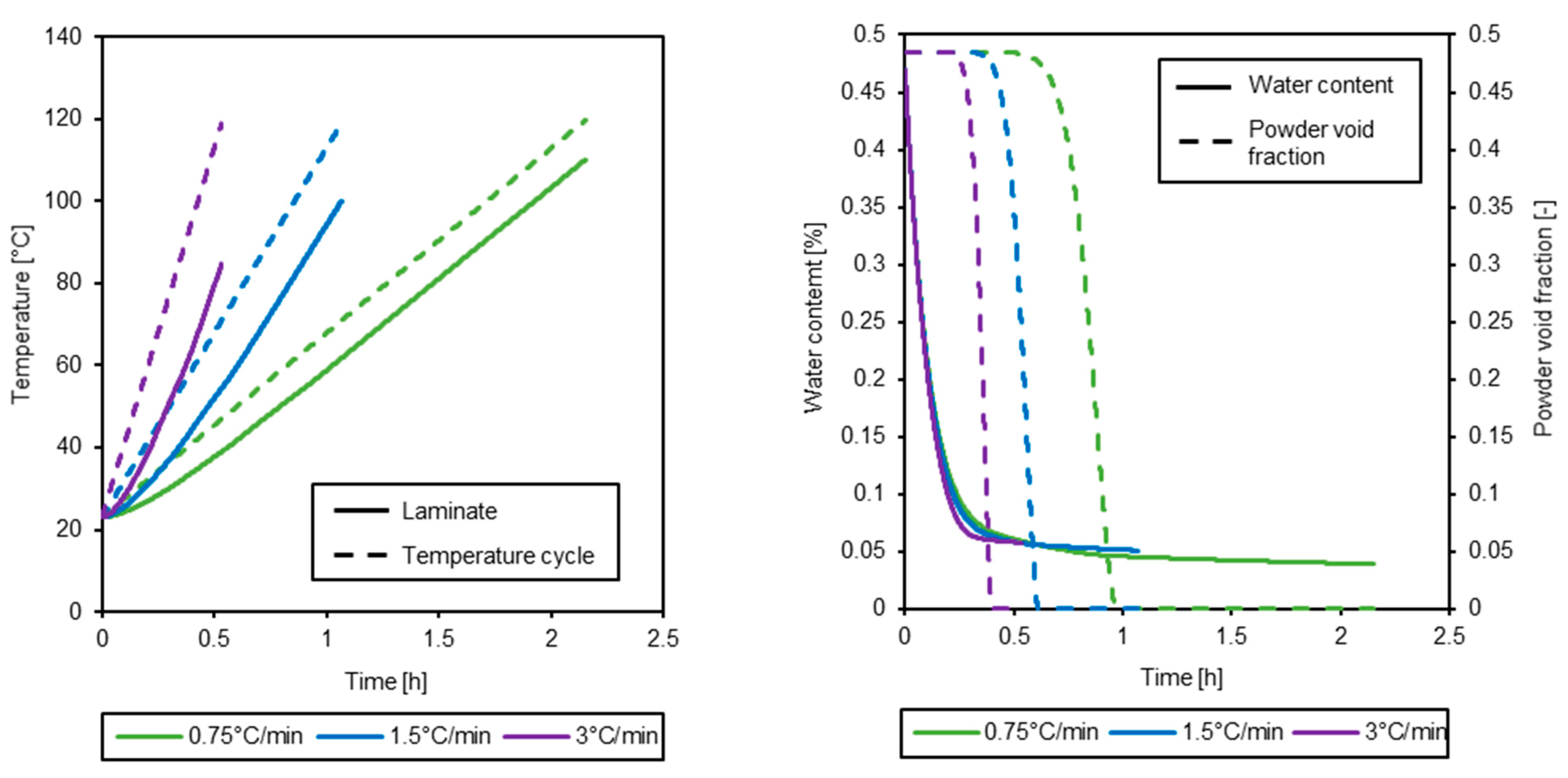
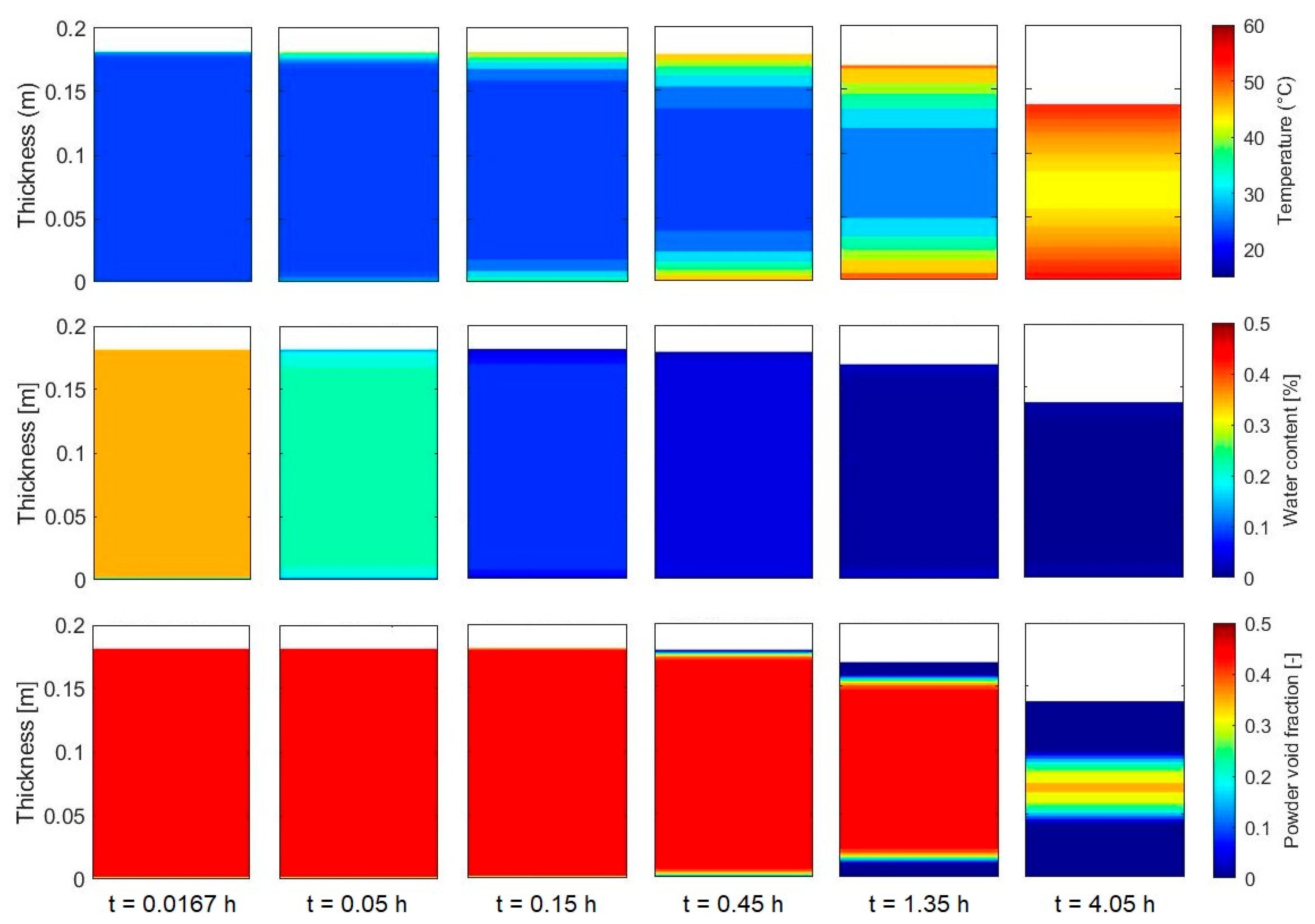
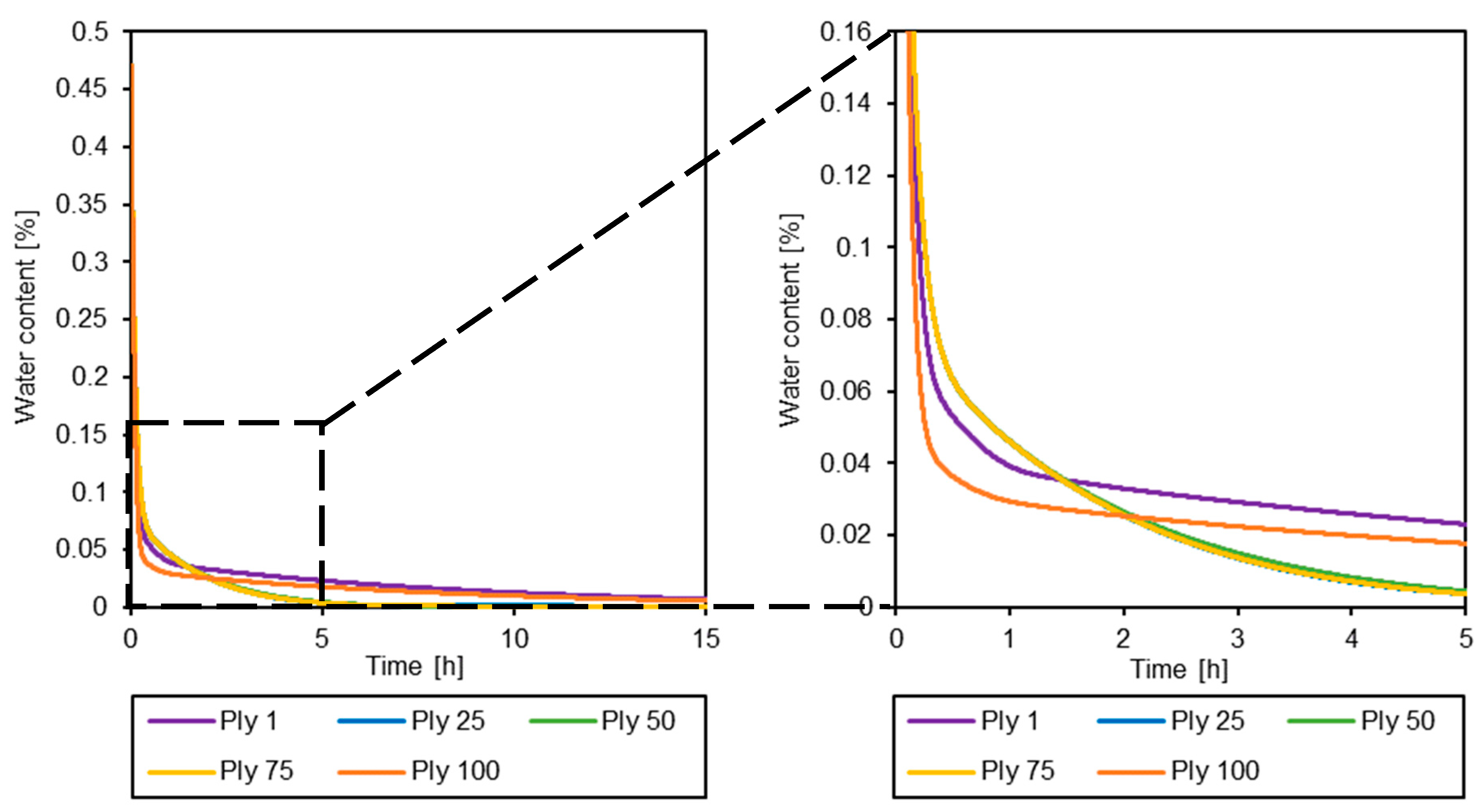
3.3. Simulation of the Drying Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, T. Boeing’s 787 Dreamliner—How Composites and Carbon Fiber Are Used. Available online: https://www.thoughtco.com/boeings-787-dreamliner-820385 (accessed on 29 December 2023).
- NES Fircroft. The Biggest Wind Turbines in the World. Available online: https://www.nesfircroft.com/resources/blog/the-biggest-wind-turbines-in-the-world/ (accessed on 29 December 2023).
- Agarwal, B.D.; Broutman, L.J.; Chandrashekhara, K. Chapter 2—Fibers, Matrices, and Fabrication of Composites. In Analysis and Performance of Fiber Composites; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 978-0-471-26891-8. [Google Scholar]
- Advani, S.G.; Hsiao, K.-T. 1—Introduction to Composites and Manufacturing Processes. In Manufacturing Techniques for Polymer Matrix Composites (PMCs); Woodhead Publishing Limited: Cambridge, UK, 2012; pp. 1–12. ISBN 9780857090676. [Google Scholar]
- Brody, J.C.; Gillespie, J.W. Reactive and Non-Reactive Binders in Glass/Vinyl Ester Composites. Polym. Compos. 2005, 26, 377–387. [Google Scholar] [CrossRef]
- Lionetto, F.; Moscatello, A.; Maffezzoli, A. Effect of Binder Powders Added to Carbon Fiber Reinforcements on the Chemoreology of an Epoxy Resin for Composites. Compos. Part B Eng. 2016, 112, 243–250. [Google Scholar] [CrossRef]
- Daelemans, L.; van der Heijden, S.; De Baere, I.; Muhammad, I.; Van Paepegem, W.; Rahier, H.; De Clerck, K. Bisphenol A Based Polyester Binder as an Effective Interlaminar Toughener. Compos. Part B Eng. 2015, 80, 145–153. [Google Scholar] [CrossRef]
- Wu, W.; Klunker, F.; Xie, L.; Jiang, B.; Ziegmann, G. Simultaneous Binding and Ex Situ Toughening Concept for Textile Reinforced PCBT Composites: Influence of Preforming Binders on Interlaminar Fracture Properties. Compos. Part A Appl. Sci. Manuf. 2013, 53, 190–203. [Google Scholar] [CrossRef]
- Schmidt, S.; Mahrholz, T.; Kühn, A.; Wierach, P. Powder Binders Used for the Manufacturing of Wind Turbine Rotor Blades. Part 2. Investigation of Binder Effects on the Mechanical Performance of Glass Fiber Reinforced Polymers. J. Compos. Mater. 2019, 53, 2261–2270. [Google Scholar] [CrossRef]
- Edie, D.; Lickfield, G.C.; Allen, L.E.; McCollum, J.R. Thermoplastic Coating of Carbon Fibres; The National Aeronautics and Space Administration Langley Research Center: Langley, VA, USA, 1989.
- Miller, A.; Wei, C.; Gibson, A.G. Manufacture of Polyphenylene Sulfide (PPS) Matrix Composites via the Powder Impregnation Route. Compos. Part A Appl. Sci. Manuf. 1996, 27, 49–56. [Google Scholar] [CrossRef]
- Allred, R.E.; Wesson, S.P.; Babow, D.A. Powder Impregnation Studies for High Temperature Towpregs. SAMPE J. 2004, 40, 40–48. [Google Scholar]
- Novo, P.J.; Silva, J.F.; Nunes, J.P.; Marques, A.T. Pultrusion of Fibre Reinforced Thermoplastic Pre-Impregnated Materials. Compos. Part B Eng. 2016, 89, 328–339. [Google Scholar] [CrossRef]
- Çelik, M.; Noble, T.; Haseeb, A.; Maguire, J.; Robert, C.; Ó Brádaigh, C.M. Contact Resistance Heating of Unidirectional Carbon Fibre Tows in a Powder-Epoxy Towpregging Line. Plast. Rubber Compos. 2022, 51, 383–392. [Google Scholar] [CrossRef]
- Mitschang, P.; Blinzler, M.; Wöginger, A. Processing Technologies for Continuous Fibre Reinforced Thermoplastics with Novel Polymer Blends. Compos. Sci. Technol. 2003, 63, 2099–2110. [Google Scholar] [CrossRef]
- Maguire, J.M.; Sharp, N.D.; Pipes, R.B.; Ó Brádaigh, C.M. Advanced Process Simulations for Thick-Section Epoxy Powder Composite Structures. Compos. Part A Appl. Sci. Manuf. 2022, 161, 107073. [Google Scholar] [CrossRef]
- Finnegan, W.; Allen, R.; Glennon, C.; Maguire, J.; Flanagan, M.; Flanagan, T. Manufacture of High-Performance Tidal Turbine Blades Using Advanced Composite Manufacturing Technologies. Appl. Compos. Mater. 2021, 28, 2061–2086. [Google Scholar] [CrossRef] [PubMed]
- Feuillerat, L.; De Almeida, O.; Fontanier, J.C.; Schmidt, F. Effect of Poly(Ether Ether Ketone) Degradation on Commingled Fabrics Consolidation. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106482. [Google Scholar] [CrossRef]
- Janzen, J.P.; May, D. Solid Epoxy Prepregs with Patterned Resin Distribution: Influence of Pattern and Process Parameters on Part Quality in Vacuum-Bag-Only Processing. Polym. Compos. 2023, 44, 8153–8167. [Google Scholar] [CrossRef]
- Çelik, M.; Maguire, J.M.; Noble, T.; Robert, C.; Ó Brádaigh, C.M. Numerical and Experimental Investigation of Joule Heating in a Carbon Fibre Powder Epoxy Towpregging Line. Compos. Part A Appl. Sci. Manuf. 2023, 164, 107285. [Google Scholar] [CrossRef]
- Asensio, M.; Esfandiari, P.; Núñez, K.; Silva, J.F.; Marques, A.; Merino, J.C.; Pastor, J.M. Processing of Pre-Impregnated Thermoplastic Towpreg Reinforced by Continuous Glass Fibre and Recycled PET by Pultrusion. Compos. Part B Eng. 2020, 200, 108365. [Google Scholar] [CrossRef]
- Ramasamy, A.; Wang, Y.; Muzzy, J. Braided Thermoplastic Composites from Powder-Coated Towpregs. Part I: Towpreg Characterization. Polym. Compos. 1996, 17, 497–504. [Google Scholar] [CrossRef]
- Gruber, M.B.; Lockwood, I.Z.; Dolan, T.L.; Funck, S.B.; Tierney, J.; Simacek, P.; Gillespie, J.; Advani, S.G.; Jensen, B.J.; Cano, R.J.; et al. Thermoplastic in Situ Placement Requires Better Impregnated Tapes and Tows. In Proceedings of the International SAMPE Technical Conference, Baltimore, MD, USA, 21–24 May 2012. [Google Scholar]
- Grunenfelder, L.K.; Nutt, S.R. Prepreg Age Monitoring via Differential Scanning Calorimetry. J. Reinf. Plast. Compos. 2012, 31, 295–302. [Google Scholar] [CrossRef]
- Grunenfelder, L.K.; Centea, T.; Hubert, P.; Nutt, S.R. Effect of Room-Temperature out-Time on Tow Impregnation in an out-of-Autoclave Prepreg. Compos. Part A Appl. Sci. Manuf. 2013, 45, 119–126. [Google Scholar] [CrossRef]
- Maguire, J.M.; Nayak, K.; Ó Brádaigh, C.M. Characterisation of Epoxy Powders for Processing Thick-Section Composite Structures. Mater. Des. 2018, 139, 112–121. [Google Scholar] [CrossRef]
- Floreani, C.; Cuthill, F.; Steynor, J.; Maguire, J.M.; McCarthy, E.D.; Niessink, M.J.; Di Noi, S.; Wittevrongel, L.; Flanagan, T.; Ó Brádaigh, C.M.; et al. Testing of a 6 m Hybrid Glass/Carbon Fibre Powder Epoxy Composite Wind Blade Demonstrator. SAMPE J. 2021, 57, 6–14. [Google Scholar]
- Kratz, J.; Hubert, P. Anisotropic Air Permeability in Out-of-Autoclave Prepregs: Effect on Honeycomb Panel Evacuation Prior to Cure. Compos. Part A Appl. Sci. Manuf. 2013, 49, 179–191. [Google Scholar] [CrossRef]
- Kourkoutsaki, T.; Comas-Cardona, S.; Binetruy, C.; Upadhyay, R.K.; Hinterhoelzl, R. The Impact of Air Evacuation on the Impregnation Time of Out-of-Autoclave Prepregs. Compos. Part A Appl. Sci. Manuf. 2015, 79, 30–42. [Google Scholar] [CrossRef]
- Zhang, D.; Heider, D.; Gillespie, J.W. Void Reduction of High-Performance Thermoplastic Composites via Oven Vacuum Bag Processing. J. Compos. Mater. 2017, 51, 4219–4230. [Google Scholar] [CrossRef]
- Sequeira Tavares, S.; Michaud, V.; Månson, J.-A. Through Thickness Air Permeability of Prepregs during Cure. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1587–1596. [Google Scholar] [CrossRef]
- Grunenfelder, L.K.; Dills, A.; Centea, T.; Nutt, S. Effect of Prepreg Format on Defect Control in Out-of-Autoclave Processing. Compos. Part A Appl. Sci. Manuf. 2017, 93, 88–99. [Google Scholar] [CrossRef]
- Schechter, S.G.K.; Centea, T.; Nutt, S. Effects of Resin Distribution Patterns on Through-Thickness Air Removal in Vacuum-Bag-Only Prepregs. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105723. [Google Scholar] [CrossRef]
- Schechter, S.G.K.; Grunenfelder, L.K.; Nutt, S.R. Air Evacuation and Resin Impregnation in Semi-Pregs: Effects of Feature Dimensions. Adv. Manuf. Polym. Compos. Sci. 2020, 6, 101–114. [Google Scholar] [CrossRef]
- Grunenfelder, L.K.; Nutt, S.R. Void Formation in Composite Prepregs—Effect of Dissolved Moisture. Compos. Sci. Technol. 2010, 70, 2304–2309. [Google Scholar] [CrossRef]
- Allada, R.; Maruthapillai, A.; Palanisamy, K.; Chappa, P. Hygroscopicity Categorization of Pharmaceutical Solids by Gravimetric Sorption Analysis: A Systematic Approach. Asian J. Pharm. 2016, 10, 279–286. [Google Scholar]
- Mohan, J.; Ivanković, A.; Murphy, N. Effect of Prepreg Storage Humidity on the Mixed-Mode Fracture Toughness of a Co-Cured Composite Joint. Compos. Part A Appl. Sci. Manuf. 2013, 45, 23–34. [Google Scholar] [CrossRef]
- Agius, S.L.; Magniez, K.J.C.; Fox, B.L. Cure Behaviour and Void Development within Rapidly Cured Out-of-Autoclave Composites. Compos. Part B Eng. 2013, 47, 230–237. [Google Scholar] [CrossRef]
- Sharp, N.; Li, C.; Strachan, A.; Adams, D.; Pipes, R.B. Effects of Water on Epoxy Cure Kinetics and Glass Transition Temperature Utilizing Molecular Dynamics Simulations. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 1150–1159. [Google Scholar] [CrossRef]
- Kim, D.; Centea, T.; Nutt, S.R. Modelling and Monitoring of Out-Time and Moisture Absorption Effects on Cure Kinetics and Viscosity for an out-of-Autoclave (OoA) Prepreg. Compos. Sci. Technol. 2017, 138, 201–208. [Google Scholar] [CrossRef]
- Netzel, C.; Hoffmann, D.; Battley, M.; Hubert, P.; Bickerton, S. Effects of Environmental Conditions on Uncured Prepreg Characteristics and Their Effects on Defect Generation during Autoclave Processing. Compos. Part A Appl. Sci. Manuf. 2021, 151, 106636. [Google Scholar] [CrossRef]
- Toribio, F.; Bellat, J.P.; Nguyen, P.H.; Dupont, M. Adsorption of Water Vapor by Poly(Styrenesulfonic Acid), Sodium Salt: Isothermal and Isobaric Adsorption Equilibria. J. Colloid Interface Sci. 2004, 280, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Padaki, S.; Drzal, L.T. A Simulation Study on the Effects of Particle Size on the Consolidation of Polymer Powder Impregnated Tapes. Compos. Part A Appl. Sci. Manuf. 1999, 30, 325–337. [Google Scholar] [CrossRef]
- Maguire, J.M.; Nayak, K.; Ó Brádaigh, C.M. Novel Epoxy Powder for Manufacturing Thick-Section Composite Parts under Vacuum-Bag-Only Conditions. Part II: Experimental Validation and Process Investigations. Compos. Part A Appl. Sci. Manuf. 2020, 136, 105970. [Google Scholar] [CrossRef]
- Sircar, S.; Hufton, J.R. Why Does the Linear Driving Force Model for Adsorption Kinetics Work? Adsorption 2000, 6, 137–147. [Google Scholar] [CrossRef]
- Maguire, J.M.; Simacek, P.; Advani, S.G.; Ó Brádaigh, C.M. Novel Epoxy Powder for Manufacturing Thick-Section Composite Parts under Vacuum-Bag-Only Conditions. Part I: Through-Thickness Process Modelling. Compos. Part A Appl. Sci. Manuf. 2020, 136, 105969. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Gorbatikh, L.; Verpoest, I.; Lomov, S.V. Voids in Fiber-Reinforced Polymer Composites: A Review on Their Formation, Characteristics, and Effects on Mechanical Performance. J. Compos. Mater. 2019, 53, 1579–1669. [Google Scholar] [CrossRef]
- Patou, J.; Bonnaire, R.; De Luycker, E.; Bernhart, G. Influence of Consolidation Process on Voids and Mechanical Properties of Powdered and Commingled Carbon/PPS Laminates. Compos. Part A Appl. Sci. Manuf. 2019, 117, 260–275. [Google Scholar] [CrossRef]
- Yuan, X.; Carter, B.P.; Schmidt, S.J. Determining the Critical Relative Humidity at Which the Glassy to Rubbery Transition Occurs in Polydextrose Using an Automatic Water Vapor Sorption Instrument. J. Food Sci. 2011, 76, E78–E89. [Google Scholar] [CrossRef] [PubMed]
- Hasrin, H.; Noble, T.; Kamarudin, A.; Ó Brádaigh, C.M.; Robert, C. Powder Epoxy Towpreg Consolidation Using Compaction Roller System. In Proceedings of the SAMPE Europe Conference, Madrid, Spain, 3–5 October 2023. [Google Scholar]
- Burnett, D.J.; Thielmann, F.; Booth, J. Determining the Critical Relative Humidity for Moisture-Induced Phase Transitions. Int. J. Pharm. 2004, 287, 123–133. [Google Scholar] [CrossRef]
- Greco, A.; Maffezzoli, A. Polymer Melting and Polymer Powder Sintering by Thermal Analysis. J. Therm. Anal. Calorim. 2003, 72, 1167–1174. [Google Scholar] [CrossRef]
- Maguire, J.M. Processing of Thick Section Epoxy Powder Composite Structures. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2019. [Google Scholar]
- Centea, T.; Grunenfelder, L.K.; Nutt, S.R. A Review of Out-of-Autoclave Prepregs—Material Properties, Process Phenomena, and Manufacturing Considerations. Compos. Part A Appl. Sci. Manuf. 2015, 70, 132–154. [Google Scholar] [CrossRef]







| Parameter [Units] | Value |
|---|---|
| [h] | 0.170 |
| [h−1] | 4.937 |
| [°C−1] | 0.030 |
| [h−1] | 4.580 |
| [°C−1] | 0.031 |
| Laminate | Fibre Volume Fraction [%] | Void Content [%] |
|---|---|---|
| Undried | 47.7 | 4.80 |
| Dried | 48.1 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maguire, J.M.; Wang, J.-Y.; Ó Brádaigh, C.M. Hygroscopicity in Epoxy Powder Composites. Powders 2024, 3, 168-189. https://doi.org/10.3390/powders3020011
Maguire JM, Wang J-Y, Ó Brádaigh CM. Hygroscopicity in Epoxy Powder Composites. Powders. 2024; 3(2):168-189. https://doi.org/10.3390/powders3020011
Chicago/Turabian StyleMaguire, James M., Jin-Yu Wang, and Conchúr M. Ó Brádaigh. 2024. "Hygroscopicity in Epoxy Powder Composites" Powders 3, no. 2: 168-189. https://doi.org/10.3390/powders3020011
APA StyleMaguire, J. M., Wang, J.-Y., & Ó Brádaigh, C. M. (2024). Hygroscopicity in Epoxy Powder Composites. Powders, 3(2), 168-189. https://doi.org/10.3390/powders3020011







