New Die-Compaction Equations for Powders as a Result of Known Equations Correction: Part 2—Modernization of M Yu Balshin’s Equations

Abstract

Based on the generalization of M. Yu. Balshin’s well-known equations in the framework of a discrete model of powder compaction process (PCP), two new die-compaction equations for powders have been derived that show the dependence of the compaction pressure p on the relative density ρ of the powder sample. The first equation, $p=\frac{w}{{(1-{\rho }_0)}^{(n-m)}}·\frac{{(\rho -{\rho }_0)}^n}{{(1-\rho )}^m}$, contains, in addition to the initial density ρ₀ of the powder in die, three constant parameters—w, n and m. The second equation in the form $p=\frac{H}{{\left(1-{\rho }_0\right)}^{\left(b-c\right)}}·\frac{{\left(\rho -{\rho }_0\right)}^b}{\left[{\left(1-{\rho }_0\right)}^c-a{\left(\rho -{\rho }_0\right)}^c\right]}$ also takes into account the initial density of the powder and contains four constant parameters H, a, b, and c. The values of the constant parameters in both equations are determined by fitting the theoretical curve according to these equations to the experimental powder compaction curve. The adequacy of the PCP description with these equations has been verified by approximating experimental data on the compaction of various powders, including usual metal powders such as iron, copper, and nickel, highly plastic powders such as tin and lead, a mixture of plastic powder (Ni) with non-plastic powder (Al₂O₃), nickel-plated alumina powder, as well as powder of a brittle compound, in particular titanium carbide TiC. The proposed equations make it possible to describe PCP with high accuracy, at which the coefficient of determination R² reaches values from 0.9900 to 0.9999. The four-constant equation provides a very accurate description of PCP from start to finish when the density of the samples stops increasing once the pressure increases to an extremely high level, despite the presence of porosity.

1. Introduction

In Part 1 of this article [1], the frequently used equations for describing PCP in a rigid die are considered, analyzed, and, in some cases, refined. They were proposed mainly in the form of mathematical functions for an adequate description of PCP as well as in the form of semi-empirical equations. A peculiarity of the mathematical dependencies is that, in most cases, the parameters of such equations, determined from the experiment, are not related to the properties of the powders, and their physical meaning is hidden. Some physical parameters of the powder material are taken into account in the semi-empirical equations, for example, the yield strength and the strengthening law, the forces of internal and external friction of the powders, as well as such physical phenomena as the rearrangement of particles and their plastic deformation. In this regard, of increased interest are the equations obtained as a result of using an approach that initially takes into account the properties of particles, the shape of particles, the features of their interaction, and other physical processes. Such an approach, in contrast to the search for mathematical functions, can be designated as “discrete”, since it considers the features of interaction during the compaction of a large number of individual particles and operates with average statistical characteristics and values. One of the pioneers of the “discrete” approach was the famous Soviet scientist M. Yu. Balshin.

2. Correction of the Balshin’s Equations

2.1. Correction of One of the Main Equations

The main statements and results on the compaction of powders are presented by M. Balshin in his last two books [2,3]. According to M. Balshin, PCP in a rigid die consists of three different stages that cannot be described by a single equation. Therefore, in the general case, each stage requires its own equation, and so he proposed such equations [2]. One of them describes PCP as consisting of two stages—the first and second or the second and third. Here, the general statement for all stages is that the external pressure during powder compaction is equal to the product of the contact pressure p_k by the dimensionless contact section α:

$$p=p_k\times \alpha .$$

(1)

It is known that when compacting plastic powders, their plastic deformation occurs, and as a result, the particle material is strengthened. Therefore, the contact pressure p_k increases during compaction. To take into account the strengthening of particles during PCP, M. Balshin refined Equation (1) and wrote it as:

$$p={\left(p_k\right)}_{eff}\times \alpha \times f$$

(2)

where (p_k)_eff is the effective contact pressure that does not change under powder compaction during the first two stages (up to ρ = 0.9–0.95) and is equal to the Brinell hardness of the non-hardened powder material if the annealed powder is used; α is the contact section, which is a function of the relative density, and f is the strengthening coefficient, which also depends on the density.

M. Balshin proposed the following dependence of the contact cross-section α on the relative density ρ [4]:

$$\alpha ={\rho }^2\left(\frac{∆\rho }{{\theta }_0}\right)={\rho }^2\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)$$

(3)

where ρ and ρ₀ are the current and initial relative densities, θ₀ = 1 − ρ₀ is the initial porosity.

As for the strengthening coefficient, M. Balshin [3] proposed three options for the dependence f on the contact section α, but we will use one of them (since they do not differ significantly) presented in the form:

$$f=\frac{1}{\left(1-\frac{2}{3}\alpha \right)}$$

(4)

After substituting Equation (3) into Equation (4), we obtain the dependence of the strengthening coefficient f on the relative density ρ:

$$f={\left(1-\frac{2}{3}{\rho }^2\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)\right)}^{-1}$$

(5)

A feature of such strengthening coefficients is that, with a relative density equal to 1.0, they have a final value equal to 3. That is, Balshin’s strengthening coefficient provides a finite value of the compaction pressure of plastic powders pressed to a compact state. However, most of the known equations for describing PCP show that as the relative density approaches 1.0, the compaction pressure tends to infinity. M. Balshin did not foresee such a change in the compaction pressure. However, it is quite evident that as the porosity approaches zero, the possibility for plastic deformation of the particles disappears. In this case, the absence of plastic deformation is mathematically expressed through an infinite pressure during PCP.

Based on this fact, it can be suggested that the real strengthening coefficient should take into account not only strain strengthening but also strengthening associated with increasing difficulty in deformation with decreasing porosity, that is, with constraining plastic deformation. When compacting the powder in a rigid die, the particles experience an increasing degree of deformation constraint with decreasing porosity (or with increasing density). The strengthening coefficient, which takes into account two types of strengthening, namely due to the amount of deformation and due to the degree of constraint of deformation, is unambiguously related to the change in porosity. Let us denote such a coefficient by the symbol $\overline{\beta }$ and offer the following generalized dependence of this new strengthening coefficient on porosity or relative density:

$$\overline{\beta }=\frac{1}{{\theta }^{\overline{m}}}=\frac{1}{{(1-\rho )}^{\overline{m}}}$$

(6)

where the exponent $\overline{m}$ reflects the intensity of the change in the degree of constraint with decreasing porosity and must be greater than zero.

The limits of change in the strengthening coefficient $\overline{\beta }$ based on Formula (6), are 1.0 (when there is no constraint and strain strengthening, that is, at a relative density equal to zero) and infinity (when the porosity is zero and there is no possibility of plastic deformation for the powder particle material). However, when compacting powders, it is necessary to consider that there is no strain strengthening and constraint in the presence of an initial relative density equal to ρ₀. Thus, it is more correct to use the strengthening coefficient β (without a dash), which takes into account the initial density of the powder in the die and has the following form:

$$\beta ={\left(\frac{1-{\rho }_0}{1-\rho }\right)}^m$$

(7)

where m is the intensity indicator of the change in the strengthening coefficient during the compaction of the powder from the initial relative density to ρ = 1.

It is important to note that dependence (7) makes it possible to use the strengthening coefficient with sufficiently different strengthening laws in comparison with dependence (5), as shown in Figure 1. Therefore, it is likely that the exponent m is able to take into account not only the degree of constraint of plastic deformation but also the degree of strain strengthening.

Furthermore, it is possible to correct the dependence of the contact section α on the relative density offered by M. Balshin according to Equation (3) and to write it in the form:

$$\alpha ={\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^n$$

(8)

In accordance with this dependence, the contact cross-section α = 0 at an initial density equal to ρ_0, and α = 1 at a relative density equal to 1.0. In this case, the exponent n stands for the possibility of changing the contact cross-section with a change in the relative density along significantly different curves that reflect the effect of various shapes and sizes of powder particles on the contact cross-section.

With the proposed formulas for the dependence of the contact section and the strengthening coefficient on the relative density, along with an assumption that the parameter (p_k)_eff, which we denote as w, is constant throughout the entire PCP, the dependence of the compaction pressure on the relative density represented by Equation (2) acquires a different look:

$$p=w·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^n·{\left(\frac{1-{\rho }_0}{1-\rho }\right)}^m=\frac{w}{{(1-{\rho }_0)}^{(n-m)}}·\frac{{(\rho -{\rho }_0)}^n}{{(1-\rho )}^m}$$

(9)

where w, n, and m are constant parameters not known in advance and determined by fitting the theoretical curve according to this equation to the corresponding experimental curve.

The dimension of parameter w corresponds to that of pressure, i.e., MPa, or the dimension of specific energy, J/cm³. Therefore, in the first approximation, the physical meaning of this constant may be associated with the specific energy spent on the plastic deformation of the powder during compaction, whereas the physical meanings of the constants n and m are associated with the intensity of the changes in the contact cross-section and the strengthening coefficient, respectively, during PCP in a rigid die.

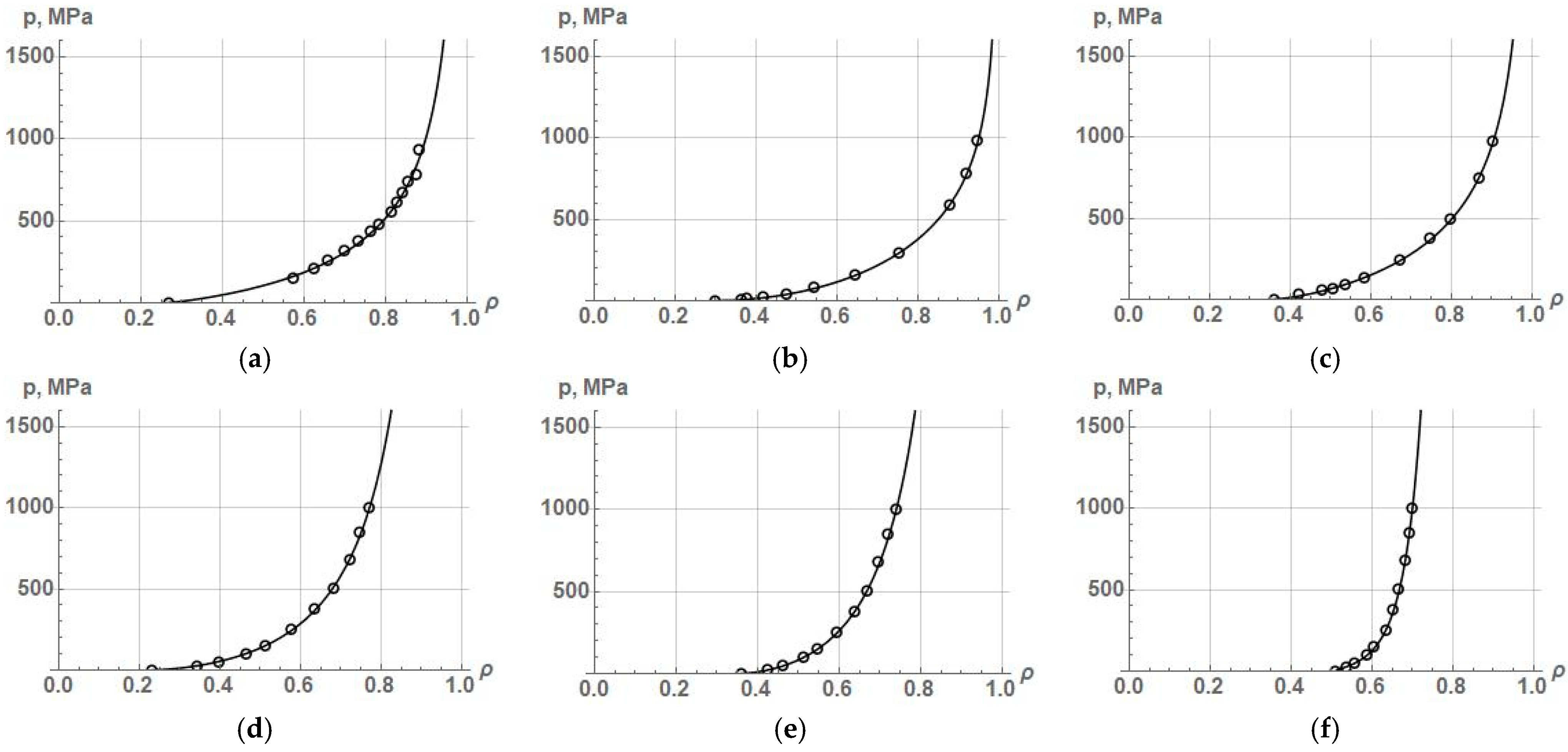
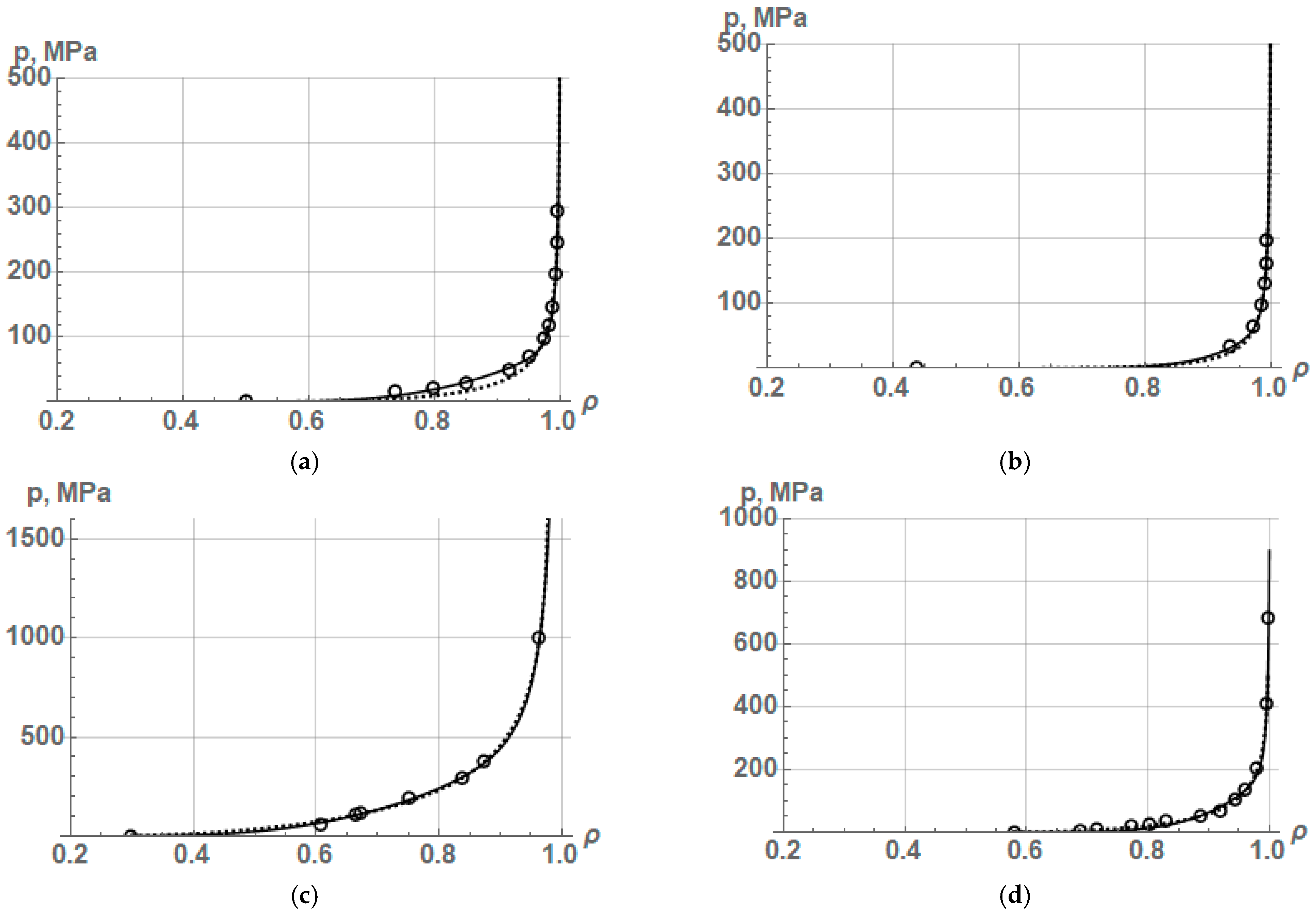
The proposed equation has three constant parameters, which allows it to describe PCP for various powders and, in many cases, with a fairly high accuracy. Let us show this with examples of approximation with Equation (9) of the experimental data on the compaction of various powders. To begin, of interest is the ability of Equation (9) to describe the compaction process of iron, copper, and nickel powders from [5,6,7], respectively, which we used in article [1], as well as nickel powder, an equivolume mixture of nickel powder with oxide aluminum, and powder of Al₂O₃ plated with 15.1 mass% Ni. The values of the experimental points of relative density and the corresponding compaction pressure during densification of Ni, Ni + 50 vol.% Al₂O₃, Al₂O₃ + 15.1 wt.% Ni powders were obtained by digitizing the points on the graphs from ([8] Figures 6 and 7), and they are shown in

Table 1. Experimental values of relative density ρ at various densification pressures for three different powders, taken from [8] via digitizing the graphs.

Powders	Densification Pressure, p, MPa
	0	25	50	100	150	250	375	500	675	850	1000
Ni	0.234	0.344	0.4	0.466	0.514	0.577	0.6345	0.682	0.724	0.747	0.772
Ni-50Al2O3	0.361	0.425	0.464	0.515	0.549	0.595	0.638	0.67	0.698	0.722	0.741
Al2O3-15.1Ni	0.512	0.537	0.558	0.589	0.607	0.637	0.653	0.666	0.682	0.694	0.699

.

The approximation results of the compaction process of these powders are shown in Figure 2, and the values of constant parameters and coefficient R² are listed in

Table 2. Values of the constants w, n, m, and coefficient R² obtained through approximation by Equation (9) the experimental data on the compaction of iron [5], copper [6], and nickel [7] powders, as well as nickel powder, an equivolume mixture of Ni and Al₂O₃ powders, and aluminum oxide coated with nickel taken from [8].

Parameters	Powders
	Fe [5]	Cu [6]	Ni [7]	Ni [8]	Ni-50 vol% Al2O3 [8]	Al2O3-15.1 mass% Ni [8]
ρ0	0.268	0.3	0.36	0.234	0.361	0.512
w, (MPa)	309.37	458.48	436.38	390.77	557.38	106.50
n	1.1730	1.8683	1.3527	1.4964	1.5044	0.5785
m	0.6819	0.3453	0.5394	1.2147	1.5179	5.7128
R2	0.99333	0.99985	0.99977	0.99896	0.99964	0.99853

.

The approximation results show high accuracy of the description by Equation (9) of the compaction process of both plastic powders and a mixture of plastic powder with non-plastic aluminum oxide powder, as well as even non-plastic Al₂O₃ coated with a small amount of nickel. In this regard, the possibility of the new equation to describe PCP of brittle powders, for example, titanium carbide from [9] and highly plastic powders, for example, tin, lead, and annealed copper from [10], and lead from [6], as well as stainless steel Kh18N15 with a particle size of less than 60 µm from [11] is also of interest. The results of the approximation of these powders by Equation (9) are shown in Figure 3, and the values of the constant parameters and R² are given in

Table 3. Values of constant parameters and coefficient of determination R² obtained through approximation by Equation (9) of the experimental data on compaction of powders of titanium carbide [9], tin, lead, and annealed copper [10], as well as lead from [6], and stainless steel Kh18N15 powders from [11].

Parameters	Powders
	TiC [9]	Sn [10]	Pb [10]	Cu [10]	Pb [6]	Kh18N15 [11]
ρ0	0.37	0.501	0.439	0.3	0.58	0.281
w (MPa)	382.5	21.71	8.547	180.79	74.02	865.34
n	2.5556	0.9015	0.9983	1.5169	2.711	1.6938
m	2.8268	0.5081	0.6666	0.6028	0.3687	0.3779
R2	0.99761	0.99768	0.99919	0.99946	0.99916	0.99969

.

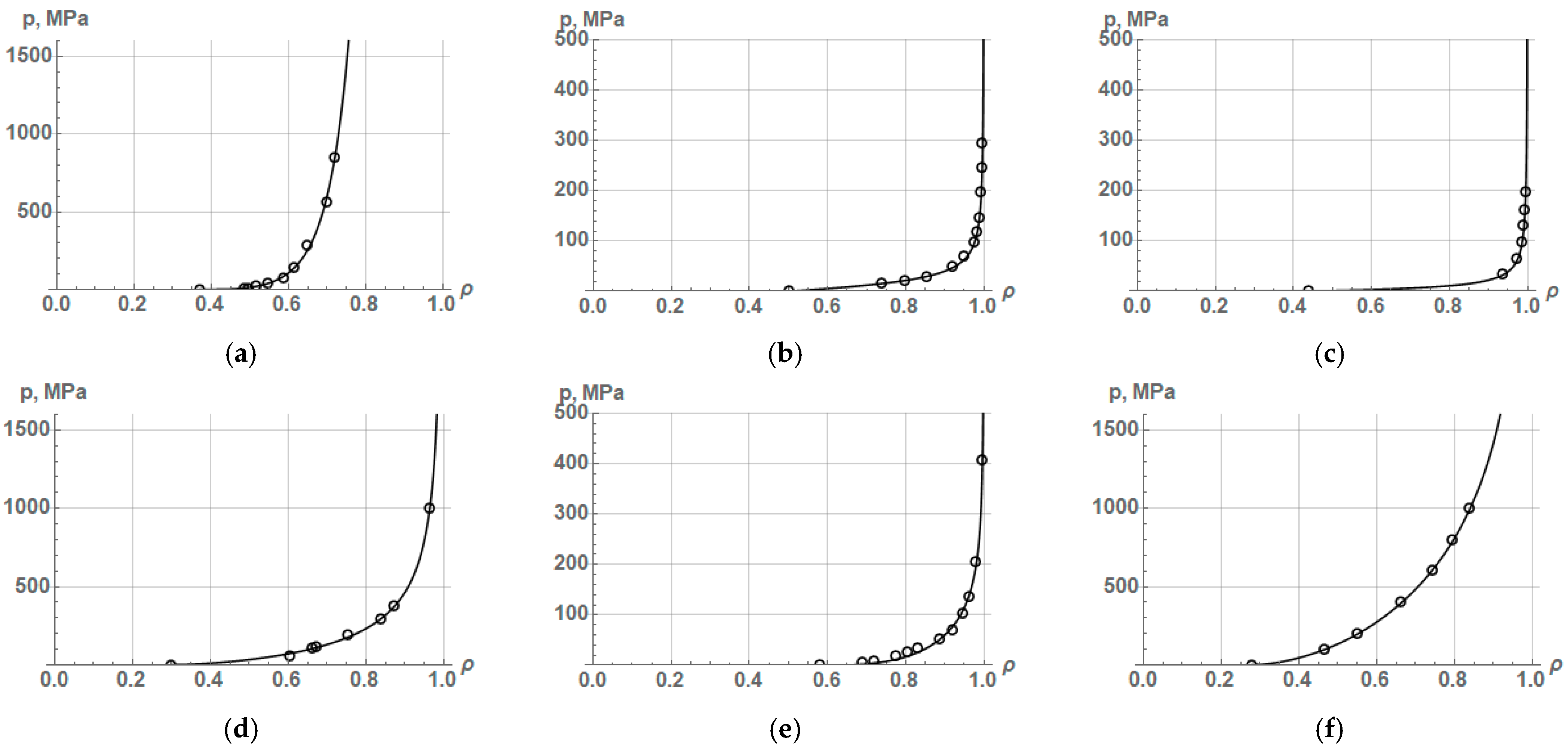
The approximation results by Equation (9) of both brittle and highly plastic powders confirm the possibility of describing the process of their compaction with high accuracy. At the same time, a question arises about the ability of Equation (9) to describe with high accuracy the compaction process for powders that cannot be compacted to a dense state even under very high pressures. Experimental data on the compaction of such powders are available in the book [12], which presents the results of compaction of iron powders of various origins under increasing compaction pressure up to 3000 MPa. It is reasonable to present these unique experimental data, which can be used to control the results of approximation by various equations and perform other calculations. Therefore, we present in

Table 4. Experimental data on the compaction of various iron powders given in the book by R. Kieffer and W. Hotop (1948) [12] (Table 30). (The pressure values have been converted to the SI system).

Pressure, p (MPa)	Powders *
	FeKH1	FeKH2	FeKH4	FeKH5	FeKH7	FeKH8
	Relative Density, ρ
0	0.285	0.266	0.389	0.344	0.403	0.427
196	0.698	0.699	0.676	0.679	-	0.755
392	0.809	0.821	0.778	0.808	0.707	0.852
588	0.862	0.886	0.820	0.869	0.796	0.898
784	0.897	0.917	0.843	0.910	0.849	0.919
980	0.921	0.929	0.875	0.928	0.889	0.935
1470	0.967	0.949	0.928	0.958	0.937	0.956
1960	0.978	0.955	0.951	0.965	0.958	0.964
2450	0.983	0.956	0.962	0.969	0.969	0.970
2940	0.987	0.960	0.976	0.972	0.972	0.976

* Iron powders were produced by the following methods: FeKH1—reduction from oxide; FeKH2—recovery from scale; FeKH4—spraying on a centrifuge; FeKH5—electrolytic; FeKH7—spraying cast iron on a centrifuge; FeKH8—spraying under gas pressure.

the experimental data for only six of nine iron powders since the data for three more powders (FeKH3, FeKH6, and FeKH9) have been presented in Part 1,

Table 5. Values of the constant parameters and coefficient of determination R² obtained through approximation by Equation (9) of the experimental data on compaction of various iron powders from [12].

Parameters	Powders
	FeKH1	FeKH2	FeKH4	FeKH5	FeKH7	FeKH8
ρ0	0.285	0.266	0.389	0.344	0.403	0.427
w (MPa)	237.93	14.974	902.88	74.897	287.09	107.88
n	0.7993	0.1575	2.5426	0.0582	0.3091	0.5960
m	0.6261	1.7843	0.3999	1.1412	0.7468	1.0550
R2	0.99449	0.96607	0.99673	0.98158	0.99327	0.99773

[1].

The results of approximation by Equation (9) of the experimental data on the compaction of various iron powders shown in Table 4 are presented in Figure 4, and the values of constant parameters and the coefficient of determination are given in Table 5.

The results of approximation by Equation (9) of the experimental data on the compaction of iron powders show that this equation describes the PCP in two of six cases with a reduced accuracy. Herein, for the FeKH2 and FeKH5 powders, Equation (9) less accurately describes the intermediate stage of the compaction process (see Figure 4b,d). Therefore, the value of the parameter w for these powders turns out to be lower than the values of w for other powders. These facts indicate that Equation (9) is not able to accurately describe the compaction process of some powders at the intermediate stage if they are compacted to high densities. Another feature of Equation (9) appears when approximating the compaction process of some powders. This means that the curve starts in Figure 4d,e is somewhat unusual: it is characterized by a rapid rise in compaction pressure, not characteristic of the beginning of a real compaction process. It follows that this equation is not able to adequately describe some experimental data on the compaction of plastic (but hard) powders despite the presence of three empirical constants. This also indicates that Equation (7) proposed above for the strengthening coefficient does not provide certain laws of strengthening during PCP, especially for cases where the powder is not compacted to a dense state, even under high pressures. Therefore, one more equation for the compaction of powders in a rigid die has been derived along with one more equation for the strengthening coefficient, which made it possible to describe with high accuracy specific experimental data difficult to describe by various known equations and the new Equation (9).

2.2. Correction of the Last Balshin’s Equations

Our second new equation was derived through the generalization of the last of Balshin’s equations presented in [2]. To describe the first and second stages of PCP in a die, when the processes of rearrangement of particles along with their elastic and plastic deformation in the contact zones of particles prevail, M. Balshin proposed the following equation:

$$p=\frac{{\left({p\prime }_k\right)}_0}{\left(1-2{\nu }^{\prime }\right)}\times \alpha =\frac{{\left({p\prime }_k\right)}_0}{\left(1-2{\nu }_0\sqrt{\alpha }\right)}\times \alpha$$

(10)

where (p′_k)₀ is the effective contact stress equal approximately to the Brinell hardness HB or Vickers hardness HV of the powder particle material [2], ν′ is the contact Poisson ratio of a porous sample, ν₀ is the Poisson ratio of the powder particle material, α is the dimensionless contact section, which here is determined by a different formula than Formula (3):

$$\alpha ={\rho }^2{\left(\frac{∆\rho }{{\theta }_0}\right)}^b={\rho }^2{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^b$$

(11)

where the exponent b > 1 for the first stage and b = 1 for the second stage of PCP in a rigid die [2].

Further, M. Balshin focused on the fact that powder particles do not have a single-valued Poisson’s ratio [2]. The value of Poisson’s ratio depends on the method of determination. Therefore, there are two Poisson’s ratios, namely the contact (${\nu }^{\prime }={\nu }_0\sqrt{\alpha }$) and the inertial ($\nu ={\nu }_0\sqrt{\alpha /\rho }$) ones. It follows that if the inertial Poisson’s ratio is used, then the form of the powder compaction equation changes:

$$p={\left({p\prime }_k\right)}_0\times \frac{\alpha }{\left(1-2{\nu }_0\sqrt{\alpha /\rho }\right)}$$

(12)

At the same time, M. Balshin did not answer the following question: In which case is it necessary to use the equation with the contact Poisson ratio, and in which case is it necessary to use the inertial equation? In addition, an ambiguous situation is also associated with the determination of the contact section α by Formula (11), since the exponent b depends, according to M. Balshin, on the compaction stage, and when describing two stages of compaction, its value is unknown in advance. Attention should also be paid to the choice of the value of the effective contact stress ${\left({p\prime }_k\right)}_0$. 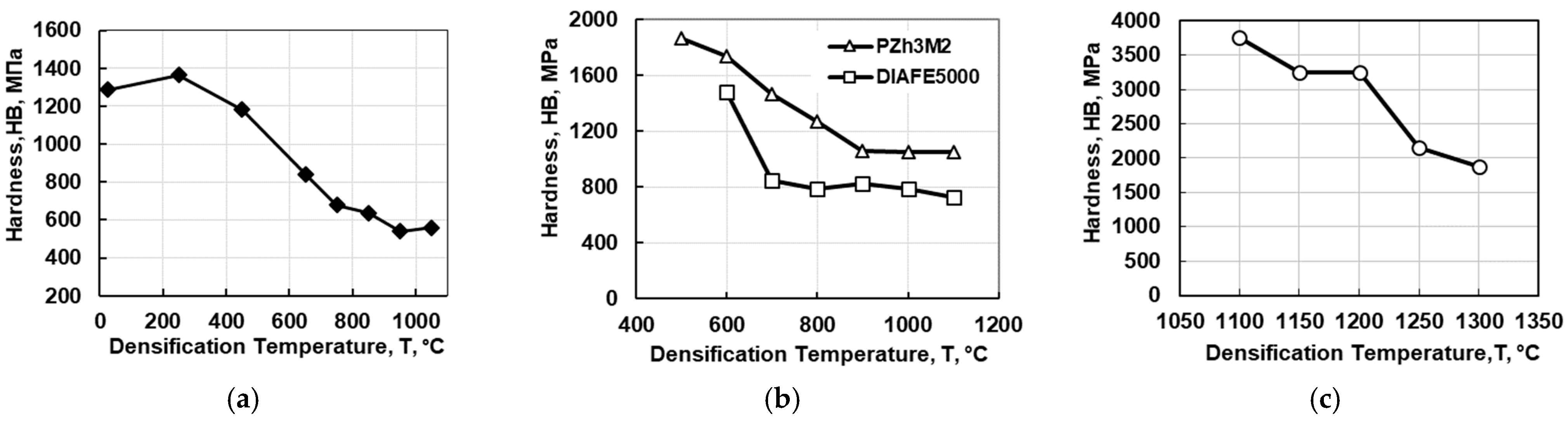It is difficult to agree with Balshin’s opinion that this value is equal to the hardness of the compact particle material, so it can be taken from a reference book. It is well-known that the hardness of a compact plastic material is a structure-sensitive characteristic, and with a decrease in the grain size, the hardness increases. Moreover, since the powder particle size can be several times smaller than the grain size in a compact or cast material, the hardness of the original, e.g., iron powders, can be much greater than the hardness of undeformed massive samples and even greater than the hardness of deformed or cold-hardened samples. To confirm this statement, it is reasonable to present here our previous findings in studying the hardness of dense powder samples obtained by hot densification at low and high temperatures. At low densification temperatures, as experiments have shown, the initial size of the powder particles is practically preserved, and at high densification temperatures, recrystallization is observed, and the structure becomes coarse-grained. Such changes in the structure are accompanied by a significant change in the sample hardness. Figure 5 shows the hardness of samples made of copper, iron (with different initial particle sizes) and “nichrome” (Cr20Ni80) obtained by impact densification at different temperatures [13,14,15].

In particular, as shown in [13], the Brinell hardness of copper powder samples compacted at 250 and 950 °C is 1364 and 540 MPa, respectively. The hardness of compact sheet (6 mm thick) copper is 580 MPa. It follows from the analysis of the reference data [16] that the hardness of deformed copper reaches 900–1050 MPa, and the hardness of copper annealed at 600 °C is 340–400 MPa. In [14], where impact densification at different temperatures of coarse and fine iron powders was studied, the following findings on the hardness of the samples were presented. The compaction of PZh3M2 powders (particle size of 50–150 µm) and DIAFE5000 (2.5–5.0 µm) at temperatures of 600 and 1100 °C leads to the following hardness values: 1740 and 1050 MPa (PZh3M2) and 1490 and 720 MPa (DIAFE5000). The hardness of the samples from PZh3M2 powder obtained at 500 °C is 1870 MPa, and the hardness of armco iron, according to [16], is 785–1180 MPa. In addition, according to the results of hardness measurements in “nichrome” powder samples [15], the increase in the nichrome densification temperature from 1100 to 1300 °C leads to a decrease in the Brinell hardness from 3800 to 1800 MPa (the hardness of cast nichrome is 1400–1500 MPa). Thus, based on the experimental data presented in Figure 5, it can be argued that the hardness of powder samples with a fine-grained structure is at least the doubled hardness of related undeformed monolithic materials. Therefore, for a more accurate description of PCP, it is necessary to know the true hardness of the powder particles, which can differ significantly for the same material. Since the hardness of powder particles, especially small particles, is not easy to determine, it is problematic to use Equation (10) or (12) without experiment. In addition, without experimental data on powder densification, it is also difficult to establish the exponent b in Equation (11) to determine the contact cross-section. An ambiguous situation with the determination of the contact cross-section α is also associated with the presence of another dependence of the contact cross-section on the relative density proposed by G. M. Zhdanovich [17]:

$${\alpha }_{\mathsf{к}}={\rho }^2\frac{ln\left(\rho /{\rho }_0\right)}{ln\left(1/{\rho }_0\rho \right)}$$

(13)

This indicates that no matter how much we would like to a priori describe the process of powder compaction, this is still impossible. Therefore, it seems appropriate to generalize the Balshin and Zhdanovich equations and introduce arbitrary parameters into the generalized equation that could be determined by fitting the theoretical dependence of the compaction pressure on the relative density to the experimental dependence. In this regard, the effective contact pressure ${\left({p\prime }_k\right)}_0$, which, according to M. Balshin, is constant up to a relative density of 0.9–0.95 and equal to the particle hardness, is generally unknown and can be denoted by the symbol H. The formula for the contact section α can be taken according to Equation (8). Thus, the expression in the denominator of Equations (10) and (12) will be generalized and replaced by the following expression:

$$\left[1-a·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^c\right]$$

(14)

where $a=2{\nu }_0^{\prime }$ and c are constant parameters, and ν₀′ is the elastic-plastic Poisson ratio, which can take values in the range from ν₀′ = ν₀ (for elastic deformation) to ν₀′ = 0.5 (for plastic deformation).

As a result of the proposed generalization, a new equation for describing PCP acquires the form:

$$p=H·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^b·\frac{1}{\left[1-a·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^c\right]}=\frac{H}{{\left(1-{\rho }_0\right)}^{\left(b-c\right)}}·\frac{{\left(\rho -{\rho }_0\right)}^b}{\left[{\left(1-{\rho }_0\right)}^c-a{\left(\rho -{\rho }_0\right)}^c\right]}$$

(15)

where H, a, b, and c are constant parameters determined through approximation of related experimental data on PCP using this equation.

When considering Equation (15) and comparing it to Equation (9), it should be taken into account that the former includes a strengthening coefficient that significantly differs from that in Equation (9) since it has two constants, a and c:

$${\beta }^{\prime }=1/\left[1-a·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^c\right]$$

(16)

Due to the presence of two constants, this strengthening coefficient has broader possibilities in describing various strengthening processes during powder compaction. According to Formula (16), it can reproduce a very wide range of strengthening laws and even laws that provide an infinite increase in pressure at a relative density below 1.0. In this case, the constant parameter a, which is equal to the doubled elastic-plastic Poisson’s ratio, becomes greater than 1.0, which has no physical explanation yet. In this regard, we will show graphical examples of various strengthening laws in one case for the parameter a ≤ 1 and the other case for the parameter a > 1. Curves for various real and unusual strengthening laws are shown in Figure 6. For comparison, the strengthening curve (dotted) is depicted in Figure 6a according to the Balshin Equation (5), whereas in Figure 6b—according to the new Equation (7) with one constant.

Of significance is the fact that the strengthening coefficient according to Equation (16) with the values of the parameters a = 0.667, c = 2.38 and the initial density ρ₀ = 0.3 almost exactly coincides with the strengthening coefficient according to Balshin’s Equation (5) with the same initial density:

$${\beta }^{\prime }=1/\left[1-0.667·{\left(\frac{\rho -0.3}{1-0.3}\right)}^{2.38}\right]\cong f=1/\left[1-\frac{2}{3}·{\rho }^2\left(\frac{\rho -0.3}{1-0.3}\right)\right]$$

(17)

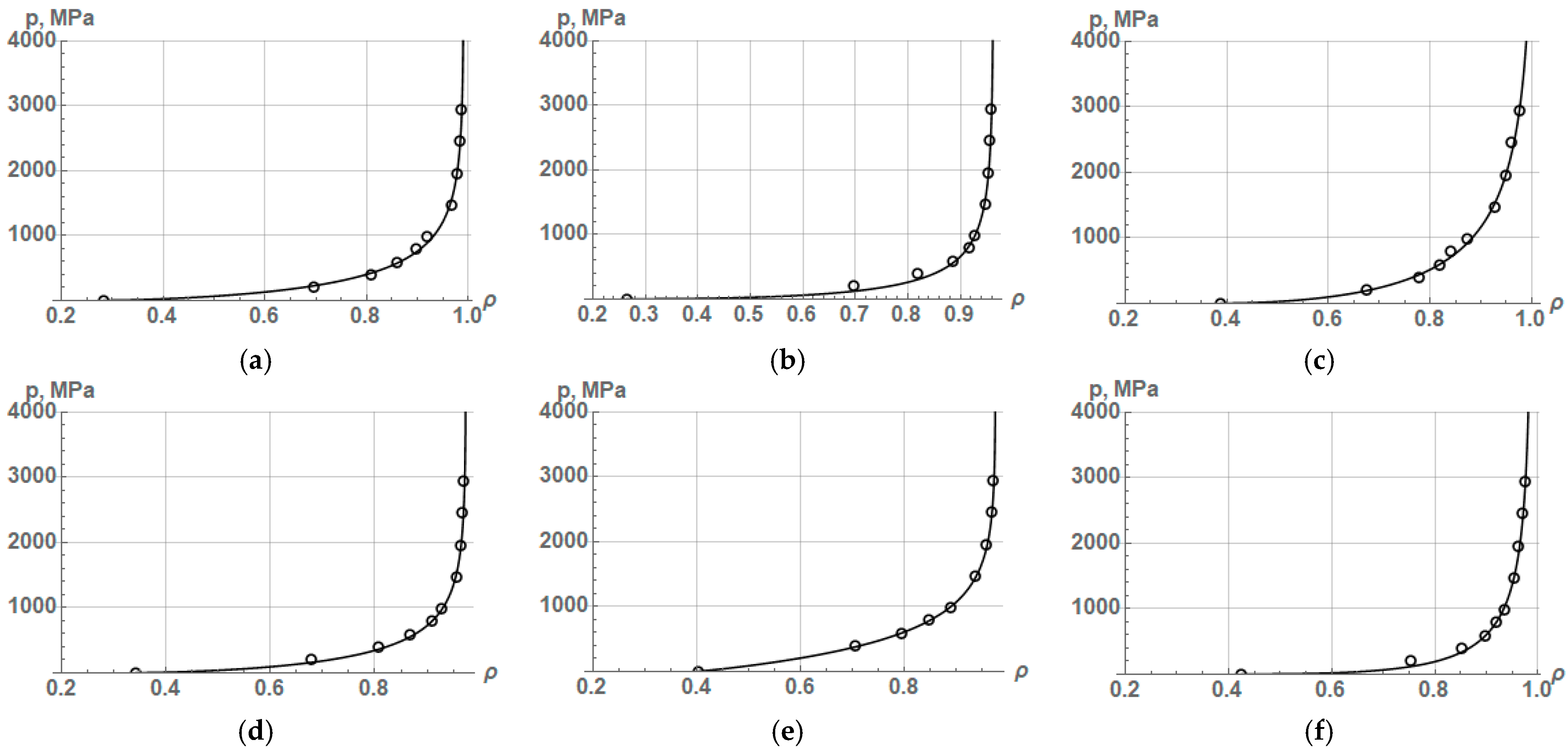
Therefore, Figure 6 and expression (17) indicate that the strengthening coefficient, according to Equation (16), is able to describe a wide variety of PCP in a rigid die. In this regard, we will perform an approximation by Equation (15) of the unique experimental data on the densification of iron powders presented in Table 4 and in Table 5 of Part 1 [1]. The results of the performed approximation are presented in Figure 7, and the values of the constant parameters are listed in

Table 6. Values of the constant parameters H, a, b, c and coefficient of determination R² obtained through approximation by Equation (15) of the experimental data on compaction of various iron powders from [12] and data on the specific work of plastic deformation W_pd.

Parameters	Iron Powders Obtained by Different Methods from [12]
	FeKH1	FeKH2	FeKH4	FeKH5	FeKH7	FeKH8	FeKH3	FeKH6	FeKH9
ρ0	0.284	0.265	0.388	0.343	0.402	0.426	0.253	0.438	0.396
H (MPa)	1460	850	1590	1145	1490	5.0	680	1590	1660
a	1.0135	2.1948	0.7023	1.9057	1.2490	1.00006	1.0592	38.5926	8.3876
b	4.0390	2.7775	2.9115	2.9011	2.1292	0.4338	1.9901	2.8520	3.1864
c	34.137	19.0504	7.3564	24.385	17.8699	0.0399	11.868	54.3505	41.1105
ρ∞	0.9997	0.9700	1.0301 *	0.9988	0.9926	0.9991	0.9964	0.9635	0.9696
R2	0.99873	0.99050	0.99715	0.99876	0.99663	0.99764	0.99683	0.99236	0.99792
Wpd (J/cm3)	282.92	257.17	372.11	269.87	402.63	227.76	337.46	253.79	270.78

* Calculated densification pressure at ρ = 1 corresponds to ∼5338.2 MPa.

.

Table 6 shows the data on the specific work of plastic deformation, W_pd, obtained through numerical integration of the equation that, in the general case, has the form:

$$W_{pd}={\int }_{{\rho }_0}^{\rho }\frac{H}{{\left(1-{\rho }_0\right)}^{\left(b-c\right)}}·\frac{{\left(\rho -{\rho }_0\right)}^b}{\left[{\left(1-{\rho }_0\right)}^c-a{\left(\rho -{\rho }_0\right)}^c\right]}·\frac{d\rho }{{\rho }^2}$$

(18)

Numerical integration was performed within the limits of relative density change from the initial one, ρ₀, to the density ρ corresponding to the compaction pressure of 2940 MPa.

As seen from Figure 7 and Table 6, the approximation Equation (15) describes the process of compaction of various iron powders quite accurately. In all cases, the value of R² is above 0.99, which indicates the adequacy of the description of the entire PCP by this equation. At the same time, it is necessary to pay attention to the fact that Equation (15), which contains four constant parameters, leads, in some cases, to an ambiguous decision regarding the values of the constants while providing a high level of accuracy in describing the compaction process. This ambiguity manifested itself when approximating experimental data on the compaction of FeKH8 powder by Equation (15), where the value of the parameter H turned out to be very low.

The fact is that when approximating the compaction of powders with this equation, the value of the parameter H is selected by comparing the values of the coefficient of determination for different predetermined values of H. As a rule, when changing the values of H, the coefficient of determination passes through a maximum, which determines the value of H given in Table 6. However, for FeKH8 powder, approximation by Equation (15) gives a high value of the coefficient of determination for a wide range of H values. In particular, when the parameter H changes from 500.0 to 5.0, the coefficient of determination constantly increases, as shown in

Table 7. Values of constant parameters and coefficient of determination R² obtained as a result of approximation by Equation (15) of experimental data on the compaction of three iron powders at different values of the constant H.

Parameters	Iron Powders Obtained in Different Ways
	FeKH8			FeKH5			FeKH2
ρ0	0.426			0.343			0.265
H, MPa	500	200	5.0	1200	1145	1100	900	855	800
a	1.00942	1.00263	1.00006	2.01400	1.90567	1.82401	2.32567	2.20746	2.07299
b	2.15588	1.16431	0.43378	3.08053	2.90112	2.75565	2.97656	2.79737	2.57792
c	4.09217	1.60108	0.03987	26.1237	24.3850	22.9962	20.3554	19.1804	17.7575
R2	0.99749	0.99762	0.99764	0.99873	0.99876	0.99874	0.99048	0.99050	0.99047

, where, as an example, the results of approximation of the compaction process of FeKH2 and FeKH5 powders with different preset values of H are also given. From the data in Table 7, it can be seen that for FeKH2 and FeKH5 powders, there is an optimal value of H, which corresponds to the maximum coefficient of determination. However, for FeKH8 powder, there is no optimal value of H, since there is no extremum in the coefficient of determination, although the value of R2 changes very slightly and remains at a high level. That is, in relation to FeKH8 powder, we can say that Equation (15) with four constants does not provide an unambiguous approximation. However, the accuracy of the approximation is ensured by high accuracy. An unambiguous approximation with high accuracy is provided for this powder when using Equation (9) with three constants. Nevertheless, an important feature of Equation (15) is that it allows one to establish the ultimate value of the relative density, which in most cases is below 1.0 and cannot be increased up to 1.0 even under infinite pressure. The mathematical result for infinite pressure at a certain value of relative density indicates the impossibility of completely eliminating porosity due to plastic deformation.

Hence, it is appropriate to recall the J. Secondi equation, which was considered in Part 1 [1] and describes cases of PCP in a rigid die when it is impossible to achieve the density of a compact material. In Part 1 [1], an approximation by the Secondi Equation (18) was performed for three powders from [12] (FeKH3, FeKH6, and FeKH9), and a high approximation accuracy for the experimental PCP was shown as well (see Table 6 in [1]). If we compare the accuracy of approximation by the Secondi equation to the new Equation (15) for the above three powders, we will see that in two of the three cases, the Secondi equation gives a slightly higher accuracy. In this regard, it is of interest to consider the accuracy of approximation for the other six iron powders presented in Table 4. The results of the Secondi approximation of the experimental data on the compaction of FeKH1, FeKH2, FeKH4, FeKH5, FeKH7, and FeKH8 iron powders are shown in Figure 8, and the values of constant parameters are listed in

Table 8. Values of the constant parameters and coefficient of determination R² obtained through approximation by the Secondi Equation ((17) in [1]) of the experimental data on compaction of various iron powders taken from [12].

Parameters	Powders
	FeKH1	FeKH2	FeKH4	FeKH5	FeKH7	FeKH8
ρ0	0.285	0.266	0.389	0.344	0.403	0.427
$K^{\prime }$ (MPa)	273.35	130.36	439.25	238.51	512.49	157.14
m	1.4236	1.8459	1.7283	1.4629	1.0436	2.1814
ρ∞	0.9904	0.9630	1.0062	0.9743	0.9749	0.9879
R2	0.99702	0.98644	0.99694	0.99683	0.99906	0.99599

.

It follows that the Secondi equation describes PCP as an extremely high density with a high enough accuracy as well (Table 8). However, in five of six cases, the accuracy of approximation by the Secondi equation is slightly lower than that by the new Equation (15). Thus, of the nine iron powders studied, the Secondi equation describes PCP more accurately in three cases, namely, for FeKH6, FeKH7, and FeKH9 powders. Hence, comparing the new to previous equations for the description of PCP to a high density reveals that the new equation makes it possible to describe PCP more precisely in most cases under extremely high density.

In the literature, other experimental data on PCP can be found that are difficult to describe with high accuracy by known equations. In Part 1 [1], such experimental data were taken from F. Lenel’s book [18], and they referred to the compaction of fine powders of iron and copper. Based on these experimental data, they were approximated by the new Equation (15) and the transformed J. Secondi Equation (18) from [1]. The approximation results are shown in Figure 9, and the values of constant parameters and the coefficient of determination are given in

Table 9. Values of the constant parameters and coefficient of determination R² obtained through approximation by new Equation (15) and well-known Secondi Equation ((18) in [1]) when describing the experimental data on the compaction of coarse and fine powders of iron and copper taken from [18].

Parameters	Powders
	Fe (Coarse)		Fe (Fine)		Cu (Coarse)		Cu (Fine)
	Equation Type
	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]
ρ0	0.350		0.183		0.391		0.165
H, K′ (MPa)	970	254.1	970	272.9	815	219.0	1278	313.2
a, m	27593	0.8475	161344000	0.7867	456.9	0.8872	197938	1.2165
b	2.8505	-	2.1792	-	2.7957	-	2.6457	-
c	201.25	-	211.09	-	187.02	-	221.6	-
ρ∞	0.9677	0.9654	0.9300	0.9273	0.9803	0.9782	0.9552	0.9776
R2	0.99951	0.98876	0.999998	0.99054	0.99976	0.99222	0.99997	0.98994

.

These results of the approximation of experimental data on the compaction of coarse and fine powders of iron and copper by the new Equation (15) and the Secondi Equation ((18) in [1]) show that the Secondi equation is inferior to the new equation in terms of the accuracy of the description of the experimental PCP for iron and copper powders. The new equation demonstrates its ability to describe PCP with very high accuracy (Table 9). It can be seen from this comparison that the new equation (15) describes the experimental PCP very well when the sample density stops increasing despite the increase in pressure to extremely high values. At the same time, there are cases when the density stops increasing due to achieving a compact (practically pore-free) state. Such cases are observed in the compaction of highly plastic powders. Therefore, it is relevant to evaluate the possibilities of the new Equation (15) and Secondi Equation ((18) in [1]) in describing the experimental data on the compaction of highly plastic powders, in particular, powders of lead, tin, and annealed copper. Experimental data on the compaction of lead can be taken from the article by M. Balshin [6] and those for lead, tin, and annealed copper [10]. We have used these experimental data for approximation by the first new Equation (9), which made it possible to compare the results of approximation of the same experimental data using different equations. The results of the approximation of these data by the second new Equation (15) and the Secondi equation are shown in Figure 10, and the values of constant parameters and the coefficient of determination are listed in

Table 10. Values of the constant parameters and coefficient of determination R², obtained through approximation by the new Equation (15) and the well-known equation of J. Secondi (18) [1] when describing the experimental data on the compaction of coarse and fine powders of iron and copper presented in [18].

Parameters	Powders
	Sn [10]		Pb [10]		Cu [10]		Pb [6]
	Equation Type
	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]	New (15)	Secondi (18) [1]
ρ0	0.501		0.439		0.3		0.58
H, K′ (MPa)	89.0	11.68	75.0	3.24	565.0	154.99	202.0	32.46
a, m	0.8384	1.9374	0.8894	2.6319	2.5926	1.4378	0.7749	1.6242
b	2.9815	-	7.1293	-	0.9673	-	4.3125	-
c	30.393	-	36.331	-	12.2454	-	39.511	-
ρ∞	1.0029	0.9999	1.0018	1.0	1.0019	0.9816	1.0027	0.9996
R2	0.99743	0.98821	0.99936	0.99587	0.99983	0.99949	0.99755	0.99971

.

From the presented results of approximation of the experimental PCP of highly plastic powders of tin, lead, and annealed copper using the new Equation (15) and the well-known Secondi equation, it can be seen that the new equation provides a higher accuracy of approximation in three of four cases. Perhaps this is due to the fact that there are four constant parameters in Equation (15) against three constants in the Secondi equation. However, three constants are also present in the first new Equation (9), which also provides a higher approximation accuracy compared to the Secondi equation for the tin and lead from [10], the same accuracy for annealed copper, and a slightly lower accuracy for lead from work [6] (see the R² values for these powders in Table 3 and Table 10).

The above results of approximating experimental data on the compaction of various powders by new Equations (9) and (15) indicate the possibility of a high-accuracy description of PCP in most cases. This is ensured by the presence of three or four constants in the new equations, which makes it possible to predict any behavior of the powder during compaction and which take into account a wide variety in the shape and size of particles, in their strength and deformation resistance, as well as in the amount and nature of the action of internal and external friction forces. At this stage in the evaluation of new equations for PCP in a rigid die, there is still no unambiguous understanding of the physical meaning of the constants of the equations proposed. In particular, one of the constants in Equations (9) and (15) has the dimension of pressure—MPa—therefore, this constant can reflect the average hardness of particles, the average yield strength, and the specific work of plastic or general deformation of particles, since the dimension of pressure (MPa) coincides with the unit of specific work of deformation (J/cm³). The two dimensionless constants n and m in Equation (9) reflect, respectively, the intensity of the change in the contact cross-section and the degree of restriction of particle deformation with increasing density of the powder preform in a rigid die.

It is more difficult to understand the physical meaning of three dimensionless constants a, b and c in Equation (15) since, for example, the constant a cannot take values above 1.0 in view of its initial definition as a double elastic-plastic Poisson’s ratio. However, with a computer approximation of the compaction of some powders, the constant a can reach a nine-digit number (Table 9), which is still difficult to explain in terms of physics. At this stage, we can only note that a very high value of parameter a indicates that the hardening coefficient β′ (16) tends to infinity at lower values of the relative density. Some examples of how the hardening coefficient can change with the value of the parameter “a” at a constant value of the parameter “c” are shown in Figure 11. This Figure shows that a change in the value of parameter “a” from 1.2 to 12,000 (that is, by 10,000 times) leads to a decrease in the limiting density (above which the density does not increase even at infinite pressure) by approximately ∆ρ = 0.4 at c = 10 or by ∆ρ = 0.06 at c = 100.

Very large values of the constant “a” in Table 9 are the result of a computer approximation by Equation (15) of real experimental data on powder compaction. They show that even ductile metal powders can be very hard and cannot be compacted to a non-porous state. In addition, compaction of hard powders occurs mainly due to the rearrangement of particles, whereas strengthening due to both deformation and deformation constraints occurs only at the end of the compaction process.

The other two dimensionless constants b and c in Equation (15) can be related to the intensity of change in the degree of particle contact and the degree of restriction of particle deformation. To clarify the physical meaning of the constants in the new equations for PCP in a rigid die, it is necessary to conduct, firstly, additional experiments on the compaction of model or specially selected powders and, secondly, a deeper theoretical analysis of the equations proposed.

3. Conclusions

1. The proposed equations for PCP as a rigid die include, in one case, three constant parameters and in the other case—four parameters. It is almost impossible to predetermine the values of these parameters or constants, but they can be easily determined by computer approximation of the experimental data on the compaction of various powders. At the same time, the proposed equations make it possible to describe the experimental PCP with a sufficiently high accuracy, at which the coefficient of determination R² lies in the range of 0.9900 and 0.9999.

2. The equation with three constants provides a high accuracy of description of the experimental PCP, especially in the case of compaction of highly plastic powders or when the experimental compaction is limited to a low relative density, within 0.8 and 0.9. The equation with four constants provides a high accuracy of approximation of experimental data in the case of pressing powders to the maximum possible relative density, which in most cases is below 1.0. Such experimental data can be described in some cases quite accurately by the well-known Secondi equation containing three constants. However, to perform an approximation by the Secondi equation, careful selection of a predetermined range of changes in the constant ρ_∞ is required.

3. The new equations allow PCP description from the initial relative density in a die to the maximum possible one, which excludes consideration of PCP as a multi-stage process with different mechanisms of powder compaction and suggests the possibility of the existence of a single mechanism that can be a constantly growing constraint of elastic and plastic deformation of a set of contacting particles, which exists throughout the entire PCP, that is, from the beginning of powder compaction in a rigid die to the state of compaction at which the relative density stops increasing with increasing pressure to infinity.