New Die-Compaction Equations for Powders as a Result of Known Equations Correction: Part 1–Review and Analysis of Various Die-Compaction Equations

Abstract

The well-known equations for the powder compaction process (PCP) in a rigid die published from the beginning of the last century until today were considered in this review. Most of the considered equations are converted into the dependences of densification pressure on the powder’s relative density. The equations were analyzed and their ability to describe PCP was assessed by defining the coefficient of determination when approximating experimental data on the compaction of various powders. It was shown that most of the equations contain two constants the values of which are determined by fitting the mathematical dependence to the experimental curve. Such equations are able to describe PCP with high accuracy for the compaction of powders up to a relative density of 0.9–0.95. It was also shown that different equations can describe PCP in the density range from the initial density to 0.9 with the same high accuracy, but when the process of compaction is extrapolated to higher values of density, the curves diverge. This indicates the importance of equations that can unambiguously describe PCP to a relative density equal to or close to 1.0. For an adequate description of PCP for relative density greater than 0.95, equations containing three or four constants have proven useful.

1. Introduction

The powder compaction process (PCP) in a rigid die is one of the main processes in final product fabrication from various powders. Thus, the comprehensive study and description of PCP has attracted the attention of many specialists in the field of powder metallurgy. There are many equations that describe PCP, and various approaches have been used to derive them. Initially, to describe PCP, simple mathematical functions were used, e.g., exponential [1,2,3], power [4,5,6], and logarithmic [7,8,9,10,11]. Later the proposed equations took into account various physical phenomena occurring in PCP such as contact interaction of particles, local and general deformation, hardening, shear between particles and within particles, friction, etc. [12,13,14,15,16,17]. To derive the equations with physical constants, some researchers considered a powder body as a combination of a large number of individual particles contacting each other [14,18,19]. An approach based on the evolution of the contact interaction between individual particles under the effect of pressure can be designated as a discrete PCP theory. There is also an approach that considers a powder sample as a quasi-continuous two-phase body that can decrease in volume under the effect of pressure. In this case, the compaction of the quasi-continuous body in a rigid die makes it possible to obtain the corresponding equations for describing PCP [20,21,22,23,24,25]. This approach can be considered a continuous one.

However, the equations for PCP in a rigid die are not able to describe the entire compaction process with high accuracy, since the process itself is complex and multi-stage. The known equations are able to adequately describe only one or two of the three available stages [18]. In addition, there are fundamental discrepancies between the equations, which are associated with the description of PCP upon approaching a pore-free state, where some equations give a finite value of the compaction pressure while other ones give infinite pressure. It is therefore difficult to choose an equation that allows one to determine the compaction pressure accurately enough to achieve a relative density close to 1.0.

Certain difficulties are associated with the determination of the true plastic deformation of particles during PCP in a rigid die because of particle rearrangement that can take place and that depends on the shape of particles and on their yield strength. Many equations for PCP do not explicitly reflect the effect of particle rearrangement on the increase in sample density. Some authors [17,26] have made an attempt to take into account the degree of density change due to particle rearrangement. These authors believe that rearrangement takes place throughout almost the entire compaction process. However, according to other researchers [27], rearrangement ends at the initial stage of the compaction process. This implies the existence of a porosity threshold beyond which no rearrangement occurs. The presence of a threshold or critical phenomena during PCP in a rigid die can be described based on percolation theory [28,29,30], but the modification of the powder compaction equations using this theory has not yet led to adequate equations.

Another issue occurs when describing the compaction of “high” samples, i.e., samples with a height-to-diameter ratio exceeding 1.0. It refers to the non-uniform distribution of density along both the height and the diameter of the sample. To solve the problem of determining the density of a sample at its different points the finite element method known for metal forming is used. This method allows one to determine the density at any point of a sample with known parameters of powder particle strength, using the hardening law and the friction forces between the particles and the die wall [31,32,33]. However, the task of determining the true strength of particles and the law of hardening during their deformation is not easy.

To determine the properties of a specific powder, experiments are required on tri-axial powder compression and on the determination of the yield surface depending on the sample density. Such experiments are relatively complex and must be carried out in special laboratories [34,35,36], which makes it difficult to obtain quick results for different powders. In addition, information about the properties of a powder can also be obtained from experiments on compaction in a rigid die of “low” samples in which, after compaction, the height becomes half the diameter. In these samples the effect of friction forces can be neglected. It should be noted that most of the experiments are performed with low samples, and that compaction equations are tested mainly on such samples. Therefore, before solving the problems of determining the density distribution in high samples (height/diameter ≥ 1) and samples of complex shape (stepped), it is necessary to have an equation that allows one to describe the compaction process of low samples with the highest accuracy and with a change in density from initial density to close to 1.0.

The adequacy of an equation for PCP in rigid die is determined by assessing the accuracy of fitting the equation to the experimental data, that is, by finding the determination coefficient R². However, in many cases the adequacy of equations is unknown. To confirm this thesis, two review papers on the equations of PCP in a rigid die, published in 2007 and 2017, can be noted. The author of one of them is T. Çomoğlu (2007) [37], who considered the equations proposed by Walker, Bal’shin, Heckel, Kawakita and Lüdde, Cooper and Eaton, Leuenberger, Shapiro, Sonnergaard. In that review, it was noted that the PCP in a rigid die typically consists of three stages and it is difficult or impossible to describe it by a single equation. The author analyzes known equations with various constant parameters and tries to relate these parameters to the particular stage of compaction and to the mechanical properties of materials. He also contrasts or compares some equations and shows their similarities and differences. An attempt was made to evaluate the equations for their ability to describe the compaction process of plastic and ceramic powders, and a possibility was also considered of describing the compaction of powder mixtures consisting of plastic and brittle powders. However, in that review there is no graphical representation of the experimental and theoretical curves of the compaction process, and there is also no quantitative assessment of the accuracy of the powder compaction process description by different equations.

In the second review, by Popescu and Vidu (2017) [38], the equations of Shapiro-Kolthoff and Konopicky, Bal’shin, Heckel, Cooper and Eaton, Kawakita and Lüdde, Ge Rong-de, Panelli and Filho, Parilak and Dudrova, Castagnet and Leal Neto, Gerdemann and Jablonski were considered. That review compares different equations describing the compaction process of powder mixtures consisting of plastic and non-plastic powders, and also establishes, in some cases, the influence of the shape and size of brittle particles on the constants of equations. However, in that review, as in the previous one, there are no graphical examples (with the exception of one figure) showing the correspondence of theoretical curves to experimental data, and there is also no quantitative assessment of the agreement degree. This does not make it possible to understand how a wider range of density changes affects the accuracy of the PCP description, and also does not allow us to evaluate the compaction process at the stage of powder compression in the region of relative density close to unity.

Therefore, the purpose of this communication is to review the known equations for PCP in a die. An attention will be focused on assessing the accuracy of PCP description by various equations, as well as on a graphical representation (visualization) of correspondence theoretical curves to experimental data. In this case, it seems to be appropriate to convert the known equations that show the dependence of relative or absolute density on the compacting pressure into the dependence of pressure on relative density, since such dependence can have a simpler form and thus makes it easy to determine the specific compaction energy of the powder using the formula:

$$w(\rho )={\int }_{{\rho }_0}^{\rho }\frac{p\left(\rho \right)}{{\rho }^2}d\rho ,$$

(1)

where w is the specific energy in J/m³ or in Mpa, p(ρ) is the experimental or theoretical external pressure (on the punch) dependence on the relative density, and ρ₀ and ρ are the initial and current relative densities of the sample, respectively.

The assessment of accuracy of PCP description by various equations was performed by computer approximation with these equations of the experimental data on compaction different powders. For approximation, the Russified program “Wolfram Mathematica 10.4” was used.

2. Accuracy Assessment of PCP Description Using Equations Obtained by Selecting Mathematical Functions

Equations in the form of simple mathematical functions were among the first formulated ones, and they appeared at the beginning of the 20th century. Most researchers point out that the first powder compaction equation was proposed by E. Walker (1923) [1]. Then, almost the same equation was proposed by M. Balshin (1948) [2] and H. Lipson (1950) [3]. If we take the compaction pressure as a function and the relative density as an argument, then the compaction equation for the powders, by these authors, will be an exponential function:

$$p=Exp\left[k_1-k_2\beta \right]=a_1·Exp\left[-(k_2/\rho \right)],$$

(2)

where p is the compaction pressure, β = 1/ρ is the relative volume of the powder sample, ρ is the relative density, k₁ and k₂ are the constants, and a₁ = Exp(k₁).

Other researchers, e.g., W. Rutkowski and H. Rutkowska (1949) [4], C. Agte and M. Petrdlik (1951) [5], and G. Meyerson (1962) [6] used a power function to describe PCP in the form of the following relationship between compaction pressure and relative density:

$$p=a_2·{\rho }^b,$$

(3)

where $a_2$ and b are constant parameters determined by approximating experimental data on powder compaction.

The presented mathematical functions (exponential (2) and power (3)) are quite simple, but there is no clear understanding what range of density change can be accurately described by them. It is only clear that the smaller this range, the more accurately it is described by these equations. The accuracy of approximation of real experimental data on various PCPs by these exponential and power dependences is shown by approximation of experimental data on the compaction of iron, copper, and nickel powders from publications [39,40,41], respectively. The experimental data on the compaction of these powders are given in

Table 1. Experimental data on the compaction of iron, copper, and nickel powders in a rigid die taken from [39,40,41], respectively.

Material	Relative Density and Corresponding Densification Pressure
Fe [39]	ρ	0.268	0.576	0.627	0.659	0.702	0.734	0.764	0.786	0.815	0.829	0.842
	p, Mpa	0	148.83	205.65	259.78	316.66	375.23	434.7	476.26	549.32	608.86	666.55
	ρ	0.857	0.876	0.884
	p, Mpa	734.91	780.48	935.45
Cu [40]	ρ	0.3	0.363	0.377	0.42	0.476	0.545	0.647	0.756	0.88	0.92	0.949
	p, Mpa	0	4.9	9.8	19.6	39.2	78.4	157.0	294.0	588.0	784.0	980
Ni [41]	ρ	0.36	0.423	0.479	0.507	0.537	0.584	0.674	0.749	0.797	0.869	0.903
	p, Mpa	0	28.03	53.7	64.39	89.08	130.44	240.79	372.4	490.0	745.39	971.57

. This makes it possible to use them to checkup the approximation carried out and approximate with equations by other researchers.

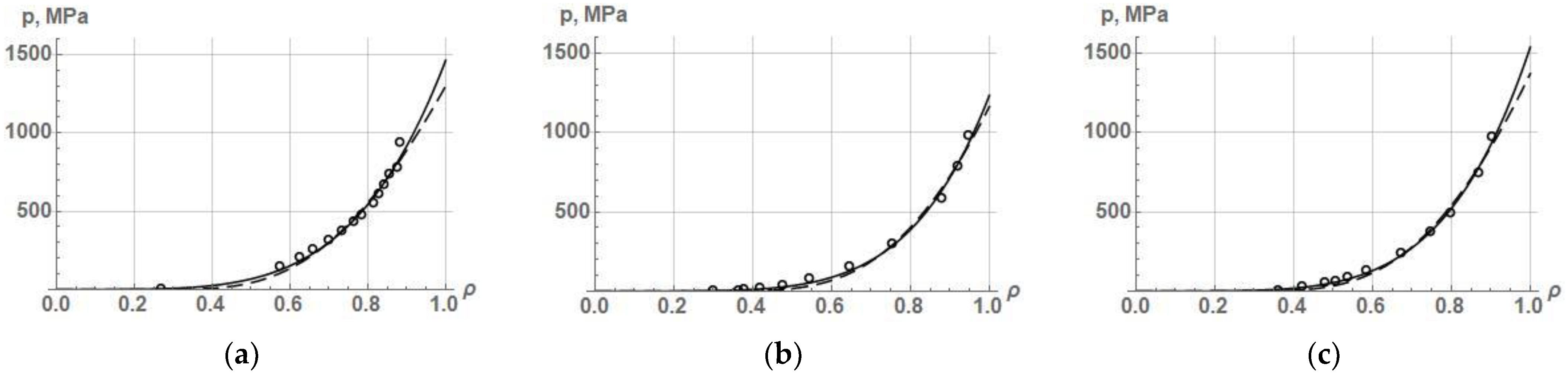
The results of the approximation of experimental data by exponential (2) and power (3) equations are shown in Figure 1, and the values of the constants of these equations and the coefficient of determination R² are presented in

Table 2. Constants and coefficient of determination R² obtained via approximation of experimental data on PCP for iron, copper, and nickel using exponential (2) and power (3) equations.

Parameter	Powder
	Iron		Copper		Nickel
	Equation Type
	(2)	(3)	(2)	(3)	(2)	(3)
ρ0	0.268		0.3		0.36
a1, a2	39313	1462.8	81834	1233.5	56561	1537.6
k2, b	3.410	4.442	4.253	5.182	3.720	4.849
pmax, MPa	1298.9	1462.8	1163.2	1233.5	1370.1	1537.6
R2	0.9763	0.9843	0.9901	0.9954	0.9897	0.9964

. As seen, the exponential (2) and power (3) dependences describe PCP quite accurately from the initial relative density to a density of 0.95, and power dependence (3) describes PCP with a higher accuracy that was also noted in another research [6].

In the above equations, PCP is conceded to be a monotonous process without any indication that, in reality, it proceeds in several stages with their own mechanisms of powder densification. Most experts agree on the existence of three stages of PCP, although according to some authors, there are 4 stages [42,43]. The three stages are characterized as follows. The first stage is the rearrangement of particles when elastic and slight plastic deformation can occur. The second stage is the compaction due to the local plastic deformation of the particles during their contact. The third stage is interpreted ambiguously: it is either the localization of plastic deformation near the pore or the general plastic deformation of particles. These stages are clearly manifested in case of constructing a graphical dependence of the experimental relative density on the densification pressure in logarithmic coordinates [44]. Moreover, each stage can be described, as the authors [44] suggested, by a power equation with its own constants:

$$p=p^{*}{\left(\frac{\rho }{{\rho }^{*}}\right)}^m,$$

(4)

where m is a constant different for each stage, ρ* and $p$* are the minimum relative density and pressure, respectively, for a particular compaction stage.

We note that the PCP staging was also established when considering one of the most common equations for PCP in a rigid die. This equation was proposed by different authors, e.g., L.F. Athy (1930) [7], I. Shapiro and I. M. Kolthoff (1947) [8], K. Konopicky (1948) [9], T. N. Znatokova and V. I. Likhtman (1954) [10], and R.W. Heckel (1961) [11], and in the original record it has the form:

$$ln\left(\frac{1}{1-\rho }\right)=kp+a$$

(5)

where k and a are constants.

This equation is often referred to as the Konopicky’s equation or as the Heckel’s equation. If the experimental data on the compaction of powders are presented in coordinates “ln(1/1 – ρ)” and “p”, then a broken line is obtained, indicating different stages of compaction with their own values k and a. The Equation (5) often met in literature [45,46], and after transformation, where the pressure is a function and the relative density is an argument, It takes the following form:

$$p=k\prime ·\left[ln\left(\frac{1}{1-\rho }\right)-a\right]$$

(6)

where k′ = 1/k is a new constant.

It is important to note that the Equation (6) allows one to describe only the intermediate or second stage of powder compaction. Therefore, in most cases, when experimental data on powder compaction are limited by low density (ρ ≤ 0.9), the Equation (6) describes the compaction process without an initial stage. It should also be noted that Equation (6) can be written otherwise if the value of the constant $a$ is determined by substituting pressure equal to zero (p = 0) into this equation. In this case, Equation (6) will look as:

$$p=k\prime ·ln\left(\frac{1-{\rho }_0^{\prime }}{1-\rho }\right)$$

(7)

Here, the parameter ${\rho }_0^{\prime }$ means the conditional initial density that is greater which the actual initial density of the powder ρ₀. This indicates that Equations (6) and (7) cannot take into account the initial process of powder compaction.

Furthermore, Equation (5) has been modernized several times. In one case, modernization was proposed by M. Kuntz and H. Leuenberger [30]. They transformed the Heckel’s equation, i.e., Equation (6), to the form:

$$p=\frac{1}{C}\left[{\rho }_c-\rho -\left(1-{\rho }_c\right)ln\left(\frac{1-\rho }{1-{\rho }_c}\right)\right],$$

(8)

where C is a constant, ρ_c is the conditional initial density of the powder or the second constant.

The use of Equation (8) for approximation of the experimental process of various powders compaction showed that it was more adequate than the Equation (6). In particular, the experimental data on the compaction of iron, copper, and nickel powders presented in Table 1 were used for approximation by Equations (6) and (8). The results of approximation are shown in Figure 2, and the values of the equations constants and the coefficient of determination R² are presented in

Table 3. Constants and coefficient of determination R² obtained via approximation of experimental data on PCP for iron, copper, and nickel using Equations (6) and (8).

Parameter	Powder
	Iron		Copper		Nickel
	Equation Type
	(6)	(8)	(6)	(8)	(6)	(8)
ρ0	0.268		0.3		0.36
k, C, ×10−3	1.9981	1.0996	2.6300	1.5437	1.9570	0.9692
1/k, 1/C, MPa	500.5	909.4	380.2	647.8	511.0	1031.8
a	0.51893	-	0.50561	-	0.56648	-
${\rho }_0^{\prime }$, ρC	0.4048	0.1504	0.3969	0.1694	0.4325	0.2228
R2	0.96549	0.99163	0.98983	0.99899	0.98464	0.99927

. In addition, Table 3 shows the value of the conditional initial density ${\rho }_0^{\prime }$, which is used in Equation (7) and is also determined by fitting the curve to the experimental data.

Figure 2 and Table 3 show that the new Equation (8) describes PCP with higher accuracy than the original Heckel’s equation (6). In this case, the value of the conditional initial density ρ_c in Equation (8), obtained as a result of the approximation, turns out to be lower than the actual initial density ρ₀ that makes it possible to accurately describe the initial stage of the compaction process.

A higher accuracy of approximation of experimental data on PCP compared to the equation of K. Konopicky or R. W. Heckel can be reached by another modernization of the equation, which leads to the appearance of the so-called double logarithmic form of the equation for powder compaction in a rigid die. Three different teams of authors proposed such an equation independently. First, the work of Ge Rong-de (1991) [47] should be noted, in which he proposed a new differential equation for PCP in a rigid die:

$$\frac{d\rho }{dp}=K\frac{(1-\rho ){\rho }^n}{p^m},$$

(9)

where K, n, and m are constants.

At the same time, Ge Rong-de claimed that at n = 0, the integration of Equation (9) leads to an equation that describes PCP at low and high pressures with high accuracy. This equation in the original record is as follows:

$$log\left[ln\frac{(1-{\rho }_0)}{(1-\rho )}\right]=Alogp + B,$$

(10)

where A and B are constants.

In another case, the same equation was proposed by other authors—A. B. Yu and Z. H. Gu (1993) [48], who used their own differential equation in the form:

$$-\frac{d(1-\rho )}{dp}=k·{\left(1-\rho \right)}^a·p^b,$$

(11)

where k, a, b are constants.

Upon integrating Equation (11), these authors obtained an equation for PCP in the form:

$$ln\left[ln\frac{(1-{\rho }_0)}{(1-\rho )}\right]=lnK+nlnp,$$

(12)

where K = k/(1 + b) and n = 1 + b are new constants.

In the third case, L. Parilak and E. Dudrova (1994) [49] proposed an equation that in its original form was written as

$$\theta ={\theta }_0·Exp\left(-K·p^n\right),$$

(13)

where θ and θ₀ are the current porosity and the initial porosity, respectively, of the powder in the die, p is the compaction pressure, K and n are constants.

Equation (13), after making double logarithm and replacement of porosity by relative density, takes the form of Equation (12) into which Equation (10) can also be easily converted. Consequently, the analysis of PCP by at least three groups of authors led to the derivation of the same equation, which contains the powder initial density ρ₀, i.e., the powder density after filling the die, and two constants that can be determined by fitting the curve of Equation (12) to experimental data on PCP. If in the Equation (12) we interchange the function and the argument, i.e., we take the pressure as a function and the relative density as an argument, then we obtain a simpler equation:

$$p=B{\left[\mathit{ln}\left(\frac{1-{\rho }_0}{1-\rho }\right)\right]}^m,$$

(14)

where m = 1/n and B = (1/K)^m are new constants.

It is of interest to check the accuracy of PCP description for different powders by Equation (12), or rather by Equation (14). Prior to this, we need to remember one more equation which also contains the powder initial density and two constants, and which was proposed much earlier than the Equation (12). We are talking about the equation of K. Kawakita and K.H. Ludde (1970) [50]. That equation is rather often referred in the literature, and in original form it is as:

$$C=\frac{V_0-V}{V_0}=\frac{abP}{1+bP}$$

(15)

where C is the degree of volume reduction, V₀ is the initial volume of the powder, V is the volume of the powder under pressure P, a and b are constants characterizing the powder.

If we transform it in such a way that the compacting pressure p is a function, and the relative density ρ is an argument, then it takes the form:

$$p=\frac{1}{b}·\frac{(\rho -{\rho }_0)}{\left[\rho \left(a-1\right)+{\rho }_0\right]}=b^{\prime }·\frac{\left(\rho -{\rho }_0\right)}{\left[a\rho -\left(\rho -{\rho }_0\right)\right]}$$

(16)

where ρ₀ is the initial relative density of the powder filled into the die, a and b′ = 1/b are constants.

To check the approximation accuracy of the experimental data on PCP by the equation of K. Kawakita and K.H. Lüdde (16) and the equation of Ge Rong-de, A. B. Yu and Z. H. Gu, L. Parilak and E. Dudrova (14), we used the experimental data on the compaction of powders of iron, copper and nickel presented in Table 1. The results of approximation are presented in the form of graphs in Figure 3, and the values of the constants of Equations (16) and (14) and the coefficient of determination R² are shown in

Table 4. Constants and coefficient of determination R² obtained via approximation of experimental data on the compaction of powders of iron, copper, and nickel using Equations (14) and (16).

Parameter	Powder
	Iron		Copper		Nickel
	Equation Type
	(16)	(14)	(16)	(14)	(16)	(14)
ρ0	0.268		0.3		0.36
b′, B, MPa	64.1376	56.7495	56.7136	62.2247	101.354	83.2898
a, m	0.7474	1.4566	0.7231	1.3547	0.6642	1.3579
pmax, MPa	3055.1	∞	1713.2	∞	2675.4	∞
R2	0.99283	0.99212	0.99879	0.99935	0.99928	0.99958

.

Accuracy assessment of the experimental data approximation on the compaction of iron, copper and nickel powders by Equations (14) and (16) show that these equations describe PCP very accurately and practically in the same way, since the coefficient of determination differs slightly. In this case, the coefficient of determination by Equation (14) for copper and nickel is slightly higher than that by Equation (16), and for iron it is slightly lower (Table 3). In addition, these equations take into account the initial density of the powder and accurately describe the initial stage of powder compaction. But the fundamental difference between them consists in the fact that at a relative density ρ = 1, the compaction pressure by Equation (16) has a finite value, while by Equation (14), it is equal to infinity. It is still difficult to say, which equation is more adequate, but the higher accuracy of Equation (14) in two cases out of three may indicate that the equation in which the pressure tends to infinity as the relative density increases up to 1.0 seems to be more valid.

The above comparison of two equations shows how important it is to accurately describe the entire PCP, including the process of compaction to a relative density close to 1.0. Alongside with this, it should be noted that there are very few experimental data in the literature on the compaction of metal powders with a final density that exceeds 0.95. Such experimental data, in particular, on the compaction of various iron powders, are available in the book by R. Kieffer and W. Hotop (1948) [51]. They also showed that it is difficult to achieve a relative density ρ = 1.0, even at a pressure of 3000 MPa. In this regard, of great interest are the equations which are able to describe PCP with high accuracy when the pressure tends to infinity at a relative density ρ < 1.0. In practice, it occurs when metal powders with low plasticity or very hard powders, such as ceramics, are compacted. To describe such a case, the J. Secondi’s equation (2002) [52] that contains the relative density parameter at infinite pressure is used. This parameter is denoted as ρ_∞, and it means that the infinite pressure can occur at a relative density ρ < 1.0. In the original record, the J. Secondi’s equation [52] had the form:

$$ln\left(\frac{{\rho }_{\infty }-{\rho }_0}{{\rho }_{\infty }-\rho }\right)=K·p^n,$$

(17)

where ρ_∞ is the relative density at which the compaction pressure tends to infinity, ρ₀ is the initial relative density of the powder, p is the compaction pressure, K and n are constant parameters which control the hardening and plasticity of the powder material.

With taking the compacting pressure p as a function and the relative density ρ as an argument, the J. Secondi’s Equation (17) is converted to the form:

$$p=K^{\prime }·{\left[\mathit{ln}\left(\frac{{\rho }_{\infty }-{\rho }_0}{{\rho }_{\infty }-\rho }\right)\right]}^m$$

(18)

where K′ = 1/K^m and m = 1/n are new constants.

One should pay attention to the fact that Equation (17) turns into Equation (14), if the limiting relative density ρ_∞, will be substituted by the limiting density ρ_∞ = 1.0. Therefore, the Secondi’s equation can describe a wider class of powder materials including both hard or brittle and plastic powders. As an example of the approximation by this equation of experimental data on compaction of hard-to-deform plastic and almost non-deformable brittle powders, we used the experimental data on compaction of titanium carbide powder [53] and three iron powders [51] that were compacted to an extremely high density. The values of relative density at different compaction pressures for titanium carbide and three iron powders are given in

Table 5. Experimental data on compaction of titanium carbide powders [53] and some iron powders [51].

Material *	Relative Density ρ and Corresponding Densification Pressure p (MPa)
TiC [53]	ρ	0.37	0.485	0.498	0.518	0.547	0.587	0.614	0.65	0.699	0.719
	p	0	4.41	8.82	17.64	35.28	70.56	141.12	282.24	564.48	846.72
FeKH3 [51]	ρ	0.253	0.640	0.831	0.890	0.920	0.941	0.966	0.971	0.978	0.981
	p	0	196	392	588	784	980	1470	1960	2450	2940
FeKH6 [51]	ρ	0.439	0.677	0.772	0.846	0.885	0.914	0.944	0.955	0.956	0.958
	p	0	196	392	588	784	980	1470	1960	2450	2940
FeKH9 [51]	ρ	0.397	0.673	0.773	0.841	0.884	0.905	0.942	0.955	0.959	0.961
	p	0	196	392	588	784	980	1470	1960	2450	2940

* Iron powders correspond to the following methods of their preparation: FeKH3—vibration grinding, FeKH6—carbonyl, and FeKH9—steel.

.

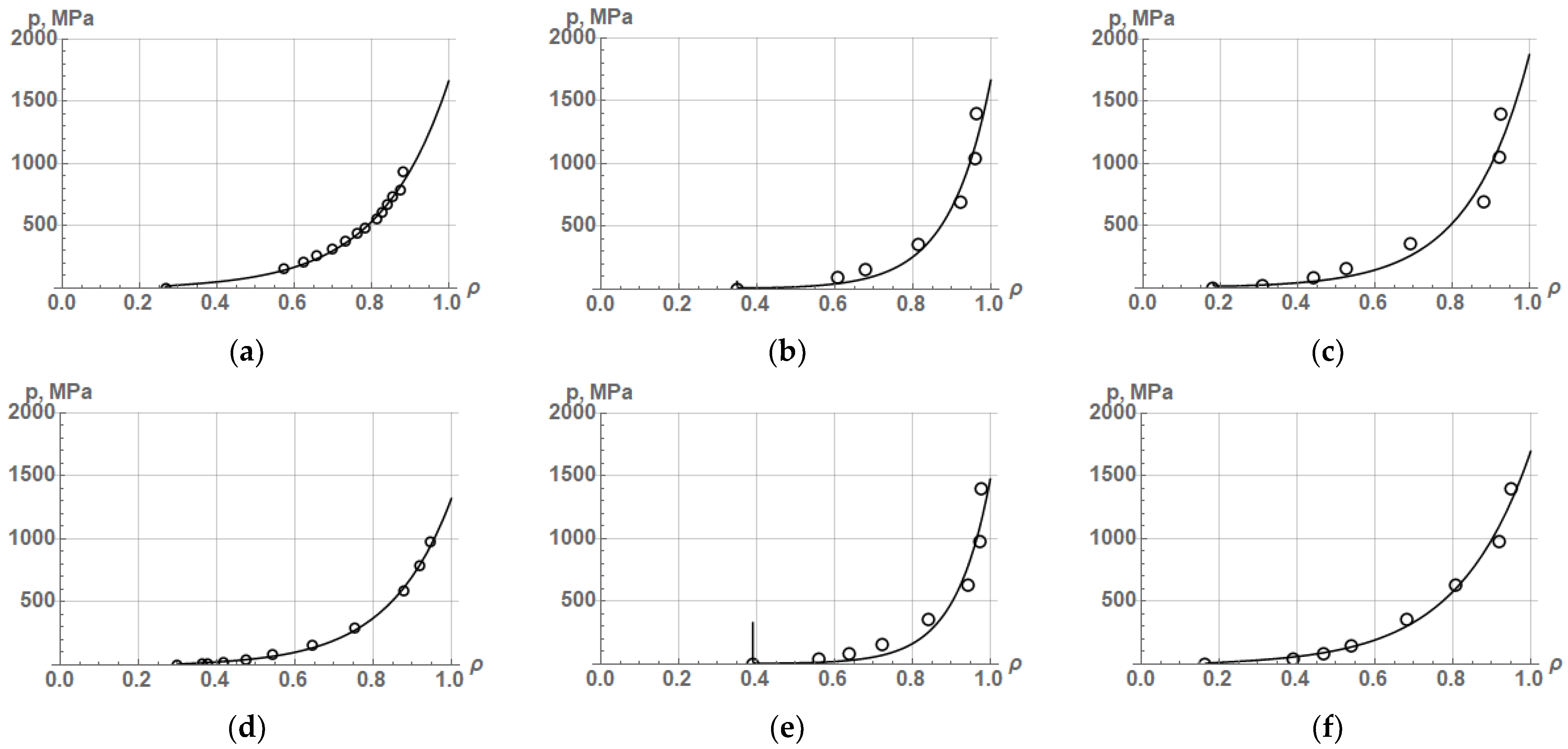
The results of approximation by the Secondi’s Equation (18) of these powders are shown in Figure 4, and the values of constant parameters and the coefficient of determination are listed in

Table 6. Constants and coefficient of determination R² obtained via approximation of experimental data on the compaction of titanium carbide powder [53] and three iron powders from [51] using Equations (18) and (14).

Parameter	Powder
	TiC [53]		FeKH3 [51]		FeKH6 [51]		FeKH9 [51]
	Equation Type
	(17)	(13)	(17)	(13)	(17)	(13)	(17)	(13)
ρ0	0.37		0.256		0.439		0.397
ρ∞	0.8146	1.0	0.985	1.0	0.9587	1.0	0.9623	1.0
$K\prime$, B, MPa	257.4	1793.1	171.4	81.19	364.5	214.9	355.9	221.3
m	2.739	3.642	1.725	2.715	1.102	2.561	1.175	2.428
R2	0.99787	0.99719	0.99519	0.98109	0.99344	0.93326	0.99952	0.95782

. In addition, Figure 4 and Table 6 also show for comparison the results of these powders approximation by Equation (14). As seen, the Equation (18) describes PCP for brittle and ductile powders with higher accuracy than Equation (14) does.

One of the factors that cause the increased accuracy of the Secondi’s Equation (18) when describing the compaction process to an extremely high density is probably the presence of three constants. Another important advantage of the Secondi’s equation is the fact that it provides for a real powder compaction process, where the compaction pressure tends to infinity at a relative density of significantly below 1.0. The equation of the authors Ge Rong-de, A. B. Yu and Z. H. Gu, L. Parilak and E. Dudrova (14) does not provide for such a possibility. It follows that the equations for PCP with two empirical constants cannot describe this process to the relative density level of 0.96–0.99 with high accuracy.

It was important to analyze another modified Konopicky-Heckel’s equation describing PCP to a high density. We mean the equation of R. Panelli and F. Ambrosio Filho (1998) [54], which in the original record had the form:

$$\mathit{ln}\left(\frac{1}{1-\rho }\right)=A\sqrt{p}+B,$$

(19)

where A and B are constants, and which can also be written in a shorter form:

$$\mathit{ln}\left(\frac{1-{\rho }_0^{\prime }}{1-\rho }\right)=A\sqrt{p,}$$

(20)

where ${\rho }_0^{\prime }$ = 1 − Exp(−B) is also constant.

If pressure is taken as a function, then the Equation (19) takes the form:

$$p=A^{\prime }{\left[\mathit{ln}\left(\frac{1}{1-\rho }\right)-B\right]}^2,$$

(21)

where A′ = 1/A² is a new constant.

To evaluate the accuracy of the PCP description by this equation, we have approximated the experimental data on the compaction of two groups of powders. In one group the experimental data show a final relative density less than 0.95, and in the other group—more than 0.95. 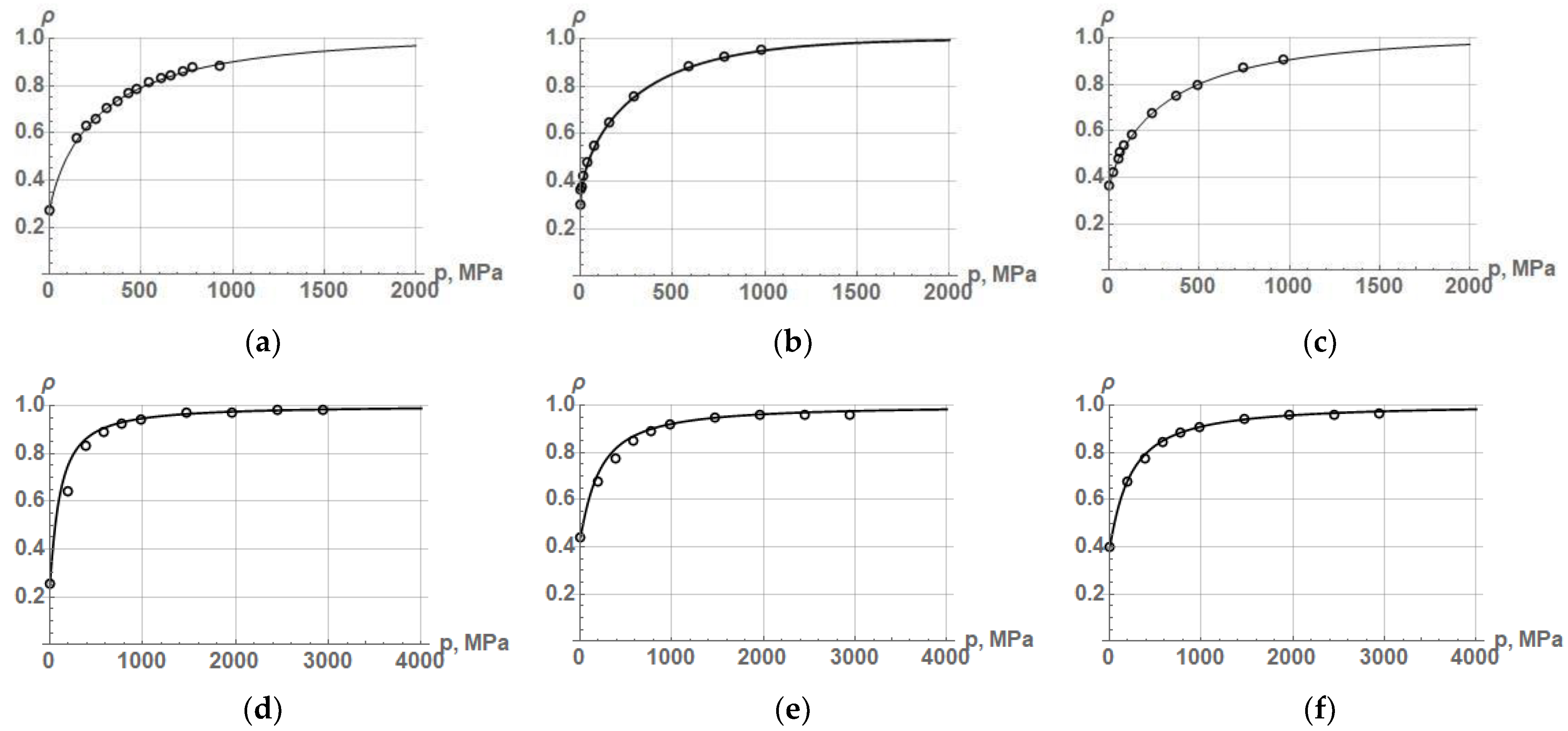That is, for the first group we use the data on iron, copper, and nickel powders from Table 1, and for the latter one—iron powders from Table 5. The results of the approximation of PCP for these powders by Equation (21) are shown in Figure 5, and the values of the constant parameters and the coefficient of determination R²—in

Table 7. Constants and coefficient of determination R² obtained via approximation of experimental data on the compaction of powders of iron, copper, nickel, and FeKH3, FeKH6 and FeKH9 using Equation (21).

Parameter	Powder
	Iron	Copper	Nickel	FeKH3	FeKH6	FeKH9
ρ0	0.268	0.3	0.36	0.256	0.439	0.397
A′, MPa	172.4	106.6	188.1	276.2	439.2	394.8
A	−0.0761	−0.0969	0.0729	0.0602	0.0477	0.0503
B	−0.1179	−0.1340	0.0362	0.8435	0.8248	0.7225
${\rho }_0^{\prime }$	−0.1252	−0.1434	0.0355	0.5698	0.5617	0.5288
R2	0.99161	0.99076	0.99496	0.97272	0.92665	0.95315

.

As seen from the results of this approximation, Equation (21) describes PCP quite accurately when the powders are compacted to a density of less than 0.95. If the powders are compacted to a density close to 1.0, then the Equation (21) describes the PCP with low accuracy, at which the beginning and middle of PCP are distorted. In this case, it is impossible to correctly assess the features of the powder and its mechanical and deformation properties. It follows that in order to determine the real properties of a powder during its compaction in a die, it is necessary to have, firstly, experimental data on the compaction of a particular powder to a density close to 1.0 and, secondly, an equation that allows to describe such a process with high accuracy. In this regard, the equations for PCP that contain some physical characteristics of the materials used for powder production are of interest.

3. Equations in Which the Physical Characteristics of Compact Materials Are Used

The above equations for PCP description have basically two constants. In some cases, attempts were made to establish the physical meaning of these constants. e.g., two constants, K and n, in Equations (13) and (17) characterize, according to the authors, the powder material plasticity and the hardening work during powder deformation. These constants are similar to the coefficients characterizing the plasticity and strain hardening of compact materials. In this regard, some researchers have tried to obtain an equation for PCP taking the strength and plasticity characteristics of the material used for powder production from reference books.

An attempt to relate one of the equation constants to the yield strength of the powder material was made by S. Torre (1948) [12] and A. N. Nikolaev (1962) [13]. They proposed the following equations:

$$p=2{\sigma }_{S}ln\frac{{\theta }_0}{\theta }=2{\sigma }_{S}ln\frac{1-{\rho }_0}{1-\rho }$$

(22)

and

$$p=C\times {\sigma }_S\times \rho \times ln\frac{\rho }{1-\rho },$$

(23)

where σ_S is the yield strength of the powder material and C = 2.5 ÷ 3 is a constant.

The Equation (23) was modified by G. M. Zhdanovich (1999) [14] as follows:

$$p=C\times {\sigma }_S\times \rho \times ln\frac{1-{\rho }_0}{1-\rho }$$

(24)

Equation (24) does not have the disadvantage inherent in Equation (23), where the pressure becomes negative when the relative density is less than 0.5, but the parameter C is not known in advance and must be determined, as G. M. Zhdanovich points out, from the experiment. The above equations are difficult to use for description of PCP, since the yield strength of particles can differ significantly from the yield strength of an absolutely dense material.

Of interest is an equation that takes into account the features of both ductile and brittle powders, as well as the effect of powder friction against the die wall during PCP. Such an equation was proposed in the work of Li S., Khosrovabadi P.B., Kolster B.H. (1994) [16]. Moreover, these authors presented experimental data on the compaction of not only plastic Ni powder but also a mixture of plastic (Ni) and ceramic (Al₂O₃) powders, as well as nickel-coated ceramic (Al₂O₃, SiC) powders. They took into account the forces of powder friction against the walls of the die and, as a result, proposed the following equation (in original form):

$$lnP=mln\left(ln\frac{D}{D_0}\right)-n\left(1-\frac{D}{D_m}\right)+ln\frac{M_0}{K}$$

(25)

where P is the external pressure, D is the absolute density of the powder blank at pressure P, D₀ is the initial density of the powder, D_m is the theoretical density of the powder material, M₀ is the compaction modulus for a dense sample, K is a dimensionless parameter associated with the friction coefficient of the powder (against the die wall) and workpiece geometry, and m and n are empirical constants. In this case, the parameters M₀ and K are also constant.

If the above equation is potentiated and the absolute density is converted into relative density, then the following equation is obtained which associates pressure with the relative density:

$$p=A{\left(ln\frac{\rho }{{\rho }_0}\right)}^{m}Exp\left[-n(1-\rho )\right],$$

(26)

where the three constants A = M/K, m and n can be determined by fitting the equation to the experimental curve.

The authors of this equation showed that the compaction of nickel powder, equivolume mixture of nickel and aluminum oxide powders, as well as aluminum oxide and silicon carbide powder coated with aluminum can be described by Equation (25) with high accuracy [16]. However, it should be kept in mind that the experimental data obtained by authors apply to the materials with a final relative density less than 0.8. For approximation by Equation (26) the experimental data for higher final density, e.g., the data on the compaction of iron and copper powders from Table 1, as well as unusual data on the compaction of coarse and fine iron and copper powders from the book by F. V. Lenel [55], (p. 96, Figures 3–25) were of interest. The experimental data on compaction of coarse and fine Fe and Cu powders, presented in [55], were obtained by digitizing the experimental points on the corresponding curves, and these data are given in

Table 8. Experimental data on the compaction of coarse and fine iron and copper powders [55].

Powder	Relative Density Values (ρ) and Corresponding Densification Pressure (p, MPa)
Fe (coarse)	ρ	0.35	0.609	0.68	0.814	0.925	0.963	0.965
	p	0	88.3	148.7	351.5	692.3	1042	1400
Cu (coarse)	ρ	0.391	0.561	0.64	0.725	0.844	0.945	0.976	0.978
	p	0	38.7	77.4	148.7	348.5	628.8	972.6	1400
Fe (fine)	ρ	0.183	0.312	0.442	0.527	0.694	0.882	0.925	0.927
	p	0	17	79	148.7	348.5	692	1044	1400
Cu (fine)	ρ	0.165	0.392	0.471	0.541	0.685	0.808	0.922	0.95
	p	0	35.6	74.3	144	351.5	627.5	975.7	1400

. Note that in [55] only the bulk or apparent density of coarse and fine iron and copper powders is indicated without information on the sizes of the powders.

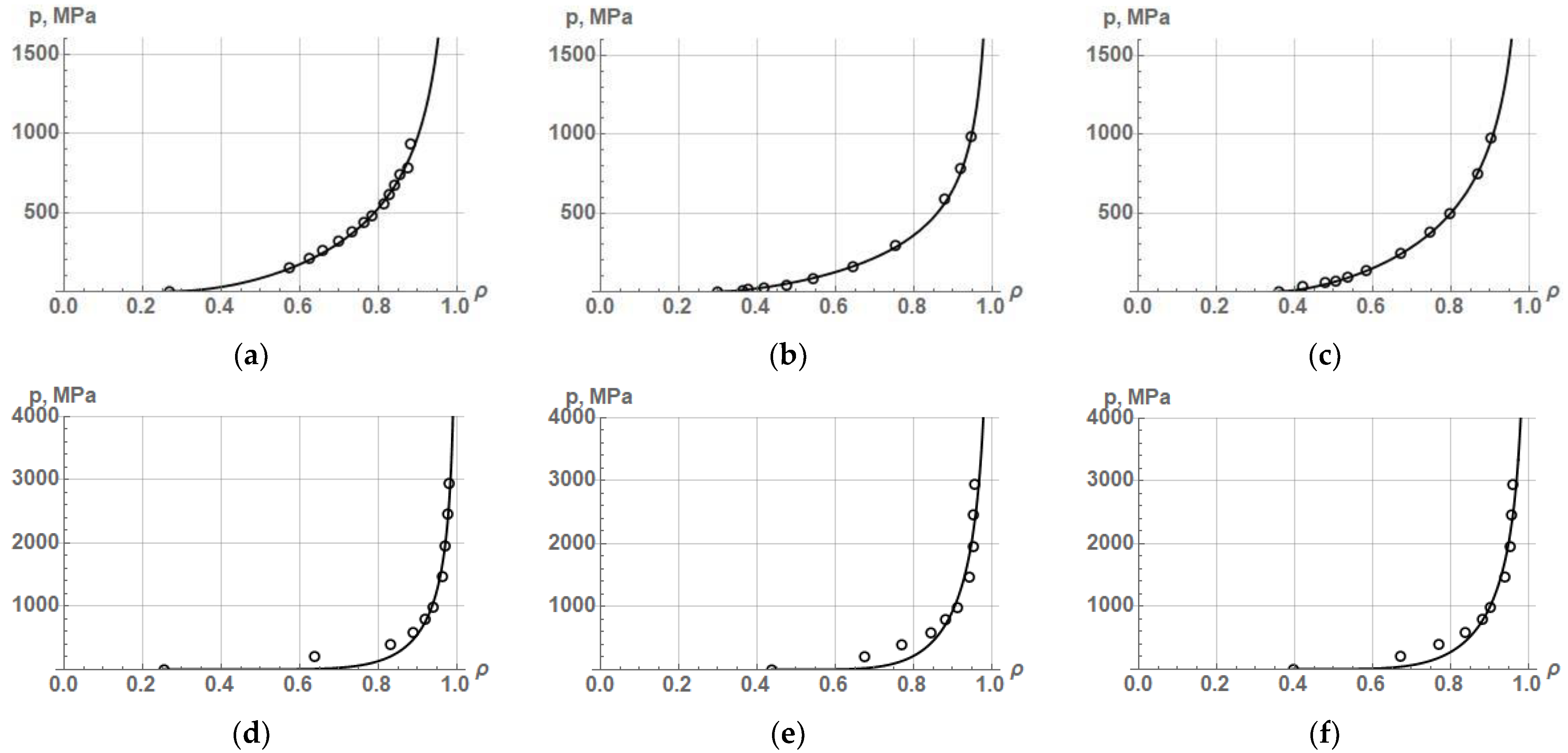
The results of approximation by Equation (26) of experimental data on the compaction of various iron and copper powders are shown in Figure 6, and the values of the constant parameters of Equation (26) and the coefficient of determination R² are listed in

Table 9. Constant parameters of Equation (26) obtained via approximation of experimental data on the compaction of iron and copper powders from Table 1 and iron and copper powders from Table 8.

Parameter	Powder
	Fe	Fe (Coarse)	Fe (Fine)	Cu	Cu (Coarse)	Cu (Fine)
ρ0	0.268	0.35	0.183	0.3	0.391	0.165
A, MPa	1596.6	1689.5	2006.5	1245.7	1436.0	1380.7
m	0.1505	−0.2869	−0.1256	0.3088	−0.4430	0.3484
n	5.5610	9.6759	6.5183	6.0371	11.623	5.1606
pmax, MPa	1664.8	1664.7	1876.6	1320.4	1474.8	1697.1
R2	0.98895	0.94972	0.94289	0.99791	0.92831	0.98167

.

The presented results of approximation of experimental data on the compaction of various iron and copper powders by Equation (26) show that the equation proposed by previously mentioned authors [16] allows description of PCP quite accurately in cases where the powder is compressed to a low density. And this happens despite the fact that the proposed equation has three constants that implicitly take into account the resistance of the powder material to deformation, the powder friction against the die walls, and the compacted powders geometry. In addition, a characteristic feature of Equation (26) is the fact that it provides for obtaining a final pressure when the relative density of the powder reaches 1.0. Moreover, the value of this pressure (see p_max in Table 9) is unexpectedly low that confirms the impossibility of this equation to accurately describe PCP at the final stage.

Noteworthy is another equation for PCP presented in one of the works by G. Aryanpour and M. Farzaneh (2015) [17]. When deriving the equation, the authors analyzed various mechanisms of PCP, in particular—particles rearrangement and plastic deformation. With that, they made the assumption that these two mechanisms work together up to a sufficiently high relative density of 0.95, at which, as they believe, there are no more open pores, and the particle rearrangement mechanism does not operate. To describe compaction due to the particle rearrangement mechanism, the authors suggested the following equation:

$$p=b\ast {\left(\frac{\rho -{\rho }_0}{1-\rho }\right)}^a$$

(27)

where b and a are constants determined from the experiment, ρ₀ is the initial density of the powder in the die.

After a simple transformation and taking logarithm, the Equation (27) takes a form:

$$ln\left(\frac{1-{\rho }_0}{1-\rho }\right)=ln\left(\frac{p^c}{b^c}+1\right),$$

(28)

where c = 1/a is a constant.

To describe the powder compaction due to plastic deformation, the researchers [17] used the Heckel’s Equation [11] written in the form:

$$ln\left(\frac{1-{\rho }_0^{\prime }}{1-\rho }\right)=kp,$$

(29)

where k is a constant, but ${\rho }_0^{\prime }$ is the conditional initial density of the powder.

According to G. Aryanpour and M. Farzaneh, these two mechanisms are summed up during compaction of the powder, and as a result, the following equation was proposed (in this case, the conditional initial density ${\rho }_0^{\prime }$ in Equation (29) is replaced by the actual initial density ${\rho }_0$):

$$ln\left(\frac{1-{\rho }_0}{1-\rho }\right)=ln\left(\frac{p^c}{b^c}+1\right)+kp$$

(30)

The Equation (30), as noted by its authors, can be used to describe PCP in the density range from ρ₀ to ρ = 0.95. It takes into account the action of two mechanisms—particles rearrangement and particles deformation. In this case, at the beginning of the compaction process, the rearrangement mechanism prevails, and at the end of the compaction, the deformation mechanism does. Unfortunately, this equation cannot be transformed in such a way that it could be solved with regard to the pressure p and an appropriate approximation can be made. However, to estimate the accuracy of approximation of various experimental data by Equation (30), it is necessary to transform it so that the function is the relative density ρ. In this case, it will acquire the following form:

$$\rho =1-\frac{\left(1-{\rho }_0\right)b^c}{\left(b^c+p^c\right)Exp\left[kp\right]}$$

(31)

But the Equation (31) hides compaction mechanisms, making it less useful. At the same time, this equation makes it possible to approximate experimental data on powder compaction and determine the values of three constants—b, c, and k. Taking into consideration that this equation has three constants, its adequacy in describing PCP not only up to a relative density of 0.95 but also up to a higher density is of interest. Therefore, to approximate the experimental data on PCP by this equation, we chose the experimental results previously used by us on the compaction of iron, copper, and nickel powders, presented in Table 1, as well as on iron powders compacted to high density presented in Table 5. The results of the approximation of experimental data on the compaction of these powders are shown in Figure 7. The values of the constants of Equation (31) and the coefficient of determination R² are given in

Table 10. Constant parameters in Equation (31) resulted from the approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1 and iron powders FeKH3, FeKH6, and FeKH9 from Table 5.

Parameter	Powder
	Fe	Cu	Ni	FeKH3	FeKH6	FeKH9
ρ0	0.268	0.3	0.36	0.256	0.439	0.397
ρlim	0.884	0.949	0.903	0.981	0.958	0.961
c	0.70715	0.51827	0.84085	1.14893	1.14893	1.10063
a = 1/c	1.4141	1.9295	1.1893	0.8704	0.8704	0.9086
b	437.1	637.8	406.3	108.21	208.21	227.31
k	0.00102	0.00184	0.00078	0.00001	0.0001	0.00009
R2	0.99883	0.99985	0.99927	0.97092	0.98165	0.99710

.

As seen from presented results, the accuracy of the approximation of experimental data on the compaction of various powders by Equation (31) is high for cases of powder compaction up to a density of 0.95. This may indicate the adequacy of the hypothesis that allows the simultaneous existence of the mechanisms of rearrangement and deformation of particles during the compaction process up to a relative density of 0.95. Alongside with this, the Equation (31) can, in some cases, describe with high accuracy the PCP up to a relative density exceeding 0.95 (Table 10, FeKH9 powder). It is also important that this equation allows one to estimate the degree of density change during powder compaction due to both particles rearrangement (Δρ_r) and plastic deformation (Δρ_d).

In order to evaluate the change in density by two mechanisms, it was suggested to determine the derivatives of the relative density with regard to pressure separately for the rearrangement and plastic deformation mechanisms [17]. If we fully expand these derivatives, then they will look as:

$$\frac{d\rho }{dp}=\frac{\left(1-{\rho }_0\right)c{b}^c}{{\left(b^c+p^c\right)}^2{p}^{(1-c)}Exp\left[kp\right]}—\mathrm{for} \mathrm{particles} \mathrm{rearrangement}$$

(32)

and

$$\frac{d\rho }{dp}=\frac{\left(1-{\rho }_0\right)b^{c}k}{\left(b^c+p^c\right)Exp\left[kp\right]}—\mathrm{for} \mathrm{plastic} \mathrm{deformation}$$

(33)

The areas under the curves (32) and (33) within the pressure range from zero to a value corresponding to a given density will show the degree of change in density for the corresponding compaction mechanism. Numerical integration of dependences (32) and (33) for the examples shown in Figure 7, within the pressure range from zero to the pressure corresponding to a density of 0.95, led to the results presented in

Table 11. Degree of change in density due to rearrangement and plastic deformation of particles during compaction of the powder from the initial density to a density of 0.95, as well as the true degree of plastic deformation of the particles and the degree of change in the relative density from initial to 0.95.

Density Change Mechanism	Powders
	Fe [37]	Cu [38]	Ni [39]	FeKH3	FeKH6	FeKH9
Rearrangement, Δρr	0.3937	0.2890	0.3805	0.7053	0.5037	0.5335
Plastic deformation, Δρd	0.3141	0.3787	0.2245	0.0019	0.0234	0.0247
True plastic deformation of particles, δpl	0.40135	0.50861	0.26958	0.00198	0.02494	0.02638
Degree of change in density, Δρ = 0.95 − ρ0	0.682	0.65	0.59	0.694	0.511	0.553

. In addition, this Table 11 presents the true value of particles plastic deformation, which, for the case of reaching the relative density of 0.95, was calculated using the following formula:

$${\delta }_{pl}=ln\left(\frac{1}{1-\mathsf{\Delta }{\rho }_d/0.95}\right).$$

(34)

By the data in Table 11, the degree of change in the powder density due to rearrangement during compaction in a rigid die can exceed the degree of change in density through plastic deformation of the particles. In relatively hard powders, such as FeKH3, FeKH6, and FeKH9, densification occurs practically due to the particles rearrangement. There cannot be excluded the case when description of solid powders particles rearrangement with the Equation (27) is very approximate. In this regard, I would also like to draw attention to the fact that the Equation (27) exactly corresponds to the equation of M. Yu. Bal’shin (1972) [18] (p. 163, Eq. V.47) which he proposed to describe the third stage of the densification process, i.e., the stage where practically there is no rearrangement of the particles.

It should also be noted that the process of particle rearrangement during compaction of powders in a rigid die is explicitly reflected in the equation proposed as far back as in the middle of the last century (1962) by A. R. Cooper and L. E. Eaton [26]. In the original record this equation is as follows:

$$V^{*}=\frac{V_0-V}{V_0-V_{\infty }}=a_1·exp\left(-\frac{k_1}{P}\right)+a_2·exp\left(-\frac{k_2}{P}\right),$$

(35)

where V* is the degree of powder sample volume change under pressure, V₀, V and V_∞ are initial volume at zero pressure, current volume at pressure P, and volume at infinite pressure, respectively, P is the compaction pressure, a₁ and k₁ are constants characterizing the rearrangement process, and a₂ and k₂ are constants characterizing the process of plastic deformation.

When compacting the powder, it is advisable to operate with the relative density ρ = V_com/V (V_com is the volume of a pore-free sample), then the Equation (35) can be converted into the dependence of relative density (ρ) on pressure (p):

$$\rho =\frac{{\rho }_0}{\left\{1-\left(1-\frac{{\rho }_0}{{\rho }_{\infty }}\right)·\left[a_{1}exp\left(-\frac{k_1}{p}\right)+a_{2}exp\left(-\frac{k_2}{p}\right)\right]\right\}}$$

(36)

where ρ₀ is the initial density of powder, ρ_∞ ≤ 1 is the density at infinite pressure.

This equation was proposed in order to describe the compaction process of ceramic powders. Therefore, it can be used to approximate the compaction process of any hard powders. In this regard, the applicability of Equation (36) was tested for describing the process of compaction of titanium carbide powders and iron powders presented in Table 5. The results are shown in Figure 8, and the values of the constant parameters of Equation (36) and the coefficient of determination R² are listed in

Table 12. Constant parameters in Equation (36) resulted from the approximation of experimental data on the compaction of titanium carbide and iron powders FeKH3, FeKH6, and FeKH9 from Table 5.

Parameter	Powder
	TiC	FeKH3	FeKH6	FeKH9
ρ0	0.37	0.256	0.439	0.397
ρ∞	0.8	0.985	0.97	0.965
a1	0.5999	0.8089	0.8159	0.8144
k1	1.5592	37.908	100.57	87.620
a2	0.3338	0.2086	0.2173	0.2165
k2	108.40	37.945	76.678	51.647
R2	0.99324	0.99386	0.99687	0.99844

. The approximation was performed at a given value of the parameter ρ_∞ for each powder.

It follows from the presented approximation results that Equation (36) that contains four constant parameters (the fifth parameter ρ_∞ is predetermined) is capable of describing the compaction process of hard metal and ceramic powders with high accuracy. The most important result of approximating the process of compaction of hard powders by this equation is the fact that the process of particle rearrangement affects the change in porosity to a much greater extent than the process of powder deformation. This is evidenced by the value of the constant a₁ in Table 12, which reaches 80% of the entire compaction process. A similar result follows when describing the process of compaction of hard iron powders by Equation (31), Table 11.

4. Modern Works Describing the Process of Powder Compaction in a Rigid Die

Recently published papers with new equations for PCP are of increased interest. First of all, a new article by L. Parilak, E. Dudrova et al. (2017) [56] is worth of attention. As said above, these authors previously proposed an equation with two constants, which in many cases allows one to describe PCP quite accurately. In new article, they proposed a novel equation based on their former one (13) which was transformed into an equation with one constant due to the relation established between the constants K and n in the form ln(K) = 1.2952 − 7.3349n. With this, Equation (13) after taking a double logarithm acquires the form:

$$ln\left[ln\left(\frac{P_0}{P}\right)\right]=1.2952-7.3349·n+n·ln\left(p\right),$$

(37)

where P₀ and P are the initial and current porosities of the powder sample.

After potentiation, the Equation (37) is transformed into the following expression:

$$ln\left(\frac{P_0}{P}\right)=3.6517·{\left(\frac{p}{1532.9}\right)}^n$$

(38)

from which one can get an equation where the compaction pressure is a function, and porosity or relative density (ρ = 1 − P) is an argument:

$$p=1532.87·{\left[0.2738·ln\left(\frac{1-{\rho }_0}{1-\rho }\right)\right]}^m,$$

(39)

where m = 1/n is a new constant.

There is an ambiguous attitude to this new equation for PCP. On one hand, with an equation containing one constant parameter it is easier to describe the compaction of different powders, but, on the other hand, such an equation is not capable of taking into account the great diversity in the morphology and properties of powders. All differences in the behavior of powders during compaction are averaged in one parameter. This may reduce the accuracy of the densification process description of certain powders. Indeed, the approximation by Equation (39) of experimental data on the compaction of iron, copper and nickel powders (Table 1) showed a lower accuracy in two cases out of three (

Table 13. The value of the constant m in Equation (39) and the coefficient of determination R² obtained after the approximation of experimental data on compaction of iron, copper, and nickel powders from Table 1.

Parameter	Powder
	Fe	Cu	Ni
ρ0	0.268	0.3	0.36
m	1.0219	1.3317	0.9755
n = 1/m	0.9786	0.7509	1.0251
R2	0.93988	0.99925	0.95445

) as compared with the approximation by two-parameter equation (14) (Table 4).

With a reduced accuracy in describing PCP, we will get to know with reduced accuracy the degree of plastic deformation of particles, the work of plastic deformation, the magnitude of the resistance of particles to deformation, as well as other characteristics of the powder. Therefore, a one-parameter equation can be used to approximate assessment of the compaction process and powder properties.

Another recent work on compressibility of powders during compaction in a die deserves an attention, namely, the article of J.M. Montes, F.G. Cuevas, J. Cintas et al. (2018) [57]. When developing their equation, the authors aimed at minimizing the number of experimental constants in the equation and using physical parameters, which are characteristic of the powder material and known in advance from reference books. Unfortunately, in many cases, such a desire cannot lead to obtaining an adequate compaction equation due to significant differences in the strength and plastic properties of powders and bulk material they are made of. The researches [57] proposed the following equation to describe PCP:

$$P_N=\frac{\sqrt{3}}{2}·\xi ·k{\left[ln\left(\frac{1-\mathsf{\Theta }}{1-{\mathsf{\Theta }}_M}\right)\right]}^n·\frac{\left(1-\mathsf{\Theta }/{\mathsf{\Theta }}_M\right)}{\sqrt{\mathsf{\Theta }/{\mathsf{\Theta }}_M}},$$

(40)

where P_N is the external pressure during compaction of the powder, Θ and Θ_M are the current and initial porosity of the powder sample, ξ is the coefficient that takes into account the friction of the powder against the die wall, k and n are the Hollomon equation parameters which characterize the law of hardening during deformation of a dense sample obtained from compacted powder.

According to the authors of [57], the parameters k and n are very close to the reference values for the powder material. Therefore, in Equation (40), the parameters k and n are known in advance, and the parameters Θ_M and ξ are determined by fitting the curve according to Equation (40) to the experimental compaction curve of a particular powder. In the authors’ opinion, the advantage of Equation (40) is the use of previously known parameters k and n with a clear physical meaning. However, the proposed equation does not take into account the phenomenon of particle rearrangement during powder compaction, as well as the possible discrepancy between the strain hardening of particles themselves and the strain hardening of a compact sample made from these particles.

In reality, such factors as the rearrangement of particles and the specific nature of the particle strain hardening, especially in the compaction of fine-grained particles, are of fundamental importance in describing the compaction process and for the adequacy of the corresponding equation. Therefore, the free status of the parameters k and n in Equation (40) can take into account both the particle rearrangement factor and the specific nature of the strain hardening of these particles. In this regard, an attempt was made to use Equation (40) to approximate the experimental curves for the compaction of various powders, provided that the parameters k and n are free, and the initial porosity is known. To perform the approximation, we transformed Equation (40) into the dependence of the compaction pressure p on the relative density ρ:

$$p=K·{\left[ln\left(\frac{\rho }{{\rho }_0}\right)\right]}^n·\frac{\left(\rho -{\rho }_0\right)}{\sqrt{\left(1-{\rho }_0\right)}·\sqrt{\left(1-\rho \right)}},$$

(41)

where K ≈ k (since ($\sqrt{3}$/2) × ξ ≈ 1) and n are constant parameters obtained from the experiment, ρ₀ is the initial relative density of the powder in the die.

To carry out the approximation, the experimental data for iron, copper and nickel powders from Table 1 as well as hard-to-compact iron powders from Table 5 were used. The results of the approximation are shown in Figure 9, and the values of the constants are listed in

Table 14. Constant parameters in Equation (41) obtained via approximation of experimental data on the compaction of iron [39], copper [40], and nickel [41] powders, as well as FeKH3, FeKH6, and FeKH9 iron powders from the book [51].

Parameter	Powder
	Fe	Cu	Ni	FeKH3	FeKH6	FeKH9
ρ0	0.268	0.3	0.36	0.256	0.439	0.397
K	345.01	270.37	462.51	26.4885	2343.95	1184.07
n	0.9927	0.5818	0.5946	9.45042	4.83775	4.58858
R2	0.99216	0.99803	0.99960	0.97298	0.92296	0.94935

.

The results of the approximation of various powders by Equation (41) show that in some cases this equation allows one to describe very accurately the PCP, despite the change in some principles underlying the derivation of Equation (40). However, hard powders compacted to a density greater than 0.95 cannot be adequately described by this equation.

A. Molinari et al. (2018) [27] also proposed a new equation for powder compaction in a rigid die. The authors studied the compaction of low-alloyed iron powders (alloyed with CuMo, Mo, CrMo, or CuMoNi) in a mixture with graphite and lubricant, and suggested describing PCP by the absolute density dependence on the average compaction pressure in the form of a power law:

$$1-\frac{{\overline{\rho }}_0}{\overline{\rho }}=A·{\left(P_m\right)}^B,$$

(42)

where ${\overline{\rho }}_0$ and $\overline{\rho }$ are the absolute initial and current density of the powder in the die (the dash above the symbol distinguishes the absolute density from the relative density, which we denote as ρ), respectively, P_m is the average compaction pressure, A and B are constant parameters obtained from the experiment.

It should be noted that a feature of the experimental PCP in article [27] is a relatively narrow range of compaction pressure up to 540 MPa, as well as the use of the absolute density of the material instead of the relative density. If we transform Equation (42) into the dependence of pressure on relative density, then we obtain power law:

$$p_m=A\prime ·{\left(1-\frac{{\rho }_0}{\rho }\right)}^{B\prime },$$

(43)

where ρ₀ and ρ are relative initial and current densities, respectively, A′ = 1/A^(1/B) and B′ = 1/B are constant parameters obtained from the experiment.

Note that using of the power law to describe PCP is not a new solution (see Equation (3)), but Equation (42) takes into account the real fact that at a density equal to the initial density ρ₀, the compaction pressure is zero. However, in the long-known equation (3), it is easy to take into account this fact if instead of the current relative density ρ we substitute the expression (ρ − ρ₀)/(1 − ρ₀), that allows taking into account not only the initial density but also the entire range of density changes from ρ₀ to ρ = 1.Then Equation (3) will acquire the form:

$$p=c·{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^d,$$

(44)

where c and d are constant parameters obtained from the experiment.

Comparison of the adequacy of Equations (43) and (44) showed that in describing the compaction of iron, copper, and nickel powders that we used the Equation (44) was more accurate. This follows from the approximation results presented in Figure 10 and in

Table 15. Constants in Equations (43) and (44) after approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1.

Parameter	Powder
	Iron		Copper		Nickel
	Equation Type
	(43)	(44)	(43)	(44)	(43)	(44)
ρ0	0.268		0.3		0.36
A′, c	16141.4	1377.9	28987.9	1192.8	15597.6	1398.8
B′, d	8.2798	2.8891	9.1188	3.2732	5.6115	2.5511
pmax, MPa	1233.2	1377.9	1135.9	1192.8	1286.0	1398.8
R2	0.97066	0.98030	0.98623	0.99207	0.97954	0.98932

.

As seen from Figure 10 and Table 15, the power-law dependence of pressure on relative density does not provide a high accuracy of the PCP description, especially in the initial stage of compaction, which is described by Equation (43) less accurately. Obviously by this reason the authors [27] divided PCP into two stages, in one of which particles are rearranging, and in the other, plastic deformation occurs. In this case, each stage of compaction was approximated by a power equation with its own constant parameters. However, such a method for PCP description was proposed by researches [44] as early as in 1975.

The ability to describe almost the entire compaction process with a single equation raises the question of how one equation can describe the different stages of PCP. In this case, two possibilities may exist: either the compaction process occurs according to one yet unknown mechanism, or the equation must contain a number of constants, which take into account, to varying degrees, the manifestation of different mechanisms. In the next two messages of this article (Part 2 and Part 3), new equations for powders compaction in a rigid die are proposed, which contain three and four constants. But in one case (Part 2), to obtain such equations, various equations of M. Yu. Bal’shin were corrected, and in another case (Part 3), the plasticity equations of a porous body proposed by Kuhn and Downey or Skorokhod, Martynova and Shtern were transformed.

According to the results of analysis concerning the equations presented in the form of simple mathematical functions or in the form of semi-empirical equations, which take into account some physical constants of the powder material, the following conclusion can be formulated.

5. Conclusions

• The considered equations for the compaction of powders in a rigid die in most cases contain two constants, which depend on the powder material and the type of equation and are determined from the experiment. At the same time, the accuracy of describing the process of powder compaction by equations with two constants is different. In addition, some equations lead to a finite value of compaction pressure upon reaching the pore-free state of the sample, while the others lead to an infinite pressure.
• High accuracy in describing the process of powder compaction using different equations is observed in the case of using a shortened range of density changes, i.e., up to 0.8–0.9, but such a description of the compaction process is not complete, since fundamental differences in the behavior of powders are observed when a relative density close to unity is reached. When compacting powders to a density greater than 0.95, the highest accuracy in describing the compaction process can be provided by equations with three constants, for example, such as the J. Secondi’s equation.
• Increasing the number of constants in the equation to three or four allows us to identify compaction mechanisms such as particle rearrangement and plastic deformation. This is shown by discussing the equations of A. R. Cooper and L. E. Eaton or G. Aryanpour and M. Farzaneh, which consider that the rearrangement and plastic deformation mechanisms operate in parallel throughout the compaction of powders to a relative density of 0.95.
• In a number of proposed equations, there was an attempt to take into account both the strength and plasticity characteristics of a powder compact material and the shape and size of particles, as well as the internal friction forces between particles and external friction forces between particles and the die wall. But this came down to setting the appropriate coefficients, which are constant throughout the entire compaction process. Moreover, in most cases, the value of these coefficients must be determined in the experiment and this neutralizes the desire of researchers to work without using empirical constants.