Performance Rank Variation Score (PRVS) to Measure Variation in Ensemble Member’s Relative Performance with Introduction to “Transformed Ensemble” Post-Processing Method
Abstract
1. Introduction
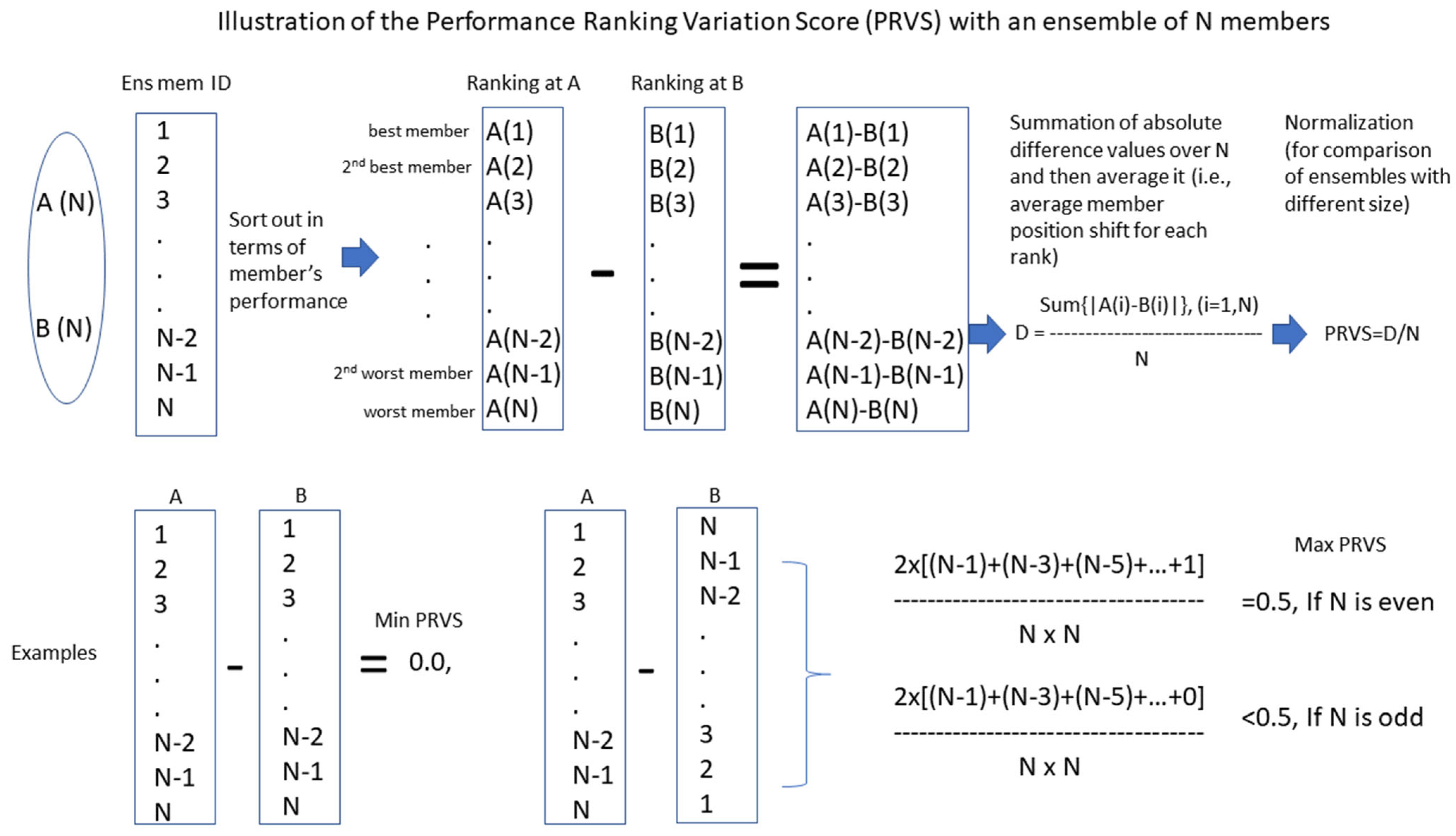
2. Performance Rank Variation Score (PRVS)
2.1. Definition
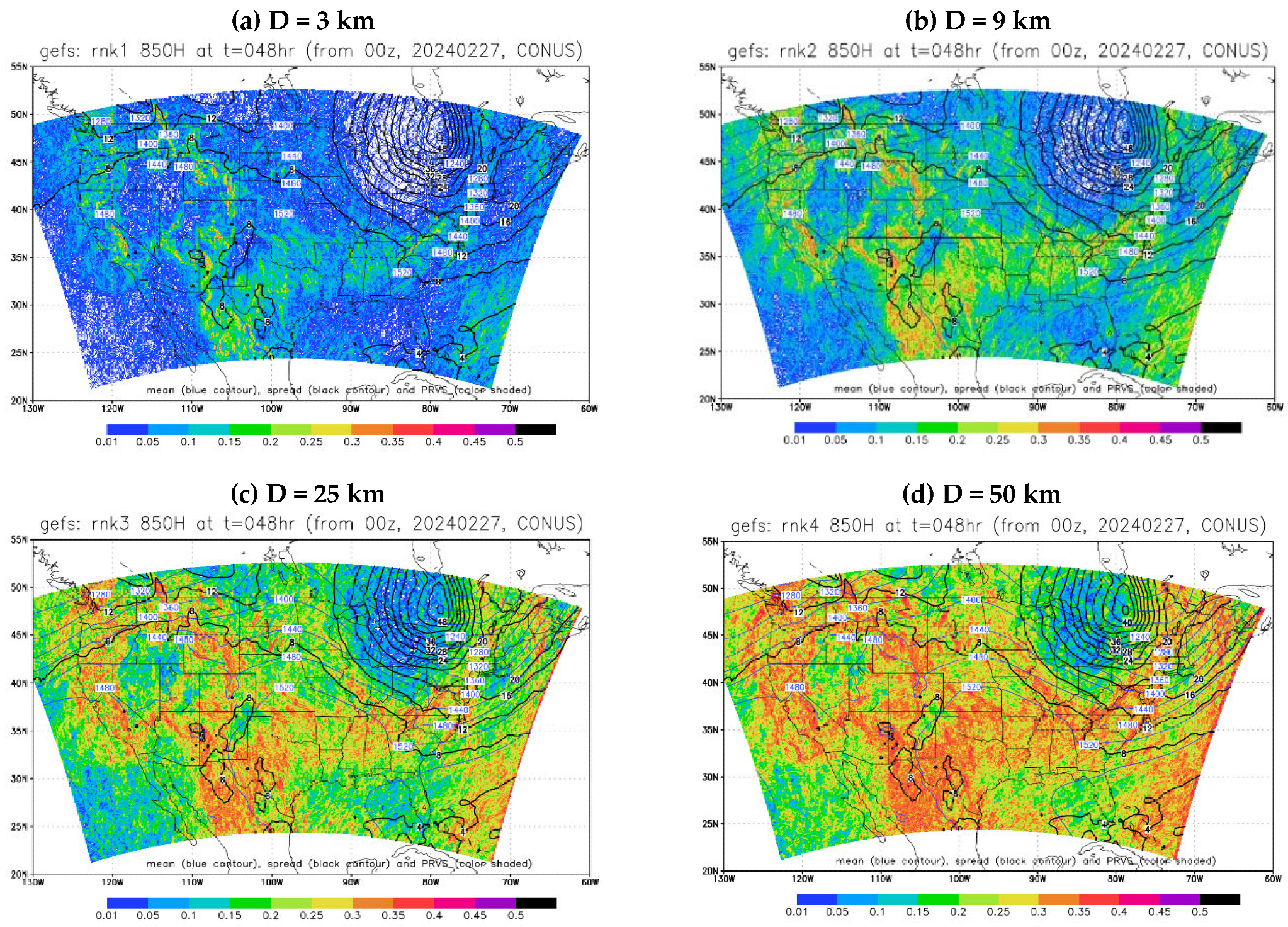
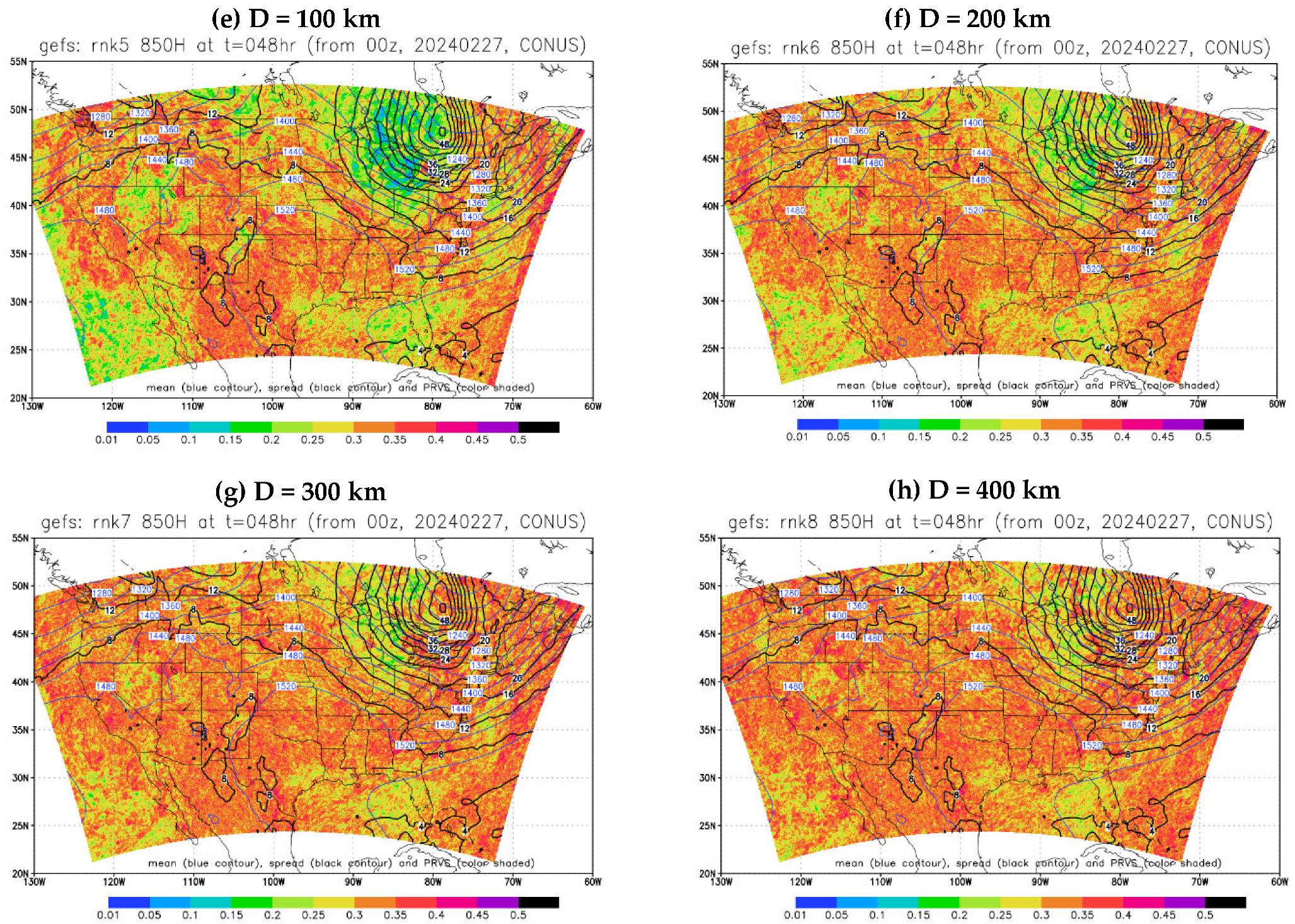
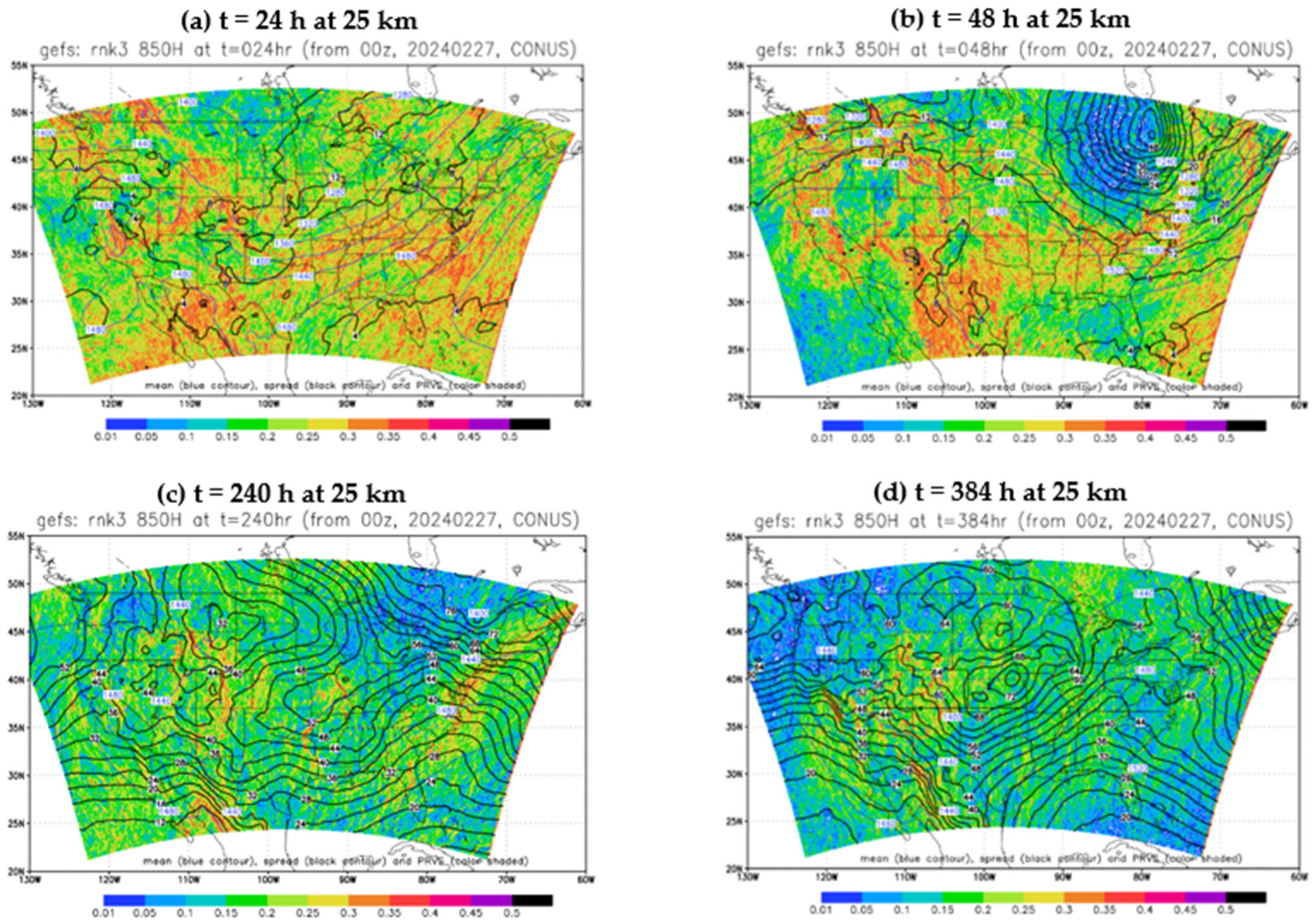
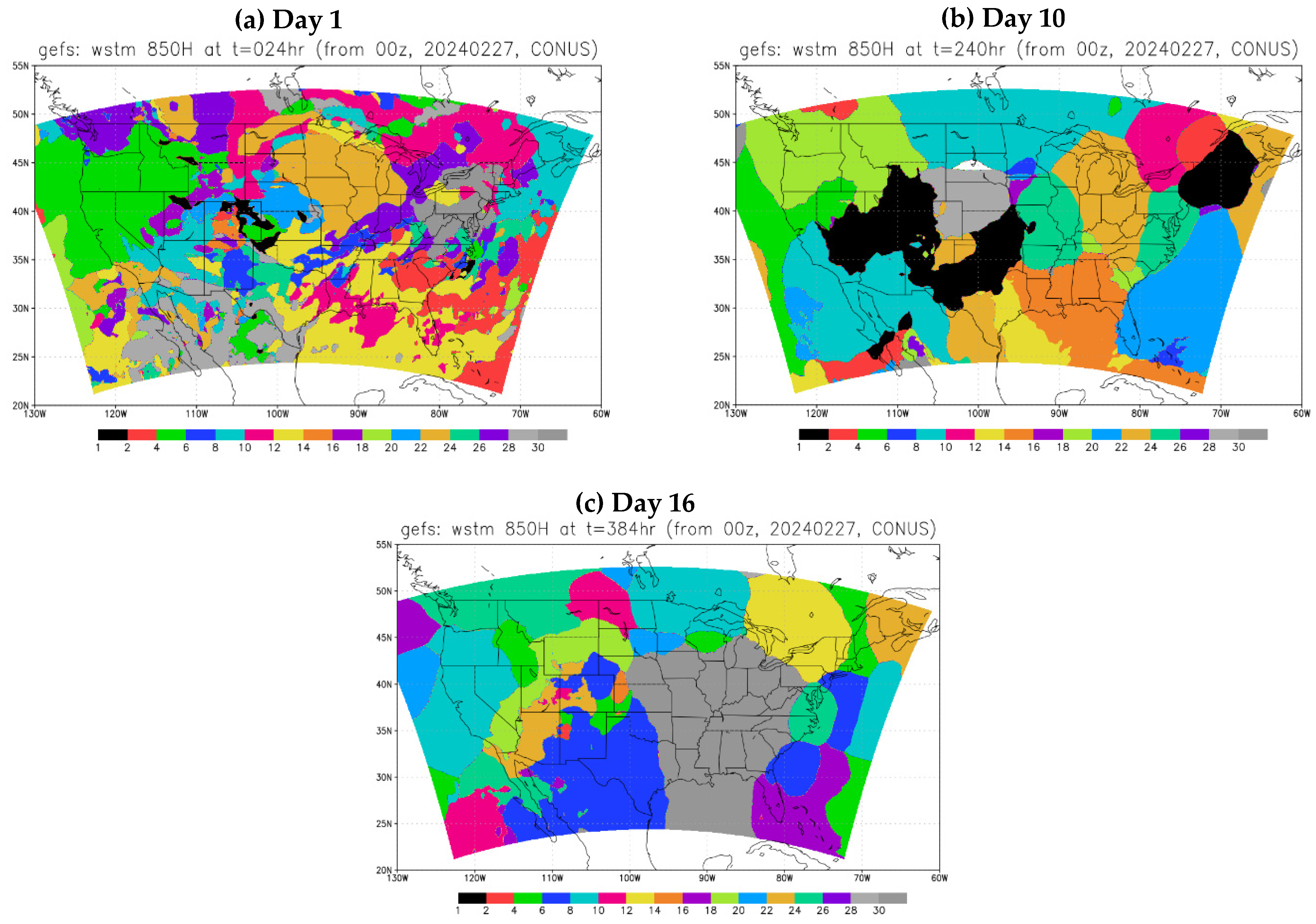
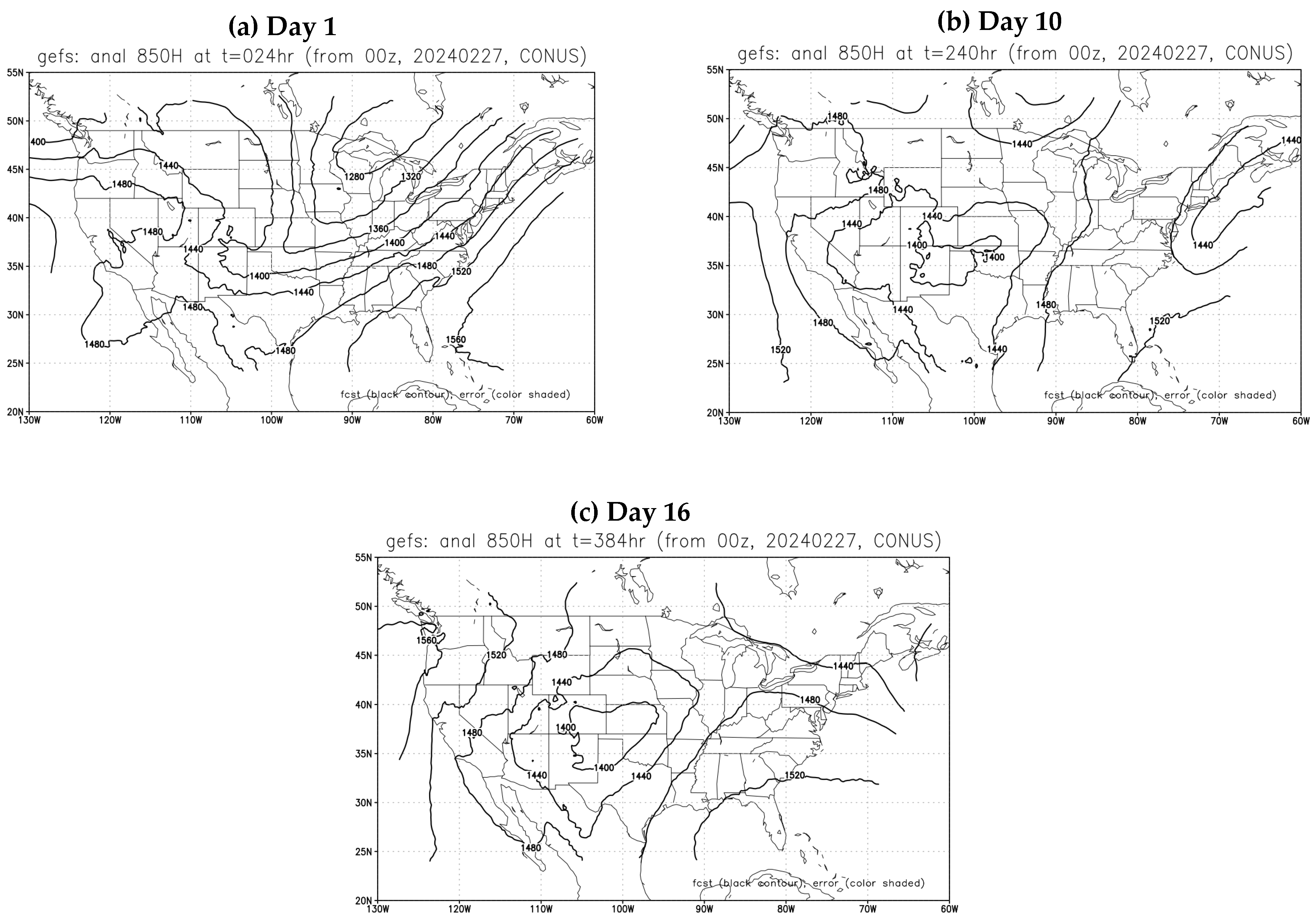
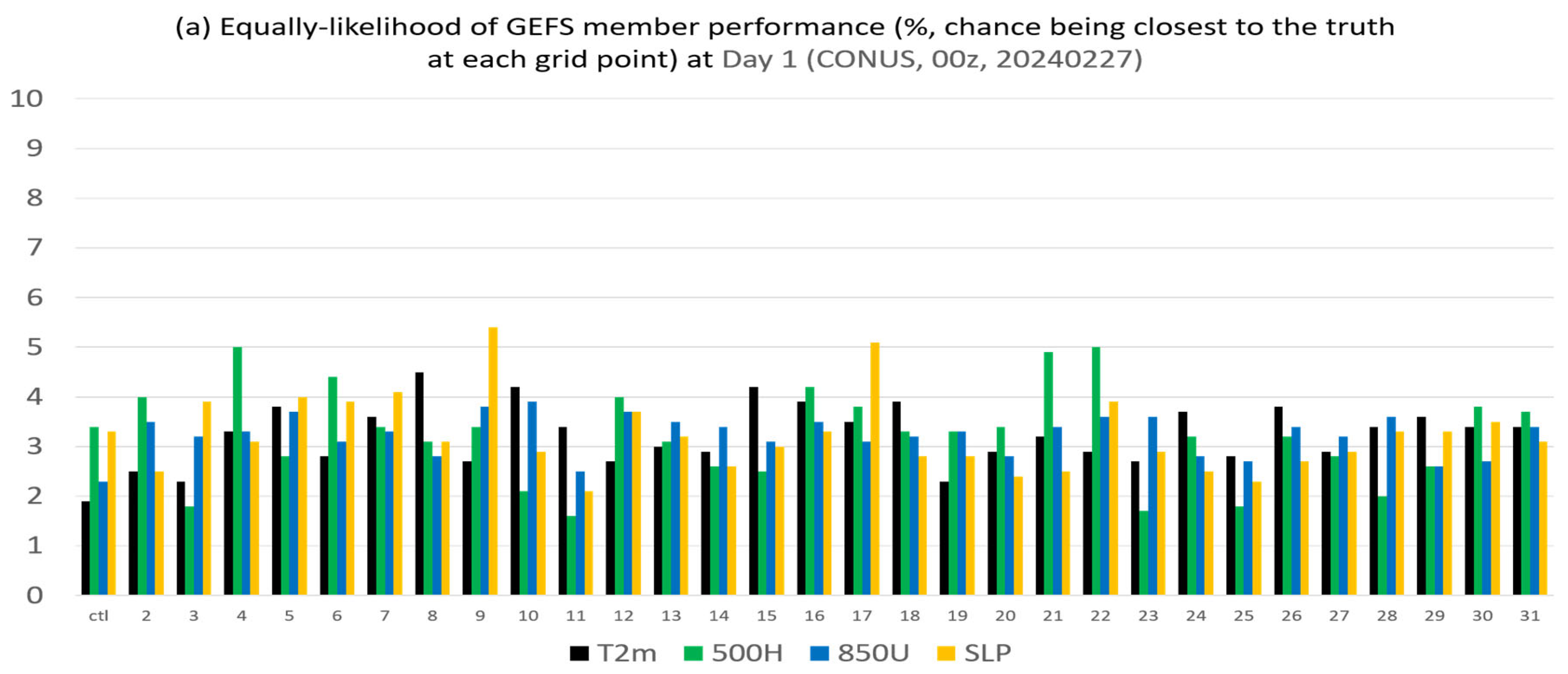
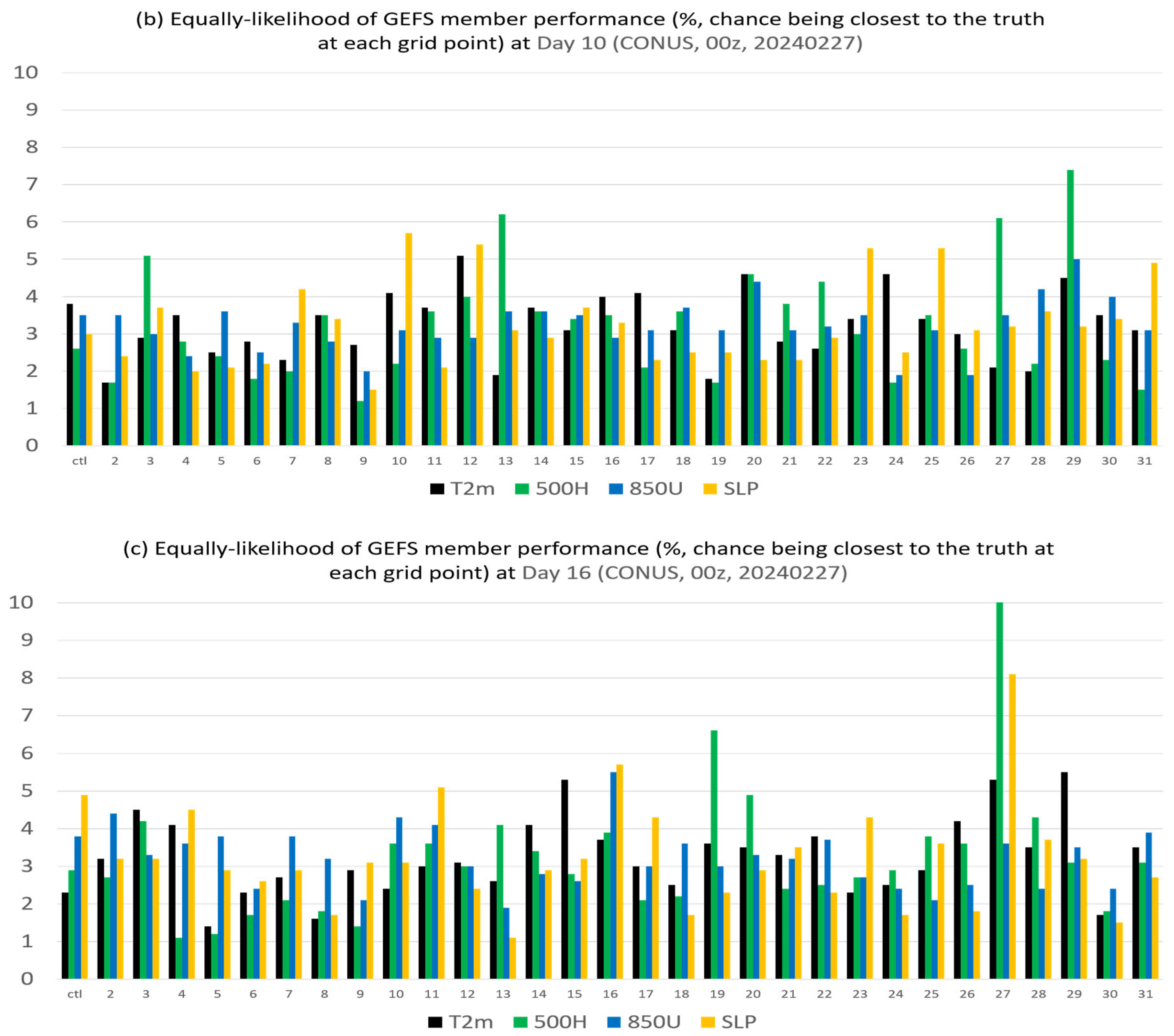
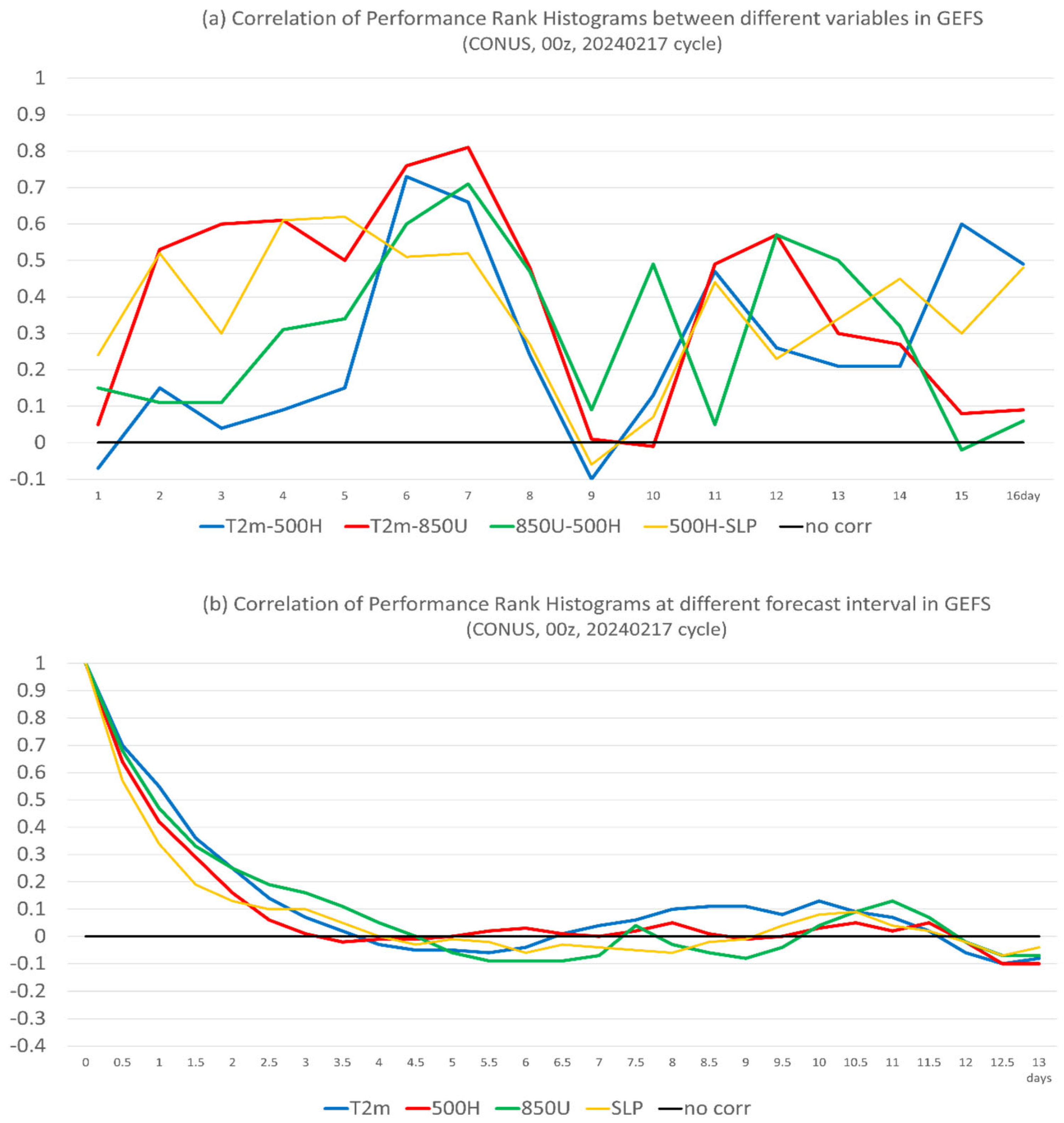
2.2. Application in GEFS Forecasts
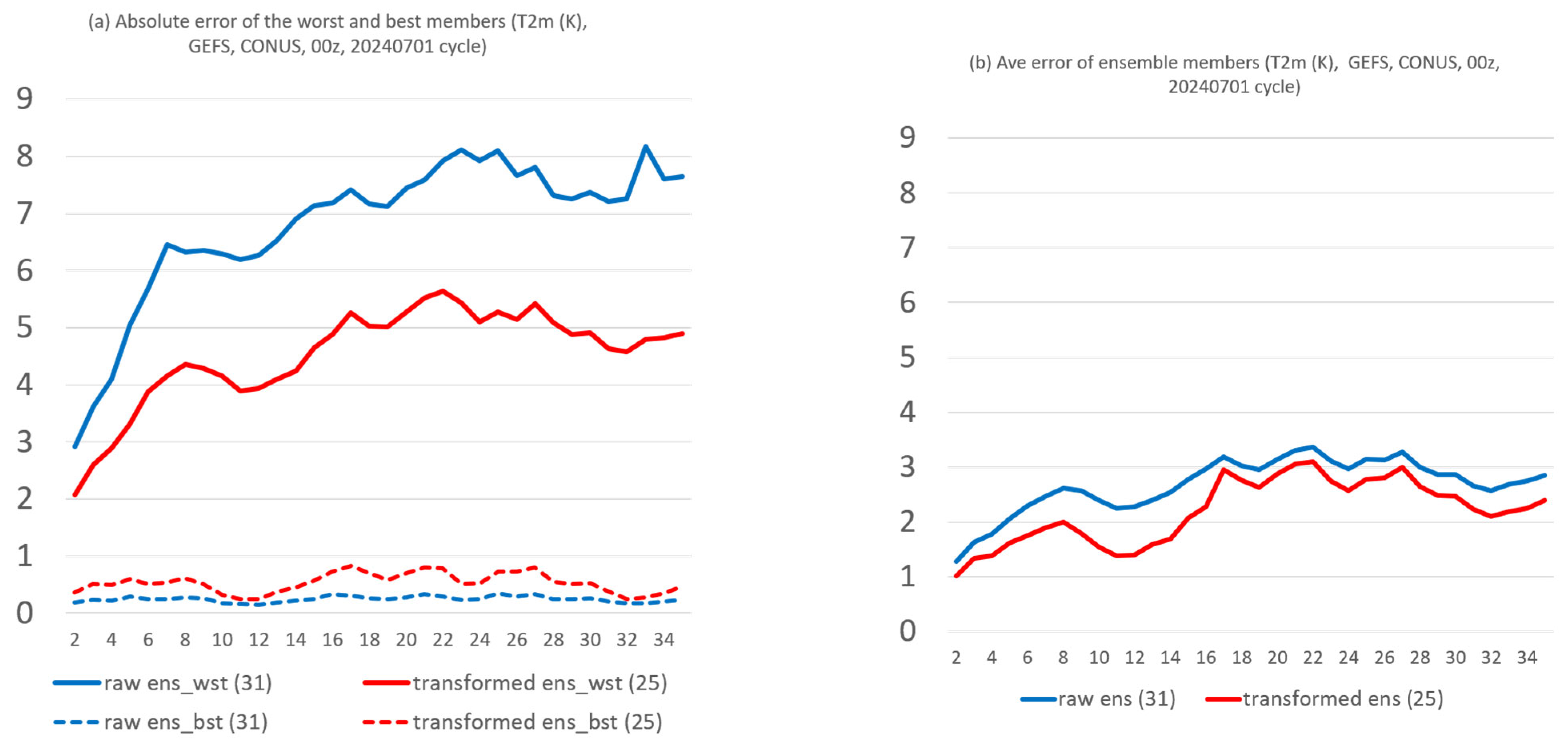
3. Discussion of Possible Ensemble Post-Processing Methods
4. Summary
- (1)
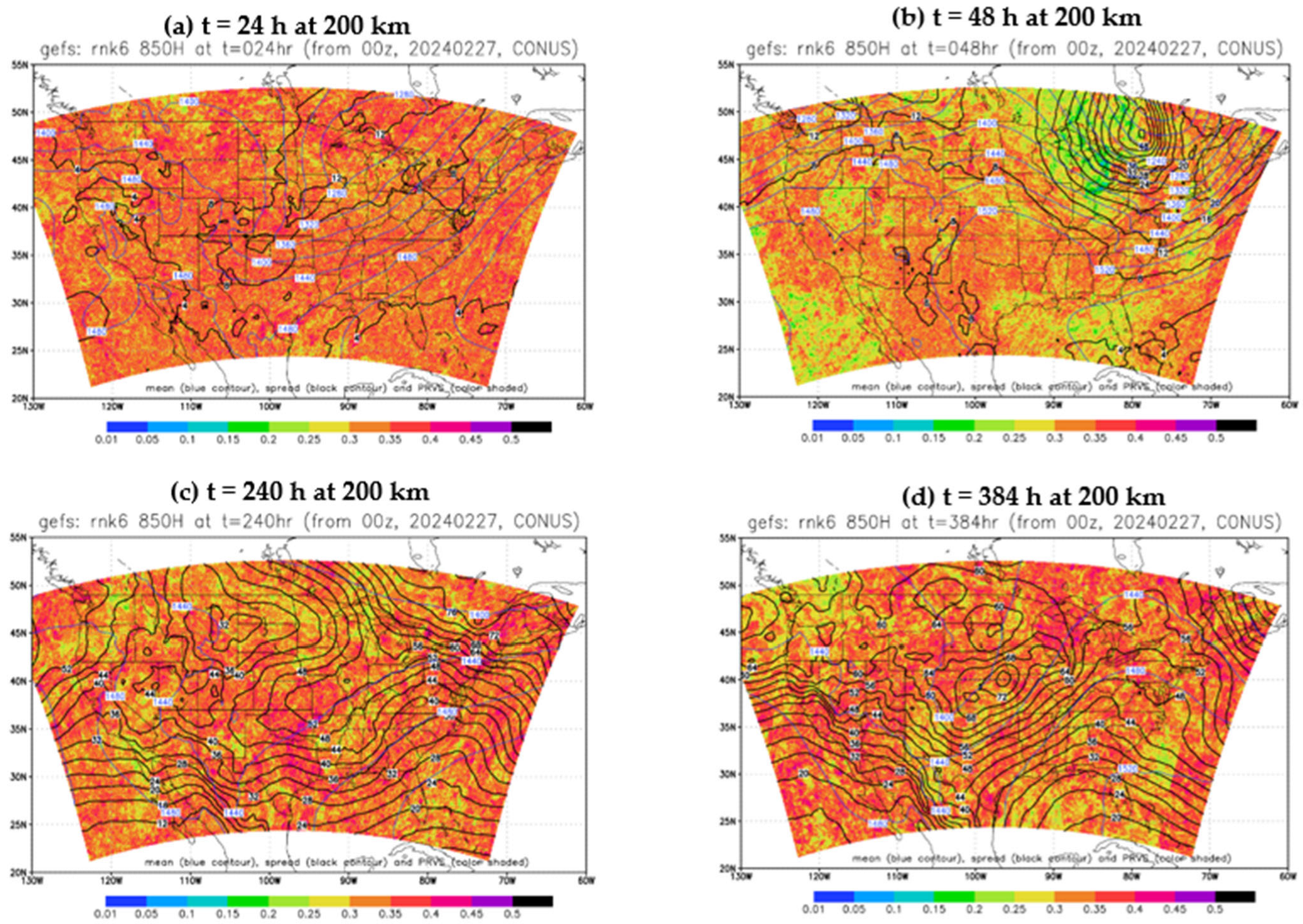
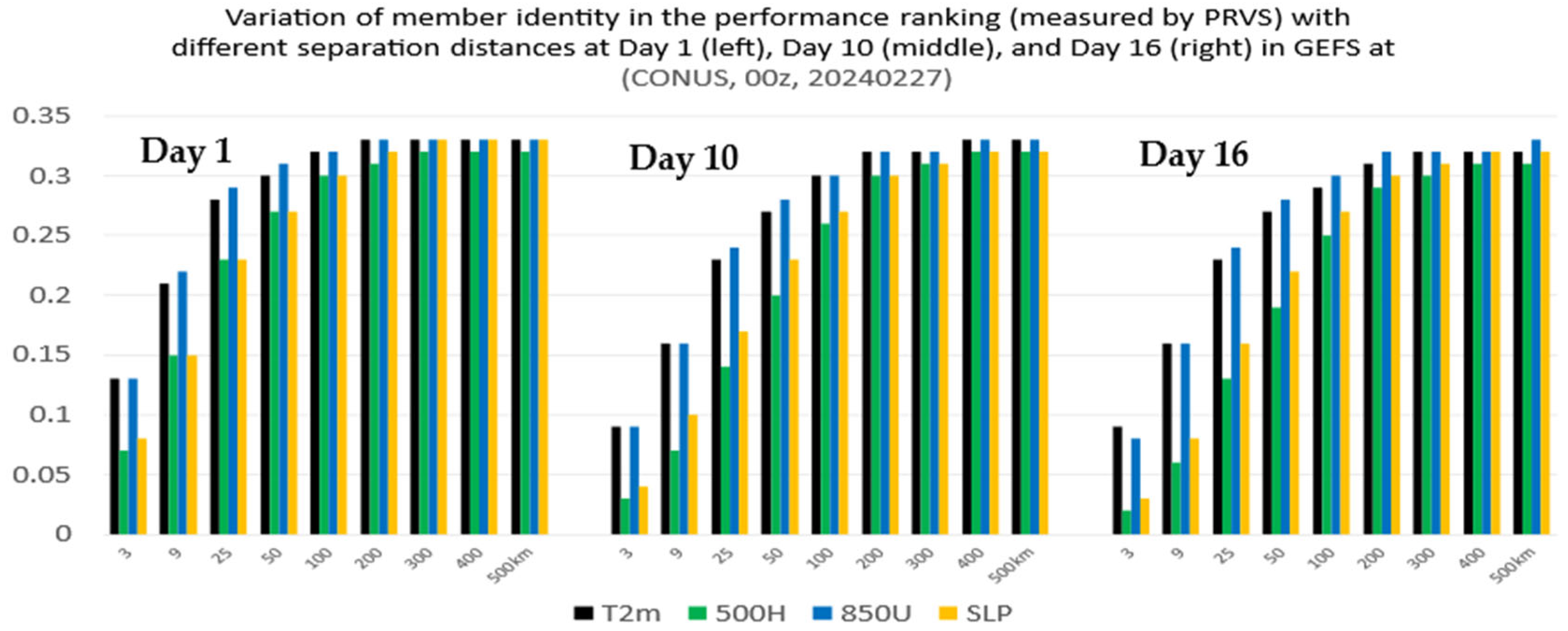
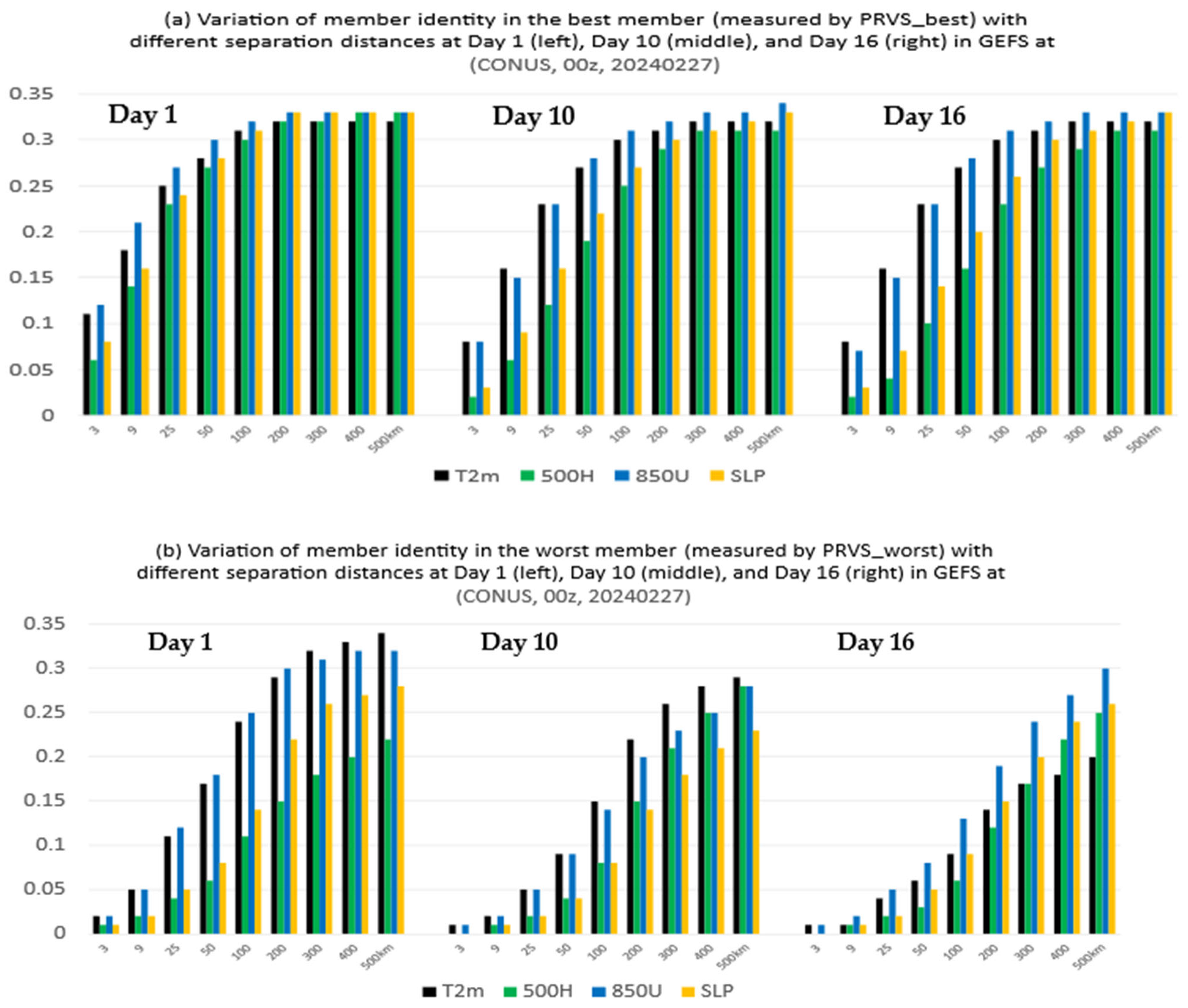
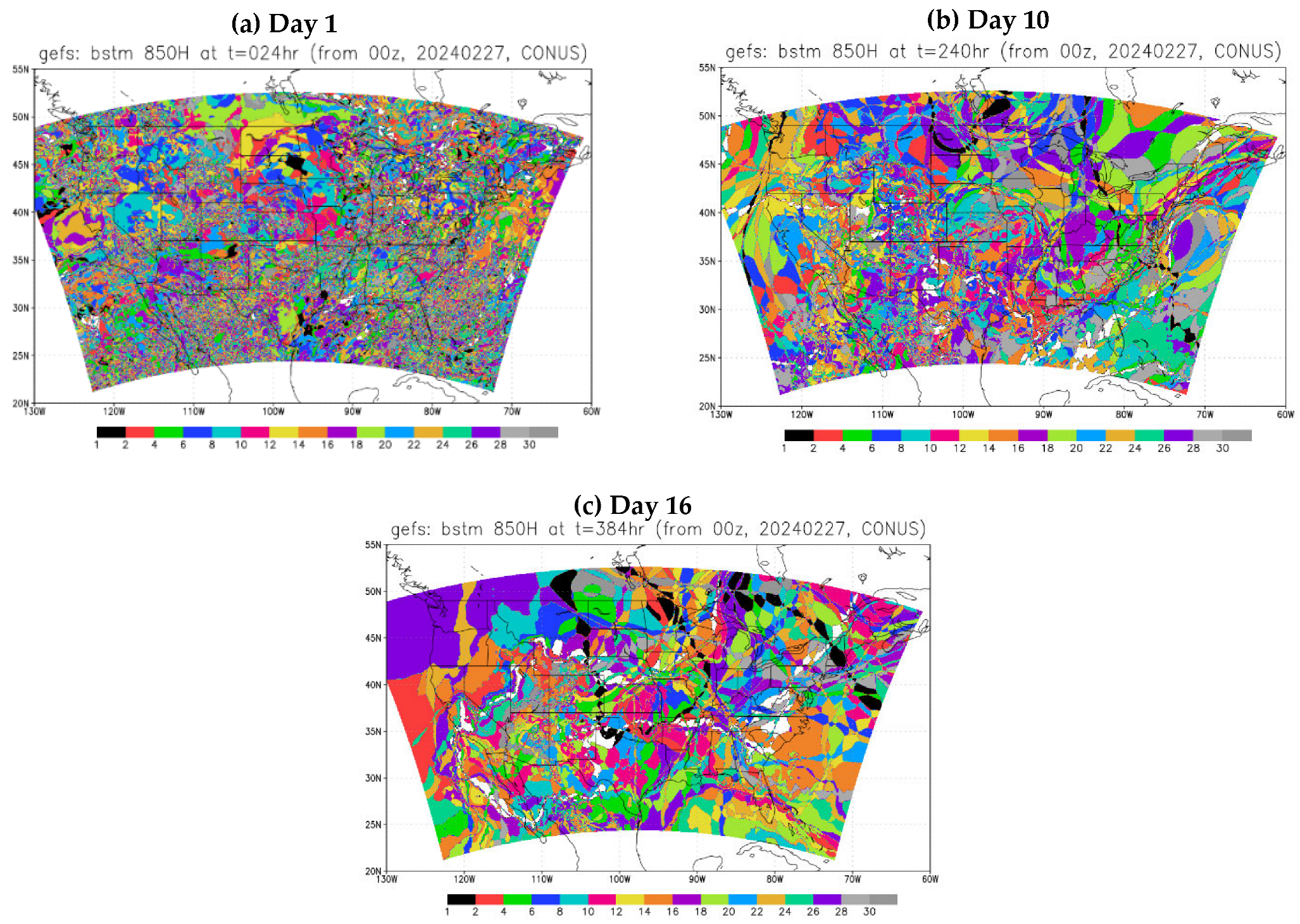
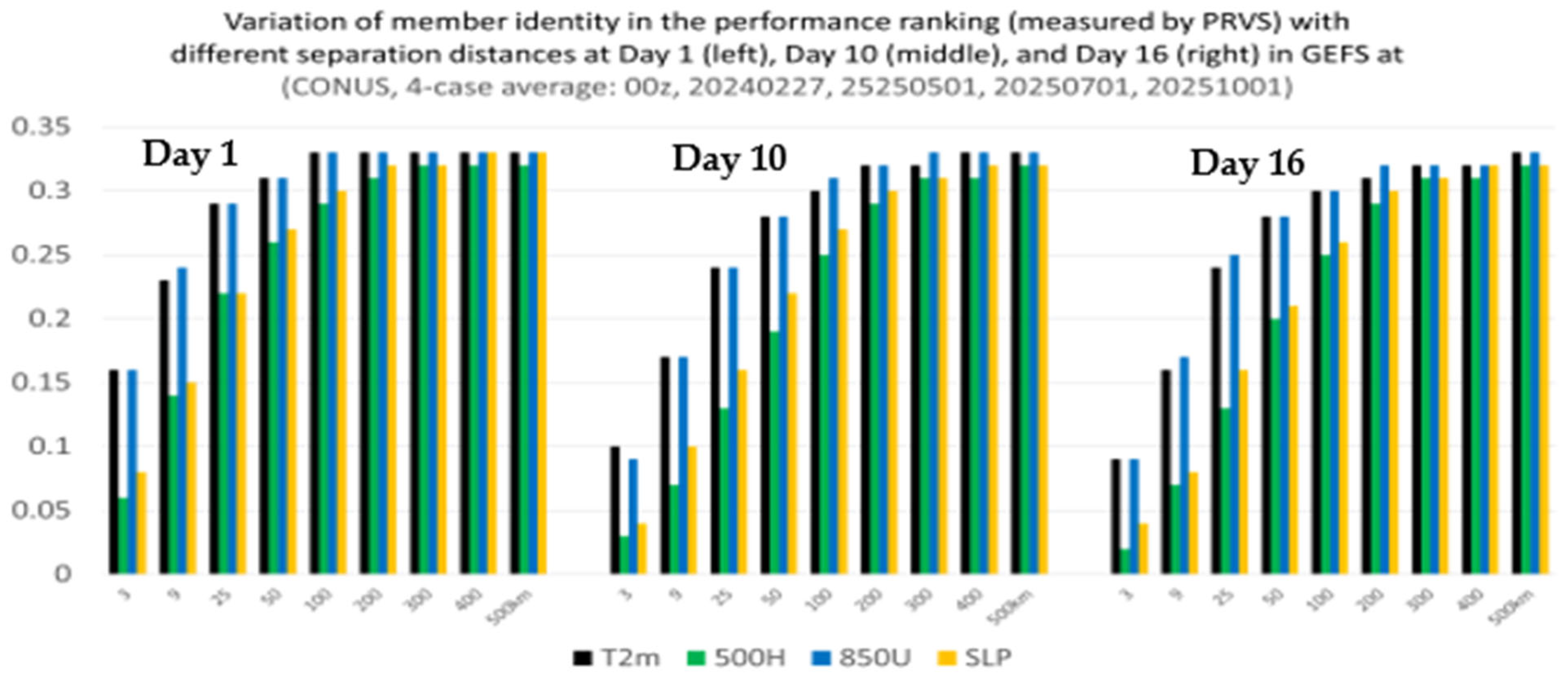
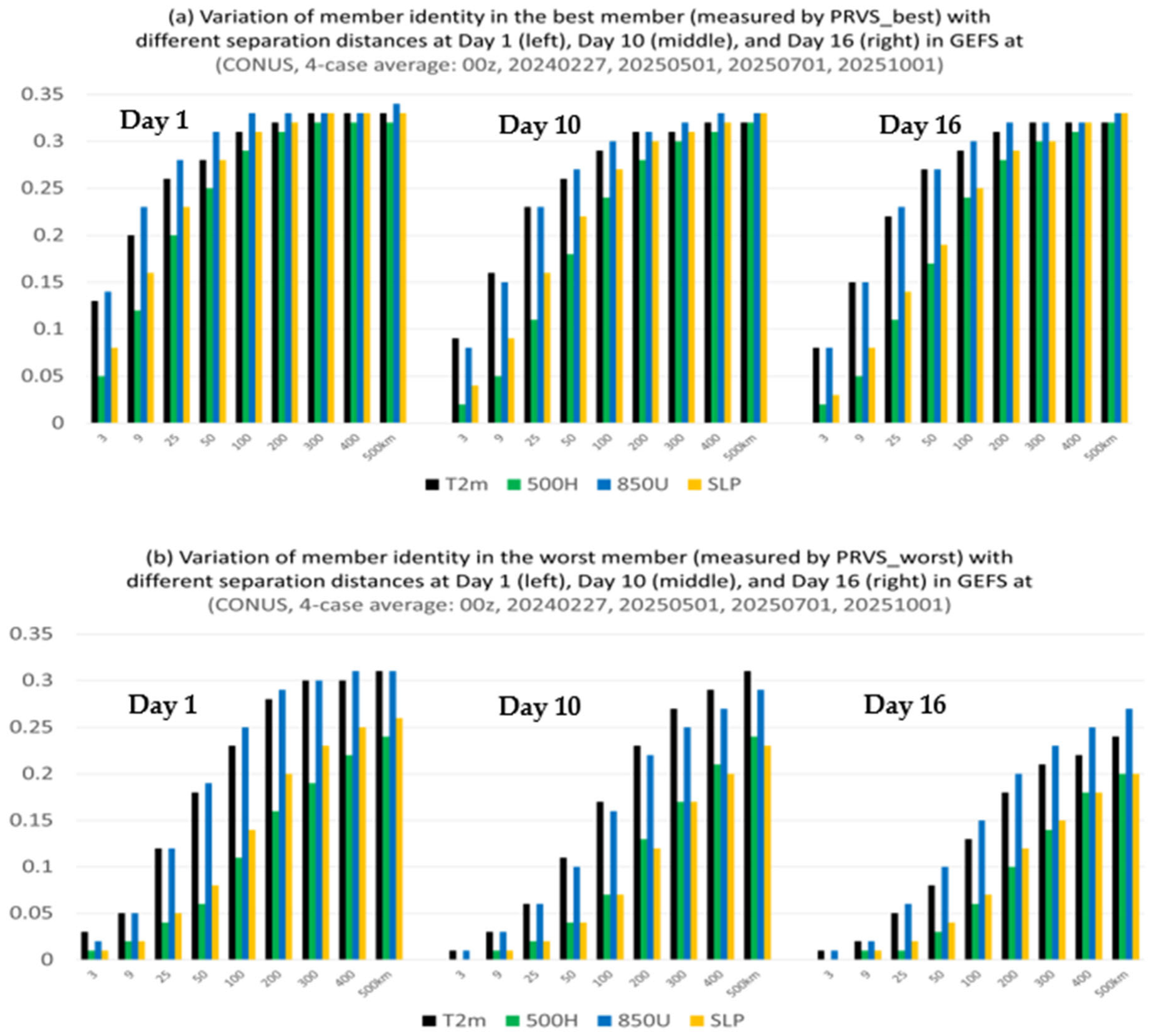
- The membership in the best members, worst members, and full members’ performance rank is found to vary significantly (if not randomly) in both space and time. Thus, it will be challenging to steadily extract “correct” information out of an ensemble cloud in advance. This reminds us of the chaotic nature of the atmosphere and emphasizes that the primary mission of an ensemble forecast should provide a spectrum of probable outcomes of a future weather event but not a single outcome.
- (2)
- From a forecast calibration point of view, there are a few encouraging results that could be explored as possible ensemble post-processing methods. First, the member identity in the best forecast varies much more rapidly than that of the worst forecast across the space, which hints that the bad forecasts could be relatively easier to identify and separate. Therefore, ensemble post-processing should focus on bad performers rather than good performers by excluding a few worst outliers to produce a more accurate and reliable final forecast product, especially for an over-dispersive ensemble. This exclusion of bad performers should work more effectively for longer time range forecasts given the fact that the membership variation decreases with forecast length for both the best and worst members. Following this finding, a new ensemble post-processing method called “transformed ensemble” is demonstrated as a proof of concept. In-depth research into the transformed ensemble method is ongoing and will be reported separately in due course.
- (3)
- Second, the performance rank histograms are positively correlated between different forecast times if the difference is less than about 2–3 days, and there is no correlation if the forecast time has a difference of more than three days. The shorter time memory of the ensemble member’s relative performance implies that the potential value of using the performance of an earlier-hour forecast to calibrate a later-hour forecast will be limited in ensemble post-processing. For example, based on this result, we can anticipate that the sensitivity-based ensemble subletting approach will not work well beyond 2–3 days in real-world practice. However, it is still possible to calibrate short-range weather forecasts about 1–2 days in advance.
- (4)
- Third, the fact that members’ performance rank has similarities to each other (positively correlated) among different variables implies that it is possible to use some variables as predictors to calibrate other variables for both short- and long-range forecasts.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; 240p. [Google Scholar]
- Thompson, P.D. Uncertainty of initial state as a factor in the predictability of large scale atmospheric flow patterns. Tellus 1957, 9, 275–295. [Google Scholar] [CrossRef]
- Du, J.; Berner, J.; Buizza, R.; Charron, M.; Houtekamer, P.; Hou, D.; Jankov, I.; Mu, M.; Wang, X.; Wei, M.; et al. Ensemble methods for meteorological predictions. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Wood, A., Cloke, H.L., Schaake, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; p. 52. [Google Scholar] [CrossRef]
- Buizza, R.; Du, J.; Toth, Z.; Hou, D. Major operational ensemble prediction systems (EPS) and the future of EPS. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Wood, A., Cloke, H.L., Schaake, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; p. 43. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NCEP: The generation of perturbations. Bull. Amer. Meteor. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF Ensemble Prediction System: Methodology and validation. Q. J. Roy. Meteor. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Lefaivre, L.; Derome, J.; Ritchie, H.; Mitchell, H.L. A system simulation approach to ensemble prediction. Mon. Weather Rev. 1996, 124, 1225–1242. [Google Scholar] [CrossRef]
- Du, J.; Mullen, S.L.; Sanders, F. Short-range ensemble forecasting of quantitative precipitation. Mon. Weather Rev. 1997, 125, 2427–2459. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Y.; Duan, W.; Zhi, X.; Min, J.; Li, X.; Deng, G.; Yuan, H.; Feng, J.; Du, J.; et al. A review on development, challenges, and future perspectives of ensemble forecast. J. Meteorol. Res. 2025, 39, 534–558. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Y.; Hou, D.; Fu, B.; Li, W.; Guan, H.; Sinsky, E.; Kolczynski, W.; Xue, X.; Luo, Y.; et al. The Development of the NCEP Global Ensemble Forecast System Version 12. Weather Forecast. 2022, 37, 1069–1084. [Google Scholar] [CrossRef]
- Fu, B.; Zhu, Y.; Guan, H.; Sinsky, E.; Yang, B.; Xue, X.; Pegion, P.; Yang, F. Weather to seasonal prediction from the UFS Coupled Global Ensemble Forecast System. Weather Forecast. 2024; in press. [Google Scholar] [CrossRef]
- Lin, S.J.; Putman, W.; Harris, L. FV3: The GFDL Finite-Volume Cubed-Sphere Dynamical Core (Version 1), NWS/NCEP/EMC. 2017. Available online: https://www.gfdl.noaa.gov/wp-content/uploads/2020/02/FV3-Technical-Description.pdf (accessed on 23 July 2025).
- Houtekamer, P.L.; Mitchell, H.L. Data assimilation using an ensemble Kalman filter technique. Mon. Weather Rev. 1998, 126, 196–811. [Google Scholar] [CrossRef]
- Kleist, D.T.; Ide, K. An OSSE-based evaluation of hybrid variational-ensemble data assimilation for the NCEP GFS, Part I: System description and 3D-hybrid results. Mon. Weather Rev. 2015, 143, 433–451. [Google Scholar] [CrossRef]
- Du, J.; Zhou, B. A dynamical performance-ranking method for predicting individual ensemble member’s performance and its application to ensemble averaging. Mon. Weather Rev. 2011, 129, 3284–3303. [Google Scholar] [CrossRef]
- Bright, D.R.; Nutter, P.A. On the challenges of identifying the “best” ensemble member in operational forecasting. In Proceedings of the 16th Conference on Numerical Weather Prediction/20th Conference on Weather Analysis and Forecasting, Seattle, WA, USA, 14 January 2004; Available online: https://ams.confex.com/ams/84Annual/techprogram/paper_69092.htm (accessed on 23 July 2025).
- Du, J. An assessment of ensemble forecast performance: Where we are and where we should go. In Proceedings of the 33rd Conference on Weather Analysis and Forecasting (WAF)/29th Conference on Numerical Weather Prediction (NWP), New Orleans, LA, USA, 12–16 January 2025. [Google Scholar]
- Du, J.; Tabas, S.S.; Wang, J.; Levit, J. Understanding similarities and differences between data-driven based and physics model-based ensemble forecasts. NCEP Off. Notes 2025, 523, 31p. [Google Scholar] [CrossRef]
- Ancell, B.C. Improving High-Impact Forecasts Through Sensitivity-Based Ensemble Subsets: Demonstration and Initial Tests. Weather Forecast. 2016, 31, 1019–1036. [Google Scholar] [CrossRef]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Graphcast: Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef] [PubMed]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium range global weather forecasting with 3-D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J. Performance Rank Variation Score (PRVS) to Measure Variation in Ensemble Member’s Relative Performance with Introduction to “Transformed Ensemble” Post-Processing Method. Meteorology 2025, 4, 20. https://doi.org/10.3390/meteorology4030020
Du J. Performance Rank Variation Score (PRVS) to Measure Variation in Ensemble Member’s Relative Performance with Introduction to “Transformed Ensemble” Post-Processing Method. Meteorology. 2025; 4(3):20. https://doi.org/10.3390/meteorology4030020
Chicago/Turabian StyleDu, Jun. 2025. "Performance Rank Variation Score (PRVS) to Measure Variation in Ensemble Member’s Relative Performance with Introduction to “Transformed Ensemble” Post-Processing Method" Meteorology 4, no. 3: 20. https://doi.org/10.3390/meteorology4030020
APA StyleDu, J. (2025). Performance Rank Variation Score (PRVS) to Measure Variation in Ensemble Member’s Relative Performance with Introduction to “Transformed Ensemble” Post-Processing Method. Meteorology, 4(3), 20. https://doi.org/10.3390/meteorology4030020






