Aerosol, Clouds and Radiation Interactions in the NCEP Unified Forecast Systems
Abstract
1. Introduction
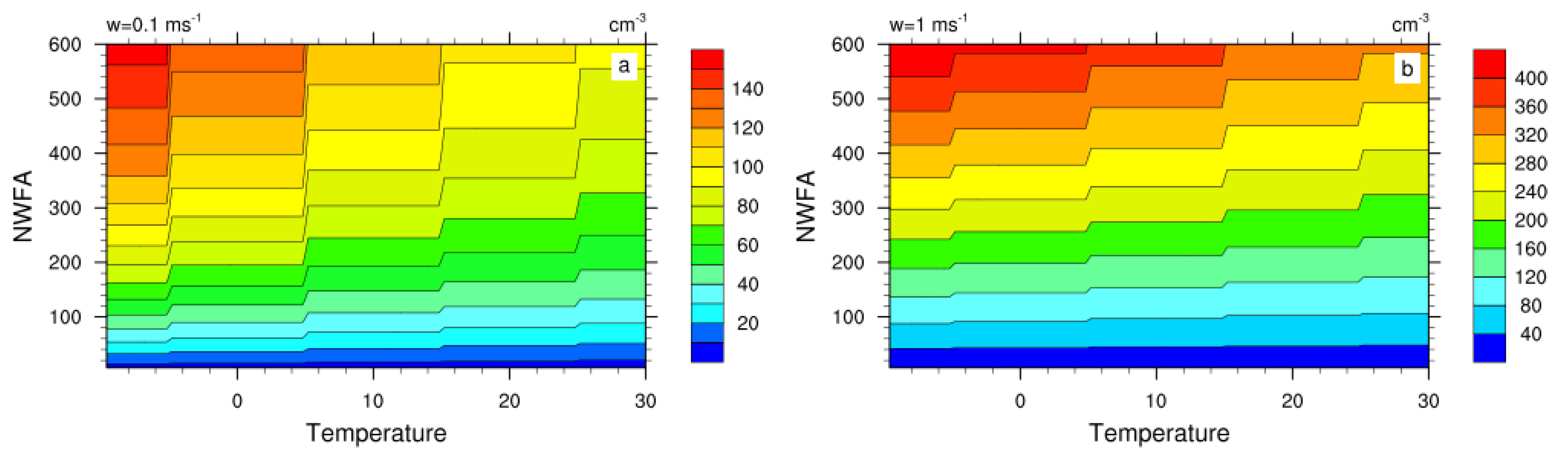
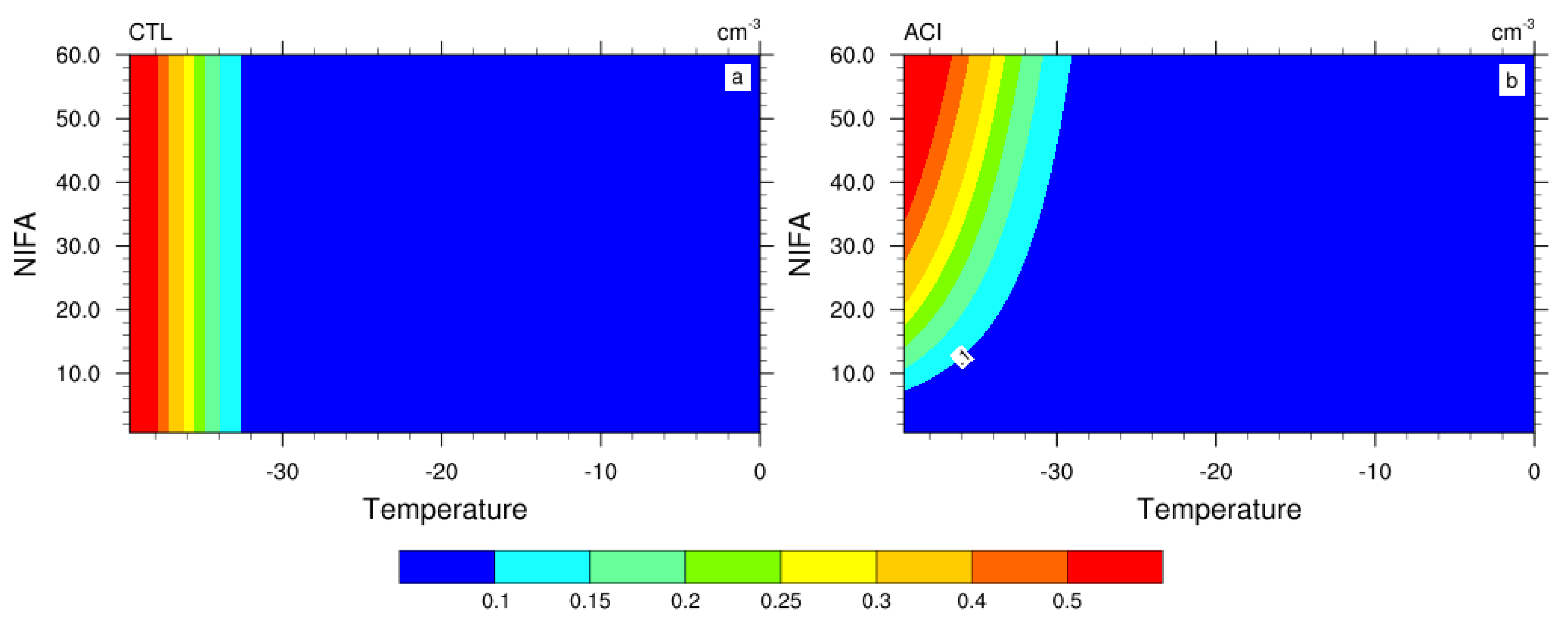
2. Experimental Design and Model Description
3. Results
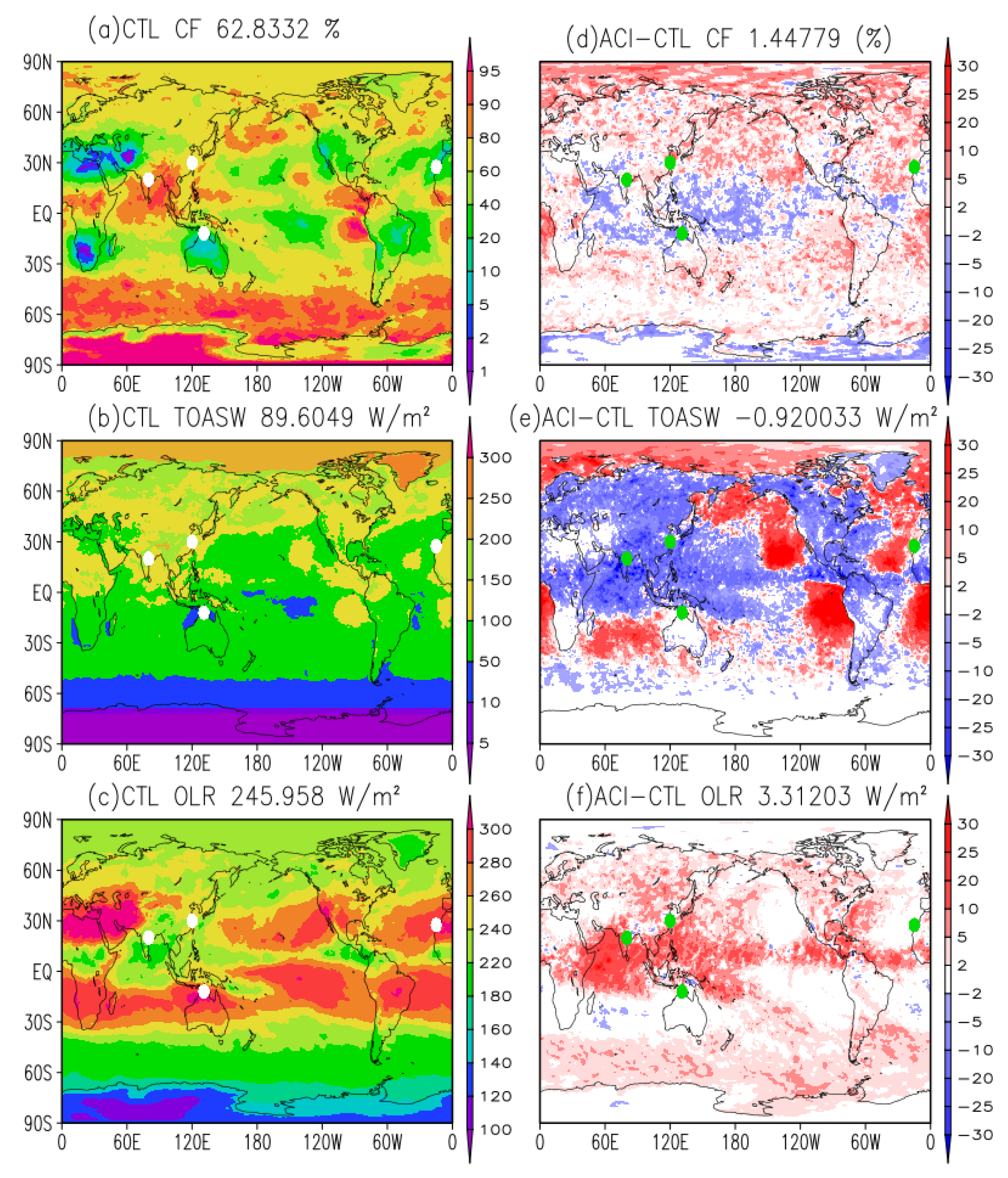
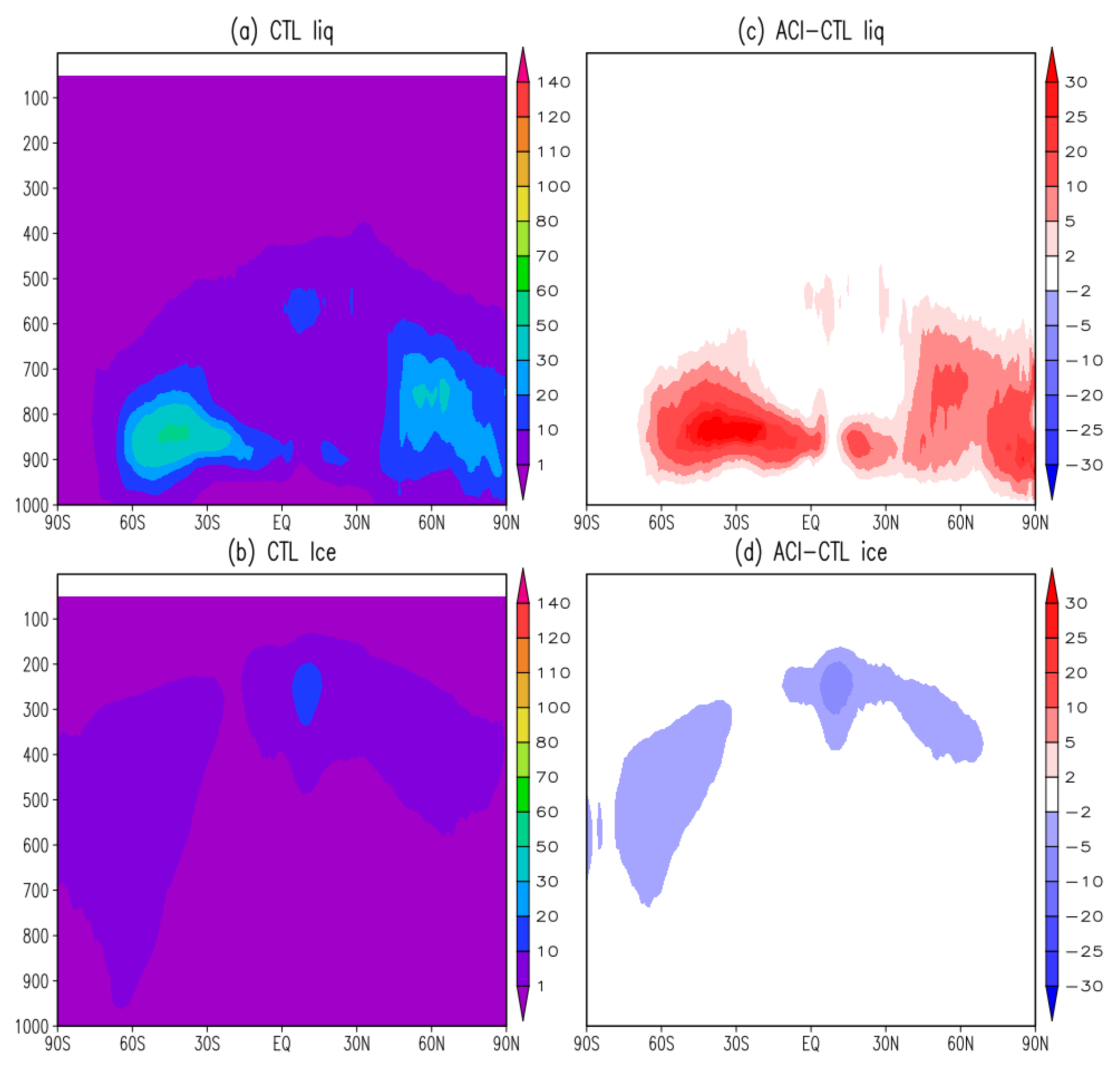
3.1. Global Distribution of Cloud Fractions and Radiation Fluxes
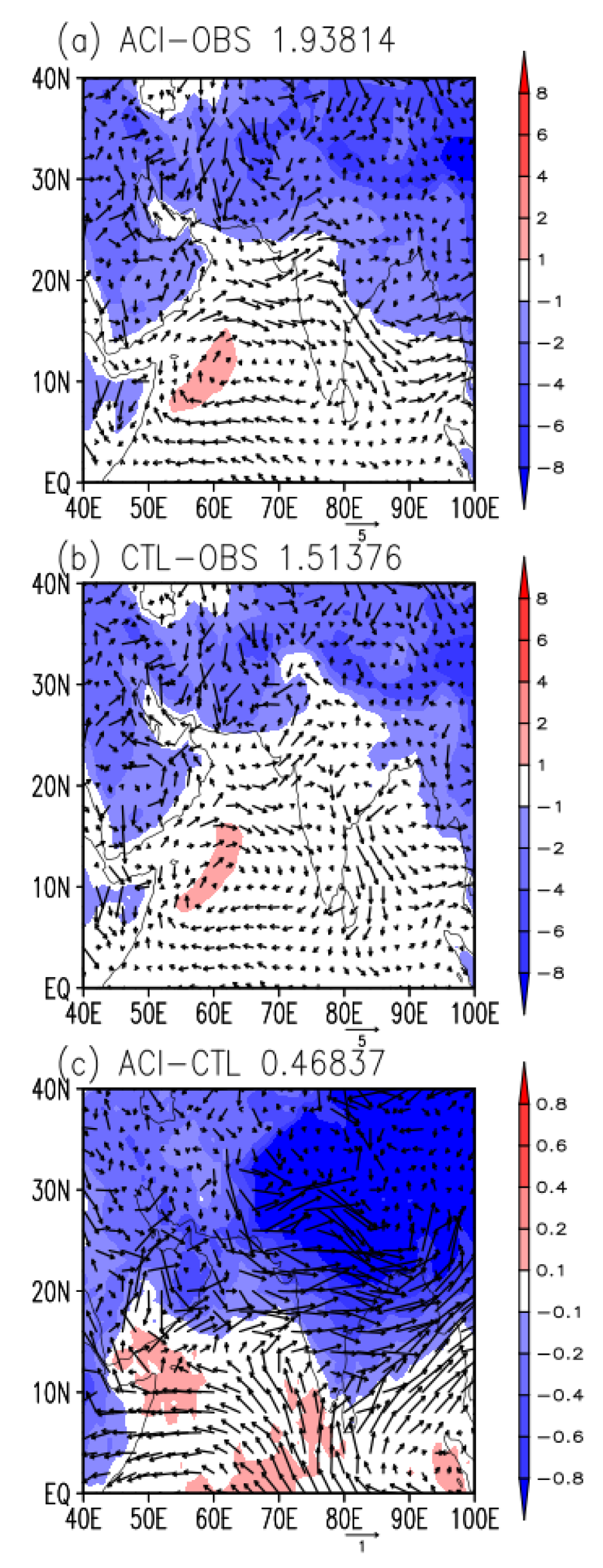
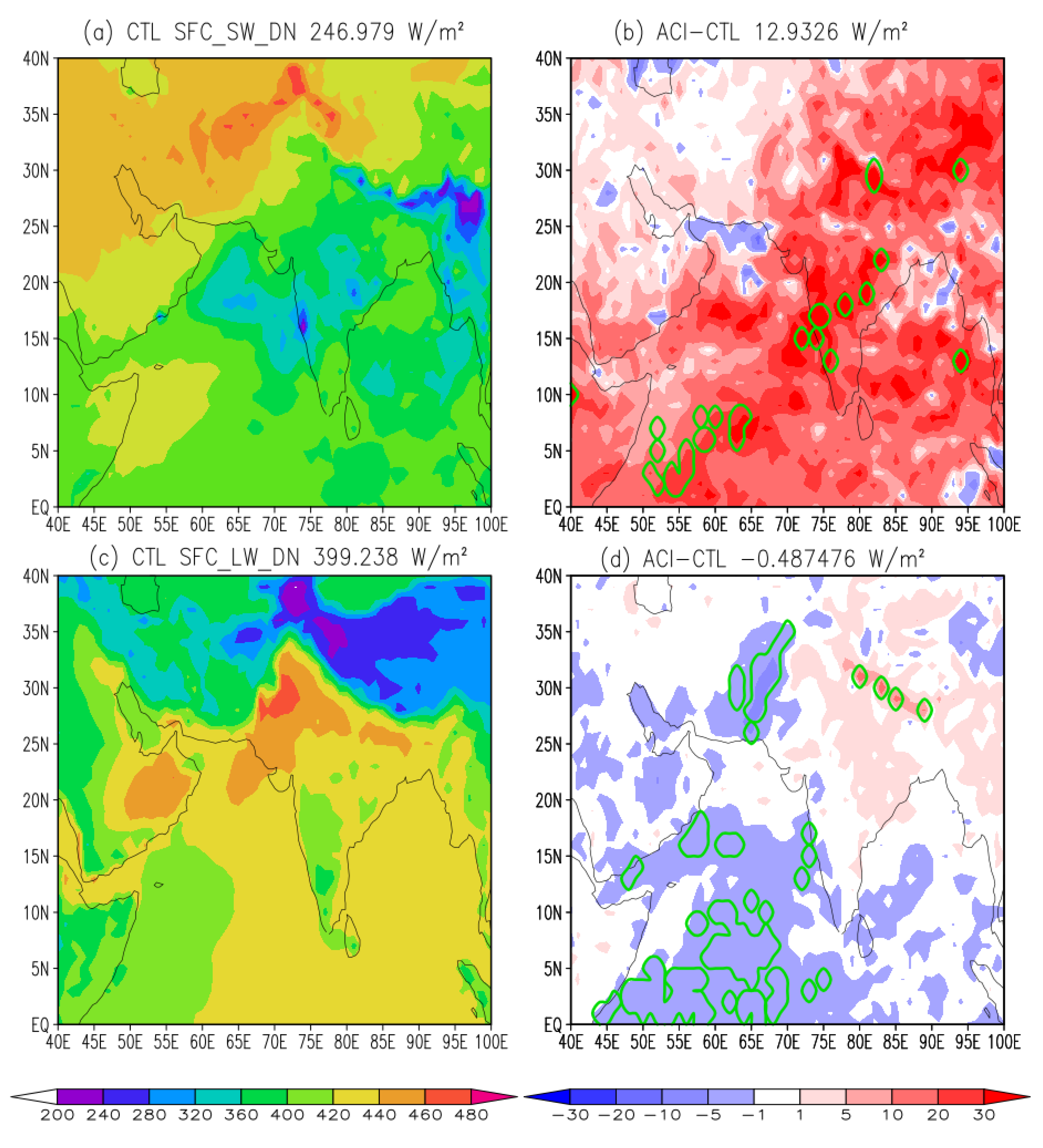
3.2. Impact on India Monsoon
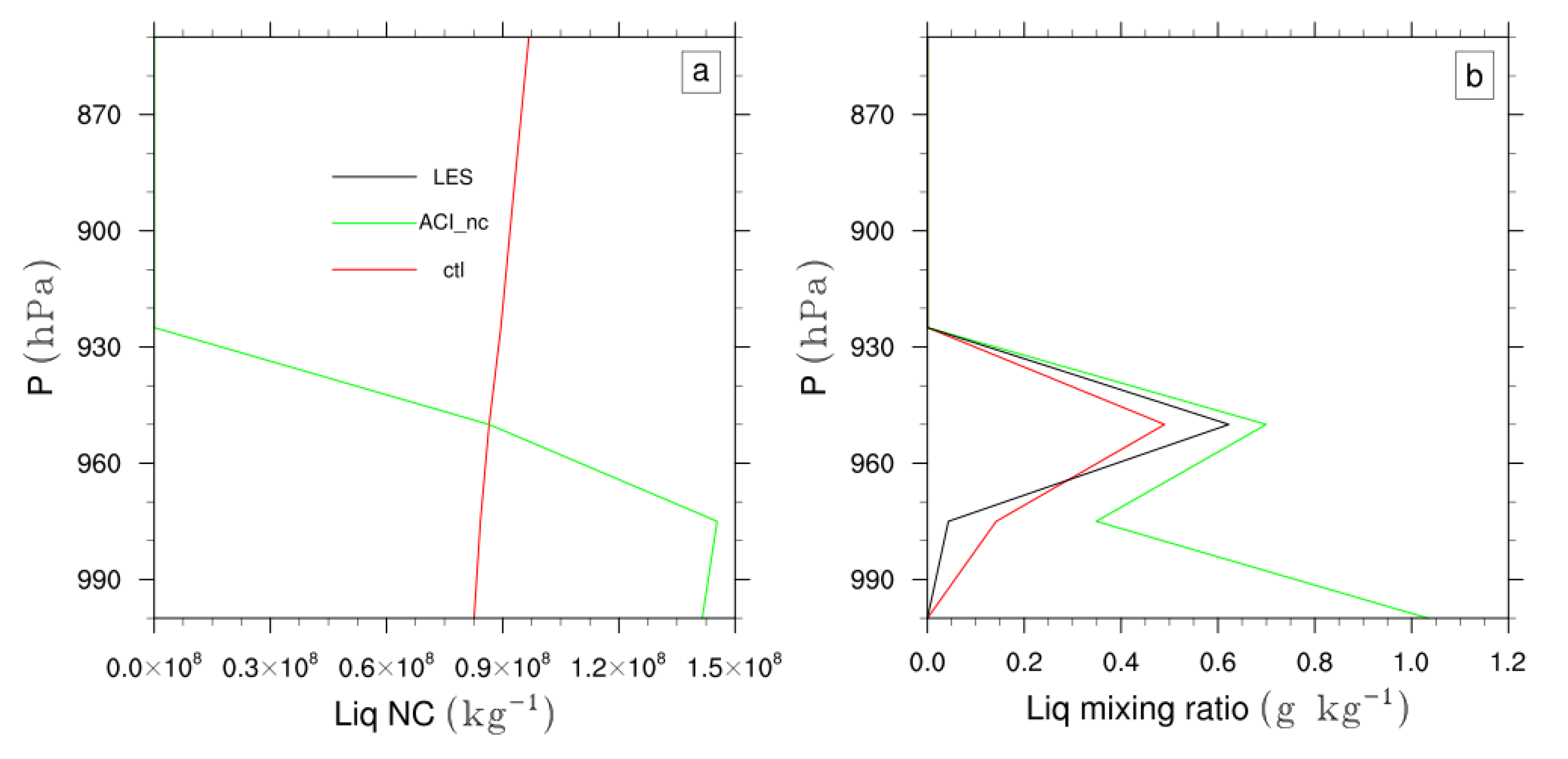
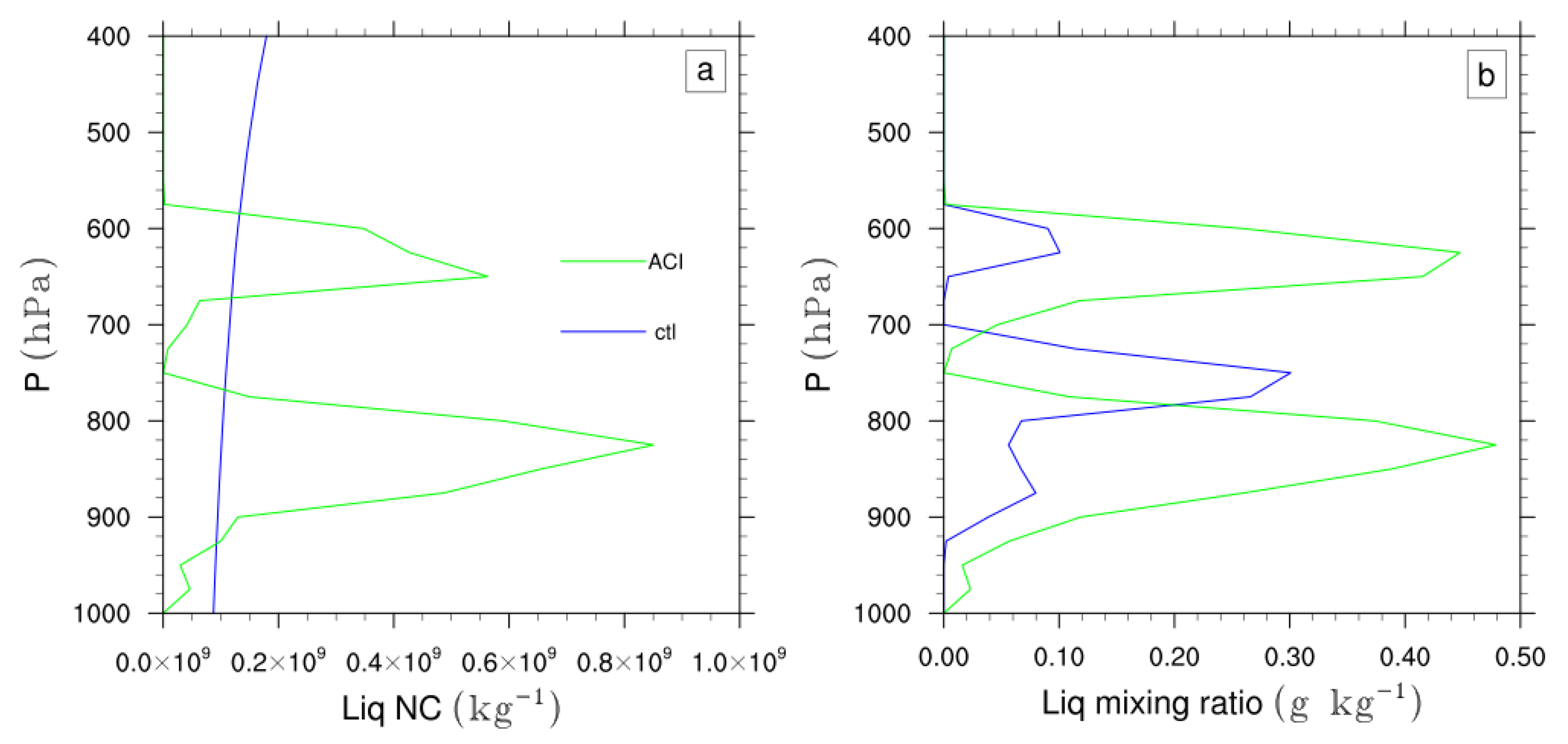
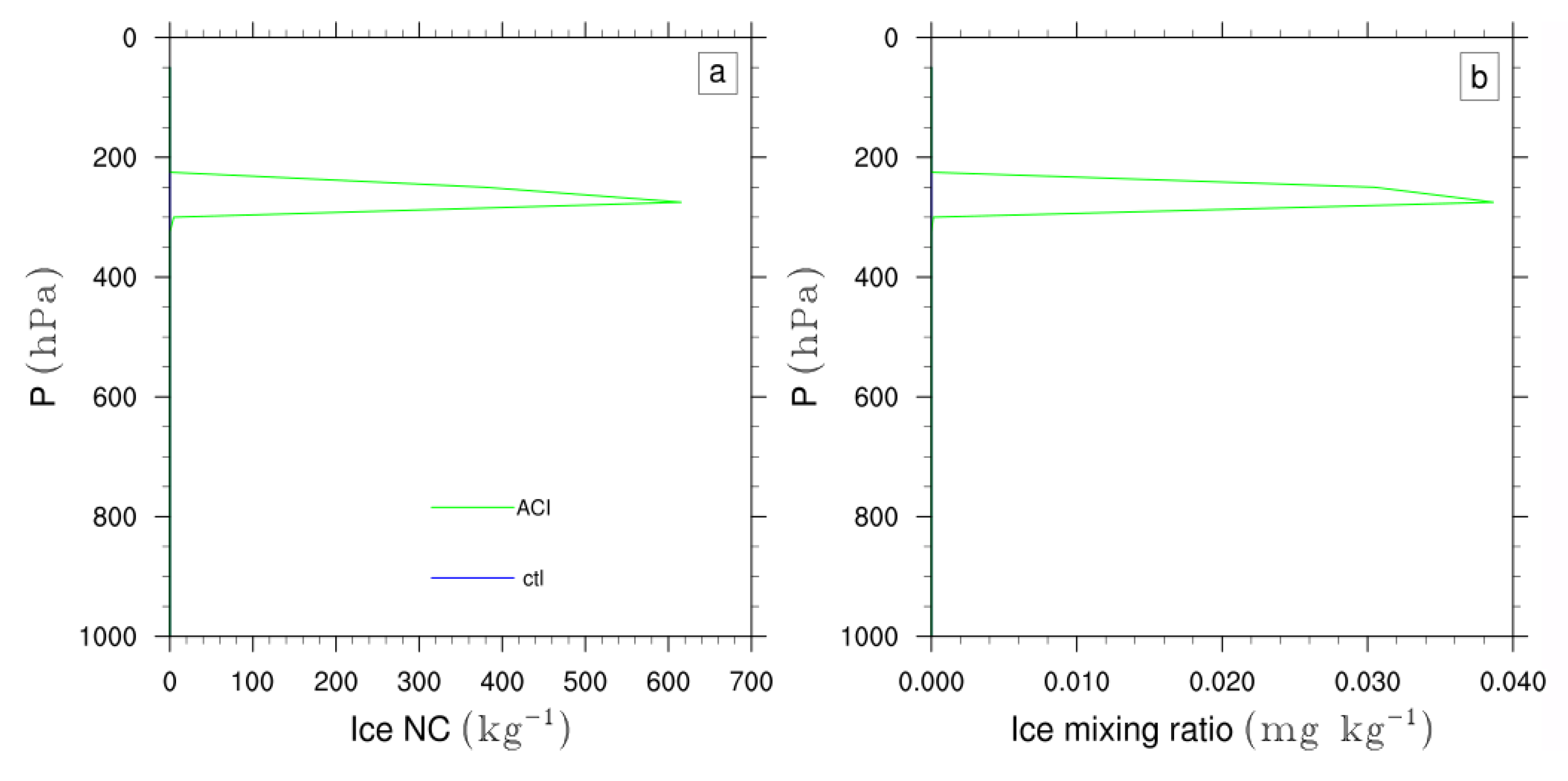
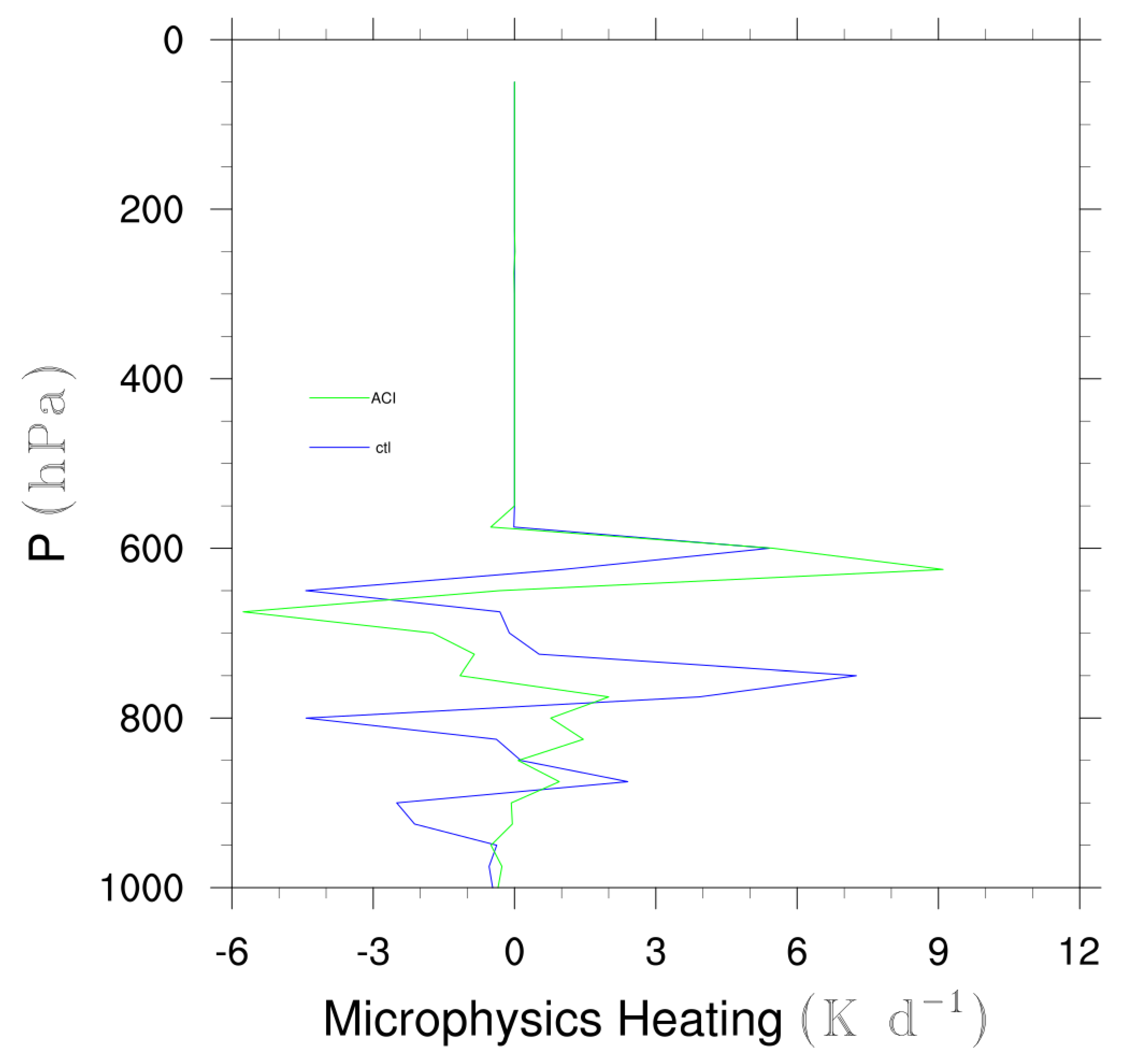
3.3. Stratocumulus Clouds
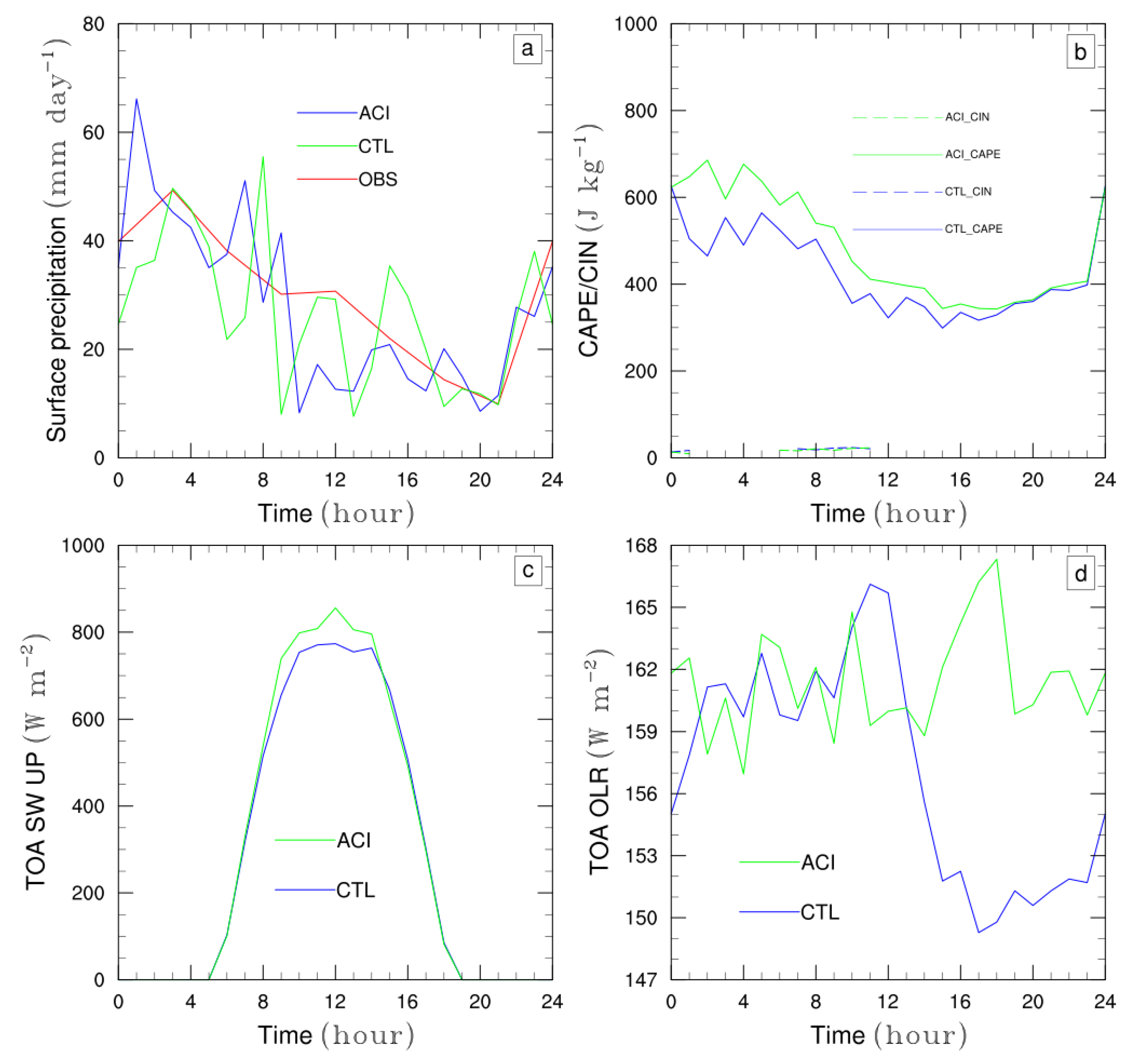
3.4. Diurnal Cycle
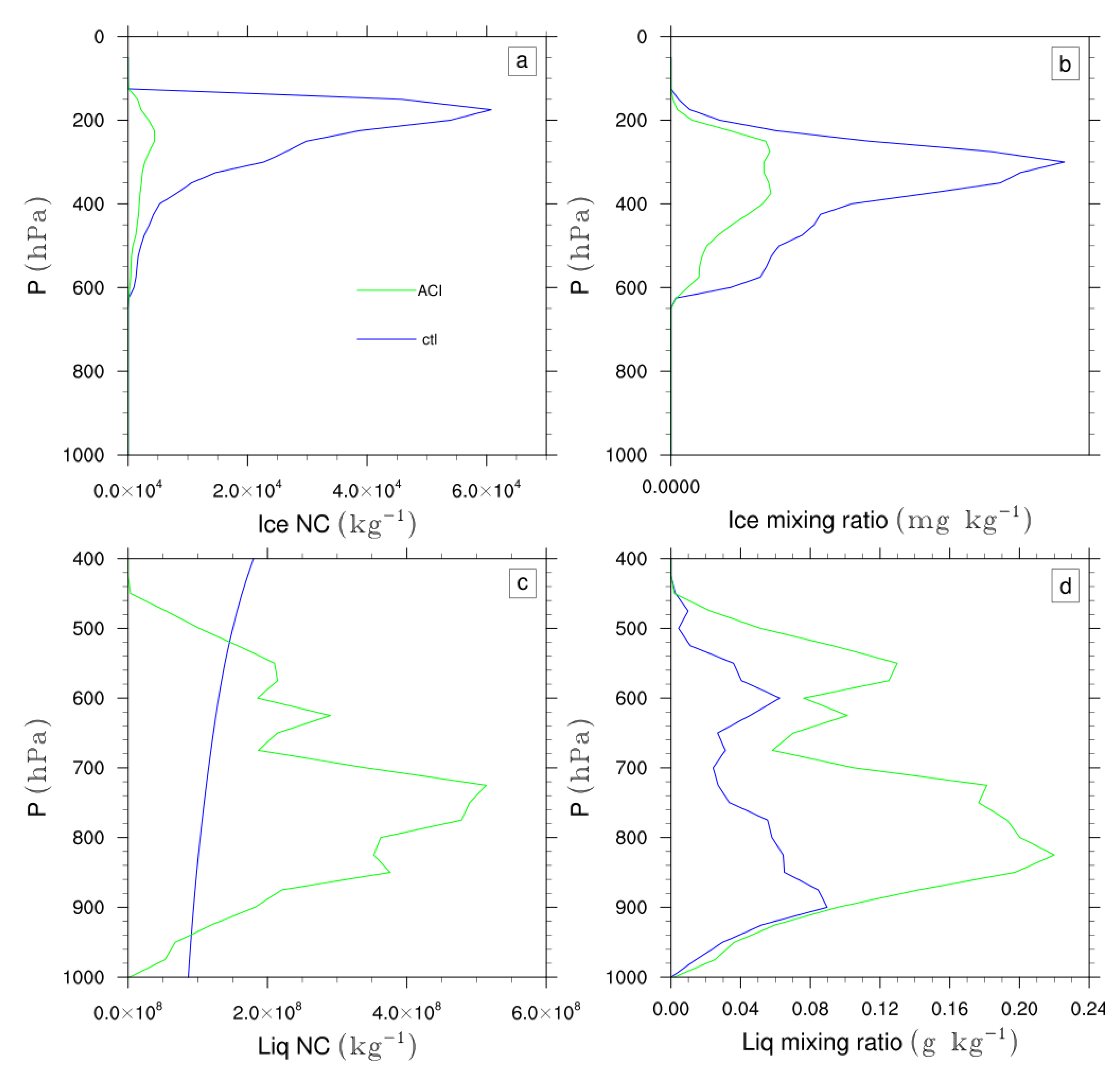
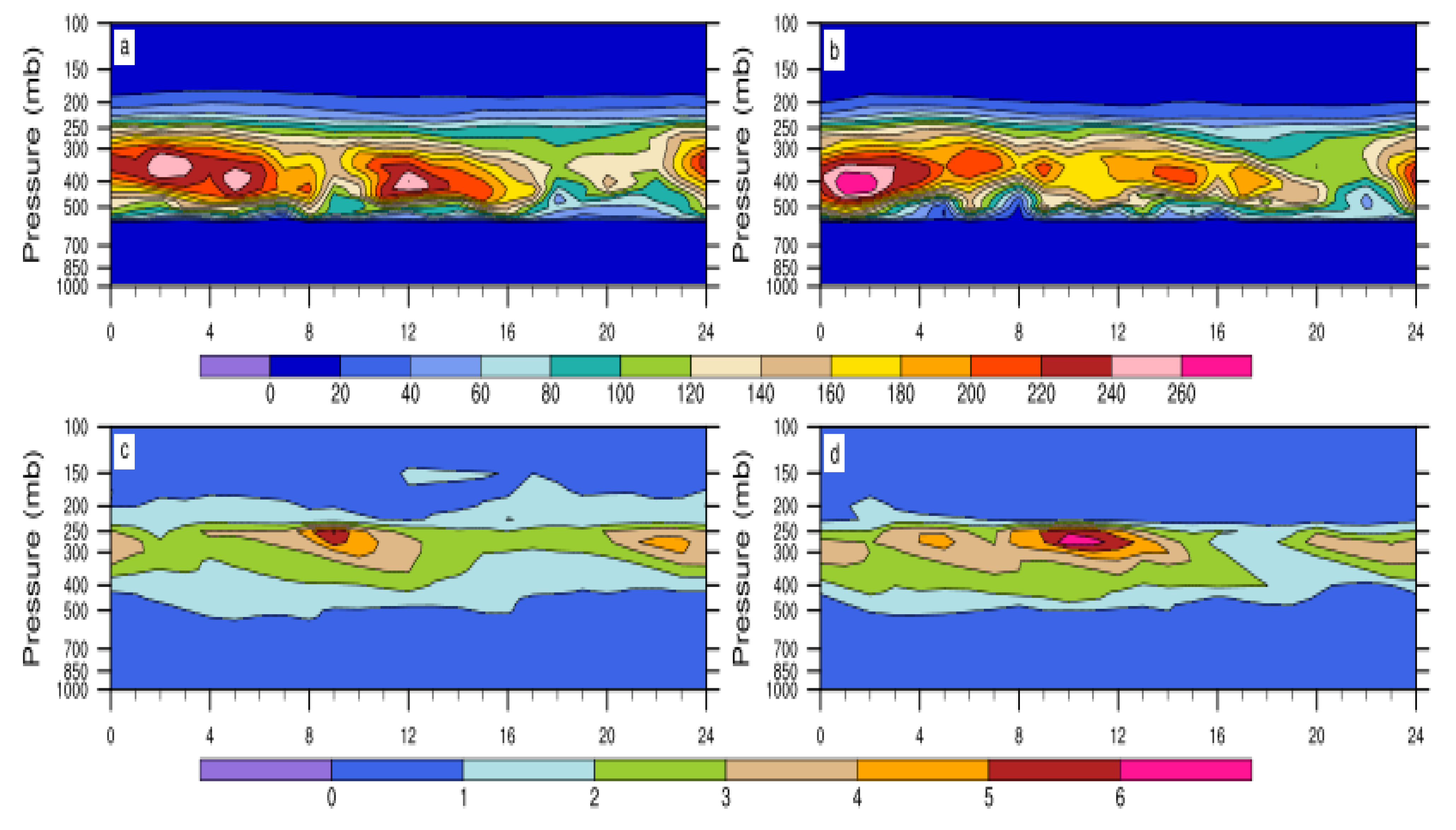
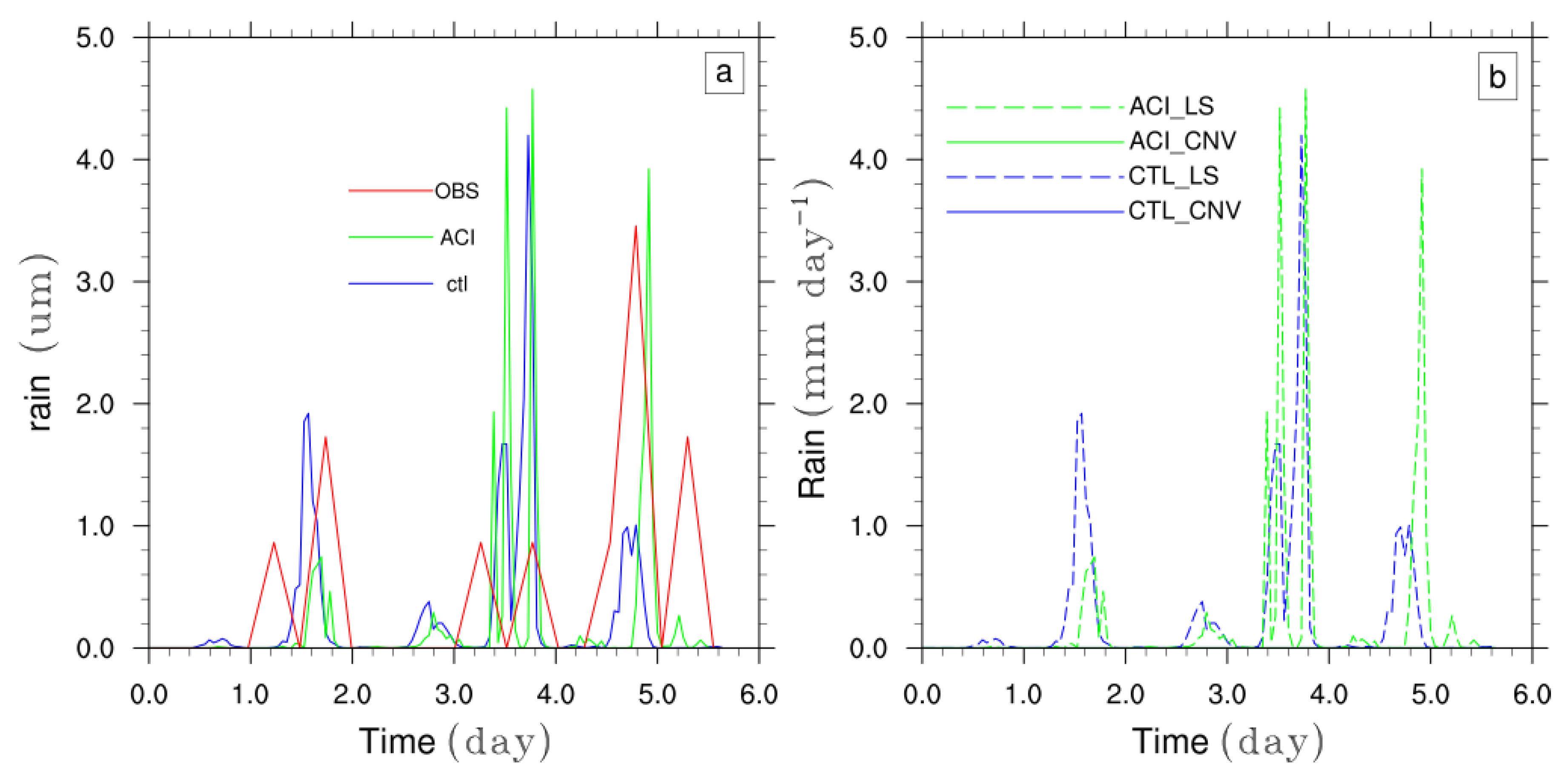
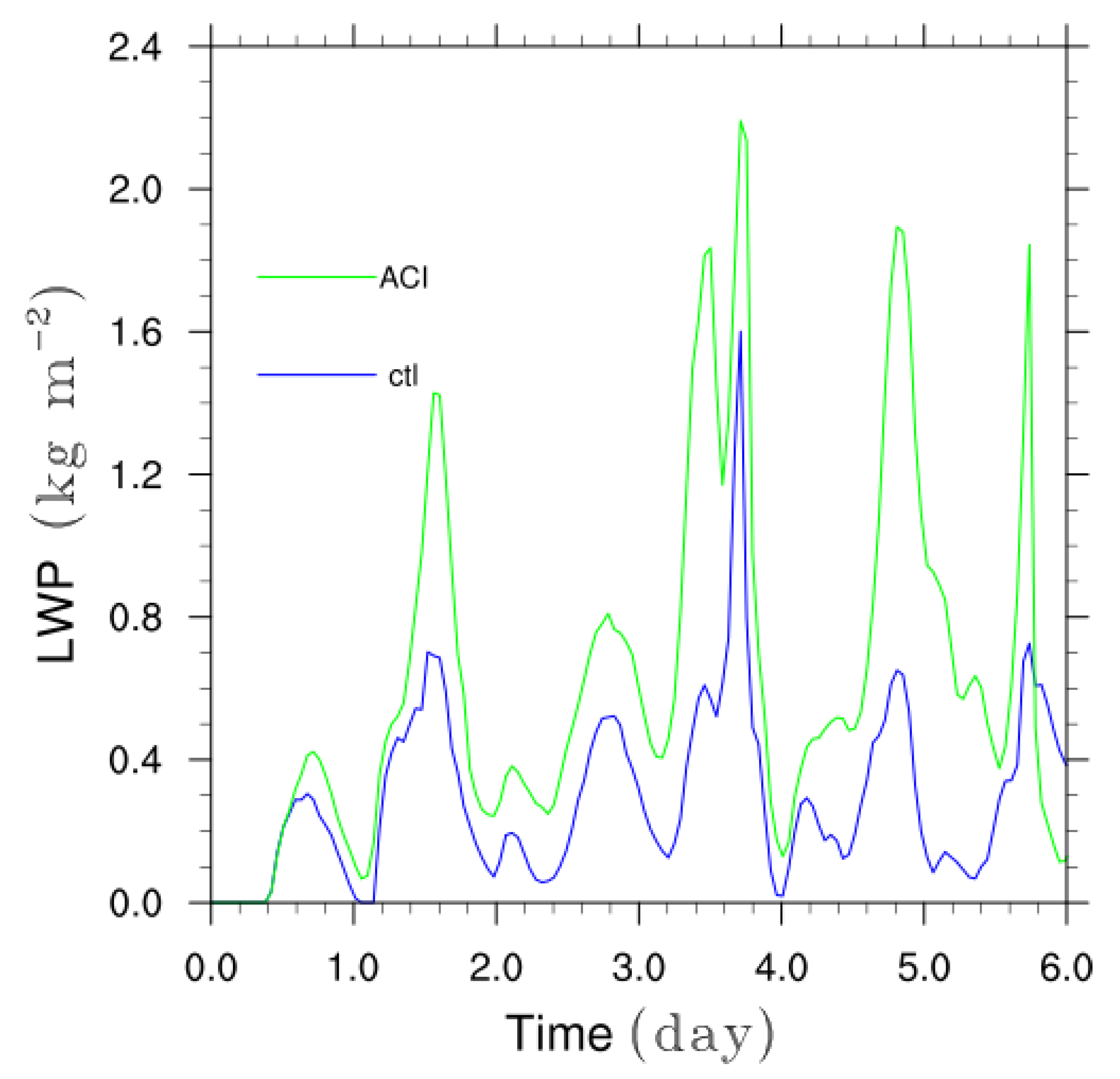
3.5. Deep Convection Invigoration and Cloud System Life Cycle
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Haywood, J.; Boucher, O. Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review. Rev. Geophys. 2000, 38, 513–543. [Google Scholar] [CrossRef]
- Myhre, G. Consistency Between Satellite-Derived and Modeled Estimates of the Direct Aerosol Effect. Science 2009, 325, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Koch, D.; Del Genio, A.D. Black carbon absorption effects on cloud cover: Review and synthesis. Atmos. Chem. Phys. 2010, 10, 7685–7696. [Google Scholar] [CrossRef]
- Twomey, S. The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Penner, J.E.; Andreae, M.; Annegarn, H.; Barrie, L.; Feichter, J.; Hegg, D.; Jayaraman Leaitch, R.; Murphy, D.; Nganga, J.; Pitari, G. Aerosols, Their Direct and Indirect Effects7, in Climate Change 2001: The Scientific Basis, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., Van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: New York, NY, USA, 2001; p. 881. [Google Scholar]
- Fan, J.; Yuan, T.; Comstock, J.M.; Ghan, S.; Khain, A.; Leung, L.R.; Li, Z.; Martins, V.J.; Ovchinnikov, M. Dominant role by vertical wind shear in regulating aerosol effects on deep convective clouds. J. Geophys. Res. Atmos. 2009, 114, D22206. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.; Rosenfeld, D.; Liu, X. Review of aerosol–cloud interactions: Mechanisms, significance, and challenges. J. Atmos. Sci. 2016, 73, 4221–4252. [Google Scholar] [CrossRef]
- Khain, A.; Rosenfeld, D.; Pokrovsky, A. Aerosol impact on the dynamics and microphysics of deep convective clouds. Q. J. R. Meteorol. Soc. 2005, 131, 2639–2663. [Google Scholar] [CrossRef]
- Li, Z.; Niu, F.; Fan, J.; Liu, Y.; Rosenfeld, D.; Ding, Y. Long-term impacts of aerosols on the vertical development of clouds and precipitation. Nat. Geosci. 2011, 4, 888–894. [Google Scholar] [CrossRef]
- Hoeve, J.E.T.; Jacobson, M.Z.; Remer, L.A. Comparing results from a physical model with satellite and in situ observations to determine whether biomass burning aerosols over the Amazon brighten or burn off clouds. J. Geophys. Res. Atmos. 2012, 117, D08203. [Google Scholar] [CrossRef]
- Heever, S.C.V.D.; Carrió, G.G.; Cotton, W.R.; DeMott, P.J.; Prenni, A.J. Impacts of Nucleating Aerosol on Florida Storms. Part I: Mesoscale Simulations. J. Atmos. Sci. 2006, 63, 1752–1775. [Google Scholar] [CrossRef]
- Devasthale, A.; Kruger, O.; Grassl, H. Change in Cloud-Top Temperatures Over Europe. IEEE Geosci. Remote Sens. Lett. 2005, 2, 333–336. [Google Scholar] [CrossRef]
- Jiang, H.; Feingold, G. Effect of aerosol on warm convective clouds: Aerosol-cloud-surface flux feedbacks in a new coupled large eddy model. J. Geophys. Res. Atmos. 2006, 111, D1. [Google Scholar] [CrossRef]
- Xue, H.; Feingold, G.; Stevens, B. Aerosol Effects on Clouds, Precipitation, and the Organization of Shallow Cumulus Convection. J. Atmos. Sci. 2008, 65, 392–406. [Google Scholar] [CrossRef]
- Altaratz, O.; Koren, I.; Remer, L.; Hirsch, E. Review: Cloud invigoration by aerosols—Coupling between microphysics and dynamics. Atmos. Res. 2014, 140–141, 38–60. [Google Scholar] [CrossRef]
- Khain, A.P. Notes on state-of-the-art investigations of aerosol effects on precipitation: A critical review. Environ. Res. Lett. 2009, 4, 015004. [Google Scholar] [CrossRef]
- Morrison, H.; Grabowski, W.W. Response of Tropical Deep Convection to Localized Heating Perturbations: Implications for Aerosol-Induced Convective Invigoration. J. Atmos. Sci. 2013, 70, 3533–3555. [Google Scholar] [CrossRef]
- Guo, L.; Turner, A.G.; Highwood, E.J. Local and Remote Impacts of Aerosol Species on Indian Summer Monsoon Rainfall in a GCM. J. Clim. 2016, 29, 6937–6955. [Google Scholar] [CrossRef]
- Lau, K.-M.; Ramanathan, V.; Wu, G.-X.; Li, Z.; Tsay, S.C.; Hsu, C.; Sikka, R.; Holben, B.; Lu, D.; Tartari, G.; et al. The Joint Aerosol–Monsoon Experiment: A New Challenge for Monsoon Climate Research. Bull. Am. Meteorol. Soc. 2008, 89, 369–384. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Lelieveld, J.; Mitra, A.P.; Althausen, D.; Anderson, J.; Andreae, M.O.; Cantrell, W.; Cass, G.R.; Chung, C.E.; et al. Indian Ocean Experiment: An integrated analysis of the climate forcing and effects of the great Indo-Asian haze. J. Geophys. Res. Atmos. 2001, 106, 28371–28398. [Google Scholar] [CrossRef]
- Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic Aerosols and the Weakening of the South Asian Summer Monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef]
- Ackerman, A.S.; Toon, O.B.; Stevens, D.E.; Heymsfield, A.J.; Ramanathan, V.; Welton, E.J. Reduction of Tropical Cloudiness by Soot. Science 2000, 288, 1042–1047. [Google Scholar] [CrossRef] [PubMed]
- Chung, C.E.; Ramanathan, V.; Kiehl, J.T. Effects of the South Asian Absorbing Haze on the Northeast Monsoon and Surface–Air Heat Exchange. J. Clim. 2002, 15, 2462–2476. [Google Scholar] [CrossRef]
- Bozzo, A.; Remy, S.; Benedetti, A.; Flemming, J.; Bechtold, P.; Rodwell, M.J.; Morcrette, J.-J. Implementation of a CAMS-Based Aerosol Climatology in the IFS; ECMWF Technical Memoranda; ECMWF: Reading, UK, 2017; Volume 801, 33p. [Google Scholar]
- Cheng, A.; Yang, F. Direct radiative effects of aerosols on numerical weather forecast—A comparison of two aerosol datasets in the NCEP GFS. Weather Forecast. 2023, 38, 753–772. [Google Scholar] [CrossRef]
- Zhang, L.; Montuoro, R.; McKeen, S.A.; Baker, B.; Bhattacharjee, P.S.; Grell, G.A.; Henderson, J.; Pan, L.; Frost, G.J.; McQueen, J.; et al. Development and evaluation of the Aerosol Forecast Member in the National Center for Environment Prediction (NCEP)’s Global Ensemble Forecast System (GEFS-Aerosols v1). Geosci. Model Dev. 2022, 15, 5337–5369. [Google Scholar] [CrossRef]
- Mulcahy, J.P.; Walters, D.N.; Bellouin, N.; Milton, S.F. Impacts of increasing the aerosol complexity in the Met Office global numerical weather prediction model. Atmos. Chem. Phys. 2014, 14, 4749–4778. [Google Scholar] [CrossRef]
- Yang, F.; Tallapragada, V.; Kain, J.; Wei, H.; Yang, R.; Yudin, A.V.; Moorthi, S.; Han, J.; Hou, Y.-T.; Wang, J.; et al. Model Upgrade Plan and Initial Results from a Prototype NCEP Global Forecast System Version 16. In Proceedings of the 10th Conference on Transition of Research to Operations, 100th AMS Annual Meeting, Boston, MA, USA, 12–16 January 2020; Available online: https://ams.confex.com/ams/2020Annual/meetingapp.cgi/Paper/362797 (accessed on 1 February 2020).
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Thompson, G.; Rasmussen, R.M.; Manning, K.W. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis. Mon. Wea. Rev. 2004, 132, 519–542. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Clough, S.A. Shortwave and longwave enhancements in the rapid radiative transfer model. In Proceedings of the Seventh Atmospheric Radiation Measurement (ARM) Science Team Meeting, San Antonio, TX, USA, 3–7 March 1997; United States Department of Energy: Washington, DC, USA, 1998; pp. 409–413. [Google Scholar]
- Mlawer, E.J.; Iacono, M.J.; Pincus, R.; Barker, H.W.; Oreopoulos, L.; Mitchell, D.L. Contributions of the ARM Program to Radiative Transfer Modeling for Climate and Weather Applications. Meteorol. Monogr. 2016, 57, 15.1-15.19. [Google Scholar] [CrossRef]
- Buchard, V.; Randles, C.A.; da Silva, A.M.; Darmenov, A.; Colarco, P.R.; Govindaraju, R.; Ferrare, R.; Hair, J.; Beyersdorf, A.J.; Ziemba, L.D.; et al. The MERRA-2 Aerosol Reanalysis, 1980-Onward, Part II: Evaluation and Case Studies. J. Clim. 2017, 30, 6851–6872. [Google Scholar] [CrossRef]
- Randles, C.A.; Da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 Aerosol Reanalysis, 1980 Onward. Part I: System Description and Data Assimilation Evaluation. J. Clim. 2017, 30, 6823–6850. [Google Scholar] [CrossRef] [PubMed]
- DeMott, P.J.; Prenni, A.J.; Rogers, D.C. Predicting global atmospheric ice nuclei distributions and their impacts on climate. Proc. Natl. Acad. Sci. USA 2010, 107, 11217–11222. [Google Scholar] [CrossRef] [PubMed]
- Feingold, G.; Heymsfield, A.J. Parameterizations of Condensational Growth of Droplets for Use in General Circulation Models. J. Atmos. Sci. 1992, 49, 2325–2342. [Google Scholar] [CrossRef]
- Cooper, W.A. Ice Initiation in Natural Clouds. Meteorol. Monogr. 1986, 43, 29–32. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Wood, R. Stratocumulus clouds. Mon. Weather Rev. 2012, 140, 2373–2423. [Google Scholar] [CrossRef]
- Huang, H.; Gu, Y.; Xue, Y.; Jiang, J.; Zhao, B. Assessing aerosol indirect effect on clouds and regional climate of East/South Asia and West Africa using NCEP GFS. Clim. Dyn. 2019, 52, 5759–5774. [Google Scholar] [CrossRef]
- Quaas, J.; Boucher, O. Constraining the first aerosol indirect radiative forcing in the LMDZ GCM using POLDER and MODIS satellite data. Geophys. Res. Lett. 2005, 32, L17814. [Google Scholar] [CrossRef]
- Schwartz, S.E. The whitehouse effect—Shortwave radiative forcing of climate by anthropogenic aerosols: An overview. J. Aerosol. Sci. 1996, 27, 359–382. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteor. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Klein, S.A.; Hartmann, D.L. The Seasonal Cycle of Low Stratiform Clouds. J. Clim. 1993, 6, 1587–1606. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, Cloud Microphysics, and Fractional Cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Zuidema, P.; Westwater, E.R.; Fairall, C.; Hazen, D. Ship-based liquid water path estimates in marine stratocumulus. J. Geophys. Res. Atmos. 2005, 110, D20206. [Google Scholar] [CrossRef]
- Albrecht, B.A.; Bretherton, C.S.; Johnson, D.; Scubert, W.H.; Frisch, A.S. The Atlantic Stratocumulus Transition Experiment—ASTEX. Bull. Am. Meteor. Soc. 1995, 76, 889–904. [Google Scholar] [CrossRef]
- Chlond, A.; Wolkau, A. Large-Eddy Simulation of a Nocturnal Stratocumulus-Topped Marine Atmospheric Boundary Layer: An Uncertainty Analysis. Bound. Layer Meteorol. 2000, 95, 31–55. [Google Scholar] [CrossRef]
- Duynkerke, P.G.; Jonker, P.J.; Chlond, A.; Van Zanten, M.C.; Cuxart, J.; Clark, P.; Sanchez, E.; Martin, G.; Lenderink, G.; Teixeira, J. Intercomparison of Three- and one-Dimensional Model Simulations and Aircraft Observations of Stratocumulus. Bound. Layer Meteorol. 1999, 92, 453–487. [Google Scholar] [CrossRef]
- Wood, R. Drizzle in stratiform boundary layer clouds. Part I: Vertical and horizontal structure. J. Atmos. Sci. 2005, 62, 3011–3033. [Google Scholar] [CrossRef]
- Painemal, D.; Xu, K.-M.; Cheng, A.; Minnis, P.; Palikonda, R. Mean Structure and Diurnal Cycle of Southeast Atlantic Boundary Layer Clouds: Insights from Satellite Observations and Multiscale Modeling Framework Simulations. J. Clim. 2015, 28, 324–341. [Google Scholar] [CrossRef]
- Stevens, B.; Graham, F. Untangling aerosol effects on clouds and precipitation in a buffered system. Nature 2009, 461, 1476–4687. [Google Scholar] [CrossRef]
- Xie, S.; Hume, T.; Jakob, C.; Klein, S.; McCoy, R.; Zhang, M. Observed large-scale conditions and diabatic heating and drying profiles during TWP-ICE. J. Clim. 2010, 23, 57–79. [Google Scholar] [CrossRef]
- Sandu, I.; Brenguier, J.-L.; Geoffroy, O.; Thouron, O.; Masson, V. Aerosol Impacts on the Diurnal Cycle of Marine Stratocumulus. J. Atmos. Sci. 2008, 65, 2705–2718. [Google Scholar] [CrossRef]
- May, P.T.; Mather, J.H.; Vaughan, G.; Jakob, C.; McFarquhar, G.M.; Bower, K.N.; Mace, G.G. The Tropical Warm Pool International Cloud Experiment. Bull. Am. Meteorol. Soc. 2008, 89, 629–646. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Zipser, E.J. The diurnal cycle of rainfall and convective intensity according to three years of TRMM measurements. J. Clim. 2003, 16, 1456–1475. [Google Scholar] [CrossRef]
- Thompson, G.; Eidhammer, T. A Study of Aerosol Impacts on Clouds and Precipitation Development in a Large Winter Cyclone. J. Atmos. Sci. 2014, 71, 3636–3658. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, A.; Yang, F. Aerosol, Clouds and Radiation Interactions in the NCEP Unified Forecast Systems. Meteorology 2025, 4, 14. https://doi.org/10.3390/meteorology4020014
Cheng A, Yang F. Aerosol, Clouds and Radiation Interactions in the NCEP Unified Forecast Systems. Meteorology. 2025; 4(2):14. https://doi.org/10.3390/meteorology4020014
Chicago/Turabian StyleCheng, Anning, and Fanglin Yang. 2025. "Aerosol, Clouds and Radiation Interactions in the NCEP Unified Forecast Systems" Meteorology 4, no. 2: 14. https://doi.org/10.3390/meteorology4020014
APA StyleCheng, A., & Yang, F. (2025). Aerosol, Clouds and Radiation Interactions in the NCEP Unified Forecast Systems. Meteorology, 4(2), 14. https://doi.org/10.3390/meteorology4020014







