Next Article in Journal
Study of Extreme Cold Surges in Hong Kong
Next Article in Special Issue
Influence of Underlying Topography on Post-Monsoon Cyclonic Systems over the Indian Peninsula
Previous Article in Journal
Evaluating Possible Changes in Air Temperature and Precipitation Patterns in Mozambique by Comparing Present and Future RegCM4 Simulation
Previous Article in Special Issue
Heat Waves Amplify the Urban Canopy Heat Island in Brno, Czechia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Meteorology
Volume 2
Issue 1
10.3390/meteorology2010003
meteorology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of Air Mass Advection on the Amount of Global Solar Radiation Reaching the Earth’s Surface in Poland, Based on the Analysis of Backward Trajectories (1986–2015)

by
Kinga Kulesza
1,2
1
Centre of Applied Geomatics, Institute of Geodesy and Cartography (IGiK), 02-679 Warsaw, Poland
2
Department of Climatology, Chair of Physical Geography, Faculty of Geography and Regional Studies, University of Warsaw, 00-927 Warsaw, Poland
Meteorology 2023, 2(1), 37-51; https://doi.org/10.3390/meteorology2010003
Submission received: 29 November 2022 / Revised: 19 December 2022 / Accepted: 5 January 2023 / Published: 9 January 2023
(This article belongs to the Special Issue Early Career Scientists' (ECS) Contributions to Meteorology (2023))
Browse Figures
Versions Notes

Abstract

:
The paper aims to analyse the relationship between the amount of global solar radiation (GSR) reaching the Earth’s surface in Poland and the direction of air mass advection, using 72-h backward trajectories (1986–2015). The study determined average daily sums of GSR related to groups of trajectories with certain similarities in shape. It was found that the average daily sums of GSR during air mass inflow from all the directions (clusters) identified were significantly different from the average daily sum in the multi-year period. A significant increase in the amount of GSR over Poland is accompanied by air mass inflow from the north and east. The frequency of these advection directions is 27% of all days. The western directions of advection prompt different GSR sums: from slightly increased during advection from the north-west, to significantly decreased during advection from the west (from the central and western part of the North Atlantic). Special attention was given to days with extremely large (above the 0.95 percentile) and with the largest (above the 0.99 percentile) GSR sums. These are prompted by two main types of synoptic conditions: the Azores High ridge covering Central and Southern Europe; and the high-pressure areas which appear in Northern and Central Europe.

1. Introduction

Incoming solar radiation is the most important factor shaping climate system on Earth and the main element of the surface heat balance [1]. Approximately 1361 W·m−2 of the Sun’s radiant energy [2] reaches the upper limit of the atmosphere every second. Thus, conditions related to the latitude (and the resulting length of the day and the solar zenith angle) are the most important to shape the amount of global solar radiation (GSR) reaching the Earth’s surface in a given place throughout the year. However, the differences in GSR sums received in the places located on the same latitude can be substantial. The reason for this is the circulation of the atmosphere and the related changes in the amount of aerosols contained in the atmosphere (which reduce the inflow of GSR), as well as the associated cloudiness changes. Therefore, the circulation (movement) of the atmosphere, might be considered as the key factor that affects the inflow of radiant energy to the Earth’s surface.
Moving air masses have certain characteristics—such as the content of water vapour and aerosols (which affects the transparency of the mass) and the presence and size of cloud cover—which directly affect the amount of radiant energy that reaches the Earth’s surface. The relationship between cloud cover and atmospheric circulation have been described in many studies [3,4,5]. But one should remember that cloud cover is very important, but not the only element which influences the amount of GSR reaching the Earth’s surface. Analyses of cloudless air masses have shown that Arctic air is responsible for the highest intensity of direct solar radiation in Europe, while tropical air prompts the lowest irradiance [6,7,8,9]. In central Poland, on days with relative sunshine duration equalling more than 80% (meaning when cloudiness has practically no impact on solar radiation), the amount of GSR reaching the Earth’s surface depends greatly on the direction of air mass inflow. In winter, larger GSR sums occur during air mass inflow from the E, N and NW directions, and smaller sums occur during advection from the SW and S directions. In summer, larger GSR sums are typically accompanied by advection from the N, NE and E directions, and smaller sums occur during advection from the SE and NW directions (1971–2014) [10].
Moreover, the relation between atmospheric aerosols concentration (which is measured by aerosol optical depth, AOD) and atmospheric circulation have been analysed in many papers [6,9,11,12,13,14]. But a comprehensive description of the influence of atmospheric circulation on the amount of GSR reaching the Earth’s surface is presented in few studies. To describe the relation between GSR and atmospheric circulation, different classifications of atmospheric circulation types are used. In these classifications, individual circulation types are determined based on the data on sea level atmospheric pressure or on the geopotential height at 500, 700, 850 or 925 hPa. The circulation type on a given day is often identified on the basis of synoptic conditions at 12:00 UTC. In Europe, the following classifications are most frequently used to describe the relation between GSR and atmospheric circulation: the German Grosswetterlagen classification [3,15,16], the British Lamb classification [17] and the Polish Lityński classification [10,18]. The disadvantage to circulation type classifications is that they only take the current state of the atmosphere (for example at 12:00 UTC every day) into account, without analysing from where the air flowed over a given area. Degirmendžić and Kożuchowski [19] pointed out that pressure system over Poland and the resulting geostrophic wind vector (which serves as the basis for determining circulation types in many numerical classifications) determined the origin of air masses only in 45–61% of cases of the strongest advections. In fact, trajectories of air mass movement have significant curvatures. As a result, the wind direction over Poland has a weak correlation with the actual direction of air mass movement. For this reason, backward trajectories of air masses seem to be a better basis for analysing the relations between meteorological elements (such as GSR) and atmospheric circulation.
The Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model was developed by the National Oceanic and Atmospheric Administration (NOAA) from the United States [20]. It is one of the most widely used models in the world for tracking the movement of air particles in the atmosphere and for analysing the dispersion of pollutants. It was used in studies on the dispersion of pollutants and dust in such countries as the United States [21], China [22], Iran [23] and Poland [24,25], as well as to forecast the movement of volcanic ash [26,27]. Backward trajectories determined by the HYSPLIT model are often used to describe the meteorological background of research (e.g., [28]), as well as to analyse circulation conditions of different meteorological elements, such as high precipitation sums [29,30] and heavy snowfall [31]. They have not been used in research on GSR so far. When using HYSPLIT backward trajectories, the total error ranges from 15 to 30% of the travel distance [32,33]. Studies have shown that HYSPLIT backward trajectories tend to differ with different input meteorological data, when air masses are passing through areas with complex topography, diversified land use, or with complicated meteorological pattern [34]. It should also be remembered that unlike atmospheric circulation types determined by classifications, backward trajectories show where the air came from, but do not identify the character of circulation (cyclonic/anticyclonic).
This paper aimed to analyse the relationship between the amount of GSR reaching the Earth’s surface in Poland and the direction of air mass advection. The paths of air mass inflow were identified using 72-h backward trajectories. This study determined average daily sums of GSR related to groups of trajectories with certain similarities in shape. Moreover, special attention was given to days with extremely large (above the 0.95 percentile) and with the largest (above the 0.99 percentile) GSR sums. Identifying the causes of the variability in the most important element of the Earth’s energy balance, solar radiation, is particularly important in the context of the dynamic development of solar energy, as well as the necessity of climate change adaptation and mitigation.

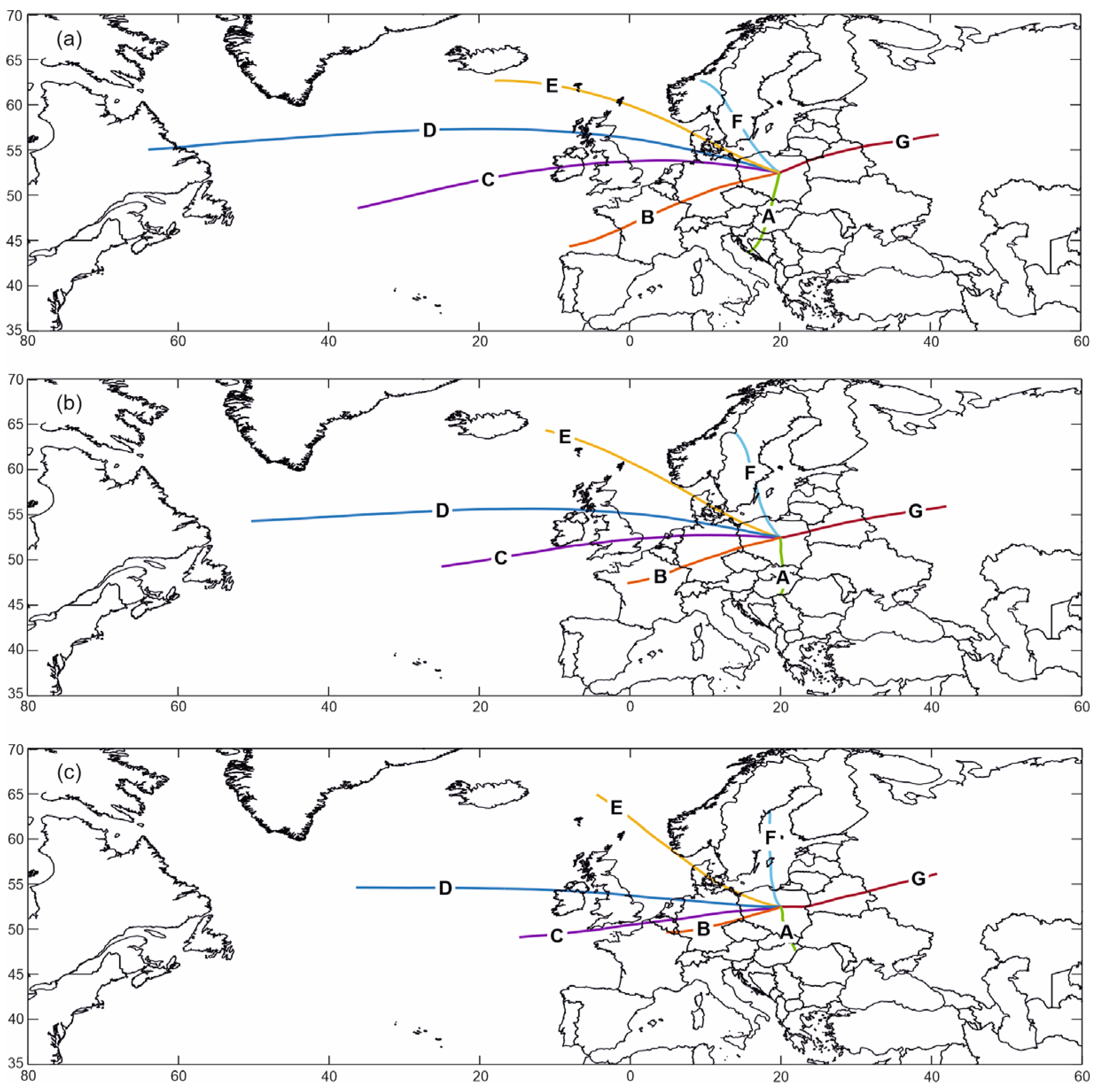
2. Data and Methods

Satellite-derived data prepared by European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT)—Satellite Application Facility on Climate Monitoring (CM SAF), concerning global solar radiation (SIS product—Surface Incoming Shortwave Radiation) and originating from the Surface Solar Radiation Data Set—Heliosat, Edition 2 (SARAH-2 database) [35], are used in this paper, in order to calculate GSR sums over Poland. SARAH-2 covers the period from 1983 to 2015 and provides data based on satellite measurements made by Meteosat Visible and Infrared Imager (MVIRI) and Spinning Enhanced Visible and Infrared Imager (SEVIRI) instruments which have been on board Meteosat geostationary satellites [35], with a spatial resolution of 0.05° × 0.05°. Pfeifroth et al. [35] proved the high quality of SARAH-2 data in relation to ground-based measurement data in Europe. The SIS product was additionally validated over Poland [36]. This paper uses SIS product with a daily resolution for the 30-year period 1986–2015. Average sums of GSR over Poland were calculated as area averages of all values in the grid points 0.05° × 0.05° within the borders of Poland.
Moreover, 72-h backward trajectories, identified using the HYSPLIT model, were analysed [20]. For this purpose, this study used data from the NCEP/NCAR reanalysis [37] from the period 1985–2015 and the openair package [38] which was implemented in the R computing environment. In the period 1986–2015 under consideration, the study identified backward trajectories ending at 12:00 UTC every day which trace air mass movement backwards in time, up to 72 h. The backward trajectories were determined for air masses ending their movement at three levels: close to the Earth’s surface (500 m above ground level), at the upper limit of the atmospheric boundary layer (1500 m above ground level) and in the free troposphere (3000 m above ground level). The NCEP/NCAR reanalysis grid point which is the closest to Warsaw (capital city, central Poland)—52.5° N, 20° E—was taken as the end point of trajectories. The starting points of trajectories, meaning the places from where the air flowed over Poland, were clustered using the k-means method [39]. In this method, k centroids (midpoints of k groups) are randomly chosen and then the entire population (in this case all starting points of trajectories) is assigned to the nearest centroids. To measure the distance between the points and centroids, this paper used squared Euclidean distance, which is commonly used in studies concerning clustering of backward trajectories [40,41]. Next, a new position of centroids was calculated as the arithmetic mean of the positions of all observations assigned to a given group. In successive iterations, the observations (starting points) were transferred between groups, and the position of centroids was recalculated until the moment when the points stayed in the same groups. This results in clusters that are as different from one another as possible, in which the sum of within-group variance is the smallest. A certain limitation of the k-means method is that the number of clusters into which all observations will be divided has to be determined in advance. There are, however, methods for searching for an optimal number of clusters, e.g., Bayesian Information Criterion (BIC) or Akaike Information Criterion (AIC) [42,43]. Other procedures can also be applied, e.g., the silhouette statistic [44], or the gap statistic [45]. In this study, after running simulations with different numbers of clusters, the silhouette statistic was calculated. The maximum value of the silhouette statistic was obtained when the observations were divided into 7 clusters. In the next step, the shape of the backward trajectories assigned to a given cluster was averaged and the main paths of air mass inflow over Poland were established in this way. The study examined the amount of GSR reaching the Earth’s surface in Poland depending on the source area and the direction of air mass inflow. The analyses were carried out for the year and the seasons (hereinafter III-V refers to spring, VI-VIII to summer, IX-XI to autumn, and XII-II to winter) as well as for days with extremely large sums of GSR (above the 0.95 percentile) in individual seasons of the year. In addition, backward trajectories were determined for days with the largest GSR sums (above the 0.99 percentile), broken down by seasons of the year.

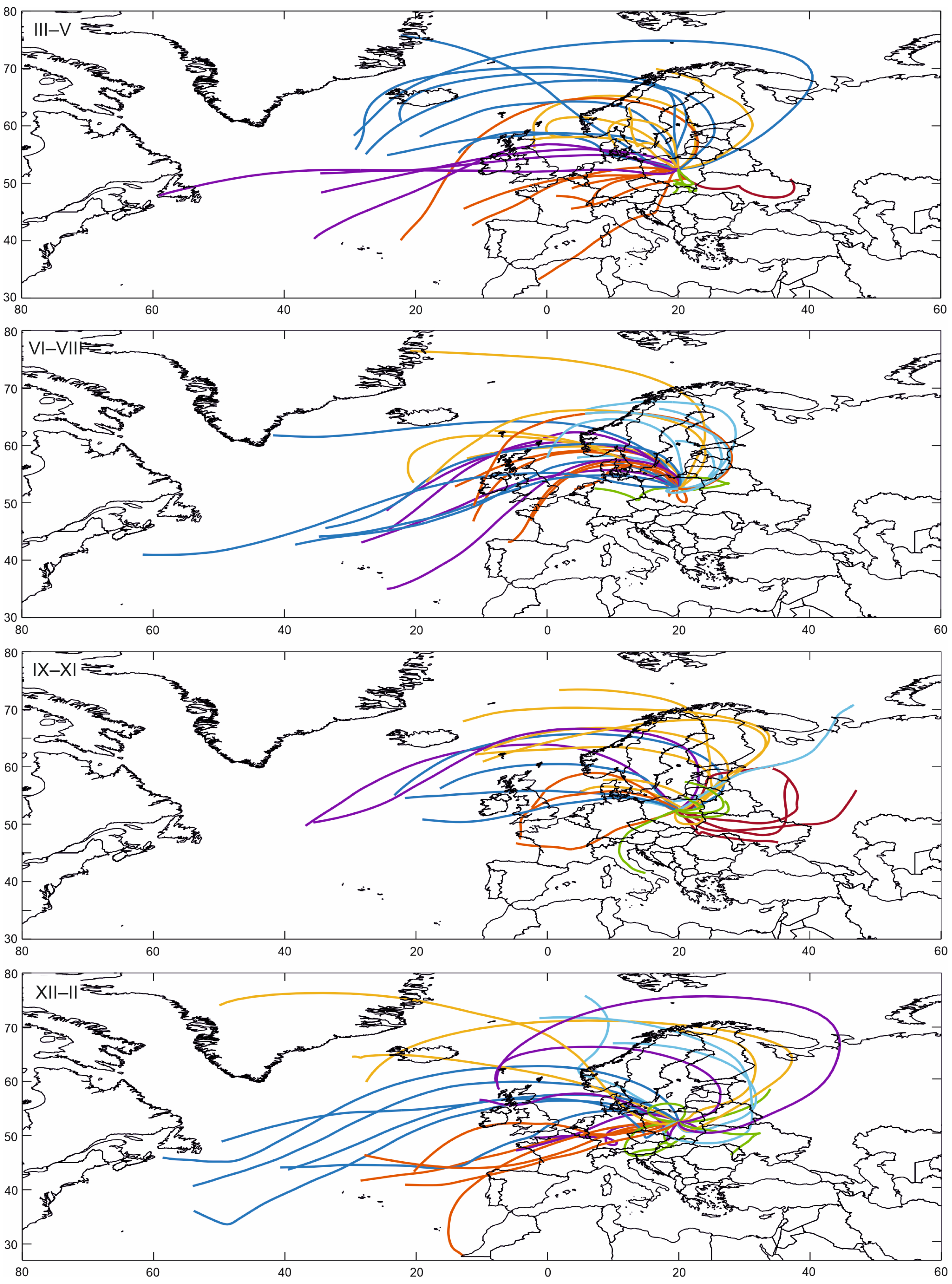
3. Results

The amount of GSR over Poland is related, among others, to the properties of the air mass over the area of the country. Using 72-h backward trajectories, one can trace the path travelled by air masses before they reach Poland. Averaged backward trajectories in 7 clusters ending at three levels: close to the Earth’s surface (500 m above ground level), at the upper limit of the atmospheric boundary layer (1500 m above ground level) and in the free troposphere (3000 m above ground level) have similar shapes, but they differ in trajectory length (Figure 1). The air moving in the free troposphere, where the friction is the lowest, moves faster than the air in lower layers, so within 72 h it can travel greater distances. However, regardless of the height at which air masses end their movement, the frequency of air mass inflow from each cluster is similar (Table 1). As a result, the average daily sum of GSR in each cluster is similar. In almost all clusters, the average daily sum is significantly different from the average daily sum in the multi-year period. Only air inflow from the cluster covering Central and Southern Europe (A) ending at 500 and 1500 m above ground level generates average GSR sums which do not differ significantly from the average multi-year sum (Table 1). For this reason, and because the backward trajectories at three levels provide similar information, only the backward trajectories at 3000 m above ground level have been used for further analysis.
Averaged trajectory in cluster A shows the path of air masses that start over the central part of Southern Europe, but the area of air mass inflow in this cluster is much larger (Figure 2). It includes air masses coming from Central and Southern Europe, as well as from the Mediterranean Sea and North Africa. In cluster A, the air travels the shortest distance of all the clusters, so it moves relatively slowly. The frequency of air inflow from this cluster is more than 17%, and the average daily sum of GSR during the inflow of air masses from cluster A is similar to the multi-year mean and amounts to 10.29 MJ·m−2·day−1 (Table 1). Cluster B contains starting points of trajectories of air masses coming from the western part of Europe (British Isles, Spain, Portugal), as well as from western Algeria, Morocco and the eastern part of the Atlantic Ocean. The air that reaches Poland in 72 h travels a fairly short distance, but this cluster contains the largest number of trajectories of all the clusters (Table 1). In this area, mid-latitude lows are often forming at the polar front and moving later to north-eastern Europe, affecting the weather in Poland, among others [46,47]. Cluster C contains the air flowing from the central part of the Atlantic Ocean. Moist air masses coming from the regions spreading from the Azores to the south coast of Greenland travel over sea areas most of the time. They move quite quickly and can, therefore, retain maritime characteristics for a long time after reaching the European continent. They often bring clouds and relatively low air transparency. This is why the average daily sum of GSR when the air flows from cluster C is significantly lower than the average multi-year sum and amounts to 9.31 MJ·m−2·day−1. The longest distance within 72 h is covered by air masses that start their movement in the eastern part of North America (cluster D). Air masses usually move from west to east so quickly during a positive phase of the North Atlantic Oscillation. This happens more often in winter than in summer and causes strong wind, heavy rainfall and high cloudiness. Therefore, the average daily sum of GSR is the smallest in cluster D and amounts only to 6.37 MJ·m−2·day−1. It should also be noted that this cluster contains the smallest number of trajectories of all the clusters: the frequency of air mass inflow from this area is less than 8%. Cluster E contains the air flowing from the central and northern part of the Atlantic Ocean. Cool air masses that start their movement in the area of Iceland and the east and north-east coast of Greenland prompt significantly increased daily sums of GSR over Poland, amounting, on average, to 11.42 MJ·m−2·day−1. Cluster F consists of trajectories of air masses flowing over Poland from the north and north-west, that is from the North Sea, Scandinavia and the European Arctic. Arctic air which often flows from this area is usually dry and highly transparent. This is why the average daily sum of GSR is high in this case and amounts to 12.08 MJ·m−2·day−1. The last cluster, G, contains trajectories of air masses starting their movement to the east of Poland, from Arctic areas in the north-east, through Eastern Europe and Transuralia, to Transcaucasia in the south-east. Even though it is certainly the largest cluster in terms of area, the frequency of air inflow from this cluster (10.0%) is much lower than the frequency of air mass inflow from all ‘western’ clusters. The eastern advection direction is related to weather conditions with small cloudiness which prompt large sums of GSR over Poland. The average daily sum of GSR in cluster G is the largest of all the clusters and amounts to 12.74 MJ·m−2·day−1.
The division into clusters and averaged air mass inflow paths over Poland in individual seasons of the year are very similar to the division into clusters of data from the entire multi-year period. However, it should be noted that in summer the air moves slower, and the starting points of backward trajectories are more concentrated geographically: most of them are located between meridians 70° W and 50° E (Figure 3). On the other hand, in winter a positive phase of the North Atlantic Oscillation occurs more often and strengthens zonal circulation [48,49], which results in the air flowing over Poland from very distant locations: the starting points of backward trajectories are located between meridians 100° W and 100° E.
Average daily GSR sums during air inflow from individual clusters show some diversity (Table 2). In spring, the average daily sum of GSR amounts to 14.05 MJ·m−2·day−1. The average daily sums in clusters A and B are significantly smaller than that. These clusters contain air mass inflow from Central and Western Europe, as well as from the Central Atlantic. Atmospheric circulation over Poland in spring is also characterised by a relatively large share of Arctic air in May [7] which prompts a significantly increased average daily sum in cluster F. In summer, the starting points of backward trajectories are not only more concentrated geographically, but also the frequency of air mass inflow from individual clusters is less diversified. This season is characterised by a relatively large share (up to 12%) of air mass inflow from Eastern Europe and Asia (cluster G), compared to all seasons of the year. In summer, the average daily sum of GSR when the air flows from cluster G is significantly higher than the average daily sum in this season of the year which amounts to 18.61 MJ·m−2·day−1. A significantly higher average daily sum of GSR can also be observed when the air flows from the Central and North Atlantic (cluster C and E). In autumn, usually meridional circulation develops (and zonal circulation weakens), which results in a statistically significant increase in the average daily sum of GSR during air mass inflow from the north (cluster F) and north-east (cluster G). The air inflow from cluster G, which is often related to the anticyclonic distribution of pressure in European Russia, prompts a particularly large GSR sum. On the other hand, the average daily sum of GSR is significantly decreased during the advection of air masses coming from Canada (cluster D), as well as from Central and Southern Europe and North Africa (cluster A). Interestingly, the air mass coming from Africa, even though it often contains a lot of dust, brings sunny and cloudless weather over Poland in autumn. However, cluster A contains mostly trajectories of air masses coming from nearby locations in Central and Southern Europe, which can cause smog and subsidence inversion in autumn. The strongest western circulation occurs in winter. In this season, a significantly decreased average daily sum of GSR is accompanied by advection from Canada (cluster D). On the other hand, dry, highly transparent air coming from European Russia and Asia (cluster G) prompts a significantly increased average daily sum of GSR.
The analysis of backward trajectories on days with extremely large GSR sums (above the 0.95 percentile) leads to interesting observations. In this case, none of the average daily GSR sums in individual clusters differs significantly from average daily GSR sums in corresponding seasons of the year (Table 3). In other words, in a given season average daily sums on days with extremely large GSR are similar in all clusters. Yet, it is interesting to analyse the frequencies of individual clusters. In spring, extreme GSR sums occur most frequently during air mass inflow from the Atlantic Ocean, from clusters B, C and D. This accounts in total for over 63% of all cases (Figure 4, Table 3). The characteristic curve of average air inflow paths, visible in particular in cluster D, is related to the anticyclonic movement of air masses flowing over Poland. Within 72 h, the air coming from the area of Iceland makes a curve and flows over Poland directly from the north or even north-east, which is particularly visible on maps that show backward trajectories on days with GSR sums exceeding the 0.99 percentile (Figure 5). Interestingly, in spring the air coming from the far north, over the Arctic Ocean (cluster F), which is most often associated with extremely high transparency and the largest GSR sums, not only very rarely causes extremely large GSR sums (its frequency is less than 3%), but also does not prompt GSR sums exceeding the 0.99 percentile (this is why in Figure 5 in spring there is no light blue colour which indicates cluster F). In summer, extremely large sums of GSR are most often related to air inflow from clusters B, E and F: this accounts for over 57% of all cases in total (Table 3). The trajectory of air masses, similarly as in cluster D in spring, indicates the anticyclonic movement of air masses which within 72 h flow from the Atlantic and reach Poland from the north or north-west (orange, yellow and light blue trajectories respectively in Figure 5 in summer). Extreme GSR sums are slightly less often (30.4% of all cases) related to air mass inflow from the Central Atlantic (cluster C and D). On these days, such high GSR is caused by the largely expanded Azores High which prompts sunny weather in Europe, mainly in the south. Similarly to summer, in autumn extremely large GSR sums are most often related to air inflow from the eastern part of the Atlantic Ocean (clusters B and E). This accounts for over 40% of all cases in total (Table 3). In autumn, cluster G (which represents air inflow from the east, from European Russia) has the biggest share of all seasons (almost 12% of all cases). This is related to a high-pressure system, when the high-pressure area is centred east of Poland and the air flows to Poland from the south-east (this is visible in autumn in Figure 5 which shows trajectories on days with GSR sums exceeding the 0.99 percentile—dark red trajectories indicate cluster G). It is also worth noting that among autumn days with extremely large GSR sums, there are no trajectories that start over Africa. As mentioned above, tropical air that flows in autumn from North Africa often contains a lot of dust, which is why it is not accompanied by GSR sums exceeding the 0.95 percentile. In winter, air masses most often flow from cluster A, from Central Europe. This accounts for over 25% of all cases (Table 3). In this case, the air moves very slowly, and large GSR sums may be caused by the strengthening of a high-pressure area over Poland. As in other seasons of the year, clusters C, D and E occur often—their total frequency is over 48%. In these clusters, the air often flows from the west, makes a huge curve and reaches Poland from the north, north-east or east. It is worth noting that extremely large GSR sums are rarely related to air inflow from the east (cluster G), even though the air coming from Eastern Europe is most often associated with cloudless weather and high air transparency. Among backward trajectories that precede days with the largest GSR sums (above the 0.99 percentile), there is no air inflow from the east (in Figure 5 in winter there is no dark red trajectory which indicates cluster G).

4. Discussion and Conclusions

The main aim of this paper was to determine the impact of the direction of air mass advection on the amount of GSR reaching the Earth’s surface in Poland. The analysis was based on source material from the period 1986–2015.
72-h HYSPLIT backward trajectories seem to be a good tool for analysing circulation conditions of GSR reaching the Earth’s surface. However, they have some limitations that should be noticed. The accuracy of an individual trajectory is limited by i.e., temporal and spatial resolution of input meteorological data, measurement errors and simplifying assumptions used in the trajectory model [34,40]. As mentioned before, the total error of a trajectory can amount up to 30% of the travel distance [32,33]. In this study the relatively coarse resolution of input meteorological data was used (2.5° × 2.5°), leading to possible uncertainties in the resulting trajectories. Yet, analysing trajectories over a relatively long period of time (in this case 30-years of daily trajectories) can compensate this problem, as generally, the confidence in the cluster analysis results increases with the number of trajectories analysed [41].
Choosing the right end point is also an important issue, because even small perturbations in final coordinates may result in different trajectories. Although HYSPLIT enables computing the matrix of end points, that could cover the whole area of Poland, in this work only one end point (close to Warsaw, central Poland) was used. That was because the GSR values were averaged within the area of Poland, and as such had to be assigned to one point. On the contrary, using many end points would require many different GSR sums. As a result, each end point should be analysed separately. This would constitute an interesting research question: whether the relationship between GSR and direction of the air masses differs spatially. In order to fully understand such problem a further research is needed.
The characteristics of the certain air mass depend on the place of its formation (here the starting point of the trajectory), but also on its transformation along the way. In this study only the starting points were taken to explain the observed GSR values. This might also be the source of minor uncertainty, especially in the case of slowly moving air masses. In order to reduce this potential uncertainty, only the air masses fast moving in in the free troposphere were taken (i.e., trajectories ending and 3000 m above ground level).
Using 72-h backward trajectories, it was found that the average daily sum of GSR during air mass inflow from all the directions (clusters) identified was significantly different from the average daily sum in the multi-year period. Throughout the year, a significant increase in the amount of GSR over Poland is accompanied by air mass inflow from the north and east. The frequency of these advection directions is not high. In total, they occur on 27% of all days. On most days, incoming air masses have a western component. The western direction of advection prompts different GSR sums: from slightly increased (in relation to the multi-year average) during advection from the north-west, to significantly decreased during advection from the west (from the central and western part of the North Atlantic).
Extremely large (above the 0.95 percentile) and the largest (above the 0.99 percentile) daily sums of GSR are usually related to air inflow from the Atlantic Ocean. The shape of backward trajectories on these days indicates the anticyclonic character of circulation. Days with extremely large and the largest sums of GSR are prompted by two main types of synoptic conditions. The first one is the Azores High ridge covering Central and Southern Europe which generates air mass inflow from the central part of the North Atlantic. The second type of conditions involves high-pressure areas which appear in Northern and Central Europe in spring, summer and autumn in particular. At that time of the year, air mass inflow over Poland follows trajectories with anticyclonic curvatures which often make a huge curve over the northern part of Europe and enter the territory of Poland from the NW-N-NE directions.
In general, in the period 1986–2015 the direction of air mass advection influenced strongly GSR sums in Poland. Similar conclusion concerning the influence of atmospheric circulation on the amount of solar radiation reaching the ground in Poland can be found in our previous works [18,50]. However, using backward trajectories in this paper, a method which is rarely used, leads to objectifying the results. Unlike methods that analyse only the current “state of the atmosphere” (e.g., most circulation type classifications), backward trajectories allow to examine from where the air actually flowed. For this reason, backward trajectories of air masses seem to be a very good basis for analysing the relations between any meteorological elements (solar radiation in this case) and atmospheric circulation.

Funding

This research was funded by the Faculty of Geography and Regional Studies of the University of Warsaw, grant number SOP-I-117/19.

Data Availability Statement

Publicly available datasets were analyzed in this study. The data on backward trajectories can be found here: https://www.ready.noaa.gov/HYSPLIT.php. The data on GSR in Poland can be found here: https://danepubliczne.imgw.pl/data/dane_pomiarowo_obserwacyjne/ (accessed on 28 November 2022).

Acknowledgments

This paper is based on a doctoral dissertation which was written under the supervision of Elwira Żmudzka, at the University of Warsaw, in the Department of Climatology of the Faculty of Geography and Regional Studies at the University of Warsaw.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wild, M.; Ohmura, A.; Schär, C.; Müller, G.; Folini, D.; Schwarz, M.; Hakuba, M.Z.; Sanchez-Lorenzo, A. The Global Energy Balance Archive (GEBA) version 2017: A database for worldwide measured surface energy fluxes. Earth Syst. Sci. Data 2017, 9, 601–613. [Google Scholar] [CrossRef] [Green Version]
  2. Gueymard, C.A. A reevaluation of the solar constant based on a 42-year total solar irradiance time series and a reconciliation of spaceborne observations. Sol. Energy 2018, 168, 2–9. [Google Scholar] [CrossRef]
  3. Parding, K.; Olseth, J.A.; Liepert, B.G.; Dagestad, K.F. Influence of atmospheric circulation patterns on local cloud and solar variability in Bergen, Norway. Theor. Appl. Climatol. 2016, 125, 625–639. [Google Scholar] [CrossRef]
  4. Sanchez-Lorenzo, A.; Calbó, J.; Brunetti, M.; Deser, C. Dimming/brightening over the Iberian Peninsula: Trends in sunshine duration and cloud cover and their relations with atmospheric circulation. J. Geophys. Res. Atmos. 2009, 114, D00D09. [Google Scholar] [CrossRef] [Green Version]
  5. Żmudzka, E. Zmienność Zachmurzenia Nad Polską I Jej Uwarunkowania Cyrkulacyjne (1951–2000); Wydawnictwo Uniwersytetu Warszawskiego: Warsaw, Poland, 2007. [Google Scholar]
  6. Smirnov, A.; Villevalde, Y.; O’Neill, N.T.; Royer, A.; Tarussov, A. Aerosol optical depth over the oceans: Analysis in terms of synoptic air mass types. J. Geophys. Res. Atmos. 1995, 100, 16639–16650. [Google Scholar] [CrossRef]
  7. Uscka-Kowalkowska, J. Bezpośrednie Promieniowanie Słoneczne I Jego Ekstynkcja W Atmosferze Na Przykładzie Puław I Papowa Toruńskiego; Wydawnictwo Naukowe Uniwersytetu Mikołaja Kopernika: Torun, Poland, 2008. [Google Scholar]
  8. Uscka-Kowalkowska, J. An analysis of the extinction of direct solar radiation on Mt. Kasprowy Wierch, Poland. Atmos. Res. 2013, 134, 175–185. [Google Scholar] [CrossRef]
  9. Uscka, J. Direct solar radiation and its attenuation by the atmosphere with different air masses in the suburban area of Toruń. Acta Univ. Wratislav. Stud. Geogr. 2003, 75, 268–281. [Google Scholar]
  10. Nelken, K. Impact of atmospheric circulation on the amount of global solar radiation reaching the Earth’s surface in Belsk (1971-2014). Bad. Fizjogr. VII Ser. A Geogr. Fiz. 2016, 67, 155–168. [Google Scholar] [CrossRef]
  11. Gkikas, A.; Houssos, E.E.; Hatzianastassiou, N.; Papadimas, C.D.; Bartzokas, A. Synoptic conditions favouring the occurrence of aerosol episodes over the broader Mediterranean basin. Q. J. R. Meteorol. Soc. 2012, 138, 932–949. [Google Scholar] [CrossRef]
  12. Nilsson, E.D.; Paatero, J.; Boy, M. Effects of air masses and synoptic weather on aerosol formation in the continental boundary layer. Tellus Ser. B Chem. Phys. Meteorol. 2001, 53, 462–478. [Google Scholar] [CrossRef]
  13. Ponczkowska, A.; Zieliński, T.; Petelski, T.; Markowicz, K.; Chourdakis, G.; Georgoussis, G. Aerosol Optical Depth Measured at Different Coastal Boundary Layers and Its Links with Synoptic-Scale Features. Remote Sens. 2009, 1, 557–576. [Google Scholar] [CrossRef]
  14. Power, H.C.; Sheridan, S.C.; Senkbeil, J.C. Synoptic climatological influences on the spatial and temporal variability of aerosols over North America. Int. J. Climatol. 2006, 26, 723–741. [Google Scholar] [CrossRef]
  15. Panziera, L.; Giovannini, L.; Laiti, L.; Zardi, D. The relation between circulation types and regional Alpine climate. Part I: Synoptic climatology of Trentino. Int. J. Climatol. 2015, 35, 4655–4672. [Google Scholar] [CrossRef] [Green Version]
  16. Parding, K.M.; Liepert, B.G.; Hinkelman, L.M.; Ackerman, T.P.; Dagestad, K.-F.; Olseth, J.A. Influence of Synoptic Weather Patterns on Solar Irradiance Variability in Northern Europe. J. Clim. 2016, 29, 4229–4250. [Google Scholar] [CrossRef]
  17. Lawrence, E.N. Solar radiation trends and weather patterns. Weather 1972, 27, 320. [Google Scholar] [CrossRef]
  18. Kulesza, K. Wpływ cyrkulacji atmosferycznej na ilość całkowitego promieniowania słonecznego docierającego do powierzchni ziemi w Polsce w latach 1986–2015 (The influence of atmospheric circulation on the amount of global solar radiation reaching the Earth’s surface in Poland in years 1986–2015). Prz. Geogr. 2020, 92, 341–359. [Google Scholar]
  19. Degirmendžić, J.; Kożuchowski, K. O drogach i kierunkach adwekcji mas powietrza nad obszar Polski. In Klimatyczne Aspekty Środowiska Geograficznego; Trepińska, J., Olecki, Z., Eds.; Instytut Geografii i Gospodarki Przestrzennej Uniwersytetu Jagiellońskiego: Krakow, Poland, 2006; pp. 339–350. [Google Scholar]
  20. Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.B.; Cohen, M.D.; Ngan, F. NOAA’s HYSPLIT Atmospheric Transport and Dispersion Modeling System. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
  21. Bella, D.; Culpepper, J.; Ealy, J.; King, Z.; Skeete, D.; Blaszczak-Boxe, C.S.; Khaimova, J.; Ahmed, N.; Belkalai, A.; Arroyo, I.; et al. Characterization of pollution transport into Texas using OMI and TES satellite, GIS and in situ data, and HYSPLIT back trajectory analyses: Implications for TCEQ State Implementation Plans. Air Qual. Atmos. Health 2016, 9, 569–588. [Google Scholar] [CrossRef]
  22. Lu, X.; Mao, F.; Pan, Z.; Gong, W.; Wang, W.; Tian, L.; Fang, S. Three-dimensional physical and optical characteristics of aerosols over central China from long-term CALIPSO and HYSPLIT data. Remote Sens. 2018, 10, 314. [Google Scholar] [CrossRef] [Green Version]
  23. Mohammadi, F.; Kamali, S.; Eskandary, M. Tracing dust sources in different atmosphere levels of Tehran using hybrid single-particle lagrangian integrated trajectory (HYSPLIT) model. Sci. J. Pure Appl. Sci. 2014, 3, 559–571. [Google Scholar] [CrossRef]
  24. Godłowska, J.; Hajto, M.J.; Tomaszewska, A.M. Spatial analysis of air masses backward trajectories in order to identify distant sources of fine particulate matter emission (Analiza przestrzenna wstecznych trajektorii mas powietrza w celu rozpoznania odległych źródeł emisji pyłu drobnego). Arch. Environ. Prot. 2015, 41, 28–35. [Google Scholar] [CrossRef] [Green Version]
  25. Szkop, A.; Pietruczuk, A. Analysis of aerosol transport over southern Poland in August 2015 based on a synergy of remote sensing and backward trajectory techniques. J. Appl. Remote Sens. 2017, 11, 016039. [Google Scholar] [CrossRef]
  26. Chai, T.; Crawford, A.; Stunder, B.; Draxler, R.; Stein, A.; Pavolonis, M.J. Improving volcanic ash predictions with the HYSPLIT dispersion model by assimilating MODIS satellite retrievals. Atmos. Chem. Phys. 2017, 17, 2865–2879. [Google Scholar] [CrossRef] [Green Version]
  27. Hurst, T.; Davis, C. Forecasting volcanic ash deposition using HYSPLIT. J. Appl. Volcanol. 2017, 6, 5. [Google Scholar] [CrossRef] [Green Version]
  28. Zawadzka, O.; Posyniak, M.; Nelken, K.; Markuszewski, P.; Chilinski, M.T.; Czyzewska, D.; Lisok, J.; Markowicz, K.M. Study of the vertical variability of aerosol properties based on cable cars in-situ measurements. Atmos. Pollut. Res. 2017, 8, 968–978. [Google Scholar] [CrossRef]
  29. Jędruszkiewicz, J.; Zieliński, M. Zróżnicowanie wysokich dobowych sum opadów w Łodzi i okolicach na tle cyrkulacji atmosferycznej (Variability in high daily precipitation sums in Łódź and its surroundings in relation to atmospheric circulation). Acta Geogr. Lodz. 2016, 104, 201–211. [Google Scholar]
  30. Miller, J.M.; Moody, J.L.; Harris, J.M.; Gaudry, A. A 10-year trajectory flow climatology for Amsterdam Island, 1980–1989. Atmos. Environ. Part A Gen. Top. 1993, 27, 1909–1916. [Google Scholar] [CrossRef]
  31. Tomczyk, A.M.; Bednorz, E. Synoptyczne uwarunkowania intensywnych opadów śniegu w wybranych regionach Europy (Synoptic conditions of heavy snowfall in selected regions of Europe). Prz. Geogr. 2014, 86, 365–380. [Google Scholar] [CrossRef]
  32. Draxler, R.R. How do I Estimate the Absolute (in km) and Relative (%) Errors when Using the Hysplit4 Trajectory Model? Where does the Error Mostly Come from (e.g., Truncation Error, Interpolation Error or Wind Field Error)? 2019. Available online: https://hysplitbbs.arl.noaa.gov/viewtopic.php?f=27&t=2368 (accessed on 28 November 2022).
  33. Stohl, A. Computation, accuracy and applications of trajectories—A review and bibliography. Atmos. Environ. 1998, 32, 947–966. [Google Scholar] [CrossRef]
  34. Su, L.; Yuan, Z.; Fung, J.C.H.; Lau, A.K.H. A comparison of HYSPLIT backward trajectories generated from two GDAS datasets. Sci. Total Environ. 2015, 506–507, 527–537. [Google Scholar] [CrossRef]
  35. Pfeifroth, U.; Sanchez-Lorenzo, A.; Manara, V.; Trentmann, J.; Hollmann, R. Trends and variability of surface solar radiation in Europe based on surface- and satellite-based data records. J. Geophys. Res. Atmos. 2018, 123, 1735–1754. [Google Scholar] [CrossRef]
  36. Kulesza, K. Spatiotemporal variability and trends in global solar radiation over Poland based on satellite-derived data (1986–2015). Int. J. Climatol. 2020, 40, 6526–6543. [Google Scholar] [CrossRef]
  37. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
  38. Carslaw, D.; Ropkins, K. Openair—An R package for air quality data analysis. Environ. Model. Softw. 2012, 27–28, 52–61. [Google Scholar] [CrossRef]
  39. MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA; Los Angeles, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
  40. Abdalmogith, S.S.; Harrison, R.M. The use of trajectory cluster analysis to examine the long-range transport of secondary inorganic aerosol in the UK. Atmos. Environ. 2005, 39, 6686–6695. [Google Scholar] [CrossRef] [Green Version]
  41. Borge, R.; Lumbreras, J.; Vardoulakis, S.; Kassomenos, P.; Rodrıguez, E. Analysis of long-range transport influences on urban PM 10 using two-stage atmospheric trajectory clusters. Atmos. Environ. 2007, 41, 4434–4450. [Google Scholar] [CrossRef]
  42. Chakrabarti, A.; Ghosh, J.K. AIC, BIC and Recent Advances in Model Selection. In Handbook of the Philosophy of Science, Philosophy of Statistics; Bandyopadhyay, P.S., Forster, M.R., Eds.; North-Holland Publishing: Amsterdam, The Netherlands, 2011; Volume 7, pp. 583–603. [Google Scholar] [CrossRef]
  43. Bai, Z.; Choi, K.P.; Fujikoshi, Y. Consistency of AIC and BIC in estimating the number of significant components in high-dimensional principal component analysis. Ann. Stat. 2018, 46, 1050–1076. [Google Scholar] [CrossRef]
  44. Kaufman, L.; Rousseeuw, R. Finding Groups in Data: An introduction to Cluster Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
  45. Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
  46. Degirmendžić, J.; Kożuchowski, K. Szlaki niżów śródziemnomorskich nad Europą Środkowo-Wschodnią a opady w Polsce (Trajectories of Mediterranean lows over Central and Eastern Europe and precipitation in Poland). Prz. Geogr. 2015, 87, 477–496. [Google Scholar] [CrossRef]
  47. Kożuchowski, K. Meteorologia I Klimatologia; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2012. [Google Scholar]
  48. Przybylak, R.; Maszewski, R. Zmienność cyrkulacji atmosferycznej w regionie Bydgosko-Toruńskim w latach 1881–2005. (Atmospheric circulation variability in Bydgoszcz-Toruń area in the period 1881–2005). Acta Agrophys. 2009, 14, 427–447. [Google Scholar]
  49. Wanner, H.; Brönnimann, S.; Casty, C.; Gyalistras, D.; Luterbacher, J.; Schmutz, C.; Stephenson, D.B.; Xoplaki, E. North Atlantic Oscillation—Concepts And Studies. Surv. Geophys. 2001, 22, 321–381. [Google Scholar] [CrossRef]
  50. Kulesza, K. Influence of air pressure patterns over Europe on solar radiation variability over Poland (1986–2015). Int. J. Climatol. 2021, 41, E354–E367. [Google Scholar] [CrossRef]
Meteorology 02 00003 g001 550
Figure 1. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at the following heights: 3000 m above ground level (a), 1500 m above ground level (b), 500 m above ground level (c), during the period 1986–2015.
Figure 1. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at the following heights: 3000 m above ground level (a), 1500 m above ground level (b), 500 m above ground level (c), during the period 1986–2015.
Meteorology 02 00003 g001
Meteorology 02 00003 g002 550
Figure 2. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, during the period 1986–2015 and clustered starting points of all backward trajectories in the period 1986–2015.
Figure 2. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, during the period 1986–2015 and clustered starting points of all backward trajectories in the period 1986–2015.
Meteorology 02 00003 g002
Meteorology 02 00003 g003 550
Figure 3. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, in individual seasons of the year during the period 1986–2015 and clustered starting points of all backward trajectories in individual seasons of the year in the period 1986–2015.
Figure 3. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, in individual seasons of the year during the period 1986–2015 and clustered starting points of all backward trajectories in individual seasons of the year in the period 1986–2015.
Meteorology 02 00003 g003
Meteorology 02 00003 g004 550
Figure 4. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, on days with extremely large sums of global solar radiation (above the 0.95 percentile) over Poland, broken down by seasons of the year during the period 1986–2015 and clustered starting points of all backward trajectories on days with extremely large sums of global solar radiation in individual seasons of the year in the period 1986–2015.
Figure 4. Averaged 72-h backward trajectories in 7 clusters ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level, on days with extremely large sums of global solar radiation (above the 0.95 percentile) over Poland, broken down by seasons of the year during the period 1986–2015 and clustered starting points of all backward trajectories on days with extremely large sums of global solar radiation in individual seasons of the year in the period 1986–2015.
Meteorology 02 00003 g004
Meteorology 02 00003 g005 550
Figure 5. 72-h backward trajectories ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level on days with the largest sums of global solar radiation (above the 0.99 percentile) over Poland, broken down by seasons of the year in the period 1986–2015. The colours of the trajectories correspond to the colours of the clusters in Figure 4.
Figure 5. 72-h backward trajectories ending at the grid point 52.5° N, 20° E at 12:00 UTC at 3000 m above ground level on days with the largest sums of global solar radiation (above the 0.99 percentile) over Poland, broken down by seasons of the year in the period 1986–2015. The colours of the trajectories correspond to the colours of the clusters in Figure 4.
Meteorology 02 00003 g005
Table
Table 1. The average daily sum of GSR, a (MJ·m-2·day-1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters during the period 1986–2015. Values that are statistically significantly different from the average daily sum in the multi-year period 1986–2015 are in bold type (α = 0.05). The letters indicating the clusters correspond to Figure 1.
Table 1. The average daily sum of GSR, a (MJ·m-2·day-1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters during the period 1986–2015. Values that are statistically significantly different from the average daily sum in the multi-year period 1986–2015 are in bold type (α = 0.05). The letters indicating the clusters correspond to Figure 1.
Height above Ground LevelCluster
ABCDEFG
3000a (MJ·m−2·day−1)10.2911.339.316.3711.4212.0812.74
f (%)17.219.017.87.614.613.710.0
1500a (MJ·m−2·day−1)10.4111.609.036.0911.4912.2111.96
f (%)17.120.515.67.913.713.911.3
500a (MJ·m−2·day−1)10.8111.009.156.5811.4312.7011.09
f (%)17.520.914.27.812.214.113.3
Table
Table 2. The average daily sum of GSR, a (MJ·m−2·day−1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters in individual seasons of the year (III-V refers to spring, VI-VIII to summer, IX-XI to autumn, and XII-II to winter) during the period 1986–2015. Values that are statistically significantly different from the seasonal average of daily sums in the multi-year period 1986–2015 are in bold type (α = 0.05). The letters indicating the clusters correspond to Figure 3.
Table 2. The average daily sum of GSR, a (MJ·m−2·day−1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters in individual seasons of the year (III-V refers to spring, VI-VIII to summer, IX-XI to autumn, and XII-II to winter) during the period 1986–2015. Values that are statistically significantly different from the seasonal average of daily sums in the multi-year period 1986–2015 are in bold type (α = 0.05). The letters indicating the clusters correspond to Figure 3.
Season of the YearCluster
ABCDEFG
III-Va (MJ·m−2·day−1)13.7313.7313.4211.5114.5715.3915.93
f (%)17.321.717.27.415.814.06.6
VI-VIIIa (MJ·m−2·day−1)17.0518.4619.1418.6618.9819.2918.93
f (%)14.521.514.910.014.412.811.9
IX-XIa (MJ·m−2·day−1)6.306.836.436.107.197.609.47
f (%)17.317.319.28.514.812.610.4
XII-IIa (MJ·m−2·day−1)2.922.782.682.682.873.013.56
f (%)17.718.422.79.312.913.75.3
Table
Table 3. The average daily sum of GSR, a (MJ·m−2·day−1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters on days with extremely large solar radiation sums (above the 0.95 percentile), broken down by seasons of the year (III-V refers to spring, VI-VIII to summer, IX-XI to autumn, and XII-II to winter), during the period 1986–2015. All values are statistically insignificant (α = 0.05). The letters indicating the clusters correspond to Figure 4.
Table 3. The average daily sum of GSR, a (MJ·m−2·day−1), over Poland during air inflow from individual clusters and the frequency, f (%), of air inflow from individual clusters on days with extremely large solar radiation sums (above the 0.95 percentile), broken down by seasons of the year (III-V refers to spring, VI-VIII to summer, IX-XI to autumn, and XII-II to winter), during the period 1986–2015. All values are statistically insignificant (α = 0.05). The letters indicating the clusters correspond to Figure 4.
Season of the YearCluster
ABCDEFG
III-Va (MJ·m−2·day−1)26.0926.6026.4426.6026.3226.2926.15
f (%)10.921.021.720.315.22.98.0
VI-VIIIa (MJ·m−2·day−1)28.3128.4028.6528.4228.4028.4028.22
f (%)8.018.114.515.921.018.14.4
IX-XIa (MJ·m−2·day−1)17.9817.1617.1017.6717.5617.7417.81
f (%)16.919.810.314.720.65.911.8
XII-IIa (MJ·m−2·day−1)8.017.888.218.068.078.487.31
f (%)25.215.617.018.512.67.43.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kulesza, K. Influence of Air Mass Advection on the Amount of Global Solar Radiation Reaching the Earth’s Surface in Poland, Based on the Analysis of Backward Trajectories (1986–2015). Meteorology 2023, 2, 37-51. https://doi.org/10.3390/meteorology2010003

AMA Style

Kulesza K. Influence of Air Mass Advection on the Amount of Global Solar Radiation Reaching the Earth’s Surface in Poland, Based on the Analysis of Backward Trajectories (1986–2015). Meteorology. 2023; 2(1):37-51. https://doi.org/10.3390/meteorology2010003

Chicago/Turabian Style

Kulesza, Kinga. 2023. "Influence of Air Mass Advection on the Amount of Global Solar Radiation Reaching the Earth’s Surface in Poland, Based on the Analysis of Backward Trajectories (1986–2015)" Meteorology 2, no. 1: 37-51. https://doi.org/10.3390/meteorology2010003

APA Style

Kulesza, K. (2023). Influence of Air Mass Advection on the Amount of Global Solar Radiation Reaching the Earth’s Surface in Poland, Based on the Analysis of Backward Trajectories (1986–2015). Meteorology, 2(1), 37-51. https://doi.org/10.3390/meteorology2010003

Article Metrics

Back to TopTop