Response and Damage Characteristics of Roadway Wall Under Impact Load Action of Methane Explosion
Abstract
1. Introduction
2. Establishment of Numerical Model
2.1. Mathematical Model
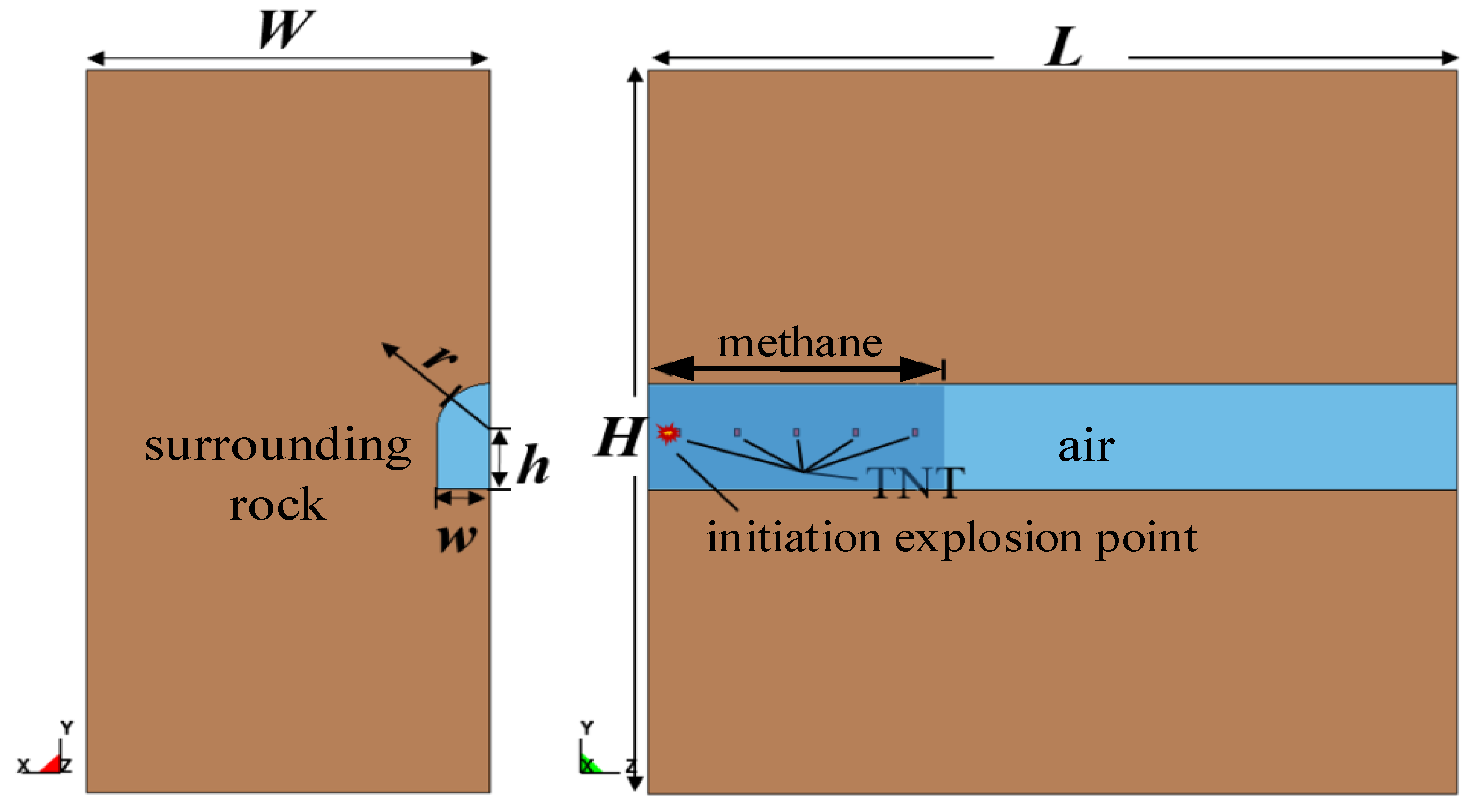
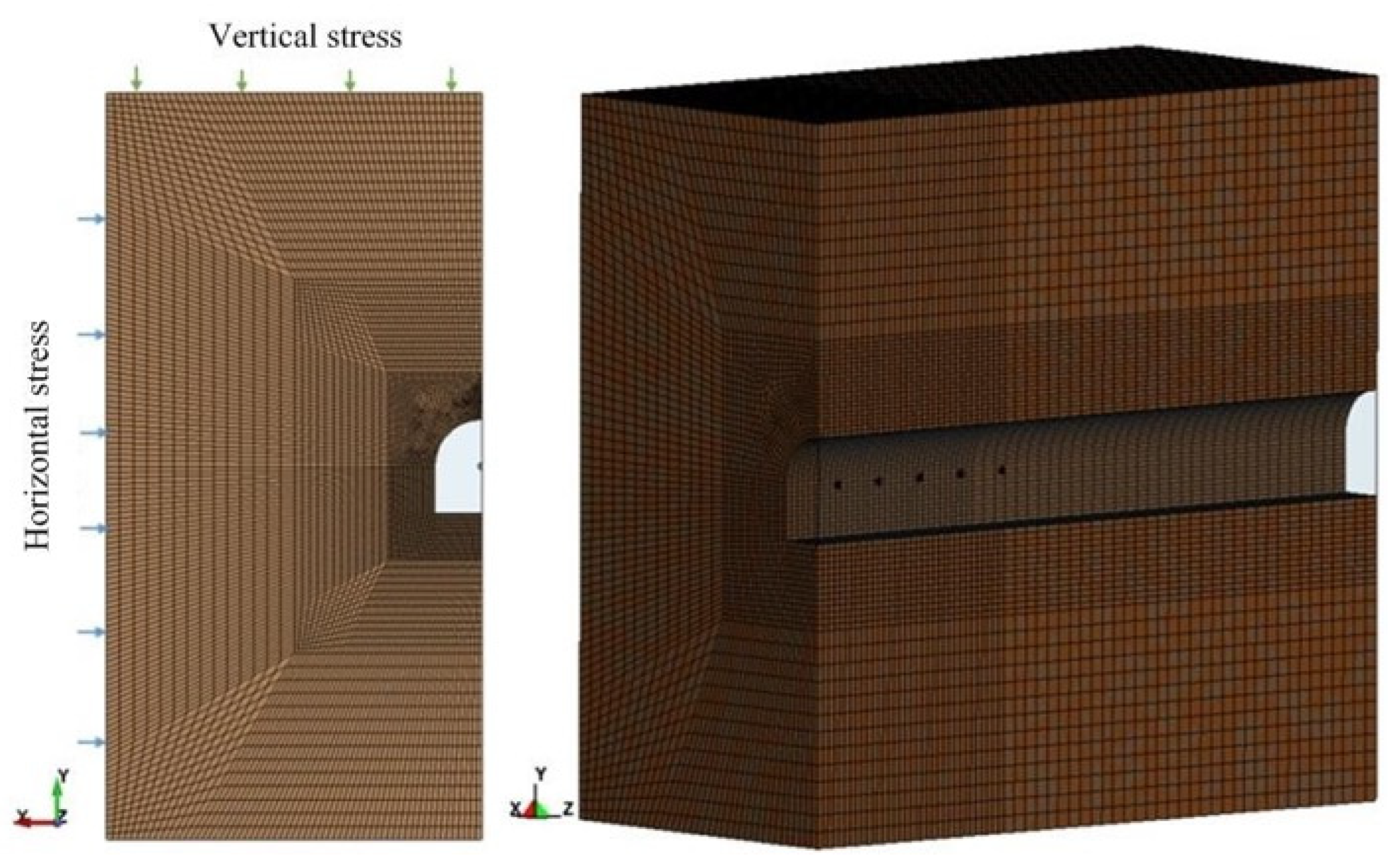
2.2. Physical Model
2.3. Material Model
3. Results Analysis and Discussion
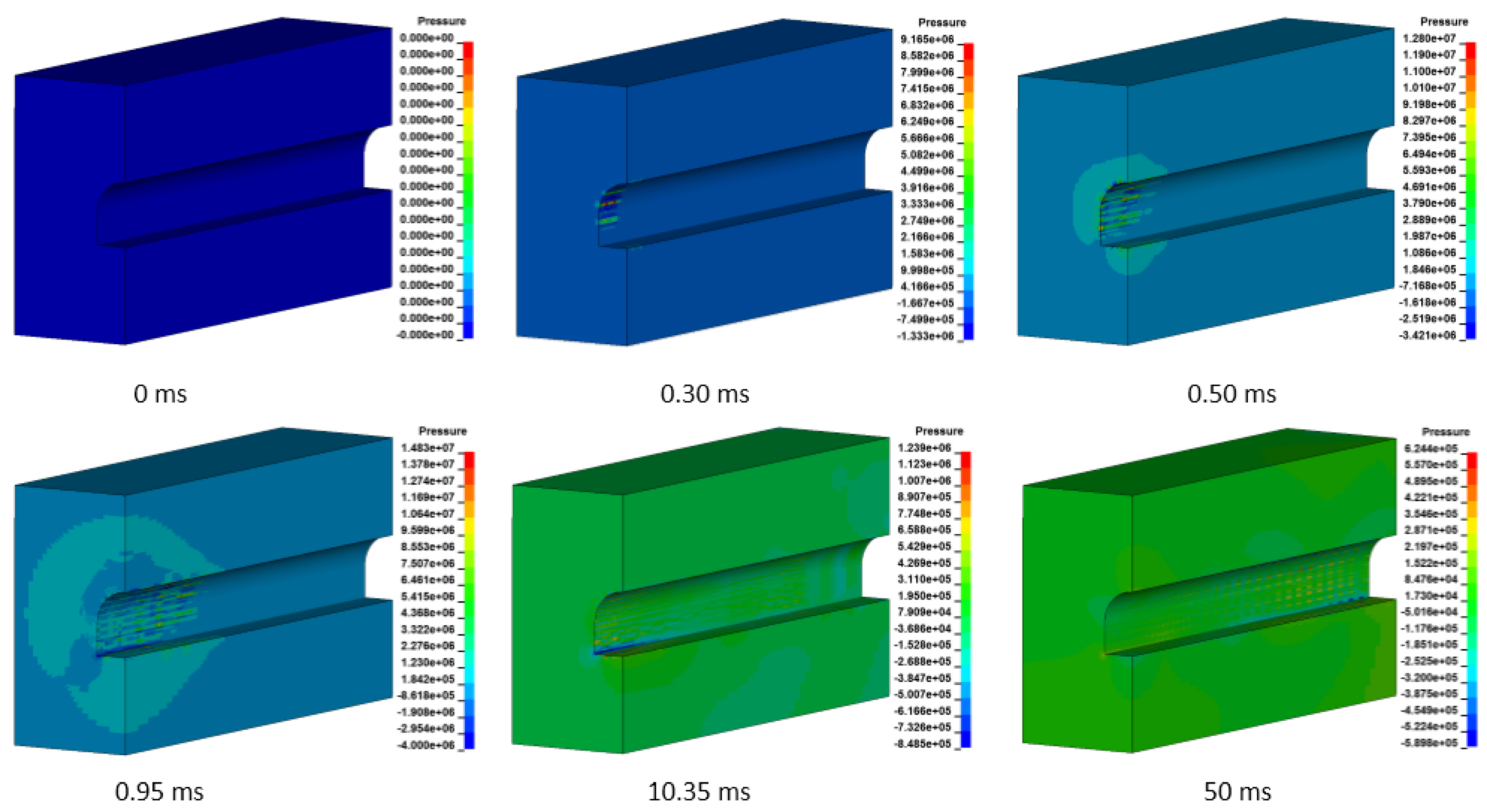
3.1. Propagation Characteristics of Methane Explosion
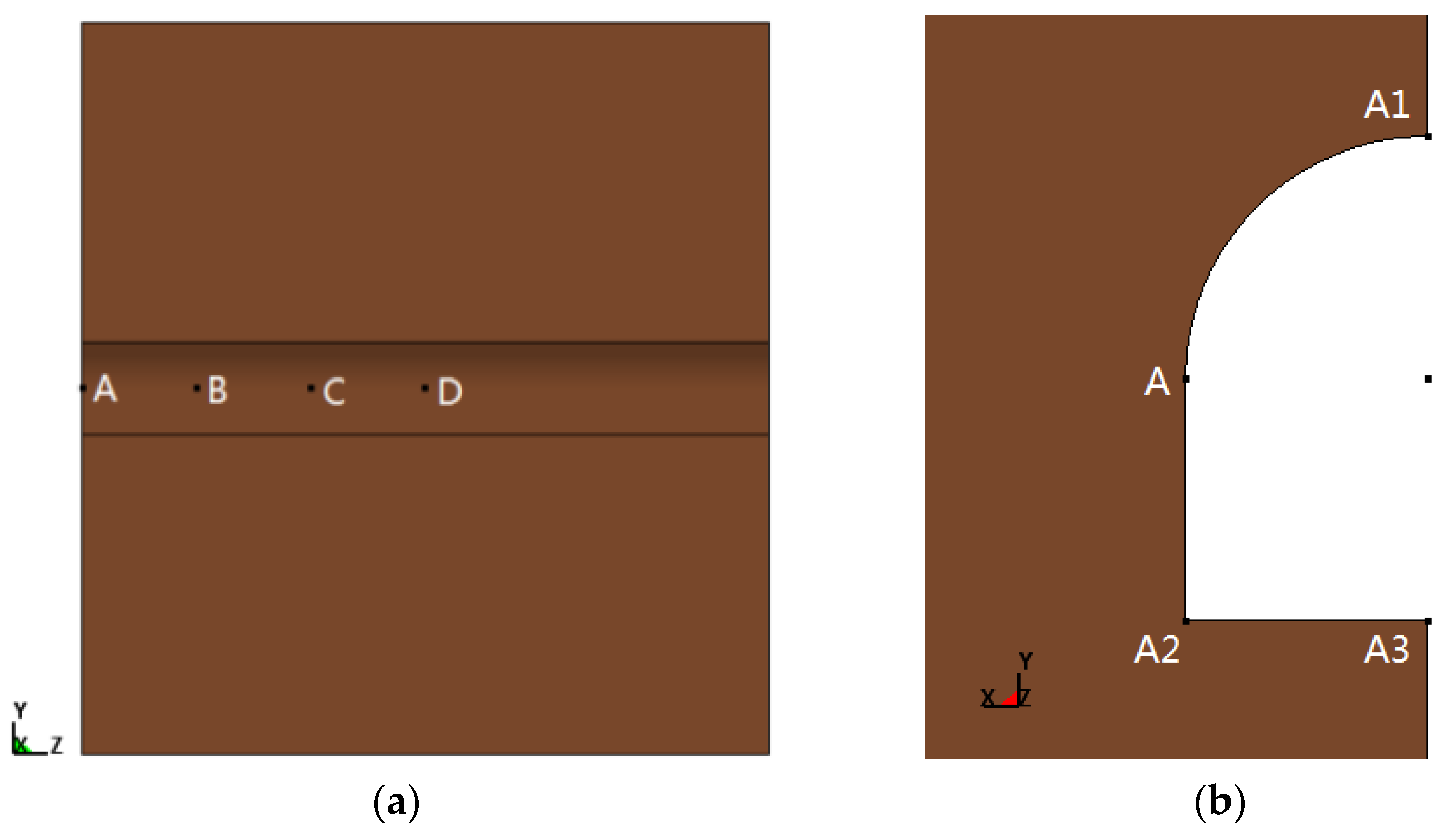
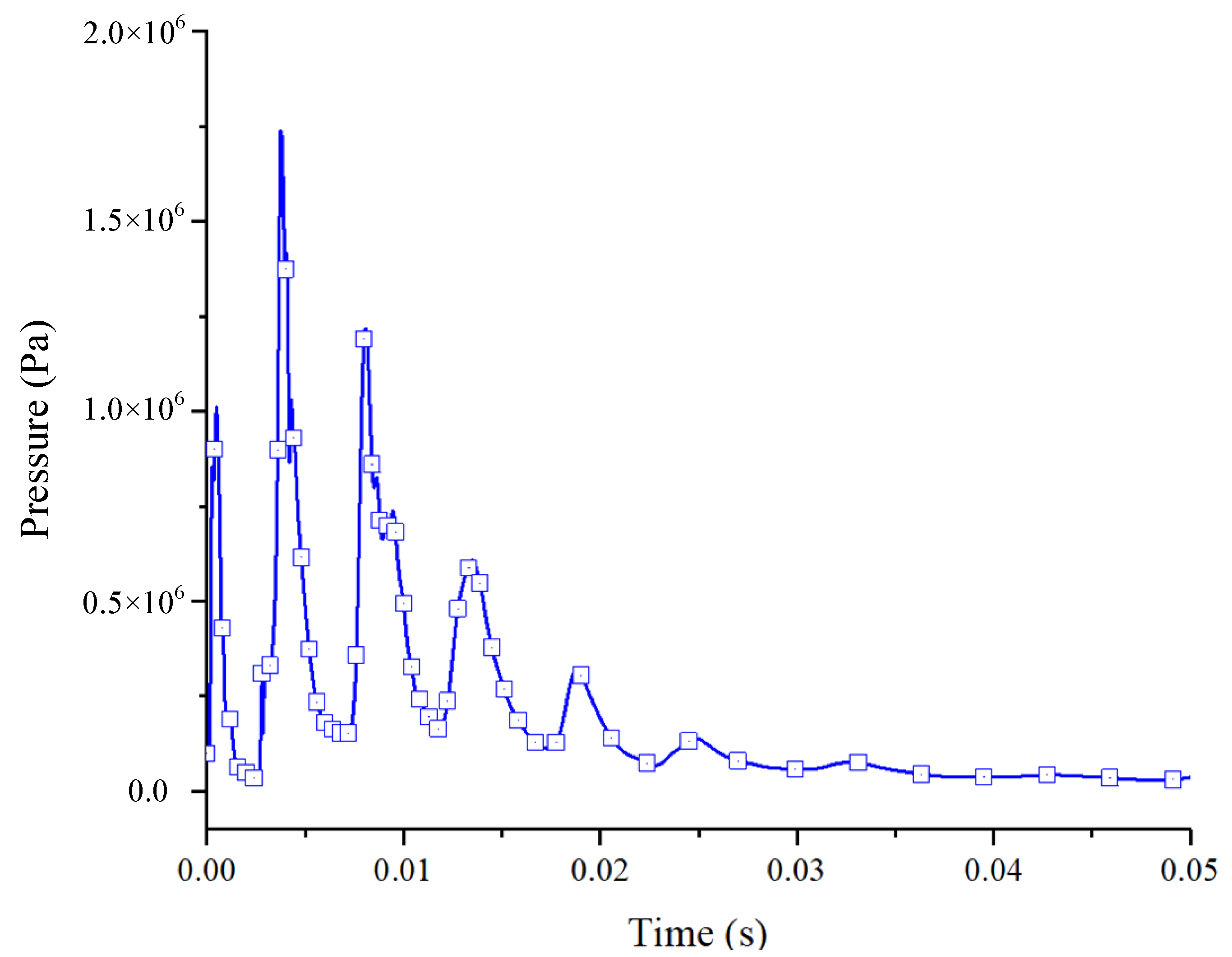
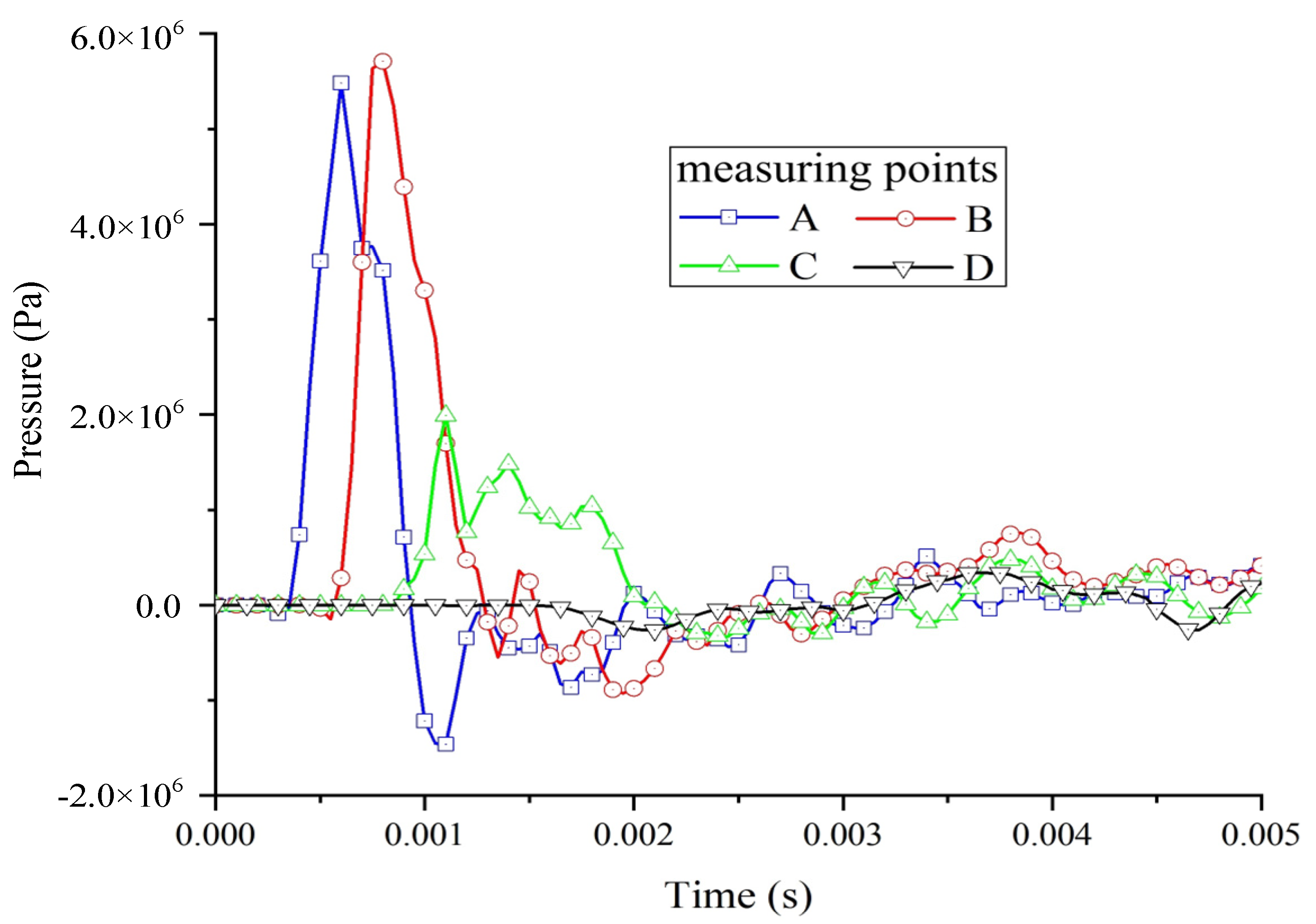
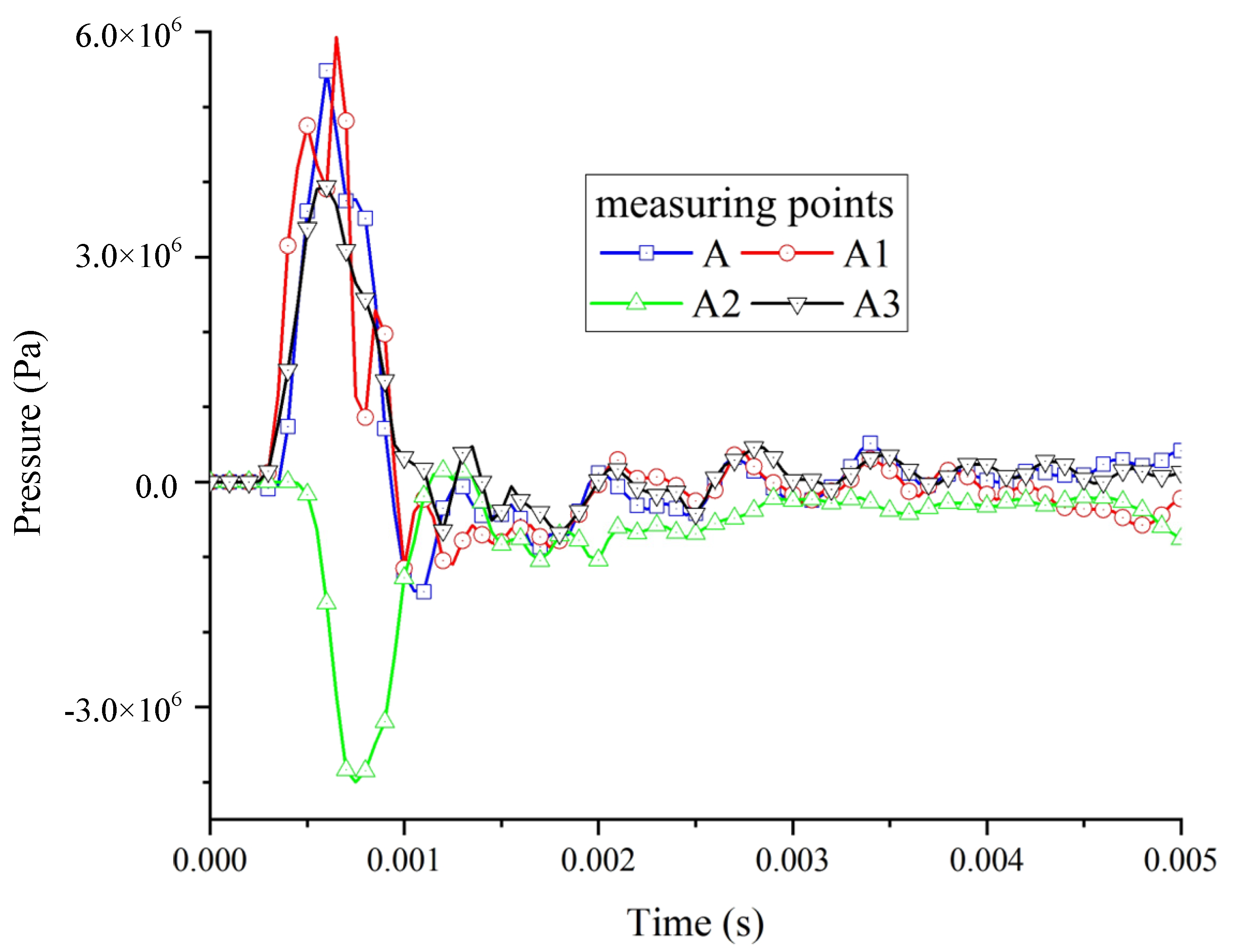
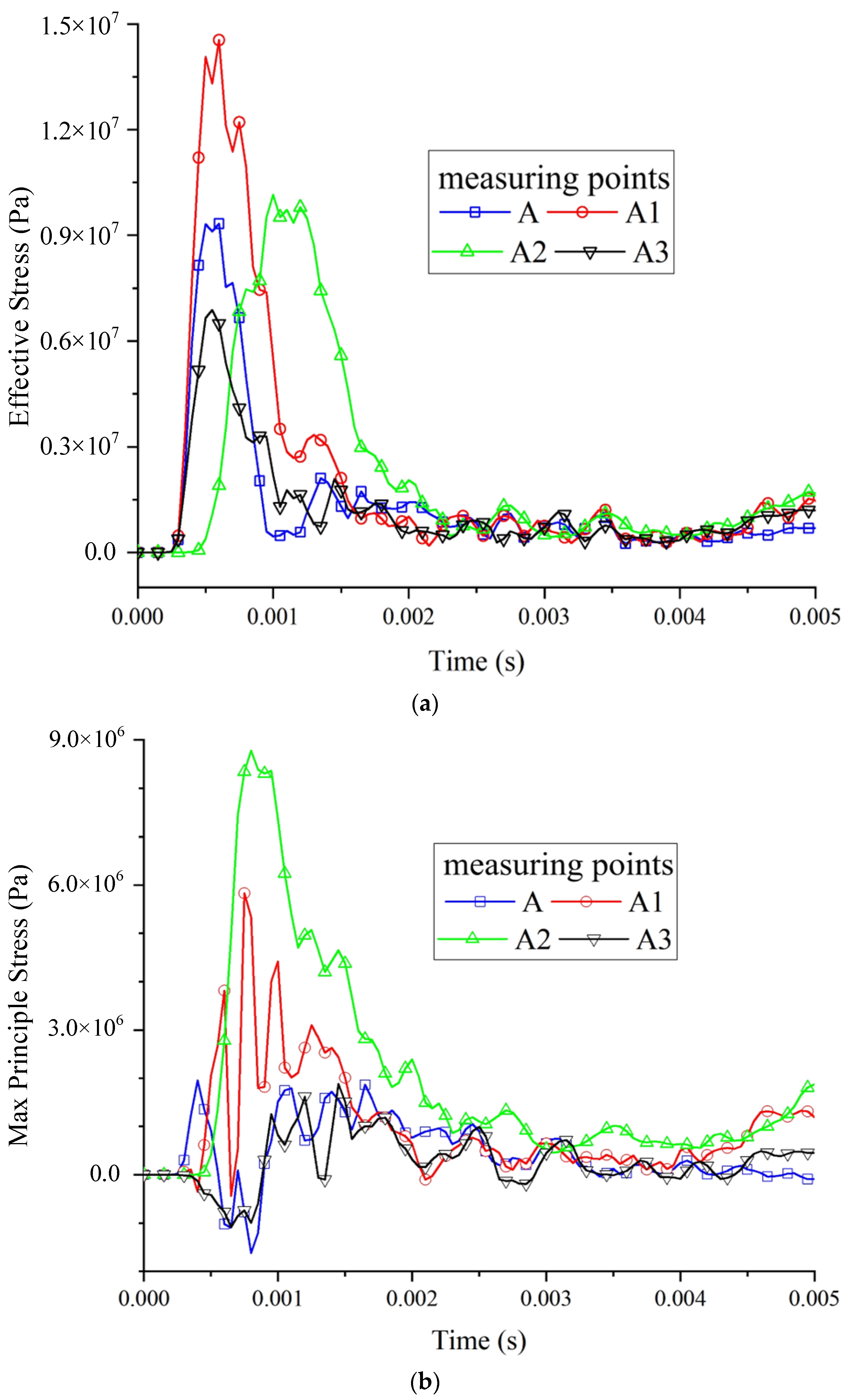
3.2. Change Law of Wall Stress
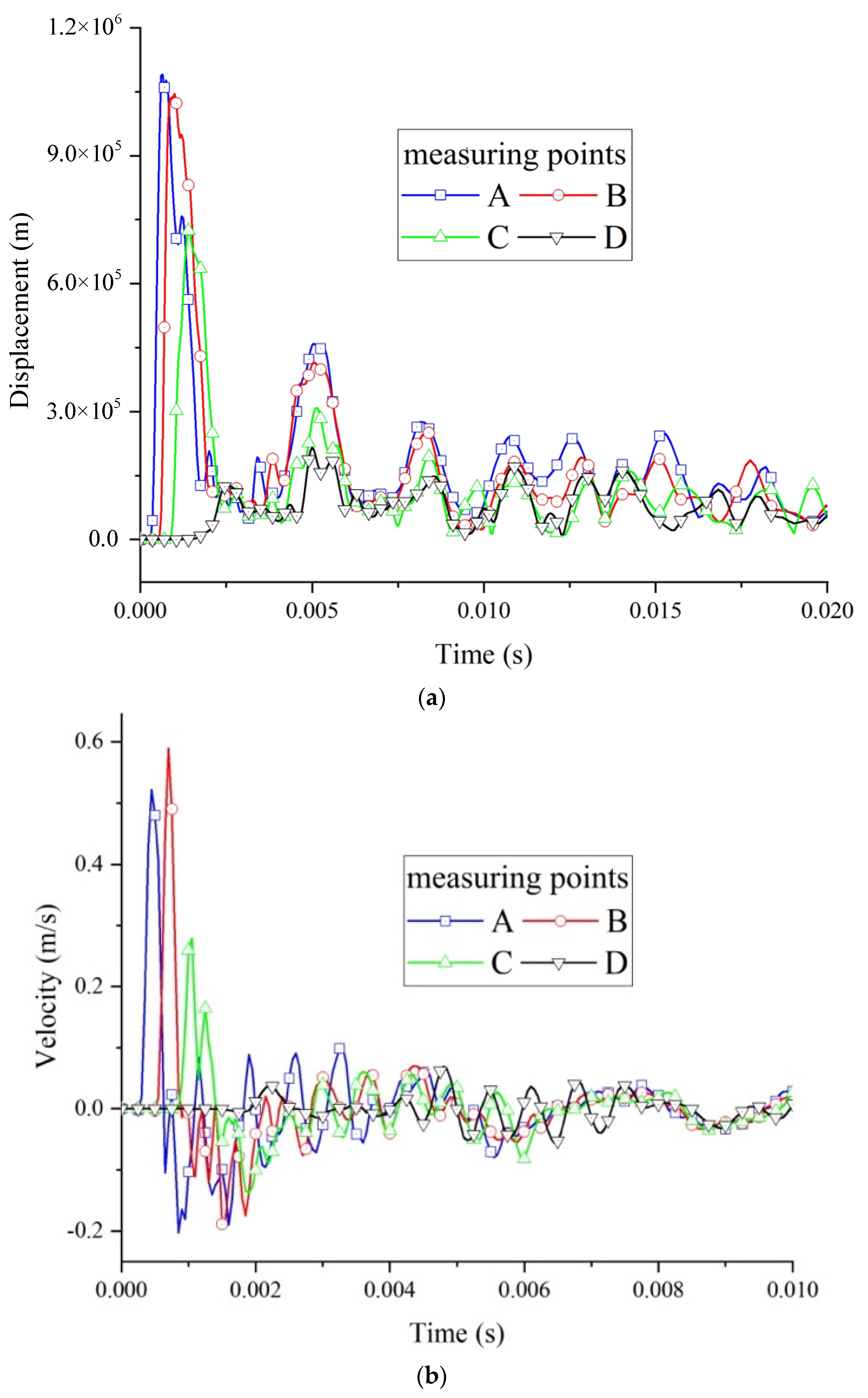
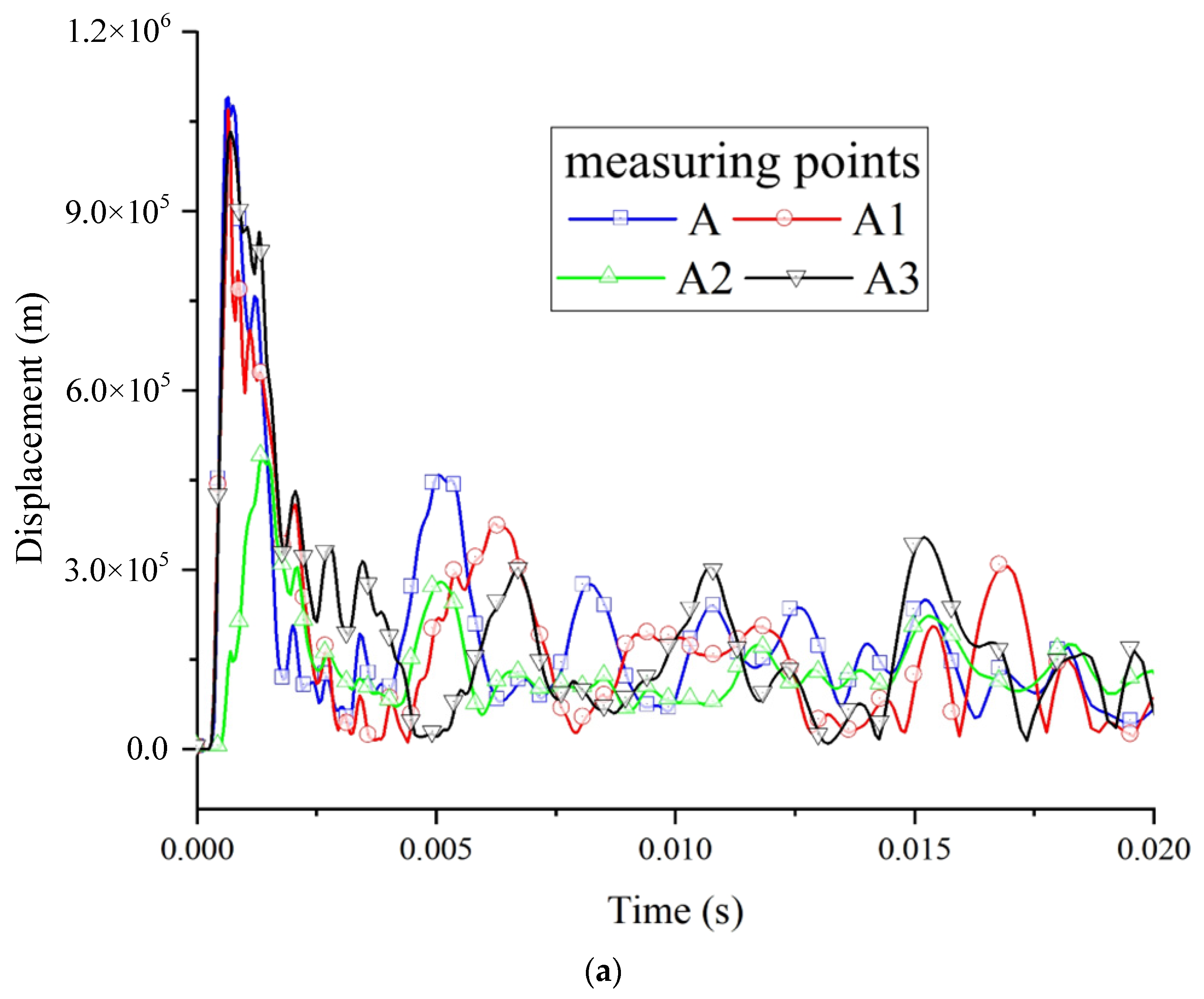
3.3. Wall Deformation Characteristics
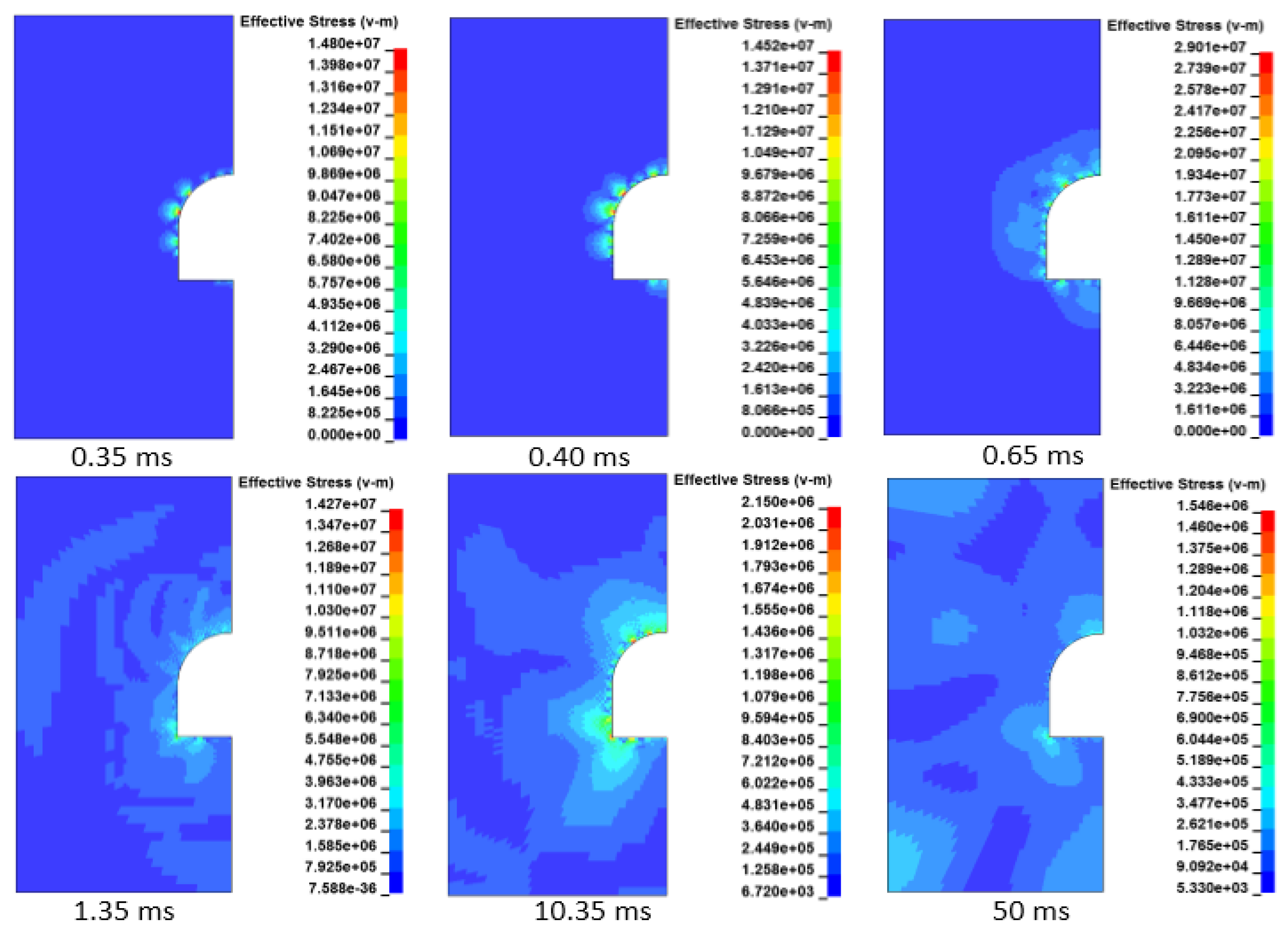
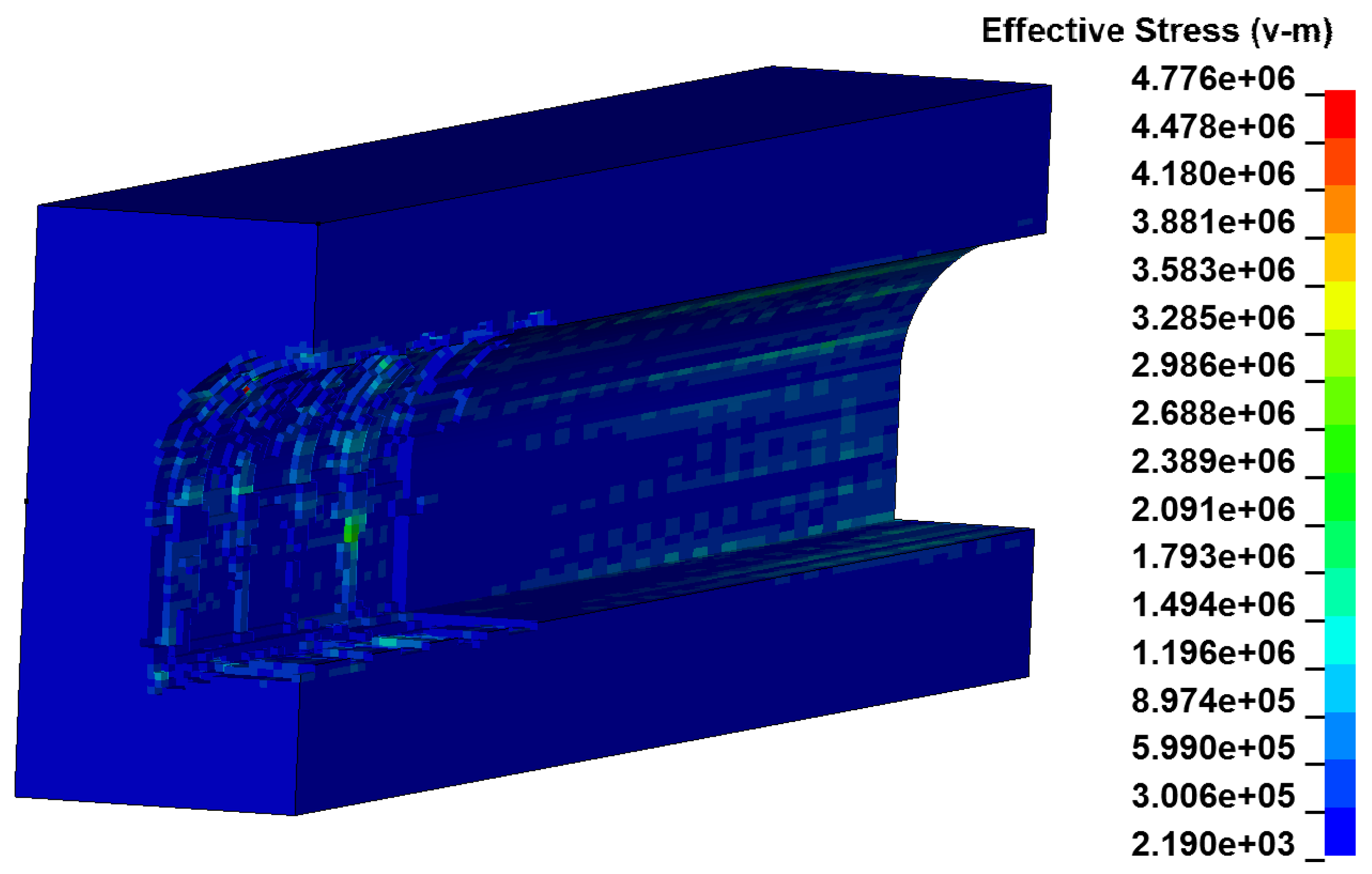
3.4. Damage Evolution Process of Wall Under Methane Explosion Load
4. Conclusions
- (1)
- The wall damage caused by the load action of the methane explosion was mainly concentrated in the methane accumulation region, in which the stresses at the roof and corner were the most concentrated and the damage was the most serious. The maximum peak principal stress of the upper and lower plates was close to the peak stress of the top plate, reaching 1.9 MPa. The duration of high stress at the roof and corners was longer, and the deformation time of the surrounding rock was longer. Under the methane explosion load, the dynamic response of the roadway wall decreased with the increase in the distance from the initiation explosion point.
- (2)
- The pressure and stress response at the curved part of the roadway roof were the most severe; the pressure and stress response of the upper part were secondary to that of the top plate, and the degree of deformation and damage was the highest. The stress change at the corners was significant, but the deformation was relatively small, and the bottom plate was minimally affected by the methane explosion loads.
- (3)
- The arch top and two sides of the roadway were first subjected to significant impact, resulting in a high-pressure zone. Subsequently, the explosion load continued to impact the walls, and a high-pressure zone appeared at the bottom plate. The distance from the explosion center at the lower corner was relatively larger, and the pressure appeared last.
- (4)
- The peak pressure of the upper part was relatively high, and there was not much difference in the peak pressures between the corner and the bottom plate, which was about 4 MPa. Plastic damage occurred on the top plate and corner walls, resulting in residual stress at the deformation site.
- (5)
- Under the load action of explosion, the wall first expanded outward, with the shock wave propagating along the axial direction, and the expansion velocity of each measuring point reached its peak successively.
- (6)
- After the shock wave reached the wall, various positions of the roadway section were constantly vibrating and deforming. The vibration amplitude of the support and roof was the largest, followed by the bottom plate, and the vibration amplitude at the corner was the smallest.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Wang, H.; Chen, C.; Wang, P.; Xu, L. Experimental study to assess the explosion hazard of CH4/coal dust mixtures induced by high-temperature source surface. Process Saf. Environ. Prot. 2021, 154, 60–71. [Google Scholar] [CrossRef]
- Li, R.; Zhang, Z.; Si, R.; Wang, L.; Li, S.; Wu, W.; Cao, J.; Ren, W. Experimental study on injuries to animals caused by a gas explosion in a large test laneway. Shock Vib. 2021, 2021, 6632654. [Google Scholar] [CrossRef]
- Luo, Z.; Kang, X.; Wang, T.; Su, B.; Cheng, F.; Deng, J. Effects of an obstacle on the deflagration behavior of premixed liquefied petroleum gas-air mixtures in a closed duct. Energy 2021, 234, 121291. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, L.; Wang, C.; Wang, X.; Jin, H.; Fu, Y. Effect of ignition position and inert gas on hydrogen/air explosions. Int. J. Hydrogen Energy 2021, 46, 8820–8833. [Google Scholar] [CrossRef]
- Cui, C.; Shao, H.; Jiang, S.; Zhang, X. Experimental study on gas explosion suppression by coupling CO2 to a vacuum chamber. Powder Technol. 2018, 335, 42–53. [Google Scholar] [CrossRef]
- Gao, K.; Liu, Z.; Wu, C.; Li, J.; Liu, K.; Liu, Y.; Li, S. Effect of low gas concentration in underground return tunnels on characteristics of gas explosions. Process Saf. Environ. Prot. 2021, 152, 679–691. [Google Scholar] [CrossRef]
- Jia, Z.; Ye, Q.; Yang, Z. Influence of wall heat effect on gas explosion and its propagation. Processes 2023, 11, 1326. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Hu, W. Numerical simulation study on the propagation and disaster mechanism of coal mine gas explosion waves. J. North China Univ. Nat. Sci. Ed. 2020, 41, 73–78+90. [Google Scholar]
- Yang, Z.; Ye, Q.; Jia, Z.; Li, H. Numerical simulation of pipeline-pavement damage caused by explosion of leakage gas in buried pe pipelines. Adv. Civ. Eng. 2020, 10, 4913984. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, G.; Zhang, Q.; Xie, M.; Ma, J. Simulation of the dynamic response of an urban utility tunnel under a natural gas explosion. Tunn. Undergr. Space Technol. 2021, 108, 103713. [Google Scholar] [CrossRef]
- Jia, Z.; Ye, Q. Analysis of the response characteristics of a roadway wall under the impact of gas explosion. Energy Sci. Eng. 2023, 11, 2486–2504. [Google Scholar] [CrossRef]
- Gao, W.; Wang, G.; Zhang, Y. Dynamic response of mountain tunnel lining under blasting. Chin. J. Appl. Mech. 2020, 37, 1737–1744. [Google Scholar]
- Zhou, J.X.; Zhu, C.J.; Lu, X.M.; Ren, J.; Si, R.J.; Ye, Q. Experimental investigation on the mechanical response of coals to uniaxial compression and low-speed dynamic loading. Shock Vib. 2021, 2021, 8871458. [Google Scholar] [CrossRef]
- Tian, Y.; Dong, Y. Dynamic response characteristics of underground roadway under blasting vibration. Explos. Mater. 2019, 48, 60–65. [Google Scholar] [CrossRef]
- Zhu, C.J.; Gao, Z.S.; Lin, B.Q.; Tan, Z.; Sun, Y.M.; Ye, Q.; Guo, C. Flame acceleration in pipes containing bends of different angles. J. Loss Prev. Process Ind. 2016, 43, 273–279. [Google Scholar] [CrossRef]
- Li, Z.; Wu, S.; Yan, Q.; Jiang, Y. Numerical analysis on the tunnel gas explosion and study on the method for determining the type of burst source. J. Vib. Shock 2018, 37, 94–101. [Google Scholar] [CrossRef]
- Wu, Y. Analysis on Dynamic Responses and Progressive Collapse of Steel Frame Structure Subject to Internal Gas Explosion. Master’s Thesis, Northeast Forestry University, Harbin, China, 2012. [Google Scholar]
- Lu, X. Study on Damage and Failure Mechanism of Roadway Under Coupling Action of Gas Explosion Load and High Stress. Master’s Thesis, China University of Mining and Technology, Beijing, China, June 2019. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Q.; Liu, J.; Jia, Z. Response and Damage Characteristics of Roadway Wall Under Impact Load Action of Methane Explosion. Methane 2025, 4, 4. https://doi.org/10.3390/methane4010004
Ye Q, Liu J, Jia Z. Response and Damage Characteristics of Roadway Wall Under Impact Load Action of Methane Explosion. Methane. 2025; 4(1):4. https://doi.org/10.3390/methane4010004
Chicago/Turabian StyleYe, Qing, Jialin Liu, and Zhenzhen Jia. 2025. "Response and Damage Characteristics of Roadway Wall Under Impact Load Action of Methane Explosion" Methane 4, no. 1: 4. https://doi.org/10.3390/methane4010004
APA StyleYe, Q., Liu, J., & Jia, Z. (2025). Response and Damage Characteristics of Roadway Wall Under Impact Load Action of Methane Explosion. Methane, 4(1), 4. https://doi.org/10.3390/methane4010004





