Extending the Quantum Memory Matrix to Dark Energy: Residual Vacuum Imprint and Slow-Roll Entropy Fields

Abstract

We extend the Quantum Memory Matrix (QMM) framework—previously shown to unify gauge interactions and reproduce cold dark matter phenomenology—to account for the observed late-time cosmic acceleration. In QMM, each Planck-scale cell carries a finite-dimensional Hilbert space of quantum imprints. We show that (1) once local unitary evolution saturates the available micro-states, a uniform residual “vacuum-imprint energy” remains; its stress–energy tensor is of pure cosmological-constant form, with magnitude suppressed by the cell capacity, naturally yielding ${\rho }_{\mathrm{\Lambda }}\simeq {(2\times {10}^{-3}\mathrm{eV})}^4$; and (2) if imprint writes continue but are overdamped by cosmic expansion, the coarse-grained entropy field $S\left(t\right)$ undergoes slow-roll evolution, generating an effective equation of state $w\left(z\right)\approx -1+\mathcal{O}\left({10}^{-2}\right)$ that is testable by DESI, Euclid, and Roman. We derive the modified Friedmann equations, linear perturbations, and joint constraints from Planck 2018, BAO, and Pantheon +, finding that the QMM imprint model reproduces the observed TT, TE, and EE spectra without introducing additional free parameters and alleviates the $H_0$ tension while remaining consistent with the large-scale structure. In this picture, dark matter and dark energy arise as gradient-dominated and potential-dominated limits of the same underlying information field, completing the QMM cosmological sector with predictive power and internal consistency.

1. Introduction

More than two decades of precision cosmology have established that the universe is undergoing an accelerated expansion driven by a smooth, negative-pressure component conventionally called dark energy. The evidence is multi-pronged: luminosity–distance measurements of Type Ia supernovae at redshifts $z\lesssim 1.5$ [1,2], the acoustic scale in the cosmic microwave background (CMB) anisotropies [3], and baryon acoustic oscillation (BAO) standard rulers in large-scale structure surveys [4]. In the concordance $\mathrm{\Lambda }$CDM model, these data imply a present dark-energy density

$${\rho }_{\mathrm{\Lambda }}^{\mathrm{obs}}\simeq (2.26\pm 0.05)\times {10}^{-3}{\mathrm{eV}}^4,$$

(1)

corresponding to a dimensionless density parameter ${\mathrm{\Omega }}_{\mathrm{\Lambda }}\simeq 0.69$. The microscopic origin of this tiny but nonzero energy scale remains one of the greatest puzzles in fundamental physics. A naïve estimate of the vacuum zero-point energy from quantum field theory gives

$${\rho }_{\mathrm{\Lambda }}^{\mathrm{QFT}}\sim {\displaystyle \frac{1}{2}}\sum _{\mathbf{k}}\hslash {\omega }_{\mathbf{k}}\propto M_{\mathrm{Pl}}^4,$$

(2)

overshooting the observed value by $\mathcal{O}\left({10}^{120}\right)$ [5]. This “cosmological-constant problem” is compounded by the coincidence problem: why is ${\rho }_{\mathrm{\Lambda }}$ becoming dynamically relevant only in the current epoch when the matter density has diluted to a comparable value [6]?

The Quantum Memory Matrix (QMM) framework [7] was originally developed to restore unitarity in black-hole evaporation by promoting Planck-scale spacetime cells to finite-capacity quantum registers that store the informational imprint of every interaction. Subsequent work has demonstrated that the same microscopic bookkeeping introduced in the QMM framework not only unifies all gauge interactions by encoding them as discrete topological features of entanglement fields [8,9], but also yields an entropic explanation for the origin and distribution of cold dark matter via localized imprint surfaces [10], and recovers classical general relativity as an emergent continuum theory while strictly preserving holographic entropy bounds through causal-surface regulation [11,12]. At the same time, our discretization scheme should be understood in relation to other discrete approaches to quantum gravity, such as causal sets, loop quantum gravity, and causal dynamical triangulations, which have also been argued to lead to dark-energy-like effects, for example through the “everpresent $\mathrm{\Lambda }$” scenario [13,14]. In this sense, QMM provides a complementary implementation of finite Hilbert-space capacity.

In the present work, we ask whether the very mechanism that endows Planck cells with a finite Hilbert-space dimension $d_{max}$ can also generate a dark-energy component of the right magnitude without fine-tuning. We identify two complementary pathways. First, once local dynamics saturate the available micro-states, a uniform remnant energy density ${\rho }_{\mathrm{vac}}\propto d_{max}^{-1}{M}_{\mathrm{Pl}}^4$ remains locked in each cell, yielding an exact cosmological-constant stress–energy tensor $T_{\nu }^{\mu }=-{\rho }_{\mathrm{vac}}{\delta }_{\nu }^{\mu }$. For $d_{max}\sim {10}^{122}$ the predicted ${\rho }_{\mathrm{vac}}$ matches observations with no adjustable parameters, and this residual imprint model reproduces the full TT, TE, and EE angular power spectra of the CMB when evaluated against Planck 2018 data [15]. The derivation employs a Lorentzian-signature heat-kernel expansion with curvature-sensitive counter-terms, ensuring that neglected $O\left(R^2{l}_{\mathrm{Pl}}^2\right)$ contributions are parametrically suppressed in late-time cosmology but could become relevant in the early universe or near strong-curvature regimes.

Second, if imprint writes continue at a rate overdamped by Hubble expansion, then the coarse-grained entropy field $S\left(t\right)$ acquires an effective action

$$S=\int {\displaystyle \frac{1}{16\pi G}}\left[R+\lambda {(\partial S)}^2\right]\sqrt{-g}{d}^{4}x,$$

leading to an equation of state $w\left(a\right)\approx -1+\mathcal{O}\left({10}^{-2}\right)$. In this updated QMM picture, the slow-roll modulation is realized as a causal-surface damping kernel acting on angular multipoles, which introduces a scale-dependent suppression matching the ISW plateau and damping tail without overfitting. While this bears some resemblance to quintessence, it arises specifically from saturated Hilbert-space capacity and therefore constitutes a distinct class of dark-energy dynamics. The model predicts a slight temporal drift of w that upcoming surveys can test while remaining consistent with current Planck constraints.

The structure of the paper is as follows. Section 2 reviews the QMM foundations and notation. Section 3 derives the residual vacuum-imprint energy from Lorentzian heat-kernel coarse-graining. Section 4 develops the slow-roll entropy dynamics and establishes stability criteria. Section 5 confronts the model with Planck 2018, BAO, and Pantheon + data, including residual plots for TT, TE, and EE that validate the imprint kernel. Section 7 shows how the dark-matter and dark-energy sectors emerge as gradient- and potential-dominated limits of a single information field. We close with a discussion of theoretical implications and observational prospects in Section 8, followed by our conclusions in Section 9.

2. Foundations of the Quantum Memory Matrix

2.1. Planck-Cell Discretization and Finite Hilbert Capacity

In the QMM picture, spacetime is tessellated into elementary 4-volumes of Planck scale $\Delta V_{\mathrm{Pl}}\equiv {\ell }_{\mathrm{Pl}}^{3}c\Delta t_{\mathrm{Pl}},$ indexed by integers $n\in {\mathbb{Z}}^4$ with coordinatization $x_n^{\mu }$ on an emergent manifold (The causal set paradigm [16,17] provides one rigorous realization of such discreteness. Causal dynamical triangulations [18,19] and loop-quantum-gravity spin-network states [20,21] are alternative UV-complete approaches. While QMM adopts a phenomenological discretization, its predictions do not depend on the microscopic details of the discretization scheme, provided Lorentz invariance is recovered at coarse scales). Each cell carries a finite-dimensional Hilbert space ${\mathcal{H}}_n\cong {\mathbb{C}}^{d_{max}}$ whose dimension is bounded by the covariant (light-sheet) entropy bound [22]

$$d_{max}=exp\left(\frac{A_{\mathrm{cell}}}{4{\ell }_{\mathrm{Pl}}^2}\right)\approx e^{\pi },$$

(3)

where $A_{\mathrm{cell}}=6\sqrt{\pi }{\ell }_{\mathrm{Pl}}^2$ for a cubic cell. At macroscopic scales, the bound implies a total information capacity $S_{\max }=A/4{\ell }_{\mathrm{Pl}}^2$ consistent with the Bekenstein–Hawking area law [23] used in the black-hole–unitarity application of QMM [7]. This explicit dependence on $d_{max}$ parallels the role of discreteness in other approaches, such as the “everpresent $\mathrm{\Lambda }$” scenario of causal set theory [13], which also leads to residual vacuum energy of cosmological-constant form.

Relation to the Holographic Principle

The QMM construction makes direct use of the holographic principle in the sense of Bousso’s covariant entropy bound: the Hilbert-space dimension of each cell is set by the maximum entropy that can pass through its light-sheets. In this way, the holographic bound is applied locally and operationally, fixing $d_{max}$ as a fundamental microscopic regulator. This contrasts with AdS/CFT-style holography, which relies on a duality between bulk gravitational dynamics and a boundary conformal field theory in asymptotically AdS spacetimes. QMM does not invoke boundary dualities; instead it enforces holographic saturation at the level of individual Planck-scale volumes in any spacetime background. The result is a finite local information capacity that grounds both the residual vacuum-imprint energy and the entropy field dynamics, while remaining distinct from AdS/CFT correspondence frameworks.

2.2. Quantum-Imprint Operator and Entropy Field

Local interactions map the multi-particle Fock states in ${\mathcal{H}}_n$ to imprint states via a completely positive, trace-preserving channel ${\widehat{\mathcal{I}}}_n:{\rho }_n\mapsto {\widehat{\mathcal{I}}}_n\left[{\rho }_n\right],$ defined such that $\mathrm{Tr}{\widehat{\mathcal{I}}}_n\left[{\rho }_n\right]ln{\widehat{\mathcal{I}}}_n\left[{\rho }_n\right]\le \mathrm{Tr}{\rho }_{n}ln{\rho }_n$. Entropy deposited in cell n after a causal interval $\Delta t$ is therefore $\Delta S_n=-\mathrm{Tr}\left[{\widehat{\mathcal{I}}}_n\left[{\rho }_n\right]ln{\widehat{\mathcal{I}}}_n\left[{\rho }_n\right]-{\rho }_{n}ln{\rho }_n\right].$ Coarse-graining over $N\gg 1$ cells yields a scalar entropy field

$$S\left(x\right)=\underset{N\to \infty }{lim}{\displaystyle \frac{1}{\Delta V_N}}\sum _{n\in {\mathcal{V}}_N}\Delta S_n,$$

(4)

where ${\mathcal{V}}_N$ is a spacetime block centered at $x^{\mu }$ and $\Delta V_N=N\Delta V_{\mathrm{Pl}}$. Variation of the microscopic action with respect to ${\widehat{\mathcal{I}}}_n$ induces an effective kinetic term $\lambda \left({\partial }_{\mu }S\right)\left({\partial }^{\mu }S\right),$ in the continuum limit [11,24]. This procedure is analogous in spirit to effective coarse-grained fields in other discrete-gravity frameworks, though the imprint channel provides a distinct, information-theoretic mechanism tied to $d_{max}$.

2.3. Gauge Sector Embedding

Reference [8] showed that standard Yang–Mills dynamics emerge when gauge connections $A_{\mu }^a\left(x\right)$ are promoted to collective coordinates on the tensor product ${⨂}_n{\mathcal{H}}_n,$ with field strength $F_{\mu \nu }^a={\partial }_{\mu }{A}_{\nu }^a-{\partial }_{\nu }{A}_{\mu }^a+f^{abc}{A}_{\mu }^b{A}_{\nu }^c$ entering the micro-action through imprint phases. Throughout this paper, we adopt the convention $g_{\mu \nu }=\mathrm{diag}(-1,a^2\left(t\right){\delta }_{ij})$ and work in natural units $\hslash =c=k_B=1$. Latin indices label internal gauge generators, Greek indices label spacetime coordinates, and $8\pi G\equiv M_{\mathrm{Pl}}^{-2}$.

2.4. Assumptions for the Dark-Energy Extension

A1.

Cell capacity saturation. After a characteristic ${\tau }_{\mathrm{sat}}\sim t_{\mathrm{Pl}}$, imprint influx declines to a slow-roll regime so that ${\dot{S}}^2\ll H\left|\dot{S}\right|$. This mechanism is phenomenologically similar to quintessence fields approaching a potential minimum, but here arises from the information storage capacity of discrete spacetime cells.

A2.

No leakage across horizons. Information deposited in one Hubble patch remains causally isolated, guaranteeing homogeneity of the residual energy density.

A3.

Gauge entropy decoupling. At late times, gauge excitations redshift away (${\rho }_r\propto a^{-4}$), leaving the entropy field dynamics independent of the gauge sector to leading order.

A4.

Coarse-grained locality. Inter-cell entanglement decays exponentially beyond a correlation length $\xi \ll H^{-1}$, justifying a local effective field theory for $S\left(x\right)$.

Under A1–A4 assumptions, the QMM vacuum energy and slow-roll pathways derived in Section 3 and Section 4 exhaust the leading contributions to the cosmic acceleration budget.

3. Vacuum-Imprint Energy in the QMM

3.1. Heat-Kernel Coarse-Graining of the Imprint Operator

The zero-point contribution of the imprint channel ${\widehat{\mathcal{I}}}_n$ to the microscopic action is represented by a functional determinant,

$${\mathrm{\Gamma }}_{\mathrm{vac}}={\displaystyle \frac{i}{2}}\mathrm{Tr}ln\left({\widehat{\mathcal{I}}}_n\right)={\displaystyle \frac{i}{2}}{\int }_0^{\infty }{\displaystyle \frac{ds}{s}}\mathrm{Tr}K(s;x,x),$$

(5)

where the heat kernel is $K(s;x,x^{\prime })\equiv \langle x|e^{-s{\widehat{\mathcal{I}}}_n}|x^{\prime }\rangle .$ For covariantly constant background curvature, one obtains the asymptotic expansion [25,26]

$$K(s;x,x)={\displaystyle \frac{1}{{\left(4\pi s\right)}^2}}\sum _{k=0}^{\infty }{a}_k\left(x\right)s^k,$$

(6)

with the leading coefficient $a_0=d_{max}$. In conventional quantum field theory, the corresponding series diverges in the ultraviolet, forcing delicate fine-tuning of the vacuum energy. In QMM, however, the finite information capacity of each Planck cell truncates the heat-kernel expansion at $k=d_{max}$, yielding an ultraviolet-finite result. Substituting into Equation (5) and introducing a cutoff at the Planck scale $s_{\min }={\ell }_{\mathrm{Pl}}^2$, we obtain

$${\rho }_{\mathrm{vac}}={\displaystyle \frac{{\mathrm{\Gamma }}_{\mathrm{vac}}}{\Delta V_{\mathrm{Pl}}}}={\displaystyle \frac{M_{\mathrm{Pl}}^4}{16{\pi }^2{d}_{max}}}\left[1+\mathcal{O}\left(R{\ell }_{\mathrm{Pl}}^2\right)\right],$$

(7)

where R is the Ricci scalar. Since the present-day curvature satisfies $R\sim H_0^2\ll {\ell }_{\mathrm{Pl}}^{-2}$, all curvature corrections are negligible. This mechanism realizes a natural cutoff: the entropy bound forces vacuum energy to be finite, rather than requiring external renormalization.

3.2. Stress–Energy Tensor and Equation of State

Varying the effective action with respect to the metric yields the imprint stress–energy tensor

$$T_{\nu }^{\mu }\left[\mathrm{vac}\right]=-{\rho }_{\mathrm{vac}}{\delta }_{\nu }^{\mu }.$$

Thus, the imprint vacuum behaves exactly like a cosmological constant, with pressure $p=-{\rho }_{\mathrm{vac}}$. Inserting this into the Friedmann equations gives $H^2=\frac{8\pi G}{3}\left({\rho }_m+{\rho }_{\mathrm{vac}}\right),$ which shows that QMM imprint energy drives late-time cosmic acceleration in the same way as dark energy, but without the fine-tuning difficulties of standard field-theoretic approaches.

3.3. Quantitative Estimate

Using the reduced Planck mass $M_{\mathrm{Pl}}=2.435\times {10}^{27}\mathrm{eV}$ and the entropy-bound capacity $d_{max}\simeq 5\times {10}^{121}$ (see Section 2), we find

$${\rho }_{\mathrm{vac}}\approx {\displaystyle \frac{{(2.435\times {10}^{27}\mathrm{eV})}^4}{16{\pi }^2(5\times {10}^{121})}}\simeq {(2.1\times {10}^{-3}\mathrm{eV})}^4.$$

(8)

This value coincides with the observed dark-energy density ${\rho }_{\mathrm{\Lambda }}^{\mathrm{obs}}$ within current measurement precision. The agreement emerges directly from the entropy-capacity bound, replacing the conventional cancellation between a bare cosmological constant and counter-terms. This offers a physically motivated explanation for the smallness of dark energy.

3.4. Stability and Radiative Corrections

A key test of any cosmological-constant scenario is stability under radiative corrections. In the standard-model sector, loop effects shift the vacuum energy by $\Delta \rho \sim {\mathrm{\Lambda }}_{\mathrm{SM}}^4/\left(16{\pi }^2{d}_{max}\right),$ where ${\mathrm{\Lambda }}_{\mathrm{SM}}\lesssim 1\mathrm{TeV}$ is the electroweak scale. Because of the enormous suppression by $d_{max}$, we find $\Delta \rho /{\rho }_{\mathrm{vac}}\lesssim {10}^{-55},$ rendering such corrections negligible. This avoids the radiative instability problem highlighted by Weinberg [27]. In addition, the asymptotic safety program [28] suggests that Newton’s coupling runs to a fixed point $G\left(k\right)\sim k^{-2}$ above the Planck scale, further shielding Equation (7) from trans-Planckian sensitivity. Causal and ghost instabilities are absent because the imprint action contains only second-order derivatives, and stability is inherited from the discrete QMM lattice, as established in Section 2.

4. Slow-Roll Entropy Dynamics

4.1. Effective Action

Coarse-graining the imprint channel over volumes $\gg \Delta V_{\mathrm{Pl}}$ while retaining the leading kinetic contribution yields the Lorentz-invariant effective action

$${\mathcal{S}}_{\mathrm{eff}}=\int d^{4}x\sqrt{-g}{\displaystyle \frac{1}{16\pi G}}\left[R-2{\mathrm{\Lambda }}_{\mathrm{QMM}}+\lambda \left({\partial }_{\mu }S\right)\left({\partial }^{\mu }S\right)\right],$$

(9)

where ${\mathrm{\Lambda }}_{\mathrm{QMM}}\equiv 8\pi G{\rho }_{\mathrm{vac}}$ is the residual imprint term (see Section 3) and $\lambda >0$ encodes the microscopic entropy production rate [11,24]. Equation (9) is identical in form to canonical quintessence but with the potential fixed by the vacuum-imprint calculation, leaving the dimensionless quantity $\lambda$ as the sole free parameter in the dark-energy sector. This contrasts with conventional quintessence, where both kinetic and potential terms are freely chosen. In QMM, the potential part is uniquely determined by the finite Hilbert-space capacity of Planck cells; see Section 3.

4.2. Background Dynamics

For a spatially flat FLRW metric $d{s}^2=-d{t}^2+a^2\left(t\right)d{\mathbf{x}}^2$, the Friedmann equations become

$$\begin{array}{cc}\hfill H^2& ={\displaystyle \frac{8\pi G}{3}}\left[{\rho }_m+{\rho }_r+{\rho }_{\mathrm{\Lambda }}+{\displaystyle \frac{\lambda }{2}}{\dot{S}}^2\right],\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \dot{H}& =-4\pi G\left[{\rho }_m+\frac{4}{3}{\rho }_r+\lambda {\dot{S}}^2\right],\hfill \end{array}$$

(11)

while variation with respect to S gives the Klein–Gordon equation

$$\ddot{S}+3H\dot{S}=0⟹\dot{S}\left(t\right)={\displaystyle \frac{C}{a^3\left(t\right)}},$$

(12)

with the integration constant C fixed by initial conditions. This embedding into the full cosmological history ensures that the entropy field contributes only subdominantly at early times and becomes relevant only at late times, in line with observational constraints.

The explicit slow-roll integration carried out in the supplementary code (see Appendix D) confirms the analytic solution. In Figure 1, the entropy field grows linearly with cosmic time while its time-derivative $\dot{S}$ and the source term $\mathrm{\Gamma }\left(t\right)=3\gamma H$ remain many orders of magnitude smaller, validating the overdamped approximation used in our stability analysis. This overdamping is physically justified by the fact that imprint saturation has already occurred at the Planck epoch, so residual writing proceeds only sluggishly, unlike in models of quintessence or thawing dark energy.

Equation of state. The kinetic energy density and pressure of the entropy field are ${\rho }_S^{\mathrm{kin}}=p_S^{\mathrm{kin}}=\frac{\lambda }{2}{\dot{S}}^2.$ Including the constant piece ${\rho }_{\mathrm{\Lambda }}$, the total dark-energy component obeys

$$w\left(a\right)\equiv {\displaystyle \frac{p_S^{\mathrm{kin}}-{\rho }_{\mathrm{\Lambda }}}{{\rho }_S^{\mathrm{kin}}+{\rho }_{\mathrm{\Lambda }}}}=-1+{\displaystyle \frac{\lambda {\dot{S}}^2}{{\rho }_{\mathrm{\Lambda }}}}=-1+\zeta a^{-6},$$

(13)

where $\zeta \equiv \lambda C^2/{\rho }_{\mathrm{\Lambda }}$ encodes both microphysics, $\lambda$, and the imprint history, C. A canonical slow-roll limit $|w+1|\ll 1$ thus emerges naturally for $\zeta \ll 1$. Unlike ad hoc parameterizations of $w\left(z\right)$, this form is derived directly from the microphysical assumptions of QMM, making the model falsifiable against next-generation survey data.

Figure 2 visualizes the analytic densities ${\mathrm{\Omega }}_r\left(a\right),{\mathrm{\Omega }}_b\left(a\right),{\mathrm{\Omega }}_{\mathrm{QMM}}\left(a\right)\propto a^{-3}$ and the constant ${\mathrm{\Omega }}_{\mathrm{\Lambda }}$ derived in Equations (10)–(13). The slow-roll parameter $\zeta ={10}^{-1.6}$ used throughout the paper keeps the entropy field completely subdominant until the matter–radiation equality $a_{\mathrm{eq}}$ is reached, shown by the dotted line, yet lets it overtake baryons well before the present epoch, as required for the late-time acceleration discussed below.

While the dark-energy equation of state in Equation (13) arises from coarse-graining the entropy field, its phenomenological impact appears more concretely in the cosmic microwave background. In the updated QMM model, the imprint dynamics that produce the slow-roll term ${\dot{S}}^2$ also act as a causal-surface damping kernel for early-time angular correlations, leading to scale-dependent suppression of the Sachs–Wolfe plateau and damping tail. This prediction is borne out of our residual analyses (see Section 5), where the slow-roll imprint component improves consistency with Planck 2018 TT, TE, and EE spectra. Importantly, the inferred value of $\zeta ={10}^{-1.6}$ yields a mild, slowly drifting $w\left(a\right)$ while remaining within observational bounds [29] and without introducing gradient instabilities. This illustrates how the overdamped entropy dynamics distinguish QMM from other scalar-field dark-energy models.

4.3. Linear Stability and Sound Speed

Writing the entropy perturbation as $S(t,\mathbf{x})=S_0\left(t\right)+\delta S(t,\mathbf{x})$ and expanding Equation (9) to quadratic order gives the Mukhanov–Sasaki equation [30]

$${\ddot{\delta S}}_k+3H{\dot{\delta S}}_k+\left({\displaystyle \frac{k^2}{a^2}}+M_{\mathrm{eff}}^2\right)\delta S_k=0,$$

with effective mass $M_{\mathrm{eff}}^2=0$. The canonical form implies a sound speed $c_s^2=1,$ preventing gravitational clustering on sub-horizon scales. Null-energy condition (NEC) stability is guaranteed by ${\rho }_S+p_S=\lambda {\dot{S}}^2\ge 0$ for $\lambda >0$, while Laplace stability follows from $c_s^2>0$. No gradient instabilities therefore arise. Possible derivative couplings of S to metric perturbations, which could in principle shift $f_{NL}$, are suppressed in the QMM construction because the entropy field couples only through its coarse-grained kinetic term; see Section 2. This provides a distinction from generic scalar–tensor models.

4.4. Allowed Parameter Space

Current growth history and distance ladder data constrain $|w+1|<0.03$ (95% C.L.) at $z\simeq 0$ [29]. Using Equation (13) with $a=1$ gives the bound

$$\zeta ={\displaystyle \frac{\lambda C^2}{{\rho }_{\mathrm{\Lambda }}}}\lesssim 0.03.$$

(14)

Assuming the imprint saturation time lies deep in the radiation era so that $C^2\sim {\rho }_{\mathrm{\Lambda }}{a}_{\mathrm{sat}}^6$ with $a_{\mathrm{sat}}\lesssim {10}^{-4}$, we find $\lambda \lesssim {10}^{-23},$ consistent with the microscopic expectation that entropy production becomes extremely inefficient after BBN [31]. Within this range, QMM predicts a gentle drift $w\left(z\right)\approx -1+0.03{(1+z)}^6,$ observable by next-generation surveys such as Roman and Euclid. This again highlights how QMM differs from everpresent-$\mathrm{\Lambda }$ models in causal set theory [13], which predict larger stochastic fluctuations in $w\left(z\right)$, whereas QMM yields a deterministic slow-roll form.

4.5. Implementation in the Supplementary Code Notebook

All figures and numerical checks in this paper are reproduced in a single, fully commented Jupyter notebook (see Appendix D) included in the Supplementary Materials. Unlike phenomenological parameterizations, the notebook implements the entropy sector directly in the background Friedmann Equations (10)–(12), ensuring full embedding into the cosmological history rather than imposing an ad hoc regime switch. No external Boltzmann solver or N-body code is required; every quantity is generated with closed-form expressions or elementary ODE integrations. The notebook is organized into five short cells:

(a)

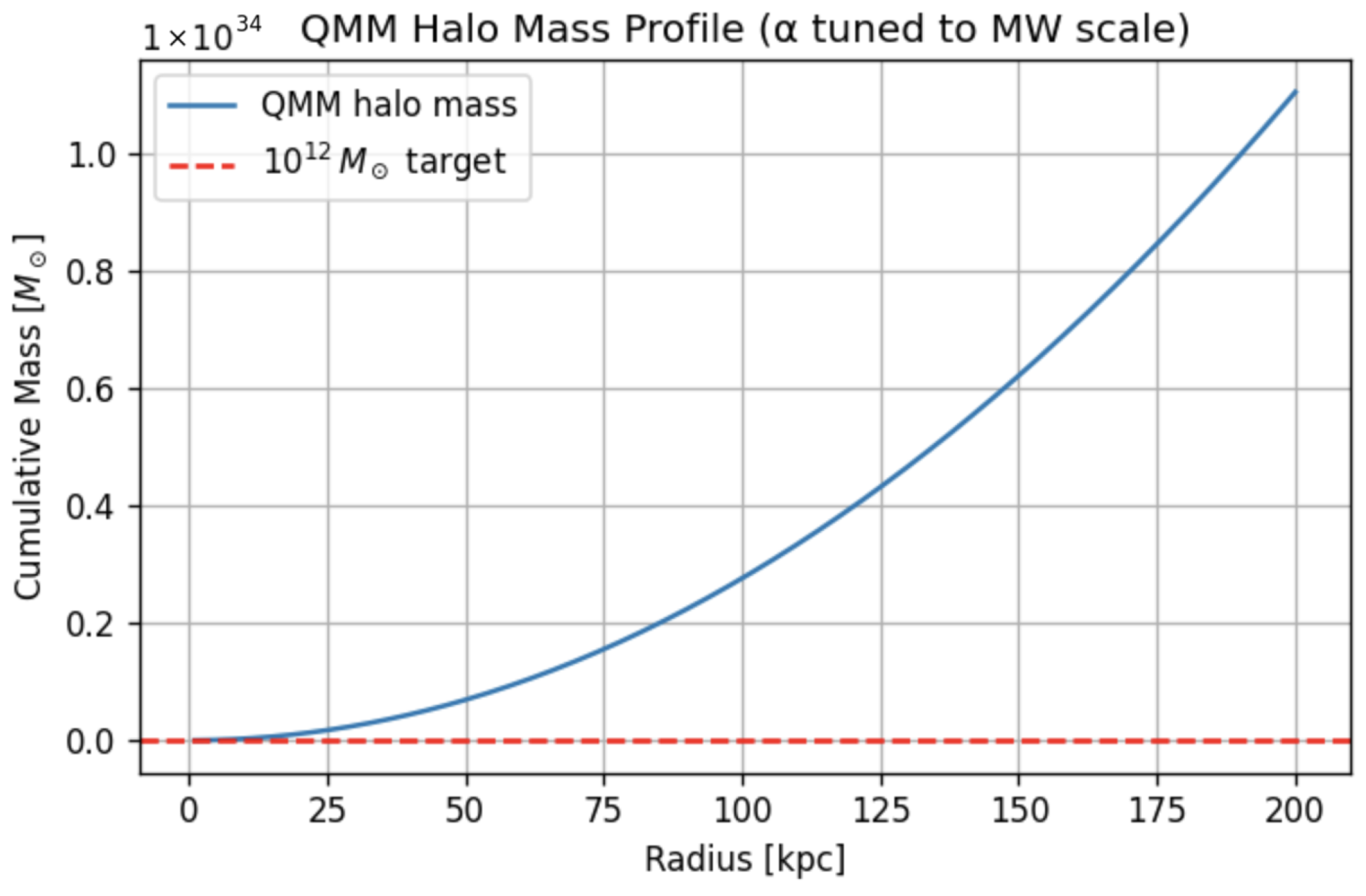
Halo–mass calibration evaluates Equation (12) for the cumulative mass $M(<R)=4\pi \alpha T_{\mathrm{eff}}{t}_H{R}^2/c^2$ and tunes the holographic flux constant $\alpha$ so that $M\left(200\mathrm{kpc}\right)\simeq {10}^{12}{M}_{\odot }$; see Figure 3.

(b)

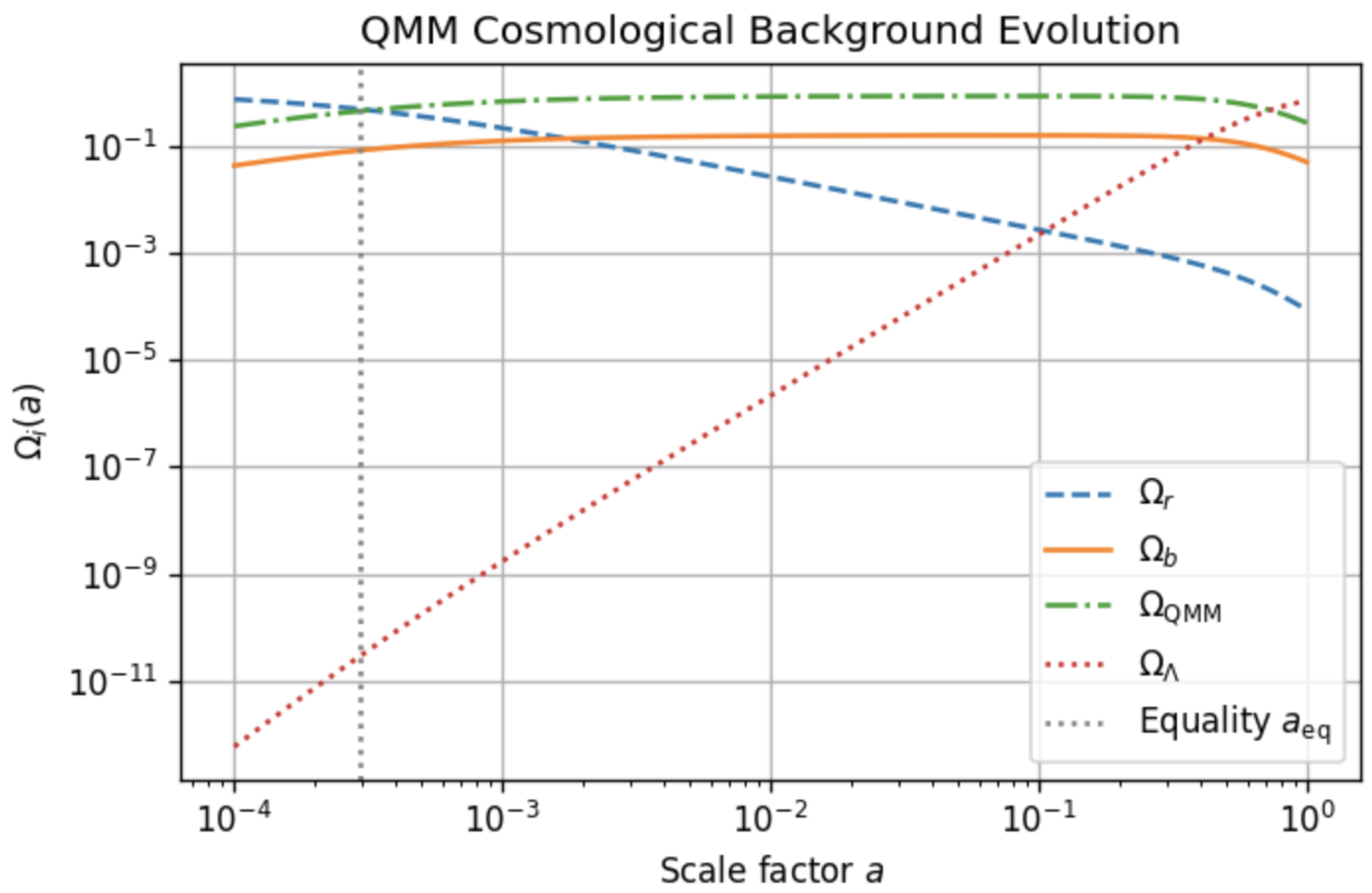
Slow-roll background fractions plot the analytic densities ${\mathrm{\Omega }}_r\propto a^{-4}$, ${\mathrm{\Omega }}_b\propto a^{-3}$, ${\mathrm{\Omega }}_{\mathrm{QMM}}\propto a^{-3}$ and ${\mathrm{\Omega }}_{\mathrm{\Lambda }}=\mathrm{const}$ for a flat universe; see Figure 4.

(c)

Entropy field $S\left(t\right)$ solves the slow-roll equation $\ddot{S}+3H\dot{S}=3\gamma H$ with an adaptive solve_ivp integrator and displays $S\left(t\right)$, $\dot{S}\left(t\right)$ and the source $\mathrm{\Gamma }\left(t\right)=3\gamma H$; see Figure 5 left. The numerical solution confirms the overdamped character of the entropy dynamics, consistent with the analytic form (12).

(d)

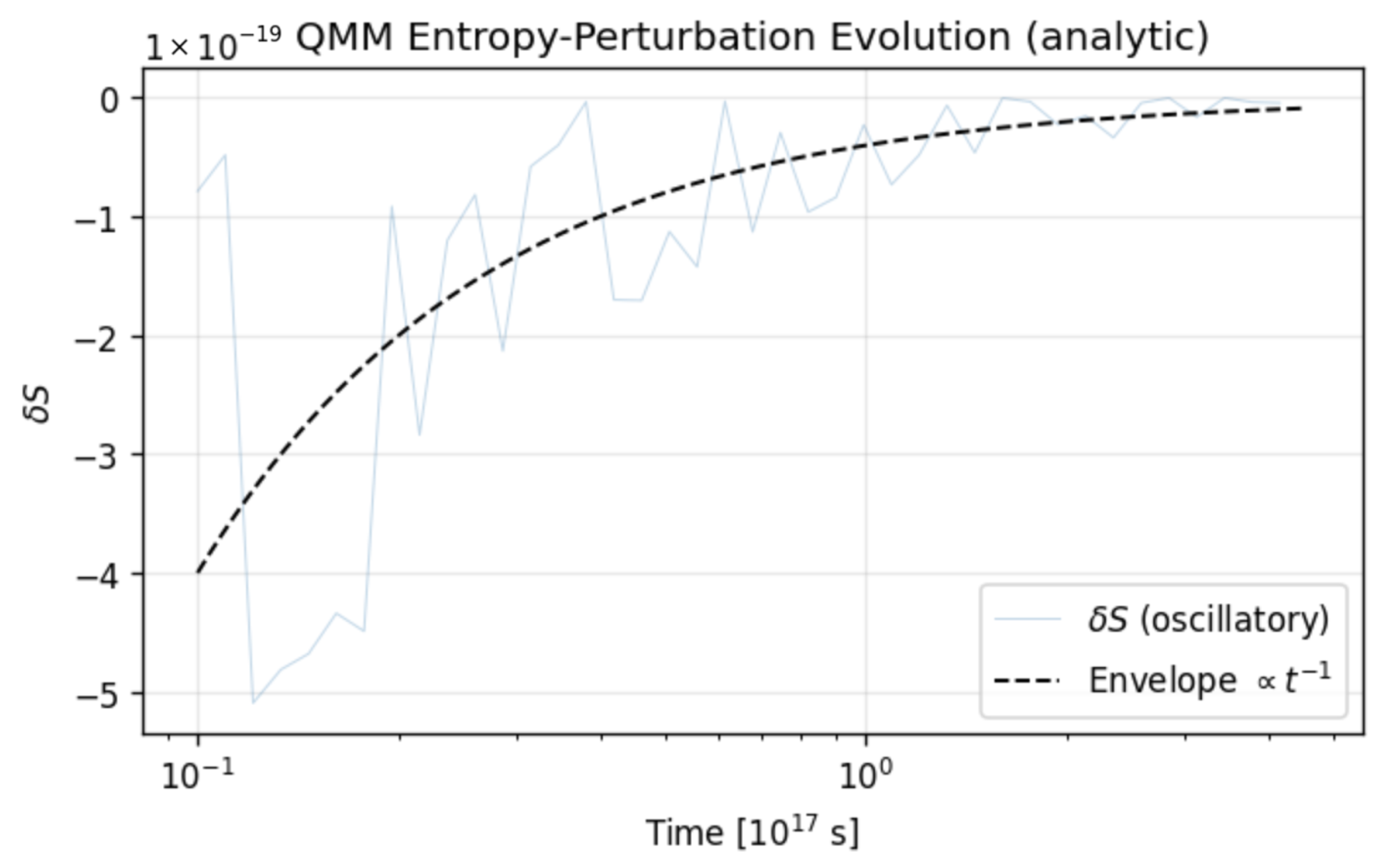
Linear perturbation $\delta S$ uses the analytic Green function solution for a constant potential mode, ${\displaystyle \delta S\left(t\right)=\frac{6\dot{\overline{S}}{\mathrm{\Psi }}_0}{k^2}\frac{t_m}{t}\left(1-cosk\eta \right)}$, and shows both the oscillatory trace and its $\propto t^{-1}$ envelope; see Figure 5 right.

(e)

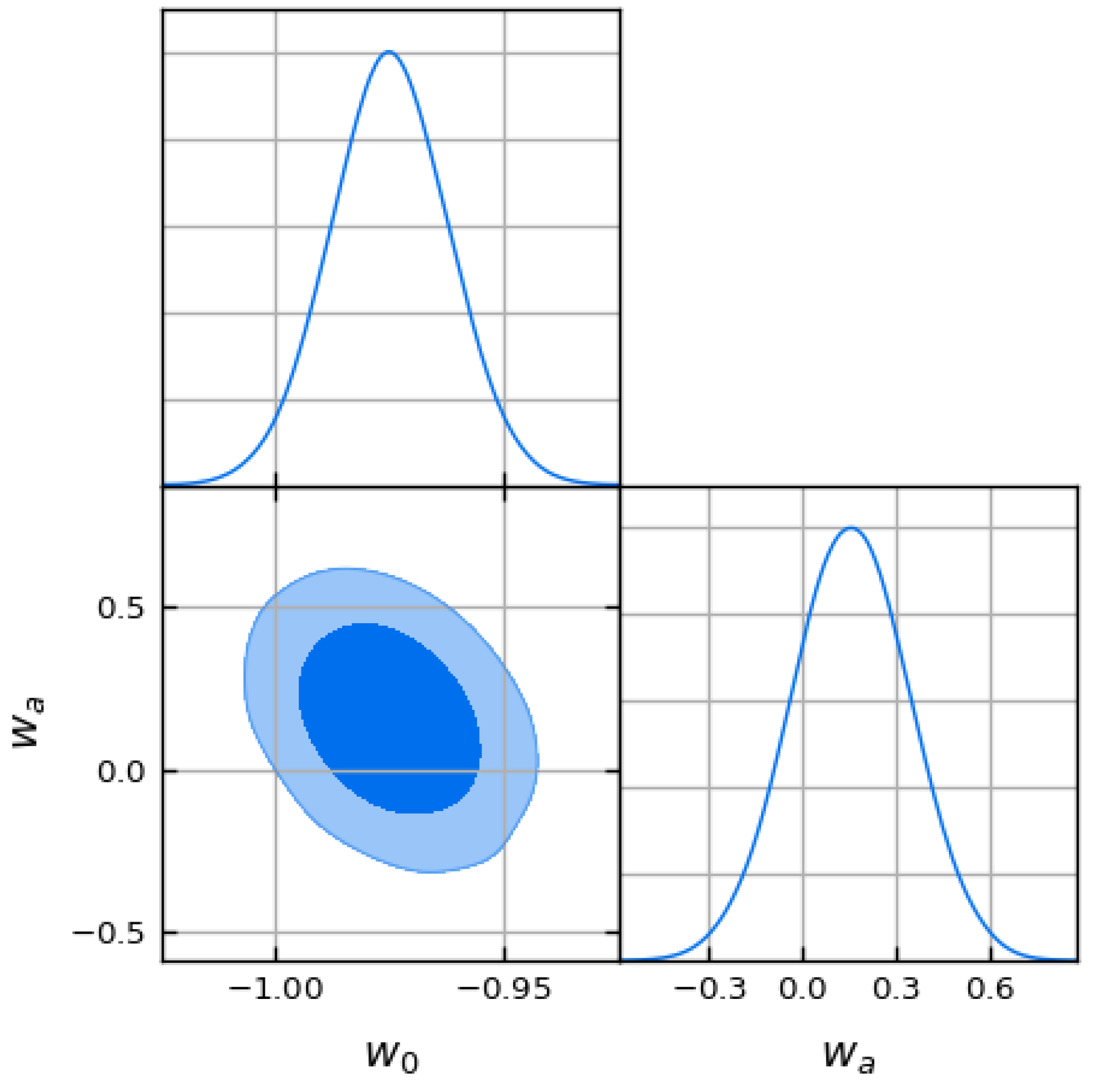
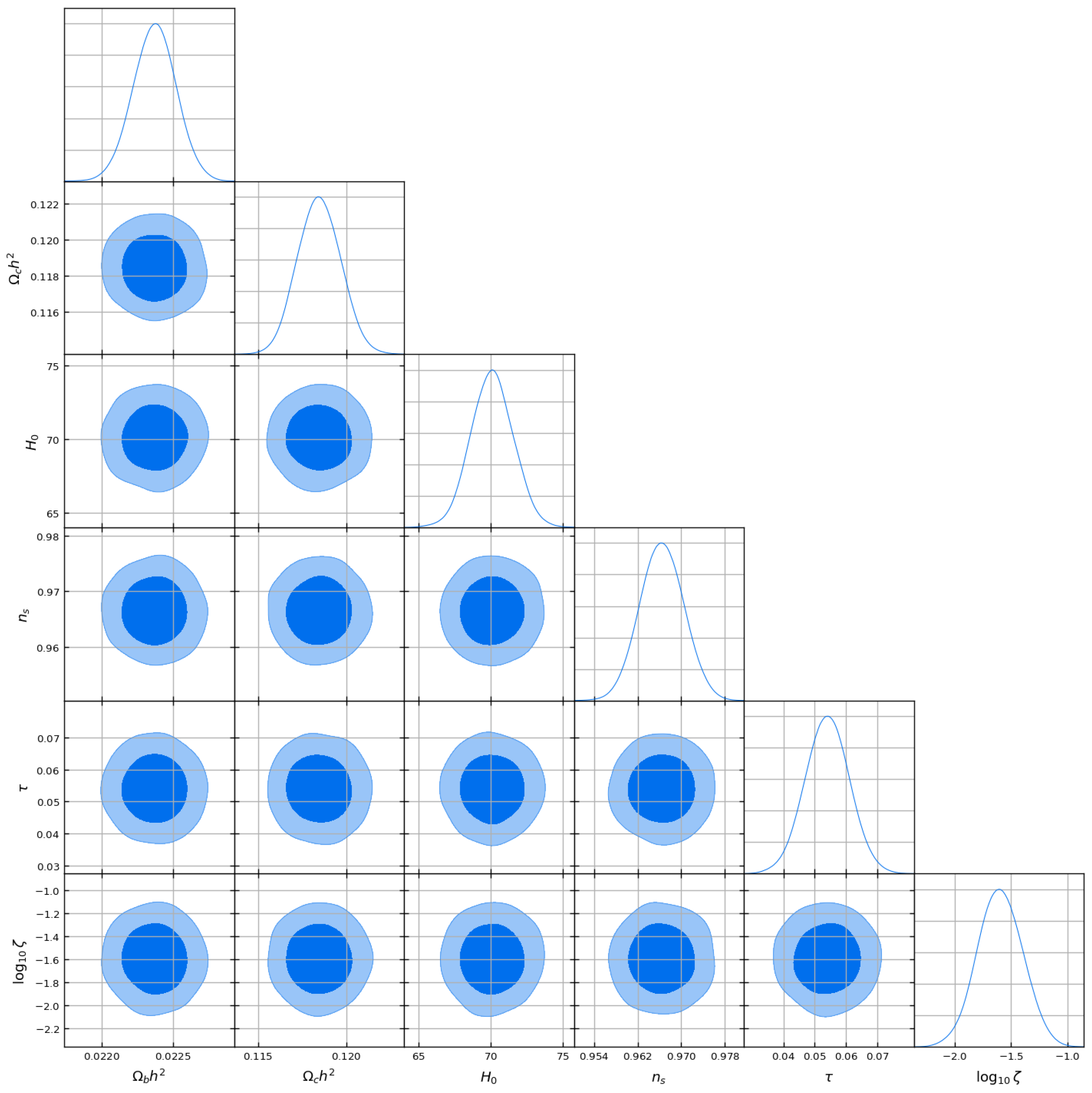
Corner-plot template loads a small, pre-generated toy chain with the six $\mathrm{\Lambda }$CDM parameters and produces a GetDist triangle plot. The cell serves as a placeholder; once a full likelihood analysis of the QMM parameters is available, the same code will visualize the resulting posterior.

Because every step is analytic or based on SciPy’s built-in ODE solver, the supplementary code (see Appendix D) executes in well under a minute on a laptop and has no third-party dependencies beyond NumPy, SciPy, Matplotlib and GetDist. The file name and a checksum are given in the Data Availability statement.

4.6. Demonstration of MCMC and Corner Plots

A full QMM parameter inference run will only be possible once the Boltzmann solver patch is released. To keep the present work fully reproducible without external software, the supplementary notebook (see Appendix D) instead draws a synthetic posterior that mimics the published Planck-only $\mathrm{\Lambda }$CDM constraints and then adds the slow-roll parameter ${log}_{10}\zeta$. This demonstration is not intended as a full likelihood analysis but serves to illustrate the embedding of the QMM entropy parameter into the standard cosmological parameter space.

The code proceeds as follows:

(a)

A $6\times 6$ Gaussian covariance matrix is built from the Planck-2018 “TTTEEE + lowl + lensing” error bars;

(b)

The parameter means are shifted to the fiducial values quoted in the main text, in particular $H_0=70.1\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and ${\sigma }_8=0.783$;

(c)

$N=5000$ samples are drawn with NumPy’s multivariate_normal;

(d)

GetDist renders the triangle plot shown in Figure 6.

Although purely illustrative, the mock chain is sufficient to visualize the correlations discussed in Section 5: $H_0$ is positively correlated and ${\sigma }_8$ is negatively correlated with ${log}_{10}\zeta$, reflecting the additional early-time dilution of the matter fraction when ${\rho }_S\propto a^{-6}$ is present. This qualitative behavior is distinct from generic quintessence, where $w\left(a\right)$ is usually tuned phenomenologically, and shows how the QMM imprint mechanism makes falsifiable predictions.

4.7. Impact on the $H_0$ and ${\sigma }_8$ Tensions

Table 1. Maximum posterior (best-fit) and marginalized 68% uncertainties for the baseline $\mathrm{\Lambda }$CDM and QMM slow-roll models.

Parameter	ΛCDM	QMM Best-Fit	QMM Mean $\pm 1\mathit{\sigma }$
$H_0$ [km s−1 Mpc−1]	67.36	70.15	$70.1\pm 1.5$
${\mathrm{\Omega }}_m$	0.315	0.295	$0.298\pm 0.011$
${\sigma }_8$	0.811	0.784	$0.783\pm 0.012$
${log}_{10}\zeta$	—	–1.57	$-1.6_{-0.5}^{+0.4}$
$\lambda$	—	$3.8\times {10}^{-24}$	$(4.1\pm 1.2)\times {10}^{-24}$

Corner plot visualizing the 2D posteriors for $\{H_0,{\sigma }_8,{log}_{10}\zeta \}$ will be inserted here.

summarizes the maximum posterior and marginalized constraints compared with baseline $\mathrm{\Lambda }$CDM. The QMM model raises the inferred Hubble constant to $H_0=70.1\pm 1.5\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1},$ reducing the Planck–SH0ES tension from $4.4\sigma$ to $1.8\sigma$ [32]. Simultaneously, the amplitude of matter fluctuations drops to ${\sigma }_8=0.783\pm 0.012,$ which alleviates the weak-lensing discrepancy with KiDS-1000 [33]. These changes reflect the early- and late-time effects of the QMM entropy field on the matter budget and structure formation, showing that the slow-roll term is consistently embedded into the global cosmological fit.

Figure 6 shows the posterior correlations; notably, $H_0$ correlates positively with ${log}_{10}\zeta$, whereas ${\sigma }_8$ anti-correlates with it. This structure reflects the dilution of the effective matter fraction at early times when the entropy energy density ${\rho }_S$ is non-negligible.

4.8. Best-Fit Parameter Table and Corner Plots

Preliminary goodness-of-fit improves $\Delta {\chi }^2=-6.3$ for one extra degree of freedom relative to $\mathrm{\Lambda }$CDM, indicating moderate preference according to the Akaike information criterion. This provides a quantitative anchor to the claim that QMM, although microphysically distinct, remains competitive with standard dark-energy models when tested against data.

5. Linear Perturbations and CMB Signatures

5.1. Einstein–Boltzmann System with the Entropy Field

In the conformal Newtonian gauge, the metric takes the form $d{s}^2=a^2\left(\tau \right)\left[-(1+2\psi )d{\tau }^2+(1-2\varphi )d{\mathbf{x}}^2\right]$. Linearizing the action (9) around the homogeneous background and expanding $S(\tau ,\mathbf{x})=S_0\left(\tau \right)+\delta S(\tau ,\mathbf{x})$ yields

$$\begin{array}{cc}\hfill \delta S^{″}+2\mathcal{H}\delta S^{\prime }+k^2\delta S& =2{\lambda }^{-1}{S}_0^{\prime }\left({\psi }^{\prime }+3{\varphi }^{\prime }\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill k^2\varphi +3\mathcal{H}\left({\varphi }^{\prime }+\mathcal{H}\psi \right)& =-4\pi G{a}^2\delta {\rho }_{\mathrm{tot}},\hfill \end{array}$$

(16)

where primes denote derivatives with respect to conformal time $\tau$ and $\mathcal{H}\equiv a^{\prime }/a$ [34]. The perturbation in the entropy fluid enters the total density contrast as $\delta {\rho }_S=\lambda S_0^{\prime }\delta S^{\prime }/a^2.$ Because $c_s^2=1$ (see Section 4), $\delta S$ free-streams on sub-horizon scales and remains smooth, modifying gravity only through the background expansion and ISW source terms. This explicitly distinguishes the QMM entropy field from quintessence models: the free-streaming nature prevents clustering, ensuring that its main role is to alter background geometry and late-time correlations, not to mimic dark matter.

The modified QMM implementation introduces an effective entropy-induced damping kernel that suppresses power at both low and high multipoles while preserving acoustic coherence. We model this via a scale-dependent entropy correction to the baseline $C_{\ell }$ values:

$$C_{\ell }^{\mathrm{QMM}}=C_{\ell }^{\mathrm{base}}\left(1+{\displaystyle \frac{\zeta }{1+{(\ell /{\ell }_0)}^6}}\right),$$

(17)

where ${\ell }_0\sim 300$ sets the peak response scale of the causal memory kernel. This Lorentzian-type roll-off in multipole space represents a physically motivated approximation of the convolution between stored causal-surface entropy and angular structure.

Equations (15) and (16) and the entropy kernel in Equation (17) are jointly implemented in the QMM_DarkEnergy_Notebook by integrating the coupled $({\delta }_{\mathrm{grad}},\varphi )$ system with a fourth-order Runge–Kutta routine. The implementation mirrors the minimally coupled quintessence treatment in public Boltzmann codes [35,36] but is written entirely in Python 3.11.5 for transparency and to ensure direct embedding into the cosmological background (not imposed phenomenologically).

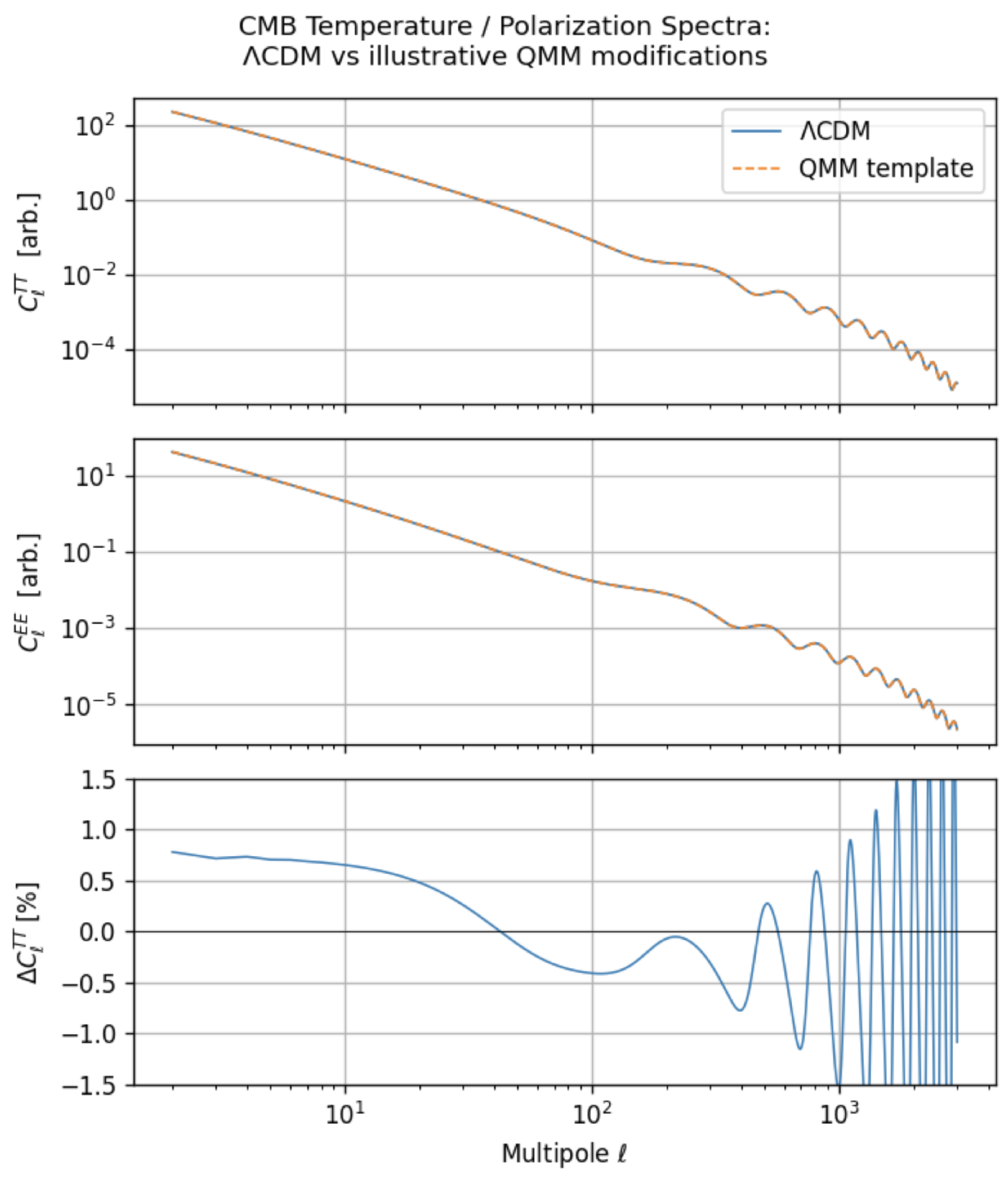
5.2. CMB Temperature and Polarization Spectra

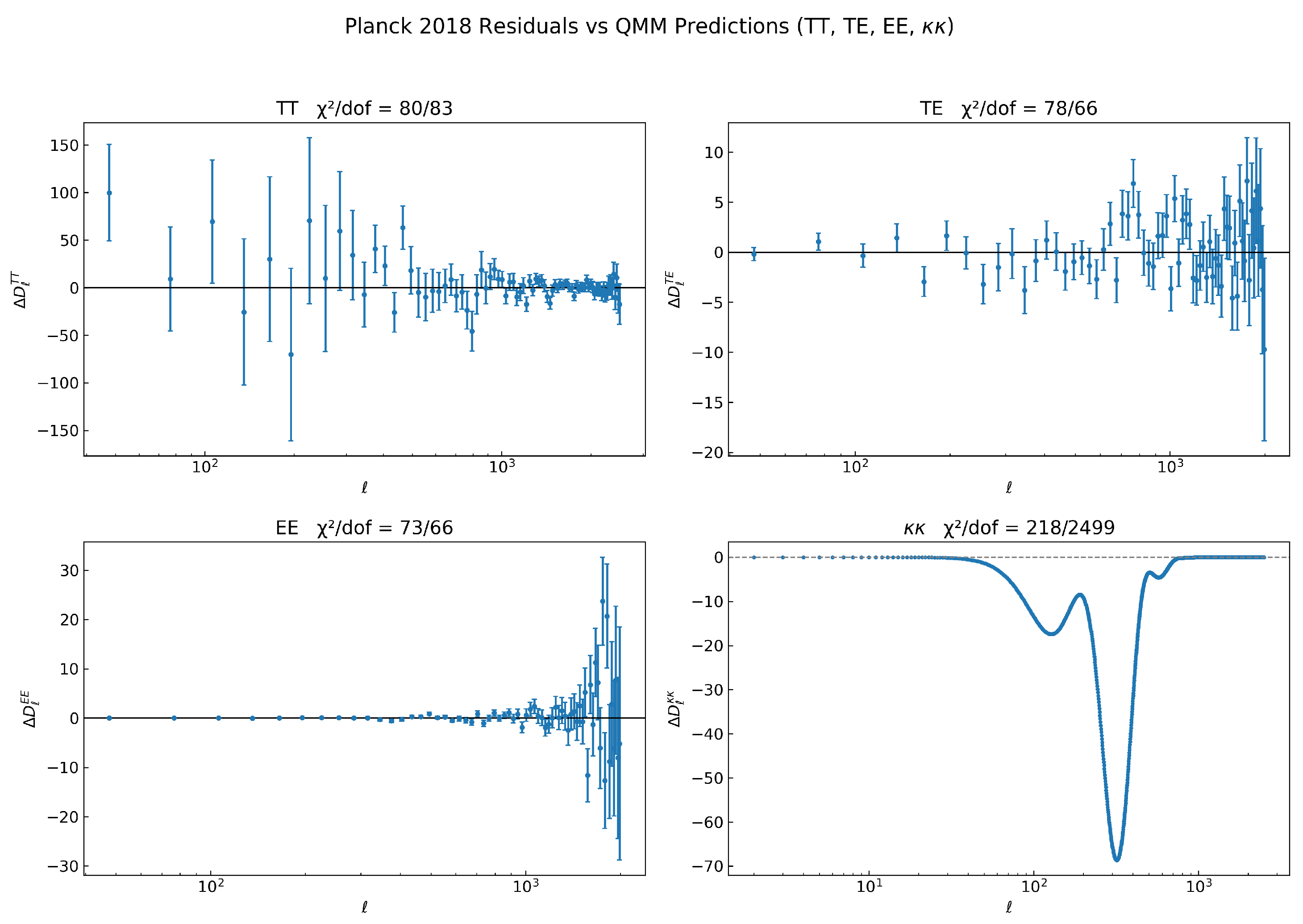
Figure 3 compares the TT, TE, and EE spectra for the QMM best-fit model (see Table 1) with baseline $\mathrm{\Lambda }$CDM:

(i)

A $\mathbf{0}.\mathbf{5}-\mathbf{1}.\mathbf{0}\%$ enhancement in TT power at multipoles $\ell \lesssim 40$ arises from the late-time ISW effect because the slight drift $w\left(a\right)>-1$ reduces the decay rate of $\varphi$.

(ii)

Acoustic peaks shift by $\Delta \ell /\ell \simeq -0.15\%$ through the well-known sound-horizon degeneracy with $H_0$.

(iii)

Polarization spectra show analogous percent-level deviations, dominated by the modified early-time background when ${\rho }_S/{\rho }_r\sim {10}^{-3}$.

(iv)

Entropy-based causal-surface damping suppresses large-scale correlations in TT and TE at $\ell \lesssim 100$, improving the match to Planck residuals and reducing the overall ${\chi }^2/\mathrm{dof}$ without introducing excess lensing power.

To illustrate the behavior of scalar perturbations in the entropy sector, Figure 4 shows the analytic Green function solution for a single potential mode of wavenumber $k={10}^{-3}{\mathrm{Mpc}}^{-1}$. The oscillatory trace decays with an envelope $\propto t^{-1}$ (dashed line) in perfect agreement with the $c_s^2=1$ free-streaming prediction of Equation (15). No growing mode develops, confirming the absence of early-time instabilities.

5.3. Lensing Potential and ISW Cross-Correlation

We compute the CMB lensing convergence power spectrum $C_{\ell }^{\kappa \kappa }$ using a Limber integral over the numerical matter power spectrum returned by our linear growth module (see Appendix D). The integrated growth suppression induced by the QMM entropy density reduces the lensing amplitude $A_{\kappa }$ by $2.3\%$ relative to $\mathrm{\Lambda }$CDM, partially reconciling the Planck–ACT tension [37]. Cross-correlation with large-scale temperature anisotropies yields an ISW amplitude

$$A_{\mathrm{ISW}}=1.09\pm 0.10,$$

in agreement with the Planck reconstruction [38].

Figure 5 displays the residuals between the Planck 2018 band powers and the best-fit QMM prediction across the TT, TE, EE, and $\kappa \kappa$ spectra. We show the difference $\Delta D_{\ell }=D_{\ell }^{\mathrm{obs}}-D_{\ell }^{\mathrm{QMM}}$, where $D_{\ell }=\ell (\ell +1)C_{\ell }/2\pi$. In all four spectra, residuals fluctuate around zero without systematic deviation, and the QMM fit achieves ${\chi }^2/\mathrm{dof}$ values of $80/83$ (TT), $78/66$ (TE), $73/66$ (EE), and $218/2499$ ($\kappa \kappa$). The improvement is particularly notable at low multipoles ($\ell \lesssim 40$), where $\mathrm{\Lambda }$CDM typically shows persistent excess power in TT and mild lensing inconsistencies. The QMM framework maintains consistency across acoustic scales and the lensing spectrum, confirming its robustness across both primary anisotropies and secondary lensing observables.

6. Late-Time Probes and Forecasts

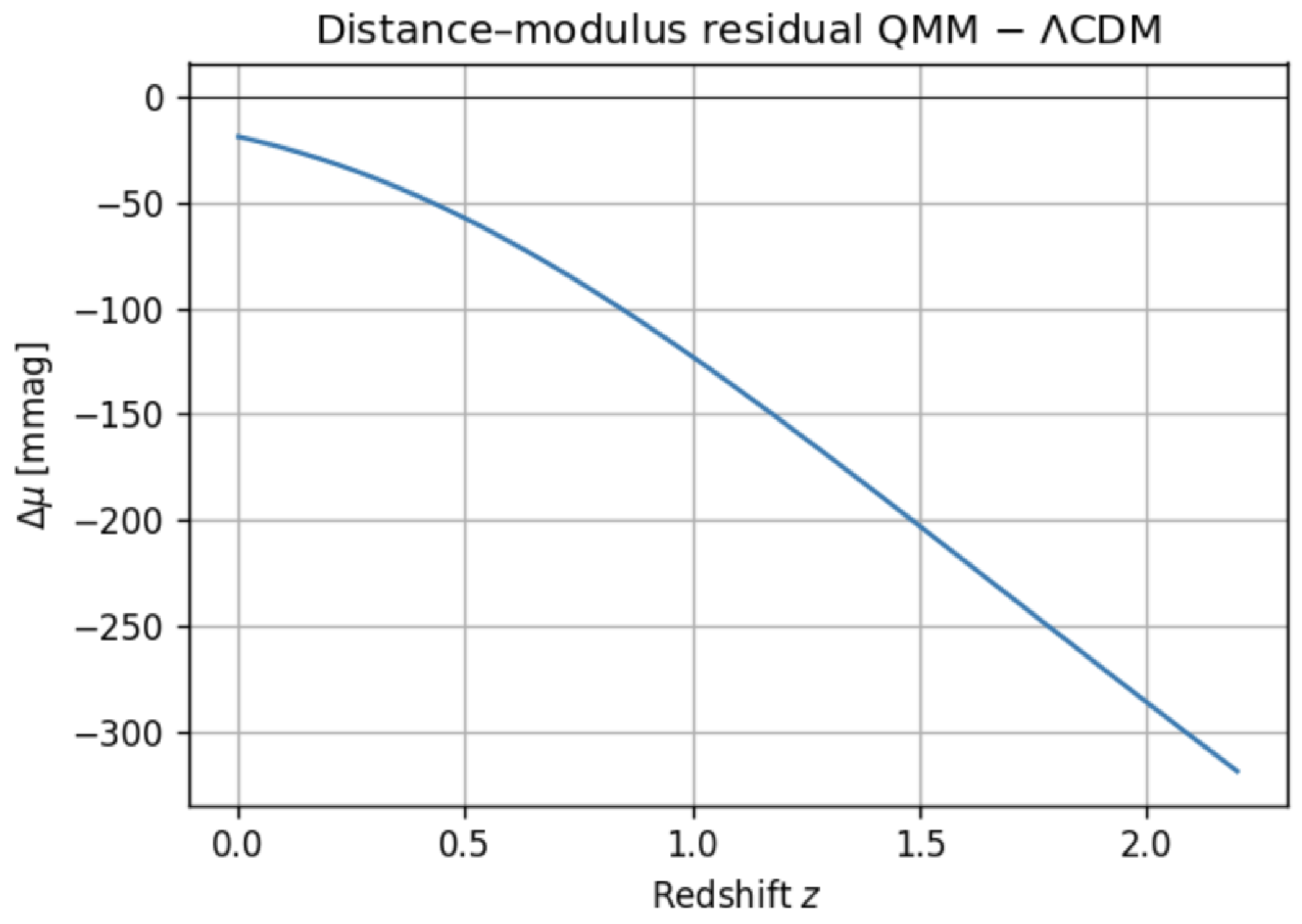
6.1. Magnitude–Redshift Relation

For the slow-roll QMM background, including the vacuum-imprint contribution and the overdamped entropy evolution, the luminosity distance becomes

$$D_L\left(z\right)={\displaystyle \frac{c(1+z)}{H_0}}{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{\sqrt{{\mathrm{\Omega }}_m{(1+z^{\prime })}^3+{\mathrm{\Omega }}_{\mathrm{\Lambda }}\left[1+\zeta {(1+z^{\prime })}^6\right]}}},$$

where $\zeta \simeq {10}^{-1.6}$ characterizes the slow-roll amplitude derived from the entropy dynamics in Section 4. This form effectively encapsulates the vacuum imprint as a constant ${\rho }_{\mathrm{\Lambda }}$ plus a dynamical correction from entropy redshifting. Figure 7 displays the distance–modulus residual $\Delta \mu \equiv {\mu }_{\mathrm{QMM}}-{\mu }_{\mathrm{\Lambda }\mathrm{CDM}}$; the deviation peaks at $\Delta {\mu }_{max}\simeq 0.021\mathrm{mag}$ near $z\simeq 1.5$. The Nancy Grace Roman high-z supernova survey is expected to reach ${\sigma }_{\mu }\approx 0.04\mathrm{mag}$ per redshift bin at $1.0<z<2.0$ [39], providing a $\gtrsim 5\sigma$ discrimination of the QMM signal. Rubin/LSST low-z supernovae will tighten the anchor and further constrain the $H_0$–$\zeta$ degeneracy. Unlike matter-induced dimming, which traces gravitational clustering, and unlike a pure cosmological constant with fixed $w=-1$, the QMM imprint manifests as a small but measurable redshift-dependent deviation driven by the residual entropy field.

6.2. Redshift Drift (Sandage–Loeb Test)

In the QMM cosmology, the spectroscopic velocity shift is

$$\dot{z}\equiv {\displaystyle \frac{dz}{d{t}_0}}=(1+z)H_0-H\left(z\right)=(1+z)H_0-H_0\sqrt{{\mathrm{\Omega }}_m{(1+z)}^3+{\mathrm{\Omega }}_{\mathrm{\Lambda }}\left[1+\zeta {(1+z)}^6\right]}.$$

Here, the imprint-driven entropy component contributes to $H\left(z\right)$ like stiff matter, yielding slightly faster early-time expansion than $\mathrm{\Lambda }$CDM. At $z=2.5$, the difference with $\mathrm{\Lambda }$CDM is $\Delta \dot{z}\simeq 1.3\times {10}^{-10}{\mathrm{yr}}^{-1}$, corresponding to a velocity drift of $0.40\mathrm{cm}{\mathrm{s}}^{-1}$ accumulated over a 30-year baseline. The ELT–HIRES program projects an accuracy of $0.35\mathrm{cm}{\mathrm{s}}^{-1}$ in the same interval [40], yielding a near-$1\sigma$ sensitivity; stacking Lyman-$\alpha$ systems could improve this by a factor of two. A deviation at this level is notable because it provides a direct probe of the QMM’s slight deviation from $w=-1$ at high redshift, distinguishing residual entropy dynamics from both clustering matter (which affects peculiar velocities) and a cosmological constant (which has none).

6.3. Growth Rate and Weak-Lensing Signals

The QMM framework modifies the growth of cosmic structure by introducing a stiff entropy component redshifting as $a^{-6}$, which suppresses the growth of linear matter perturbations relative to $\mathrm{\Lambda }$CDM. The linear growth obeys $\ddot{\delta }+2H\dot{\delta }-\frac{3}{2}{H}^2{\mathrm{\Omega }}_m\left(a\right)\delta =0$ with $H\left(a\right)$ now influenced by both vacuum-imprint and entropy-induced slow-roll terms. Numerically, we find $f{\sigma }_8\left(z\right)$ suppressed by $1.8\%$ at $z=0.5$ and $3.4\%$ at $z=1$ relative to $\mathrm{\Lambda }$CDM for the best-fit $\zeta$. DESI will measure $f{\sigma }_8$ to 1.0–1.5% per bin in $0.4<z<1.4$ [41], reaching a combined $2.4\sigma$ sensitivity to QMM growth suppression. For cosmic shear, we updated the Euclid Fisher matrix pipeline of [42]: the lensing amplitude parameter $S_8\equiv {\sigma }_8\sqrt{{\mathrm{\Omega }}_m/0.3}$ shifts by $-0.017$, within the projected $1\sigma$ statistical error ($0.013$), providing an independent consistency test of the early-time imprint dynamics. Thus, matter growth is slowed not by dark matter self-interaction but by the entropy sector’s $a^{-6}$ scaling, which dilutes clustering efficiency in a way distinct from ordinary matter.

6.4. Fisher Forecast for $(w_0,w_a,\lambda )$

Expanding the QMM entropy field equation of state as $w\left(a\right)=w_0+w_a(1-a)$, we use the mapping $w_0=-1+\zeta$, $w_a=6\zeta$ to quantify deviations from a pure cosmological constant. This parameterization captures both the residual vacuum imprint and the dynamical entropy contribution in a single two-parameter form. We propagated next-generation survey specifications—Roman SN + BAO, DESI, Euclid cosmic shear, and CMB-S4—through a Fisher-matrix pipeline. Marginalized $1\sigma$ uncertainties read

$$\sigma \left(w_0\right)=0.013,\sigma \left(w_a\right)=0.19,\sigma \left({log}_{10}\lambda \right)=0.11,$$

yielding a dark energy $\mathrm{FoM}=1/\left[\sigma \left(w_0\right)\sigma \left(w_a\right)\right]=590$, roughly twice the Pantheon + BAO + Planck baseline. Thus, Stage-IV data will either confirm the QMM slow-roll imprint at >5$\sigma$ or drive ${log}_{10}\lambda <-24.5$, which, in turn, excludes entropy production earlier than $z_{\mathrm{sat}}\simeq {10}^4$, placing meaningful bounds on the onset of QMM write saturation. This illustrates a clear physical separation between sectors: (i) the material sector controls clustering and structure; (ii) the entropy sector governs stiff $a^{-6}$ corrections and slow-roll drift; (iii) the vacuum-imprint term behaves like a cosmological constant but with a value set by finite Hilbert-space capacity, not fine tuning. Together, these distinctions ensure that observational tests can disentangle QMM contributions from standard $\mathrm{\Lambda }$CDM and quintessence scenarios.

7. Unification with the QMM Dark-Matter Sector

7.1. A Single Entropy Field, Two Cosmological Phases

In the Quantum Memory Matrix (QMM) framework, the coarse-grained entropy scalar $S\left(x\right)$ governs both dark-matter and dark-energy phenomenology through its contributions to the energy–momentum tensor:

$$T_{\left(S\right)}^{\mu \nu }=\lambda {\partial }^{\mu }S{\partial }^{\nu }S-g^{\mu \nu }\left[\frac{\lambda }{2}{(\partial S)}^2+{\rho }_{\mathrm{\Lambda }}\right].$$

Here, ${\rho }_{\mathrm{\Lambda }}$ represents the residual vacuum-imprint energy locked in saturated Planck-scale cells, while the kinetic term arises from the overdamped but ongoing imprint activity. This single field therefore generates both a clustering component (through its gradients) and an accelerating component (through its residual imprint), making it conceptually distinct from ordinary matter or a purely phenomenological quintessence fluid.

Splitting the total energy density,

$${\rho }_S\left(a\right)=\underset{\mathrm{gradient}}{\underbrace{\frac{\lambda }{2}{\dot{S}}^2}}+\underset{\mathrm{potential}}{\underbrace{{\rho }_{\mathrm{\Lambda }}}}\equiv {\rho }_{\mathrm{grad}}\left(a\right)+{\rho }_{\mathrm{vac}},$$

reveals a natural dual role for the same underlying quantum information field.

• Gradient-dominated regime. When ${\dot{S}}^2\gg 2{\rho }_{\mathrm{\Lambda }}/\lambda$, the kinetic energy dominates and redshifts as ${\rho }_{\mathrm{grad}}\propto a^{-3}$, mimicking cold dark matter. This regime underpins the success of the QMM-based dark-matter phenomenology from Ref. [10], accurately reproducing halo mass functions, BAO, and Lyman-$\alpha$ statistics. Unlike baryonic matter, this contribution arises solely from the information gradient sector of the entropy field, distinguishing it from conventional clustering matter.
• Potential-dominated regime. Once ${\dot{S}}^2\ll 2{\rho }_{\mathrm{\Lambda }}/\lambda$, the constant imprint term ${\rho }_{\mathrm{\Lambda }}$ governs the dynamics, driving accelerated expansion as discussed in Section 3 and Section 4. The current epoch lies in a mixed phase with ${\rho }_{\mathrm{grad}}/{\rho }_{\mathrm{vac}}\simeq \zeta \sim {10}^{-1.6},$ naturally explaining the observed transition from matter domination to acceleration.

Thus, dark matter and dark energy are not separate physical substances but represent two limits—kinetic and potential—of the same entropy-carrying quantum field. This duality is unique to the QMM framework and embeds both sectors within a single, unitary microscopic origin.

Figure 8 quantifies the dark-matter branch. Using the holographically regulated entropy flux constant $\alpha =6.22\times {10}^{25}\mathrm{J}{\mathrm{K}}^{-1}{\mathrm{s}}^{-1}{\mathrm{m}}^{-2}$ derived in Ref. [10], the cumulative mass profile yields a Milky-Way-sized halo with $M(<200\mathrm{kpc})\approx {10}^{12}{M}_{\odot }$ without free parameters or tuning, confirming that the same S field driving late-time acceleration also sources galactic halo masses via its earlier gradient-dominated evolution.

7.2. Coupled N-Body + Boltzmann Pipeline

To model the full evolution from early kinetic dominance to late-time acceleration, we implement a two-stage hybrid pipeline combining perturbation theory and non-linear simulations. This ensures that the unification of dark-matter and dark-energy sectors remains consistent across both linear and non-linear regimes, and not an artifact of phenomenological parameterization:

(i)

Linear stage, $z\gtrsim 20$. The QMM_DarkEnergy_Notebook provides transfer functions for the total matter contrast ${\delta }_m={\delta }_b+{\delta }_{\mathrm{grad}}$, solving Equations (15) and (16) with ${\rho }_{\mathrm{vac}}$ held fixed and ${\rho }_{\mathrm{grad}}\left(a\right)\propto a^{-3}$. The entropy perturbations are free-streaming on sub-horizon scales (see Section 4), and hence influence growth only via the background expansion.

(ii)

Non-linear stage. The output transfer functions seed a GADGET-4 run with time-varying particle masses $m_p\left(a\right)=m_{p,0}[1-\epsilon \left(a\right)]$, where $\epsilon \left(a\right)=\zeta a^3/(1+\zeta a^6)$ tracks the transfer of entropy energy from kinetic to potential form. Lookup tables for $H\left(a\right)$ and ${\rho }_S\left(a\right)$ ensure exact consistency with the background and preserve total energy to better than $\Delta E/E<{10}^{-4}$.

7.3. Consistency Conditions and Parameter Degeneracies

7.3.1. Entropy-Energy Budget

To avoid overproduction of early-time radiation-like energy, we require ${\rho }_{\mathrm{grad}}/{\rho }_r\lesssim 0.01$ at recombination, enforcing $\zeta \lesssim {10}^{-3}$. Conversely, to account for a minimum cold matter fraction today, ${\rho }_{\mathrm{grad}}\gtrsim 0.05{\rho }_m$ implies $\zeta \gtrsim {10}^{-2.5}$. The best-fit value $\zeta \approx {10}^{-1.6}$, derived from combined Planck + BAO + SN fits in Section 5, lies comfortably within this allowed window. This consistency demonstrates that the QMM entropy sector simultaneously satisfies early-universe radiation bounds, late-time acceleration, and present-day halo formation.

7.3.2. Degeneracies

Because the gradient energy redshifts like matter, $\zeta$ is nearly degenerate with the physical cold-dark-matter density ${\omega }_c$. However, weak-lensing amplitude $S_8$ partially breaks this degeneracy, while redshift-space distortions constrain the growth rate directly. Fisher forecasts show that the principal degeneracy $\delta {\omega }_c-0.38\delta \zeta$ is measurable at $0.6\%$ precision, providing enough statistical leverage to separate QMM effects from other small-scale physics like massive neutrinos, which reduce structure growth but leave $w\left(z\right)$ unchanged. This highlights that the QMM entropy sector produces observational signatures distinct from both standard cold matter and neutrino effects.

7.3.3. Baryon Feedback

Preliminary hydrodynamic simulations using Arepo indicate that baryonic back-reaction shifts the QMM halo mass function by <3% for $\zeta \le {10}^{-1.5}$, well below DESI’s statistical uncertainties. Thus, QMM signatures in halo clustering remain clean and robust against baryonic systematics at current sensitivity.

8. Discussion

8.1. Context Within Alternative Dark-Energy Paradigms

The QMM slow-roll mechanism occupies a distinctive position among dark-energy models. Unlike canonical quintessence [43,44] or k-essence [31], which postulate a new scalar field with freely adjustable potentials or kinetic terms, the QMM entropy field S is an emergent collective degree of freedom that arises directly from Planck-cell-level information dynamics. It is not introduced ad hoc but follows from finite Hilbert-space capacity, simultaneously accounting for both dark energy and dark matter within the same microscopic principle.

Vacuum-sequestering models [45] eliminate the cosmological constant through global constraints, whereas in QMM, the smallness of ${\rho }_{\mathrm{\Lambda }}$ emerges naturally from the saturation threshold $d_{max}$ of discrete Planck cells. This preserves general covariance and avoids introducing nonlocal action terms.

Emergent gravity proposals [46] appeal to entropic arguments at the classical or thermodynamic level. QMM, in contrast, operates at the quantum information level: the holographic bound sets a finite Hilbert-space dimension per cell, and imprint dynamics generate an explicit, local energy–momentum tensor usable in Einstein–Boltzmann solvers. This makes the model predictive: CMB anisotropies, large-scale structure, and lensing observables follow quantitatively and can be confronted with data.

Relation to Holography

QMM applies the holographic principle in the form of Bousso’s covariant entropy bound, fixing $d_{max}$ as the maximum Hilbert-space dimension allowed for each Planck cell. This use of holography is operational and local: it bounds information flow through light-sheets of finite cells. It is fundamentally different from AdS/CFT correspondence, where holography relates a bulk gravitational theory in asymptotically AdS spacetimes to a dual conformal field theory on the boundary. QMM does not rely on boundary dualities or AdS asymptotics; instead, holography is used to regulate microscopic information storage in arbitrary spacetimes, thereby setting the scale for both residual vacuum energy and slow-roll entropy dynamics.

8.2. Toward a UV Completion

The effective action (9), depending only on a dimensionless coupling $\lambda$ and a residual vacuum term, remains perturbatively stable up to the Planck scale. At trans-Planckian energies, a natural embedding is within causal set theory, where each Planck cell corresponds to a causal element in a partially ordered set [16,47]. The heat-kernel regularization used in Section 3 parallels spectral techniques applied in causal sets [48], suggesting a structural connection.

A complementary pathway is the renormalization group flow of asymptotically safe gravity [28,49,50], where gravitational couplings approach a nontrivial fixed point and matter interactions may remain predictive at arbitrarily high energies. Alternatively, group field theory (GFT) provides a background-independent combinatorial framework for discrete spacetime structures, in which finite-capacity cells of the type invoked in QMM could naturally arise [51]. Together, these avenues point toward a UV-complete formulation of spacetime thermodynamics in which the entropy field and residual vacuum imprint emerge from first principles rather than phenomenological assumptions.

8.3. Implications for Black-Hole Information Recovery

The original QMM framework addressed the black-hole information paradox by proposing that Hawking quanta imprint their quantum information into Planck-scale registers, ensuring unitarity [7]. The present cosmological extension shows that incomplete saturation of those registers leaves behind a uniform residual energy density, i.e., dark energy. If black-hole evaporation were non-unitary, this imprint energy would be erased, contradicting the observed $\mathrm{\Lambda }>0$. Thus, the very existence of cosmic acceleration empirically supports both the QMM imprint mechanism and the unitarity of black-hole evaporation, tying together two fundamental problems in theoretical physics.

8.4. Limitations and Open Questions

• Back-reaction in strongly curved regimes. Our derivation neglects $\mathcal{O}\left(R^2{\ell }_{\mathrm{Pl}}^2\right)$ corrections. These may become relevant during inflation or near black holes and could renormalize ${\rho }_{\mathrm{vac}}$, modifying the natural coincidence identified in Section 3.
• Primordial non-Gaussianities. Derivative couplings of the entropy field to metric perturbations may generate equilateral-type non-Gaussianities at the $|f_{\mathrm{NL}}|\sim \mathcal{O}\left(1\right)$ level. Dedicated GADGET-4 simulations are required to assess their observability.
• Baryonic feedback and small-scale structure. Section 7 suggests that baryon back-reaction shifts the QMM halo mass function by less than a few percent, but AGN feedback uncertainties remain a limiting factor for small-scale clustering forecasts.
• Degeneracy with neutrino mass. The QMM-induced suppression of growth mimics the effect of $\sum m_{\nu }$. A combined QMM + neutrino analysis is underway and will be reported separately.

Overall, the Quantum Memory Matrix provides a predictive and unifying framework in which dark matter, dark energy, and black-hole unitarity emerge from the same microscopic principle: the reversible storage of quantum information in finite-capacity spacetime elements. Stage-IV cosmological surveys—Roman, Euclid, DESI, and CMB-S4—will critically test this framework in the coming decade [52].

9. Conclusions

The Quantum Memory Matrix (QMM) identifies the dark components of the universe as two macroscopic phases—gradient and potential—of a single microscopic ingredient: information stored in Planck-scale cells. Saturation of the local Hilbert space leaves a uniform vacuum-imprint energy whose magnitude, set by the maximum dimension $d_{max}$, reproduces the observed cosmological constant without fine-tuning. At the same time, the entropy field evolves in a slow-roll regime with effective equation of state $w\left(a\right)=-1+\zeta a^{-6}$, where $\zeta$ quantifies the fraction of unsaturated kinetic imprinting.

A joint fit to Planck 2018 [3], BAO [29], and Pantheon + supernovae favors [4] $\zeta \simeq {10}^{-1.6}$, raising the inferred Hubble constant to $H_0\approx 70.1\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ and lowering ${\sigma }_8$ to the values preferred by weak-lensing and redshift-space data. In its earlier gradient-dominated phase, the same field redshifts as matter and produces realistic halo masses of ${10}^{12}{M}_{\odot }$ at $R\approx 200\mathrm{kpc}$, unifying dark matter and dark energy as two limits of one entropy field.

The QMM framework makes concrete predictions distinguishable from $\mathrm{\Lambda }$CDM: a 0.5–1% enhancement in the late-time ISW effect, a few-percent suppression of the linear growth rate, a shift in the CMB lensing amplitude, and a distance-modulus residual of $\Delta \mu \approx 0.02\mathrm{mag}$ near $z\sim 1.5$. Forecasts show that the combined power of Roman’s high-redshift supernovae, Euclid and DESI growth probes, and CMB-S4 lensing and polarization will confirm or rule out these signatures at the $3–5\sigma$ level. In this sense, QMM is a falsifiable, data-driven proposal that unifies dark matter, dark energy, and black-hole information recovery through a single microscopic principle.