Cosmic-Ray Boosted Diffuse Supernova Neutrinos

Abstract

The subject of boosted fluxes of dark matter or cosmic relic neutrinos via scattering on cosmic rays has received considerable attention recently. This article investigates the boosted neutrino flux from the scattering of cosmic rays and the so-far undetected diffuse supernova neutrino background, taking into account both galactic and extragalactic cosmic rays. The calculated flux is many orders of magnitude smaller than either the galactic diffuse neutrino emission, the extragalactic astrophysical flux measured by IceCube, or the cosmogenic neutrino flux expected at the highest energies.

1. Introduction

Core collapse supernovæ emit many orders of magnitude more energy in neutrinos than in photons; the most recent core-collapse supernova in the near-neighborhood of the Milky Way, SN1987A, was the first extraterrestrial neutrino source ever detected apart from the Sun. For a long time, a diffuse isotropic background of neutrinos from the integrated emission of many core collapse supernovæ has been predicted, but so far it has escaped detection. Theoretical predictions vary by a factor of 2 to 5, and existing experimental limits are about an order of magnitude higher than predictions [1,2].

Recently, there has been an increased interest in calculations of the flux of relic neutrinos upscattered by elastic scattering on cosmic ray particles to ultra-high energies [3,4]. The comparison of the computed fluxes to experimental upper limits on ultra-high-energy neutrino fluxes have allowed the authors to determine strong upper limits on the density of relic neutrinos.

This article calculates the expected neutrino flux, resulting from the scattering of the diffuse supernova neutrino background on cosmic rays in order to investigate the possibility of an indirect detection of this neutrino background through the observation of high-energy neutrinos. There are two contributions with different angular distributions. On the one hand, galactic cosmic rays can upscatter the diffuse supernova neutrinos; the resulting neutrino flux will then be concentrated around the galactic plane, similar to the diffuse galactic neutrino flux from hadronuclear interactions of cosmic rays with the interstellar medium [5]. On the other hand, extragalactic cosmic rays can upscatter the diffuse supernova neutrino background, resulting in an isotropic flux of ultra-high-energy neutrinos, similar to the cosmogenic neutrino flux expected from photohadronic interactions of ultra-high-energy cosmic rays with the cosmic neutrino background [6], which has so far not been detected [7,8,9].

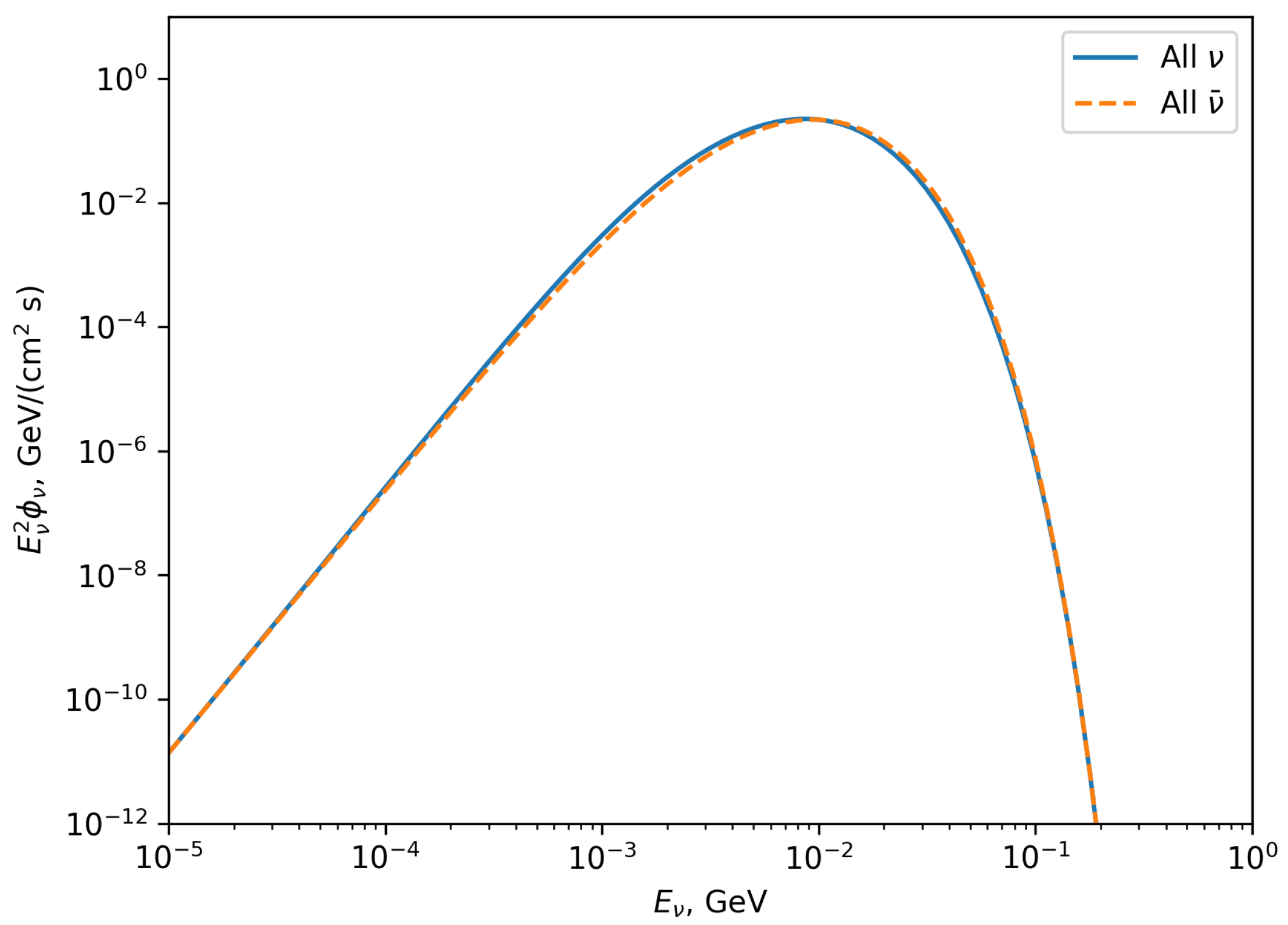
2. Diffuse Supernova Neutrino Background

For this calculation, the flux prediction by the authors of [10] is used, who present a convenient parametrization of SN simulations presented in [11]. Since the neutral-current neutrino cross-sections do not depend on the neutrino flavor, only the total sum of neutrinos and antineutrinos is needed. The flux prediction is given by the following integral:

$${\varphi }_{v_l}=c{\int }_{8M_{\odot }}^{125M_{\odot }}dM{\int }_0^{5}dz(1+z)\left|{\displaystyle \frac{d{t}_c}{dz}}\right|R_{\mathrm{SN}}(z,M)Y_{v_l}(E_v(1+z),M),$$

(1)

where $Y_{v_l}$ refers to the parametrized neutrino yield.

$$R_{\mathrm{SN}}(z,M)={\dot{\rho }}_{\ast }\left(z\right){\displaystyle \frac{\varphi \left(M\right)dM}{{\int }_{0.5M_{\odot }}^{125M_{\odot }}\varphi \left(M\right)MdM}}$$

(2)

is the supernova rate, which is determined from star formation history ${\dot{\rho }}_{\ast }$ and initial mass function $\varphi$ with M the stellar mass, and

$$\left|{\displaystyle \frac{d{t}_c}{dz}}\right|={\left[H_0(1+z)\sqrt{{\Omega }_{\Lambda }+{(1+z)}^3{\Omega }_m}\right]}^{-1}.$$

(3)

describes the expansion history of the universe with redshift z. The fiducial spectrum of the diffuse supernova neutrino background is shown in Figure 1.

3. Cosmic Ray Flux

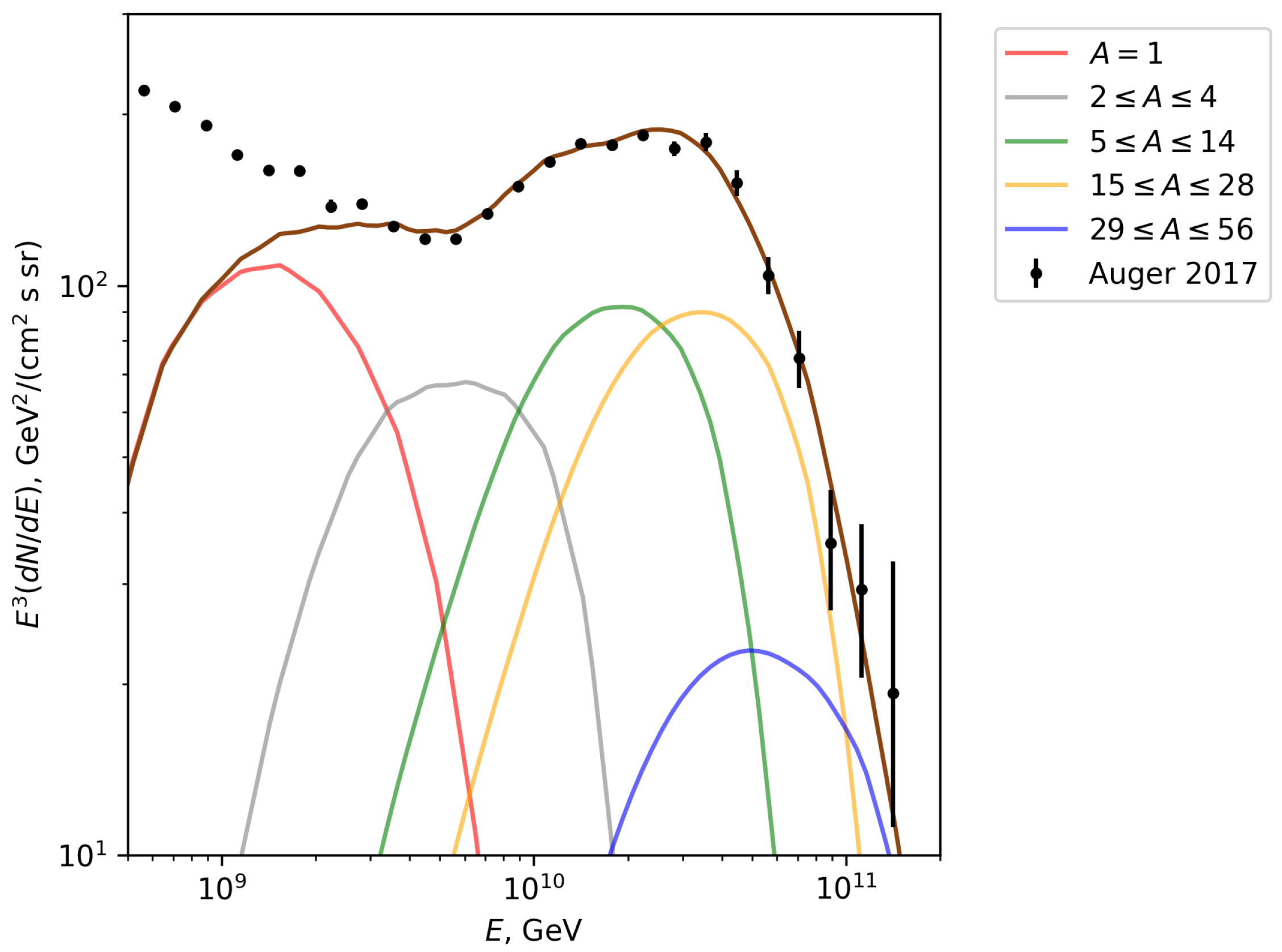
3.1. Galactic Cosmic Ray Flux

For the galactic cosmic ray flux, the parametrization presented in [12] is adopted, which describes the cosmic ray spectrum as the sum of several exponentially cutoff power-law spectra in rigidity $R=E/Ze$ (cf. Figure 2). The flux for a nucleus i is then given as follows:

$${\displaystyle \frac{d{\Phi }_i}{d{E}_i}}=\sum _{j=1}^3{a}_{ij}{E}_i^{-{\gamma }_j-1}exp\left(-{\displaystyle \frac{E_i}{Z_i{R}_j^{\mathrm{cut}}}}\right)$$

(4)

This corresponds to three populations of cosmic rays with cutoff rigidity $R_j^{\mathrm{cut}}$ and spectral index ${\gamma }_j$ common for each population (except for the spectral index of the first population, which is different for each species, based on direct measurements).

The third generation of this parametrization corresponds to the extragalactic cosmic ray flux. This is treated differently (see following section); therefore, the normalization of the third generation is set to zero.

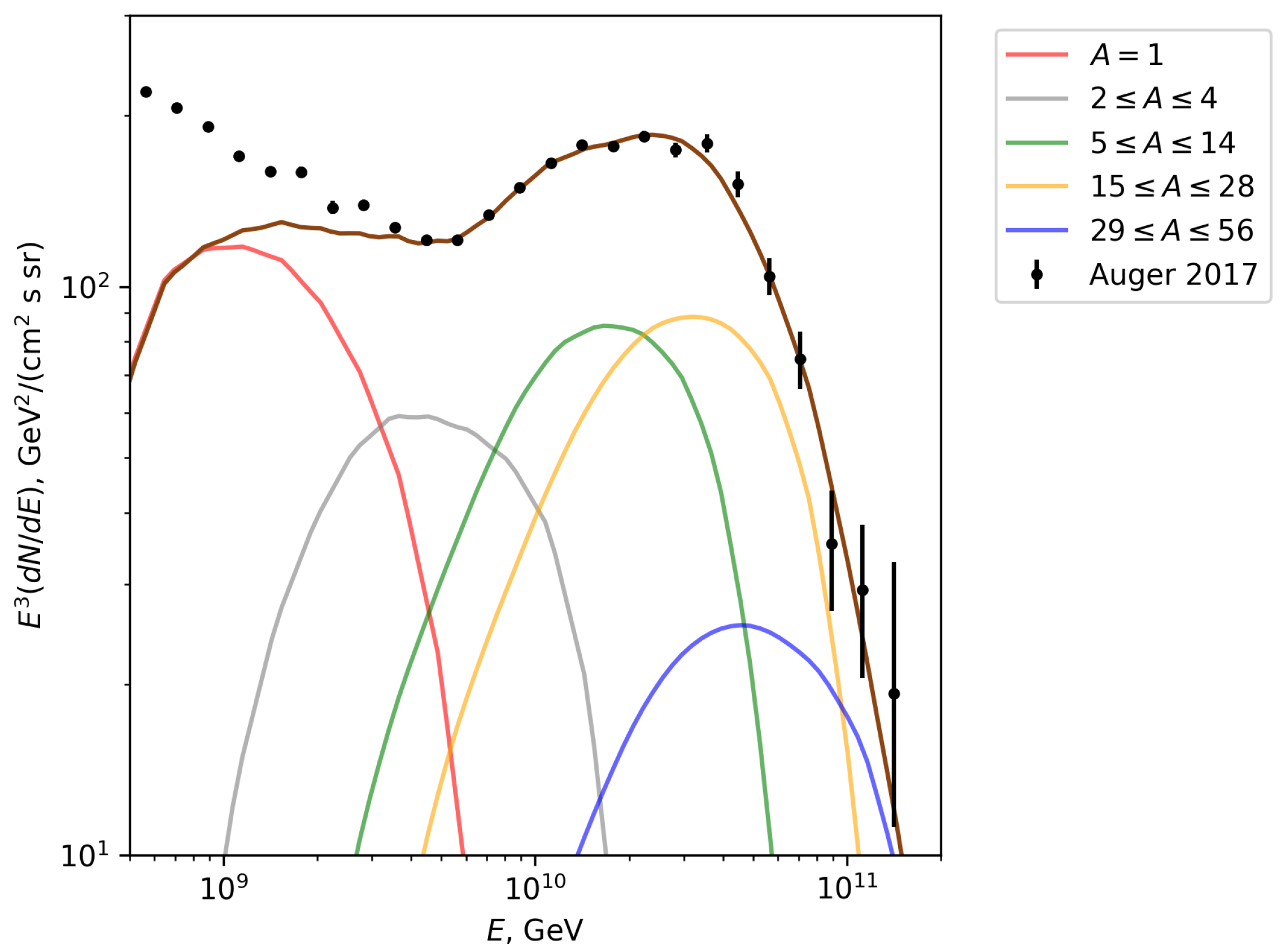
3.2. Extragalactic Cosmic Ray Flux

The extragalactic cosmic ray flux is determined using simulation results of the UHECR propagation code PriNCe [15]. Since the sources of UHECRs are thus far unknown, we assume three possible source density scalings in this work, namely the star formation rate, as follows: [16]

$$N_{\mathrm{SFR}}\left(z\right)={\displaystyle \frac{1+a_{2}z/a_1}{1+{(z/a_3)}^{a_4}}}$$

(5)

with $a_1=0.0170, a_2=0.13, a_3=3.3, a_4=5.3$; the quasar rate [17], as follows:

$$N_{\mathrm{QSO}}\left(z\right)=exp\left(a_{1}z-a_2{z}^2+a_3{z}^3-a_4{z}^4\right)$$

(6)

with $a_1=2.704, a_2=1.145, a_3=0.1796, a_4=0.01019$; and the gamma-ray burst rate, as follows:

$$N_{\mathrm{GRB}}\left(z\right)=N_{\mathrm{SFR}}\left(z\right){(1+z)}^{\delta }$$

(7)

with $\delta =1.26$. In each case, the normalization of the source density is chosen such that $N_i(z=0)=1$. This does not necessarily imply that star-forming galaxies, quasars, or gamma ray bursts are the sources of ultra-high-energy cosmic rays; the assumption is only that they scale with redshift in the same way.

The spectrum of the injected cosmic rays is assumed to follow the following spectral form: [18]

$$J_A\left(E\right)=N_{\mathrm{evol}}\left(z\right)f_A{\left({\displaystyle \frac{E}{{10}^9\mathrm{GeV}}}\right)}^{-\gamma }\left\{\begin{array}{cc}1\hfill & E<Z{R}_{\max },\hfill \\ exp\left(1-{\displaystyle \frac{E}{Z{R}_{\max }}}\right)\hfill & E>Z{R}_{\max },\hfill \end{array}\right.$$

(8)

where $A, Z$ are the mass and charge number of the injected nucleus, E is its energy, $R_{\max }$ is the maximum rigidity, $\gamma$ is the spectral index, $N_{\mathrm{evol}}\left(z\right)\in \{N_{\mathrm{SFR}},N_{\mathrm{QSO}},N_{\mathrm{GRB}}\}$ is the redshift evolution of the source density, and $f_A$ is the normalization. Through a fit to measurements from the Pierre Auger Observatory [19], the spectral index, maximum rigidity, and normalizations of the injected source spectrum is determined (see

Table 1. Fit parameters of the UHECR fit for the specified source distribution.

Source Density Scaling	Star Formation Rate	Quasar Rate	Gamma Ray Burst Rate
$R_{\max }$, $\mathrm{GV}$	${10}^{9.25}$	${10}^{9.20}$	${10}^{9.25}$
$\gamma$	−0.8	−1.0	−0.8
$f_{\mathrm{H}}$, ${\mathrm{GeV}}^{-1}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$	1.0 × 10 −45	2.2 × 10 −45	1.7 × 10 −46
$f_{\mathrm{He}}$, ${\mathrm{GeV}}^{-1}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$	4.5 × 10 −46	7.7 × 10 −46	4.6 × 10 −47
$f_{\mathrm{N}}$, ${\mathrm{GeV}}^{-1}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$	6.2 × 10 −47	6.1 × 10 −47	5.5 × 10 −47
$f_{\mathrm{Si}}$, ${\mathrm{GeV}}^{-1}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$	4.1 × 10 −48	2.3 × 10 −48	3.9 × 10 −48
$f_{\mathrm{Fe}}$, ${\mathrm{GeV}}^{-1}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$	9.0 × 10 −50	6.6 × 10 −50	9.5 × 10 −50

).

The cosmological parameters used in this fit are H₀ = 70.5 km/s/Mpc for the Hubble constant, as well as ${\Omega }_m=0.27,{\Omega }_{\Lambda }=0.73$. The photodisintegration cross-section used is the TALYS parametrization [20]. The fitted spectrum is shown in Figure 3 for density scaling according to the star formation rate, while Figure A1 and Figure A2 report fit assuming a source density scaling according to the quasar and gamma ray burst rate, respectively.

4. Neutrino–Nucleon and Neutrino–Nucleus Scattering Cross-Sections

For the elastic scattering of neutrinos on nucleons, the parametrization of [21] is utilized, as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\sigma }{d{Q}^2}}& ={\displaystyle \frac{G_{\mathrm{F}}^2{M}_p^2}{8\pi {\left(E_v^{\ast }\right)}^2}}\left(A\left(Q^2\right)\pm {\displaystyle \frac{s-u}{M_p^2}}B\left(Q^2\right)+{\displaystyle \frac{{(s-u)}^2}{M_p^4}}C\left(Q^2\right)\right),\hfill \\ \hfill s-u& =4M_p\left(E_v^{\ast }\right)-Q^2,\hfill \end{array}$$

(9)

The ± in front of $B\left(Q^2\right)$ refers to + for neutrinos and − for antineutrinos. The coefficients $A\left(Q^2\right), B\left(Q^2\right), C\left(Q^2\right)$ are functions of the vector and axial vector form factors of the proton (see Appendix A). The neutrino energy in the rest frame of the nucleon is denoted by $E_v^{\ast }$, the momentum transfer squared is denoted by $Q^2$, and the proton mass is denoted by $M_p$; $s, u$ are Mandelstam variables of two-particle scattering [22].

The coherent elastic neutrino–nucleus scattering cross-section can be written as follows [23]:

$${\displaystyle \frac{d\sigma }{d{Q}^2}}={\displaystyle \frac{G_{\mathrm{F}}^2}{8\pi }}{Q}_{\mathrm{W}}^2\left(1-{\displaystyle \frac{Q^2}{4{\left(E_v^{\ast }\right)}^2}}\right)F{\left(Q^2\right)}^2$$

(10)

with $F\left(Q^2\right)$ as the nuclear formfactor [24] and

$$Q_W=(A-Z)-Z(1-4{sin}^2{\theta }_{\mathrm{W}})$$

(11)

demonstrating the weak charge of the nucleus. The incoherent elastic neutrino–nucleus scattering cross-section can be written as follows:

$${\displaystyle \frac{d\sigma }{d{Q}^2}}={\left.{\displaystyle \frac{d\sigma }{d{Q}^2}}\right|}_{\mathrm{elastic}\mathrm{scattering}}A[1-F{\left(Q^2\right)}^2].$$

(12)

The differential cross-section of deep inelastic scattering is given as follows:

$${\displaystyle \frac{d^2\sigma }{dyd{Q}^2}}={\displaystyle \frac{G_{\mathrm{F}}^2{M}_Z^4}{4\pi y{(Q^2+M_Z^2)}^2}}\{[1+{(1-y)}^2]F_2(x,Q^2)-y^2{F}_L(x,Q^2)\},$$

(13)

with y as the inelasticity and x as the Björken scaling variable. In this work, the parametrization of the structure function $F_2$ from [25] is used, in combination with the parametrization of the structure function ratio $R=F_L/(F_2-F_L)$ from [26].

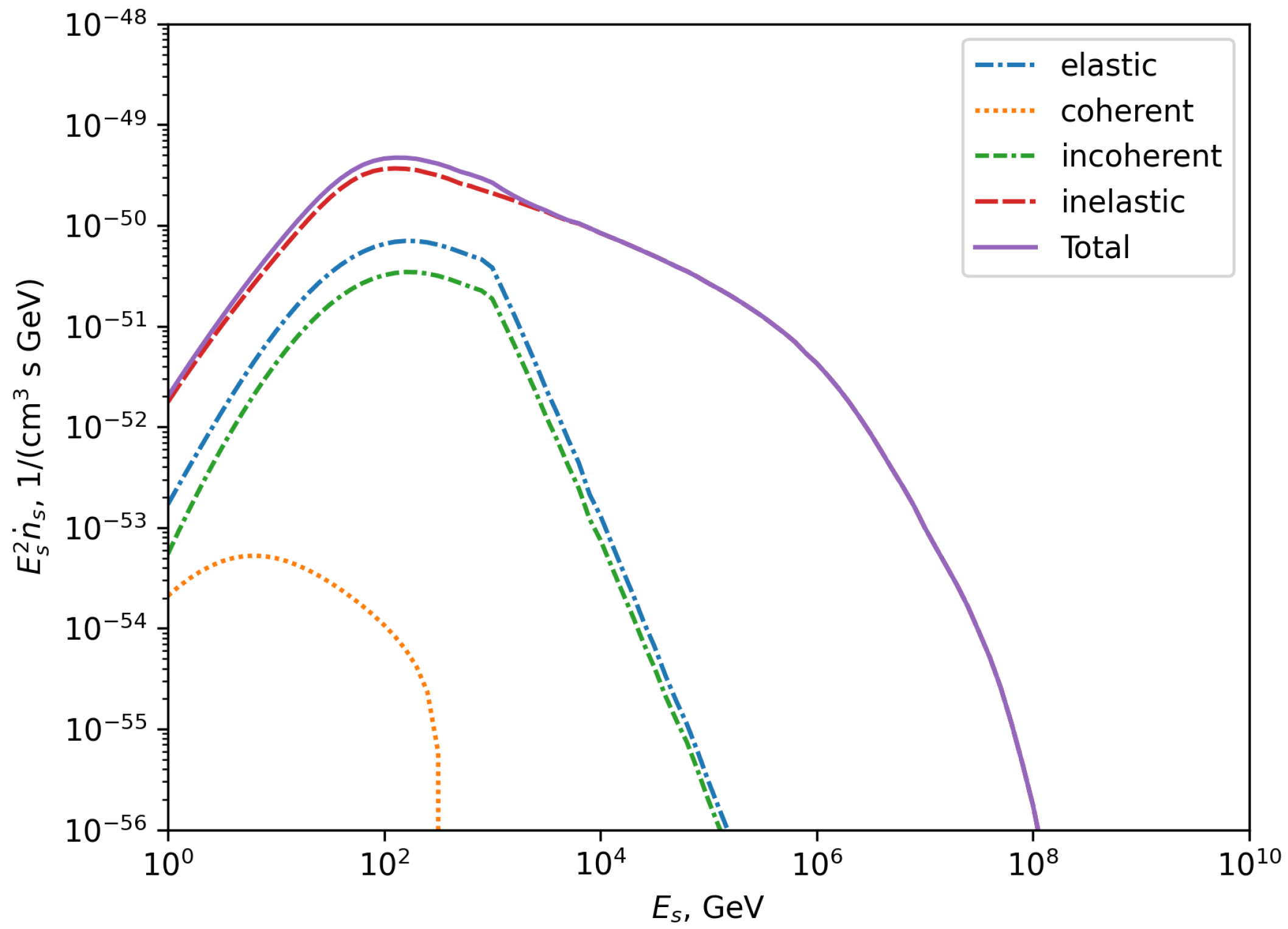
5. Galactic-Boosted Neutrino Flux

5.1. Elastic Scattering

The rate of upscattered neutrinos per volume, energy, and solid angle can be written as follows:

$$\begin{array}{cc}\hfill {\dot{n}}_s({ϵ}_s,{\Omega }_s)& ={\displaystyle \frac{d{n}_s}{d{ϵ}_{s}d{\Omega }_s}}\hfill \\ \hfill & =c{\int }_0^{\infty }d{ϵ}_v\oint d{\Omega }_v{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}\oint d{\Omega }_{\mathrm{CR}}(1-\beta cos\psi )n_v{n}_{\mathrm{CR}}{\displaystyle \frac{d\sigma }{d{ϵ}_{s}d{\Omega }_s}}\hfill \end{array}$$

(14)

with $cos\psi =cos{\theta }_{v}cos{\theta }_{\mathrm{CR}}+sin{\theta }_{v}sin{\theta }_{\mathrm{CR}}cos({\varphi }_v-{\varphi }_{\mathrm{CR}})$, the DSNvB density $n_v=d{n}_v/\left(d{ϵ}_{v}d{\Omega }_v\right)$, and the cosmic ray density $n_{\mathrm{CR}}=d{n}_{\mathrm{CR}}/\left(d{\Gamma }_{\mathrm{CR}}d{\Omega }_{\mathrm{CR}}\right)$. The polar angles $\Omega =(\theta ,\varphi )$, energies $ϵ$, and Lorentz factor $\Gamma$ refer to the upscattered neutrino (subscript s), DSNvB neutrino (subscript v), and the cosmic ray particle (subscript CR). From kinematic considerations, the head-on approximation ${\Omega }_s={\Omega }_{\mathrm{CR}}$ and relative velocity $\beta \approx 1$ are appropriate for this problem because ${\Gamma }_{\mathrm{CR}}\gg 1$.

The energy of the neutrino in the nucleus (nucleon) rest frame is given as follows:

$${ϵ}_v^{\ast }={ϵ}_v{\Gamma }_{\mathrm{CR}}(1-\beta cos\psi )$$

(15)

and the squared momentum transfer is as follows:

$$Q^2=2{ϵ}_v{ϵ}_s(1-cos\psi ).$$

(16)

Using this together with the approximations above, the following expression is obtained:

$$\begin{array}{cc}\hfill {\dot{n}}_s({ϵ}_s,{\Omega }_s)& =c{\int }_0^{\infty }d{ϵ}_v\oint d{\Omega }_v{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}2{ϵ}_v{n}_v{n}_{\mathrm{CR}}{|}_{{\Omega }_{\mathrm{CR}}={\Omega }_s}\hfill \\ \hfill & \times {\left.{\displaystyle \frac{d\sigma }{d{Q}^2}}\right|}_{Q^2=2{ϵ}_v{ϵ}_s(1-cos\psi )}^{{ϵ}_v^{\ast }={ϵ}_v{\Gamma }_{\mathrm{CR}}(1-cos\psi )}\hfill \end{array}$$

(17)

Since both the diffuse neutrino background and the cosmic ray flux are isotropic to very good approximation, we can choose the polar axis of the coordinate system of ${\Omega }_v$ to coincide with the cosmic ray direction ${\Omega }_{\mathrm{CR}}$. Then, $cos\psi =cos\theta$ and the integral over the azimuthal angle becomes trivial. The integral over the polar angle can be expressed as an integral over $Q^2$, so that we are left with the following:

$${\dot{n}}_s={\displaystyle \frac{\pi c}{2{ϵ}_s^3}}{\int }_0^{\infty }{\displaystyle \frac{d{ϵ}_v}{{ϵ}_v^2}}{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}{n}_v{n}_{\mathrm{CR}}{\int }_0^{4{ϵ}_s{ϵ}_v}d{Q}^2{Q}^4{\displaystyle \frac{d\sigma }{d{Q}^2}}.$$

(18)

5.2. Deep Inelastic Scattering

While in elastic scattering the final state is determined by a single variable, in the inelastic case, two variables are needed, requiring a separate calculation. In the head-on approximation, the inelasticity y is connected to the final energy ${ϵ}_s$ in the galactic rest frame, as follows:

$${ϵ}_s=2(1-y){ϵ}_v{\Gamma }_{\mathrm{CR}}^2(1-\beta cos\psi ),$$

(19)

so that the cross-section differential in ${ϵ}_s$ is given as follows:

$${\displaystyle \frac{d\sigma }{d{ϵ}_s}}={\displaystyle \frac{1}{2{ϵ}_v{\Gamma }_{\mathrm{CR}}^2(1-\beta cos\psi )}}{\left.{\displaystyle \frac{d\sigma }{dy}}\right|}_{y=1-{ϵ}_s/\left[2{ϵ}_v{\Gamma }_{\mathrm{CR}}^2(1-\beta cos\psi )\right]}^{{ϵ}_v^{\ast }={ϵ}_v{\Gamma }_{\mathrm{CR}}(1-\beta cos\psi )}.$$

(20)

In analogy with the above calculation, the following holds:

$$\begin{array}{cc}\hfill {\dot{n}}_s({ϵ}_s,{\Omega }_s)& =c{\int }_0^{\infty }d{ϵ}_v\oint d{\Omega }_v{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}\oint d{\Omega }_{\mathrm{CR}}(1-\beta cos\psi )n_v{n}_{\mathrm{CR}}{\displaystyle \frac{d^2\sigma }{d{ϵ}_{s}d{\Omega }_s}}\hfill \\ \hfill & \simeq c{\int }_0^{\infty }d{ϵ}_v\oint d{\Omega }_v{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}(1-\beta cos\psi )n_v{n}_{\mathrm{CR}}{\displaystyle \frac{d\sigma }{d{ϵ}_s}}\hfill \\ \hfill & =c{\int }_0^{\infty }d{ϵ}_v\oint d{\Omega }_v{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}{\displaystyle \frac{n_v{n}_{\mathrm{CR}}}{2{ϵ}_v{\Gamma }_{\mathrm{CR}}^2}}{\left.{\displaystyle \frac{d\sigma }{dy}}\right|}_{y=1-{ϵ}_s/\left[2{ϵ}_v{\Gamma }_{\mathrm{CR}}^2(1-\beta cos\psi )\right]}^{{ϵ}_v^{\ast }={ϵ}_v{\Gamma }_{\mathrm{CR}}(1-\beta cos\psi )}\hfill \\ \hfill & =\pi c{\int }_0^{\infty }d{ϵ}_v{\displaystyle \frac{n_v}{{ϵ}_v}}{\int }_1^{\infty }d{\Gamma }_{\mathrm{CR}}{\displaystyle \frac{n_{\mathrm{CR}}}{{\Gamma }_{\mathrm{CR}}^2}}{\int }_0^{2{ϵ}_v{\Gamma }_{\mathrm{CR}}}{\displaystyle \frac{d{ϵ}_v^{\ast }}{{ϵ}_v{\Gamma }_{\mathrm{CR}}}}\underset{0}{\overset{2m_p(y{ϵ}_v^{\ast }-m_{\pi })-m_{\pi }^2}{\int }}d{Q}^2{\displaystyle \frac{d^2\sigma }{dyd{Q}^2}}.\hfill \end{array}$$

(21)

Since the minimal energy in the nucleon rest frame for this process is given by ${ϵ}_{\min }^{\ast }=m_{\pi }+m_{\pi }^2/2m_p$, the integration region is more constrained compared to the elastic scattering case, leading to the following:

$$\begin{array}{cc}\hfill {\dot{n}}_s({ϵ}_s,{\Omega }_s)& =\pi c{\int }_0^{\infty }d{ϵ}_v{\int }_{{ϵ}_{\min }^{\ast }/2{ϵ}_v}^{\infty }d{\Gamma }_{\mathrm{CR}}{\int }_{{ϵ}_{\min }^{\ast }}^{2{ϵ}_v{\Gamma }_{\mathrm{CR}}}d{ϵ}^{\ast }\underset{0}{\overset{2m_p({ϵ}_v^{\ast }-{ϵ}_s/2{\Gamma }_{\mathrm{CR}}-m_{\pi })-m_{\pi }^2}{\int }}d{Q}^2\hfill \\ \hfill & \times {\displaystyle \frac{n_v{n}_{\mathrm{CR}}}{{ϵ}_v^2{\Gamma }_{\mathrm{CR}}^3}}{\displaystyle \frac{d^2\sigma }{dyd{Q}^2}}.\hfill \end{array}$$

(22)

5.3. Local Neutrino Emission Rate

The emission rate varies as a function of the local cosmic ray spectrum, while the diffuse supernova neutrino flux can be assumed to be constant over the scale of the galaxy.

The numerical results are shown in Figure 4. The dominant contribution to the emission rate is due to inelastic scattering, with elastic scattering on a proton having a small, yet non-negligible impact at energies up to about 1 TeV. For energies below a few hundred $\mathrm{GeV}$, the spectral index is about −1, while for larger energies, the emission rate roughly follows the cosmic ray spectrum with a spectral index of −2.4 and steepening at energies higher than a few $\mathrm{PeV}$.

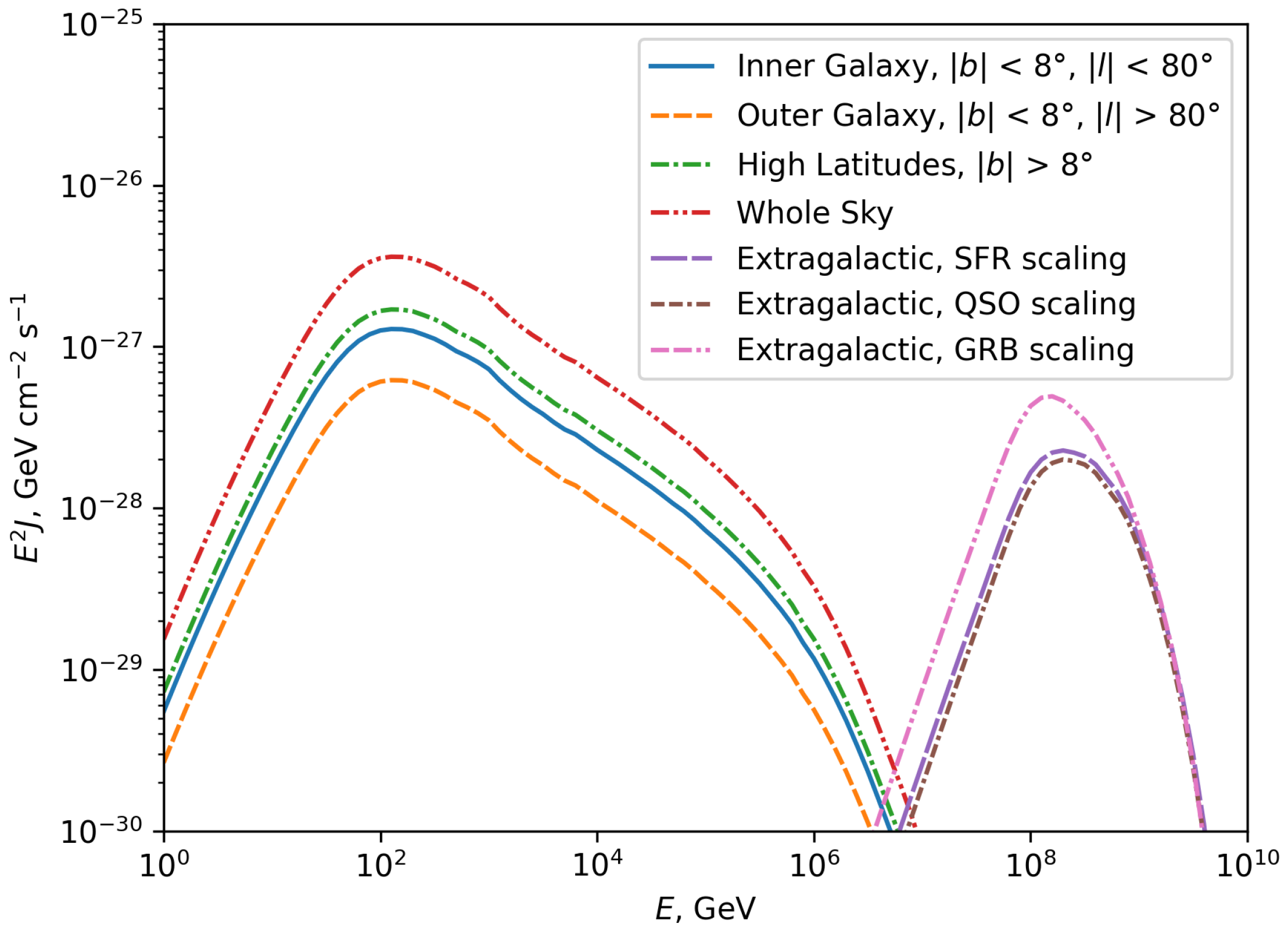
5.4. Intensity of Boosted Neutrinos from Galactic Cosmic Rays

The intensity of the boosted flux follows the spatial dependence of the cosmic ray flux, since the diffuse supernova neutrino background is homogeneous on the scale of the galaxy. Therefore, the intensity map follows by a line-of-sight integral, as follows:

$$I({ϵ}_s,\Omega )={\dot{n}}_s{|}_{\odot }{\int }_0^{\infty }f({\overrightarrow{x}}_{\odot }+\tau \widehat{\Omega })d\tau ,$$

(23)

where $\widehat{\Omega }$ denotes a unit vector in the direction $\Omega$. The spectral shape of the cosmic ray spectrum is identical everywhere, if the model describing the galactic cosmic rays assumes a steady state, the source spectra are the same everywhere if averaged over time, the diffusion coefficient factorizes in a rigidity and a spatial factor, energy losses during propagation are negligible, and escape from the galaxy is the dominant mechanism for CR losses. Under these conditions, the cosmic ray spectrum can be written as $n_{\mathrm{CR}}(E,\overrightarrow{x})=n_{\odot }\left(E\right)f\left(\overrightarrow{x}\right)$, where $n_{\odot }\left(E\right)$ is the local CR spectrum, and f is equal to 1 at the position of Earth. A simple parametrization for the space dependence in this case is given as follows [27]:

$$f\left(\overrightarrow{x}\right)=f(r,z)={\displaystyle \frac{sech(r/R_{\mathrm{cr}})sech(z/Z_{\mathrm{cr}})}{sech(r_{\odot }/R_{\mathrm{cr}})}}$$

(24)

with the hyperbolic secant $sechx=1/coshx$, $R_{\mathrm{cr}}=5.1\mathrm{kpc}$, and $Z_{\mathrm{cr}}=0.3 \mathrm{kpc}$. This function is equal to 1 at the position of the Earth $r=r_{\odot }=8.5 \mathrm{kpc},z=0$, which falls off exponentially at large distances from the center of the galaxy and has a vanishing derivative at the galactic center. Here, $r, z$ are cylindrical coordinates in the galactic plane with $r=0, z=0$ at the galactic center. As expected, the largest intensity is in the direction of the galactic center, where the line-of-sight integral $L(\Omega )={\int }_0^{\infty }f({\overrightarrow{x}}_{\odot }+\tau \widehat{\Omega })d\tau$ assumes its maximal value of the following:

$$\begin{array}{cc}\hfill L_{\max }& =cosh{\displaystyle \frac{r_{\odot }}{R_{\mathrm{cr}}}}{\int }_0^{\infty }{\displaystyle \frac{d\tau }{cosh\frac{r_{\odot }-\tau }{R_{\mathrm{cr}}}}}\hfill \\ \hfill & =2R_{\mathrm{cr}}cosh{\displaystyle \frac{r_{\odot }}{R_{\mathrm{cr}}}}arctan{e}^{r_{\odot }/R_{\mathrm{cr}}}\hfill \\ \hfill & =38.7 \mathrm{kpc}/\mathrm{sr}=1.19 \times {10}^{23}\mathrm{cm}/\mathrm{sr}.\hfill \end{array}$$

(25)

The intensity integrated over angular regions corresponding to the inner and outer galaxy, high latitudes, and the whole sky is shown in Figure 5, together with the extragalactic flux (see following section).

5.5. Intensity of Boosted Neutrinos from Extragalactic Cosmic Rays

The intensity of diffuse supernova neutrinos boosted by scattering on extragalactic cosmic rays is given as follows:

$${\displaystyle \frac{d\varphi }{d{ϵ}_s}}=c\int dz{\displaystyle \frac{1}{H_0\sqrt{{\Omega }_{\Lambda }+{(1+z)}^3{\Omega }_m}}}{\dot{n}}_{e,s}({ϵ}_s(1+z),z),$$

(26)

where $f\left(z\right)$ describes the scaling of the cosmic ray source density with redshift z, normalized to 1 at $z_{\min }=2.37 \times {10}^{-6}$, corresponding to the size of the galaxy, while the emission rate takes into account the z-dependence of the diffuse supernova neutrino background. The extragalactic emission rate ${\dot{n}}_{e,s}$ is given by the same formulae as above; however, the redshift-dependent cosmic ray flux is instead taken from a simulation of ultra-high-energy cosmic rays performed using PriNCe [15]. The flux of cosmic rays observed at ultra-high energies on Earth is dominated by nearby sources due to the short interaction length of cosmic ray nuclei at these energies; in contrast, the neutrinos produced at high redshifts will propagate unabsorbed, so that the neutrino flux also depends on the source behaviour at redshifts that cannot be investigated by fitting the cosmic ray flux observed at Earth. Since the sources of ultra-high-energy cosmic rays are unclear, the star formation rate, quasar rate [17], and gamma ray burst rate [28] are investigated as possible source densities. The parameters of the injected sources are given in Table 1. These are then propagated using the TALYS photodissociation cross-section [20] and the Gilmore cosmic infrared background [29].

The resulting flux is of similar spectral energy density, but demonstrates peaks at higher energies compared to the galactic flux (cf. Figure 5). In contrast to the galactic contribution, this flux is isotropic.

6. Conclusions

The cosmic ray boosted diffuse supernova neutrino background is predicted in this work. Due to the higher energies of supernova neutrinos compared to relic neutrinos, not only elastic scattering on nucleons and nuclei but also inelastic scattering contributes significantly to the boosted flux. Furthermore, the cosmic ray energies contributing to the observed flux are lower, such that not only extragalactic ultra-high-energy cosmic rays but also galactic cosmic rays contribute to the boosted flux.

Similar to the diffuse galactic neutrino emission produced in cosmic ray interactions, the emission from scattering on galactic cosmic rays is concentrated along the galactic plane and follows roughly an $E^{-2.4}$ spectrum. However, the cosmic ray boosted diffuse supernova neutrino background flux is smaller by about 20 orders of magnitude than current models of the galactic diffuse neutrino emission [5].

The extragalactic component peaks in the region of a few hundred $\mathrm{PeV}$. Current experimental limits on the neutrino flux are about 18 orders of magnitude higher [7,8,9]. Predictions for the as-yet-undetected cosmogenic neutrino flux expected from photon–proton interactions between ultra-high-energy cosmic ray protons and the cosmic microwave background vary depending on assumptions relating to the composition of the highest-energy cosmic rays, but even pessimistic calculations predict a much larger flux by more than 10 orders of magnitude [6].

In conclusion, neither the galactic nor the extragalactic component of the cosmic ray boosted diffuse supernova neutrino background are expected to be measurable in the foreseeable future.