The Use of Conditional Variational Autoencoders in Generating Stellar Spectra
Abstract
1. Introduction
2. Database
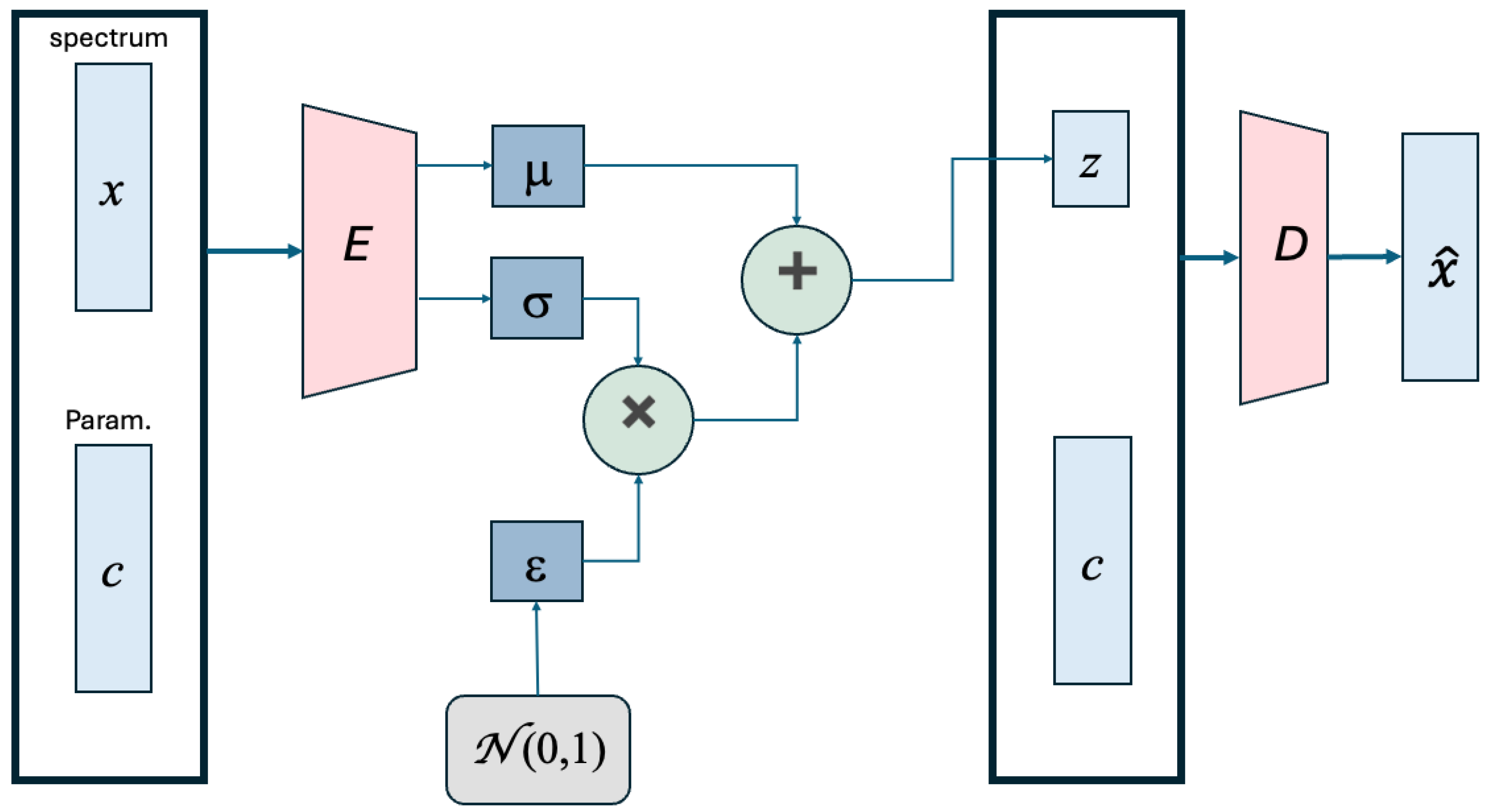
3. Variational Autoencoder
3.1. Conditional Variational Autoencoders
- is the mean squared error between the original spectrum x and the reconstructed spectrum .
- is the KL divergence term that regularizes the latent space.
- Normalize the desired stellar parameters using the previously calculated normalization factors:
- Sample a random vector z from the standard normal distribution .
- Feed z and to the decoder to generate a normalized synthetic spectrum:
- Denormalize the spectrum to obtain physical flux values (the generated spectrum):
3.2. Model Architecture
- An input layer containing the spectrum of dimension 19,000 combined with a conditional vector containing the stellar and instrumental parameters of dimension 6.
- Latent space of dimension 100.
- Encoder network: Dense layers with 4000, 2000, and 1000 units with ReLU activations.
- Decoder network: Dense layers with 1000, 2000, and 4000 units with ReLU activations, followed by a final layer with sigmoid activation.
- Training parameters: Adam optimizer with a dynamical learning rate, a batch size of 512, and early stopping based on reconstruction loss with patience of 50.
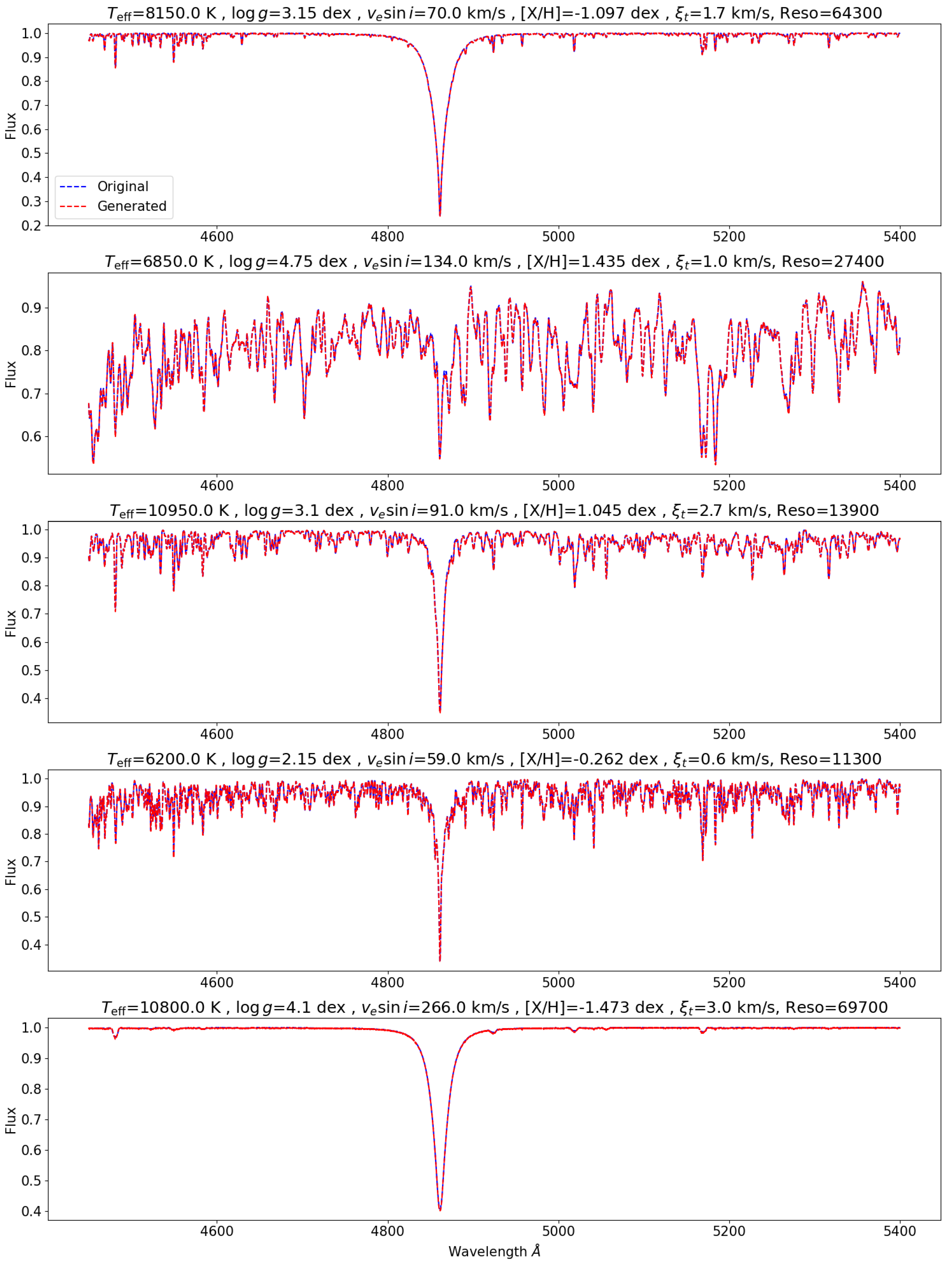
3.3. Spectra Generation
4. Determination of Parameters
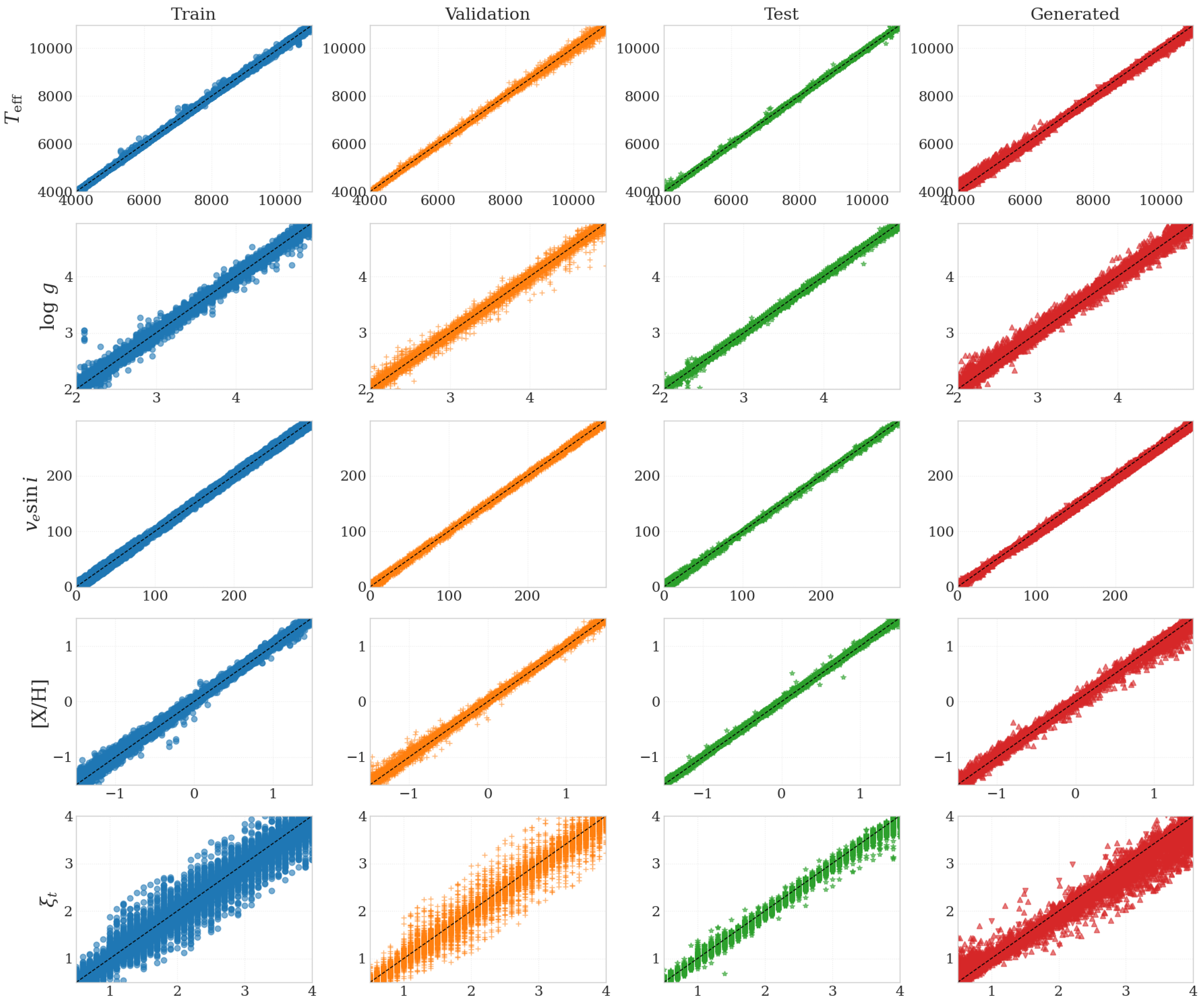
4.1. Accuracy of the Stellar Parameters
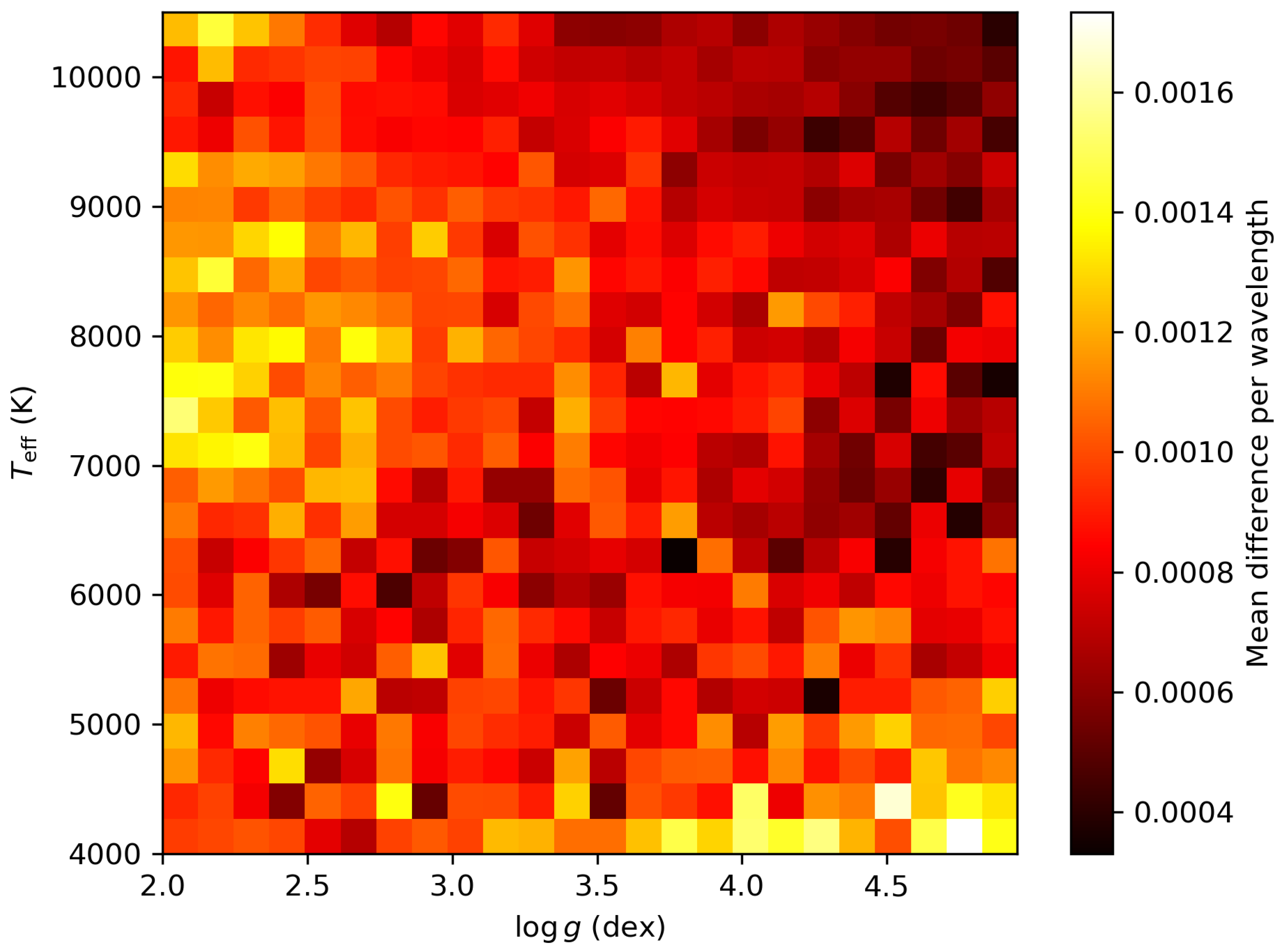
4.2. Heat-Map of Residuals over Parameter Space
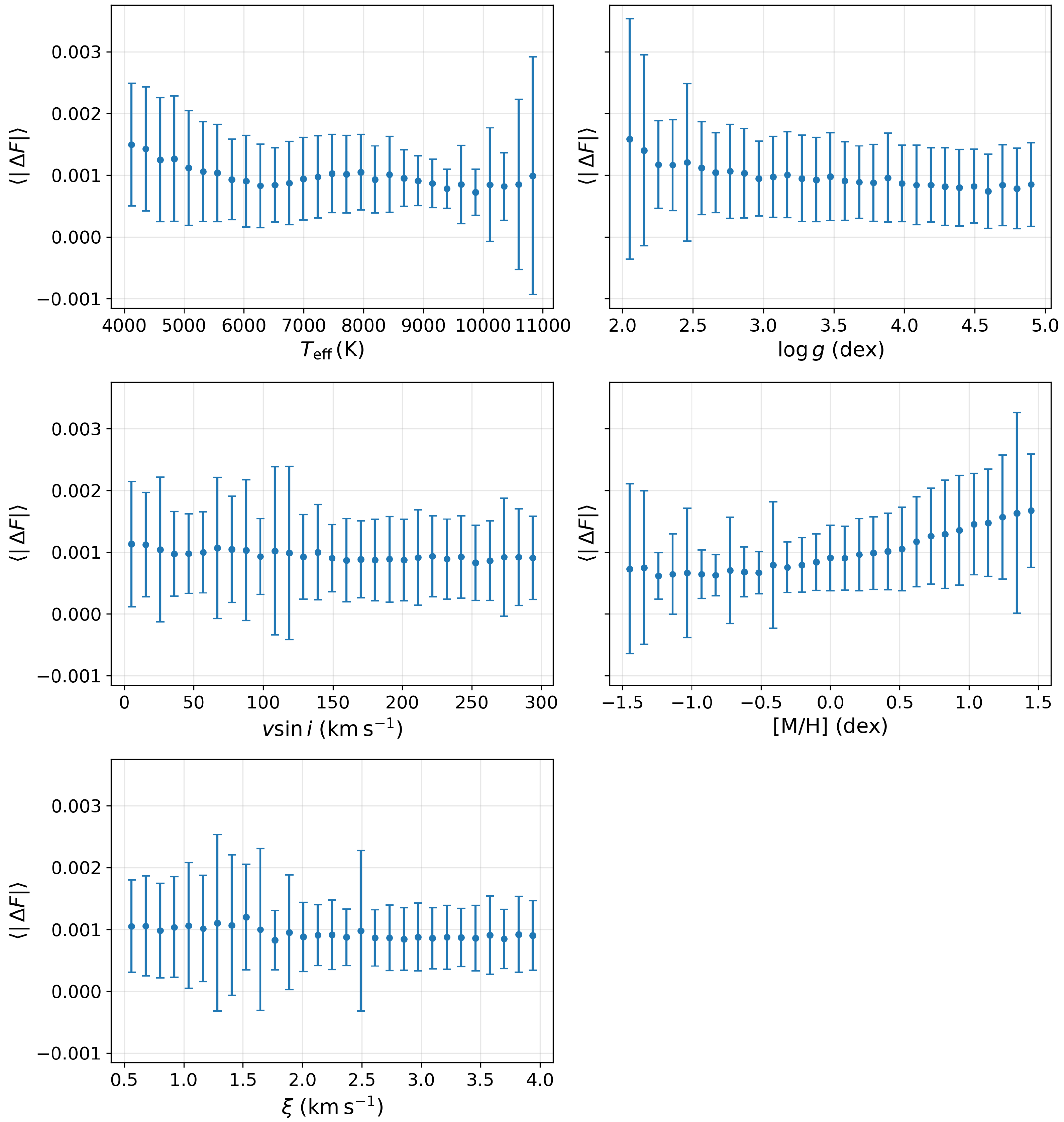
4.3. Marginal Residuals Versus Stellar Parameters
5. Conclusions and Future Work
- Spectral window: ultraviolet, optical, infrared, or a combination thereof
- Resolving power: high-resolution echelle down to broad-band photometric passbands.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Cao, J.; Xu, T.; Deng, L.; Zhou, X.; Li, S.; Liu, Y.; Zhou, W. Pulsar candidate identification using advanced transformer-based models. Chin. J. Phys. 2024, 90, 121. [Google Scholar] [CrossRef]
- Malik, R.; Garg, R.; Cengiz, K.; Ivković, N.; Akhunzada, A. MODAMS: Design of a multimodal object-detection based augmentation model for satellite image sets. Sci. Rep. 2025, 15, 12742. [Google Scholar] [CrossRef]
- Jarolim, R.; Veronig, A.M.; Pötzi, W.; Podladchikova, T. A deep learning framework for instrument-to-instrument translation of solar observation data. Nat. Commun. 2025, 16, 3157. [Google Scholar] [CrossRef]
- Doorenbos, L.; Sextl, E.; Heng, K.; Cavuoti, S.; Brescia, M.; Torbaniuk, O.; Longo, G.; Sznitman, R.; Márquez-Neila, P. Galaxy Spectroscopy without Spectra: Galaxy Properties from Photometric Images with Conditional Diffusion Models. ApJ 2024, 977, 131. [Google Scholar] [CrossRef]
- Chatterjee, S.; Muñoz-Jaramillo, A.; Malanushenko, A.V. Deep Generative model that uses physical quantities to generate and retrieve solar magnetic active regions. arXiv 2025, arXiv:2502.05351. [Google Scholar] [CrossRef]
- Leung, H.W.; Bovy, J. Towards an astronomical foundation model for stars with a transformer-based model. MNRAS 2024, 527, 1494. [Google Scholar] [CrossRef]
- O’Briain, T.; Ting, Y.-S.; Fabbro, S.; Yi, K.M.; Venn, K.; Bialek, S. Cycle-StarNet: Bridging the Gap between Theory and Data by Leveraging Large Data Sets. ApJ 2021, 906, 130. [Google Scholar] [CrossRef]
- Koblischke, N.; Bovy, J. SpectraFM: Tuning into Stellar Foundation Models. arXiv 2024, arXiv:2411.04750. [Google Scholar] [CrossRef]
- Chen, X.; Jeffery, D.J.; Zhong, M.; McClenny, L.; Braga-Neto, U.; Wang, L. Using Physics Informed Neural Networks for Supernova Radiative Transfer Simulation. arXiv 2022, arXiv:2211.05219. [Google Scholar] [CrossRef]
- Husser, T.-O.; Berg, W.; Dreizler, S.; Homeier, D.; Reiners, A.; Barman, T.; Hauschildt, P.H. A new extensive library of PHOENIX stellar atmospheres and synthetic spectra. A&A 2013, 553, A6. [Google Scholar] [CrossRef]
- Hubeny, I.; Lanz, T. Astrophysics Source Code Library. Record ascl:1109.022. 2011. Available online: https://ascl.net/1109.022 (accessed on 1 July 2024).
- Hubeny, I.; Lanz, T. A brief introductory guide to TLUSTY and SYNSPEC. arXiv 2017, arXiv:1706.01859. [Google Scholar] [CrossRef]
- Hubeny, I.; Allende Prieto, C.; Osorio, Y.; Lanz, T. TLUSTY and SYNSPEC Users’s Guide IV: Upgraded Versions 208 and 54. arXiv 2021, arXiv:2104.02829. [Google Scholar] [CrossRef]
- Gebran, M. Generating Stellar Spectra Using Neural Networks. Astronomy 2024, 3, 1. [Google Scholar] [CrossRef]
- Gebran, M.; Farah, W.; Paletou, F.; Monier, R.; Watson, V. A new method for the inversion of atmospheric parameters of A/Am stars. A&A 2016, 589, A83. [Google Scholar] [CrossRef]
- Gebran, M.; Paletou, F.; Bentley, I.; Brienza, R.; Connick, K. Deep learning applications for stellar parameter determination: II-application to the observed spectra of AFGK stars. Open Astron. 2023, 32, 209. [Google Scholar] [CrossRef]
- Kassounian, S.; Gebran, M.; Paletou, F.; Watson, V. Sliced Inverse Regression: Application to fundamental stellar parameters. Open Astron. 2019, 28, 68. [Google Scholar] [CrossRef]
- Kurucz, R.L. Model atmospheres for population synthesis. Symp. Int. Astron. Union 1992, 149, 225. [Google Scholar]
- Castelli, F.; Kurucz, R.L. New Grids of ATLAS9 Model Atmospheres. arXiv 2003, arXiv:astro-ph/0405087. [Google Scholar] [CrossRef]
- Smalley, B. Observations of convection in A-type stars. Proc. Int. Astron. Union 2004, 224, 131. [Google Scholar] [CrossRef]
- Grevesse, N.; Sauval, A.J. Standard Solar Composition. Space Sci. Rev. 1998, 85, 161. [Google Scholar] [CrossRef]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar] [CrossRef]
- van de Ven, G.M.; Li, Z.; Tolias, A.S. Class-Incremental Learning with Generative Classifiers. arXiv 2021, arXiv:2104.10093. [Google Scholar] [CrossRef]
- Gebran, M.; Connick, K.; Farhat, H.; Paletou, F.; Bentley, I. Deep learning application for stellar parameters determination: I-constraining the hyperparameters. Open Astron. 2022, 31, 38. [Google Scholar] [CrossRef]
- Paletou, F.; Böhm, T.; Watson, V.; Trouilhet, J.-F. Inversion of stellar fundamental parameters from ESPaDOnS and Narval high-resolution spectra. A&A 2015, 573, A67. [Google Scholar] [CrossRef]
- Gebran, M.; Bentley, I.; Brienza, R.; Paletou, F. Deep learning application for stellar parameter determination: III-denoising procedure. OAst 2025, 34, 20240010. [Google Scholar] [CrossRef]
- Gustafsson, B.; Edvardsson, B.; Eriksson, K.; Jørgensen, U.G.; Nordlund, Å.; Plez, B. A grid of MARCS model atmospheres for late-type stars. A&A 2008, 486, 951. [Google Scholar] [CrossRef]
- Sneden, C.; Bean, J.; Ivans, I.; Lucatello, S.; Sobeck, J. Astrophysics Source Code Library. Record ascl:1202.009. 2012. Available online: https://ui.adsabs.harvard.edu/abs/2012ascl.soft02009S (accessed on 1 July 2024).
- Royer, P.; Merle, T.; Dsilva, K.; Sekaran, S.; Van Winckel, H.; Frémat, Y.; Van der Swaelmen, M.; Gebruers, S.; Tkachenko, A.; Laverick, M.; et al. The Mercator Library of High Resolution Stellar Spectroscopy. A&A 2024, 681, A107. [Google Scholar] [CrossRef]
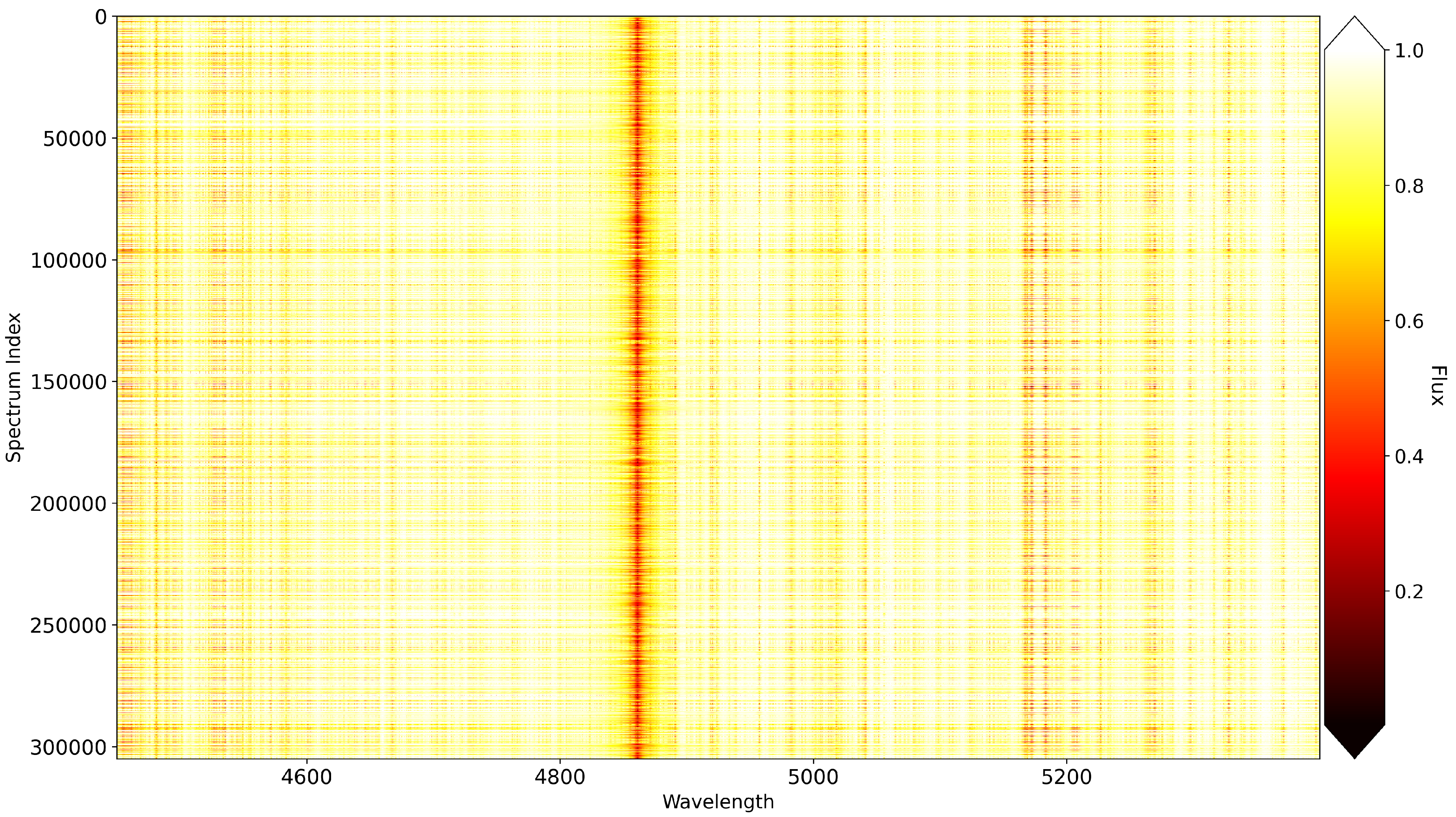
| Parameter | Range |
|---|---|
| 4000–11,000 K | |
| 2.0–5.0 dex | |
| 0–300 km/s | |
| −1.5–1.5 dex | |
| 0–4 km/s | |
| Resolution () | 1000–115,000 |
| Layer | Characteristics | Activation Function |
|---|---|---|
| Input | PCA coefficient (25 data points per spectrum) | - |
| Hidden | 5000 neurons | ReLU |
| Hidden | 2000 neurons | ReLU |
| Hidden | 1000 neurons | ReLU |
| Hidden | 64 neurons | ReLU |
| Output | Stellar Parameters (6 data points per spectrum) | - |
| Parameter | Training | Validation | Test | Generated |
|---|---|---|---|---|
| (K) | 30 | 45 | 60 | 65 |
| (dex) | 0.04 | 0.04 | 0.04 | 0.04 |
| (km/s) | 3.0 | 5.1 | 6.2 | 6.1 |
| (dex) | 0.030 | 0.035 | 0.029 | 0.030 |
| (km/s) | 0.08 | 0.10 | 0.08 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gebran, M.; Bentley, I. The Use of Conditional Variational Autoencoders in Generating Stellar Spectra. Astronomy 2025, 4, 13. https://doi.org/10.3390/astronomy4030013
Gebran M, Bentley I. The Use of Conditional Variational Autoencoders in Generating Stellar Spectra. Astronomy. 2025; 4(3):13. https://doi.org/10.3390/astronomy4030013
Chicago/Turabian StyleGebran, Marwan, and Ian Bentley. 2025. "The Use of Conditional Variational Autoencoders in Generating Stellar Spectra" Astronomy 4, no. 3: 13. https://doi.org/10.3390/astronomy4030013
APA StyleGebran, M., & Bentley, I. (2025). The Use of Conditional Variational Autoencoders in Generating Stellar Spectra. Astronomy, 4(3), 13. https://doi.org/10.3390/astronomy4030013





