Gravity Wave Phase Shift in a Cold Quark Star with a Nonconvex QCD BZT Shock Wave Van Der Waals Equation of State
Abstract
1. Introduction
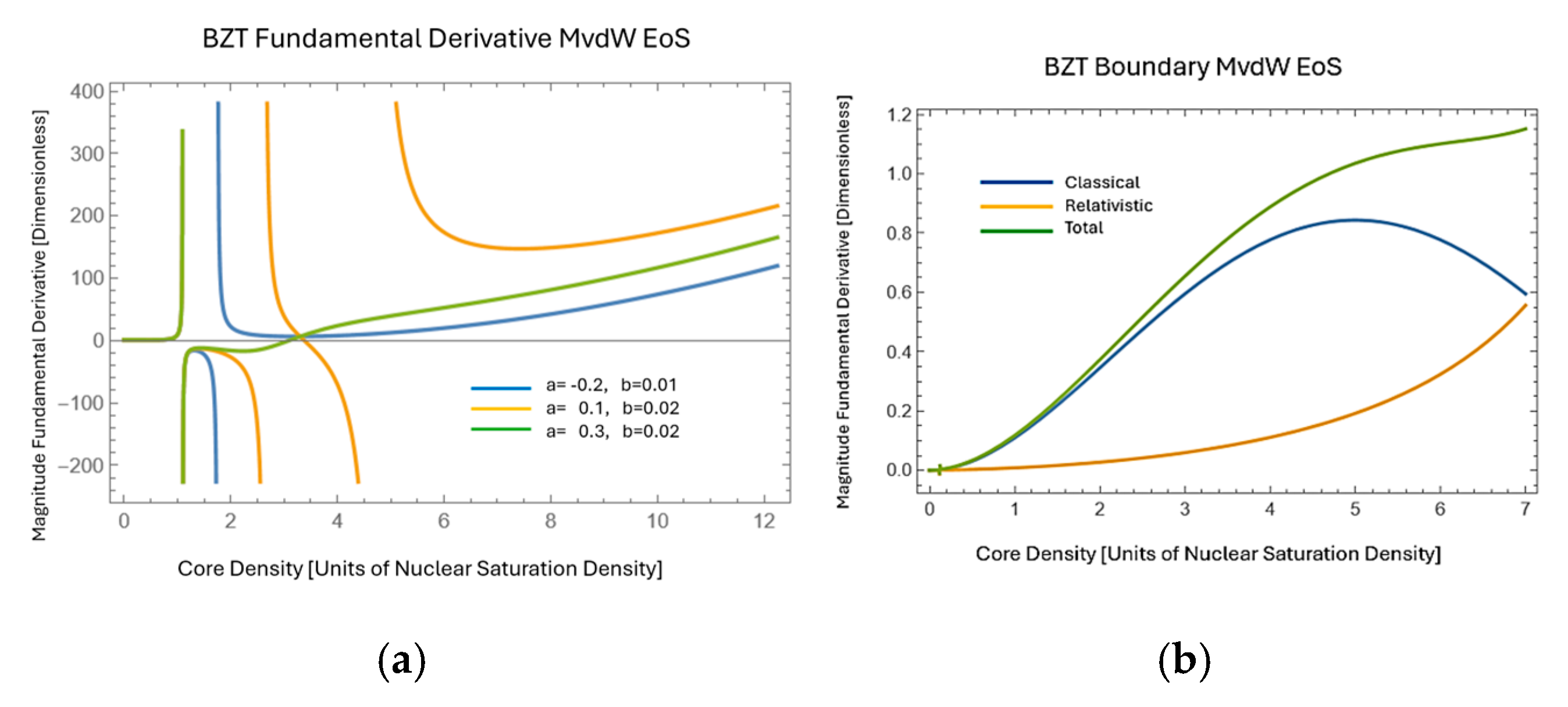
2. MvdW Partition Function and Fundamental Derivative
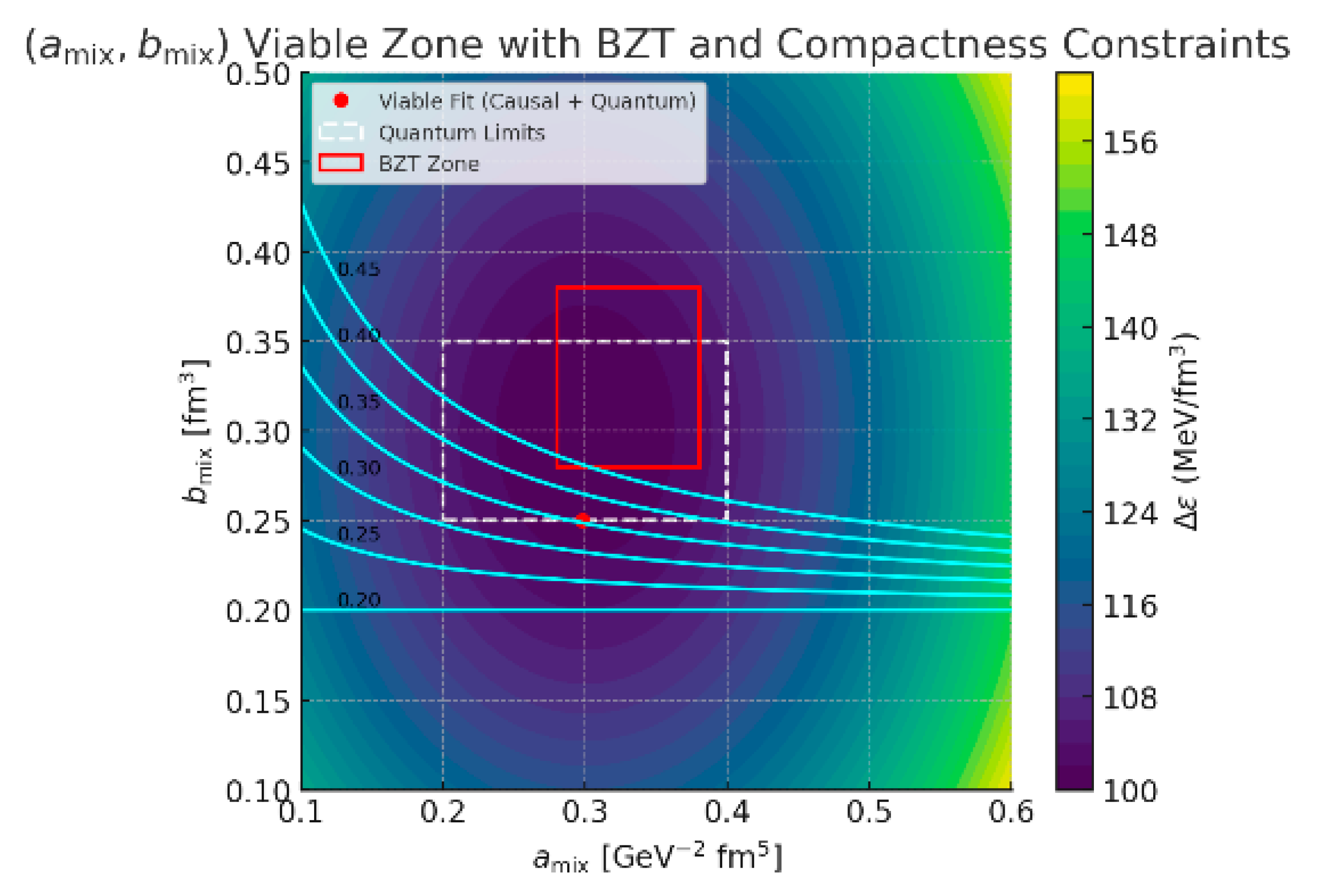
3. Peak Gravity Wave Shift Signature of BZT Shocks and Chirps
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
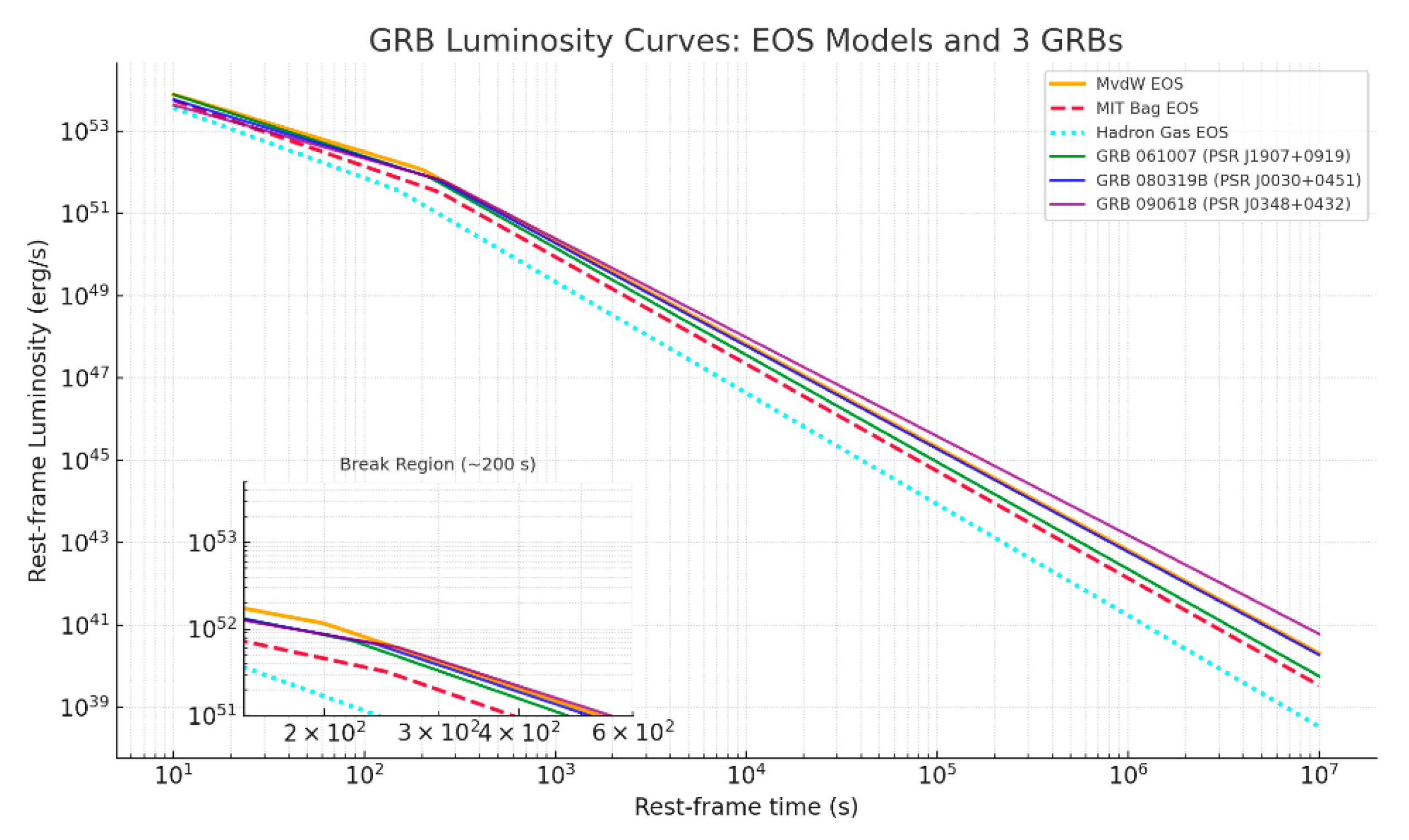
Appendix A. Models for Gamma-Ray Curves
- where the MIT bag Model with interactions has a harp phase transition and can produces strong Δε, has a simple analytic form, can produce a moderate-to-high L0, can only support a BZT region if interactions are present, the luminosity curve is symmetric and less realistic without extension, it matches mid-width GRBs like GRB 080319B.
- where the NJL model has a Δε driven by chiral symmetry restoration, naturally supports color superconducting extensions, produces long tails and plateaus in the light curve, has an L0 competitive with the MvdW model, matches GRBs with dual-phase decay (GRB 090618, GRB 080319B) see Appendix C for references.
- where the HGM matches low-temperature lattice EOS, tends to favor a transition that produces short, sharp GRBs, in general Δε is small therefore L0 is limited, so it fails to model long-duration or broad-peak GRBs, it is best for short, faint GRBs (GRB 091127); does not naturally explain long GRB luminosity tails.
- where the lattice model is based directly on a QCD first-principles EOS, stability and reproducibility are good for calibration and EOS matching, produces a small Δε and soft peak luminosity, no BZT region unless effective model interactions are added, can approximate GRB plateaus but underpredicts L0 for bright GRB events, the lattice model is most effective for events like GRB 111228.
| GRB ID | NS System | a1 (Early) | a2 (Late) |
|---|---|---|---|
| GRB 061007 | PSR J1907+0919 | 1.48 ± 0.06 | 2.42 ± 0.05 |
| GRB 080319B | PSR J0030+0451 | 1.43 ± 0.05 | 2.19 ± 0.04 |
| GRB 090618 | PSR J0348+0432 | 1.60 ± 0.07 | 2.54 ± 0.06 |
| GRB 091127 | PSR J0737–3039 | 1.79 ± 0.08 | 2.68 ± 0.07 |
| GRB 111228 | PSR J1614–2230 | 1.66 ± 0.06 | 2.41 ± 0.05 |

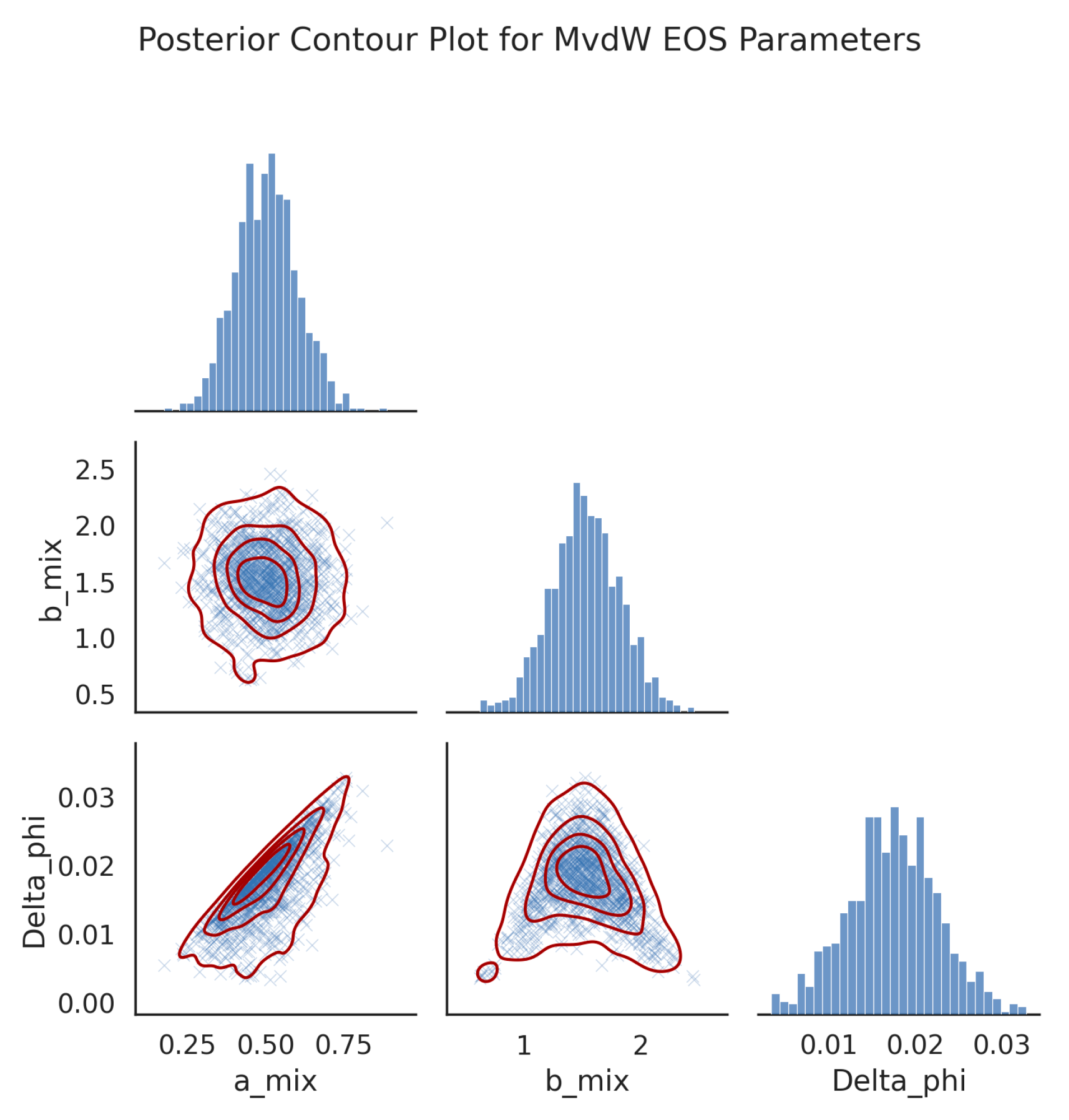
Appendix B. Bayesian Inference Corner Plot for MvdW
Appendix C. Neutron Star Sources
| Neutron Star | Reference |
|---|---|
| PSR J0030+0451 | [140] |
| PSR J0740+6620 | [141] |
| PSR J1614–2230 | [142] |
| PSR J0952–0607 | [143] |
| PSR J0348+0432 | [144] |
| PSR J2124–3358 | [145] |
| PSR J1909–3744 | [146] |
| GRB 170817A | [147] |
| GRB 190425 | [148] |
| GRB 211211A | [149] |
| GRB 230307A | [150] |
| GRB 221009A | [151] |
| GRB 150101B | [152] |
| GW 190814 | [153] |
| PSR B1642–03 | [154] |
References
- Smith, N.; Li, W.; Foley, R.J.; Wheeler, J.C.; Pooley, D.; Chornock, R.; Filippenk, A.V.; Siverman, J.M.; Quimby, R.; Bloom, J.S.; et al. SN 2006gy: Discovery of the most luminous supernova ever recorded, powered by the death of an extremely massive star like η Carinae. Astrophys. J. 2007, 666, 1116. [Google Scholar] [CrossRef]
- Xu, R. Strange quark stars: Observations and speculations. J. Phys. G Nucl. Part. Phys. 2009, 36, 064010. [Google Scholar] [CrossRef][Green Version]
- Burwitz, V.; Haberl, F.; Neuhäuser, R.; Predehl, P.; Trümper, J.; Zavlin, V.E. The thermal radiation of the isolated neutron star RX J1856. 5–3754 observed with Chandra and XMM-Newton. Astron. Astrophys. 2003, 399, 1109–1114. [Google Scholar] [CrossRef]
- Burwitz, V.; Zavlin, V.E.; Neuhäuser, R.; Predehl, P.; Trümper, J.; Brinkman, A.C. The Chandra LETGS high resolution X-ray spectrum of the isolated neutron star RX J1856. 5-3754. Astron. Astrophys. 2001, 379, L35–L38. [Google Scholar] [CrossRef]
- Xu, R.X.; Qiao, G.J.; Zhang, B. PSR 0943 + 10: A bare strange star? Astrophys. J. Lett. 1999, 522, L109. [Google Scholar] [CrossRef]
- Lyne, A.; Hobbs, G.; Kramer, M.; Stairs, I.; Stappers, B. Switched magnetospheric regulation of pulsar spin-down. Science 2010, 329, 408–412. [Google Scholar] [CrossRef] [PubMed]
- Alford, M.; Braby, M.; Paris, M.; Reddy, S. Hybrid stars that masquerade as neutron stars. Astrophys. J. 2005, 629, 969. [Google Scholar] [CrossRef]
- Jin, Z.-P.; Hotokezaka, K.; Li, X.; Tanaka, M.; D’Avanzo, P.; Fan, Y.-Z.; Covino, S.; Wei, D.-M.; Piran, T. The Macronova in GRB 050709 and the GRB-macronova connection. Nat. Commun. 2016, 7, 12898. [Google Scholar] [CrossRef]
- Von, K.A.; Veres, P.; Roberts, O.J.; Hamburg, R.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Goldstein, A.; Kocevski, D.; Preece, R.D.; et al. Fermi-GBM GRBs with characteristics similar to GRB 170817A. Astrophys. J. 2019, 876, 89. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A decade of gamma-ray bursts observed by Fermi-LAT: The second GRB catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill magnetar catalog. Astrophys. J. Suppl. Ser. 2014, 212, 6. [Google Scholar] [CrossRef]
- Gavriil, F.P.; Kaspi, V.M.; Woods, P.M. A comprehensive study of the X-ray bursts from the magnetar candidate 1E 2259 + 586. Astrophys. J. 2004, 607, 959. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Vasilis, K. Oikonomou. Extended gravity description for the GW190814 supermassive neutron star. Phys. Lett. B 2020, 811, 135910. [Google Scholar]
- Liu, B.; Lai, D. Hierarchical black hole mergers in multiple systems: Constrain the formation of GW190412-, GW190814-, and GW190521-like events. Mon. Not. R. Astron. Soc. 2021, 502, 2049–2064. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Hirvonen, J.; Komoltsev, O.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Strongly interacting matter exhibits deconfined behavior in massive neutron stars. Nat. Commun. 2023, 14, 8451. [Google Scholar] [CrossRef] [PubMed]
- Heinz, U. From SPS to RHIC: Breaking the barrier to the quark-gluon plasma. In Proceedings of the AIP Conference Proceedings, Melville, NY, USA, 13 December 2001; Volume 602, pp. 281–292. [Google Scholar]
- Emerick, A.; Zhao, X.; Rapp, R. Bottomonia in the quark-gluon plasma and their production at RHIC and LHC. Eur. Phys. J. A 2012, 48, 72. [Google Scholar] [CrossRef]
- Teaney, D.; Lauret, J.; Shuryak, E.V. Flow at the SPS and RHIC as a quark-gluon plasma signature. Phys. Rev. Lett. 2001, 86, 4783. [Google Scholar] [CrossRef] [PubMed]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark–gluon plasma and color glass condensate at RHIC? The perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Florkowski, W.; Jaiswal, A.; Maksymiuk, E.; Ryblewski, R.; Strickland, M. Relativistic quantum transport coefficients for second-order viscous hydrodynamics. Phys. Rev. C 2015, 91, 054907. [Google Scholar] [CrossRef]
- Heinz, U.; Shen, C.; Song, H. The viscosity of quark-gluon plasma at RHIC and the LHC. In Proceedings of the AIP Conference Proceedings, Melville, NY, USA, 28 September 2012; Volume 1441, pp. 766–770. [Google Scholar]
- Moore, G.D.; Saremi, O. Bulk viscosity and spectral functions in QCD. J. High Energy Phys. 2008, 2008, 015. [Google Scholar] [CrossRef]
- Miller, J.M.; Fabian, A.C.; Wijnands, R.; Reynolds, C.S.; Ehle, M.; Freyberg, M.J.; Van Der Klis, M.; Lewin, W.H.G.; Sanchez-Fernandez, C.; Castro-Tirado, A.J. Evidence of Spin and Energy Extraction in a Galactic Black Hole Candidate: The XMM-Newton/EPIC-pn Spectrum of XTE J1650–500. Astrophys. J. Lett. 2002, 570, L69. [Google Scholar] [CrossRef]
- Dey, M.; Bombaci, I.; Dey, J.; Ray, S.; Samanta, B.C. Strange stars with realistic quark vector interaction and phenomenological density-dependent scalar potential. Phys. Lett. B 1998, 438, 123–128. [Google Scholar] [CrossRef]
- Dolan, L.; Jackiw, R. Symmetry behavior at finite temperature. Phys. Rev. D 1974, 9, 3320. [Google Scholar] [CrossRef]
- Ray, S.; Dey, J.; Dey, M. Density dependent strong coupling constant of QCD derived from compact star data. Mod. Phys. Lett. A 2000, 15, 1301–1306. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Okajima, T. The Neutron star Interior Composition ExploreR (NICER): An Explorer mission of opportunity for soft x-ray timing spectroscopy. In Proceedings of the Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, Amsterdam, Netherlands, 1–6 July 2012; Volume 8443, pp. 322–329. [Google Scholar]
- Vinciguerra, S.; Salmi, T.; Watts, A.L.; Choudhury, D.; Riley, T.E.; Ray, P.S.; Bogdanov, S.; Kini, Y.; Guillot, S.; Chakrabarty, D.; et al. An Updated Mass–Radius Analysis of the 2017–2018 NICER Data Set of PSR J0030 + 0451. Astrophys. J. 2024, 961, 62. [Google Scholar] [CrossRef]
- Johnson, K. The MIT bag model. Acta Phys. Pol. B 1975, 6, 8. [Google Scholar]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Wilczek, F. Color-flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef]
- Rajagopal, K.; Wilczek, F. Enforced electrical neutrality of the color-flavor locked phase. Phys. Rev. Lett. 2001, 86, 3492. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Alford, M.; Reddy, S. Compact stars with color superconducting quark matter. Phys. Rev. D 2003, 67, 074024. [Google Scholar] [CrossRef]
- Baldo, M.; Buballa, M.; Burgio, G.F.; Lawley, F.; Bentz, W.; Thomas, A.W. Neutron stars and the transition to color superconducting quark matter. Phys. Lett. B 2003, 562, 153–160. [Google Scholar] [CrossRef]
- Lawley, S.; Bentz, W.; Thomas, A.W. Nucleons, nuclear matter and quark matter: A unified NJL approach. J. Phys. G Nucl. Part. Phys. 2006, 32, 667. [Google Scholar] [CrossRef]
- Baym, G.; Chin, S.A. Can a neutron star be a giant MIT bag? Phys. Lett. B 1976, 62, 241–244. [Google Scholar] [CrossRef]
- Källman, C.-G. Mean-field QCD model for hot/dense matter. Phys. Lett. B 1984, 134, 363–367. [Google Scholar] [CrossRef]
- Adler, S.L. Generalized bag models as mean-field approximations to QCD. Phys. Lett. B 1982, 110, 302–306. [Google Scholar] [CrossRef]
- McLerran, L.; Reddy, S. Quarkyonic matter and neutron stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef]
- Zhao, T.; Lattimer, J.M. Quarkyonic matter equation of state in beta-equilibrium. Phys. Rev. D 2020, 102, 023021. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S.D. A new method to study lattice QCD at finite temperature and chemical potential. Phys. Lett. B 2002, 534, 87–92. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Weber, F. Nuclear solid crust on rotating strange quark stars. Astrophys. J. 1992, 400., 1–15. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum elastic deformations of compact stars with exotic equations of state. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef]
- Sharma, R.; Mukherjee, S. Compact stars: A core-envelope model. Mod. Phys. Lett. A 2002, 17, 2535–2544. [Google Scholar] [CrossRef]
- Ng, C.Y.; Cheng, K.S.; Chu, M.C. Cooling properties of Cloudy Bag strange stars. Astropart. Phys. 2003, 19, 171–192. [Google Scholar] [CrossRef]
- Latifah, S.; Sulaksono, A.; Mart, T. Bosons star at finite temperature. Phys. Rev. D 2014, 90, 127501. [Google Scholar] [CrossRef]
- Andrew, K.; Andrew, K.; Brown, R.; Thornberry, B.; Harper, S.; Steinfelds, E.; Roberts, T. A QCD Model of the Chemical Potential Kaon Boundary Formation for a Compact Quark Star. Bull. Am. Phys. Soc. 2016, 61, 241. [Google Scholar]
- Thorsson, V.; Prakash, M.; Lattimer, J.M. Composition, structure and evolution of neutron stars with kaon condensates. Nucl. Phys. A 1994, 572, 693–731. [Google Scholar] [CrossRef]
- Alford, M. Color-superconducting quark matter. Annu. Rev. Nucl. Part. Sci. 2001, 51, 131–160. [Google Scholar] [CrossRef]
- Andrew, K.; Steinfelds, E.; Andrew, K. QCD Color Vector Potential Effects on Color Flavor Locked Quark Stellar Cores. Bull. Am. Phys. Soc. 2018, 63, 185. [Google Scholar]
- Alford, M.; Bowers, J.A.; Rajagopal, K. Crystalline color superconductivity. Phys. Rev. D 2001, 63, 074016. [Google Scholar] [CrossRef]
- Casalbuoni, R.; Gatto, R.; Mannarelli, M.; Nardulli, G. Effective field theory for the crystalline colour superconductive phase of QCD. Phys. Lett. B 2001, 511, 218–228. [Google Scholar] [CrossRef]
- Andrew, K.; Brown, R.; Andrew, K.; Thornberry, B.; Harper, S.; Steinfelds, E.; Roberts, T. Analysis of Mass and Radius Sensitivity of a Crystalline Quark Star to a Strong Repulsive Equation of State. Bull. Am. Phys. Soc. 2016, 61, 244. [Google Scholar]
- Berbel, P.M. On Nonconvex Special Relativistic Hydrodynamics. Ph.D. Thesis, Universatat Autonoma de Barcelona, Barcelona, Spain, 2023. [Google Scholar]
- Marquina, A.; Serna, S.; Ibanez, J.M. Capturing composite waves in non-convex special relativistic hydrodynamics. J. Sci. Comput. 2019, 81, 2132–2161. [Google Scholar] [CrossRef]
- Duez, M.D.; Liu, Y.T.; Shapiro, S.L.; Stephens, B.C. General relativistic hydrodynamics with viscosity: Contraction, catastrophic collapse, and disk formation in hypermassive neutron stars. Phys. Rev. D 2004, 69, 104030. [Google Scholar] [CrossRef]
- See, N. Technical Information Service Document No. PB 032189 H. A. Bethe, the Theory of Shock Waves for an Arbitrary Equation of State; Office of Scientific Research and Development Paper No. 545; National Technical Information Service: Springfield, VA, USA, 1942. [Google Scholar]
- Zel’dovich, Y.B. Theory of Shock Waves and Introduction to Gas Dynamics; Izdatel’stvo Akademii Nauk SSSR: Moscow, Russia, 1946. [Google Scholar]
- Thompson, P.A. A fundamental derivative in gasdynamics. Phys. Fluids 1971, 14, 1843. [Google Scholar] [CrossRef]
- Aloy, M.A.; Ibáñez, J.M.; Sanchis-Gual, N.; Obergaulinger, M.; Jose, A.; Susana Serna, F.; Marquina, A. Neutron star collapse and gravitational waves with a non-convex equation of state. Mon. Not. R. Astron. Soc. 2019, 484, 4980–5008. [Google Scholar] [CrossRef]
- Rivieccio, G.; Guerra, D.; Ruiz, M.; Font, J.A. Gravitational-wave imprints of nonconvex dynamics in binary neutron star mergers. Phys. Rev. D 2024, 109, 064032. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Stoecker, H.; Rezzolla, L. On the deconfinement phase transition in neutron-star mergers. Eur. Phys. J. A 2020, 56, 59. [Google Scholar] [CrossRef]
- Sarkar, N.; Ghosh, P. van der Waals hadron resonance gas and QCD phase diagram. Phys. Rev. C 2018, 98, 014907. [Google Scholar] [CrossRef]
- Vovchenko, V.; Gorenstein, M.I.; Stoecker, H. van der Waals interactions in hadron resonance gas: From nuclear matter to lattice QCD. Phys. Rev. Lett. 2017, 118, 182301. [Google Scholar] [CrossRef]
- Rodrigues, E.H.; Dutra, M.; Lourenço, O. Recent astrophysical observations reproduced by a short-range correlated van der Waals-type model? Mon. Not. R. Astron. Soc. 2023, 523, 4859–4868. [Google Scholar] [CrossRef]
- Andrew, K.; Steinfelds, E.V.; Andrew, K.A. The van der Waals Hexaquark Chemical Potential in Dense Stellar Matter. Particles 2023, 6, 556–567. [Google Scholar] [CrossRef]
- Poberezhnyuk, R.V.; Stoecker, H.; Vovchenko, V. Quarkyonic matter with quantum van der Waals theory. Phys. Rev. C 2023, 108, 045202. [Google Scholar] [CrossRef]
- Thirukkanesh, S.; Ragel, F.C. Anisotropic compact sphere with Van der Waals equation of state. Astrophys. Space Sci. 2014, 354, 415–420. [Google Scholar] [CrossRef]
- Vovchenko, V.; Motornenko, A.; Alba, P.; Gorenstein, M.I.; Satarov, L.M.; Stoecker, H. Multicomponent van der Waals equation of state: Applications in nuclear and hadronic physics. Phys. Rev. C 2017, 96, 045202. [Google Scholar] [CrossRef]
- Mardan, S.A.; Khalid, A.; Manzoor, R.; Riaz, M.B. Anisotropic model observing pulsars from Neutron Star Interior Composition with modified Van der Waals equation of state. Eur. Phys. J. C 2024, 84, 1018. [Google Scholar] [CrossRef]
- Lourenço, O.; Dutra, M.; Lenzi, C.H.; Bhuyan, M.; Biswal, S.K.; Santos, B.M. A density-dependent van der waals model under the gw170817 constraint. Astrophys. J. 2019, 882, 67. [Google Scholar] [CrossRef]
- Dutra, M.; Santos, B.M.; Lourenço, O. Constraints and correlations of nuclear matter parameters from a density-dependent van der Waals model. J. Phys. G Nucl. Part. Phys. 2020, 47, 035101. [Google Scholar] [CrossRef]
- Malaver, M.; Kasmaei, H.D. Analytical models for quark stars with van der Waals modified equation of state. Int. J. Astrophys. Space Sci. 2019, 7, 58. [Google Scholar] [CrossRef]
- Errehymy, A.; Mustafa, G.; Khedif, Y.; Daoud, M.; Alrebdi, H.I.; Abdel-Aty, A.-H. Self-gravitating anisotropic model in general relativity under modified Van der Waals equation of state: A stable configuration. Eur. Phys. J. C 2022, 82, 1–11. [Google Scholar] [CrossRef]
- Poberezhnyuk, R.V.; Vovchenko, V.; Gorenstein, M.I.; Stoecker, H. Noncongruent phase transitions in strongly interacting matter within the quantum van der Waals model. Phys. Rev. C 2019, 99, 024907. [Google Scholar] [CrossRef]
- Moss, T.; Poberezhniuk, R.; Vovchenko, V. Quantum van der Waals quarkyonic matter at non-zero isospin asymmetry. arXiv 2024, arXiv:2411.11996. [Google Scholar] [CrossRef]
- Guardone, A.; Vigevano, L. Roe linearization for the van der Waals gas. J. Comput. Phys. 2002, 175, 50–78. [Google Scholar] [CrossRef]
- Ibáñez, J.-M.; Cordero-Carrión, I.; Aloy, M.-Á.; Martí, J.-M.; Miralles, J.-A. On the convexity of relativistic ideal magnetohydrodynamics. Class. Quantum Gravity 2015, 32, 095007. [Google Scholar] [CrossRef]
- Kapusta, J.; Singh, M.; Welle, T. Spinodal decomposition in Bjorken flow. arXiv 2024, arXiv:2409.16525. [Google Scholar] [CrossRef]
- Vovchenko, V.; Anchishkin, D.V.; Gorenstein, M.I. Van der Waals equation of state with Fermi statistics for nuclear matter. Phys. Rev. C 2015, 91, 064314. [Google Scholar] [CrossRef]
- Keffer, D. The Statistical Mechanical Derivation of the Van Der Waals Equation of State for a Multicomponent Fluid and Its Associated Thermodynamic Properties. Available online: http://www.utkstair.org/clausius/docs/che330/pdf/vdw_statmech_multicomponent.pdf (accessed on 4 March 2023).
- Stryjek, R.; Vera, J.H. PRSV: An improved Peng—Robinson equation of state for pure compounds and mixtures. Can. J. Chem. Eng. 1986, 64, 323–333. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Blaschke, D.; Typel, S.; Farrar, G.R.; Alvarez-Castillo, D.E. Sexaquark dilemma in neutron stars and its solution by quark deconfinement. Phys. Rev. D 2022, 105, 103005. [Google Scholar] [CrossRef]
- CompOSE Core Team; Typel, S.; Oertel, M.; Klähn, T.; Chatterjee, D.; Dexheimer, V.; Ishizuka, C.; Manchini, M.; Novak, J.; Paos, H.; et al. CompOSE reference manual: Version 3.01, CompStar Online Supernovæ Equations of State, “harmonising the concert of nuclear physics and astrophysics”. Eur. Phys. J. A 2022, 58, 221. [Google Scholar]
- Zeng, J. Non-Classical Behavior of BZT Gas in Isentropic Quasi-One-Dimensional Flow. Master’s Thesis, University of California, Irvine, CA, USA, 2020. [Google Scholar]
- Colonna, P.; Nannan, N.R.; Guardone, A.; van der Stelt, T.P. On the computation of the fundamental derivative of gas dynamics using equations of state. Fluid Phase Equilibria 2009, 286, 43–54. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The ground state of matter at high densities: Equation of state and stellar models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Ghosh, S.; Pradhan, B.K.; Chatterjee, D.; Schaffner-Bielich, J. Multi-physics constraints at different densities to probe nuclear symmetry energy in hyperonic neutron stars. Front. Astron. Space Sci. 2022, 9, 864294. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Rahmansyah, A.; Purnamasari, D.; Kurniadi, R.; Sulaksono, A. Generalized Tolman-Oppenheimer-Volkoff model and neutron stars. Phys. Rev. D 2022, 106, 084042. [Google Scholar] [CrossRef]
- Smoller, J.; Temple, B. On the Oppenheimer-Volkoff Equations in General Relativity. Arch. Ration. Mech. Anal. 1998, 142, 177–191. [Google Scholar] [CrossRef][Green Version]
- Wolfram, S. The Mathematica Book; Wolfram Research, Inc.: Oxfordshire, UK, 2003. [Google Scholar]
- Abell, M.L.; Braselton, J.P. Differential Equations with Mathematica; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Relativ. Gravit. 2017, 49, 1–21. [Google Scholar] [CrossRef]
- Casali, R.H.; Menezes, D.P. Adiabatic index of hot and cold compact objects. Braz. J. Phys. 2010, 40, 166–171. [Google Scholar] [CrossRef]
- Carney, M.F.; Wade, L.E.; Irwin, B.S. Comparing two models for measuring the neutron star equation of state from gravitational-wave signals. Phys. Rev. D 2018, 98, 063004. [Google Scholar] [CrossRef]
- Hartle, J.B.; Thorne, K.S. Slowly rotating relativistic stars. II. Models for neutron stars and supermassive stars. Astrophys. J. 1968, 153, 807. [Google Scholar] [CrossRef]
- Bauböck, M.; Berti, E.; Psaltis, D.; Özel, F. Relations between neutron-star parameters in the hartle–thorne approximation. Astrophys. J. 2013, 777, 68. [Google Scholar] [CrossRef]
- Bocquet, M.; Bonazzola, S.; Gourgoulhon, E.; Novak, J. Rotating neutron star models with magnetic field. arXiv 1995, arXiv:gr-qc/9503044. [Google Scholar] [CrossRef]
- Romani, R.W. A unified model of neutron-star magnetic fields. Nature 1990, 347, 741–743. [Google Scholar] [CrossRef]
- Pretel, J.M.Z. Equilibrium, radial stability and non-adiabatic gravitational collapse of anisotropic neutron stars. Eur. Phys. J. C 2020, 80, 726. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from binary neutron stars. Arab. J. Math. 2022, 11, 105–118. [Google Scholar] [CrossRef]
- Vines, J.; Flanagan, E.E.; Hinderer, T. Post-1-Newtonian tidal effects in the gravitational waveform from binary inspirals. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2011, 83, 084051. [Google Scholar] [CrossRef]
- Fraga, E.S.; Kurkela, A.; Vuorinen, A. Interacting quark matter equation of state for compact stars. Astrophys. J. Lett. 2014, 781, L25. [Google Scholar] [CrossRef]
- Li, H.; Luo, X.-L.; Zong, H.-S. Bag model and quark star. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2010, 82, 065017. [Google Scholar] [CrossRef]
- Huovinen, P.; Petreczky, P. QCD equation of state and hadron resonance gas. Nucl. Phys. A 2010, 837, 26–53. [Google Scholar] [CrossRef]
- Kojo, T.; Powell, P.D.; Song, Y.; Baym, G. Phenomenological QCD equation of state for massive neutron stars. Phys. Rev. D 2015, 91, 045003. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Equation of state in (2 + 1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Laermann, E. The equation of state from lattice QCD. Acta Phys. Pol. Ser. B Proc. Suppl. 2010, 3, 611–620. [Google Scholar]
- Schady, P.; Baumgartner, W.H.; Beardmore, A.P. Swift Observation of GRB 090618. GCN Report 232, No. 1. 2009. Available online: http://gcn.gsfc.nasa.gov (accessed on 12 May 2024).
- Jain, T. Analytic Modelling of Gravitational-Wave Source in General Relativity and Alternative Theories of Gravity. Ph.D. Thesis, Cambridge University, Cambridge, UK, 2024. [Google Scholar]
- Martynov, D.V.; Hall, E.D.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Adams, C.; Adhikari, R.X.; Anderson, R.A.; Anderson, S.B.; Arai, K.; et al. Sensitivity of the Advanced LIGO detectors at the beginning of gravitational wave astronomy. Phys. Rev. D 2016, 93, 112004. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.; Accadia, T.; Acernese, F.; Adams, C.; Addesso, P.; et al. The characterization of Virgo data and its impact on gravitational-wave searches. Class. Quantum Gravity 2012, 29, 155002. [Google Scholar] [CrossRef]
- KAGRA Collaboration. KAGRA: 2.5 generation interferometric gravitational wave detector. Nat. Astron. 2019, 3, 35–40. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Cutler, C. Angular resolution of the LISA gravitational wave detector. Phys. Rev. D 1998, 57, 7089. [Google Scholar] [CrossRef]
- Posselt, B.; Pavlov, G.G. The cooling of the central compact object in Cas A from 2006 to 2020. Astrophys. J. 2022, 932, 83. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics: Particle data groups. Phys. Rev. D 2018, 98, 1–1898. [Google Scholar] [CrossRef]
- Vovchenko, V.; Anchishkin, D.V.; Gorenstein, M.I.; Poberezhnyuk, R.V. Scaled variance, skewness, and kurtosis near the critical point of nuclear matter. Phys. Rev. C 2015, 92, 054901. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Strottman, D. Multiquark baryons and the MIT bag model. Phys. Rev. D 1979, 20, 748. [Google Scholar] [CrossRef]
- Hess, P.O.; Viollier, R.D. Interacting many-gluon systems within the MIT bag model. Phys. Rev. D 1986, 34, 258. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Sandin, F.; Fuchs, C.; Faessler, A.; Grigorian, H.; Röpke, G.; Trümper, J. Modern compact star observations and the quark matter equation of state. Phys. Lett. B 2007, 654, 170–176. [Google Scholar] [CrossRef]
- Karsch, F.; Redlich, K.; Tawfik, A. Thermodynamics at non-zero baryon number density: A comparison of lattice and hadron resonance gas model calculations. Phys. Lett. B 2003, 571, 67–74. [Google Scholar] [CrossRef]
- Endrődi, G. QCD equation of state at nonzero magnetic fields in the Hadron Resonance Gas model. J. High Energy Phys. 2013, 2013, 23. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. QCD equation of state to O (μ B 6) from lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Kahangirwe, M.; Bass, S.A.; Bratkovskaya, E.; Jahan, J.; Moreau, P.; Parotto, P.; Price, D.; Ratti, C.; Soloveva, O.; Stephanov, M. Finite density QCD equation of state: Critical point and lattice-based T′ expansion. Phys. Rev. D 2024, 109, 094046. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.N.; Kara, R.; Katz, S.D.; Parotto, P.; Pásztor, A.; Ratti, C.; Lattice, K.K.S. QCD equation of state at finite chemical potential from an alternative expansion scheme. Phys. Rev. Lett. 2021, 126, 232001. [Google Scholar] [CrossRef] [PubMed]
- Mészáros, P.; Rees, M.J. Optical and long-wavelength afterglow from gamma-ray bursts. Astrophys. J. 1997, 476, 232. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Poynting jets from black holes and cosmological gamma-ray bursts. Astrophys. J. 1997, 482, L29. [Google Scholar] [CrossRef]
- Kulkarni, S.R.; Djorgovski, S.G.; Odewahn, S.C.; Bloom, J.S.; Gal, R.R.; Koresko, C.D.; Harrison, F.A.; Lubin, L.M.; Armus, L.; Sari, R.; et al. The afterglow, redshift and extreme energetics of the γ-ray burst of 23 January 1999. Nature 1999, 398, 389–394. [Google Scholar] [CrossRef]
- Li, L.-X. Shock breakout in Type Ibc supernovae and application to GRB 060218/SN 2006aj. Mon. Not. R. Astron. Soc. 2007, 375, 240–256. [Google Scholar] [CrossRef]
- Irwin, C.M.; Hotokezaka, K. Revisiting GRB 060218: New insights into low-luminosity gamma-ray bursts from a revised shock breakout model. arXiv 2024, arXiv:2412.06736. [Google Scholar] [CrossRef]
- Kuroda, T.; Takiwaki, T.; Kotake, K. Gravitational wave signatures from low-mode spiral instabilities in rapidly rotating supernova cores. Phys. Rev. D 2014, 89, 044011. [Google Scholar] [CrossRef]
- Ruffini, R.; Izzo, L.; Muccino, M.; Pisani, G.B.; Rueda, J.A.; Wang, Y.; Barbarino, C.; Bianco, C.L.; Enderli, M.; Kovacevic, M. Induced gravitational collapse at extreme cosmological distances: The case of GRB 090423. Astron. Astrophys. 2014, 569, A39. [Google Scholar] [CrossRef][Green Version]
- Cowsik, R.; Prabhu, T.P.; Anupama, G.C.; Bhatt, B.C.; Sahu, D.K.; Ambika, S.; Bhargavi, S.G. Optical photometry of the GRB 010222 afterglow. arXiv 2001, arXiv:astro-ph/0104363. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030 + 0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The radius of PSR J0740 + 6620 from NICER and XMM-Newton data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Zhao, X.-F.; Jia, H.-Y. Mass of the neutron star PSR J1614-2230. Phys. Rev. C—Nucl. Phys. 2012, 85, 065806. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W.K. PSR J0952− 0607: The fastest and heaviest known galactic neutron star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Zhao, X.-F. The properties of the massive neutron star PSR J0348+ 0432. Int. J. Mod. Phys. D 2015, 24, 1550058. [Google Scholar] [CrossRef]
- Zheng, S.; Han, D.; Xu, H.; Lee, K.; Yuan, J.; Wang, H.; Ge, M.; Zhang, L.; Li, Y.; Yin, Y. New Timing Results MSPs NICER Observations. Universe 2024, 10, 174. [Google Scholar] [CrossRef]
- Liu, K.; Guillemot, L.; Istrate, A.G.; Shao, L.; Tauris, T.M.; Wex, N.; Antoniadis, J.; Chalumeau, A.; Cognard, I.; Desvignes, G.; et al. A revisit of PSR J1909−3744 with 15-yr high-precision timing. Mon. Not. R. Astron. Soc. 2020, 499, 2276–2291. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R.; Wang, Y.; Aimuratov, Y.; de Almeida, U.B.; Bianco, C.L.; Chen, Y.C.; Lobato, R.V.; Maia, C.; Primorac, D.; et al. Grb 170817a-gw170817-at 2017gfo and the observations of ns-ns, ns-wd and wd-wd mergers. J. Cosmol. Astropart. Phys. 2018, 2018, 006. [Google Scholar] [CrossRef]
- Kyutoku, K.; Fujibayashi, S.; Hayashi, K.; Kawaguchi, K.; Kiuchi, K.; Shibata, M.; Tanaka, M. On the possibility of GW190425 being a black hole–neutron star binary merger. Astrophys. J. Lett. 2020, 890, L4. [Google Scholar] [CrossRef]
- Yin, Y.-H.I.; Zhang, B.-B.; Sun, H.; Yang, J.; Kang, Y.; Shao, L.; Yang, Y.-H.; Zhang, B. GRB 211211A-like events and how gravitational waves may tell their origins. Astrophys. J. Lett. 2023, 954, L17. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Z.-Q.; Zheng, T.-C.; Ren, J.; Fan, Y.-Z. A broken “α–intensity” relation caused by the evolving photosphere emission and the nature of the extraordinarily bright GRB 230307A. Astrophys. J. Lett. 2023, 953, L8. [Google Scholar] [CrossRef]
- Levan, A.J.; Lamb, G.P.; Schneider, B.; Hjorth, J.; Zafar, T.; de Ugarte Postigo, A.; Sargent, B.; Mullally, S.E.; Izzo, L.; D’aVanzo, P.; et al. The first JWST spectrum of a GRB afterglow: No bright supernova in observations of the brightest GRB of all time, GRB 221009A. Astrophys. J. Lett. 2023, 946, L28. [Google Scholar] [CrossRef]
- Ascenzi, S.; Coughlin, M.W.; Dietrich, T.; Foley, R.J.; Ramirez-Ruiz, E.; Piranomonte, S.; Mockler, B.; Murguia-Berthier, A.; Fryer, C.L.; Lloyd-Ronning, N.M. A luminosity distribution for kilonovae based on short gamma-ray burst afterglows. Mon. Not. R. Astron. Soc. 2019, 486, 672–690. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814:gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Smirnova, T.V.V.L.; Shishov, W.; Sieber, D.R.; Stinebring, V.M.; Malofeev, V.A.; Potapov, S.A.; Bashev, T.; Jessner, A.; Wielebinski, R. The interstellar turbulent plasma spectrum in the direction to PSR B1642-03 from multi-frequency observations of interstellar scintillation. Astron. Astrophys. 2006, 455, 195–201. [Google Scholar] [CrossRef][Green Version]

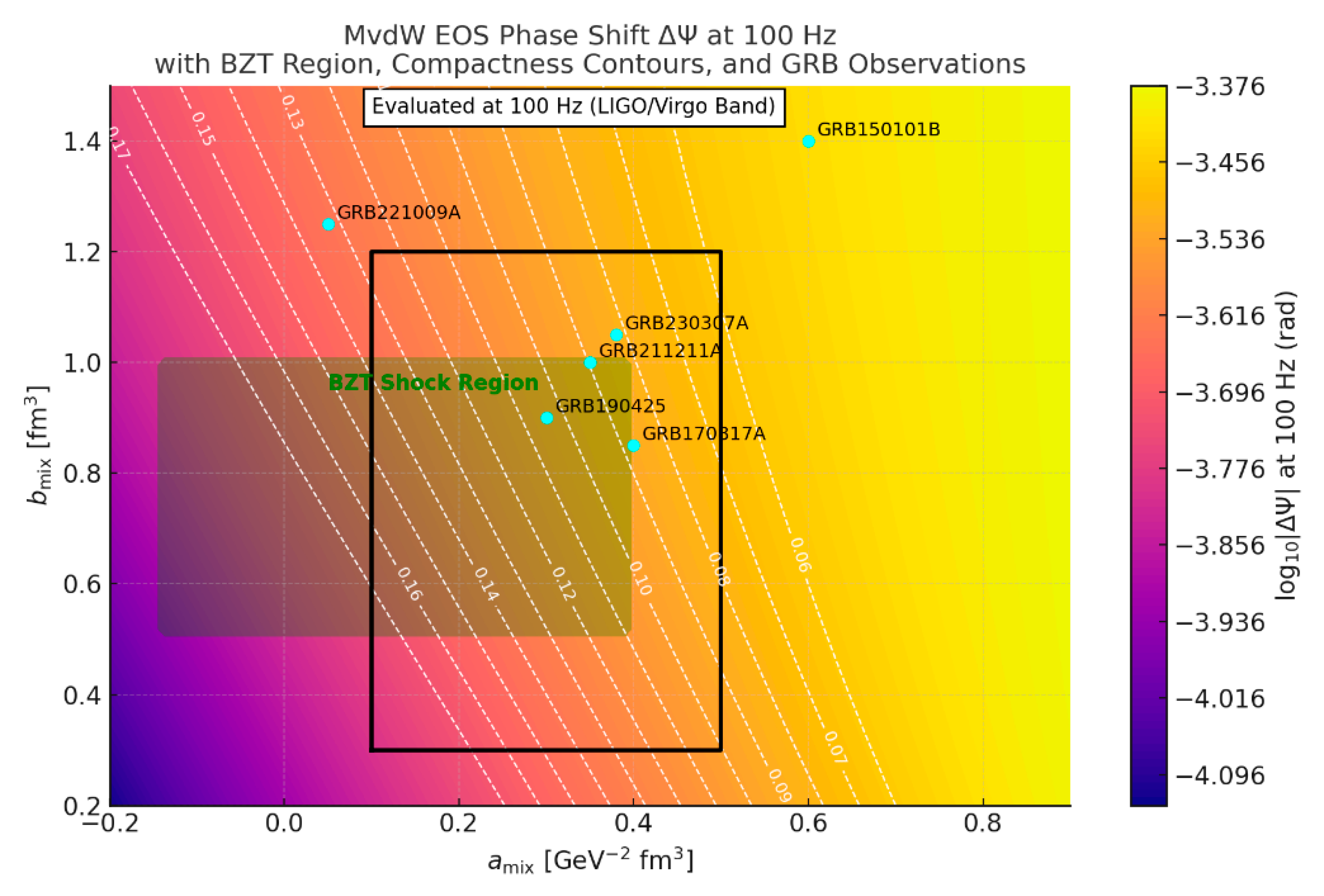

| Parameter | Neutron Stars | Quark Stars |
|---|---|---|
| Compactness (C) | 0.15–0.25 | 0.2–0.35 |
| Love Number (k2) | 0.05–0.15 | 0.01–0.05 |
| Tidal Deformability (Λ) | 200–1000 | 10–100 |
| Chirp Mass (M in solar masses) | 1.18–1.20 | 0.96–1.15 |
| Merger Tidal Deformability () | 70–720 | 10–100 |
| Detector | Frequency Range (Hz) | Sensitivity (Strain) | SNR Threshold | Application | Phase Shift Sensitivity | |
|---|---|---|---|---|---|---|
| 1 | LIGO | 10–1000 | ~10−23 | ~8 | Binary mergers, neutron stars, black holes | 10−2 |
| 2 | Virgo | 10–1000 | ~10−23 | ~8 | Binary mergers, neutron stars, black holes | 10−2 |
| 3 | LISA | 0.01–1 | ~10−21 | ~1 | Supermassive black holes, early universe | 10−5 |
| 4 | Einstein Telescope | 1–1000 | ~10−24 | ~5 | Binary mergers, cosmological signals | 10−4 |
| 5 | KAGRA | 10–1000 | ~10−23 | ~8 | Binary mergers, neutron stars, black holes | 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrew, K.; Steinfelds, E.V.; Andrew, K.A. Gravity Wave Phase Shift in a Cold Quark Star with a Nonconvex QCD BZT Shock Wave Van Der Waals Equation of State. Astronomy 2025, 4, 14. https://doi.org/10.3390/astronomy4030014
Andrew K, Steinfelds EV, Andrew KA. Gravity Wave Phase Shift in a Cold Quark Star with a Nonconvex QCD BZT Shock Wave Van Der Waals Equation of State. Astronomy. 2025; 4(3):14. https://doi.org/10.3390/astronomy4030014
Chicago/Turabian StyleAndrew, Keith, Eric V. Steinfelds, and Kristopher A. Andrew. 2025. "Gravity Wave Phase Shift in a Cold Quark Star with a Nonconvex QCD BZT Shock Wave Van Der Waals Equation of State" Astronomy 4, no. 3: 14. https://doi.org/10.3390/astronomy4030014
APA StyleAndrew, K., Steinfelds, E. V., & Andrew, K. A. (2025). Gravity Wave Phase Shift in a Cold Quark Star with a Nonconvex QCD BZT Shock Wave Van Der Waals Equation of State. Astronomy, 4(3), 14. https://doi.org/10.3390/astronomy4030014






