Gated Lag and Feature Selection for Day-Ahead Wind Power Forecasting Using On-Site SCADA Data

Abstract

Day-ahead wind power forecasting is often limited to on-site Supervisory Control and Data Acquisition (SCADA) datasets without Numerical Weather Prediction (NWP) information. In this regime, practitioners extend autoregressive windows over many variables, so the input size grows with both features and lags. Many lag–feature pairs are redundant, increasing the training time and overfitting risk. A lightweight, differentiable joint gate over the lag–feature plane trained with a temperature-annealed sigmoid is proposed. Sparsity is induced by capped penalties that (i) bound the total open mass to the top-M features and (ii), within each selected feature, bound the mass to the top-k lags. An additional budget-aware off-state term pushes unused logits negative in proportion to the excess density over the $(M\times k)$ budget. A lightweight, per-feature softmax pooling head supplies the forecasting loss during selection. After training, the learned probabilities are converted into compact, non-contiguous lag–feature subsets (top-M features; per-feature top-k lags) and reused by downstream predictors. Tests on the Offshore Renewable Energy (ORE) Catapult Platform for Operational Data (POD) from the Levenmouth Demonstration Turbine (LDT) dataset show that the joint gate reduces the input dimensionality and training time while improving accuracy and stability relative to Pearson’s correlation, mutual information, and cross-correlation function selectors.

1. Introduction

Reliable 24 h wind power forecasts are indispensable for electricity market participation, reserve allocation, and maintenance scheduling. Operational data are typically decomposed into time–frequency sub-bands using discrete wavelet transform (DWT), empirical mode decomposition (EMD) (and variations: ensemble EMD (EEMD), complete ensemble EMD with adaptive noise (CEEMDAN)), and variational mode decomposition (VMD) methodologies. These decompositions are appended in long autoregressive windows, often 24 to 96 steps for training machine learning or deep learning predictors [1,2,3,4].

Most wind farms lack access to high-resolution Numerical Weather Prediction (NWP) data and rely solely on Supervisory Control and Data Acquisition (SCADA) streams such as active power, wind speed, and direction, sampled every 10–60 min, making decomposition-based techniques unreliable, since no future information can be extracted in practice. To improve forecasts without NWP data, operators extend the autoregressive history to cover many hours. This produces large lagged input tensors and raises a key question: which lags and features are truly informative?

The literature approaches this problem in several ways. One strand fixes the variable set and optimizes history length via rolling-origin cross-validation, partial autocorrelation function (PACF) cut-offs, false nearest-neighbor rules, or simple frequency-based heuristics [5,6,7,8]. Another strand fixes the history window and prunes features using information-theoretic scores, sequential causal tests, or meta-heuristics to discard redundant channels [9,10,11,12]. Only a few recent models have jointly optimized the lags and features, using neural masks embedded into effective temporal-lag networks (ETLN) [13], a Temporal Fusion Transformer (TFT) [14], and others. These recent approaches show that aggressive joint pruning is technically feasible, yet none has been subjected to a broad algorithmic comparison that quantifies both the predictive accuracy and computational cost across multiple decomposition depths.

In short, the existing pipelines partially deal with the lag and feature expansion but still rely on manual heuristics, predictor-specific tricks, or sequential filters that add computational time. In addition, within the scope of wind power forecasting, it is rare to find research dedicated to feature and lag selection; most commonly, features are chosen via Pearson’s correlation, and lags are not discussed.

The present study introduces a unified pipeline that stacks SCADA windows into a three-dimensional array and performs joint lag–feature selection with a single differentiable mask, removing manual lag tuning and feature pruning. In practice, sequential or separate pruning (e.g., choosing a lag set first and then applying it to all features, or selecting features independently of the lag) imposes a uniform structure: the same lags are kept for every feature, or the same features are retained across all lags. This inevitably retains many irrelevant combinations. For instance, long lags in wind direction may be retained solely because long lags in wind speed are important. Informativeness is pair-specific rather than uniform: some sensors matter only at short horizons, while others only at mid- or long horizons. This way, independent or uniform pruning cannot capture this heterogeneity and often bloats the input with redundant terms.

To create the differentiable mask, a lightweight model is trained with a joint Concrete-like (sigmoid) gate over all lag–feature pairs, scoring each lag–feature pair $(\mathcal{l},f)$, allowing the model to keep only the combinations that truly carry predictive signals. The gate is annealed by a temperature schedule and regularized by cap penalties that bound the mass to the top-M features and, within each feature, to the top-k lags, plus a small off-state term that pushes unused logits negative. After training, the gate probabilities are converted into compact lag–feature subsets and reused to train downstream forecasts.

Joint optimization is theoretically superior to sequential or separate pruning because temporal relevance is not uniform across features or lags. Independent feature selection assumes that every chosen variable is informative at all time offsets, while independent lag selection assumes that the same history length is optimal for all sensors. In practice, many lag–feature interactions are localized: for example, long lags in wind speed may be informative, while long lags in wind direction are not. Sequential pruning cannot represent these cross-dependencies because each stage conditions on partially filtered information, often retaining redundant or irrelevant combinations. A joint optimization learns the importance of each lag–feature pair $(\mathcal{l},f)$ directly under the forecasting loss, capturing these interactions in a single differentiable step and resulting in a more compact and optimal subset of inputs.

The primary objectives of this study are to

(i)

Develop a single, differentiable mechanism for joint lag–feature selection on SCADA-only data using a temperature-annealed sigmoid gate with budgeted cap penalties;

(ii)

Reduce the input dimensionality by ≥96% for the evaluated dataset (top-M features; per-feature top-k non-contiguous lags) while preserving or improving 24 h forecast accuracy versus Pearson’s, mutual information, and cross-correlation and a persistence baseline.

(iii)

Lower the training time and memory by pruning redundant lag–feature pairs before training downstream predictors, reporting feasible wall-clock comparisons under the available hardware;

(iv)

Produce an interpretable, reusable mask that yields a compact design matrix for multiple deep backbones under identical splits and training protocols;

(v)

Introduce an adaptive pruning mechanism that automatically adjusts the number of retained features and lags based on the validation performance, making the method invariant to dataset size and avoiding collapse to zero inputs;

(vi)

Benchmark the selected subsets across a diverse set of deep-learning architectures to assess robustness to model choice.

A secondary set of objectives is to

(a)

Quantify the impact of decay-aware regularization on non-contiguous lag selection and on mid- to late horizon errors;

(b)

Analyze the bias and stepwise 24 h error profiles to assess the stability of the selected subsets;

(c)

Provide a practical capacity-normalization procedure from SCADA when nameplate rating is ambiguous, to ensure consistent error normalization.

2. Related Work

Dimensionality reduction in the time series forecasting domain has followed four main directions: lag length optimization, feature pruning, joint pruning of lag–feature pairs, and representation learning that avoids explicit lag enumeration. Most existing methods prioritize either accuracy or efficiency, but few provide an end-to-end solution that jointly selects lags and features while offering an interpretable and quantified computational cost. This work addresses that gap in the context of 24 h wind power forecasting.

From the lag optimization perspective, common strategies are to keep a fixed feature set and optimize the length of the autoregressive window. Neural hierarchical interpolation for time series (NHITS) and other hybrid models use cross-validation, PACF, false nearest neighbors, or frequency heuristics to search over long horizons [6]. More aggressive compression occurs via autocorrelation function peaks, mutual information, and ReliefF-based subset selection [15], yet all these approaches retain the full feature set. While globally fixed windows can simplify modeling, they often miss the scale-aligned temporal structure and introduce irrelevant lags for individual features.

Conversely, many approaches fix the lag window and prune features via relevance scores or causal tests. Maximal information coefficient driven filters [4], meta-heuristics [9], correlation shifts [2], and statistical filters like Granger or capped-${\mathcal{l}}_1$ shrinkage [11,12] remove redundant channels while keeping all time steps intact. Gate-based pruning has been explored in stochastic gates [16] and GateNet variants [17], but most operate on static tabular data and do not perform joint filtering. These approaches still feed all time steps within the window to the model, regardless of their temporal relevance.

Recent architectures have also explored joint pruning of the lags and features, by learning masks that downweight the time steps and channels simultaneously. Approaches include dual-tower attention networks that assign a softmax weight pair to each sample, allowing either the temporal branch or the feature branch to be downweighted [18]. Also, the ETLN embed causal and lag gates within each block [13]. The TFT performs per-step variable selection via interpretable attention [14], while dynamic sparse networks rewire one-dimensional kernels during training [19]. Lag–feature pruning has also been achieved with gated convolutional neural networks (CNNs), opposition-based whale optimization, and multivariate EMD-filtered signals [20,21]. A closely related gate mechanism, feature-selection gate with gradient routing (FSG-GR), attaches a sigmoid gate to every CNN and Transformer channel and performs a second optimizer pass that prunes weak channels, achieving a near-lossless dimensionality reduction on single frames but lacking temporal modeling or statistical filtering [22].

From the perspective of representation learning and topology-based alternatives that bypass explicit lag enumeration altogether, network topology evolution synchronization embeds each channel into a distance threshold graph and tracks the nonlinear coupling through edge density growth, though it relies on a single fixed embedding [23]. Ordinal-pattern probability maps are used to compress series into 720 descriptors, which are then reduced to two statistics via a small artificial neural network (ANN) [24]. A five-layer CNN trained on synthetic shift labels implicitly discovers informative offsets without enumerating lags [25]. Comprehensive surveys of ANN lag tuning summarize meta-heuristics such as particle swarm optimization, skeletonization, and optimal-brain-damage pruning but introduce no new algorithms [26]. These methods eliminate explicit lag enumeration but typically reduce interpretability and require larger datasets.

Several recent studies have proposed learnable masking mechanisms to select relevant inputs in structured or temporal data. Sampling-based selectors such as Learning to Explain (L2X) [27] and instance-wise variable selection [28] estimate discrete input masks using reinforcement learning or Gumbel-softmax reparameterization. These methods are typically optimized with gradient-based techniques and generate sample-wise importance scores. In contrast, the proposed method uses fully differentiable global masks that are learned via backpropagation and remain constant across samples, making them more stable and computationally efficient.

Other work uses continuous sparsification strategies via Concrete or Hard-Concrete gates, notably in the L0 regularization framework of Louizos et al. [29] and Maddison et al. [30]. These methods inspire our feature and lag gate design, which extend their application to time series by applying learned masks over temporal and feature axes, enabling sparse, continuous selection of relevant inputs during training.

Compared to recurrent attention models such as the TFT [14], which dynamically attends to input features per time step, our model uses static, interpretable gates that reduce model complexity and training variance. Unlike transformer-based lag scorers (e.g., PatchTST [31]) or multilayer perceptron lag importance models, the focus is to learn a global mask over lags and features, trained with sparsity regularization and annealed temperatures. This preserves interpretation (separate $P_L$ and $P_F$ vectors) and allows for independent sparsity control along both the lag and feature axes, with constrained compute and memory.

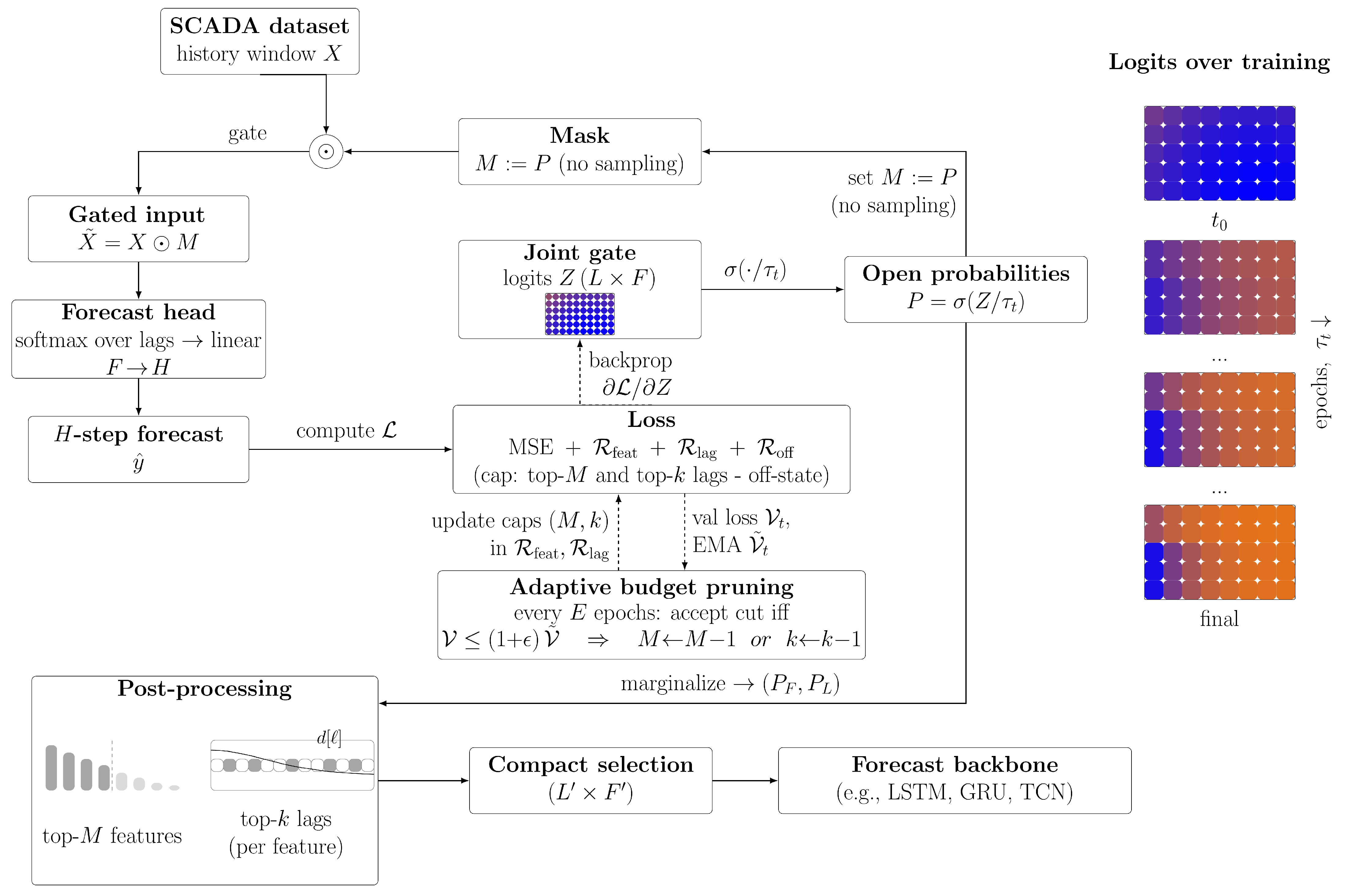
3. Methodology

The gating mechanism selectively filters informative temporal lags and features from the multivariate time series using a single joint gate $M\in {[0,1]}^{L\times F}$ applied to the input window $X\in {\mathbb{R}}^{N\times L\times F}$. The gate is a Concrete-like (sigmoid) relaxation with the annealed temperature $\tau$: for logits $Z\in {\mathbb{R}}^{L\times F}$, $P=\sigma (Z/{\tau }_t)\in {(0,1)}^{L\times F}$, $M:=P$, and standard backpropagation is used for training. Sparsity is driven by threshold penalties that keep most of the mass in the top-M features and, per feature, in the top-k lags, plus a light off-state penalty that pushes unused logits negative. A compact per-feature lag-pooling head provides the forecasting loss to learn the mask.

For context, Figure 1 summarizes the proposed pipeline. Right: A vertical overview showing logit evolution (four steps). Forward: $X\to Z\stackrel{\sigma (·/{\tau }_t)}{\to }P$, set $M:=P$ (deterministic), gate X to $\tilde{X}=X\odot M$, and then the head (softmax over lags, then linear $F\to H$) to $\widehat{y}$. Loss $\mathcal{L}=\mathrm{mean}\mathrm{squared}\mathrm{error}\left(\mathrm{MSE}\right)+{\mathcal{R}}_{\mathrm{feat}}+{\mathcal{R}}_{\mathrm{lag}}+{\mathcal{R}}_{\mathrm{off}}$. Threshold penalties enforce the top-M features and, within each, the top-k lags; ${\mathcal{R}}_{\mathrm{off}}$ pushes unused logits negative. Every E epochs, an adaptive pruning loop uses the validation loss ($\mathcal{V}$ vs. $\tilde{\mathcal{V}}$) to decrement M or k only if $\mathcal{V}\le (1+ϵ)\tilde{\mathcal{V}}$. Post-processing: choose the top-M features with $P_F$; for each, keep the top-k lags with $P_L$ (non-contiguous) to form $(L^{\prime }\times F^{\prime })$ for downstream models.

The joint mask is trained, and the best lags and features are then selected by collapsing the $L\times F$ matrix to obtain per-feature and per-lag profiles. The learned mask is post-processed to keep the top features and lags.

An overview of the gated architecture is shown in Algorithm 1, where $X\in {\mathbb{R}}^{L\times F}$ represents a multivariate time series window of length L with F features. The gate is trained in the forward step by enforcing a lag and feature minimization penalty.

Algorithm 1 Gated time series forecasting model (Concrete-like joint gate)

Require:  $X\in {\mathbb{R}}^{N\times L\times F}$, logits $Z\in {\mathbb{R}}^{L\times F}$, temperature schedule ${\tau }_t$   1: M: joint sigmoid gate $P=\sigma (Z/\tau )$, $M:=P$   2: H: forecast head (per-feature softmax pooling over lags + linear map to H steps)   3: function Forward(X)   4:    $M\leftarrow \sigma (Z/\tau )$   5:    $\tilde{X}\leftarrow X\odot M$   6:    return $H\left(\tilde{X}\right)$   7: end function   8: function Train_Step($X,y$)   9      $\widehat{y}\leftarrow \mathrm{Forward}\left(X\right)$  10:    build $P=\sigma (Z/\tau )$, $P_{\mathcal{l}f}^{\left(d\right)}=P_{\mathcal{l}f}d\left[\mathcal{l}\right]$  11:    compute ${\mathcal{R}}_{\mathrm{feat}},{\mathcal{R}}_{\mathrm{lag}},{\mathcal{R}}_{\mathrm{off}}$ (cap penalties)  12:    $\mathcal{L}\leftarrow \mathrm{MSE}(\widehat{y},y)+{\mathcal{R}}_{\mathrm{feat}}+{\mathcal{R}}_{\mathrm{lag}}+{\mathcal{R}}_{\mathrm{off}}$  13:    update parameters; anneal $\tau \leftarrow {\tau }_t$  14: end function

3.1. Joint Lag and Feature Gating

Joint lag–feature gating uses a single learnable mask $M\in {[0,1]}^{L\times F}$ applied to the input window $X\in {\mathbb{R}}^{N\times L\times F}$. Each entry $M_{\mathcal{l}f}$ controls how much of feature f at lag ℓ is retained. The mask is produced by a Concrete-like sigmoid gate parameterized by trainable logits $Z\in {\mathbb{R}}^{L\times F}$ with the temperature $\tau$. During training, $M=P=\sigma (Z/\tau )$ is set and learned via backpropagation.

The forward pass gates the input and aggregates across the lag axis with a lightweight attention head (softmax-weighted mean):

$$\begin{array}{cc}\hfill \tilde{X}& =X\odot M,\hfill \end{array}$$

(1)

$$s_{\mathcal{l}f}={\alpha }_f{\tilde{X}}_{\mathcal{l}f},\alpha \in {\mathbb{R}}^F\mathrm{trainable},$$

(2)

$$w_{\mathcal{l}f}={\displaystyle \frac{exp\left(s_{\mathcal{l}f}\right)}{{\sum }_{j=1}^{L}exp\left(s_{jf}\right)}},$$

(3)

$$c_f=\sum _{\mathcal{l}=1}^L{w}_{\mathcal{l}f}{\tilde{X}}_{\mathcal{l}f},c\in {\mathbb{R}}^{B\times F},$$

(4)

$$\widehat{y}=W_{\mathrm{out}}c\in {\mathbb{R}}^{B\times H}.$$

(5)

where ⊙ denotes elementwise multiplication, the softmax in (3) is taken along the lag axis so that ${\sum }_{\mathcal{l}=1}^L{w}_{\mathcal{l}f}=1$ for each feature f, and $W_{\mathrm{out}}$ is a linear map from F to H.

The pooling weights are sample-dependent because $s_{\mathcal{l}f}={\alpha }_f{\tilde{X}}_{\mathcal{l}f}$ enters a softmax along the lag axis, where ${\alpha }_f$ is a single scalar per feature with no cross-feature coupling.

Regularization (Decay-Aware Threshold + Budget-Aware Off-State)

The regularization terms in Equation (6) act directly on the gate probabilities, $P=\sigma (Z/\tau )$, where each entry $P_{\mathcal{l}f}$ denotes the openness of feature f at lag ℓ. A fixed lag–decay $d\left[\mathcal{l}\right]$ rescales these probabilities to $P_{\mathcal{l}f}^{\left(d\right)}=P_{\mathcal{l}f}d\left[\mathcal{l}\right]$, mildly biasing the mask toward recent lags without enforcing continuity. The feature penalty ${\mathcal{R}}_{feat}$ compares the total mass of all features against the mass of the top-M features, normalized by their total. This term vanishes when only M features carry probability and grows as mass spreads to additional features. The lag penalty, in Equation (7), ${\mathcal{R}}_{lag}$ operates within each feature column: it measures the fraction of mass lying outside the top-k lags and averages across all features.

$$\begin{array}{cc}\hfill s_f& =\sum _{\mathcal{l}=1}^L{P}_{\mathcal{l}f}^{\left(d\right)},{\mathcal{R}}_{\mathrm{feat}}={\lambda }_{\mathrm{feat}}{\displaystyle \frac{{\sum }_{f=1}^F{s}_f-{\sum }_{f\in \mathrm{TopM}\left(s\right)}{s}_f}{{\sum }_{f=1}^F{s}_f+\epsilon }},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\mathrm{lag}}& ={\lambda }_{\mathrm{lag}}{\displaystyle \frac{1}{F}}\sum _{f=1}^F{\displaystyle \frac{{\sum }_{\mathcal{l}=1}^L{P}_{\mathcal{l}f}^{\left(d\right)}-{\sum }_{\mathcal{l}\in {\mathrm{TopK}}_f\left(P_{·f}^{\left(d\right)}\right)}{P}_{\mathcal{l}f}^{\left(d\right)}}{{\sum }_{\mathcal{l}=1}^L{P}_{\mathcal{l}f}^{\left(d\right)}+\epsilon }}.\hfill \end{array}$$

(7)

The lag decay term is defined as an exponential attenuation

$$d\left[\mathcal{l}\right]=exp(-\alpha \mathcal{l}),\alpha =0.03,$$

(8)

which biases the mask toward recent lags while allowing non-contiguous long-lag selections.

The off-state regularizer ${\mathcal{R}}_{off}$ stabilizes unused logits by applying a density pressure. The mean openness ${\mathrm{dens}}_{now}$ is compared with the soft budget ${\mathrm{dens}}_{budget}$. When the openness exceeds this budget, a quadratic pressure factor amplifies the penalty, pushing excess logits further negative through the $(1-P_{\mathcal{l}f})\mathrm{softplus}\left(Z_{\mathcal{l}f}\right)$ term. Finally, a linear warm-up $\gamma \left(t\right)$ delays the activation of the cap penalties, so that the full training loss becomes

$$\begin{array}{cc}\hfill {\mathrm{dens}}_{\mathrm{now}}& ={\displaystyle \frac{1}{LF}}\sum _{\mathcal{l},f}{P}_{\mathcal{l}f},{\mathrm{dens}}_{\mathrm{budget}}={\displaystyle \frac{Mk}{LF}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathrm{pressure}& =max{\left(1,{\displaystyle \frac{{\mathrm{dens}}_{\mathrm{now}}}{{\mathrm{dens}}_{\mathrm{budget}}+\epsilon }}\right)}^2,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathcal{R}}_{\mathrm{off}}& ={\lambda }_{\mathrm{off}}\mathrm{pressure}{\displaystyle \frac{1}{LF}}\sum _{\mathcal{l},f}\left(1-P_{\mathcal{l}f}\right)\mathrm{softplus}\left(Z_{\mathcal{l}f}\right),\hfill \end{array}$$

(11)

$$\begin{array}{c}\hfill \gamma \left(t\right)=min\left(1,{\displaystyle \frac{t-t_{\mathrm{warm}}}{T-t_{\mathrm{warm}}}}\right),\mathcal{R}=\mathrm{MSE}+\gamma \left(t\right)\left({\mathcal{R}}_{\mathrm{feat}}+{\mathcal{R}}_{\mathrm{lag}}\right)+{\mathcal{R}}_{\mathrm{off}}.\end{array}$$

(12)

In practice, the threshold penalties gradually enforce the budgets M and k, while the off-state term accelerates closure when the overall density of open gates rises above the budget.

In all experiments, set ${\lambda }_{\mathrm{off}}=3\times {10}^{-3}$, ${\lambda }_{\mathrm{feat}}=3\times {10}^{-3}$, ${\lambda }_{\mathrm{lag}}=2\times {10}^{-3}$, and anneal $\tau$ linearly from temperature start to end. Neither the loss nor the post-processing enforces contiguous lags. For each selected feature f, the order-free top-k lags by $P_{\mathcal{l}f}^{\left(d\right)}$ are kept, which applies $\mathrm{TopK}$ per column without positional smoothing. A lag decay $d\left[\mathcal{l}\right]$ biases toward recent information but does not impose adjacency.

The regularization coefficients $({\lambda }_{\mathrm{off}},{\lambda }_{\mathrm{feat}},{\lambda }_{\mathrm{lag}})$ act primarily as initial scaling factors for the sparsity terms rather than strict hyperparameters. Their effective influence evolves during training through the warm-up ramp and the adaptive pruning procedure described in Section 3.3. Because pruning decisions are guided by the validation performance instead of fixed regularization strength, these parameters function only as initial sparsity biases. As a result, moderate variations within a small range (${10}^{-3}$–${10}^{-2}$) have limited effect on the final sparsity pattern or predictive accuracy. The temperature $\tau$ is linearly annealed, and its start–end values mainly affect the smoothness of gating rather than the final feature–lag configuration.

3.2. Forecast Head and Training

The forecast head follows the gated input and implements softmax pooling across lags with a linear projection to the H-step output. Concretely, each lag slice is scored by a linear map along the feature axis, the scores are normalized with a softmax over the lag dimension to produce attention weights, and the weighted feature context is mapped linearly to $\widehat{y}\in {\mathbb{R}}^{N\times H}$ (Equations (3)–(5)). An optional dropout layer is applied after gating and before pooling.

The training minimizes the mean squared error augmented by the sparsity regularizer, using AdamW optimization with a cosine learning rate schedule [32,33]. Let $g_t$ be the gradient at step t, $m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$, $v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$ with bias corrections ${\widehat{m}}_t=m_t/(1-{\beta }_1^t)$ and ${\widehat{v}}_t=v_t/(1-{\beta }_2^t)$, where the AdamW update for a parameter vector $\theta$ is

$${\theta }_{t+1}={\theta }_t-{\eta }_t{\displaystyle \frac{{\widehat{m}}_t}{\sqrt{{\widehat{v}}_t}+\epsilon }}-{\eta }_t{w}_d{\theta }_t,$$

(13)

where ${\eta }_t$ is the learning rate, $w_d$ the weight decay coefficient, and $\epsilon$ a small constant.

The gate temperature $\tau$ is updated once per epoch via a linear annealing schedule (high → low), which progressively sharpens the mask. The logits are learned jointly with the model, and the resulting probabilities lie in $[0,1]$. A warm-up factor $k\in [0,1]$ scales the regularization in early epochs. Validation is computed as the pure MSE on the forecast head outputs, and early stopping selects the best checkpoint according to the validation loss.

After training, the probabilities $P=\sigma (Z/{\tau }_{\mathrm{final}})$ are used to select the top-M features by mass $s_f={\sum }_{\mathcal{l}}{P}_{\mathcal{l}f}^{\left(d\right)}$. For each selected feature f, the top-k lags by $P_{\mathcal{l}f}^{\left(d\right)}$ are selected independently per feature. This yields a binary mask $M^{★}\in {\{0,1\}}^{L\times F}$ with exactly $M·k$ active lag–feature pairs.

The continuous probabilities $P_{\mathcal{l}f}^{\left(d\right)}$ are converted into a binary mask $M^{★}$ by retaining the top-M features ranked by the total mass $s_f={\sum }_{\mathcal{l}}{P}_{\mathcal{l}f}^{\left(d\right)}$ and, within each selected feature, the top-k lags ranked by $P_{\mathcal{l}f}^{\left(d\right)}$. All remaining entries are set to zero:

$$M_{\mathcal{l}f}^{★}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}f\in \mathrm{TopM}\left(s\right)\mathrm{and}\mathcal{l}\in {\mathrm{TopK}}_f(P_{·f}^{\left(d\right)}),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(14)

3.3. Adaptive Budget Pruning

The gate logits start fully open ($M=F$, $k=L$) and disable pruning for a burn-in of $E_{\mathrm{burn}}$ epochs, so that the model has time to learn the best feature and lag direction. Every E epochs thereafter (with $E\in 1,2$), the procedure considers reducing k and/or M based on a smoothed validation loss. Let ${\tilde{\mathcal{V}}}_t=\beta {\tilde{\mathcal{V}}}_{t-1}+(1-\beta ){\mathcal{V}}_t$ be an Exponential Moving Average (EMA) ($\beta \in [0.60,0.90]$ adaptively set from noise and density). At each prune event, up to

$$c_k\le min\{\lfloor {\rho }_{k}k\rfloor ,k-k_{min}\},c_M\le min\{\lfloor {\rho }_{M}M\rfloor ,M-M_{min}\},$$

(15)

unit cuts, where ${\rho }_k\in [0.30,0.45]$, ${\rho }_M\in [0.15,0.35]$, and a threshold $(k_{min},M_{min})=(3,1)$. The threshold is kept to avoid zeroing out one of the variables.

For a trial $k-1$ or $M-1$ cut, evaluate $\mathcal{V}(k-1,M)$ and $\mathcal{V}(M-1,M)$. A cut is accepted if the validation loss does not exceed a tolerance scaled from the EMA:

$$\mathcal{V}(·)\le (1+{ϵ}^{★}){\tilde{\mathcal{V}}}_t,{ϵ}^{★}=\left\{\begin{array}{cc}{ϵ}_{\mathrm{first}}\hfill & \mathrm{for}\mathrm{the}\mathrm{first}\mathrm{accepted}\mathrm{cut}\mathrm{of}\mathrm{this}\mathrm{type},\hfill \\ {ϵ}_{\mathrm{next}}\hfill & \mathrm{thereafter},\hfill \end{array}\right.$$

(16)

with ${ϵ}_{\mathrm{first}}=2ϵ$ and ${ϵ}_{\mathrm{next}}=0.5ϵ$, $ϵ\in [0.025,0.060]$. To avoid trimming of informative tails, the k cut additionally requires a small tail mass at the $M_{k-th}$ value of the pooled $P^{\left(d\right)}$ over the currently kept features and an absolute threshold relative to the mean pool value. If both cuts are admissible, committing both cuts jointly is also tested and accepted if they satisfy the stricter of the two tolerances. Early stopping is allowed only after two consecutive events with no accepted cuts, to prevent premature stops during active pruning.

The adaptive pruning process eliminates the need to predefine the number of features or lags to retain. Instead of hard-coding these values, the algorithm gradually reduces them during training and accepts each cut only if it does not increase the validation loss beyond a small tolerance. This allows the model to automatically find an appropriate sparsity level for each dataset, regardless of dimensionality or lag horizon. Because pruning is validation-guided, excessive reductions that would harm accuracy are rejected, and a small minimum threshold ensures that at least one feature and a few lags remain active. This prevents collapse to an empty input set and keeps the gate stable throughout training. As a result, the same configuration can be used safely across datasets with different resolutions or feature counts, without any manual tuning of the sparsity parameters.

4. Case Study

4.1. Data Description

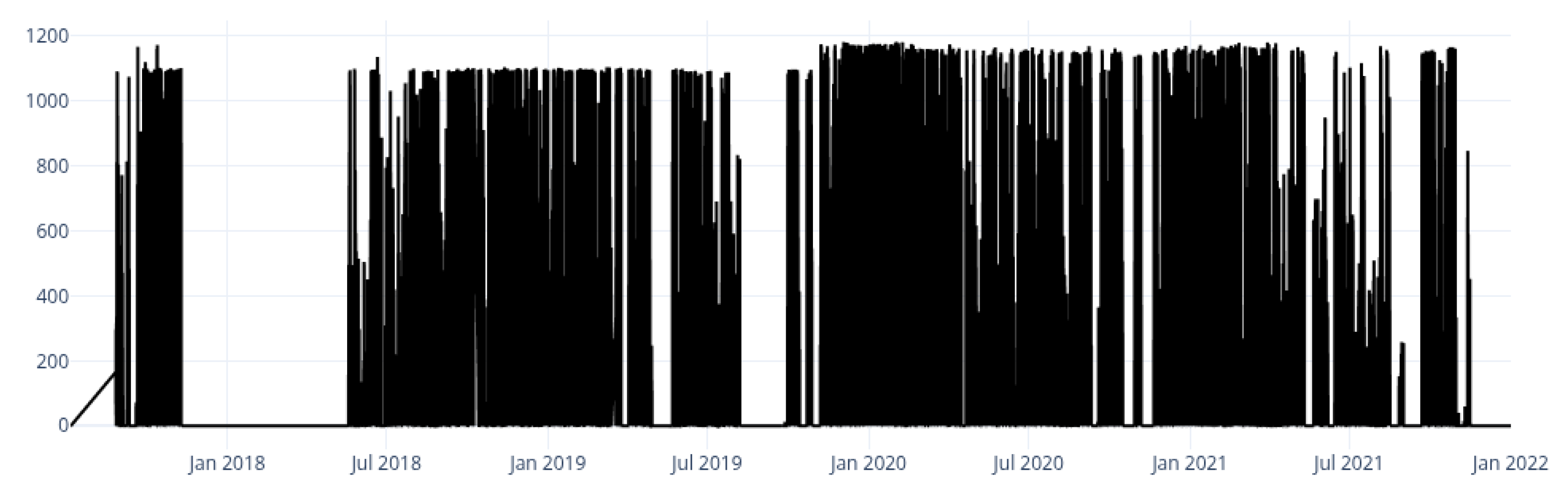
The dataset used in this study is the Offshore Renewable Energy (ORE) Catapult Platform for Operational Data (POD) from the Levenmouth Demonstration Turbine (LDT), a $7\mathrm{MW}$ offshore research turbine. The inputs are primarily the LDT’s met–mast SCADA (11 sensors of wind speed and direction at multiple heights), and the forecasting target comes from the LDT’s SCADA (574 sensors at 1 Hz covering electricity, temperature, and pressure). This study uses the met–mast SCADA as inputs and one turbine SCADA tag (CI_SubIprPrivPower_Mean) as the forecasting target variable. All variables are summarized in 10 min windows for the interval of 6 July 2017 to 31 December 2021.

The met-mast data provide repeated 10 min summaries per sensor with the fields Min, Max, Mean, Stdev, and EndVal. The variables observed are for barometers, air temperature sensors, wind vanes, and cup anemometers, each recorded at multiple mast positions. Counting the sensors and the 5 statistics yields 65 candidate inputs per timestamp.

The variable CI_SubIprPrivPower_Mean (Figure 2) is the prediction target and is used only through its lagged values (autoregressive features). Let $P_t$ denote the active power at time t in $\mathrm{MW}$. The 10 min interval energy $E_t$ in $\mathrm{MWh}$ is

$$E_t\left[\mathrm{MWh}\right]={\displaystyle \frac{P_t\left[\mathrm{MW}\right]}{6}}$$

(17)

where $P_t$ is the active power at time t.

Samples are formed by stacking an autoregressive window of $L=168$ steps (28 h) across the F input channels, resulting in $X\in {\mathbb{R}}^{N\times L\times F}$. The target is a day-ahead vector $y\in {\mathbb{R}}^{N\times H}$ with $H=144$ steps (24 h). Chronological order is preserved across the training, validation, and test sets, keeping 5000 fixed inputs for validation and testing. A contiguous slice of 2000 random inputs inside the training span is reserved for hyperparameter search. Extensive periods where $E_t=0$ were removed to prevent the model from collapsing.

The proposed method was validated using data from a single offshore wind turbine at the LDT. While this setup naturally limits the ability to generalize the findings across different geographical and climatic conditions, the wind power forecasting performance is known to vary significantly between sites due to differences in terrain complexity, surface roughness, and local atmospheric dynamics. Consequently, full verification of the model’s robustness would require testing on multiple wind farms representing both onshore and offshore environments and including sites with simple and complex terrain. Validation across at least three to five diverse locations would provide a more comprehensive assessment of the method’s generalizability.

However, the use of a single dataset remains a common and accepted practice in the field. As noted in [34], most wind power forecasting studies employ data from one site, primarily due to the limited public availability of high-quality SCADA and NWP data and the considerable heterogeneity among wind farms. Under these constraints, conducting experiments on one representative and well-documented site, such as the offshore LDT facility, is consistent with standard methodological practice and allows for reproducible benchmarking.

4.2. Capacity Estimation

As seen in Figure 2, the nominal rating inferred from the data differs from the turbine description. Accordingly, a piecewise constant capacity curve $C\left(t\right)$ is inferred directly from the smoothed power series $y\left(t\right)$, so that a capacity can be estimated for any dataset with an unknown rating. The timeline is partitioned into fixed 30-day blocks. For the block index g, the intra-block range is $R_g={max}_{g\left(t_k\right)=g}y\left(t_k\right)-{min}_{g\left(t_k\right)=g}y\left(t_k\right)$, where $g\left(t_k\right)$ assigns timestamp $t_k$ to its block.

A capacity break is identified as follows: let $R_{max}={max}_g{R}_g$, and set a tolerance $\theta =0.50$. A structural break is declared whenever $|R_g-R_{g-1}|>\theta R_{max}$, signaling a substantive alteration in the plant’s ceiling output. Capacity is then assigned by treating each run of consecutive blocks between breaks as a period p. The capacity for that period is $C_p={max}_{G_g=p}{R}_g$, and every timestamp within the period receives the same $C_p$, resulting in a piecewise constant $C\left(t\right)$.

4.3. Experimental Setup and Evaluation Metrics

While several recent architectures have addressed aspects of temporal or feature relevance, their mechanisms differ fundamentally from the global, static selection performed by the proposed joint gate. PatchTST [31] introduces a channel-independent transformer that applies self-attention across contiguous temporal patches. Each patch embedding models the local temporal continuity, and attention weights are computed per instance during inference. The model captures the temporal structure implicitly but retains all input dimensions and does not produce a stable subset of lag–feature pairs that can be reused across datasets or architectures.

The TFT [14,19] combines variable selection networks and gated residual connections to compute the feature relevance at each time step. The selection weights are conditioned on both observed past and known future covariates, producing time-dependent and sample-specific relevance scores. As a result, the feature weighting varies for each forecast window and does not produce a global mask applicable to new data. In addition, the TFT assumes access to known future variables, which are not available in the SCADA-only configuration used in this work.

The proposed gating mechanism produces a single, static mask that identifies globally relevant lag–feature combinations from historical SCADA data. This configuration remains fixed across training runs and datasets, providing a consistent input structure for different model architectures. This study therefore compares this static selection with conventional lag–feature filters, such as Pearson’s correlation, mutual information, and cross-correlation, which operate explicitly on lagged SCADA variables and are commonly used as reference methods in wind power forecasting.

To quantify the relative accuracy of the joint gate, three score-based selectors were implemented:

$$S_{\mathcal{l}f}^{\left(\mathrm{corr}\right)}=\left|\rho (X_{·,\mathcal{l},f},y)\right|,S_{\mathcal{l}f}^{\left(\mathrm{mi}\right)}=\mathrm{MI}(X_{·,\mathcal{l},f};y),S_{\mathcal{l}f}^{\left(\mathrm{ccf}\right)}=\underset{\tau }{max}\left|\mathrm{corr}(X_{·,\mathcal{l}-\tau ,f},y)\right|.$$

(18)

Here, $\rho (·,·)$ denotes the Pearson’s correlation coefficient and $\mathrm{corr}(·,·)$ the sample cross-correlation function evaluated over temporal shifts $\tau$. Scores were normalized per feature and optionally weighted by a lag decay factor $d\left[\mathcal{l}\right]$ to penalize distant lags. Fractions $g_{\mathcal{l}},g_f\in [0.02,0.20]$ of the highest-scoring lags and features were retained, and each filtered design was evaluated using a compact ExtraTrees regressor to determine the best configuration.

The selected fractions of the gate model and the comparison approaches are then validated on different deep learning models. All models share the same splits, AdamW with cosine annealing, and early stopping. Final training uses 100 epochs and 200 trials to select the model hyperparameters.

To evaluate the performance, the following metrics are computed: the Normalized Root Mean Squared Error (nRMSE), Normalized Mean Absolute Error (nMAE), and Normalized Mean Bias Error (nMBE).

$$\mathrm{nRMSE}={\displaystyle \frac{1}{D}}\sqrt{{\displaystyle \frac{1}{T}}\sum _{t=1}^T{\left({\widehat{y}}_t-y_t\right)}^2},$$

(19)

$$\mathrm{nMAE}={\displaystyle \frac{1}{D}}{\displaystyle \frac{1}{T}}\sum _{t=1}^T|{\widehat{y}}_t-y_t|,$$

(20)

$$\mathrm{nMBE}={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left({\widehat{y}}_t-y_t\right),$$

(21)

where $y_t$ and ${\widehat{y}}_t$ are the observed and forecasted values at time t, T is the number of evaluated timestamps, and D is the rated capacity. While the nRMSE and nMAE are the most commonly used metrics, this combination was chosen for its complementary behavior: the nRMSE highlights large errors (quadratic penalty) and, after normalization through D, expresses them relative to the capacity; the nMAE measures the average absolute deviation and is less sensitive to outliers; the nMBE captures systematic bias (over/underestimation).

5. Experimental Findings and Discussion

Traditional wind power forecasting pipelines handle feature and lag reduction through multiple disconnected steps: a filter score is computed (e.g., correlation, MIC, or cross-correlation), thresholds or heuristics are applied to pruning features, an autoregressive window is fixed manually, and the resulting subset is then passed to a learning model. Each stage optimizes a different proxy objective and requires manual parameter tuning, leading to accumulated selection bias and the retention of redundant lag–feature combinations. In contrast, the proposed gate performs these steps jointly and directly under the supervised forecasting loss. A single, end-to-end trainable component replaces the chain of filters and thresholds, allowing sparsity and relevance to be learned simultaneously. The result is a smaller, reproducible, and task-aligned subset of inputs without any manual lag length or feature ranking rules.

To show the practical impact of the proposed mechanism, tests were performed on a Dell laptop equipped with an Intel Core i7 processor and 32 GB of memory (Dell Technologies, Raheen Business Park, Limerick, Ireland). The experiments evaluated (i) the effectiveness of the joint gate in selecting compact and informative lag–feature subsets under the supervised forecasting loss by comparing against Pearson’s, mutual information, and cross-correlation selectors across identical splits and architectures; (ii) the influence of the decay term $d\left[\mathcal{l}\right]$ through an ablation study (with and without decay); and (iii) the practical runtime on the available hardware. The regularization coefficients $({\lambda }_{\mathrm{off}},{\lambda }_{\mathrm{feat}},{\lambda }_{\mathrm{lag}})$ are not explicitly tuned through external search but are optimized implicitly during training as part of the loss function. In the proposed setup, effective sparsity is primarily governed by the validation-guided adaptive pruning (Section 3.3) rather than by the precise numeric choice of $\lambda$ values.

5.1. Lag-Continuity- and Decay-Aware Selection

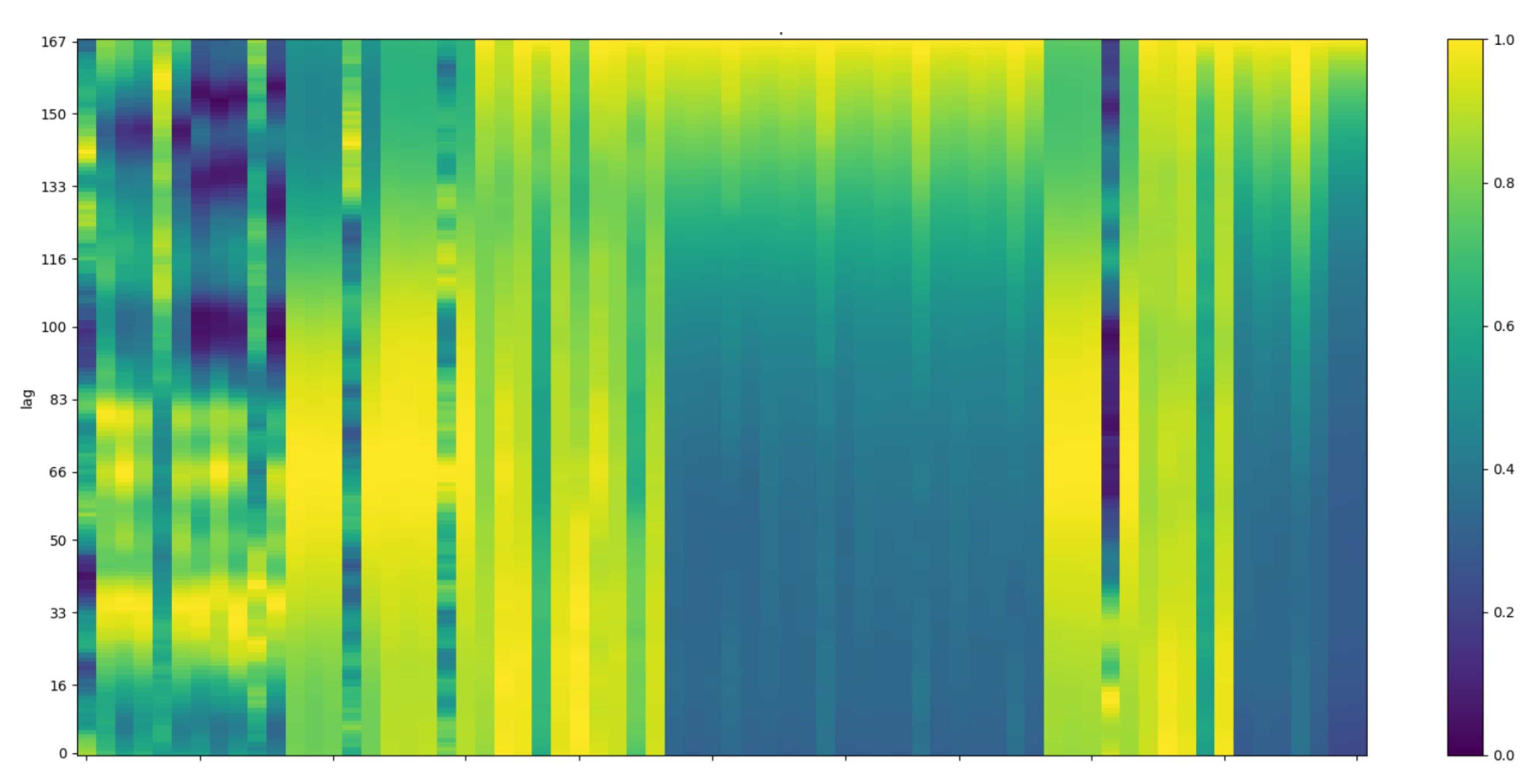
The selection of lagged steps in time series forecasting typically assumes continuity; that is, if a past value at lag $t-3$ is relevant, so are $t-2$ and $t-1$. This assumption is commonly used to simplify model input construction (the autoregressive window), which is in fact the data format given as input to the gate model. Figure 3 shows the normalized lag–feature Pearson’s correlations for the ORE Catapult POD dataset. The figure shows that not every feature has its maximum correlation at the newest lag, and relevance appears in clusters. Therefore, enforcing continuity can inflate inputs with low-signal steps and biases learning toward recent noise and toward the selection of features that follow the expected continuity.

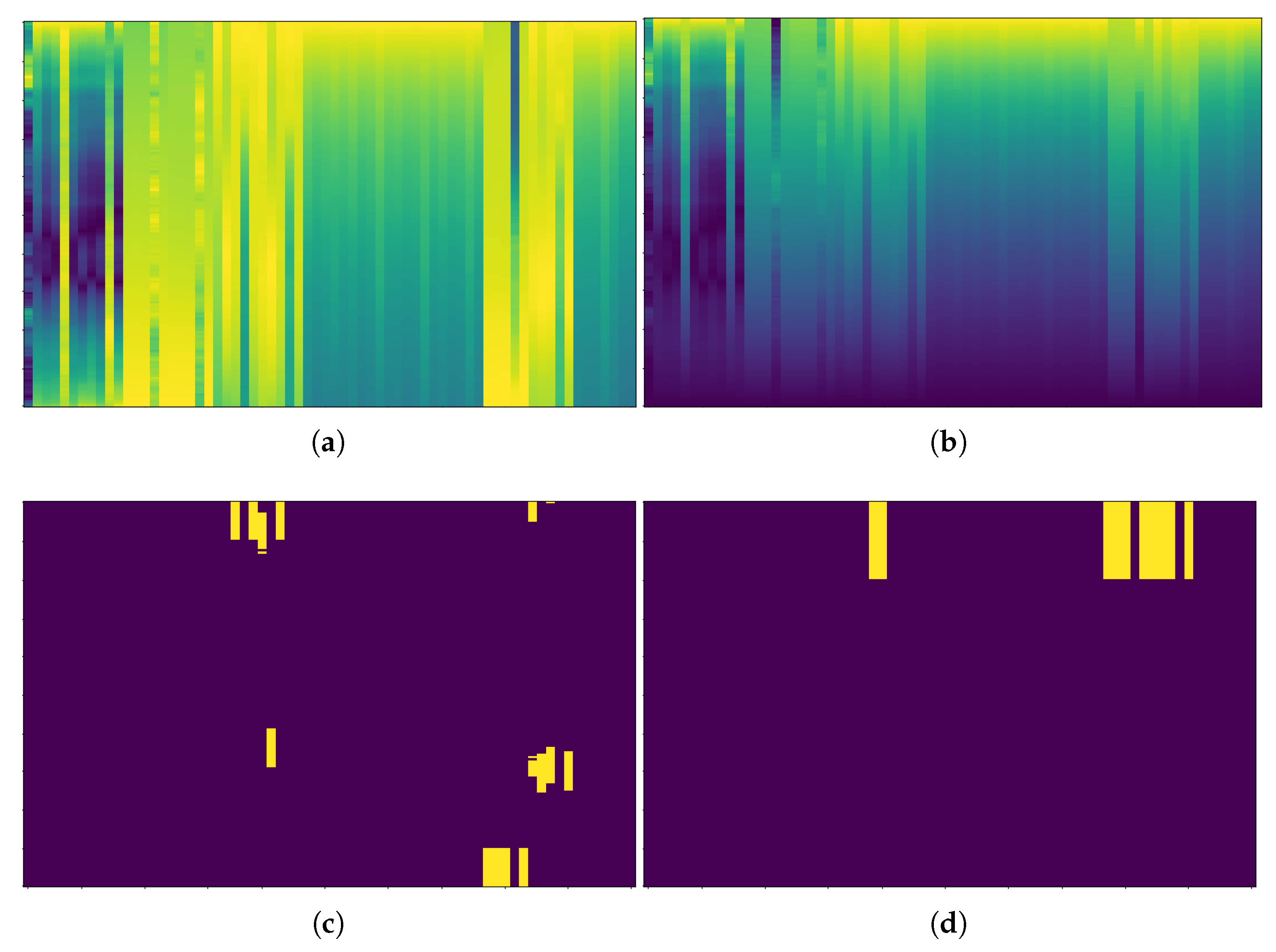
To encourage, but not force, a preference for recent lags, a lag decay factor is included in the loss (Figure 4). It acts by regularizing isolated long-lag peaks while preserving the informative mid- to long-lag structure. This way, the gate scores are order-free along the lag axis, and post-processing keeps the top-k lags per feature according to $P_{\mathcal{l}f}^{\left(d\right)}$. In practice, the decay-aware factor tends to force longer lags to add the recent knowledge available in newer lags, but it does not exclude older lags if the relationship is relevant enough.

For other methodologies, such as cross-correlation, the decay effect is quite different since the decay is directly multiplied by the correlation matrix, causing the features with correlation in older lags to fade and become falsely less relevant (Figure 5).

In order to quantify the effect of the decay bias on lag relevance, strategies that are both decay-aware and non-decay-aware without forced continuity selection are presented and compared, with the results reported in terms of forecasting accuracy and input dimensionality.

5.2. Forecast Accuracy

To evaluate the performance of the selected joint gate for lag and feature pruning, seven deep learning architectures (long short-term memory (LSTM), convolutional neural network (CNN), recurrent neural network (RNN), convolutional–recurrent network (CNN–RNN), convolutional–long short-term memory (CNN–LSTM), gated recurrent unit (GRU), and temporal convolutional network (TCN)).These models were benchmarked under four pruning strategies: the proposed joint gate and Pearson’s, mutual information (MI), and cross-correlation (CCF). Accuracy was measured on the 24 h horizon using the nRMSE, nMAE, and nMBE (

Table 1. Deep models evaluated with four lag–feature pruning approaches.

Model	Joint Gate			Pearson			MI			CCF
	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE
LSTM	0.145	0.094	0.041	0.182	0.156	0.104	0.241	0.221	0.178	0.192	0.171	0.122
CNN	0.152	0.110	0.059	0.229	0.220	0.179	0.179	0.155	0.106	0.250	0.233	0.194
RNN	0.151	0.111	0.056	0.188	0.162	0.108	0.232	0.222	0.182	0.144	0.100	0.040
CNN-RNN	0.145	0.100	0.045	0.220	0.201	0.155	0.208	0.190	0.144	0.249	0.237	0.198
CNN-LSTM	0.148	0.101	0.046	0.229	0.216	0.174	0.175	0.147	0.093	0.237	0.223	0.182
GRU	0.152	0.109	0.056	0.198	0.175	0.125	0.217	0.196	0.151	0.215	0.196	0.149
TCN	0.142	0.088	0.034	0.196	0.170	0.119	0.187	0.165	0.116	0.180	0.158	0.106

and

Table 2. Deep models evaluated with lag–feature pruning approaches, with decay.

Model	Joint Gate			Pearson			MI			CCF
	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE	nRMSE	nMAE	nMBE
LSTM	0.140	0.084	0.028	0.187	0.161	0.108	0.232	0.208	0.165	0.180	0.158	0.107
CNN	0.141	0.089	0.036	0.250	0.235	0.197	0.166	0.143	0.092	0.182	0.152	0.098
RNN	0.152	0.109	0.053	0.204	0.177	0.126	0.181	0.164	0.116	0.195	0.178	0.131
CNN-RNN	0.146	0.104	0.050	0.205	0.187	0.140	0.224	0.205	0.161	0.217	0.193	0.145
CNN-LSTM	0.145	0.102	0.049	0.188	0.165	0.114	0.198	0.185	0.141	0.214	0.194	0.147
GRU	0.143	0.094	0.039	0.181	0.152	0.099	0.186	0.162	0.112	0.198	0.173	0.123
TCN	0.143	0.093	0.040	0.206	0.189	0.143	0.163	0.125	0.067	0.185	0.158	0.105

).

For reference, a naïve persistence baseline that simply repeats the last observation over the horizon is included. Naïve (persistence): $\mathrm{nRMSE}=0.181$, $\mathrm{nMAE}=0.065$, and $\mathrm{nMBE}=0.001$. The proposed joint gate with LSTM achieves an $\mathrm{nRMSE}$ = 0.140, and similar gains appear across other architectures (Table 1 and Table 2). The naïve method achieves a very small MBE because persistence forecasts align with the series mean, but this comes at the cost of much larger variance and overall error. In contrast, the joint gate reduces the nRMSE and nMAE while keeping the bias acceptably small (e.g., LSTM with decay: $\mathrm{nMBE}$ = 0.028).

Focusing on the best overall accuracy, the joint gate with decay achieves the lowest nRMSE for all seven models (e.g., LSTM: $0.140$; CNN: $0.141$; GRU: $0.143$; TCN: $0.143$), outperforming Pearson’s, MI, and CCF in each case (Table 2). Without decay, the joint gate is best in six out of seven models (Table 1); the only exception is the RNN, where CCF achieves a marginally lower nRMSE ($0.144$ vs. $0.151$). Typical nRMSE reductions versus the best baseline range from modest to large, depending on the architecture. For example, for LSTM, the joint gate improves over Pearson’s/MI/CCF from $0.187/0.232/0.180$ to $0.140$ (relative reductions of about 25–40%), while for the CNN, the improvement is from $0.250/0.166/0.182$ to $0.141$. The joint gate also consistently achieves the smallest nMBE in each backbone (e.g., with decay: LSTM $0.028$; CNN $0.036$; GRU $0.039$; TCN $0.040$), indicating low systematic over- or underestimation. Finally, the nMAE follows the same trend as that for the nRMSE: with decay, the joint gate gives the best or tied best nMAE across the models (e.g., LSTM: $0.084$; CNN: $0.089$; GRU: $0.094$; TCN: $0.093$).

Comparing the decay and non-decay settings, decay-aware regularization is generally preferable. With decay, the joint gate achieves the lowest nRMSE across all models (e.g., LSTM: $0.140$ vs. $0.145$; CNN: $0.141$ vs. $0.152$; GRU: $0.143$ vs. $0.152$), while the performance without decay is slightly worse or unchanged depending on the model. For baselines such as Pearson’s and CCF, directly multiplying through decay can suppress informative long-lag contributions and even degrade the results (e.g., CNN with Pearson’s = $0.250$ with decay vs. $0.229$ without). Overall, the decay-aware gate provides modest but consistent improvements, especially for recurrent and convolutional models.

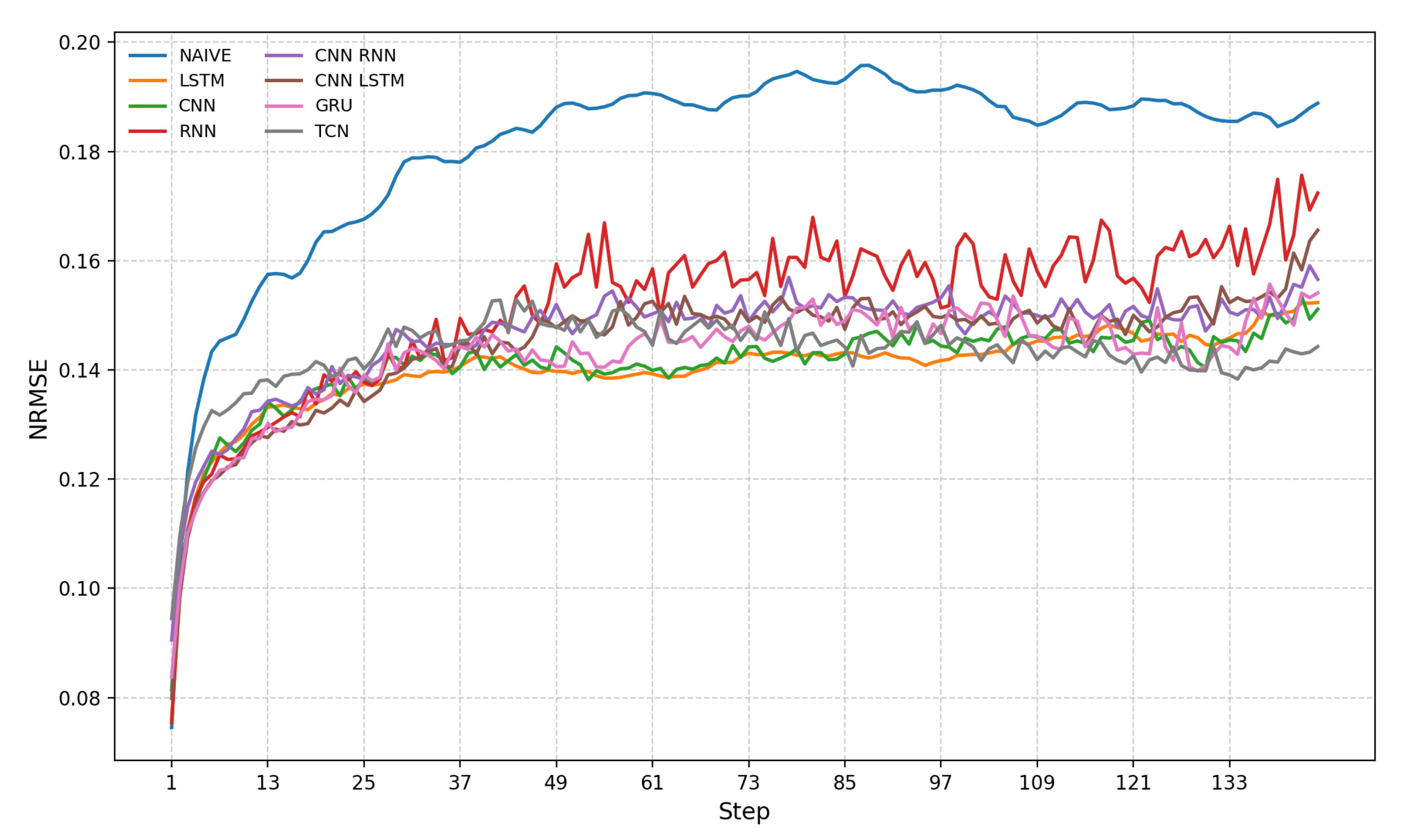
Figure 6 (joint gate) and Figure 7 (joint gate with decay) report the stepwise nRMSE across the 24 h horizon. All models show the expected pattern: a rapid increase in error during the first 10–20 steps, followed by a slow drift. The naïve persistence baseline deteriorates over the horizon and performs uniformly worse. With decay, the joint gate achieves uniformly lower and less volatile curves after step 40, where LSTM presents the lowest error for most steps, with the TCN close behind and exhibiting the most stable profile. The RNN remains the noisiest and tends to be the highest-error curve beyond mid-horizon. Without decay, the differences between models become larger, and late-horizon drift increases, especially for the RNN and (to a lesser extent) the CNN/GRU. Overall, decay regularization mainly improves the mid- to late horizon by lowering the error levels and reducing variance while preserving the ranking seen in the aggregate tables.

Across all architectures, the proposed gate is the most accurate and lowest-bias lag–feature selector. The decay-aware regularization modestly the improves performance without enforcing lag continuity, especially improving the mid- to late horizon, where stepwise errors are lower and less volatile. These advantages are consistent across convolutional and recurrent predictors under identical training conditions and data splits. Compared with baselines such as Pearson’s, MI, and CCF, the joint gate achieves systematically smaller nRMSE, nMAE, and nMBE values, while the naïve persistence baseline, although nearly unbiased, fails to capture the dynamics and incurs substantially larger variance.

Typical pipelines treat pruning as a sequence of loosely coupled stages: (i) compute the filter scores (e.g., correlations, MIC, CCF) per feature or per lag; (ii) apply thresholds or meta-heuristics to keep a subset; (iii) expand to a fixed autoregressive window (often the same lags for all features or the same features for all lags); and (iv) tune the forecast model on the resulting design. This multi-step flow has well-known side effects: (a) it accumulates compute (each stage touches the full tensor), (b) it compounds selection bias by reusing the evaluation data across stages, (c) it fixes uniform structures (the same features across all lags, or the same lags across all features) that carry irrelevant pairs, and (d) it optimizes proxies (filter scores) rather than the supervised objective.

Our approach collapses these stages into a single, end-to-end trainable component. The joint gate is optimized directly on the forecasting loss while enforcing explicit sparsity budgets (top-M features and per-feature top-k lags). Hence, the pruning decisions are made under the supervised objective, at the granularity of lag–feature pairs $(\mathcal{l},f)$, with no external thresholds, wrappers, or hand-tuned continuity rules. Practically, this (i) removes manual sequencing and ad hoc thresholds, (ii) reduces code paths and failure modes, (iii) yields a compact, reproducible subset tied to the task loss, and (iv) avoids dragging irrelevant pairs created by uniform lag or feature sets. The empirical sections show that this single-step optimization attains both higher accuracy and greater compression than multi-step filters across all tested backbones.

5.3. Dimensionality Reduction

A central motivation for lag–feature pruning is a reduction in the input dimensionality. With $L=168$ lags and $F=68$ features, the raw design contains $L\times F$ = 11,424 lag–feature pairs.

Table 3. Dimensionality reduction for different pruning strategies (LSTM).

Approach	Features	Lags/Feature	Kept Pairs	Reduction %
Joint gate (no decay)	9	20	180	98.42
Joint gate (decay)	7	52	364	96.81
Pearson’s (no decay)	13	21	273	97.61
Pearson’s (decay)	13	24	312	97.27
Mutual information	14	21	294	97.43
Mutual information (decay)	14	27	378	96.69
Cross-correlation	13	17	221	98.07
Cross-correlation (decay)	10	34	340	97.02

Percentages are relative to the full input size ($68\times 168=11,424$ lag–feature pairs).

reports the number of selected features, lags per feature, retained pairs, and the resulting percentage reduction for each method.

All methods achieve strong compression, removing more than 96% of the original inputs. The joint gate without decay is the most aggressive, retaining only 180 pairs (98.4% reduction) while still delivering the best forecast accuracy. Decay regularization increases the number of selected lags per feature, leading to a larger kept set (364 pairs, 96.8% reduction) but also stabilizes mid-horizon errors. Correlation and mutual information filters achieve similar reductions (97–97.5%), though they often cluster lags in the most recent region, as shown in the learned masks. Cross-correlation achieves a 98% reduction without decay but requires more pairs under decay (340).

Overall, these results show that aggressive dimensionality reduction is consistently possible without loss of accuracy. The exact number of retained pairs varies across runs and methods, but the joint gate achieves the strongest balance, combining the highest compression with a superior forecast accuracy. Importantly, the findings confirm that extending the lag or feature space does not improve the performance. What matters is the selection methodology, not the raw input size.

5.4. Computational Efficiency

The proposed gating mechanism was designed to reduce the computational cost of model training by pruning redundant lag–feature combinations before forecasting. In practice, full-scale training using all available inputs exceeded the local hardware limits, preventing a direct wall-clock comparison with the complete input tensor. To provide a fair and feasible efficiency assessment, all baselines, Pearson’s correlation, mutual information, and cross-correlation were evaluated using the full lag window and their respective reduced feature subsets, while the proposed gate performed both lag and feature pruning jointly. Specifically, the correlation and mutual information selectors retained 14 features each, and the CCF-based selector reduced the set to 7 features. In contrast, the gate adaptively selected a smaller number of lags and features according to the learned relevance mask, and its reported runtime included both the selection and training phases.

The runtime results in

Table 4. Total runtime (lag–feature selection + model training) under full and reduced input configurations.

Model	Gate	Pearson’s		MI		CCF
		Full-Lag	Reduced	Full-Lag	Reduced	Full-Lag	Reduced
LSTM	00:37:19	02:49:06	00:29:43	02:49:54	01:33:31	03:14:13	00:20:32
CNN	00:26:04	01:19:48	00:18:55	02:56:20	01:31:56	01:21:21	00:18:01
RNN	00:34:05	02:47:08	00:25:45	02:50:37	01:49:18	00:55:43	00:23:28
CNN–RNN	00:26:21	01:02:30	00:19:24	03:01:18	01:35:27	00:57:27	00:20:09
CNN–LSTM	00:37:34	01:14:57	00:32:37	02:24:12	01:39:25	01:16:46	00:41:08
GRU	00:32:54	03:51:12	01:27:15	02:49:06	01:43:31	00:36:32	00:42:00
TCN	00:40:39	05:24:19	00:31:14	03:25:24	01:58:35	02:43:05	00:22:19

show that when all historical lags were retained (full-lag), the gate achieved the lowest total training time across all architectures, despite performing joint lag–feature pruning rather than feature filtering alone. On average, the gate reduced the total runtime by approximately 79–81% relative to correlation- and mutual-information-based selectors and by about 65% relative to CCF. The largest gains were observed for the LSTM and TCN architectures, where the gate lowered wall-clock time by more than 75% compared with the next best method. These results indicate that the computational benefit arises primarily from lag pruning, which reduces the effective sequence length and the number of recurrent or convolutional operations per epoch.

The Full-lag columns of Table 4 isolates the effect of feature pruning while maintaining the same lag window. In this setup, Pearson’s and CCF achieved the lowest raw runtimes among classical selectors, reflecting their simplicity and linear scoring nature, while mutual information remained the most computationally demanding due to entropy estimation. Despite this, these methods do not prune lag sequences and thus cannot eliminate redundant temporal dependencies. The gate, which prunes both lags and features simultaneously, achieved a lower total training time than that of any feature-only selector, even under the reduced configuration. This suggests that its differentiable pruning not only decreases the input dimensionality but also accelerates convergence by aligning feature and lag relevance directly with the supervised forecasting loss.

Because the gate jointly prunes both lags and features, its runtime reflects the true cost of a compact input tensor. The other methods prune only features and therefore still process the full lag window, making their computational load scale with sequence length. Since recurrent and convolutional models scale approximately linearly with this dimension, lag pruning directly reduces the number of per-epoch operations. This structural difference explains the consistent runtime advantage observed for the gate across all architectures.

When all methods reduce both lags and features, the wall-clock time drops across all baselines. Pearson’s and CCF become the fastest because their naïve scoring passes are cheap and the resulting training uses much shorter sequences. MI remains the most time demanding due to the cost of estimating mutual information, which dominates even after the lag window is shortened.

Despite these speedups, the filter baselines differ fundamentally from the gate in what they can extract. Pearson’s and CCF rank each $(\mathcal{l},f)$ pair with a marginal, mostly linear statistic and then prune independently. They cannot account for nonlinear cross-lag interactions, competition among features, or redundancy across nearby lags. MI is nonlinear but still a marginal, univariate score and is sensitive to sample density and estimator settings. In contrast, the proposed gate learns $(\mathcal{l},f)$ relevance under the supervised forecasting loss while the predictor is being optimized. The selection head and the forecaster co-adapt: (i) the temperature-annealed gate produces a soft mask refined by gradients from the multi-step loss; (ii) the decay $d\left[\mathcal{l}\right]$ biases, but does not force, recent lags; and (iii) the adaptive pruning in Section 3.3 validates sparsity against performance, preventing over-pruning and collapse. Practically, this means the gate can retain a small, non-contiguous set of lags that work jointly for prediction rather than a collection of individually strong but redundant inputs.

5.5. Interpretation of the Learned Mask

The final lag–feature mask selected nine variables with a non-zero probability mass: {12, 13, 15, 29, 52, 55, 56, 60, 66}. Feature 66 corresponds to past values of the target power output and was kept only as autoregressive context. The remaining eight inputs describe the environmental and electrical conditions from the SCADA and met-mast systems.

The gate placed the highest weights on the barometric and anemometric channels (features 12–15 and 52–56), showing that short-term changes in pressure and wind speed are the main drivers of day-ahead forecasts. Barometer and anemometer end values and means appeared together in the top ranks, forming lag clusters up to about 0–18 steps (0–3 h) into the past, which reflects short-range persistence in local pressure and wind flow. Wind vane signals (feature 29) were also retained but with fewer active lags, showing a weaker directional influence.

Lags beyond 120 steps (about 20 h) were mostly inactive, except for the autoregressive power channel (feature 66), whose long-lag coverage (150–167) represented the explicit day-ahead memory window. Overall, the learned mask highlights physically consistent variables such as wind speed, pressure, and wind direction at recent time scales while downweighting distant or temperature-related inputs.

6. Conclusions

Day-ahead wind power forecasting using SCADA-only data suffers from large autoregressive windows that inflate inputs with many weak lag–feature pairs. This study presents a lightweight and interpretable joint gate that learns a global, decay-aware mask over the lag–feature plane and reuses the selected subset for forecasting, replacing multi-stage, heuristic pipelines with a single, end-to-end optimization.

Across seven deep learning backbones and two decay regimes, the proposed selector achieved the best accuracy in our study, delivering the lowest nRMSE, nMAE, and absolute bias versus Pearson’s, mutual information, and cross–correlation and a persistence baseline. The adaptive pruning mechanism automatically adjusted sparsity during training, maintaining accuracy while ensuring model compactness. The learned masks reduced the input dimensionality by 96–98% while preserving or improving accuracy, indicating that performance gains stem from structured selection rather than added model capacity. In wall–clock terms, pruning lag–feature pairs before training shortened the effective sequence length and cut the total runtime by roughly 65–80% relative to correlation- and MI-based selectors under the full-lag setting.

In practice, the joint gate provides a compact, reusable design matrix and a reproducible preprocessing stage directly integrated with the forecasting loss. Its interpretability (global mask) and simplicity (single training step) remove manual lag tuning, ad hoc thresholds, and wrapper searches common in prior pipelines.

Two key limitations should be noted. First, validation used a single offshore site. Broader multi-site studies are needed to establish generalizability. Second, the learned mask is global and static at inference time, which favors stability and interpretability but limits adaptability under non-stationary conditions. Future work will explore dynamic, context-aware gating, cross-site evaluation, and integration with control and economic valuation frameworks.

Future Work

This study was conducted using data from a single offshore wind farm. While the results demonstrate strong predictive performance and computational efficiency within this setting, further validation is required to assess the method’s generalizability across diverse environments. Future work should evaluate the proposed approach on additional sites with varying geographic and climatic characteristics, such as onshore locations, complex terrains, or other renewable power sources, to confirm its robustness under different operational conditions.

A second direction concerns the static nature of the learned mask. The current design applies a global, fixed selection of lags and features during inference, which limits adaptability under non-stationary conditions. Extending the method toward dynamic or context-aware gating could allow the selection mechanism to adjust automatically to evolving data patterns, improving responsiveness without sacrificing interpretability.

Beyond these extensions, two complementary research directions are particularly relevant. First, integrating the forecasting framework with reinforcement-learning-based control could support dynamic power dispatching in offshore networks. Fu et al. [35] proposed a reinforcement learning approach for the dynamic optimal power flow in offshore wind farms with multiple points of common coupling, demonstrating that learning-based controllers can coordinate grid and turbine operations in real time. Incorporating the proposed gating mechanism into such a control setting would allow the forecast model to provide directly optimized inputs for reinforcement-driven operational decisions.

Second, the economic benefit of improved forecasts can be examined through an option-value framework. Borozan et al. [36] introduced this concept to quantify the economic advantage of flexible investment and operational decisions under uncertainty. Applying this principle to wind power forecasting would enable assessment of how predictive accuracy improvements translate into measurable economic value under market and grid variability.

Finally, future studies should include repeated training runs with formal statistical validation, applying Diebold–Mariano or paired t-tests to ensure that the observed improvements are statistically significant and not due to random variation.