Laboratory Validation of 3D Model and Investigating Its Application to Wind Turbine Noise Propagation over Rough Ground
Abstract
1. Introduction
2. Methods
2.1. Effective Impedance Model
2.2. Sound Field Above a Locally Reacting Ground
2.3. Principles of Parabolic Equation (PE) Method
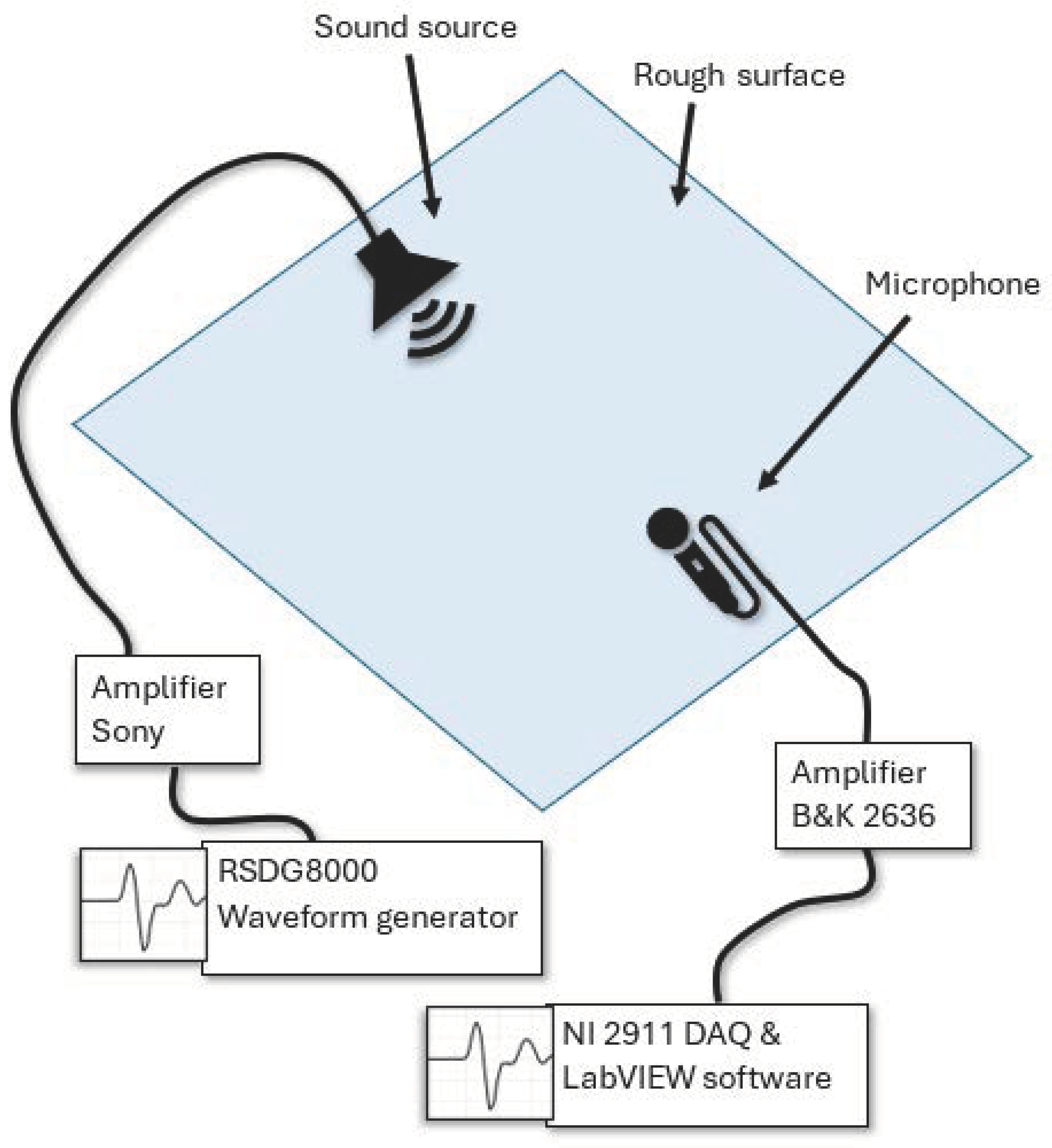
2.4. Experiment Methods
3. Results
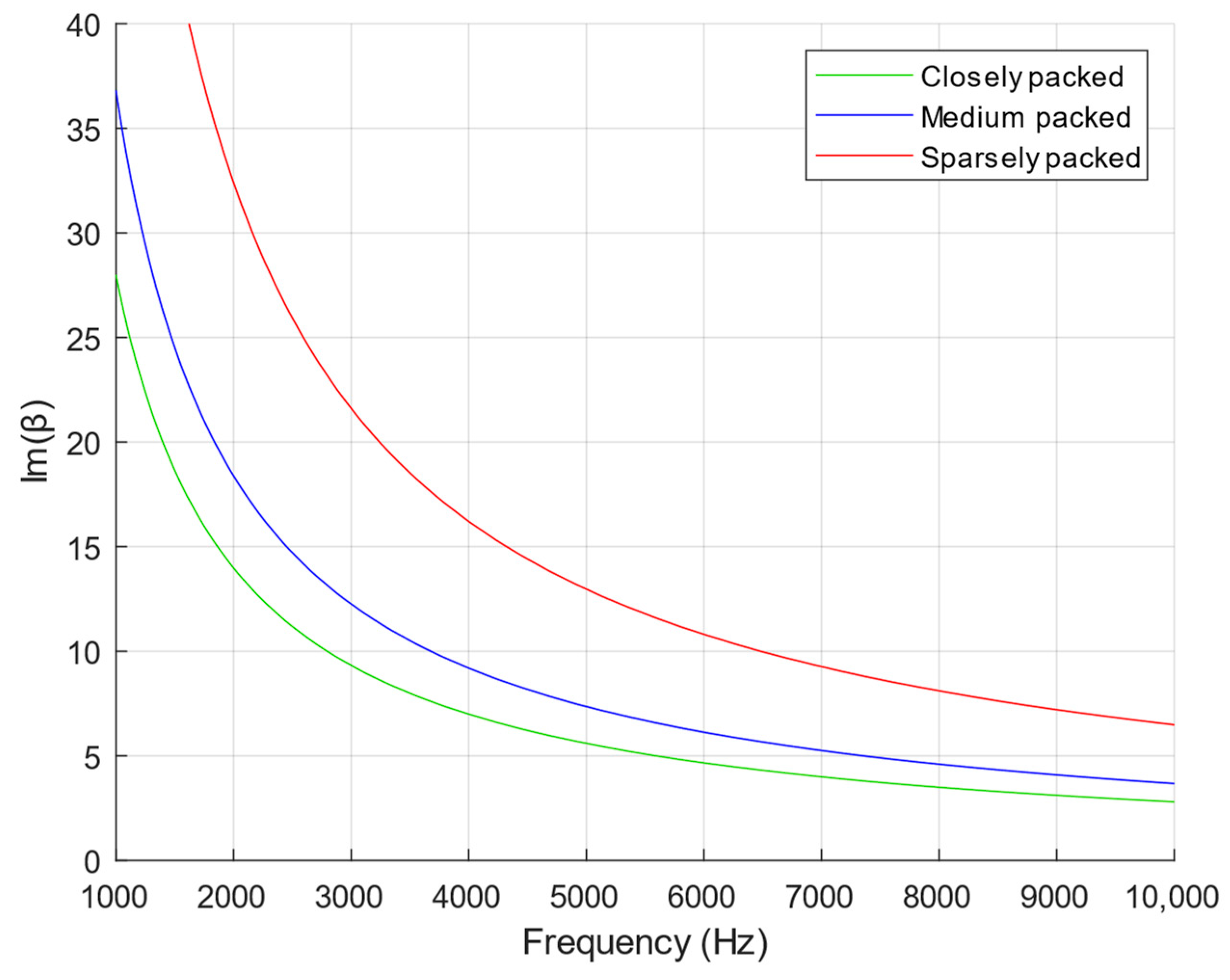
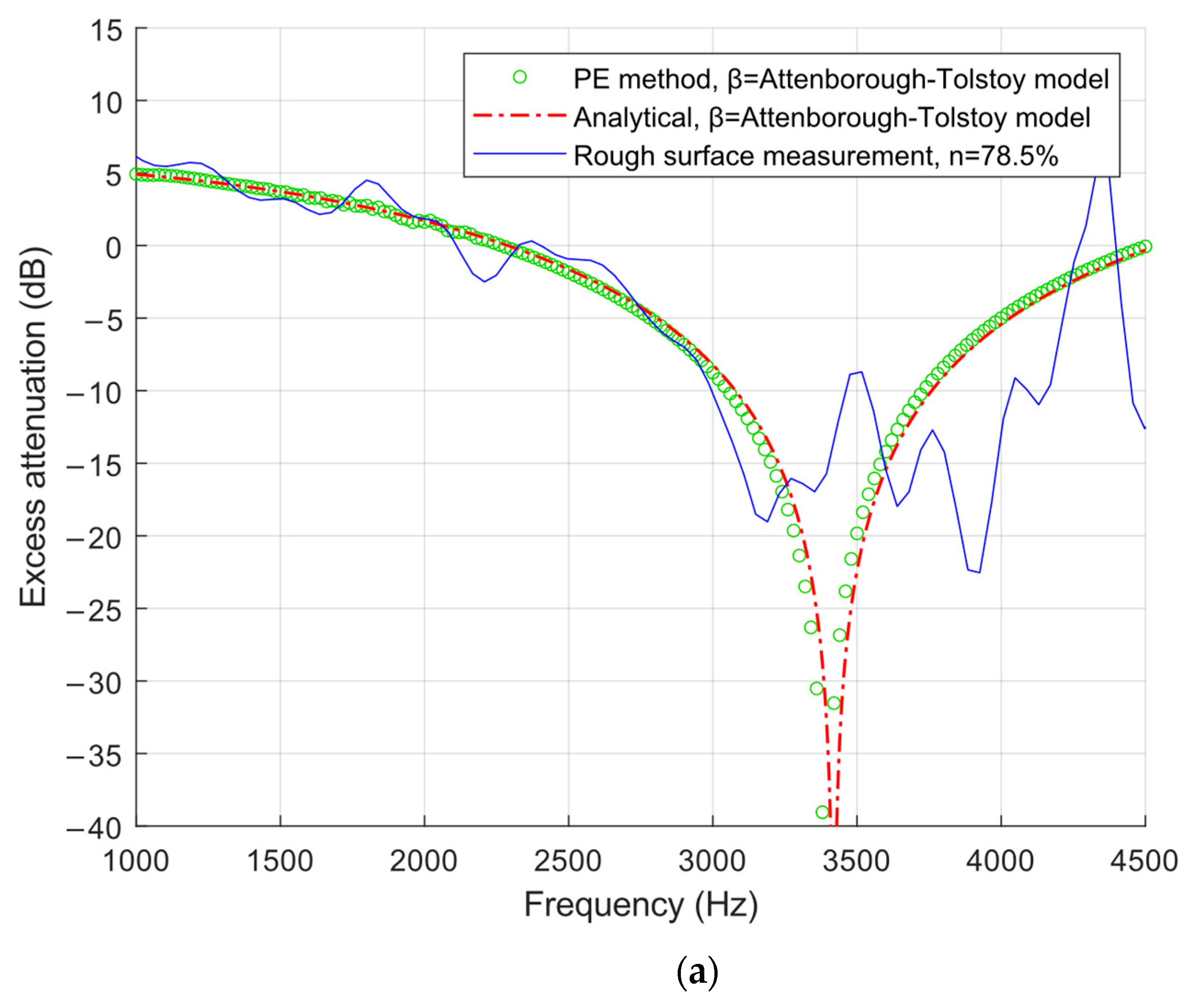
3.1. Validation of the Effective Impedance Model
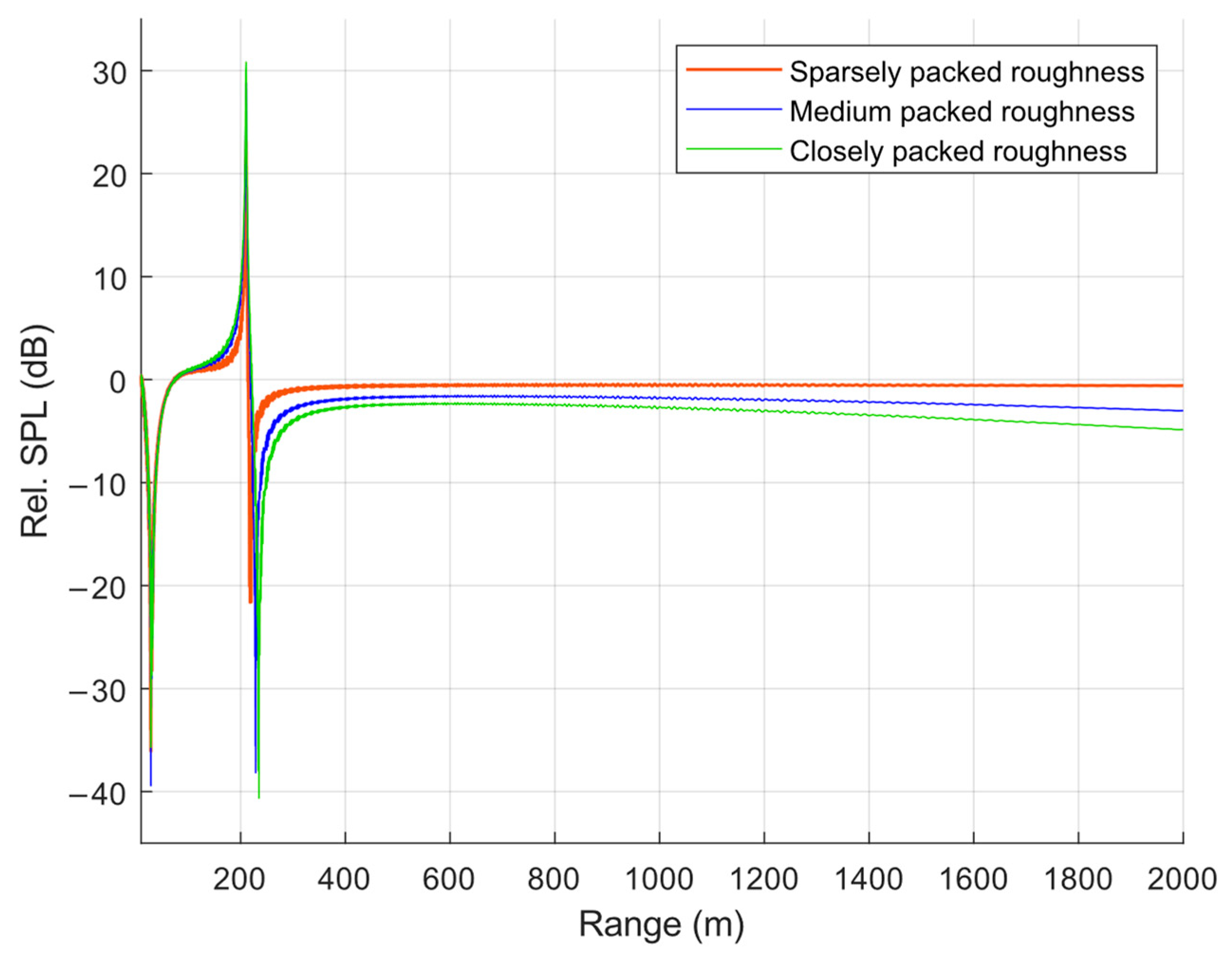
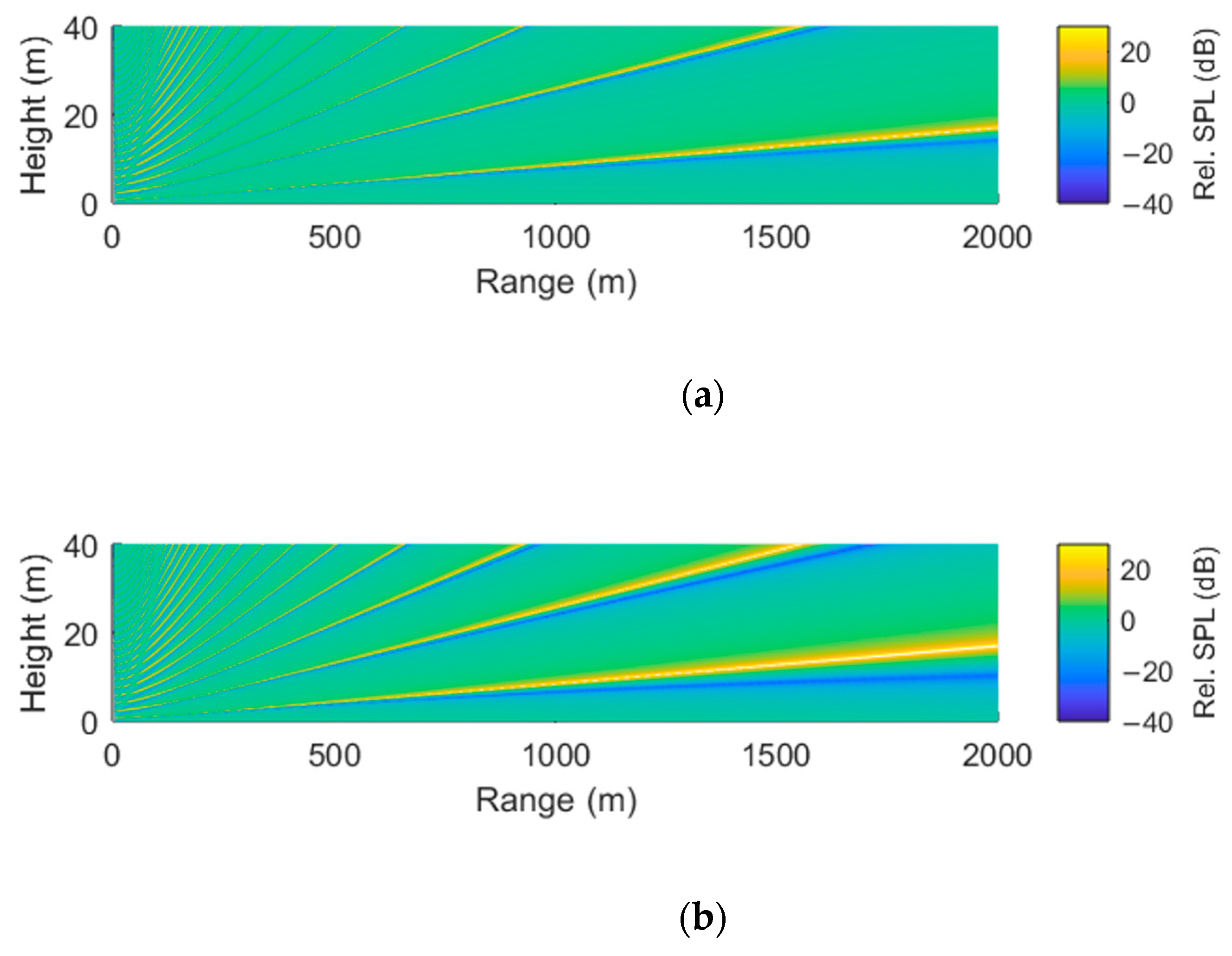
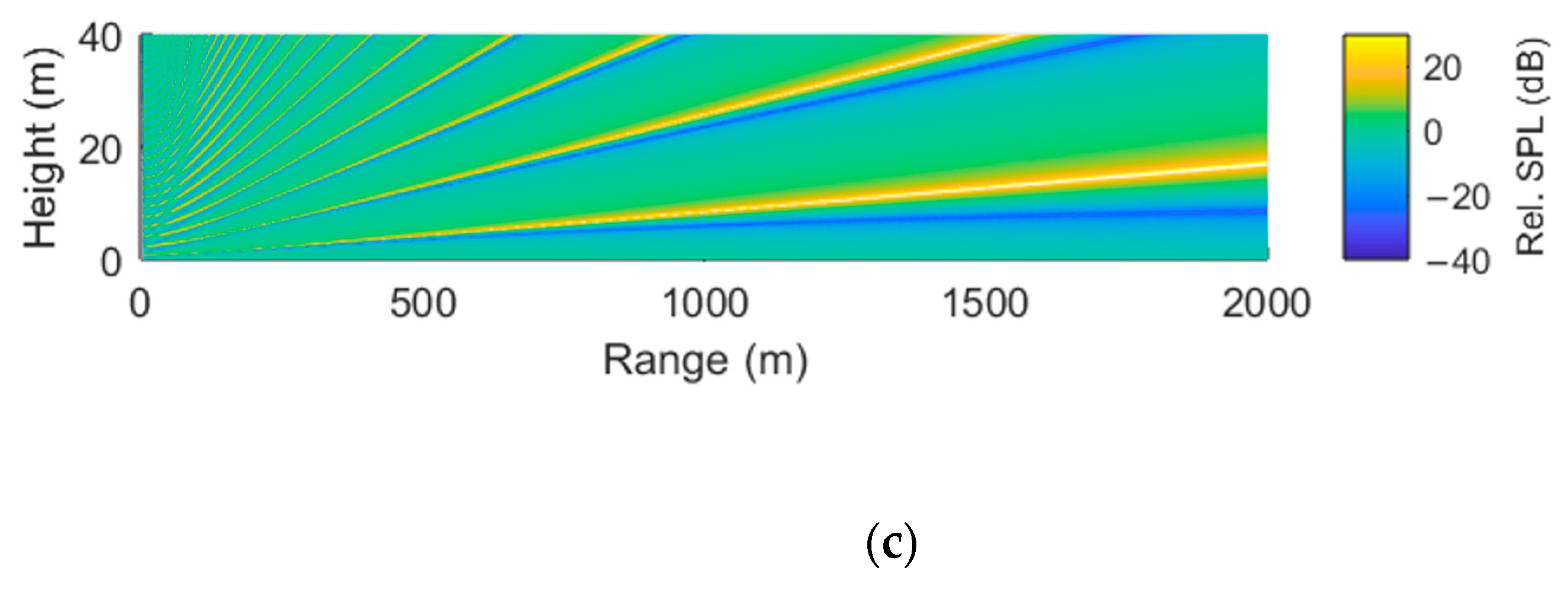
3.2. Further Parabolic Equation Method Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- van den Berg, F. A Proposal to Use Determinants of Annoyance in Wind Farm Planning and Management. Wind 2022, 2, 571–585. [Google Scholar] [CrossRef]
- da Silva, V.P.; Galvão, M.L.D.M. Onshore wind power generation and sustainability challenges in Northeast Brazil: A quick scoping review. Wind 2022, 2, 192–209. [Google Scholar] [CrossRef]
- Working Group on Noise from Wind Turbines; ETSU. The Assessment and Rating of Noise from Wind Farms; Easte Tennessess State University: Johnson City, TN, USA, 1996. [Google Scholar]
- Lotinga, M.; Lewis, T.; Powlson, J.; Berry, B. Onshore wind turbine noise: A review of the current guidance framework for the UK Government (Part 2: Conclusions and recommendations). Acoust. Bull. 2023, 49, 26–38. [Google Scholar]
- van Kamp, I.; van den Berg, F. Health effects related to wind turbine sound: An update. Int. J. Environ. Res. Public Health 2021, 18, 9133. [Google Scholar] [CrossRef] [PubMed]
- Vecchiotti, A.; Ryan, T.J.; Vignola, J.F.; Turo, D. Atmospheric Sound Propagation over Rough Sea: Numerical Evaluation of Equivalent Acoustic Impedance of Varying Sea States. Acoustics 2024, 6, 489–508. [Google Scholar] [CrossRef]
- Shen, W.Z.; Zhu, W.J.; Barlas, E.; Li, Y. Advanced flow and noise simulation method for wind farm assessment in complex terrain. Renew. Energy 2019, 143, 1812–1825. [Google Scholar] [CrossRef]
- Boulanger, P.; Attenborough, K.; Taherzadeh, S.; Waters-Fuller, T.; Li, K.M. Ground effect over hard rough surfaces. J. Acoust. Soc. Am. 1998, 104, 1474–1482. [Google Scholar] [CrossRef]
- Attenborough, K.; Taherzadeh, S. Propagation from a point source over a rough finite impedance boundary. J. Acoust. Soc. Am. 1995, 98, 1717–1722. [Google Scholar] [CrossRef]
- Brelet, Y.; Bourlier, C. SPM numerical results from an effective surface impedance for a one-dimensional perfectly-conducting rough sea surface. Prog. Electromagn. Res. 2008, 81, 413–436. [Google Scholar] [CrossRef]
- Boulanger, P.; Attenborough, K. Effective impedance spectra for predicting rough sea effects on atmospheric impulsive sounds. J. Acoust. Soc. Am. 2005, 117, 751–762. [Google Scholar] [CrossRef]
- Johansson, L. Sound Propagation Around Off-Shore Wind Turbines; Byggvetenskap: Stockholm, Sweden, 2003. [Google Scholar]
- Van Renterghem, T.; Botteldooren, D.; Dekoninck, L. Airborne sound propagation over sea during offshore wind farm piling. J. Acoust. Soc. Am. 2014, 135, 599–609. [Google Scholar] [CrossRef] [PubMed]
- Kayser, B.; Gauvreau, B.; Ecotière, D. Sensitivity analysis of a parabolic equation model to ground impedance and surface roughness for wind turbine noise. J. Acoust. Soc. Am. 2019, 146, 3222–3231. [Google Scholar] [CrossRef]
- Twersky, V. On scattering and reflection of sound by rough surfaces. J. Acoust. Soc. Am. 1957, 29, 209–225. [Google Scholar] [CrossRef]
- Biot, M.A. Reflection on a rough surface from an acoustic point source. J. Acoust. Soc. Am. 1957, 29, 1193–1200. [Google Scholar] [CrossRef]
- Biot, M.A. Generalized boundary condition for multiple scatter in acoustic reflection. J. Acoust. Soc. Am. 1968, 44, 1616–1622. [Google Scholar] [CrossRef]
- Tolstoy, I. Coherent sound scatter from a rough interface between arbitrary fluids with particular reference to roughness element shapes and corrugated surfaces. J. Acoust. Soc. Am. 1982, 72, 960–972. [Google Scholar] [CrossRef]
- Brekhovskikh, L. Diffraction of waves on an uneven surface, 2(Diffraction of acoustic and electromagnetic waves on wavy surfaces). Zh. Eksperim. Teor. Fiz. 1952, 23, 289–304. [Google Scholar]
- Ogilvy, J. Wave scattering from rough surfaces. Rep. Prog. Phys. 1987, 50, 1553. [Google Scholar] [CrossRef]
- Attenborough, K.; Van Renterghem, T. Predicting Outdoor Sound; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; United States Government Printing Office: Washington, DC, USA, 1948; Volume 55. [Google Scholar]
- Tappert, F.D. The parabolic approximation method. In Wave Propagation and Underwater Acoustics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 224–287. [Google Scholar]
- Könecke, S.; Hörmeyer, J.; Bohne, T.; Rolfes, R. A new base of wind turbine noise measurement data and its application for a systematic validation of sound propagation models. Wind. Energy Sci. Discuss. 2022, 8, 639–659. [Google Scholar] [CrossRef]
- West, M.; Gilbert, K.; Sack, R. A tutorial on the parabolic equation (PE) model used for long range sound propagation in the atmosphere. Appl. Acoust. 1992, 37, 31–49. [Google Scholar] [CrossRef]
- Salomons, E.M. Computational Atmospheric Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Bashir, I.; Taherzadeh, S.; Attenborough, K. Diffraction assisted rough ground effect: Models and data. J. Acoust. Soc. Am. 2013, 133, 1281–1292. [Google Scholar] [CrossRef] [PubMed]
- Nyborg, C.; Fischer, A.; Thysell, E.; Feng, J.; Søndergaard, L.S.; Sørensen, T.; Hansen, T.R.; Hansen, K.S.; Bertagnolio, F. Propagation of wind turbine noise: Measurements and model evaluation. J. Phys. Conf. Ser. 2022, 2265, 032041. [Google Scholar] [CrossRef]
- Ecotière, D. Can we really predict wind turbine noise with only one pointsource. In Proceedings of the 6th International Meeting on Wind Turbine Noise, Glasgow, Scotland, 20–23 April 2015. [Google Scholar]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Dag, K.O.; Moriarty, P. Consistent modelling of wind turbine noise propagation from source to receiver. J. Acoust. Soc. Am. 2017, 142, 3297–3310. [Google Scholar] [CrossRef] [PubMed]
- Oerlemans, S.; Sijtsma, P.; López, B.M. Location and quantification of noise sources on a wind turbine. J. Sound Vib. 2007, 299, 869–883. [Google Scholar] [CrossRef]
- Søndergaard, B. Low frequency noise from wind turbines: Do the Danish regulations have any impact? An analysis of noise measurements. Int. J. Aeroacoust. 2015, 14, 909–915. [Google Scholar] [CrossRef]
- Eckart, C. The scattering of sound from the sea surface. J. Acoust. Soc. Am. 1953, 25, 566–570. [Google Scholar] [CrossRef]
- Sack, R.; West, M. A parabolic equation for sound propagation in two dimensions over any smooth terrain profile: The generalised terrain parabolic equation (GT-PE). Appl. Acoust. 1995, 45, 113–129. [Google Scholar] [CrossRef]
- Chu, D.; Stanton, T. Application of Twersky’s boss scattering theory to laboratory measurements of sound scattered by a rough surface. J. Acoust. Soc. Am. 1990, 87, 1557–1568. [Google Scholar] [CrossRef]
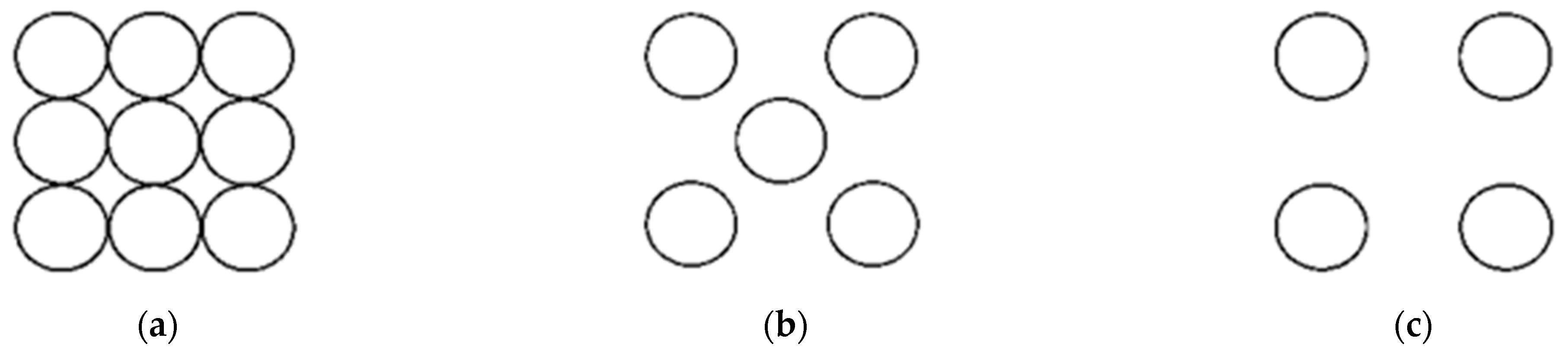
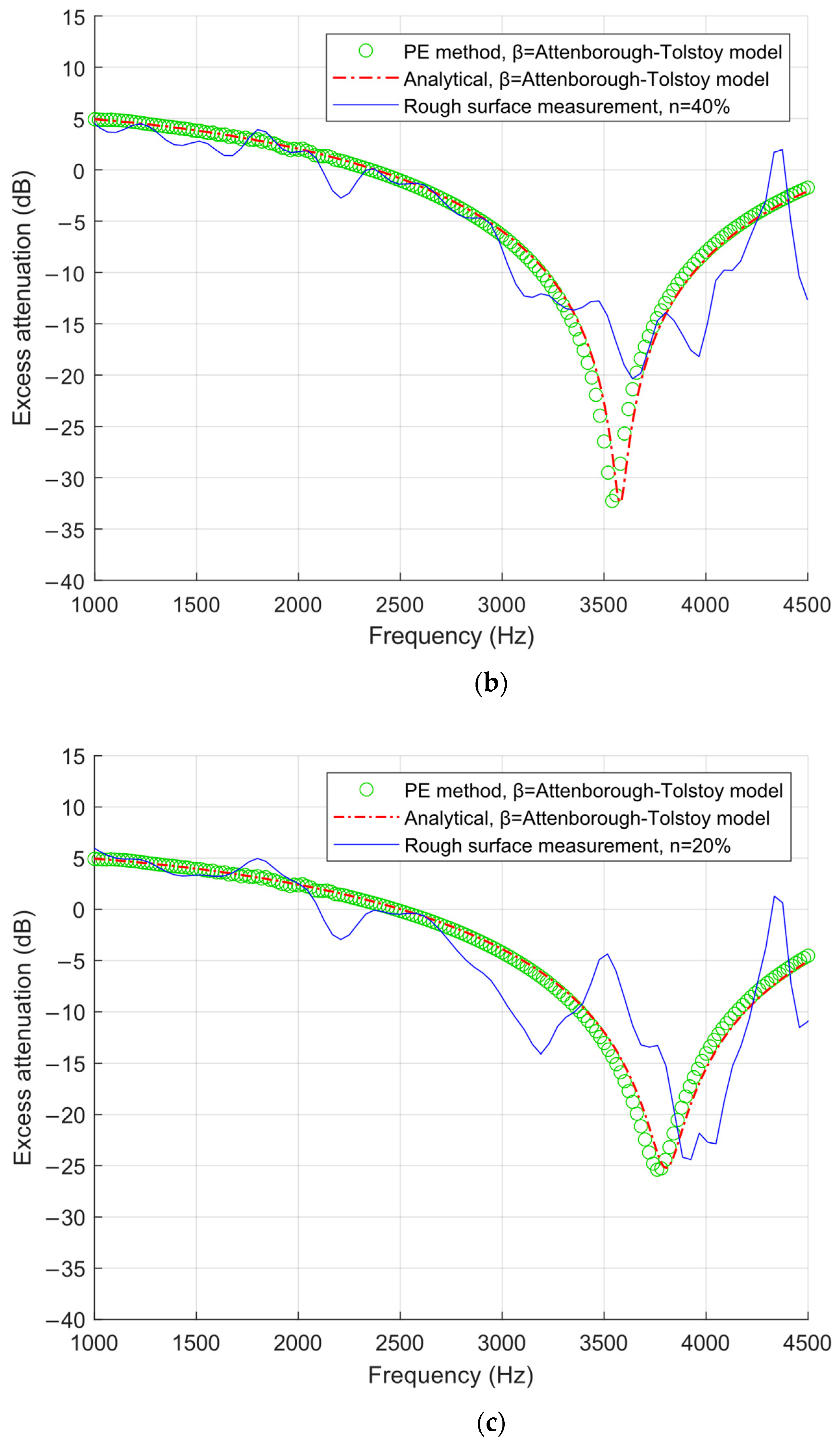
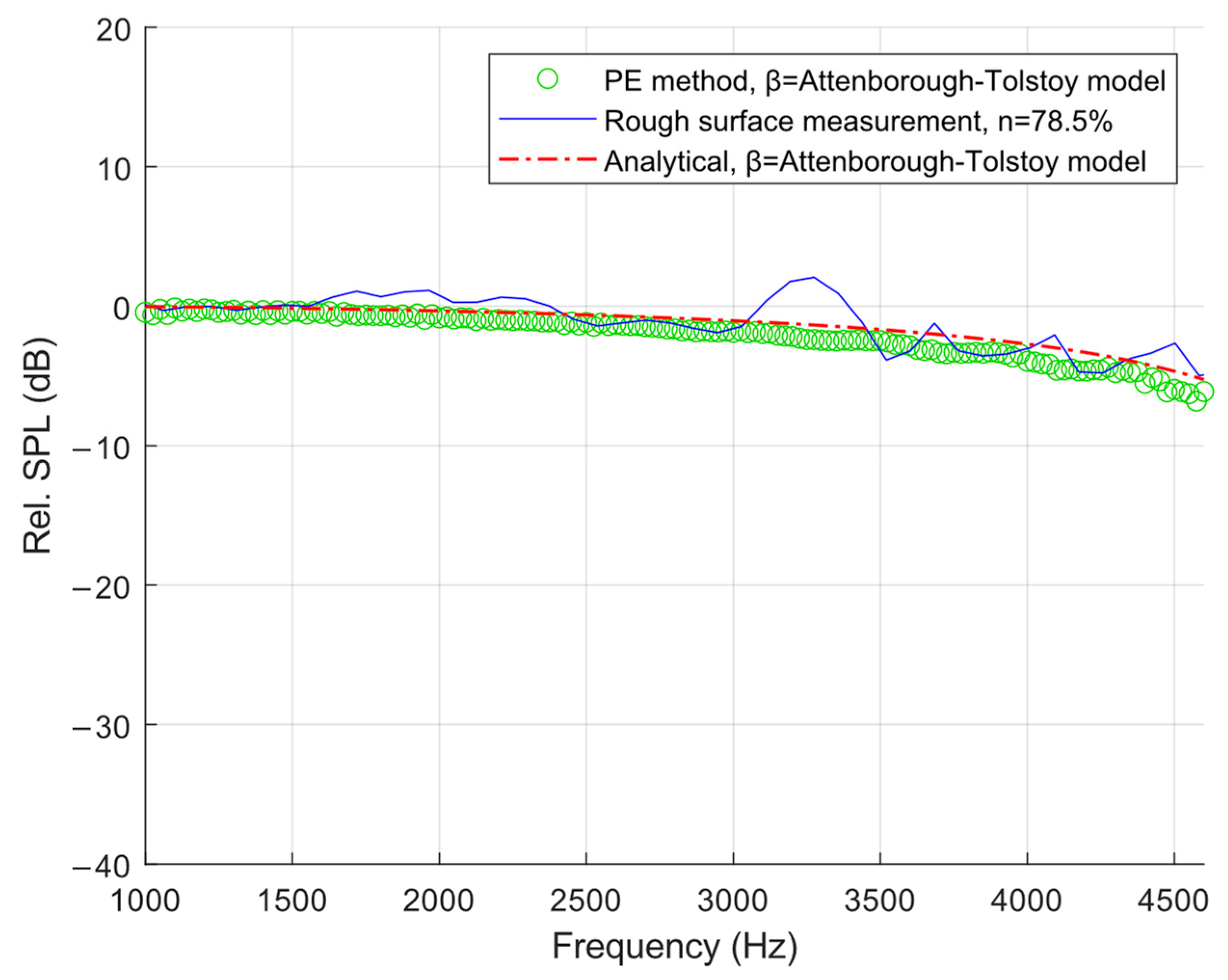

| Roughness Type | Number per Unit Area, N | Center-Center Spacing, L (m) | Coverage per Unit Area, n (%) |
|---|---|---|---|
| Closely packed | 1372 | 0.033 | 78.5 |
| Medium packed | 700 | 0.046 | 40 |
| Sparsely packed | 350 | 0.065 | 20 |
| Roughness Type | Number per Unit Area, N | Center-Center Spacing, L (m) | Coverage per Unit Area, n (%) |
|---|---|---|---|
| Closely packed | 6 | 0.483 | 75.4 |
| Medium packed | 3 | 0.683 | 37.7 |
| Sparsely packed | 1 | 1.366 | 12.6 |
| Roughness Type | Rel. SPL at 2 km (dB) |
|---|---|
| Closely packed | −4.9 |
| Medium packed | −3 |
| Sparsely packed | −0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naylor, J.; Qin, Q. Laboratory Validation of 3D Model and Investigating Its Application to Wind Turbine Noise Propagation over Rough Ground. Wind 2024, 4, 363-375. https://doi.org/10.3390/wind4040018
Naylor J, Qin Q. Laboratory Validation of 3D Model and Investigating Its Application to Wind Turbine Noise Propagation over Rough Ground. Wind. 2024; 4(4):363-375. https://doi.org/10.3390/wind4040018
Chicago/Turabian StyleNaylor, James, and Qin Qin. 2024. "Laboratory Validation of 3D Model and Investigating Its Application to Wind Turbine Noise Propagation over Rough Ground" Wind 4, no. 4: 363-375. https://doi.org/10.3390/wind4040018
APA StyleNaylor, J., & Qin, Q. (2024). Laboratory Validation of 3D Model and Investigating Its Application to Wind Turbine Noise Propagation over Rough Ground. Wind, 4(4), 363-375. https://doi.org/10.3390/wind4040018






