Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation
Abstract
1. Introduction
2. Plant Description and Control Objectives
2.1. Baseline Reference System
2.2. The Numerical Model of the FOWT
2.3. Disturbances
2.4. Control Inputs
2.5. Control Objectives
- 1.
- Maintaining the generated power around the target value
- 2.
- Repositioning the platform to reach a target position
- 3.
- Limiting the platform’s oscillation motions and velocities (including the repositioning step).
3. Controller Design
3.1. Controller Structure
3.1.1. Power Regulator
3.1.2. Position Controller
3.2. Model Predictive Controller Design
4. Case Study
4.1. Position Control Results
4.2. Power and Generator Speed Control Results
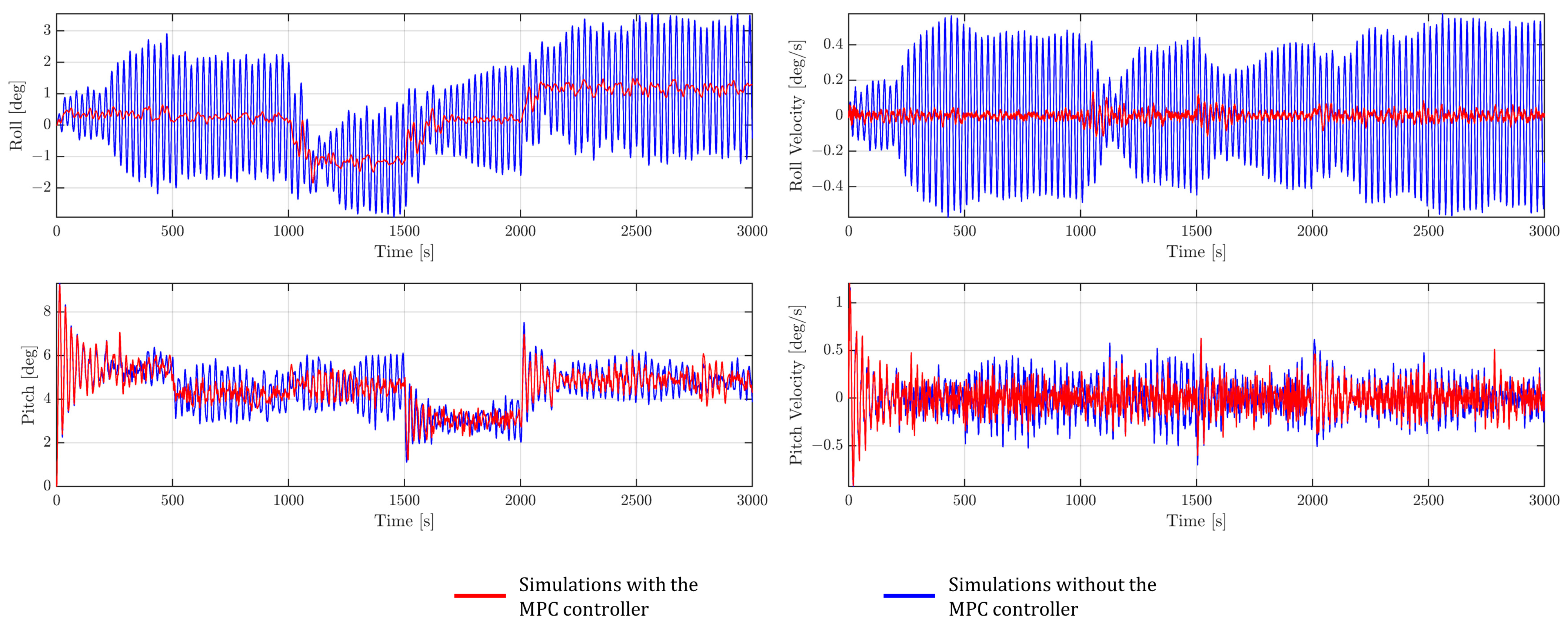
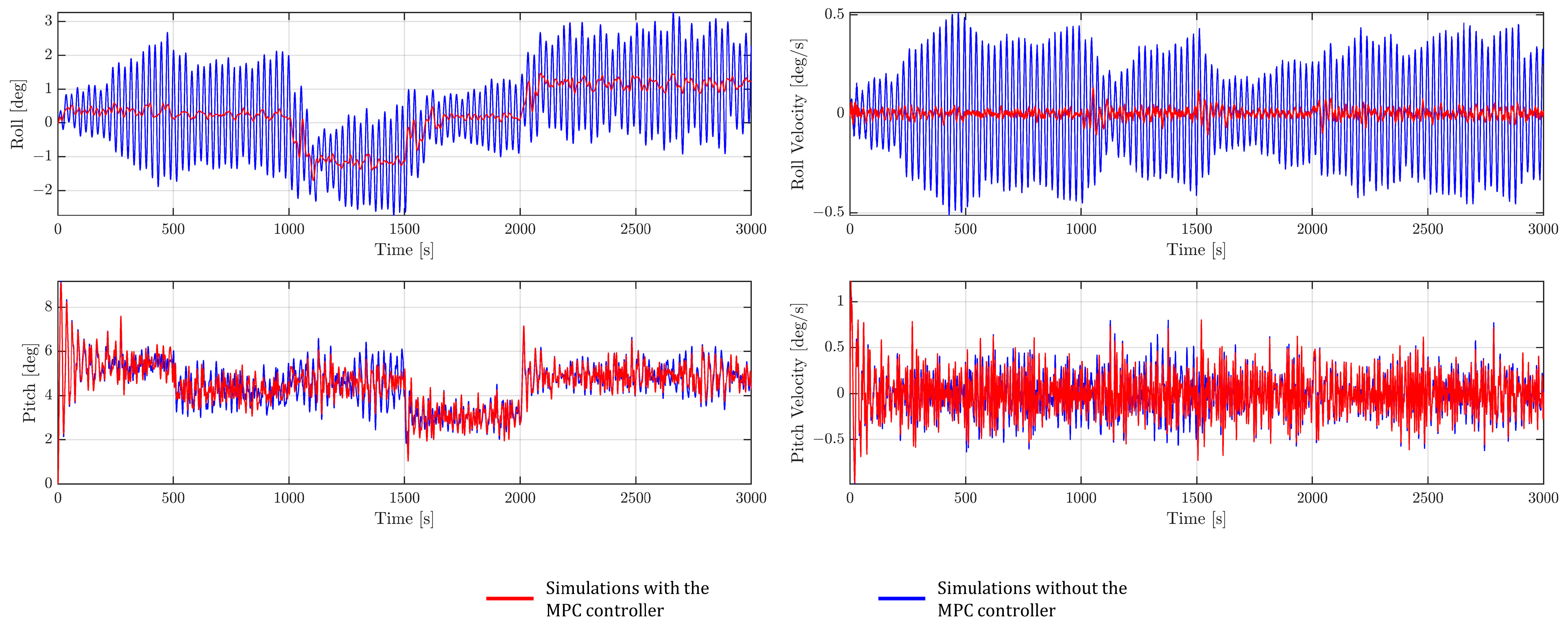
4.3. Platform Rotational Motion and Oscillation Results
4.4. Control Inputs Results
4.5. Quantitative Comparison of the Controllers’ Performances
4.6. MPC Performance under Severe Environmental Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Controller Parameters
References
- Musial, W.; Beiter, P.; Spitsen, P.; Nunemaker, J.; Gevorgian, V.; Cooperman, A.; Hammond, R.; Shields, M. 2019 Offshore Wind Technology Data Update; NREL/TP-5000-77411; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2020. [Google Scholar]
- GWEC. Global Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021; Available online: https://gwec.net/global-wind-report-2021/ (accessed on 4 October 2022).
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, USA, National Renewable Energy Laboratory, Golden, CO, USA, 2007. [Google Scholar]
- Swart, R.; Coppens, C.; Gordjin, H.; Piek, M.; Ruyssenaars, P.; Schrander, J.J.; Hoogwijk, M.; Papalexandrou, M.; Horalek, J. Europe’s Onshore Andoffshore Wind Energy Potential: An Assessment of Environmental and Economic Constraints. (No. 6/2009); European Environment Agency: København, Denmark, 2009. [Google Scholar]
- Shah, K.A.; Meng, F.; Li, Y.; Nagamune, R.; Zhou, Y.; Ren, Z.; Jiang, Z. A Synthesis of Feasible Control Methods for Floating Offshore Wind Turbine System Dynamics. Renew. Sustain. Energy Rev. 2021, 151, 111525. [Google Scholar] [CrossRef]
- Stehly, T.; Beiter, P. 2018 Cost of Wind Energy Review (Technical Report); NREL/TP-5000-74598; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [Google Scholar]
- Barthelmie, R.J.; Hansen, K.; Frandsen, S.T.; Rathmann, O.; Schepers, J.G.; Schlez, W.; Phillips, J.; Rados, K.; Zervos, A.; Politis, E.S.; et al. Modelling and Measuring Flow and Wind Turbine Wakes in Large Wind Farms Offshore. Wind. Energy 2009, 12, 431–444. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind Turbine Wake Aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.-T.; Chen, C.-H. A Numerical Study of the Effects of Wind Direction on Turbine Wakes and Power Losses in a Large Wind Farm. Energies 2013, 6, 5297–5313. [Google Scholar] [CrossRef]
- Fleming, P.A.; Gebraad, P.M.O.; Lee, S.; van Wingerden, J.-W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Evaluating Techniques for Redirecting Turbine Wakes Using SOWFA. Renew. Energy 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Steinbuch, M.; de Boer, W.W.; Bosgra, O.H.; Peters, S.A.W.M.; Ploeg, J. Optimal Control of Wind Power Plants. J. Wind. Eng. Ind. Aerodyn. 1988, 27, 237–246. [Google Scholar] [CrossRef]
- Wagenaar, J.W.; Machielse, L.; Schepers, J. Controlling wind in ECN’s scaled wind farm. In Proceedings of the European Wind Energy Association (EWEA) Annual Event, Oldenburg, Germany, 16–19 April 2012; pp. 685–694. [Google Scholar]
- Jiménez, Á.; Crespo, A.; Migoya, E. Application of a LES Technique to Characterize the Wake Deflection of a Wind Turbine in Yaw. Wind. Energy 2009, 13, 559–572. [Google Scholar] [CrossRef]
- Guntur, S.; Troldborg, N.; Gaunaa, M. Application of Engineering Models to Predict Wake Deflection Due to a Tilted Wind Turbine. In Proceedings of the EWEC 2012—European Wind Energy Conference & Exhibition, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Fleming, P.; Gebraad, P.M.O.; Lee, S.; van Wingerden, J.-W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Simulation Comparison of Wake Mitigation Control Strategies for a Two-Turbine Case. Wind. Energy 2015, 18, 2135–2143. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Nagamune, R. Modeling and Power Optimization of Floating Offshore Wind Farms with Yaw and Induction-Based Turbine Repositioning. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 5458–5463. [Google Scholar]
- Kheirabadi, A.C.; Nagamune, R. Real-Time Relocation of Floating Offshore Wind Turbine Platforms for Wind Farm Efficiency Maximization: An Assessment of Feasibility and Steady-State Potential. Ocean Eng. 2020, 208, 107445. [Google Scholar] [CrossRef]
- Rodrigues, S.F.; Teixeira Pinto, R.; Soleimanzadeh, M.; Bosman, P.A.N.; Bauer, P. Wake Losses Optimization of Offshore Wind Farms with Moveable Floating Wind Turbines. Energy Convers. Manag. 2015, 89, 933–941. [Google Scholar] [CrossRef]
- Gao, Y.; Padmanabhan, A.; Chen, O.; Kheirabadi, A.C.; Nagamune, R. A Baseline Repositioning Controller for a Floating Offshore Wind Farm. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8 June 2022; pp. 4224–4229. [Google Scholar]
- Han, C.; Nagamune, R. Platform Position Control of Floating Wind Turbines Using Aerodynamic Force. Renew. Energy 2020, 151, 896–907. [Google Scholar] [CrossRef]
- Escobar Aquino, E.E.; Nagamune, R. H∞ Position Transfer and Regulation for Floating Offshore Wind Turbines. Control Theory Technol. 2020, 18, 231–245. [Google Scholar] [CrossRef]
- Xu, S.; Murai, M.; Wang, X.; Takahashi, K. A Novel Conceptual Design of a Dynamically Positioned Floating Wind Turbine. Ocean Eng. 2021, 221, 108528. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. Stabilization of Floating Offshore Wind Turbines by Artificial Muscle Based Active Mooring Line Force Control. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2277–2282. [Google Scholar]
- Sierra-Garcia, J.E.; Santos, M.; Pandit, R. Wind Turbine Pitch Reinforcement Learning Control Improved by PID Regulator and Learning Observer. Eng. Appl. Artif. Intell. 2022, 111, 104769. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Wei, X. Reinforcement Learning-Based Structural Control of Floating Wind Turbines. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1603–1613. [Google Scholar] [CrossRef]
- Wu, T.; Snaiki, R. Applications of Machine Learning to Wind Engineering. Front. Built Environ. 2022, 8, 811460. [Google Scholar] [CrossRef]
- Li, S.; Snaiki, R.; Wu, T. Active Simulation of Transient Wind Field in a Multiple-Fan Wind Tunnel via Deep Reinforcement Learning. J. Eng. Mech. 2021, 147, 04021056. [Google Scholar] [CrossRef]
- Li, S.; Snaiki, R.; Wu, T. A Knowledge-enhanced Deep Reinforcement Learning-based Shape Optimizer for Aerodynamic Mitigation of Wind-sensitive Structures. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 733–746. [Google Scholar] [CrossRef]
- Shah, K.A.; Li, Y.; Nagamune, R.; Zhou, Y.; Ur Rehman, W. Platform Motion Minimization Using Model Predictive Control of a Floating Offshore Wind Turbine. Theor. Appl. Mech. Lett. 2021, 11, 100295. [Google Scholar] [CrossRef]
- Raach, S.; Schlipf, D.; Sandner, F.; Matha, D.; Cheng, P.W. Nonlinear Model Predictive Control of Floating Wind Turbines with Individual Pitch Control. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4434–4439. [Google Scholar]
- Homer, J.R.; Nagamune, R. Physics-Based 3-D Control-Oriented Modeling of Floating Wind Turbines. IEEE Trans. Control Syst. Technol. 2018, 26, 14–26. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060, 947422; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Buhl, M.; Greg, H.; Jason, J.; Bonnie, J.; Rafael, M.; Andy, P. Mike Sprague OpenFAST. Available online: https://github.com/OpenFAST/openfast (accessed on 2 January 2023).
- Namik, H.; Stol, K. Individual Blade Pitch Control of Floating Offshore Wind Turbines. Wind Energy 2010, 13, 74–85. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; NREL/TP-5000-60601, 1155123; National Renewable Energy Laboratory: Golden, CO, USA, 2014. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide-Updated August 2005; NREL/TP-500-38230, 15020796; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Jonkman, J.M. Dynamics of Offshore Floating Wind Turbines-Model Development and Verification. Wind. Energy 2009, 12, 459–492. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A Proposed Spectral Form for Fully Developed Wind Seas Based on the Similarity Theory of S. A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Han, C.; Homer, J.R.; Nagamune, R. Movable Range and Position Control of an Offshore Wind Turbine with a Semi-Submersible Floating Platform. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1389–1394. [Google Scholar]
- Schmid, C.; Biegler, L.T. Quadratic Programming Methods for Reduced Hessian SQP. Comput. Chem. Eng. 1994, 18, 817–832. [Google Scholar] [CrossRef]
- Collu, M.; Borg, M. Design of Floating Offshore Wind Turbines. In Offshore Wind Farms; Elsevier: Amsterdam, The Netherlands, 2016; pp. 359–385. ISBN 978-0-08-100779-2. [Google Scholar]
- Han, C. Position Control of a Floating Offshore Wind Turbine System Using Aerodynamic Force; University of British Columbia: Vancouver, BC, Canada, 2018. [Google Scholar] [CrossRef]
- Escobar Aquino, E.E. H∞ Position Control of a 5-MW Offshore Wind Turbine with a Semi-Submersible Platform; University of British Columbia: Vancouver, BC, Canada, 2019. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. Hurricane Risk Assessment of Offshore Wind Turbines under a Changing Climate Scenario; International Association for Bridge and Structural Engineering: Ghent, Belgium, 2021. [Google Scholar]
- Snaiki, R.; Wu, T. Hurricane Hazard Assessment Along the United States Northeastern Coast: Surface Wind and Rain Fields Under Changing Climate. Front. Built Environ. 2020, 6, 573054. [Google Scholar] [CrossRef]
- Snaiki, R.; Parida, S.S. A Data-Driven Physics-Informed Stochastic Framework for Hurricane-Induced Risk Estimation of Transmission Tower-Line Systems under a Changing Climate. Eng. Struct. 2023, 280, 115673. [Google Scholar] [CrossRef]
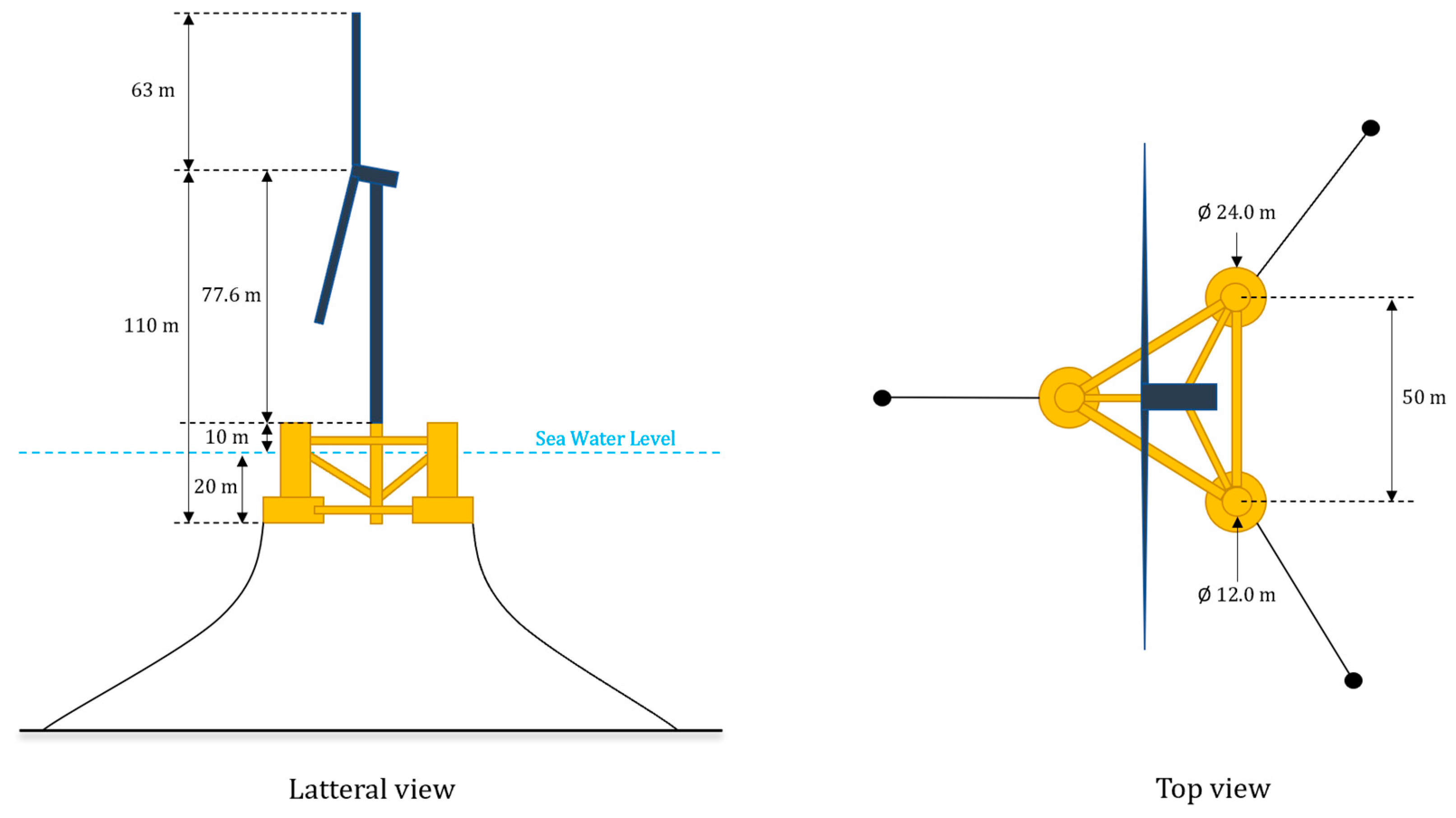

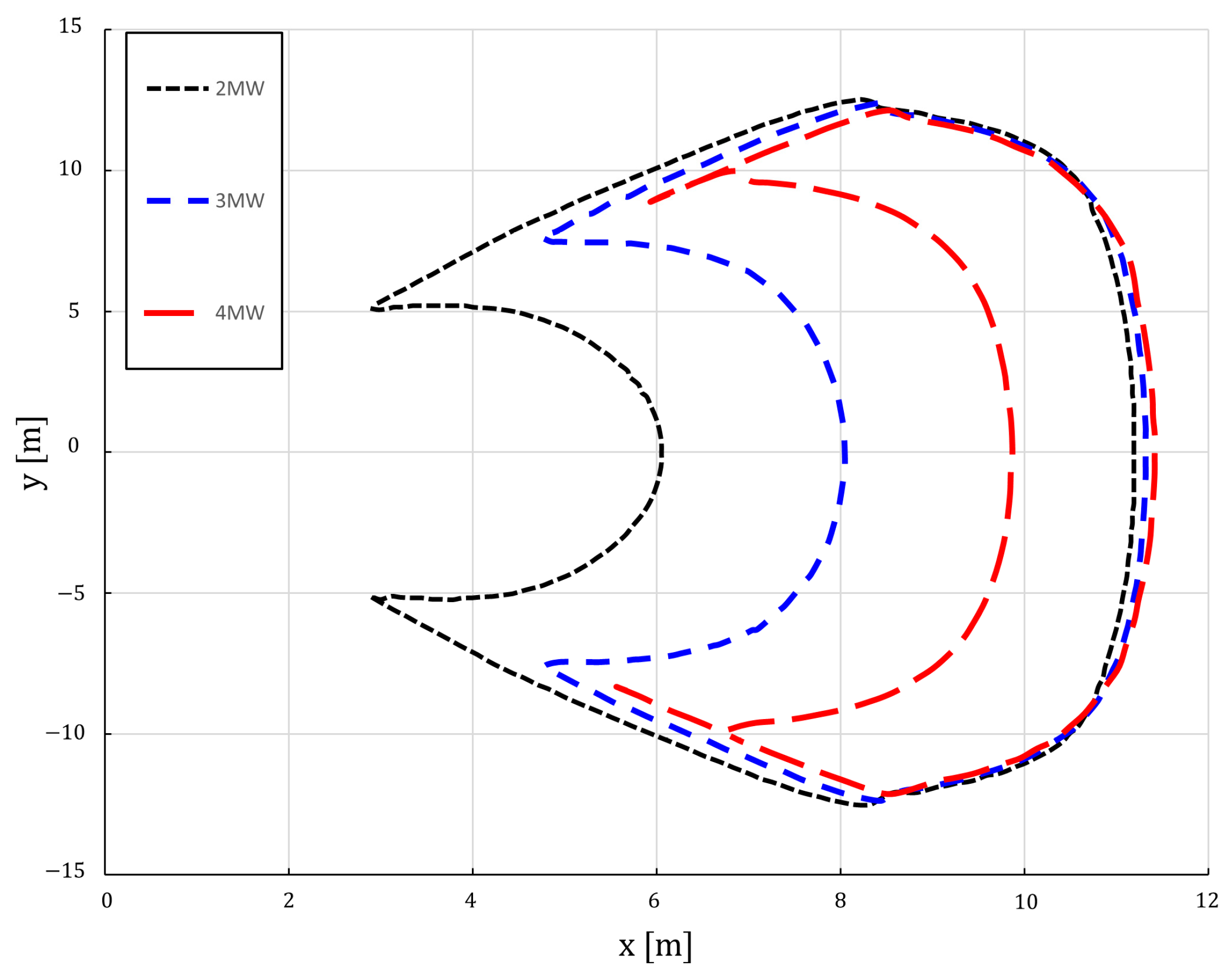
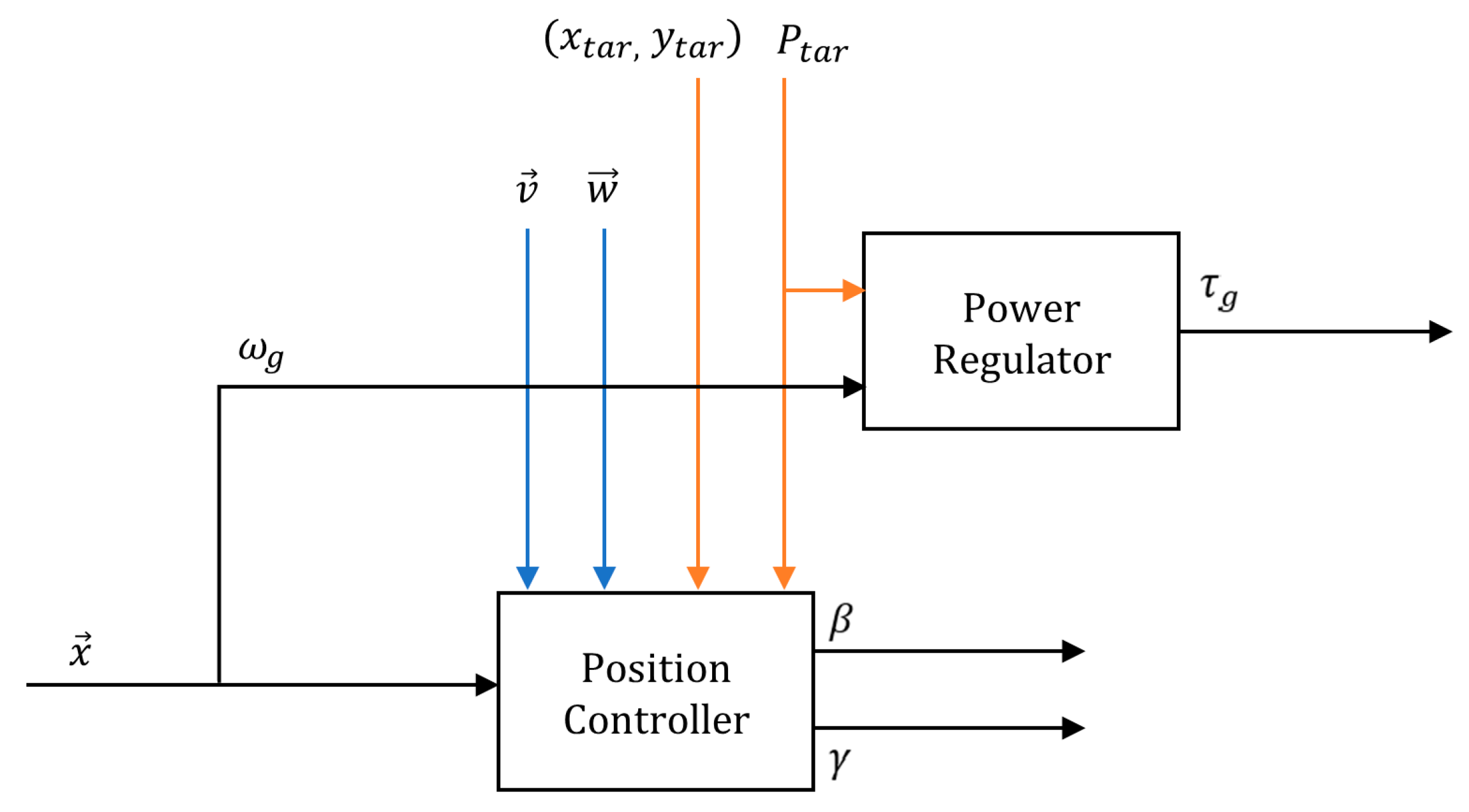
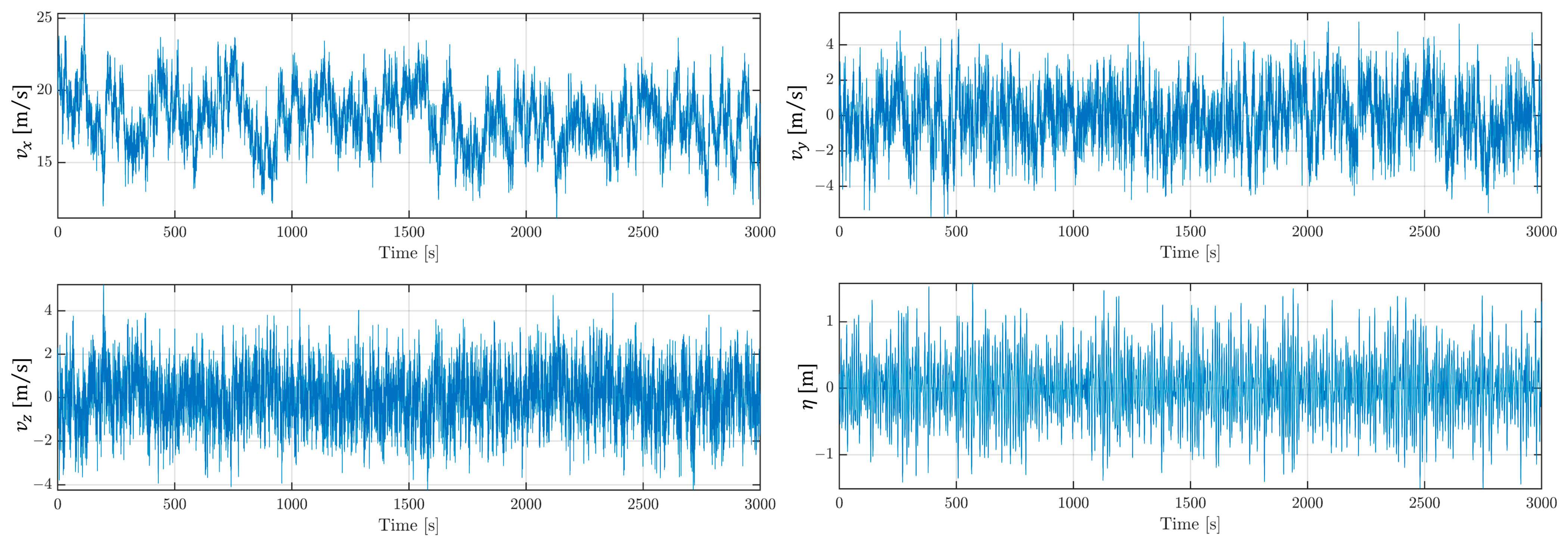





| Property | Value |
|---|---|
| Power rating | 5 [MW] |
| Rotor diameter | 126 [m] |
| Hub height | 90 [m] |
| Gear ratio | 97 |
| Generator efficiency | 94.4 [%] |
| Cut-in, rated, cut-out wind speed | 3, 11.4, 25 [m/s] |
| Cut-in, rated rotor speed | 6.9, 12.1 [rpm] |
| Water depth | 200 [m] |
| Mooring line length | 835.5 [m] |
| Property | Value |
|---|---|
| (2, 15) [m] | |
| (−15, 15) [m] | |
| (669.3, 1173.7) [rpm] | |
| (−10, 10), (−10, 10) [deg] |
| Control Inputs | Saturation | Rate Limit |
|---|---|---|
| β | [−30, 30] [deg] | [−8, 8] [deg/s] |
| [0, 47.402] [kN·m] | [−15, 15] [kN·m/s] | |
| γ | [−60, 60] [deg] | [−0.3, 0.3] [deg/s] |
| Target Number | Time (s) | Position Target (m) | Power Target (MW) |
|---|---|---|---|
| 1 | 0–500 | (11, 0) | 5 |
| 2 | 500–1000 | (9, 0) | 3 |
| 3 | 1000–1500 | (10, 5) | 4 |
| 4 | 1500–2000 | (7, 0) | 2 |
| 5 | 2000–3000 | (10, −3) | 3 |
| Controller | Position (m) | Power (kW) | Roll Velocity (deg/s) | Pitch Velocity (deg/s) |
|---|---|---|---|---|
| MPC | 1.203 | 42.154 | 0.026 | 0.167 |
| PID | 2.075 | 42.750 | 0.055 | 0.166 |
| Controller | Position (m) | Power (kW) | Roll Velocity (deg/s) | Pitch Velocity (deg/s) |
|---|---|---|---|---|
| MPC | 1.369 | 44.154 | 0.024 | 0.225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jard, T.; Snaiki, R. Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation. Wind 2023, 3, 131-150. https://doi.org/10.3390/wind3020009
Jard T, Snaiki R. Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation. Wind. 2023; 3(2):131-150. https://doi.org/10.3390/wind3020009
Chicago/Turabian StyleJard, Timothé, and Reda Snaiki. 2023. "Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation" Wind 3, no. 2: 131-150. https://doi.org/10.3390/wind3020009
APA StyleJard, T., & Snaiki, R. (2023). Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation. Wind, 3(2), 131-150. https://doi.org/10.3390/wind3020009







