Modern society faces an existential dilemma. As industrialized countries support a modern lifestyle driven by consumerism, energy consumption continues to grow. Even amongst the highest energy users, the primary source continues to be non-renewable energy sources such as oil, coal, and natural gas [
1]. Coupled with developing nations reliance on dirty fuel sources such as coal, a warming planet already seeing the effects of climate change, and increasing energy prices [
2], the need for energy source diversification has never been stronger. Offshore wind power is a resource with strong potential to fill this need in the United States. In fact, while the total U.S. energy consumption is 13 quads/year [
3], the total potential of offshore wind, accounting for losses and including conservative assumptions regarding technical, legal, regulatory, and social inhibiting factors, is still 2 quads/year [
4]. With 58% of this potential in water depths requiring floating platforms, the potential for floating offshore wind technologies as part of the United States’ power portfolio is strong.
The state of the art of floating offshore wind technology, however, is expensive. According to NREL, existing FOWT technologies have achieved a levelized cost of energy (LCOE) of USD 0.15–0.18/kWh, which is high compared to the USD 0.03–0.05/kWh for land-based turbines [
5]. Much of this cost is from the steel used to make large and heavy platforms designed to keep the system as stable as possible, survive large sea storms, and maintain similar dynamics to onshore wind turbines. An arm of the Department of Energy, the Advanced Research Projects Agency—Energy (ARPA-E), which funds emerging but unproven technologies, identified floating offshore wind as a research area with significant potential because of the untapped but currently expensive power resource. To address this cost difference, the ARPA-E Aerodynamic Turbines Lighter and Afloat with Nautical Technologies and Integrated Servo-control (ATLANTIS) program set out to generate “radically new FOWT designs with significantly lower mass/area; a new generation of computer tools to facilitate control co-design of the FOWTs; and generation of real-data from full and lab-scale experiments to validate the FOWT designs and computer tools” [
6]. To bring floating offshore wind technology down to a competitive cost, the goal of this project is to design a floating offshore wind turbine concept with a USD 0.075/kWh or less LCOE. The current work fits into the first ATLANTIS program category. Building on the University of Maine’s experience with post-tensioned concrete and a previous collaboration with NASA on tuned mass dampers utilizing ballast water to stabilize the platform, this project proposes a lightweight floating platform with significantly lower costs than the current designs. Additionally, in keeping with a controls co-design methodology, the platform is optimized for the lowest possible cost with the use of computationally efficient analysis tools.
Proposed Design and Solution Method
The three main types of floating offshore wind turbine platforms are spars, tension-leg platforms, and semi-submersibles. Spars achieve their stability with the restoring force created between the low center of gravity and the high center of buoyancy. However, they require deep drafts to achieve this stability, which also necessitates assembly offshore, increasing costs. Tension-leg platforms can be stable and light due to stability achieved from the tension in the mooring lines, but anchoring to the seabed is difficult, especially as wind turbine sizes increase. Finally, semi-submersible platforms achieve their stability from a large water plane area. Designs must be large enough to avoid typical wave period excitation ranges of 5–20 s, but since the period is inversely proportional to the water plane area, existing designs have been large, heavy, and therefore expensive [
7].
The typical design process of a floating offshore wind turbine is performed sequentially, owing to the computationally intensive time domain simulations required. To satisfy the design requirements of the International Electrotechnical Commission, the combination of winds, waves, and currents for all of the design load cases requires thousands of simulations. As a result, platforms cannot be optimized with an analytical function due to the nonlinear design constraints. Furthermore, stochastic optimization techniques are infeasible when using all design load cases with time domain simulations due to the computational time required. In order to develop the novel cruciform platform concept with tuned mass damper (TMD) elements and simultaneously minimize the cost to meet the ARPE-E project goals, a novel optimization technique was developed.
Other projects have proposed solutions to floating offshore wind turbine optimization problems. Most focus on replacing time domain simulations in the optimization with various methods. In [
8], a spar was developed by generating 12 feasible designs with a spreadsheet calculator, executing a frequency domain simulation to down-select the three best designs and then performing time domain simulations on the set to choose a finalized design. This approach is similar to the current work in the progression from hydrostatic calculations showing feasible designs to frequency domain simulations. However, with only 12 designs to choose from, there is no way to guarantee the search space is optimal, as one can accomplish by examining the statistics of repeated genetic algorithm (GA) runs. Additionally, with the manual manipulation involved in spreadsheet calculations, this limits the set of designs that could be considered, and subsequent redesigns would also be time-intensive.
Replacement of the time domain simulations was also proposed with the use of machine learning to develop a statistical model of a mooring system in [
9]. A similar approach was taken in parts of the current work; to replace the wave loadings on the hull that are typically obtained from the potential flow solver WAMIT, a response surface model was developed. However, statistical methods based on training points from the full time domain simulation were deemed unsuitable. With the number of input variables required for the floating platform problem presented here being six, the number of training points for a statistical model would have required too many time domain simulations to be practical.
A similar method to the present work was developed by [
10], where they developed an analytical model to replace the time domain simulations. Their analytical model only considered a subset of the degrees of freedom, as the frequency domain simulation in this work does. In order to verify their analytical models, they were benchmarked against the time domain solver OpenFAST, similar to the present work. While [
10] also used a damping device, their optimization only focused on the parameters for the damping device and not the platform itself to minimize the overall cost.
Overall, the existing literature has identified the need to optimize floating offshore wind platforms to help reduce costs compared with traditional sequential design methods. In particular, attempts at reducing the amount of time domain simulations have been proposed. However, the existing literature does not contain methods to optimize the entire system efficiently. For example, where tuned mass dampers have been studied, only the tuned mass damper was optimized for a pre-existing platform. Therefore, for a new generation of lighter platforms, there is a need for a comprehensive optimization technique combining the hydrostatic and dynamic models, including tuned mass damper physics with sufficient computational efficiency so as to practically generate designs.
The present work is based on the use of a TMD element to reduce the platform mass and a novel optimization approach to minimize the cost of the platform. Drawing from a 2018 proof-of-concept basin test of a 1:50 scale semi-submersible platform with TMDs utilizing water ballast, potential was seen for a platform concept taking advantage of the motion mitigation properties of the TMD [
11]. A photo of the test is shown in
Figure 1. Since semi-submersible designs already require significant amounts of ballast to float with much of their height underwater, the ballast water can be used by the TMD to stabilize the platform without adding mass. Furthermore, with the motion mitigation from the TMD, the wave periods do not need to be avoided so the waterplane area of the platform can be reduced, reducing the mass of the material used in the platform. The optimization assumed a TMD element-motivating water ballast as the effective mass of the TMD, similar to [
11].
The University of Maine has previous experience with post-tensioned concrete in the development of the VolturnUS semi-submersible floating offshore wind turbine platform [
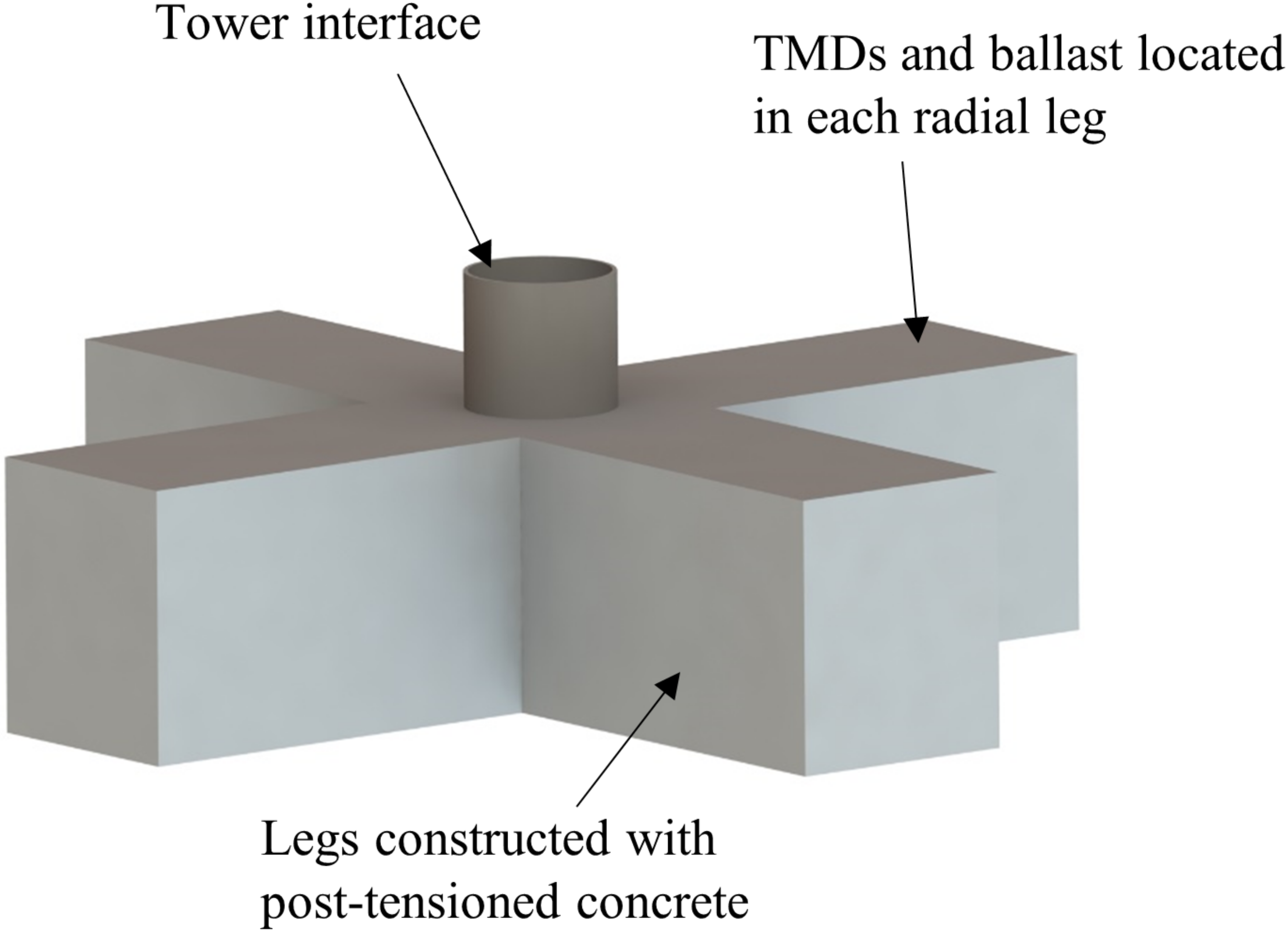
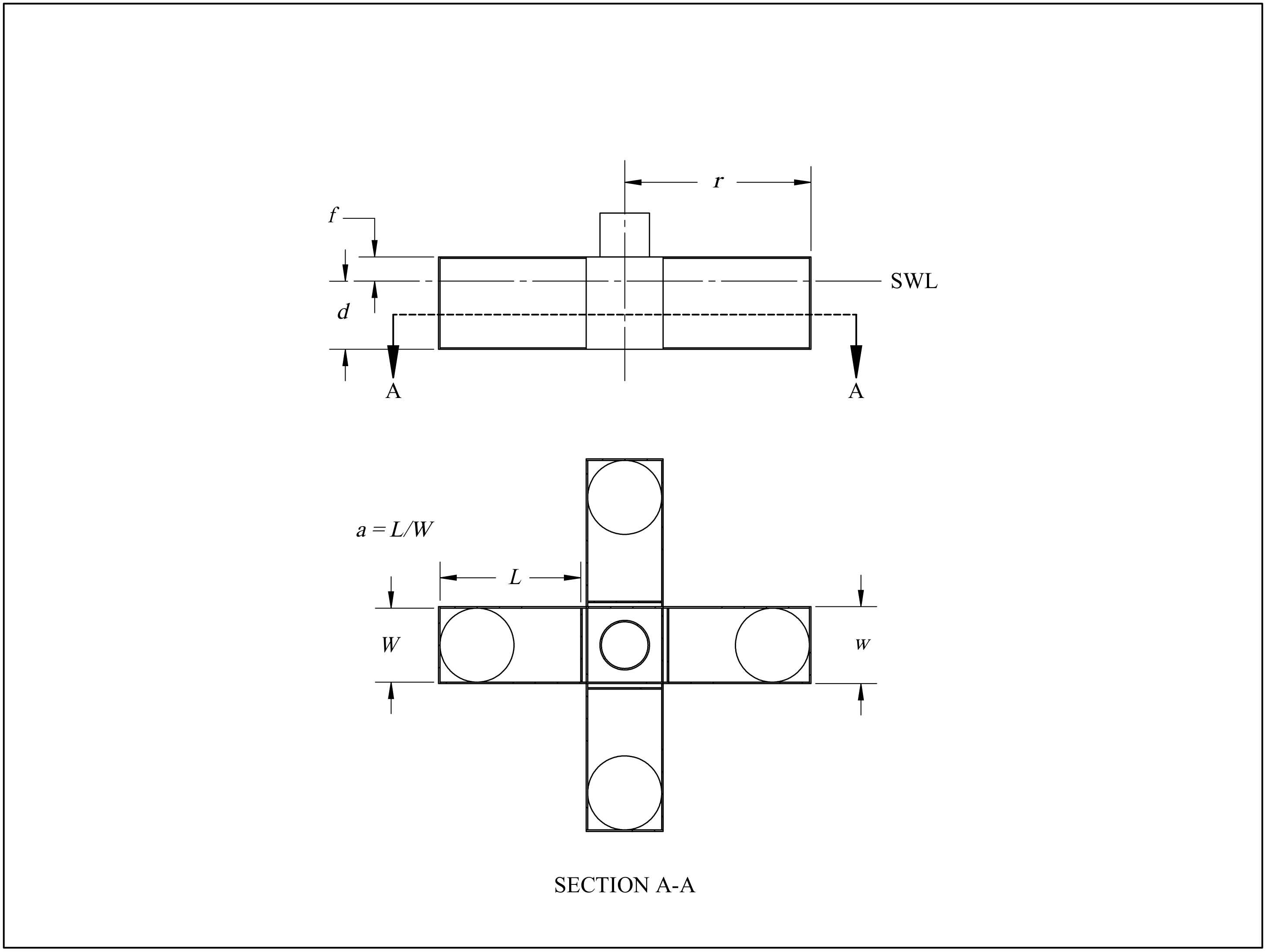
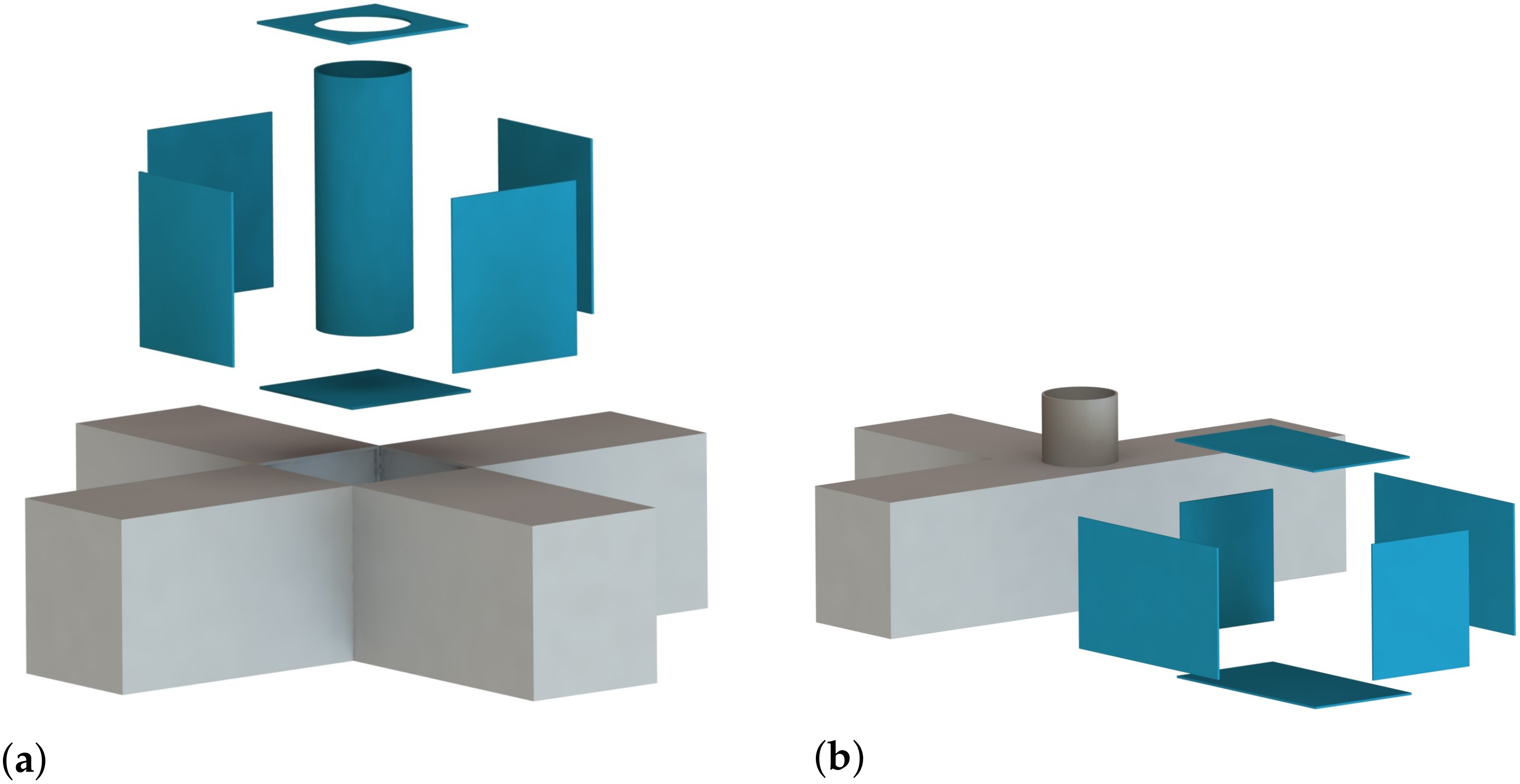
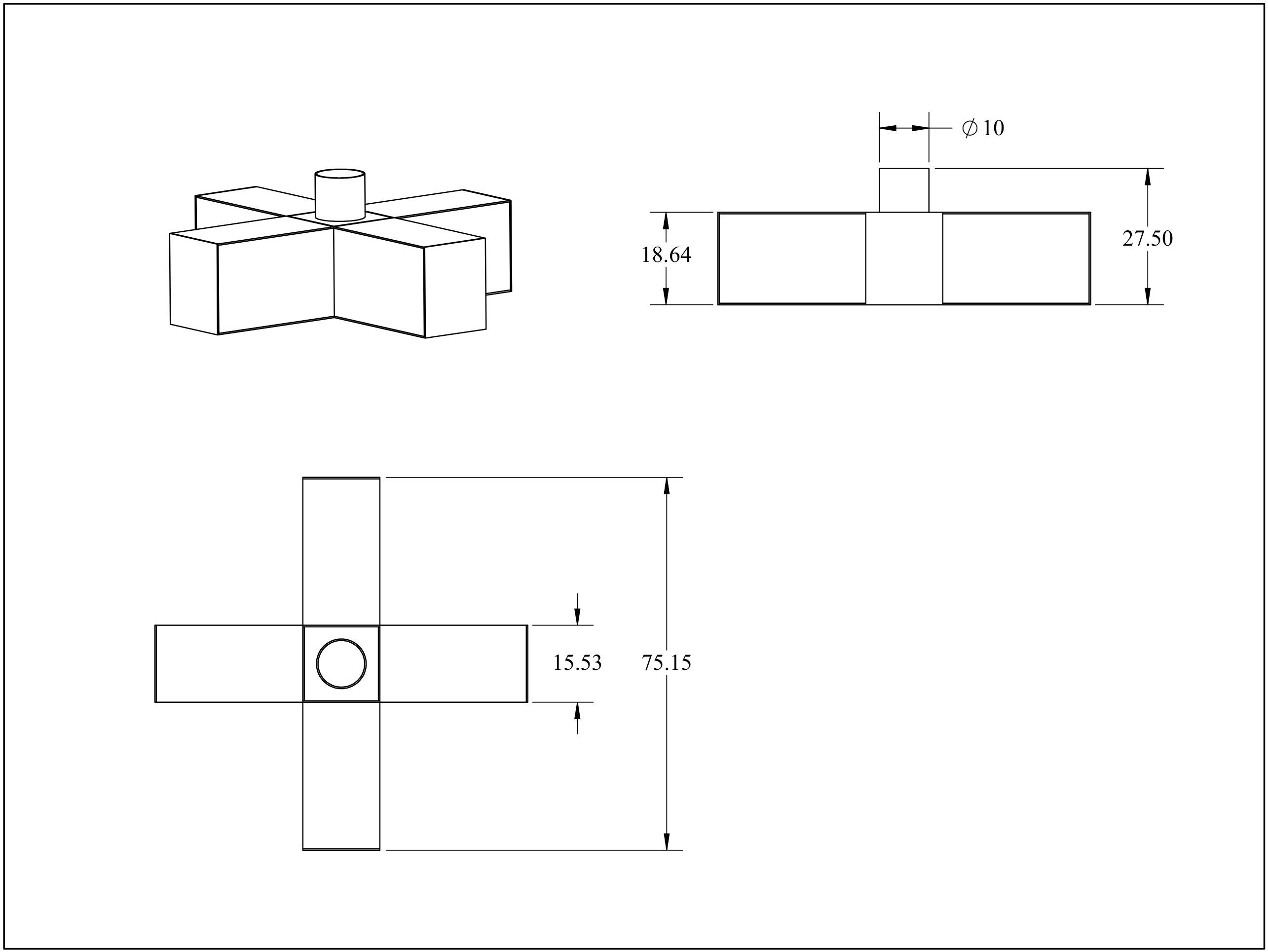
12]. Post-tensioned concrete is advantageous over steel in corrosion resistance, manufacturing cost, and material cost. With this in mind, the University of Maine developed a cruciform hull shape to be made of post-tensioned concrete, on which the current work would be based. The cruciform shape is easily constructed and allows room for ballast water and TMD equipment. The cruciform is shown in
Figure 2. In keeping with industry trends toward larger turbines, the platform was designed around the IEA 15 MW reference turbine, a research turbine with power output consistent with state-of-the art and future industry turbines.
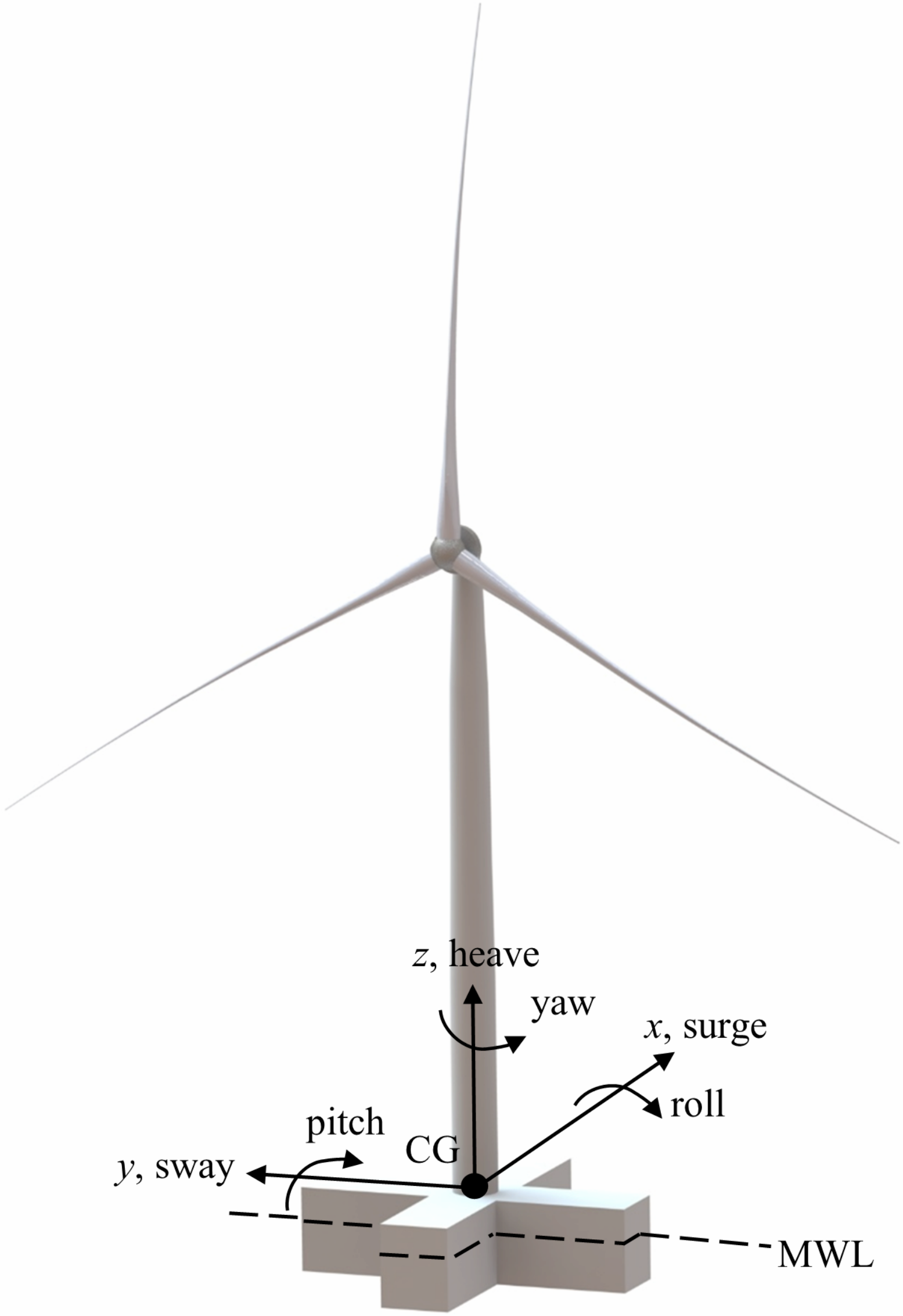
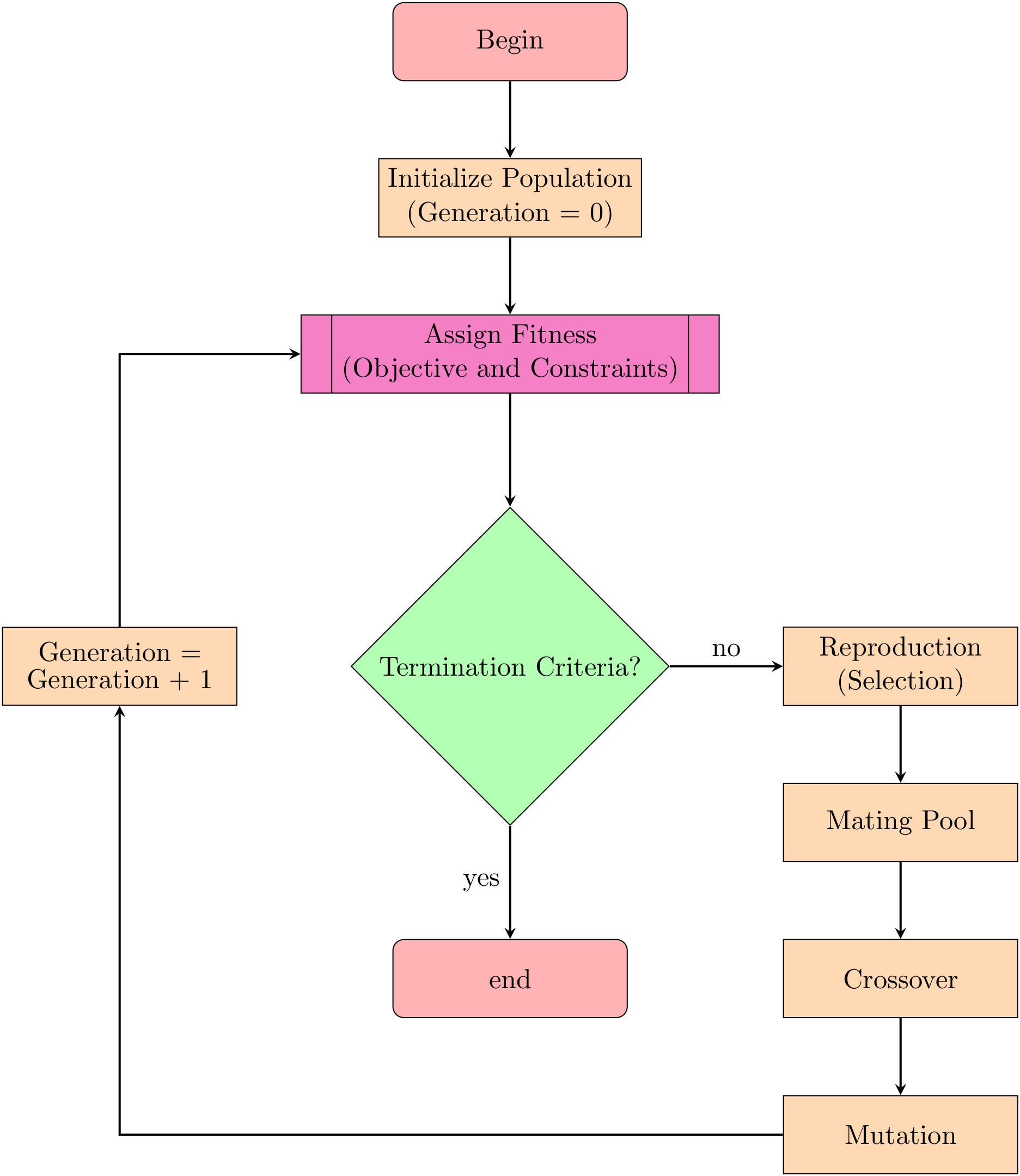
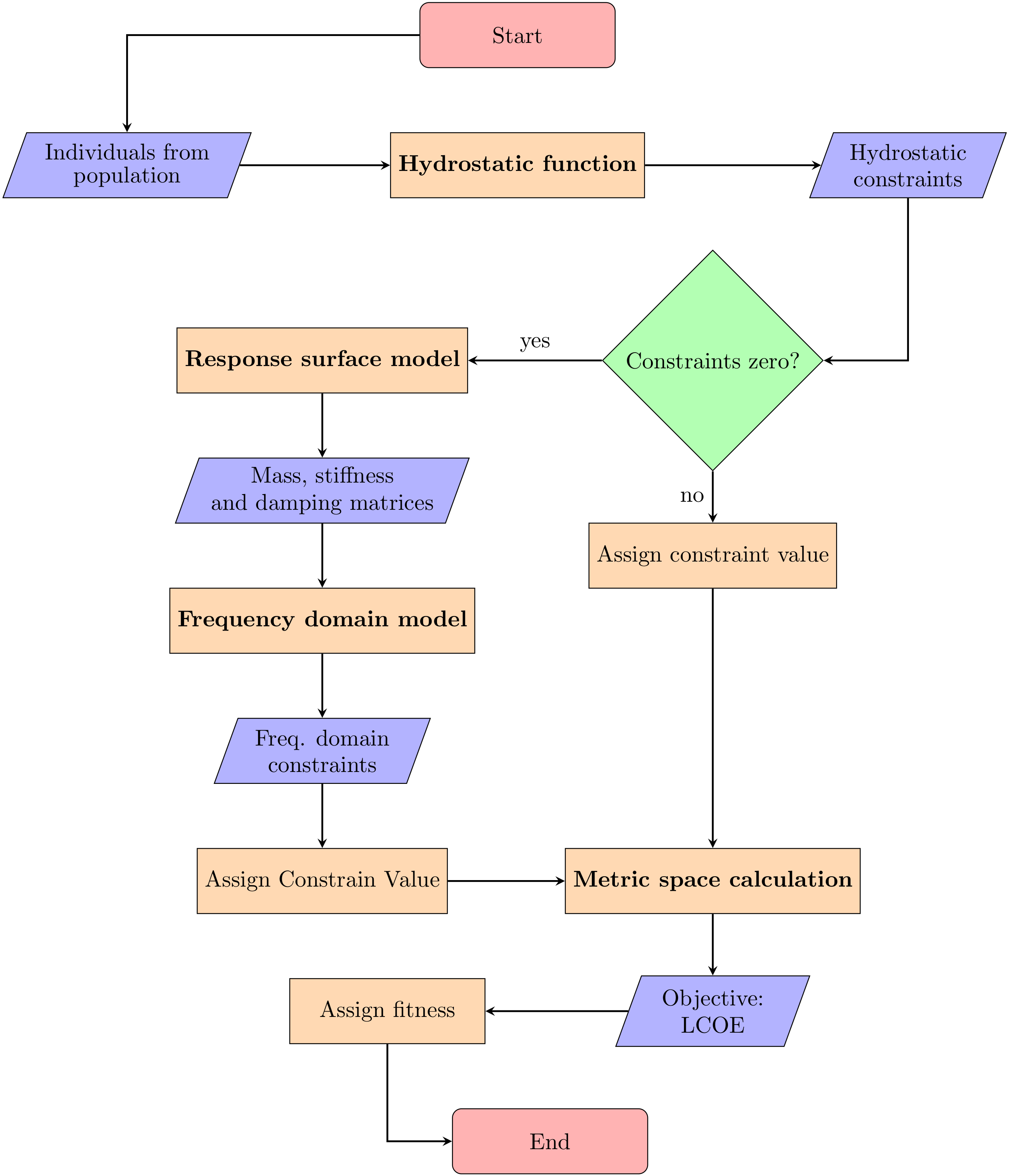
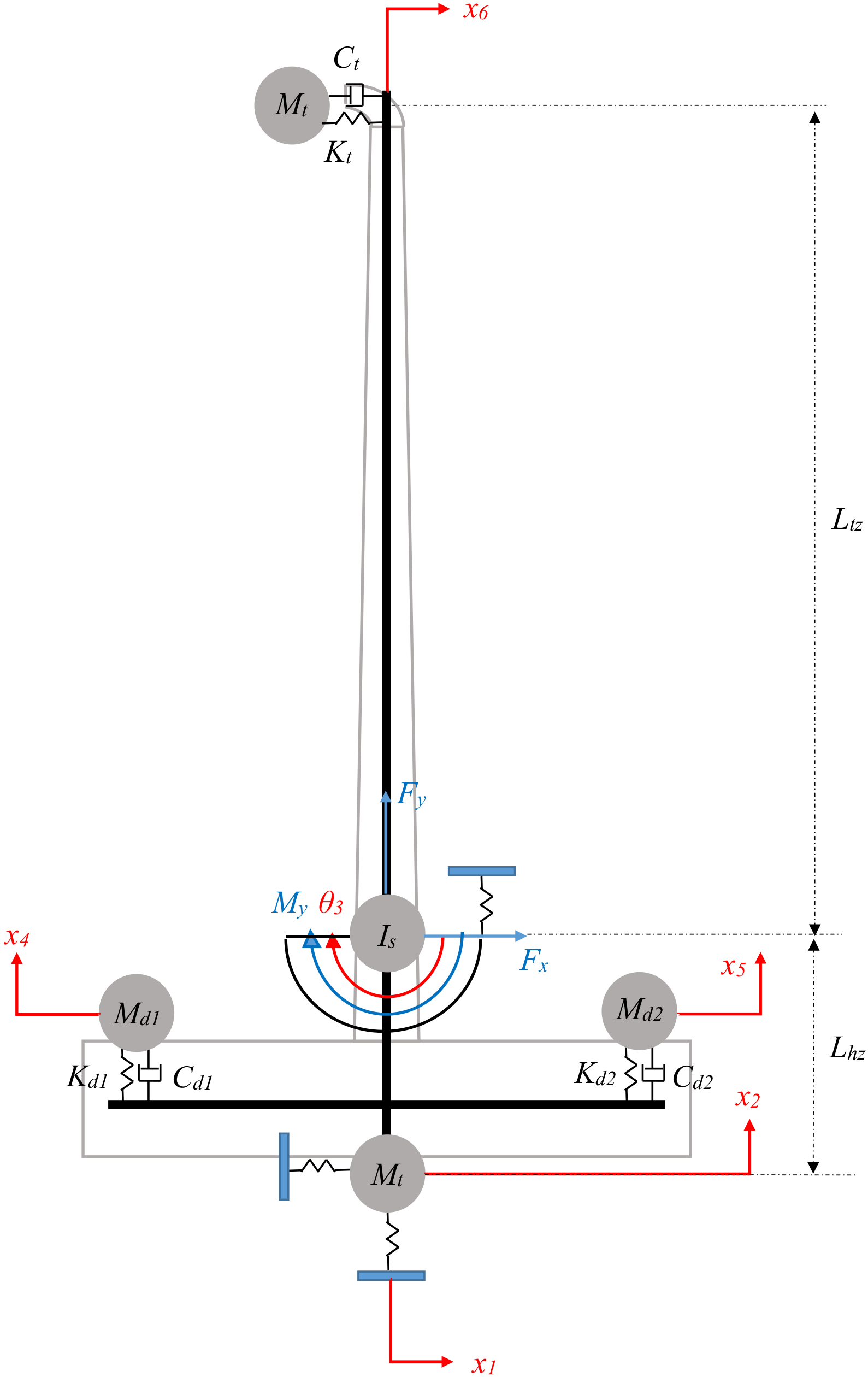
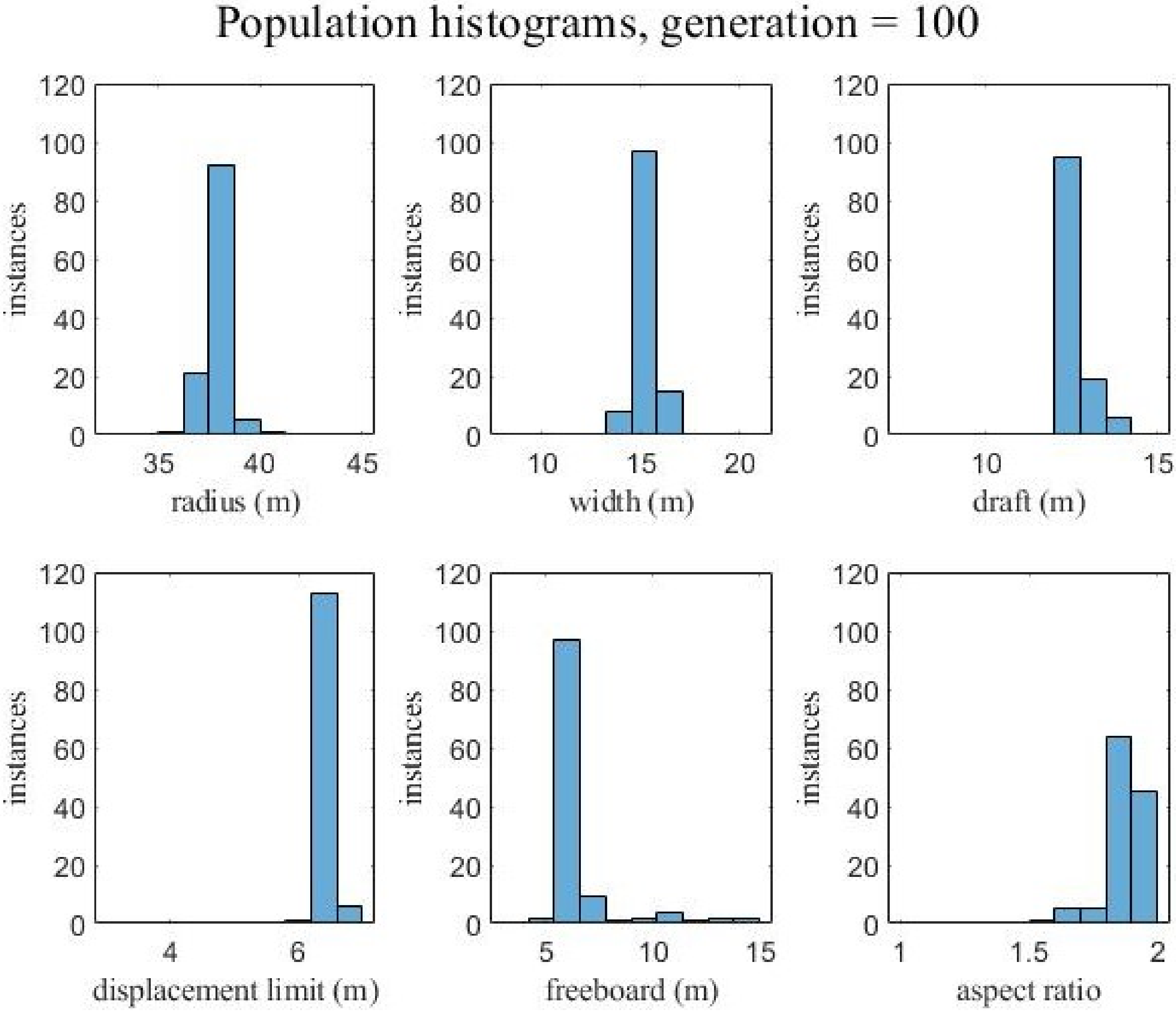
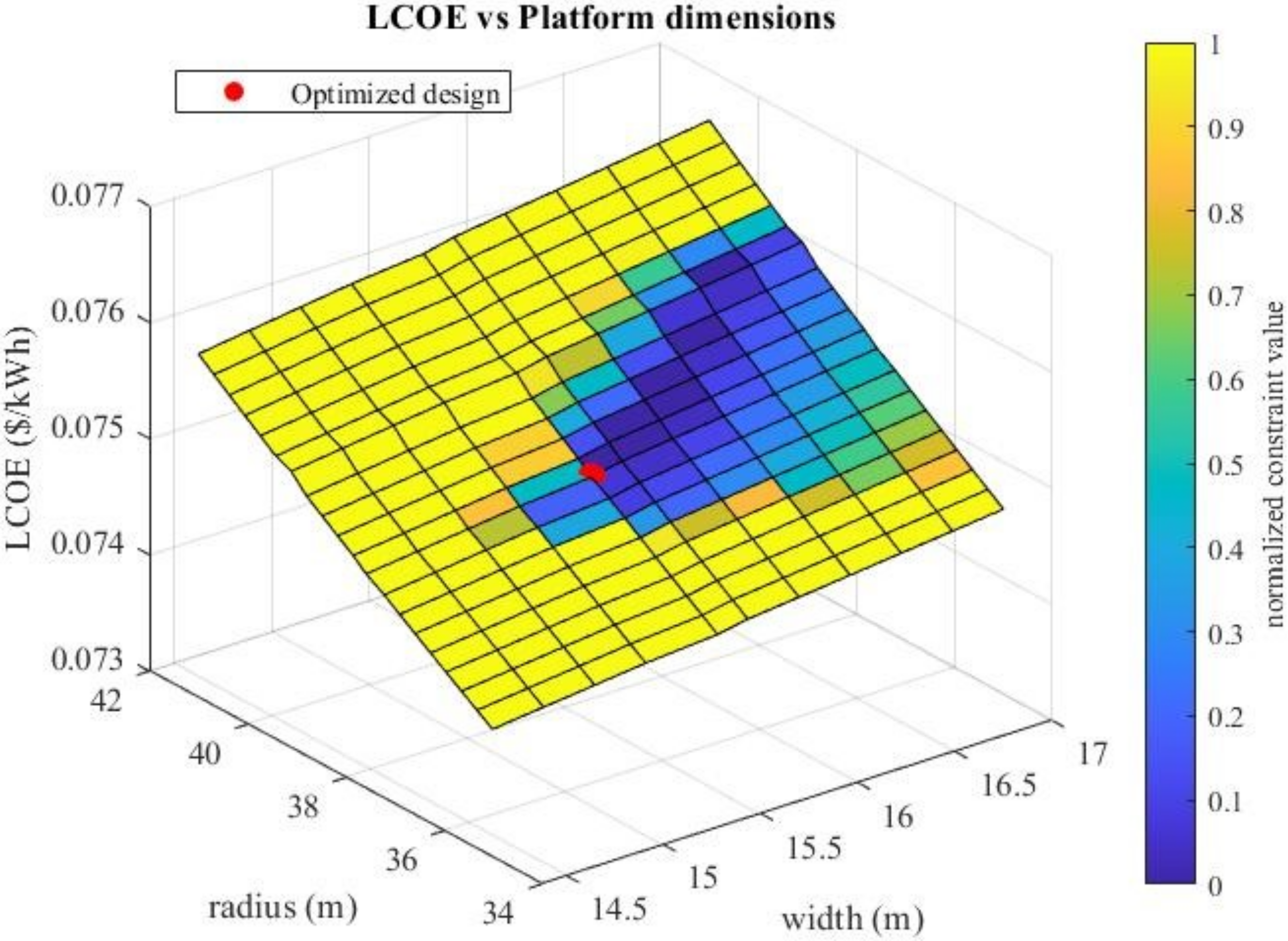
Owing to the highly nonlinear constraints, a GA was chosen for the optimization architecture. A GA assesses the fitness of a given design based on the objective of the optimization, subject to constraints. The objective, minimization of the LCOE, was calculated based on a model developed by ARPA-E for the ATLANTIS program. Significant work was conducted on the development of the constraint functions. Similar to the requirements that would be set by a turbine’s original equipment manufacturer, the typical values of horizontal and vertical acceleration and the pitch angle limits were set for an IEA 15-MW turbine. In addition, a model was required that accounted for the TMD and its travel limits. To capture these dynamic constraints, a frequency domain model was developed to save computational time over a time domain simulation. To generate the necessary inputs for the frequency domain model, a hydrostatic function was also developed. This model also outputs constraints related to geometric compatibility and initial stability. Since the hydrostatic constraints are essential to any design’s suitability (a design that does not float is obviously not practical, for example), a staged constraint handling method was developed. When the hydrostatic constraints were violated, the GA skipped the execution of the frequency domain model. This saved significant computational time, because while the frequency domain model took at least 90 s to run, the hydrostatic model required less than 1 s.
The present work focuses on the optimization of the cruciform-type hull. In particular, the main developments were the input variable selection, integration of constraint functions with the GA, development of a hydrostatic function to generate constraints and inputs to the frequency domain function, and control scheduling. The Materials and Methods section details the GA parameters, the staged constraint handling method, input variable selection, and details of the objective and constraint functions. Following that are the results, detailing the wind and wave conditions used, specifications of the IEA 15-MW turbine and the converged platform, simulation results for the platform, and convergence criteria for the GA. In all, the article describes the solution techniques required to optimize the novel cruciform hull design. This includes the numerical models developed specifically for this design and the wind and wave data necessary for their implementation. Tying together the numerical models is a genetic algorithm, with methods described to increase computational efficiency. Resulting from the optimization is a floating offshore wind platform with a significantly reduced cost compared with the state of the art.