Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database
Abstract
1. Introduction
2. Materials and Methods
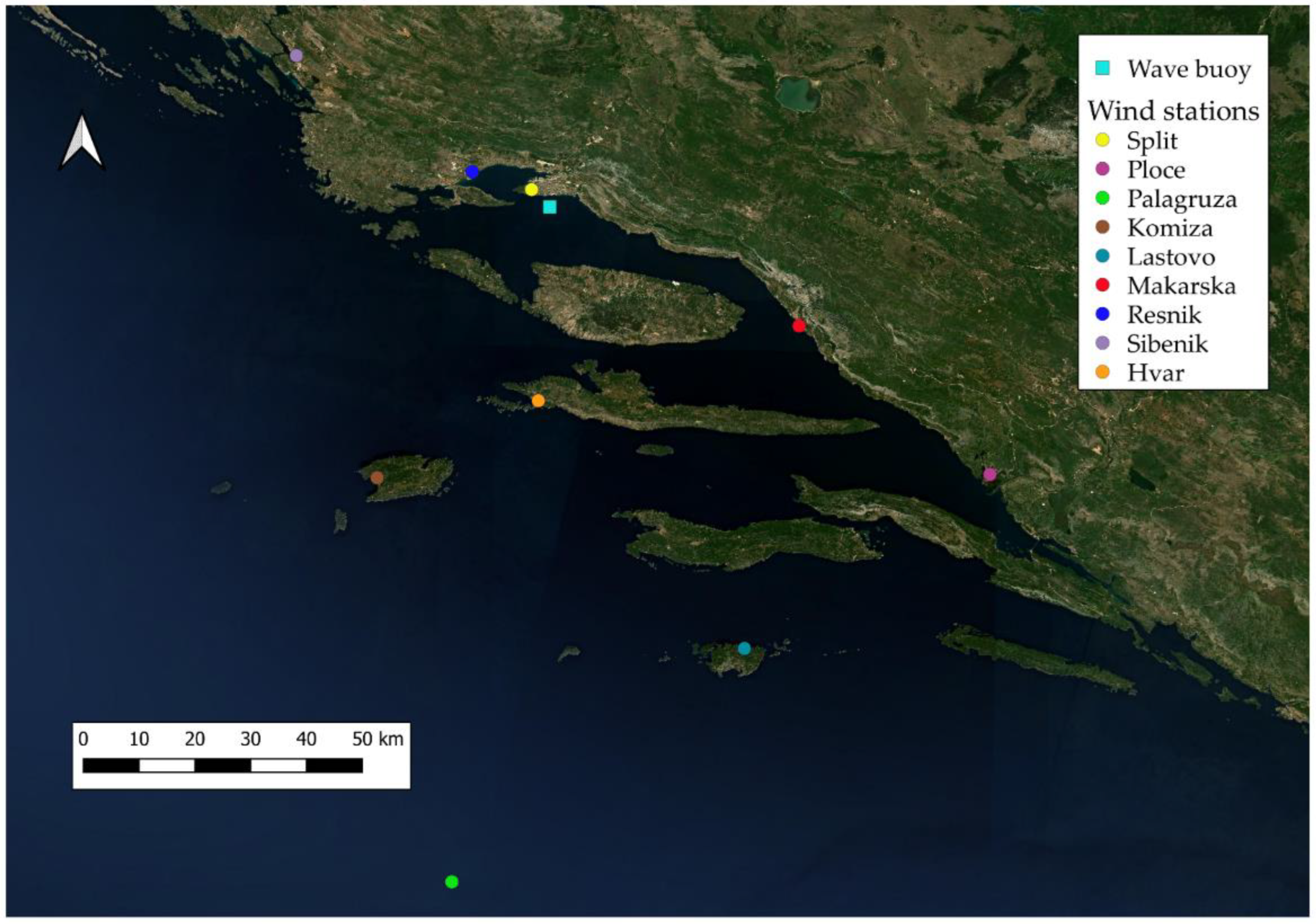
2.1. Study Site
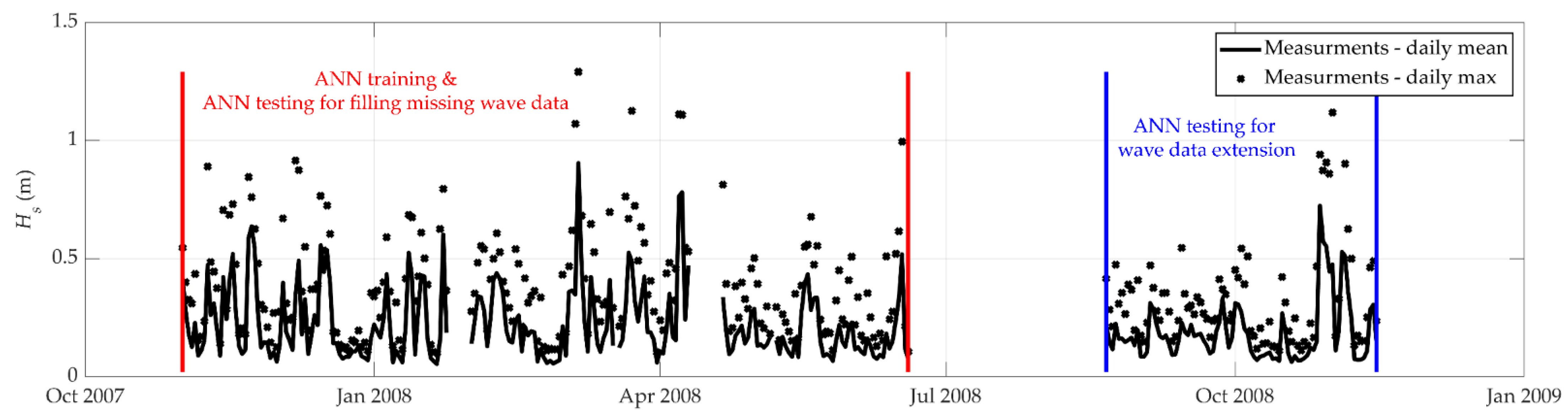
2.2. Wind and Wave Data
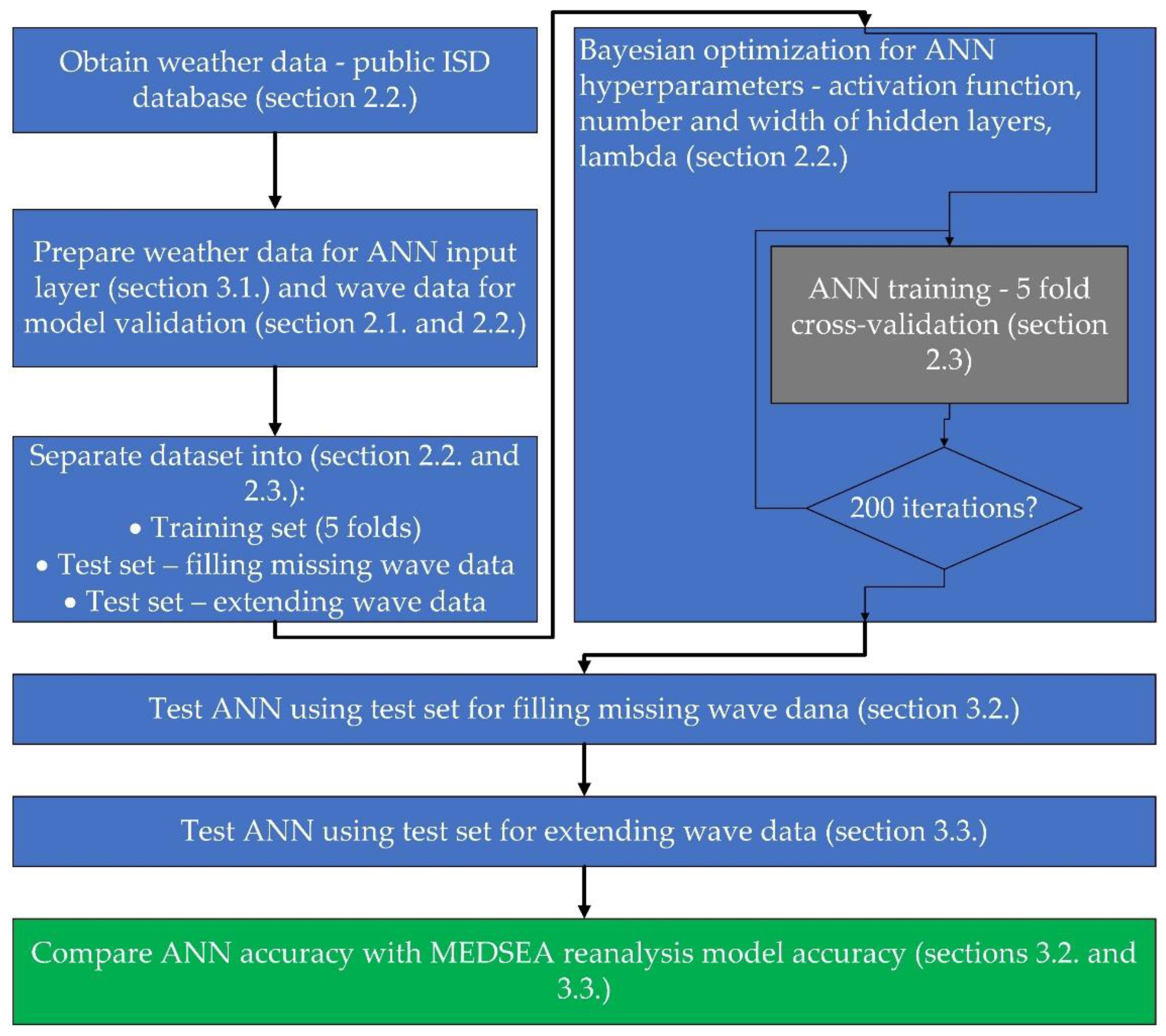
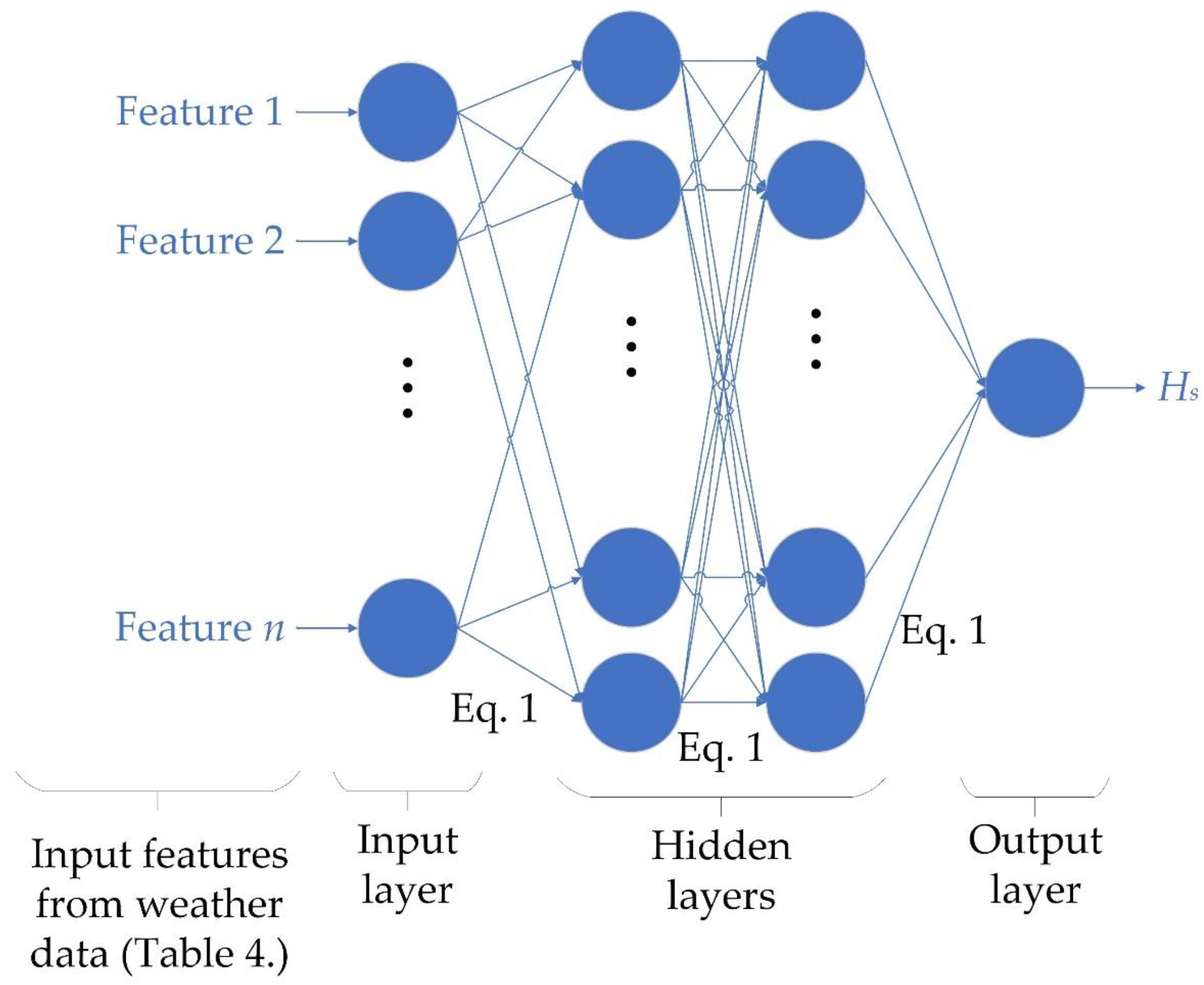
2.3. Artificial Neural Network Training and Model Building Workflow
2.4. Statistical Error Metrics
3. Results
3.1. Univariate Feature Ranking
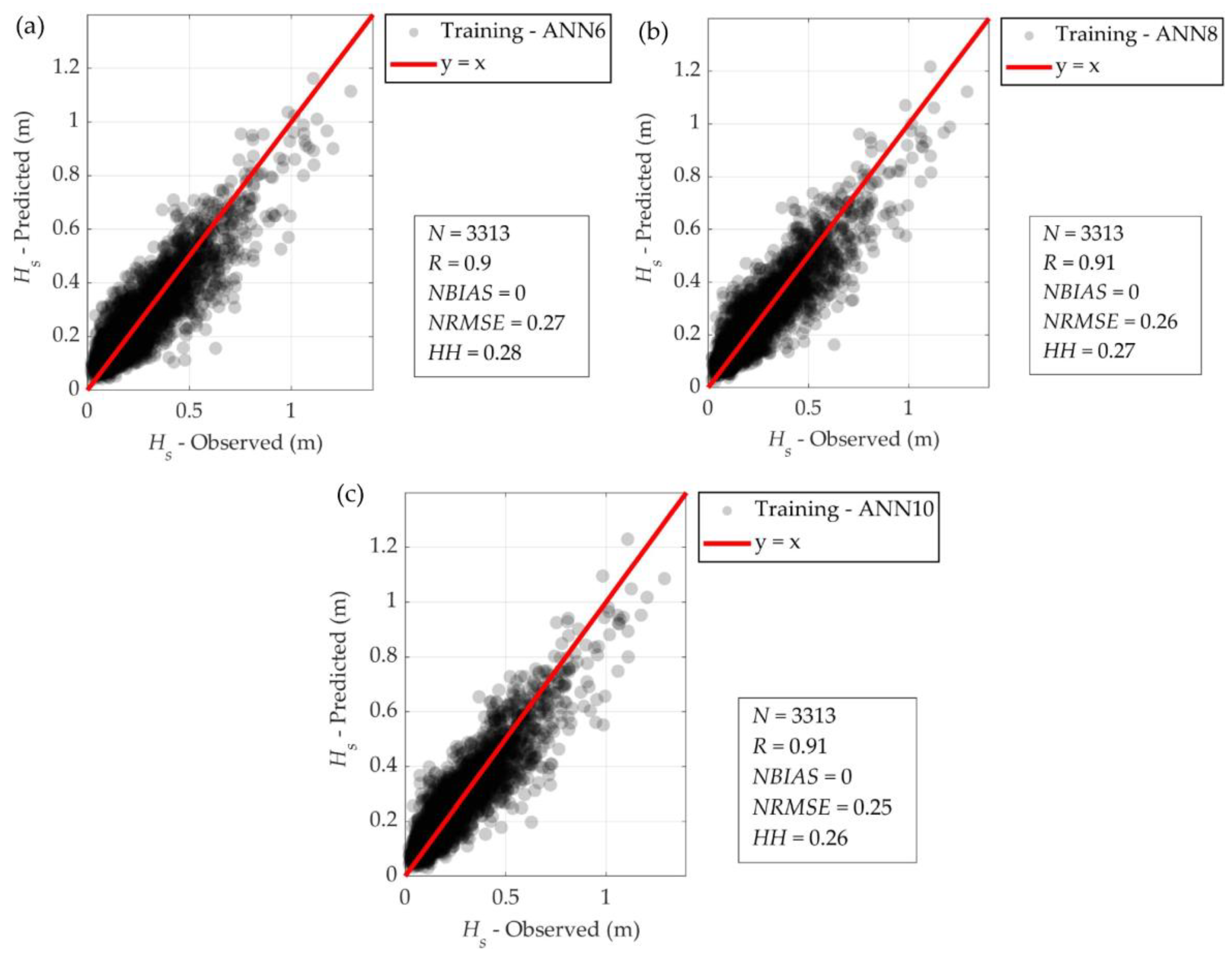
3.2. Training of ANN
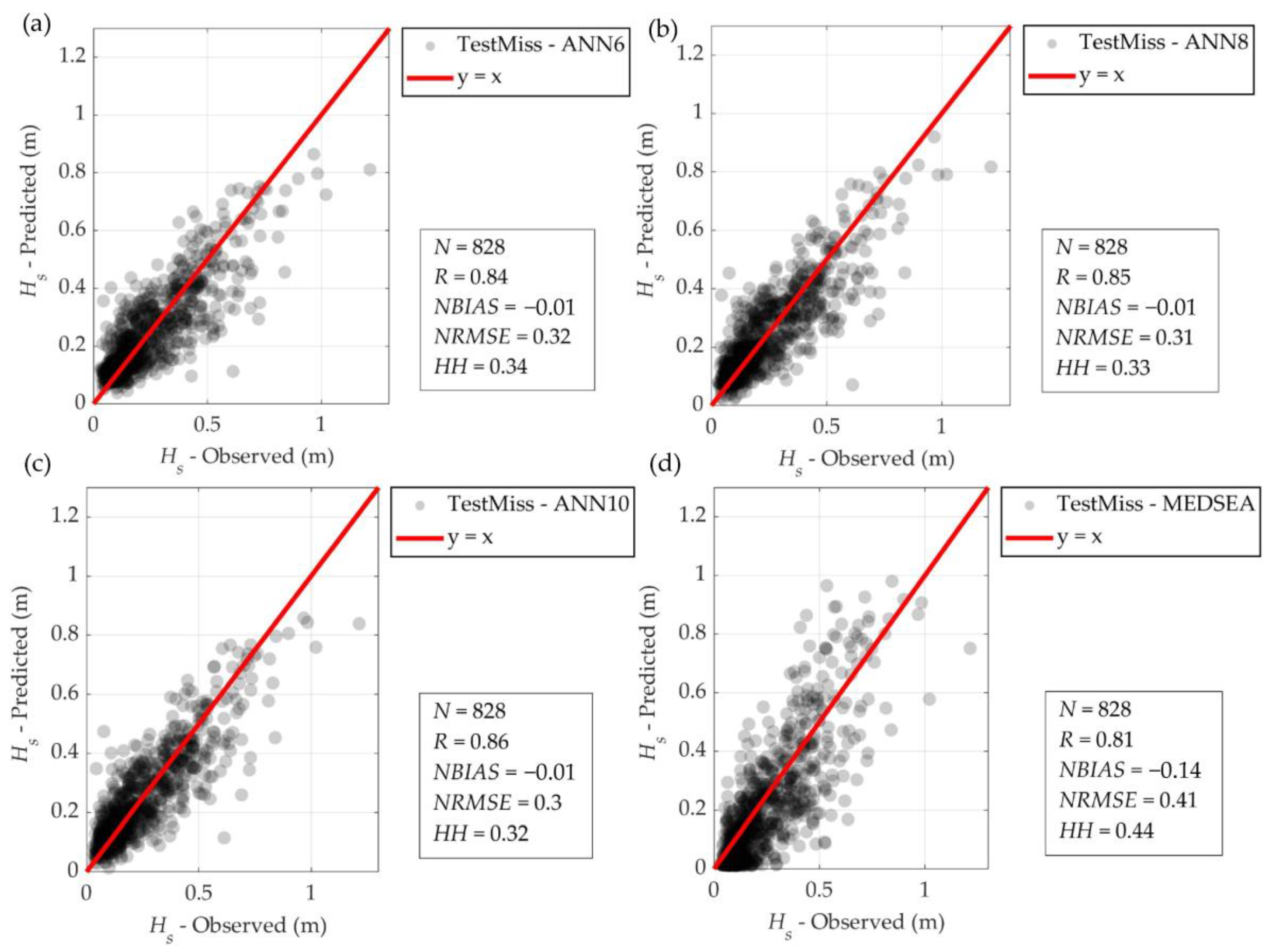
3.3. Filling Missing Wave Data Using an ANN
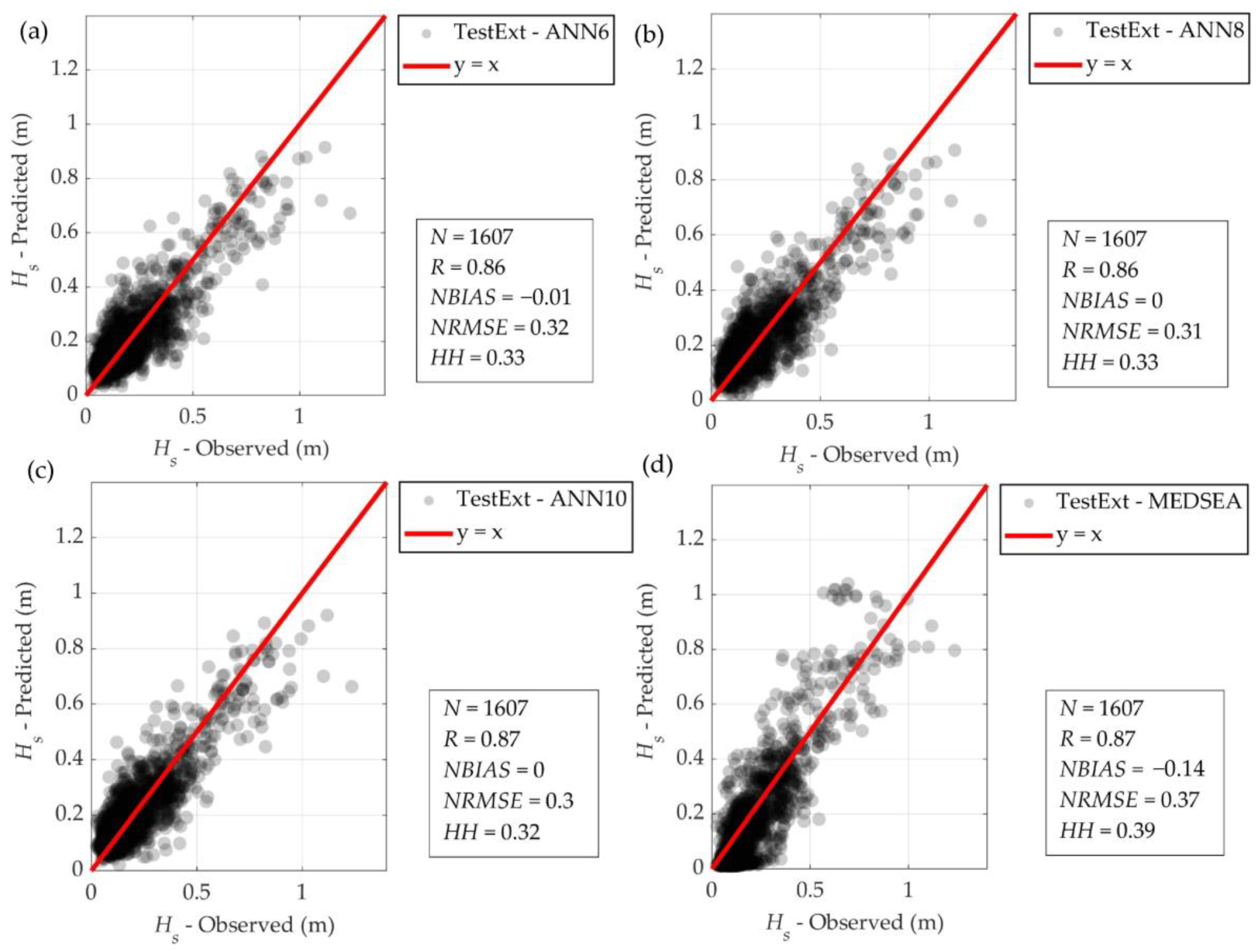
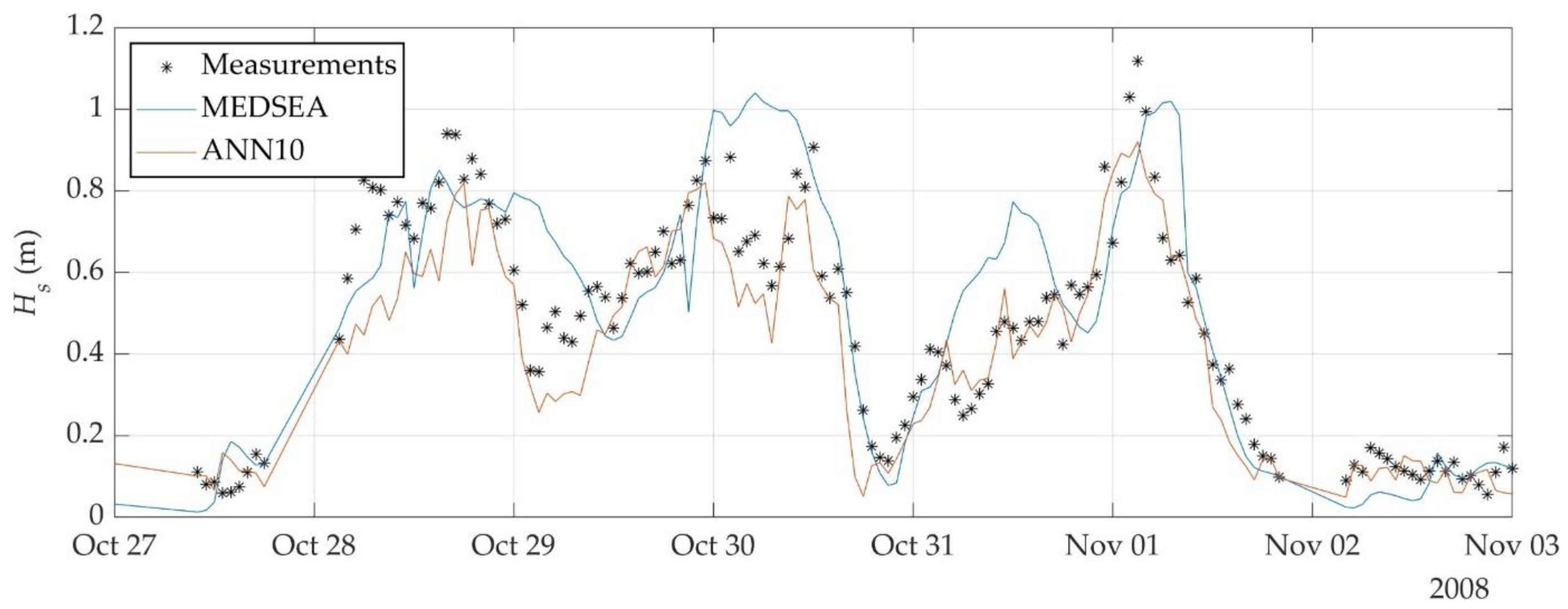
3.4. Extension of Wave Data Using a Trained ANN
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nitsure, S.P.; Londhe, S.N.; Khare, K.C. Wave forecasts using wind information and genetic programming. Ocean Eng. 2012, 54, 61–69. [Google Scholar] [CrossRef]
- Ojo, A.; Collu, M.; Coraddu, A. Multidisciplinary design analysis and optimization of floating offshore wind turbine substructures: A review. Ocean Eng. 2022, 266, 112727. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structure; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Bosom, E.; Jimenez, J.A. Probabilistic coastal vulnerability assessment to storms at regional scale—Application to Catalan beaches (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 475–484. [Google Scholar] [CrossRef]
- IEA. Renewable Power; IEA: Paris, France, 2022. [Google Scholar]
- Sacie, M.; Santos, M.; López, R.; Pandit, R. Use of State-of-Art Machine Learning Technologies for Forecasting Offshore Wind Speed, Wave and Misalignment to Improve Wind Turbine Performance. J. Mar. Sci. Eng. 2022, 10, 938. [Google Scholar] [CrossRef]
- Robertson, B.; Dunkle, G.; Gadasi, J.; Garcia-Medina, G.; Yang, Z.Q. Holistic marine energy resource assessments: A wave and offshore wind perspective of metocean conditions. Renew. Energy 2021, 170, 286–301. [Google Scholar] [CrossRef]
- Wu, M.N.; Stefanakos, C.; Gao, Z. Multi-Step-Ahead Forecasting of Wave Conditions Based on a Physics-Based Machine Learning (PBML) Model for Marine Operations. J. Mar. Sci. Eng. 2020, 8, 992. [Google Scholar] [CrossRef]
- Bahaghighat, M.; Abedini, F.; Xin, Q.; Zanjireh, M.M.; Mirjalili, S. Using machine learning and computer vision to estimate the angular velocity of wind turbines in smart grids remotely. Energy Rep. 2021, 7, 8561–8576. [Google Scholar] [CrossRef]
- Vannucchi, V.; Taddei, S.; Capecchi, V.; Bendoni, M.; Brandini, C. Dynamical Downscaling of ERA5 Data on the North-Western Mediterranean Sea: From Atmosphere to High-Resolution Coastal Wave Climate. J. Mar. Sci. Eng. 2021, 9, 208. [Google Scholar] [CrossRef]
- Peres, D.J.; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. Significant wave height record extension by neural networks and reanalysis wind data. Ocean Model. 2015, 94, 128–140. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Wave Analysis and Forecasting; WMO: Geneva, Switzerland, 2018; Volume WMO-No. 702. [Google Scholar]
- Goda, Y. Revisiting Wilson’s formulas for simplified wind-wave prediction. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 93–95. [Google Scholar] [CrossRef]
- WAMDI Group. The WAM Model—A Third Generation Ocean Wave Prediction Model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Smith, C.A.; Compo, G.P.; Hooper, D.K. Web-Based Reanalysis Intercomparison Tools (WRIT) for Analysis and Comparison of Reanalyses and Other Datasets. B. Am. Meteorol. Soc. 2014, 95, 1671–1678. [Google Scholar] [CrossRef]
- Bellotti, G.; Franco, L.; Cecioni, C. Regional Downscaling of Copernicus ERA5 Wave Data for Coastal Engineering Activities and Operational Coastal Services. Water 2021, 13, 859. [Google Scholar] [CrossRef]
- Feng, X.; Chen, X. Feasibility of ERA5 reanalysis wind dataset on wave simulation for the western inner-shelf of Yellow Sea. Ocean Eng. 2021, 236, 109413. [Google Scholar] [CrossRef]
- Bujak, D.; Loncar, G.; Carevic, D.; Kulic, T. The Feasibility of the ERA5 Forced Numerical Wave Model in Fetch-Limited Basins. J. Mar. Sci. Eng. 2023, 11, 59. [Google Scholar] [CrossRef]
- Kim, S.; Tom, T.H.A.; Takeda, M.; Mase, H. A framework for transformation to nearshore wave from global wave data using machine learning techniques: Validation at the Port of Hitachinaka, Japan. Ocean Eng. 2021, 221, 108516. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. Roy. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Law-Chune, S.; Aouf, L.; Dalphinet, A.; Levier, B.; Drillet, Y.; Drevillon, M. WAVERYS: A CMEMS global wave reanalysis during the altimetry period. Ocean Dyn. 2021, 71, 357–378. [Google Scholar] [CrossRef]
- Korres, G.; Ravdas, M.; Zacharioudaki, A. Mediterranean Sea Waves Hindcast (CMEMS MED-Waves); CMEMS, Ed.; CMEMS: Ramonville-Saint-Agne, France, 2019. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 1999; Prentice Hall: Mcmillan, NJ, USA, 2010; pp. 1–24. [Google Scholar]
- Berbić, J.; Ocvirk, E.; Carević, D.; Lončar, G. Application of neural networks and support vector machine for significant wave height prediction. Oceanologia 2017, 59, 331–349. [Google Scholar] [CrossRef]
- Elbisy, M.S.; Elbisy, A.M.S. Prediction of significant wave height by artificial neural networks and multiple additive regression trees. Ocean Eng. 2021, 230, 109077. [Google Scholar] [CrossRef]
- Mahjoobi, J.; Adeli Mosabbeb, E. Prediction of significant wave height using regressive support vector machines. Ocean Eng. 2009, 36, 339–347. [Google Scholar] [CrossRef]
- Mahjoobi, J.; Etemad-Shahidi, A.; Kazeminezhad, M.H. Hindcasting of wave parameters using different soft computing methods. Appl. Ocean Res. 2008, 30, 28–36. [Google Scholar] [CrossRef]
- Passarella, M.; Goldstein, E.B.; De Muro, S.; Coco, G. The use of genetic programming to develop a predictor of swash excursion on sandy beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 599–611. [Google Scholar] [CrossRef]
- van Maanen, B.; Coco, G.; Bryan, K.R.; Ruessink, B.G. The use of artificial neural networks to analyze and predict alongshore sediment transport. Nonlinear Proc. Geoph. 2010, 17, 395–404. [Google Scholar] [CrossRef]
- Goldstein, E.B.; Coco, G.; Plant, N.G. A review of machine learning applications to coastal sediment transport and morphodynamics. Earth-Sci. Rev. 2019, 194, 97–108. [Google Scholar] [CrossRef]
- Bujak, D.; Bogovac, T.; Carević, D.; Ilic, S.; Lončar, G. Application of Artificial Neural Networks to Predict Beach Nourishment Volume Requirements. J. Mar. Sci. Eng. 2021, 9, 786. [Google Scholar] [CrossRef]
- Londhe, S.N. Soft computing approach for real-time estimation of missing wave heights. Ocean Eng. 2008, 35, 1080–1089. [Google Scholar] [CrossRef]
- Vieira, F.; Cavalcante, G.; Campos, E.; Taveira-Pinto, F. A methodology for data gap filling in wave records using Artificial Neural Networks. Appl. Ocean Res. 2020, 98, 102109. [Google Scholar] [CrossRef]
- Alexandre, E.; Cuadra, L.; Nieto-Borge, J.C.; Candil-García, G.; del Pino, M.; Salcedo-Sanz, S. A hybrid genetic algorithm—Extreme learning machine approach for accurate significant wave height reconstruction. Ocean Model. 2015, 92, 115–123. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mosavi, A.; Rabczuk, T.; Nabipour, N.; Chau, K.-w. Prediction of significant wave height; comparison between nested grid numerical model, and machine learning models of artificial neural networks, extreme learning and support vector machines. Eng. Appl. Comput. Fluid Mech. 2020, 14, 805–817. [Google Scholar] [CrossRef]
- Kim, T.; Lee, W.-D. Review on Applications of Machine Learning in Coastal and Ocean Engineering. J. Ocean Eng. Technol. 2022, 36, 194–210. [Google Scholar] [CrossRef]
- Smith, A.; Lott, N.; Vose, R. The Integrated Surface Database Recent Developments and Partnerships. B. Am. Meteorol. Soc. 2011, 92, 704–708. [Google Scholar] [CrossRef]
- Lott, N.; Vose, R.; Del Greco, S.A.; Ross, T.F.; Worley, S.J.; Comeaux, J. The integrated surface database: Partnerships and progress. In Proceedings of the 24th Conference on Interactive Information Processing Systems for Meteorology, Oceanography and Hydrology, New Orleans, LA, USA, 20 January 2008. [Google Scholar]
- Lott, J.N. The quality control of the integrated surface hourly database. In Proceedings of the 14th Conference on Applied Climatology, Seattle, WA, USA, 10–15 January 2004. [Google Scholar]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Janssen, P.A.E.M. Wave-Induced Stress and the Drag of Air Flow over Sea Waves. J. Phys. Oceanogr. 1989, 19, 745–754. [Google Scholar] [CrossRef]
- Janssen, P. Quasi-linear Theory of Wind-Wave Generation Applied to Wave Forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Hasselmann, K. On the spectral dissipation of ocean waves due to white capping. Bound.-Layer Meteorol. 1973, 6, 107–127. [Google Scholar] [CrossRef]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015, 2, 331–345. [Google Scholar] [CrossRef]
- Lionello, P.; Gunther, H.; Janssen, P.A.E.M. Assimilation of Altimeter Data in a Global 3rd-Generation Wave Model. J. Geophys. Res. Ocean. 1992, 97, 14453–14474. [Google Scholar] [CrossRef]
- van Gent, M.R.A.; van den Boogaard, H.F.P.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Jorge, N., Ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hanna, S.R.; Heinold, D.W. Development and Application of a Simple Method for Evaluating Air Quality; American Petroleum Institute, Health and Environmental Affairs Department: Washington, DC, USA, 1985. [Google Scholar]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]




| Feature Name | Physical Measure (Units) |
|---|---|
| temp | Air temperature (°C) |
| dew | Dew point (°C) |
| rhum | Relative humidity (%) |
| wdir | Wind direction (°) |
| wmag | Wind magnitude (km/h) |
| pres | Sea-level air pressure (hPa) |
| Wind Data | Type | Spatial Resolution | Temporal Resolution | Location/Region | Altitude |
|---|---|---|---|---|---|
| MEDSEA | Gridded data (Copernicus) | 0.25° × 0.25° | 1 h | Regional, extracted at wave buoy location | N/A |
| Hvar | Weather data (ISD) | Point data | 1 h | 43° 10′ 15″ N 16° 26′ 14″ E | 20 m |
| Resnik | Weather data (ISD) | Point data | 1 h | 43° 32′ 22″ N 16° 18′ 5″ E | 19 m |
| Split | Weather data (ISD) | Point data | 1 h | 43° 30′ 30″ N 16° 25′ 35″ E | 122 m |
| Lastovo | Weather data (ISD) | Point data | 1 h | 42° 46′ 6″ N 16° 54′ 1″ E | 186 m |
| Palagruza | Weather data (ISD) | Point data | 1 h | 42° 23′ 36″ N 16° 15′ 05″ E | 98 m |
| Komiza | Weather data (ISD) | Point data | 1 h | 43° 2′ 55″ N 16° 5′ 14″ E | 20 m |
| Sibenik | Weather data (ISD) | Point data | 1 h | 43° 43′ 41″ N 15° 54′ 23″ E | 77 m |
| Ploce | Weather data (ISD) | Point data | 1 h | 43° 2′ 51″ N 17° 26′ 34″ E | 2 m |
| Makarska | Weather data (ISD) | Point data | 1 h | 43° 17′ 16″ N 17° 1′ 12″ E | 50 m |
| Feature | Available Data Points |
|---|---|
| Hvar | 98% |
| Komiza | 98% |
| Lastovo | 32% |
| Makarska | 61% |
| Palagruza | 16% |
| Ploce | 61% |
| Resnik | 99% |
| Sibenik | 98% |
| Split | 99% |
| ANN | ANN6 | ANN8 | ANN10 |
|---|---|---|---|
| wmag_Hvar | x | x | x |
| wmag_Komiza | x | x | x |
| wmag_Makarska | low amount of data points | ||
| wdir_Resnik | x | x | x |
| wmag_Resnik | x | x | x |
| wmag_Sibenik | x | x | x |
| wmag_Split | x | x | x |
| wdir_Split | - | x | x |
| wmag_Lastovo | low amount of data points | ||
| wdir_Hvar | - | x | x |
| wdir_Komiza | - | - | x |
| wmag_Ploce | low amount of data points | ||
| wdir_Sibenik | - | - | x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bujak, D.; Bogovac, T.; Carević, D.; Miličević, H. Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database. Wind 2023, 3, 151-169. https://doi.org/10.3390/wind3020010
Bujak D, Bogovac T, Carević D, Miličević H. Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database. Wind. 2023; 3(2):151-169. https://doi.org/10.3390/wind3020010
Chicago/Turabian StyleBujak, Damjan, Tonko Bogovac, Dalibor Carević, and Hanna Miličević. 2023. "Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database" Wind 3, no. 2: 151-169. https://doi.org/10.3390/wind3020010
APA StyleBujak, D., Bogovac, T., Carević, D., & Miličević, H. (2023). Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database. Wind, 3(2), 151-169. https://doi.org/10.3390/wind3020010







