Abstract
In this work, the ERA5 reanalysis dataset, with its fine spatial and temporal resolution, is used to study the wind speed and direction characteristics in the Mediterranean basin from 1979 to 2020. Their variability, trend and mean values, as well as their association, are examined in the monthly, annual and interannual/decadal time scales. The long-term variability of the wind direction is assessed using the angular variance, while the mean annual and interannual variability are used for the wind speed. The most characteristic and constant flow systems appear in the Gulf of Lion (Mistral) and the Aegean Sea during the summer (Etesian winds). The mean annual variability maximizes in the northern part of the basin, while the western part appears to have the most variable wind directions, while the fastest increasing wind speeds appear in the southwestern Levantine sub-basin. The long-term linear trend for the mean, the 95th and 99th quantiles of annual wind speed and the number of occurrences of extreme wind events have been also assessed. For particular areas, there is an increasing tendency in both intensity and frequency of occurrence of extreme wind events. Τhe linear-circular correlation coefficient has been implemented in order to quantify the linear association between the wind direction and the wind speed. This parameter demonstrates higher annual values for the Mistral wind in the Gulf of Lion and the Etesian winds in the Aegean Sea during the summer. Finally, the comparison of the results of ERA5 with the results of ERA-Interim highlighted significant differences in the Mediterranean wind speed and direction characteristics.
1. Introduction
The assessment of wind climatology is important for a wide variety of research fields such as atmospheric pollution scattering patterns [1,2,3,4,5], bird migration routes [6,7,8,9], biological mechanisms and patterns [10,11], weather forecasting along shipping lanes and optimization of ship routing [12,13] and climate change issues and impacts [14,15,16,17]. Near-surface wind speed and direction variability, in particular, are closely related to wind energy applications [18,19,20,21,22,23], coastal erosion where changes in wind direction play a predominant role [24,25,26], design and construction of buildings where, apart from wind speed, wind direction is also an important design parameter [27,28,29,30], wave propagation patterns, the assessment of local extreme metocean conditions, etc. Evidently, in the context of wind climate analysis and variability, the frequency and intensity of extreme wind events are also important [31], while the linear trends of wind speed can be used as indicators of atmospheric circulation patterns [32,33].
Wind speed and direction change over different time scales, as is evident in long-term time series, as well as atmospheric circulation patterns [34]. In order to assess the long-term behavior, trends and variability, the long-term time series of wind speed and direction are necessary [35,36,37]. This necessity is obvious in works such as the study conducted by Pogumirskis [5], where an analysis of the wind direction is presented for the Baltic Sea, and it is consequently emphasized that wind direction variability is also important as it affects human activities, transportation and temperatures in coastal zones. Another important facet of the wind direction variability emerging from this study is its importance in retrieving offshore wind speeds from satellite data [38]. In addition, the assessment of wind direction variability during night-time low wind speeds demonstrated how low wind speed values do not hinder wind direction variability in any way, while large variability has been measured even at low wind speeds. The terrain over which the wind blows seems to play a significant role, as intricate patterns increase the variability for small time scales, as well as the stratification conditions in the atmosphere [39,40,41]. Moreover, the variability in wind direction also affects the fetch length and therefore, the wave propagation schemes and sea-state intensity [42], as well as the estimation of wind and/or wave design values [43,44]. The probabilistic modeling of wind direction seems to be increasingly important for wind farm design and micro-siting, both onshore and offshore [45,46,47], for structural stability and reliability [48,49,50] and long-term economic gains from such applications [51].
However, despite the importance of both wind speed and direction, researchers focus mostly on statistical assessment and the modeling of wind speed, while wind direction is examined implicitly by using wind roses [52,53]. Some exceptions to this are [54]: where wind direction variability has been assessed using angular variance [35,45], where circular statistics have been applied in order to study directional metocean variables, including wind direction and [55] where the variability of wind direction has been examined with respect to the mean and extreme wind events. In the same work [55], it is highlighted that wind direction variability per se is important in the analysis of extreme winds since the “deviations in the direction of the mean wind are not a good indicator for deviations in the direction of extreme winds”.
Since wind variability is important for a variety of applications, several studies have focused on this subject. The evaluation of wind speed and direction from 216 stations in the United States from 1961 to 1990 indicated that monthly mean values are similar, while variance values exhibit a seasonal change [56]. McVicar [57] has identified a declining trend in wind speed of −0.014 m/s per year to a global extent. A different study resulted in a −0.011 m/s per year for the Northern Hemisphere [58], and Watson [59] concludes that there appears to be a “very slight” decline in the UK. Conversely, there has also been a study examining long-term time series for the whole of Europe that indicated no particular trend whatsoever, as the authors concluded that the measured variability falls in the area of natural variability, and that uncertainty of the results poses yet another factor for not concluding on the subject of long-term trends. However, the NE Atlantic exhibited the highest average wind speeds and daily variability [36]. A recent analysis regarding the assessment of wind variability, trend and extremes over Europe and the North Atlantic based on ERA5 data has been performed by Laurila [34], by introducing an extreme wind factor (EWF) for the assessment of extremeness of the wind speed. It has been concluded that EWF takes its higher values (on a monthly basis) in southern Europe. Finally, Yu [37] performed an analysis of ERA-Interim wind datasets for Antarctica and the Southern Ocean, focusing on the potential implications of wind energy.
Focusing on the Mediterranean Sea, it is considered to be a climate change hot-spot [60]. In addition, it is an area where offshore wind energy is currently in its development phase. In this respect, wind climate analysis and variability, estimation of trends, frequency and intensity of extreme weather events become important since it shapes to a large extent the economics of any offshore wind energy project during its lifetime. Therefore, in the last few years, what has mostly been the subject of interest for researchers is the study of wind speed variability in the span of 20–30 years, which is the normal lifetime of a wind farm.
The existing wind climate and offshore wind power potential analyses are based on gridded datasets obtained from numerical models or remote sensing techniques that cover different periods with various horizontal and temporal resolutions. For example, wind data provided by the SeaWinds scatterometer for the period 2000–2004 with a resolution of 0.25° over the entire Mediterranean and Black Seas were analyzed to produce the spatial distribution, the seasonal wind stress and the annual and seasonal vorticity [61]. In order to assess ocean surface thermal anomalies, the analysis of extreme wind fields in the western Mediterranean has been performed using a merged data product comprising remotely sensed observations and the ERA-Interim wind dataset for the period 1987–2015 with a spatial resolution of 0.25° and a temporal resolution of 6 h [62]. Soukissian [35] analyzed wind speed variability and long-term offshore wind characteristics based on the ERA-Interim product for the period 1979–2014 with a spatial resolution of 79 km and a temporal resolution of 6 h. The surface wind climate features in the Mediterranean have been described using the ERA40 dataset for the period 1957 to 2002 with horizontal and temporal resolutions of 2.5° and 6 h, respectively [54], while the interannual and multi-decadal variabilities in the eastern Mediterranean have been studied based on visual observations from ships [63]. Moreover, on the subject of the Mediterranean cyclones, an extended assessment of their dynamics in the Mediterranean basin using a variety of different datasets has been previously presented [64]; an important finding on cyclogenesis seasonality derived from a study by Flocas [65] where it is proven that after May the cyclone track frequency decreases to increase again after October. The same study indicates that the cyclone track frequency seems to decrease annually.
Long-term wind climate analyses have been also performed in the context of offshore wind energy assessment for the Mediterranean basin. For example, the effects of climate change on future offshore wind energy potential have been studied, based on hindcast wind data for the period 1979–2020 with a spatial resolution of 10 km and a temporal resolution of 1 h [66], and for the period 1961–1990 with a horizontal resolution of 25 km [16]. The offshore wind power potential in the Mediterranean Sea has been estimated using the satellite Blended SeaWinds product of NOAA (1995–2014), with 6 h and 0.25° temporal and spatial resolutions, respectively [67]. The classification of the offshore wind power potential has been performed using 40 years of 1-hour wind data from MEERA-2 reanalysis [68], while the offshore wind power potential has been estimated using wind data from ERA5 reanalysis and a combination of remotely sensed data [69] and results from ERA-Interim and NCEP [70].
This paper aims to investigate the variability of wind speed and direction in the monthly, annual and interannual/decadal time scales, using the most recent and fine spatiotemporal resolution of the ERA5 reanalysis dataset, extending from 1979 up to 2020. ERA5 is one of the few existing reanalysis products with a 1 h temporal resolution and a 0.25° × 0.25° spatial resolution, which combined with the very sufficient length of the available time series provides a robust basis for long-term analysis of the annual, seasonal and decadal timeframes. The results provided in this work will be also compared with corresponding results obtained from the ERA-Interim dataset [35]. The latter dataset covered a slightly shorter period (1979–2014) with a coarser temporal resolution (6 h) and spatial resolution (79 km). See also Section 2.
The area of interest is the entire Mediterranean basin defined by a rectangle with 5° W–36.5° E and 46° N–30° S coordinates. Apart from the long-term variability of wind speed and its extremes, wind direction will also be studied due to its importance, as already mentioned above, along with their association. In this context, the following issues will be examined in detail: (1) the angular distance at the decadal time scale; (2) the slopes of the site-specific extreme wind speed events; (3) the linear-circular association of wind speed and direction. Moreover, the comparison in the long-term time scale of the results obtained by using the ERA-Interim and ERA5 datasets reveals important differences between the two datasets as regards variability characteristics of wind speed and direction and long-term trends and extremes of wind speed.
The structure of this work is the following: Section 2 describes the ERA5 reanalysis dataset, while the theoretical background and mathematical tools used are introduced in Section 3. Section 4 presents the numerical results derived in the annual, monthly and interannual time scales along with some comparisons with the corresponding results obtained by the ERA-Interim dataset. Special emphasis is given to the variability characteristics of wind speed and direction, as well as the trends for the mean and extreme values of wind speed. Finally, in Section 5, a general discussion on the results is provided along with some concluding remarks.
2. The ERA5 Reanalysis Dataset
In this work, the ERA5 reanalysis dataset was utilized [71,72]. It has been implemented by the European Centre for Medium-Range Weather Forecasts (ECMWF), and it is a dynamical–physical coupled numerical model that uses historical records and 4D-Var data assimilation in order to produce estimations on the climate and its various parameters on a global scale. ERA5 is the product dataset of a long line of reanalysis produced by the ECMWF that was initiated in 1979 and is becoming increasingly sophisticated with higher resolution and more accurate forecasting. Its data are available and can be freely accessed from the Copernicus Climate Data Store (https://cds.climate.copernicus.eu/#!/home (accessed on 7 March 2022)). Compared to the previous ERA-Interim reanalysis, the ERA5 dataset is based on an improved numerical model and data assimilation schemes, and has a more sophisticated resolution with ~31 km for the horizontal dimension, 137 levels in the vertical dimension and 1 h for the time scale resolution, making it an adequate source of data for this particular study. In this work, the wind speed time series at a 10 m height above sea level will be analyzed and some of the derived results will be also compared with the corresponding results obtained from the ERA-Interim [35].
The ERA5 dataset has been validated by a number of studies dedicated to this task. In the Mediterranean, a validation focusing on the Tyrrhenian and the Ligurian Seas by downscaling the ERA5 atmospheric reanalysis in order to produce a hindcast for the period 1990–2018 indicated, after comparison with the ERA5 data, that the downscaling improves the hindcast’s reliability for wind speed and wind direction results [73]. The estimation of the global wind power potential has been performed using ERA5, whereas the suitability of the ERA5 wind dataset for long-term regional analyses has been highlighted [74]. ERA5 wind speeds have been also compared against lidar measurements at different heights [75]. It was concluded that the ERA5 wind speed data deviate up to 20% from lidar measurements. ERA5 wind and wave data have also been validated after comparison with the ERA-Interim data and advanced scatterometer and offshore platforms measurements obtained at the Caspian Sea. It was concluded that there is a good agreement for wind speed values of 2 m/s or more [76]. Wind speed results over the South Brazil coasts from ERA5 and two different reanalysis datasets were compared to in situ measurements, and ERA5 emerged as the most accurate reanalysis [77]. A global comparison conducted by Sharmar [74] between different reanalysis models’ hindcasts (ERA5, MERRA2, ERA-I, CFSR and WAVEWATCH III) for 37 years, accompanied also by a comparison with satellite and buoy measurements, proved again that the ERA5 reanalysis is the most accurate model. Similar conclusions were also drawn by Olauson [78]. ERA5 wave and wind parameters have been evaluated against in situ buoy measurements in the Greek Seas and it was concluded that the ERA5 reanalysis dataset, in general, tends to underestimate the actual values of the examined parameters, but the (site-specific) deviations were found to be acceptable [79]. Let it be noted that site-dependent deviations of numerical model products when compared to measured or remotely sensed data is a very common feature [80]. The ERA5 wind dataset has been also evaluated by comparison against in situ measurements from tall towers in very different offshore and onshore areas of the world and results from other reanalysis products [81]. It has been concluded that “ERA5 scores proved to be finer than those achieved on comparable offshore sites when using higher-resolution regional reanalysis products or even NWP models” [81].
3. Theoretical Background and Methodology
For the spatial analysis of wind speed and its variability at the annual, monthly and decadal times scales (Section 4.1 and Section 4.2), the terminology of Soukissian [35] will be adopted. Using the basic time index , and , will represent the time series of wind speed and wind direction, respectively. The scale of is hours, while months will be denoted with the letter and years with the letter . Accordingly, the annual mean wind speed for a particular year is
with being the number of observations of the year (in our case is the number of hours in a year).
The mean annual wind speed then is estimated as
where is the total number of years. Similarly, the monthly mean wind speed for a particular year and month is
where is the total number of hours for the particular month and year and . Consequently, the mean monthly wind speed for a particular month , will then be
The mean annual variability, denoted as (also referred to as ), provides a measure of wind speed variability within each year [35] and is estimated as the mean annual coefficient of variation of wind speed. Additionally, the wind speed variability from year to year is estimated by means of the interannual variability , which is the ratio of the standard deviation of the annual mean wind speed to the overall mean wind speed.
For the linear trend identification of wind speed and the estimation of the corresponding slope in the annual and monthly time scales (Section 4.1.3 and Section 4.2.3), the Theil–Sen estimator was used. This estimator was introduced by Theil [82] and extended by Sen [83] and provides a value for the linear slope so that the corresponding Kendall’s correlation tau (), between and equals zero [84], where is the time index corresponding to . Specifically, for the estimation of the Theil–Sen slope, the slopes
of all possible combinations of pairs of points , should be estimated, where are the time indices corresponding to , respectively [84]. The total number of slopes is , where is the sample size. The median of these slopes , is the Theil–Sen estimator.
This method was preferred in comparison to the ordinary least squares approach, for a variety of reasons as, e.g., the fact that it is resistant to outliers, while at the same time being very robust. The robustness of the estimation has been verified by calculating its breakdown point—the point after which the estimator becomes redundant—as being 0.293, indicating a robust estimator [85]. Moreover, the Theil–Sen estimator has high asymptotic efficiency and proven unbiasedness for continuous error distribution, while it is considered a good estimator for mean squares error, in comparison to other slope estimators.
Regarding the wind direction, the statistical analysis for vectorial data differs from linear data in the sense that one needs to utilize a directional statistics approach. This kind of data has a starting point and a direction (clockwise and counter-clockwise), as well as a value, making it intrinsically different from linear data, especially with respect to notions such as “larger”, “increase”, etc. The way to compare such data derives from deciding one direction as being positive. An introduction to the most important statistical parameters of directional variables (mean value, circular variance, etc.) is provided by Soukissian [45]. Moreover, the angular distance between two directional variables and is defined [86] as:
The angular distance takes values in . The variable is set as positive for the clockwise direction and negative for the counter-clockwise one.
Finally, the linear-circular correlation coefficient , indicates the degree of relationship between a linear (i.e., wind speed ) and a directional (i.e., wind direction ) variable [35].
4. Numerical Results
This section includes the analysis of the wind speed and wind direction in the MS, on the annual, monthly and interannual time scales. Some of the results that are presented in this section will be compared with the corresponding results of the ERA-Interim [35] in order to reveal potential discrepancies between the two datasets.
Before proceeding to the presentation and discussion of the results, let us describe the main intense wind regimes that are encountered in the Mediterranean Sea. See also, Lionello [64] for a detailed description of the wind systems in the Mediterranean Sea. The most important wind systems are of local nature: for example, Sirocco is a wind that blows from the Sahara Desert towards the Mediterranean, reaching high speeds, especially during spring and autumn, Tramontana is a northern wind that appears in many Mediterranean countries, Mistral is a strong northwesterly wind that blows across the Rhône River valley into the Gulf of Lion in France, the Etesians are northerly seasonal winds that blow across the Aegean Sea during summer and Bora is a north-easterly wind blowing in the Adriatic Sea, especially from November to March. These wind systems shape the wind climate of the basin, and their appearance can be traced in the following results. Note also that the same wind systems may have different names in specific regions, e.g., the Sirocco is named Khamsin in Egypt.
In Figure 1, the map of the Mediterranean basin along with the areas that are often mentioned in the text are provided.
Figure 1.
Mediterranean areas that are mentioned in the text.
4.1. Annual and Interannual Time Scales
In the following Figure 2, the areas with the highest mean wind speed emerge, namely the Gulf of Lion, the Aegean Sea and the sea surrounding the western and eastern coasts of Crete Isl., as well as the Alboran Sea. These areas are the most wind energetic areas in the Mediterranean and therefore, they are promising candidates for offshore wind energy development. The highest mean wind speed values occur in the Gulf of Lion (7.80 m/s) and the offshore area west of Crete Isl. (7.62 m/s). The spatial distribution patterns of the wind direction are similar to previous results [35,67,69]. For the areas where the wind speed values appear to be the largest, the wind direction is NW (Mistral wind) in the Gulf of Lion and NE in the N Aegean which then turns to NW in the south Aegean Sea. Another easily identified wind system is the NE Bora (blowing from the Dinaric Alps in the Adriatic Sea). The wind climate in the Aegean Sea is largely shaped by NE winds during the winter and Etesians during the summer, and in the Gulf of Lion by the Mistral and the Tramontana wind systems. Results from previous studies indicate that the areas with the highest wind speed, as well as the wind direction patterns, are the same.
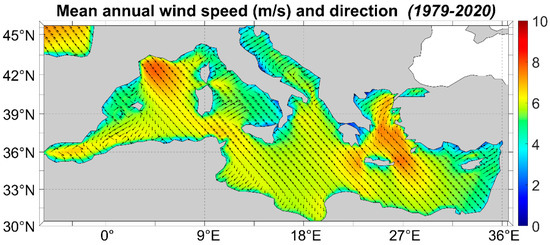
Figure 2.
Mean annual wind speed and direction.
In order to reveal the important differences that occur in the mean annual wind speed estimation between ERA5 and ERA-Interim, in Figure 3, the relative difference between the mean annual wind speed obtained from ERA-Interim and ERA5 is shown.
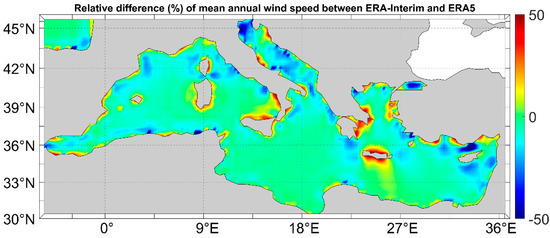
Figure 3.
Relative difference of the mean annual wind speed obtained from ERA5 and ERA-Interim datasets.
is defined as follows:
where and denote the mean annual wind speed obtained from ERA5 and ERA-Interim, respectively. The common reference period for both datasets is 1979–2014. From this figure, it can be seen that for extended areas of the Mediterranean Sea, the absolute relative difference is greater than 25%. Important relative differences in the mean annual estimates occur in the Aegean and Adriatic Seas, as well as in several nearshore areas. Specifically, in the N Adriatic Sea, the relative difference is of the order of up to −50%, while in the W Aegean Sea the relative difference is of the order of up to 35%.
4.1.1. Variability Characteristics
The variability characteristics are provided through the mean annual variability, i.e., the variability within a year (), and the interannual variability, i.e., the year-to-year variability, (). The left plot of Figure 4 illustrates the spatial distribution of the . The highest values of the appear in the Ligurian Sea and especially in the Gulf of Genoa, an area prone to regular cyclones, the N Levantine Basin and especially in the Gulf of Antalya, where tornadoes are frequent [87], the E Tyrrhenian Sea and the N Aegean Sea, while relatively high values of are also encountered in the Adriatic Sea, especially in the Gulf of Venice. The southern part of the basin exhibits lower values, and the general spatial pattern consists of declining values from the north to the south. The results presented here are in agreement with the results referring to wind power density, where the ERA5 dataset was used [69], and with the results of the Blended SeaWinds product for the period 1995–2011 [67]. On the other hand, results based on the ERA-Interim dataset [35] demonstrate that the highest MAV occurs in the Adriatic Sea with a value of 68%.
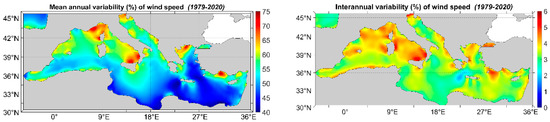
Figure 4.
Mean annual (left) and interannual (right) variability of wind speed.
The right plot of Figure 4 illustrates the spatial distribution of the . Again, the interannual variability exhibits lower values in the southern part of the basin (except for the coasts of Algeria). The largest value (6%) appears in the S Tyrrhenian sub-basin and the N Levantine Basin. The regions with the overall largest are the Balearic, the Ligurian and the Tyrrhenian Seas, as well as the N Aegean and the S coasts of Turkey. The lowest value of appears off the W coasts of Crete Isl. Note that the results based on ERA-Interim [35] demonstrate higher maximum values of (7.25%), appearing in the W Ligurian Sea.
Figure 5 depicts the angular variance of the mean annual wind direction. The angular variance is a measure of the spread of the mean annual wind direction values around the overall annual mean. The smaller the angular variance, the more concentrated the circular distribution. The majority of the Mediterranean areas presents values close to 0 (0–0.02) with a few specific areas with values above 0.03. This result suggests that the mean annual wind direction remains, to a large extent, stable. The regions that exhibit the highest angular variance are found in the western part of the Mediterranean Sea and are very localized, e.g., the middle of the Alboran Sea, the W Algerian basin, the Balearic Sea (around and especially north of Mallorca) and the N Ligurian Sea (off the coasts of Monaco and offshore the Gulf of Genoa). Values of angular variance close to 1 suggest that the mean annual wind direction is highly variable. Lower values around 0.4 appear as well in specific spots in the Adriatic Sea and the Gulf of Mersin. These results are in general similar to the results by Soukissian [35], in terms of the areas that present the highest values, however, the more sophisticated the ERA5 dataset indicates that there are more areas with high values of angular variance (higher than 0.4) in the Alboran, Balearic and Algerian basins, that had not emerged previously.
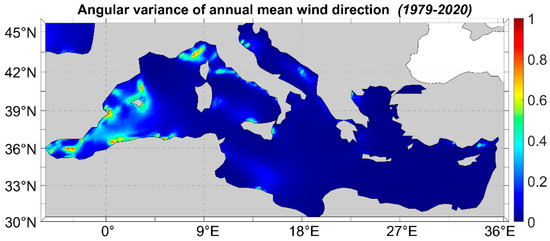
Figure 5.
Angular variance of annual mean wind direction.
In Figure 6, the angular distance between the mean decadal wind direction for the 1st (1979–1988) and 2nd (1989–1998) decades, the 2nd and 3rd (1999–2008) decades and the 3rd and 4th (2009–2018) decades, as well as between the 1st and the last decade (2012–2021) are presented.
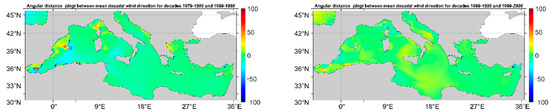
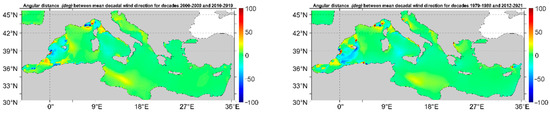
Figure 6.
Angular distance between the decadal mean wind directions.
The largest differences are observed for the decadal mean wind direction between the 3rd and 4th, as well as between the 1st and last decades. It is interesting to note that for some very particular regions positive and negative angular distances are simultaneously present in the form of dipoles. These areas are the entire Balearic Sea, the Ligurian Sea (offshore the Gulf of Genoa), across the Algerian coasts and the southern coasts of Turkey. Note also that the areas exhibiting high values of angular variance are largely the same as the areas exhibiting the highest decadal angular distances.
4.1.2. Association between Wind Speed and Direction
In Figure 7, the spatial distribution of the mean annual linear-circular correlation coefficient between the wind speed and direction is presented. The highest values (0.56) of appear in an extended offshore area in the Gulf of Lion, suggesting a positive association between wind speed and wind direction of the Tramontana and Mistral wind regimes. Other areas with relatively high circular correlation coefficients are the Alboran, the Balearic and S Tyrrhenian Seas, the Algerian basin, the S Levantine Basin, the N Adriatic and the Aegean Seas and the W coasts of Lebanon. The areas with the lowest values are the E Levantine Basin, the N Tyrrhenian, the Central Mediterranean sub-basin, the Ionian Sea and the S Adriatic. This result is in agreement with previous work [35] where the same regions emerged as having the highest correlation coefficient values, but the more detailed analysis provided by the ERA5 dataset gives higher values. Moreover, the NE Alboran Sea emerged as having one of the highest correlation coefficient values, which it had previously not.
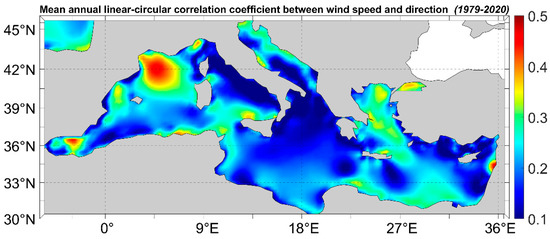
Figure 7.
Mean annual linear-circular correlation coefficient of wind speed and direction.
4.1.3. Wind Speed Trend
In Figure 8, the linear slope for the mean wind speed on the annual scale is presented. The slopes are indicative of the wind speed tendency to increase, decrease or remain constant over the time span under analysis.
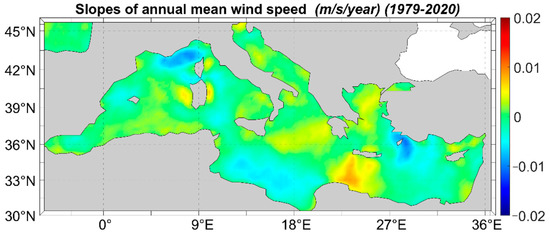
Figure 8.
Linear slope of annual mean wind speed.
The highest positive slopes appear in the area between Crete Isl. and the African coasts, and then in the E Levantine Basin, the E Balearic Sea and offshore the W and E coasts of Sardinia Isl. The overall highest slope (0.087 m/s/year) appears offshore the SW coasts of Crete Isl. Previous results [35] showed the largest positive slope to appear in the Ionian Sea. On the other hand, the Ligurian Sea, the Central Mediterranean sub-basin and the rest of the Levantine Basin exhibit negative slopes. The minimum slope (−0.011 m/s/year) appears in the Aegean Sea, offshore the island of Rodos. The negative slopes of the Ligurian Sea, the central Mediterranean sub-basin and the Levantine Basin, as well as the increasing trends in the W Levantine Basin, the Ionian and the E Balearic–W Tyrrhenian Seas, generally match the results of Soukissian [35]. The central Aegean was expected to have decreasing slopes [35,88,89], yet the results presented here are in agreement with those provided by the recent work of Weiss [90].
As another example of the discrepancies between the ERA-Interim and ERA5 datasets, in Figure 9 the Theil–Sen linear slopes of the mean annual wind speeds for the locations 43.25° N, 7.75° E (left) and 37.50° N, 19.25° E (right) are depicted. Let it be noted that the wind speed trend of these locations has been assessed by using the ERA-Interim dataset [35].
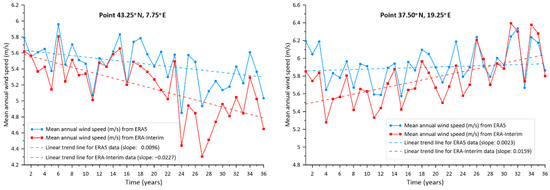
Figure 9.
Linear slope of the mean annual wind speed for the locations 43.25° N, 7.75° E (left) and 37.50° N, 19.25° E (right), as obtained from the ERA-Interim and ERA5 datasets.
Despite the fact that the indicated slopes are of the same sign, the ones that are provided by the ERA-Interim dataset are one order of magnitude different from the corresponding slopes provided by the ERA5 dataset. In addition, in Figure 10, the Theil–Sen linear slope for the mean annual wind speed obtained from the ERA-Interim and ERA5 datasets for the location 37.75° N, 25.00° E is presented. In this case, there is a difference in the sign of the slope (ERA5 provides a slightly positive slope, while ERA-Interim provides a negative slope), as well as important differences in the annual statistics. Specifically, the mean annual, standard deviation, minimum and maximum values from ERA5 are 7.572 m/s, 0.275 m/s, 6.864 m/s and 8.183 m/s, respectively, while the corresponding values from ERA-Interim are 6.706 m/s, 0.316 m/s, 5/789 m/s and 7.287 m/s.
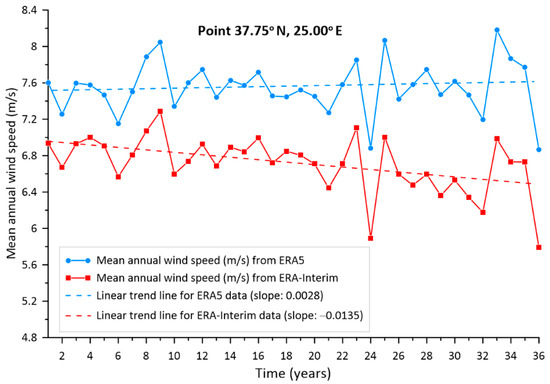
Figure 10.
Linear slope of the mean annual wind speed for the location 37.75° N. 25.00° E, as obtained from the ERA-Interim and ERA5 datasets.
Nevertheless, the qualitative differences between the ERA-Interim dataset that has previously been used, compared to the much more sophisticated ERA5 dataset, have to be taken into account when examining the differences in those sets of results.
4.1.4. Extreme Wind Events
In Figure 11, the linear slopes for the annual 95th (left) and 99th (right) quantiles of wind speed are presented.
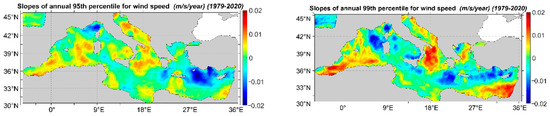
Figure 11.
Linear slope of 95th (left) and 99th (right) annual percentiles of wind speed.
By comparing Figure 11 with Figure 8, it can be seen that the rate of change (increase or decrease) of the extreme wind speeds is clearly greater (in the absolute sense) than the corresponding rate of the annual mean wind speeds. The areas where the 99th annual percentiles of wind speeds tend to increase at the fastest rates are the coasts of the Middle East, the central Aegean Sea, the sea of Alboran and the W Ionian Sea. Areas where extreme wind speeds tend to decrease are the S coasts of Turkey, the area between the S Ionian and the Libyan Sea, the NW offshore area of Corsica Isl., the N coasts of Sicily Isl. and the Ligurian Sea.
Extreme wind events have been further assessed. Since an “extreme event” is a local phenomenon that is clearly defined and related to the wind climate of a particular area, we introduce the following definition for extreme events: Let denote the annual maxima series for a particular location. A local extreme event in this area will be considered any event with . Accordingly, in Figure 12, the linear slopes for the annual number of extreme events of wind speed are depicted. It is clear that the extended areas characterized by increasing the number of occurrences of extreme wind events per year are the central Aegean Sea, the Alboran Sea, the W Ionian Sea and the SE part of the Levantine Basin. Taking also into account the results of Figure 11, it can be concluded that these areas are characterized by both increased intensities and frequencies of occurrence of extreme wind speed events.
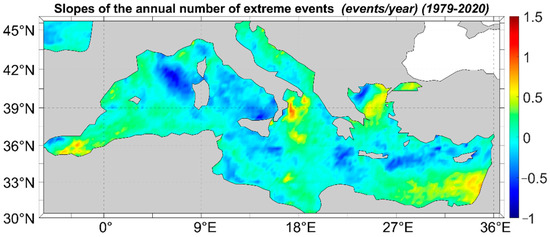
Figure 12.
Linear slope of the number of extreme wind events.
4.2. Monthly Time Scale
In Figure 13, the mean wind speed and wind direction for the monthly scale are presented for May, August, October and December, since these months are characterized by distinct features as explained below.
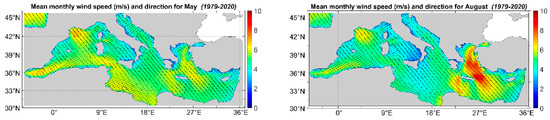
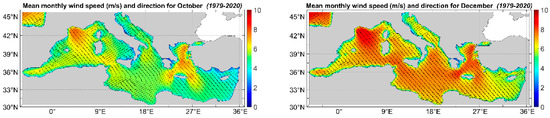
Figure 13.
Mean monthly wind speed and direction for May, August, September and December.
- From November to April, there are high wind speed values all over the basin, with the highest values in the Aegean and the Balearic Seas. Wind speed starts to increase during November and continues so until February when it peaks. Then, it decreases until April when it reaches values close to November’s. For most of the basin, the wind speed values are around 7 m/s.
- From May up to September, there are lower wind speeds all over the basin, compared to the previous period; however, the Gulf of Lion and the Aegean Sea still have the highest values. The wind speed in the Aegean Sea increases from May to August and then drops until September. For most of the basin, the wind speed values are around 4.5 m/s.
- During October, wind speed starts to increase all over the basin, especially in the Aegean Sea and the Gulf of Lion.
The month with the highest wind speeds overall is February, and the overall highest mean wind speeds are encountered in the Gulf of Lion and the central Aegean Sea. The overall lowest wind speeds occur in August, notwithstanding the existence of the Etesians (a seasonal phenomenon that is discernible in Figure 13) in the Aegean Sea. The monthly spatial wind patterns that are presented by Laurila [34] are in agreement with the results presented here.
We will focus now on five areas that exhibit some interesting seasonal patterns. In the Aegean Sea, during the summer (JJA), the wind direction is NE at the N Aegean turning to NW at the central and south Aegean Sea. This season is dominated by the Etesian winds which blow steadily during the summer [91,92,93]. In the Gulf of Lion, steady NW winds (Mistral) are present especially during the winter [62]. In the north part of the Ligurian Sea, there is a seasonal wind direction pattern. From September to March, there is a circular pattern over Corsica Isl. with winds that turn from SE off the E coasts to SW off the W coasts. From April to August, the main winds are SW and there appears no circular pattern. In the Levantine Basin and in particular, on the E coasts of Cyprus, there appears a circular pattern that advances towards the north and is not visible from May to September. In January, the pattern is located offshore the eastern coasts of Cyprus and moves northerly, until April when it is barely visible on the southern coasts of Turkey. There it appears again in October and it moves southerly until December when it is again located in the east of Cyprus. Finally, in the Adriatic Sea during the summer, the wind direction in the central part is NW while for the rest of the year, the direction changes from the east part to the west, from SE to NW, creating a semi-circular pattern. During the months of April, and October until December, there are also SW winds that complete the circular pattern.
4.2.1. Variability Characteristics
Figure 14 depicts the monthly mean angular variance. The highest values are observed during March, April, October and November. The months with the maximum angular variance values are the transitional ones, as they are representative of the transition from spring to summer and from autumn to winter. The general behavior also matches the one of previous results, with the exception of the four transitional months (March, April, October and November), where more extended areas of the basin have angular variance values that exceed 0.35. The period from October to April is characterized by higher mean angular variance values, while from May to September, the mean angular variance decreases. The reason for this pattern is that during higher temperature months (late spring–summer–early autumn) there are steadier wind pressure patterns [94,95]. During the low angular variance period, only a few specified locations have values over 0.30. Moreover, the locations that were expected to exhibit high angular variance values (Gulf of Lion, Aegean, Adriatic and Levantine) confirm this expectation.
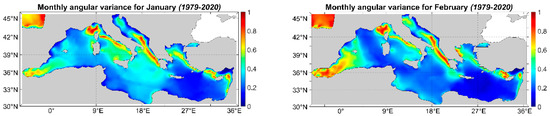
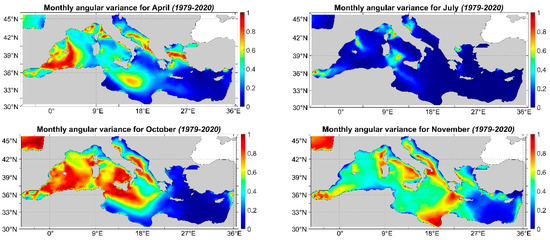
Figure 14.
Monthly mean angular variance.
4.2.2. Association between Wind Speed and Direction
In Figure 15, the mean monthly linear-circular correlation coefficient between wind speed and direction for August is shown. This month was selected as it represents the highest monthly correlation coefficient value (0.78), which appears in the Aegean Sea and the W Levantine Basin.
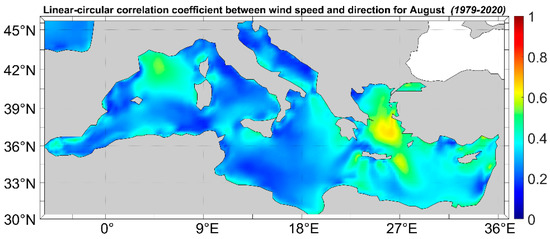
Figure 15.
Linear-circular correlation coefficient of wind speed and direction for August.
For the month of August, a comparison between this and previously reported results [35] indicates that the basin presents similar behaviors. The areas with the highest linear-circular correlation coefficient values are the Aegean Sea, the Levantine Basin and the Gulf of Lion. The Aegean Sea has the highest correlation coefficient values during the summer months (JJA) due to the presence of steady Etesian winds over the area. The Etesians are intense persistent northern winds; therefore, the wind speed and direction are two highly associated variables in this case. On the other hand, the W Algerian basin, the Ionian and the Adriatic Seas, as well as the S Levantine Basin, have the lowest values.
4.2.3. Wind Speed Trend
In Figure 16, the linear slopes for the monthly mean wind speed are presented. The highest (0.035 m/s/year) and lowest (−0.045 m/s/year) slopes are encountered during May and April, respectively, both in the Gulf of Lion. In January, the highest slopes appear in the eastern part and the lowest in the western part of the basin, while in February it takes place the opposite. In March, high slopes are encountered in the Alboran Sea and across the African coasts. In April, the lowest slopes can be found in the extended offshore area between the Gulf of Lion and Sardinia Isl. and the highest in the Alboran and the Aegean Seas. In May, a large part of the basin is characterized by positive slopes. During June, July and August, the slope spatial distribution is very similar with very low absolute slopes (close to 0) at the W Mediterranean and increasing positive slopes in the Aegean Sea (reaching values up to 0.034 m/s/month during August) due to the Etesian winds. October, November and December are characterized by rather mild slopes (either positive or negative), while October is a transitional month.
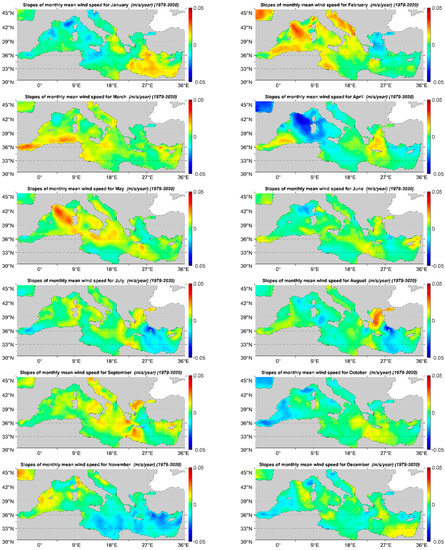
Figure 16.
Linear slope of monthly mean wind speed.
In Figure 17, the linear slopes for the monthly 99th percentiles of wind speed are depicted. The monthly 95th percentiles of wind speed have been also estimated but are not shown here. Clearly, the slopes are in this case greater than the corresponding slopes of the mean monthly values. In May, the sea area between Sardinia Isl. and the Gulf of Lion exhibits the overall maximum (positive) slopes. The slope patterns exhibit some very distinct regional features for the western, central and eastern Mediterranean. Specifically, for the western Mediterranean from January to March the 99% percentile slopes are over 0.04 for the majority of the area (except for January in the Tyrrhenian Sea). In April, the slope values abruptly decrease taking negative values, where the sea area between Sardinia Isl. and the Gulf of Lion and the Tyrrhenian Sea exhibits the overall minimum slopes, only to rise abruptly again to a maximum in May. This monthly pattern of abrupt changes from positive to negative slopes and vice versa last until December for the western part of the basin. In the central part, the months with the lowest slopes are January, March and December, while the maximum (positive) slopes appear in September and October. Finally, in the Eastern part of the basin, the months of January, May and September present increased slope values. On the contrary, July, August and November have very low values. Specifically, in the northern part of the Aegean Sea, the slopes take higher values than the rest of the east basin during August and December. For the majority of the months, the eastern part of the basin seems to present decreased slopes in comparison to the west part, with the only exception to this behavior being the month of January.
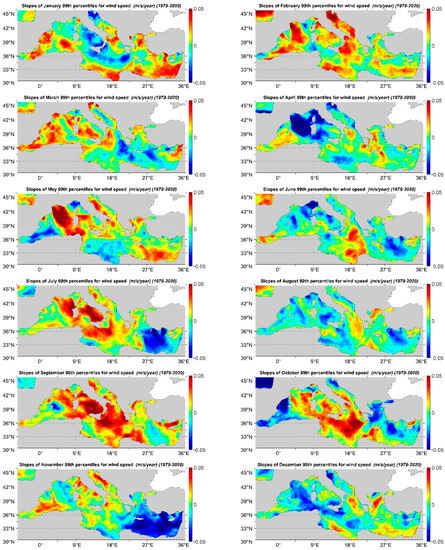
Figure 17.
Linear slopes of the monthly 99th percentile of wind speed.
5. Discussion
Several studies have indicated that the Mediterranean is a region important in its cyclogenetic characteristics, as it is impacted largely by the North Atlantic Oscillation and as indicated by the above-mentioned areas is favorable for cyclogenesis [96]. Moreover, the E Mediterranean basin has been distinguished for its cyclogenesis [65], which is also the area where present results locate the maximum angular distances. A relationship between wind direction angular distance and cyclogenesis seems possible given the previous results and mentioned research, however, this finding is not solidly established here. Climate change, which affects wind direction as indicated by the decadal time scale differentiations, is bound to also affect the cyclogenesis of the region. However, it is still not clear in what way this might happen since there have been studies indicating that cyclones may occur more often [97] and others that predict a decrease in cyclone occurrence [98,99]. Nonetheless, it has been the result of previous research that cyclogenesis in the area is affected seasonally by the large-scale wind circulation there [100]. The potential identification of the areas with intense cyclogenesis using the angular distance, as well as any association between them, is the subject of other research by the authors. While the impact of wind direction is not yet fully understood, anthropogenic climate change is another important factor that will potentially affect both wind speed and direction in the coming decades. Studies have shown slight alterations in wind speed and we can expect this behavior to continue as climate change effects get increasingly intense.
Τhe comparison analyzed above, of collocated ERA-Interim and ERA5 datasets results, revealed important differences in the wind speed and direction statistical parameters. In this work, only comparisons between the mean annual wind speed and the Theil–Sen linear trend line have been analytically shown, but relevant differences have been observed for all estimated quantities in all temporal scales. This was expected due to the improved numerical model and data assimilation schemes, as well as the better temporal and spatial resolution of the ERA5 product. Clearly, for a finer and more detailed analysis of the regional wind climate in the Mediterranean Sea, especially in nearshore areas, higher spatial resolution data are required. This can be achieved, e.g., by downscaling the ERA5 wind fields. Moreover, the definitive version of ERA5 hourly data on single levels from 1950 to 1978 will allow a more robust multi-decadal analysis of wind speed and direction and provide more insight into the long-term behavior of mean and extreme wind speeds, as well as the variability of wind direction in the Mediterranean basin.
6. Conclusions
The mean annual and the interannual variability of wind speed are reduced in the southern parts of the Mediterranean basin, compared to the corresponding northern parts. The angular variance of the mean annual wind direction exhibits an analogous behavior. The areas characterized by large variability as regards wind speed do not, in general, coincide with the areas of increased angular variance values. This is also confirmed by the spatial distribution of the mean annual linear-circular correlation coefficient between wind speed and direction, which assumes values below 0.3 and close to 0 for the majority of the basin areas. Decadal changes in wind direction, in the form of angular distance, are presented here for the first time as far as the authors are aware. The most extreme angular distances have been observed in very particular areas such as the Balearic and Alboran Seas, the coasts of Algeria, the Ligurian Sea (at the offshore area west of the Gulf of Genoa) and the northeastern part of the Levantine Sea.
The slopes of the annual mean wind speed are rather mild (either positive or negative) for the entire basin. The highest value of the slope (0.087 m/s/y) that appears on the southwestern coasts of Crete Isl. corresponds to a mean increase in wind speed of 3.65 m/s during the examined 42-year period, but this is a rather exceptional case. Additionally, the linear slopes of the extreme wind speed have been also examined: firstly, the slopes for the 95th and 99th percentiles of wind speed are clearly greater than the corresponding ones for the mean wind speed, suggesting that extreme wind states tend to increase in magnitude at the long-term time scale. Secondly, site-specific extreme wind events have also been defined and assessed. The areas with an increasing number of extreme wind events occurrences, except for the Alboran Sea, are located in the eastern Mediterranean, namely the north and central Aegean Sea, western Ionian Sea and the southeastern part of the Levantine Basin. The areas with increasing slopes for the 99th percentiles of wind speed coincide with the areas with increasing slopes for the number of extreme wind events occurrences.
Author Contributions
Conceptualization, T.S.; methodology, T.S.; software, M.-A.S.; validation, T.S. and M.-A.S.; formal analysis, T.S. and M.-A.S.; investigation, T.S. and M.-A.S.; writing—original draft preparation, M.-A.S.; writing—review and editing, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
ERA5 reanalysis data on single levels from 1979 to the present can be freely accessed and downloaded at: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 13 July 2021).
Acknowledgments
The Copernicus Climate Change Service (C3S) of the European Centre for Medium-Range Weather Forecasting is gratefully acknowledged for the ERA5 reanalysis data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramšak, V.; Malačič, V.; Ličer, M.; Kotnik, J.; Horvat, M.; Žagar, D. High-resolution pollutant dispersion modelling in contaminated coastal sites. Environ. Res. 2013, 125, 103–112. [Google Scholar] [CrossRef] [PubMed]
- Korinenko, A.E.; Malinovsky, V.V. Field study of film spreading on a sea surface. Oceanologia 2014, 56, 461–475. [Google Scholar] [CrossRef]
- Meng, C.; Cheng, T.; Bao, F.; Gu, X.; Wang, J.; Zuo, X.; Shi, S. The Impact of Meteorological Factors on Fine Particulate Pollution in Northeast China. Aerosol. Air. Qual. Res. 2020, 20, 1618–1628. [Google Scholar] [CrossRef]
- Kannemadugu, H.b.s.; Dorligjav, S.; Gharai, B.; Seshasai, M.V.R. Satellite-Based Air Pollution Potential Climatology over India. Water Air Soil Pollut. 2021, 232, 365. [Google Scholar] [CrossRef]
- Pogumirskis, M.; Sīle, T.; Seņņikovs, J.; Bethers, U. PCA analysis of wind direction climate in the baltic states. Tellus A Dyn. Meteorol. Oceanogr. 2021, 73, 1–16. [Google Scholar] [CrossRef]
- Drake, A.; Rock, C.A.; Quinlan, S.P.; Martin, M.; Green, D.J. Wind Speed during Migration Influences the Survival, Timing of Breeding, and Productivity of a Neotropical Migrant, Setophaga petechia. PLoS ONE 2014, 9, e97152. [Google Scholar] [CrossRef]
- Erni, B.; Liechti, F.; Bruderer, B. The role of wind in passerine autumn migration between Europe and Africa. Behav. Ecol. 2005, 16, 732–740. [Google Scholar] [CrossRef]
- Huang, A.C.; Bishop, C.A.; McKibbin, R.; Drake, A.; Green, D.J. Wind conditions on migration influence the annual survival of a neotropical migrant, the western yellow-breasted chat (Icteria virens auricollis). BMC Ecol. 2017, 17, 29. [Google Scholar] [CrossRef]
- Gutierrez Illan, J.; Wang, G.; Cunningham, F.L.; King, D.T. Seasonal effects of wind conditions on migration patterns of soaring American white pelican. PLoS ONE 2017, 12, e0186948. [Google Scholar] [CrossRef]
- Damschen, E.I.; Baker, D.V.; Bohrer, G.; Nathan, R.; Orrock, J.L.; Turner, J.R.; Brudvig, L.A.; Haddad, N.M.; Levey, D.J.; Tewksbury, J.J. How fragmentation and corridors affect wind dynamics and seed dispersal in open habitats. Proc. Natl. Acad. Sci. USA 2014, 111, 3484–3489. [Google Scholar] [CrossRef]
- Gibb, R.; Shoji, A.; Fayet, A.L.; Perrins, C.M.; Guilford, T.; Freeman, R. Remotely sensed wind speed predicts soaring behaviour in a wide-ranging pelagic seabird. J. R. Soc. Interface 2017, 14, 20170262. [Google Scholar] [CrossRef]
- Delitala, A.M.S.; Gallino, S.; Villa, L.; Lagouvardos, K.; Drago, A. Weather routing in long-distance Mediterranean routes. Theor. Appl. Climatol. 2010, 102, 125–137. [Google Scholar] [CrossRef]
- Życzkowski, M.; Szlapczynska, J.; Szlapczynski, R. Review of Weather Forecast Services for Ship Routing Purposes. Pol. Marit. Res. 2019, 26, 80–89. [Google Scholar] [CrossRef]
- Feng, X.; Liu, C.; Xie, F.; Lu, J.; Chiu, L.S.; Tintera, G.; Chen, B. Precipitation characteristic changes due to global warming in a high-resolution (16 km) ECMWF simulation. Q. J. R. Meteorol. Soc. 2019, 145, 303–317. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Huang, P.; Liu, F.; Murakami, H.; Hsu, P.-C. Simulated ENSO’s impact on tropical cyclone genesis over the western North Pacific in CMIP5 models and its changes under global warming. Int. J. Clim. 2019, 39, 3668–3678. [Google Scholar] [CrossRef]
- Koletsis, I.; Kotroni, V.; Lagouvardos, K.; Soukissian, T. Assessment of offshore wind speed and power potential over the Mediterranean and the Black Seas under future climate changes. Renew. Sust. Energy Rev. 2016, 60, 234–245. [Google Scholar] [CrossRef]
- Ma, J.; Foltz, G.R.; Soden, B.J.; Huang, G.; He, J.; Dong, C. Will surface winds weaken in response to global warming? Environ. Res. Lett. 2016, 11, 124012. [Google Scholar] [CrossRef]
- Chadee, X.T.; Clarke, R.M. Large-scale wind energy potential of the Caribbean region using near-surface reanalysis data. Renew. Sustain. Energy Rev. 2014, 30, 45–58. [Google Scholar] [CrossRef]
- Kotroni, V.; Lagouvardos, K.; Lykoudis, S. High-resolution model-based wind atlas for Greece. Renew. Sustain. Energy Rev. 2014, 30, 479–489. [Google Scholar] [CrossRef]
- Hasager, C.B.; Mouche, A.; Badger, M.; Bingöl, F.; Karagali, I.; Driesenaar, T.; Stoffelen, A.; Peña, A.; Longépé, N. Offshore wind climatology based on synergetic use of Envisat ASAR, ASCAT and QuikSCAT. Remote Sens. Env. 2015, 156, 247–263. [Google Scholar] [CrossRef]
- Huang, J.; McElroy, M.B. A 32-year perspective on the origin of wind energy in a warming climate. Renew. Energy 2015, 77, 482–492. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Jensen, L.E. Evaluation of wind farm efficiency and wind turbine wakes at the Nysted offshore wind farm. Wind Energy 2010, 13, 573–586. [Google Scholar] [CrossRef]
- Xoplaki, E.; Trigo, R.M.; García-Herrera, R.; Barriopedro, D.; D’Andrea, F.; Fischer, E.M.; Gimeno, L.; Gouveia, C.; Hernández, E.; Kuglitsch, F.G.; et al. 6-Large-Scale Atmospheric Circulation Driving Extreme Climate Events in the Mediterranean and its Related Impacts. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: Oxford, UK, 2012; pp. 347–417. [Google Scholar]
- Kelpšaitė, L.; Dailidienė, I. Influence of wind wave climate change on coastal processes in the eastern Baltic Sea. J. Coast. Res. 2011, 64, 220–224. [Google Scholar]
- Kondrat, V.; Šakurova, I.; Baltranaitė, E.; Kelpšaitė-Rimkienė, L. Natural and Anthropogenic Factors Shaping the Shoreline of Klaipėda, Lithuania. J. Mar. Sci. Eng. 2021, 9, 1456. [Google Scholar] [CrossRef]
- Weisse, R.; Dailidienė, I.; Hünicke, B.; Kahma, K.; Madsen, K.; Omstedt, A.; Parnell, K.; Schöne, T.; Soomere, T.; Zhang, W.; et al. Sea level dynamics and coastal erosion in the Baltic Sea region. Earth Syst. Dynam. 2021, 12, 871–898. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Alrawashdeh, H. Wind loads on buildings: A code of practice perspective. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104338. [Google Scholar] [CrossRef]
- Li, S.H. Design Wind Speed for Buildings and Facilities with Non-Standard Design Life in Canadian Wind Climates. Front. Built Environ. 2022, 8, 829533. [Google Scholar] [CrossRef]
- Snaiki, R.; Wu, T. Knowledge-enhanced deep learning for simulation of tropical cyclone boundary-layer winds. J. Wind Eng. Ind. Aerodyn. 2019, 194, 103983. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T. Statistical Investigation of Wind Duration Using a Refined Hurricane Track Model. In Proceedings of the 6th American Association for Wind Engineering Workshop, Clemson, SC, USA, 12–14 May 2021; pp. 135–137. [Google Scholar]
- Outten, S.; Sobolowski, S. Extreme wind projections over Europe from the Euro-CORDEX regional climate models. Weather Clim. Extrem. 2021, 33, 100363. [Google Scholar] [CrossRef]
- Troccoli, A.; Muller, K.; Coppin, P.; Davy, R.; Russell, C.; Hirsch, A.L. Long-Term Wind Speed Trends over Australia. J. Clim. 2012, 25, 170–183. [Google Scholar] [CrossRef]
- Wohland, J.; Folini, D.; Pickering, B. Wind speed stilling and its recovery due to internal climate variability. Earth Syst. Dynam. 2021, 12, 1239–1251. [Google Scholar] [CrossRef]
- Laurila, T.K.; Sinclair, V.A.; Gregow, H. Climatology, variability, and trends in near-surface wind speeds over the North Atlantic and Europe during 1979–2018 based on ERA5. Int. J. Clim. 2021, 41, 2253–2278. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Karathanasi, F.E.; Axaopoulos, P.; Voukouvalas, E.; Kotroni, V. Offshore wind climate analysis and variability in the Mediterranean Sea. Int. J. Clim. 2018, 38, 384–402. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E.; Clark, R.T. European wind variability over 140 yr. Adv. Sci. Res. 2013, 10, 51–58. [Google Scholar] [CrossRef]
- Yu, L.; Zhong, S.; Sun, B. The Climatology and Trend of Surface Wind Speed over Antarctica and the Southern Ocean and the Implication to Wind Energy Application. Atmosphere 2020, 11, 108. [Google Scholar] [CrossRef]
- Koch, W. Directional analysis of SAR images aiming at wind direction. IEEE Trans. Geosci. Remote 2004, 42, 702–710. [Google Scholar] [CrossRef]
- Mahrt, L. Surface Wind Direction Variability. J. Appl. Meteorol. Climatol. 2011, 50, 144–152. [Google Scholar] [CrossRef]
- Pandey, G.; Sharan, M. Accountability of wind variability in AERMOD for computing concentrations in low wind conditions. Atmos. Environ. 2019, 202, 105–116. [Google Scholar] [CrossRef]
- Lang, F.; Belusic, D.; Siems, S. Observations of Wind-Direction Variability in the Nocturnal Boundary Layer. Bound.-Layer Meteorol. 2018, 166, 51–68. [Google Scholar] [CrossRef]
- Voermans, J.J.; Smit, P.B.; Janssen, T.T.; Babanin, A.V. Estimating Wind Speed and Direction Using Wave Spectra. J. Geophys. Res. Ocean. 2020, 125, e2019JC015717. [Google Scholar] [CrossRef]
- Karathanasi, F.; Soukissian, T.; Belibassakis, K. Directional Extreme Value Models in Wave Energy Applications. Atmosphere 2020, 11, 274. [Google Scholar] [CrossRef]
- Coles, S.G.; Walshaw, D. Directional Modeling of Extreme Wind Speeds. J. R. Stat. Soc. Ser. C 1994, 43, 139–157. [Google Scholar]
- Soukissian, T.H. Probabilistic modeling of directional and linear characteristics of wind and sea states. Ocean Eng. 2014, 91, 91–110. [Google Scholar] [CrossRef]
- Song, M.X.; Chen, K.; Zhang, X.; Wang, J. Optimization of wind turbine micro-siting for reducing the sensitivity of power generation to wind direction. Renew. Energy 2016, 85, 57–65. [Google Scholar] [CrossRef]
- Stosic, T.; Telesca, L.; Stosic, B. Multiparametric statistical and dynamical analysis of angular high-frequency wind speed time series. Phys. A Stat. Mech. Its Appl. 2021, 566, 125627. [Google Scholar] [CrossRef]
- Abdelkader, A.; Aly, A.M.; Rezaee, M.; Bitsuamlak, G.T.; El Naggar, M.H. On the evaluation of wind loads for wind turbines’ foundation design: Experimental and numerical investigations. Struct. Des. Tall Spec. Build. 2017, 26, e1362. [Google Scholar] [CrossRef]
- Lamei, A.; Hayatdavoodi, M. On motion analysis and elastic response of floating offshore wind turbines. J. Ocean Eng. Mar. Energy 2020, 6, 71–90. [Google Scholar] [CrossRef]
- Moan, T.; Gao, Z.; Bachynski, E.E.; Nejad, A.R. Recent Advances in Integrated Response Analysis of Floating Wind Turbines in a Reliability Perspective. J. Offshore Mech. Arct. Eng. 2020, 142, 052002. [Google Scholar] [CrossRef]
- Himri, Y.; Merzouk, M.; Kasbadji Merzouk, N.; Himri, S. Potential and economic feasibility of wind energy in south West region of Algeria. Sustain. Energy Technol. Assess. 2020, 38, 100643. [Google Scholar] [CrossRef]
- Karagali, I.; Badger, M.; Hahmann, A.N.; Peña, A.; Hasager, C.B.; Sempreviva, A.M. Spatial and temporal variability of winds in the Northern European Seas. Renew. Energy 2013, 57, 200–210. [Google Scholar] [CrossRef]
- Alvarez, I.; Gomez-Gesteira, M.; Decastro, M.; Carvalho, D. Comparison of different wind products and buoy wind data with seasonality and interannual climate variability in the southern Bay of Biscay (2000–2009). Deep. Sea Res. Part II Top. Stud. Oceanogr. 2014, 106, 38–48. [Google Scholar] [CrossRef]
- Burlando, M. The synoptic-scale surface wind climate regimes of the Mediterranean Sea according to the cluster analysis of ERA-40 wind fields. Theor. Appl. Climatol. 2009, 96, 69–83. [Google Scholar] [CrossRef]
- Bierstedt, S.E.; Hünicke, B.; Zorita, E. Variability of wind direction statistics of mean and extreme wind events over the Baltic Sea region. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 29073. [Google Scholar] [CrossRef]
- Klink, K. Climatological mean and interannual variance of United States surface wind speed, direction and velocity1. Int. J. Clim. 1999, 19, 471–488. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Vautard, R.; Cattiaux, J.; Yiou, P.; Thépaut, J.-N.; Ciais, P. Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nat. Geosci. 2010, 3, 756–761. [Google Scholar] [CrossRef]
- Watson, S.J.; Kritharas, P.; Hodgson, G.J. Wind speed variability across the UK between 1957 and 2011. Wind Energy 2015, 18, 21–42. [Google Scholar] [CrossRef]
- Cos, J.; Doblas-Reyes, F.; Jury, M.; Marcos, R.; Bretonnière, P.A.; Samsó, M. The Mediterranean climate change hotspot in the CMIP5 and CMIP6 projections. Earth Syst. Dynam. 2022, 13, 321–340. [Google Scholar] [CrossRef]
- Zecchetto, S.; De Biasio, F. Sea surface winds over the Mediterranean basin from satellite data (2000–04): Meso- and local-scale features on annual and seasonal time scales. J. Appl. Meteorol. Climatol. 2007, 46, 814–827. [Google Scholar] [CrossRef]
- Ragone, F.; Meli, A.; Napoli, A.; Pasquero, C. Ocean Surface Anomalies after Strong Winds in the Western Mediterranean Sea. J. Mar. Sci. Eng. 2019, 7, 182. [Google Scholar] [CrossRef]
- Gomez-Delgado, F.d.P.; Gallego, D.; Peña-Ortiz, C.; Vega, I.; Ribera, P.; Garcia-Herrera, R. Long term variability of the northerly winds over the Eastern Mediterranean as seen from historical wind observations. Glob. Planet Change 2019, 172, 355–364. [Google Scholar] [CrossRef]
- Lionello, P.; Bhend, J.; Buzzi, A.; Della-Marta, P.M.; Krichak, S.O.; Jansà, A.; Maheras, P.; Sanna, A.; Trigo, I.F.; Trigo, R. Chapter 6 Cyclones in the Mediterranean region: Climatology and effects on the environment. In Developments in Earth and Environmental Sciences; Lionello, P., Malanotte-Rizzoli, P., Boscolo, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 4, pp. 325–372. [Google Scholar]
- Flocas, H.A.; Simmonds, I.; Kouroutzoglou, J.; Keay, K.; Hatzaki, M.; Bricolas, V.; Asimakopoulos, D. On Cyclonic Tracks over the Eastern Mediterranean. J. Clim. 2010, 23, 5243–5257. [Google Scholar] [CrossRef]
- Lira-Loarca, A.; Ferrari, F.; Mazzino, A.; Besio, G. Future wind and wave energy resources and exploitability in the Mediterranean Sea by 2100. Appl. Energy 2021, 302, 117492. [Google Scholar] [CrossRef]
- Soukissian, T.; Karathanasi, F.; Axaopoulos, P. Satellite-Based Offshore Wind Resource Assessment in the Mediterranean Sea. IEEE J Ocean. Eng. 2017, 42, 73–86. [Google Scholar] [CrossRef]
- Majidi Nezhad, M.; Heydari, A.; Neshat, M.; Keynia, F.; Piras, G.; Garcia, D.A. A Mediterranean Sea Offshore Wind classification using MERRA-2 and machine learning models. Renew. Energy 2022, 190, 156–166. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Karathanasi, F.E.; Zaragkas, D.K. Exploiting offshore wind and solar resources in the Mediterranean using ERA5 reanalysis data. Energy Convers Manag. 2021, 237, 114092. [Google Scholar] [CrossRef]
- Onea, F.; Deleanu, L.; Rusu, L.; Georgescu, C. Evaluation of the wind energy potential along the Mediterranean Sea coasts. Energy Explor. Exploit. 2016, 34, 766–792. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 7 March 2022).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Vannucchi, V.; Taddei, S.; Capecchi, V.; Bendoni, M.; Brandini, C. Dynamical Downscaling of ERA5 Data on the North-Western Mediterranean Sea: From Atmosphere to High-Resolution Coastal Wave Climate. J. Mar. Sci. Eng. 2021, 9, 208. [Google Scholar] [CrossRef]
- Ulazia, A.; Saenz, J.; Ibarra-Berastegi, G.; Gonzalez-Roji, S.J.; Carreno-Madinabeitia, S. Global estimations of wind energy potential considering seasonal air density changes. Energy 2019, 187, 115938. [Google Scholar] [CrossRef]
- Aniskevich, S.; Bezrukovs, V.; Zandovskis, U.; Bezrukovs, D. Modelling the Spatial Distribution of Wind Energy Resources in Latvia. Latv. J. Phys. Tech. Sci. 2017, 54, 10–20. [Google Scholar] [CrossRef][Green Version]
- Farjami, H.; Hesari, A.R.E. Assessment of sea surface wind field pattern over the Caspian Sea using EOF analysis. Reg. Stud. Mar. Sci. 2020, 35, 101254. [Google Scholar] [CrossRef]
- Tavares, L.F.D.; Shadman, M.; Assad, L.P.D.; Silva, C.; Landau, L.; Estefen, S.F. Assessment of the offshore wind technical potential for the Brazilian Southeast and South regions. Energy 2020, 196, 117097. [Google Scholar] [CrossRef]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Kardakaris, K.; Boufidi, I.; Soukissian, T. Offshore Wind and Wave Energy Complementarity in the Greek Seas Based on ERA5 Data. Atmosphere 2021, 12, 1360. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Papadopoulos, A. Effects of different wind data sources in offshore wind power assessment. Renew. Energy 2015, 77, 101–114. [Google Scholar] [CrossRef]
- Gualtieri, G. Reliability of ERA5 Reanalysis Data for Wind Resource Assessment: A Comparison against Tall Towers. Energies 2021, 14, 4169. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology; Raj, B., Koerts, J., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wilcox, R. Chapter 10—Robust Regression. In Introduction to Robust Estimation and Hypothesis Testing, 3rd ed.; Wilcox, R., Ed.; Academic Press: Boston, MA, USA, 2012; pp. 471–532. [Google Scholar]
- Peng, H.; Wang, S.; Wang, X. Consistency and asymptotic distribution of the Theil–Sen estimator. J. Stat. Plan. Infer. 2008, 138, 1836–1850. [Google Scholar] [CrossRef]
- Farrugia, P.S.; Borg, J.L.; Micallef, A. On the Algorithms Used to Compute the Standard Deviation of Wind Direction. J. Appl. Meteorol. Climatol. 2009, 48, 2144–2151. [Google Scholar] [CrossRef]
- Kahraman, A.; Kadioglu, M.; Markowski, P.M. Severe Convective Storm Environments in Turkey. Mon. Weather Rev. 2017, 145, 4711–4725. [Google Scholar] [CrossRef]
- Aarnes, O.J.; Abdalla, S.; Bidlot, J.R.; Breivik, O. Marine wind and wave height trends at different ERA-Interim forecast ranges. J. Clim. 2015, 28, 819–837. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Weiss, C.V.C.; Menendez, M.; Ondiviela, B.; Guanche, R.; Losada, I.J.; Juanes, J. Climate change effects on marine renewable energy resources and environmental conditions for offshore aquaculture in Europe. Ices. J. Mar. Sci. 2020, 77, 3168–3182. [Google Scholar] [CrossRef]
- Tyrlis, E.; Lelieveld, J. Climatology and Dynamics of the Summer Etesian Winds over the Eastern Mediterranean. J. Atmos. Sci. 2013, 70, 3374–3396. [Google Scholar] [CrossRef]
- Anagnostopoulou, C.; Zanis, P.; Katragkou, E.; Tegoulias, I.; Tolika, K. Recent past and future patterns of the Etesian winds based on regional scale climate model simulations. Clim. Dynam. 2014, 42, 1819–1836. [Google Scholar] [CrossRef]
- Dafka, S.; Xoplaki, E.; Toreti, A.; Zanis, P.; Tyrlis, E.; Zerefos, C.; Luterbacher, J. The Etesians: From observations to reanalysis. Clim. Dynam. 2016, 47, 1569–1585. [Google Scholar] [CrossRef]
- Thompson, R.; Green, D. Mediterranean precipitation and its relationship with sea level pressure patterns. Ann. Geophys. 2004, 47, 1617–1633. Available online: https://www.annalsofgeophysics.eu/index.php/annals/article/view/3364 (accessed on 7 March 2022). [CrossRef]
- Ulbrich, U.; Lionello, P.; Belušić, D.; Jacobeit, J.; Knippertz, P.; Kuglitsch, F.G.; Leckebusch, G.C.; Luterbacher, J.; Maugeri, M.; Maheras, P.; et al. 5—Climate of the Mediterranean: Synoptic Patterns, Temperature, Precipitation, Winds, and Their Extremes. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: Oxford, UK, 2012; pp. 301–346. [Google Scholar]
- Raible, C.C. On the relation between extremes of midlatitude cyclones and the atmospheric circulation using ERA40. Geophys. Res. Lett. 2007, 34, L07703. [Google Scholar] [CrossRef]
- Nissen, K.; Leckebusch, G.C.; Pinto, J.; Ulbrich, U. Mediterranean cyclones and windstorms in a changing climate. Reg. Environ. Change 2013, 14, 1873–1890. [Google Scholar] [CrossRef]
- Cavicchia, L.; von Storch, H.; Gualdi, S. Mediterranean Tropical-Like Cyclones in Present and Future Climate. J. Clim. 2014, 27, 7493–7501. [Google Scholar] [CrossRef]
- Romero, R.; Emanuel, K. Medicane risk in a changing climate. J. Geophys. Res. Atmos. 2013, 118, 5992–6001. [Google Scholar] [CrossRef]
- Hatzaki, M.; Flocas, H.A.; Simmonds, I.; Kouroutzoglou, J.; Keay, K.; Rudeva, I. Seasonal Aspects of an Objective Climatology of Anticyclones Affecting the Mediterranean. J. Clim. 2014, 27, 9272–9289. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).