Multivariate Simulation of Offshore Weather Time Series: A Comparison between Markov Chain, Autoregressive, and Long Short-Term Memory Models
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Scope of the Analysis and Overview
2. Materials and Methods
2.1. Historical Weather Data
2.2. Data Processing
2.3. Markov Chain
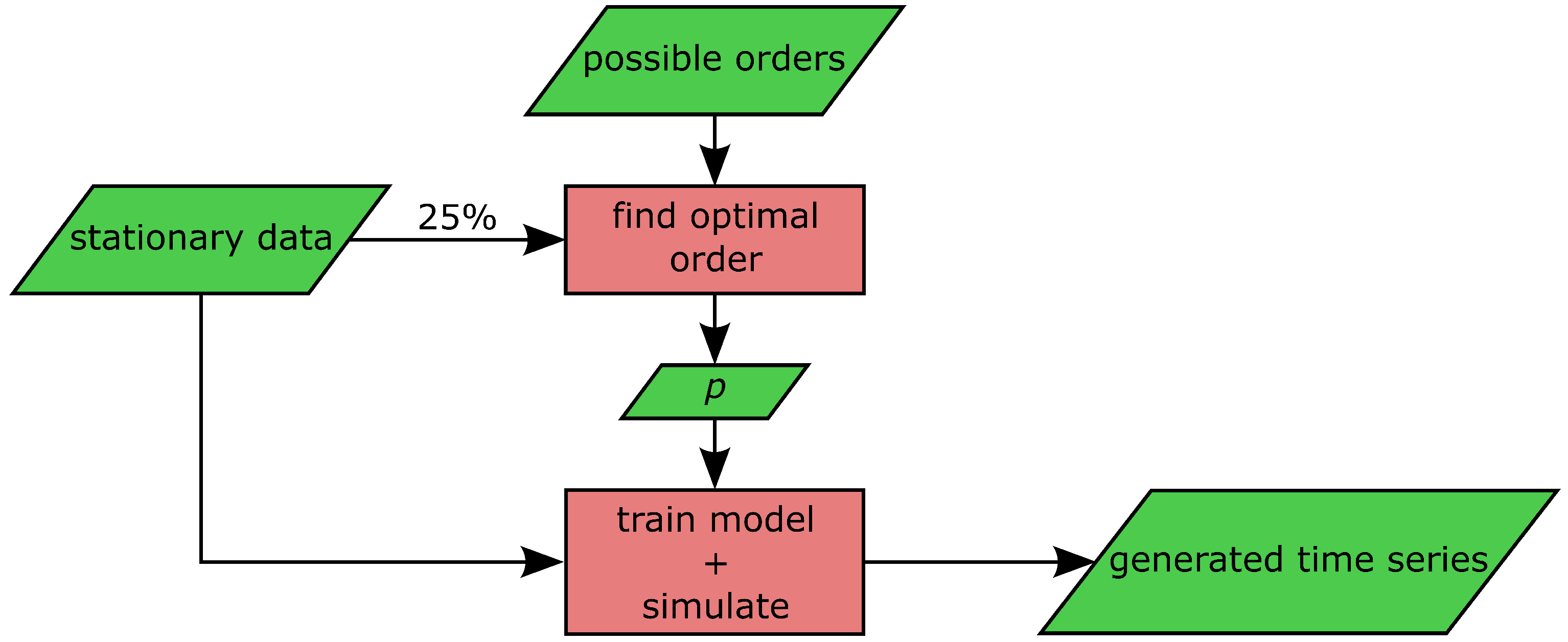
2.4. Vector Autoregressive Models
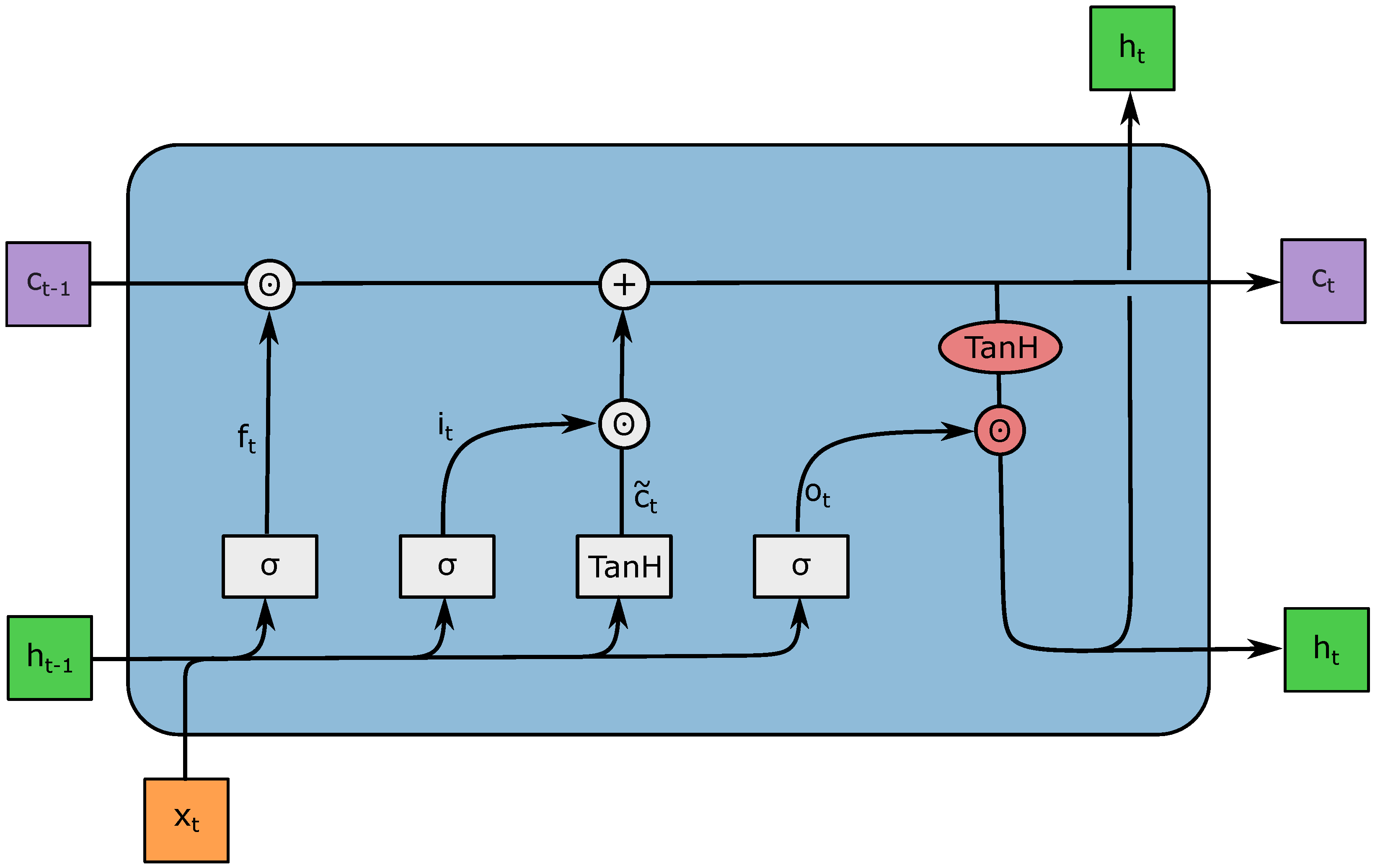
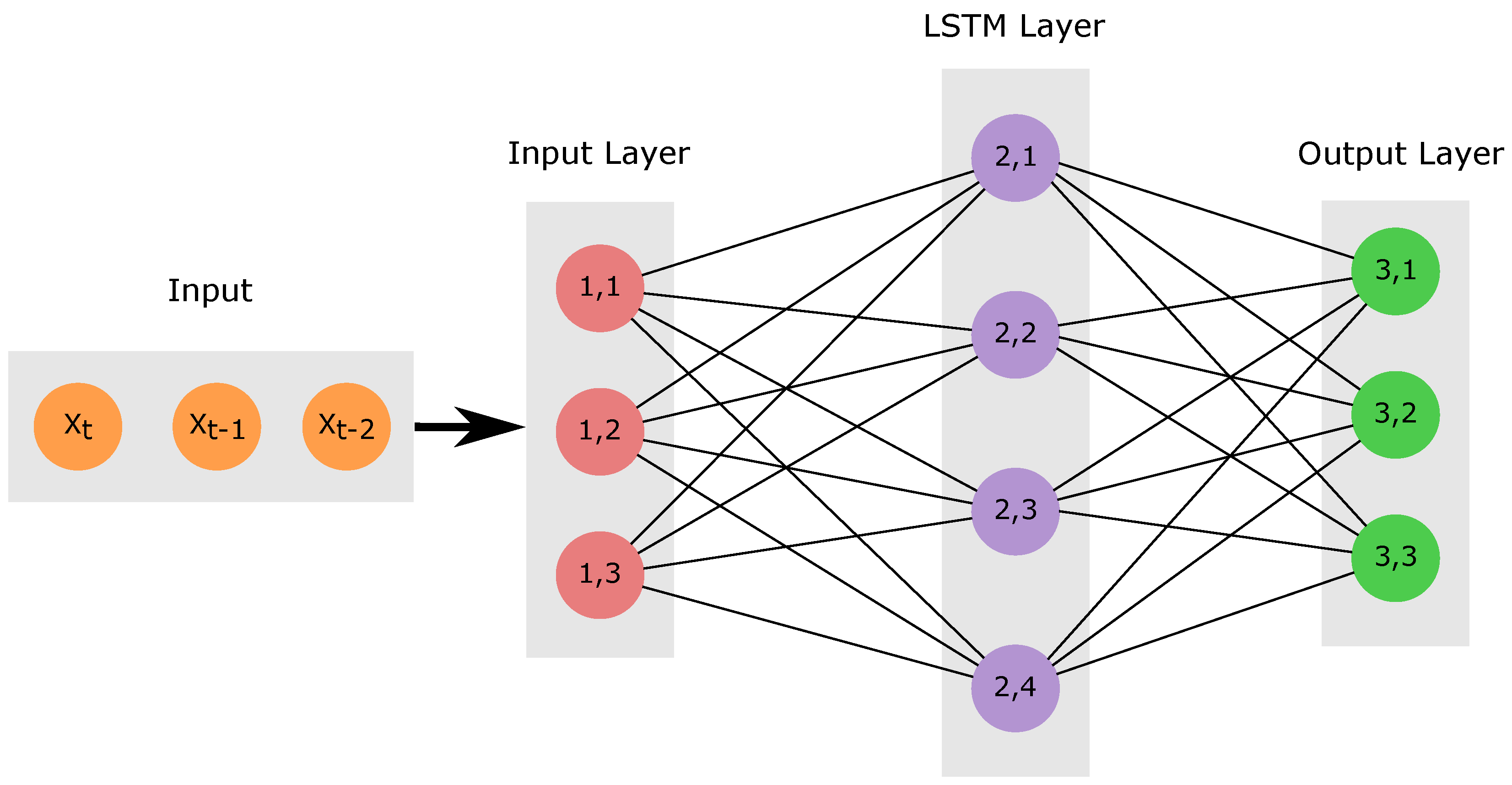
2.5. LSTM Neural Networks
- Forget gate controls how much of the old cell state is forgotten for every component;
- Input gate determines which information from the current time step is important and should be added to ;
- Output gate decides which information from (activated with the TanH) should be saved in the hidden state .
2.6. Metrics for Joint Probability Density Functions
3. Results
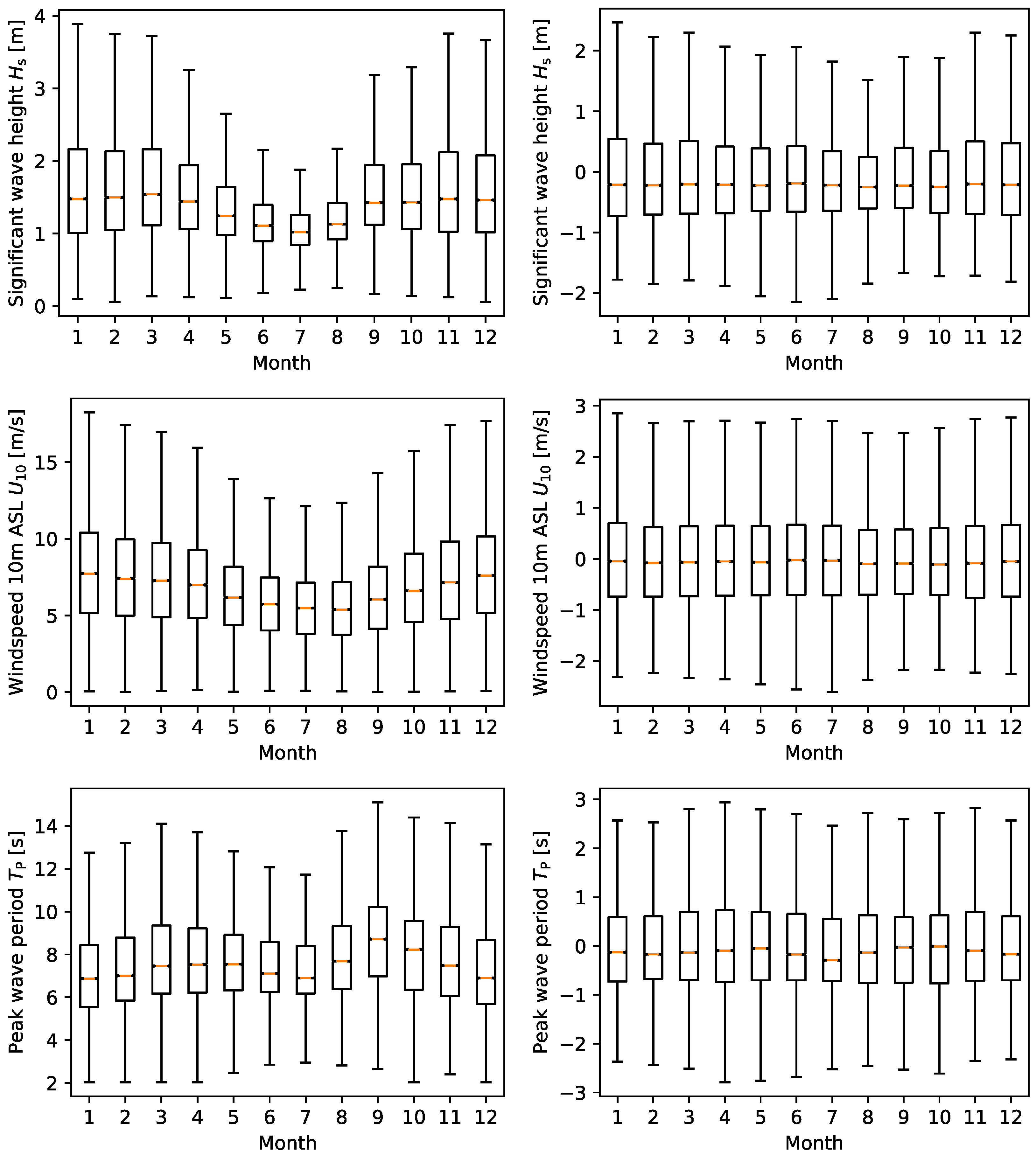
3.1. Preprocessing of the Data
3.2. Single Measurements Comparison
3.2.1. Marginal Distributions and Increments
3.2.2. Earth Mover’s Distance
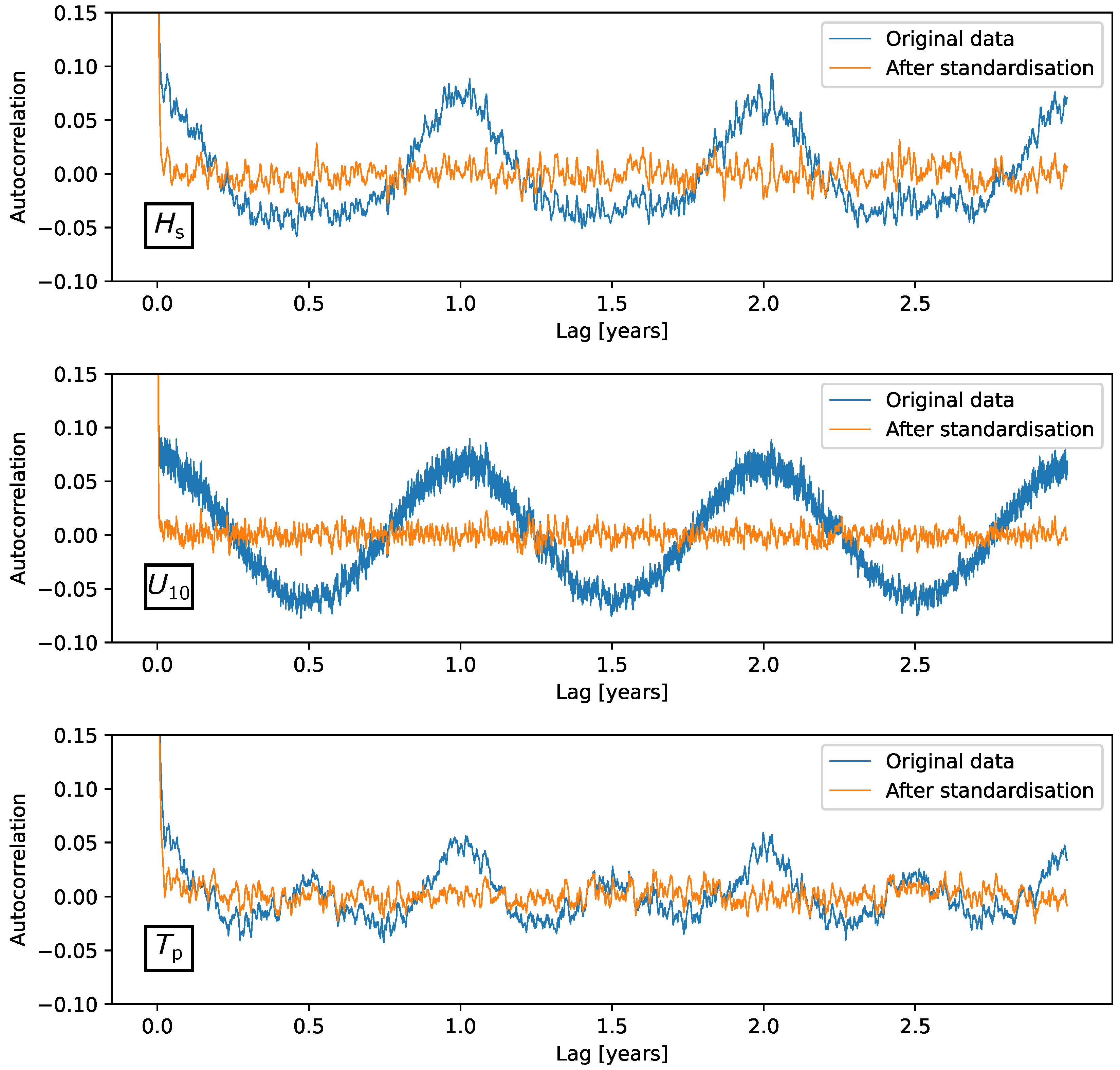
3.2.3. Autocorrelation
3.3. Multidimensional Results Comparison
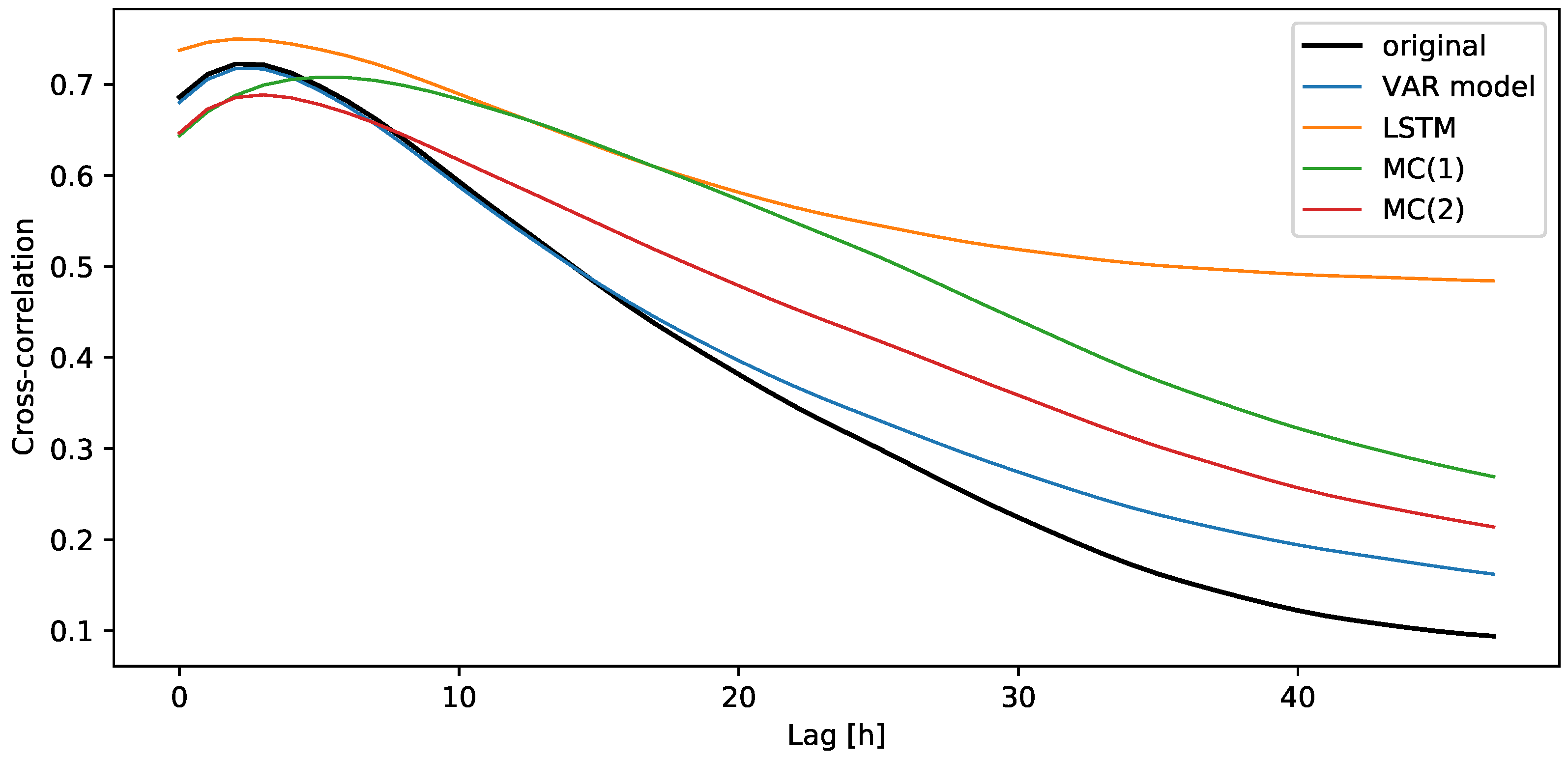
3.3.1. Cross-Correlation of the Simulations
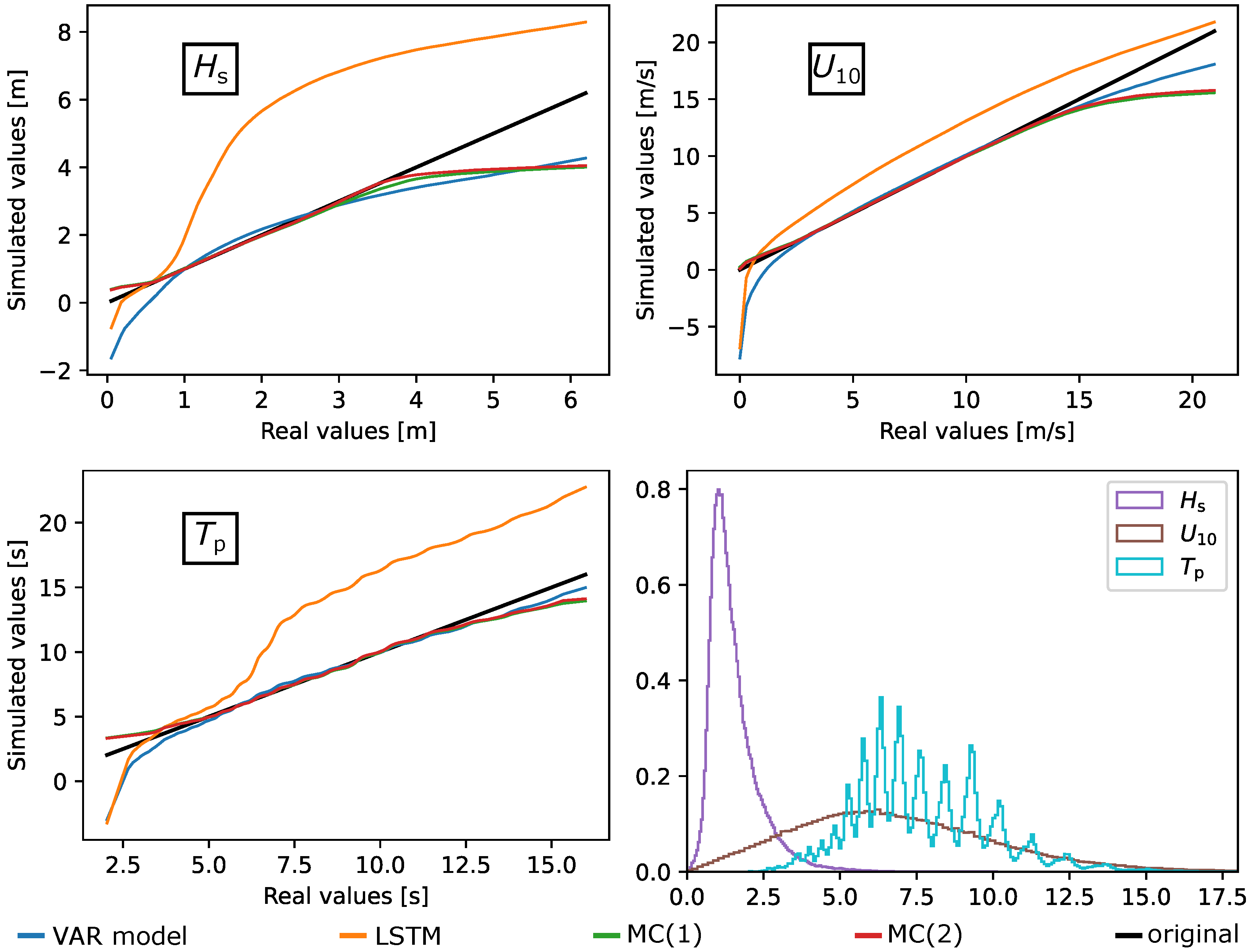
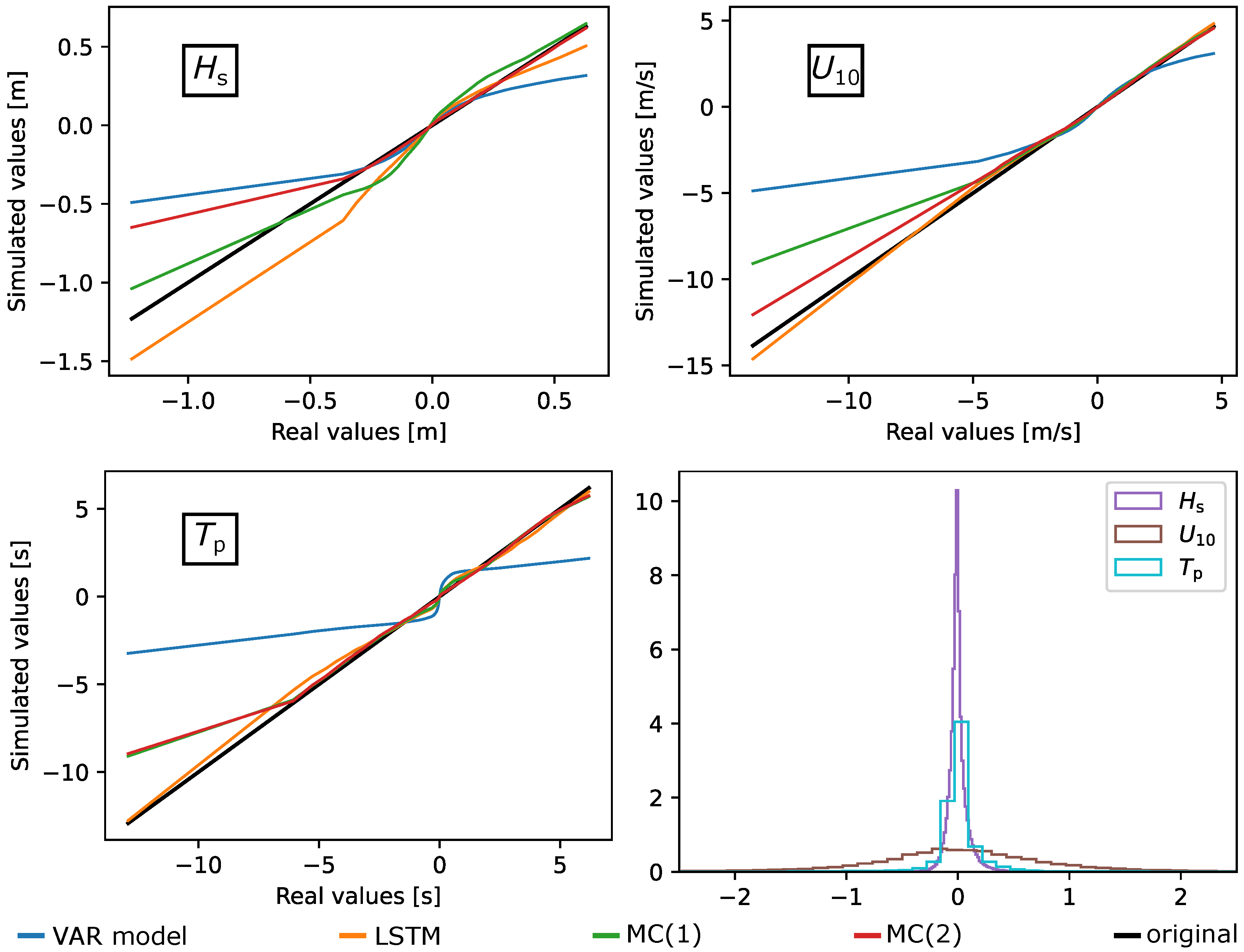
3.3.2. Joint Probability Density Functions
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| O&M | Operation and maintenance |
| LCOE | Levelised costs of energy |
| OPEX | Operational expenditures |
| Metocean data | Meteorological and oceanographic data |
| ASL | Above sea level |
| Hs | Significant wave height |
| U10 | Wind speed at 10 m ASL |
| Tp | Peak wave period |
| MC | Markov chain |
| VAR model | Vector autoregressive model |
| HQ | Hannan–Quinn criterion |
| FPE | Final prediction error |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| LSTM | Long short-term memory |
| RNN | Recurrent neural network |
| MSE | Mean squared error |
| Adam | Adaptive moment estimation |
| QQ plot | Quantile–quantile plot |
| EMD | Earth mover’s distance |
| BC | Bhattacharyya coefficient |
| Kullback–Leibler divergence | |
| Jeffrey divergence | |
| HI | Histogram intersection |
| Joint PDF | Joint probability density function |
References
- EU. Directive (EU) 2018/2001 of the European Parliament and of the Council on the Promotion of the Use of Energy from Renewable Sources; EU: Brussels, Belgium, 2018. [Google Scholar]
- Bundesverband-WindEnergie. Europa in Zahlen. 2022. Available online: https://www.wind-energie.de/themen/zahlen-und-fakten/europa/#:~:text=Windenergie%20in%20Europa&text=Mit%20458%20TWh%20produziertem%20Strom,und%20Gro%C3%9Fbritannien%20mit%2024%20GW (accessed on 26 April 2022).
- Johnston, B.; Foley, A.; Doran, J.; Littler, T. Levelised cost of energy, A challenge for offshore wind. Renew. Energy 2020, 160, 876–885. [Google Scholar] [CrossRef]
- Seyr, H.; Muskulus, M. Decision Support Models for Operations and Maintenance for Offshore Wind Farms: A Review. Appl. Sci. 2019, 9, 278. [Google Scholar] [CrossRef] [Green Version]
- Graham, C. The parameterisation and prediction of wave height and wind speed persistence statistics for oil industry operational planning purposes. Coast. Eng. 1982, 6, 303–329. [Google Scholar] [CrossRef]
- Brokish, K.; Kirtley, J. Pitfalls of modeling wind power using Markov chains. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, PSCE, Seattle, WA, USA, 15–18 March 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Ailliot, P.; Monbet, V. Markov-switching autoregressive models for wind time series. Environ. Model. Softw. 2012, 30, 92–101. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Guo, P.; Huang, X. A Review of Wind Power Forecasting Models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef] [Green Version]
- Scheu, M. Maintenance Strategies for Large Offshore Wind Farms. Energy Procedia 2012, 24, 281–288. [Google Scholar] [CrossRef] [Green Version]
- Seyr, H.; Muskulus, M. Using a Langevin model for the simulation of environmental conditions in an offshore wind farm. J. Phys. Conf. Ser. 2018, 1104, 012023. [Google Scholar] [CrossRef]
- Pandit, R.; Kolios, A.; Infield, D. Data-Driven weather forecasting models performance comparison for improving offshore wind turbine availability and maintenance. IET Renew. Power Gener. 2020, 14, 2386–2394. [Google Scholar] [CrossRef]
- BMU (Bundesministerium fuer Umwelt, Federal Ministry for the Environment, Nature Conservation and Nuclear Safety); Project Executing Organisation; PTJ (Projekttraeger Juelich). FINO3 Metrological Masts Datasets. Available online: https://www.fino3.de/en/ (accessed on 26 April 2022).
- Skobiej, B.; Niemi, A. Validation of copula-based weather generator for maintenance model of offshore wind farm. WMU J. Marit. Aff. 2022, 21, 73–87. [Google Scholar] [CrossRef]
- Niemi, A.; Torres, F.S. Application of synthetic weather time series based on four-dimensional copula for modeling of maritime operations. In Proceedings of the Oceans Conference Record (IEEE), MTS, San Diego, CA, USA, 20–23 September 2021. [Google Scholar] [CrossRef]
- MIT Data To AI Lab. Copulas Python Library; MIT Data To AI Lab: Cambridge, MA, USA, 2018. [Google Scholar]
- Soares, C.G.; Cunha, C. Bivariate autoregressive models for the time series of significant wave height and mean period. Coast. Eng. 2000, 40, 297–311. [Google Scholar] [CrossRef]
- Hagen, B.; Simonsen, I.; Hofmann, M.; Muskulus, M. A multivariate Markov Weather Model for O&M Simulation of Offshore Wind Parks. Energy Procedia 2013, 35, 137–147. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Liu, C.; Guo, Z.; Feng, Y.; Hong, F.; Huang, H. Trajectory Prediction for Ocean Vessels Base on K-order Multivariate Markov Chain. In Wireless Algorithms, Systems, and Applications; Chellappan, S., Cheng, W., Li, W., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 140–150. [Google Scholar] [CrossRef]
- Nfaoui, H.; Essiarab, H.; Sayigh, A. A stochastic Markov chain model for simulating wind speed time series at Tangiers, Morocco. Renew. Energy 2004, 29, 1407–1418. [Google Scholar] [CrossRef]
- Pesch, T.; Schröders, S.; Allelein, H.J.; Hake, J.F. A new Markov-chain-related statistical approach for modelling synthetic wind power time series. New J. Phys. 2015, 17, 055001. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), IEEE, Orlando, FL, USA, 17–20 December 2018. [Google Scholar] [CrossRef]
- Dinwoodie, I.; Quail, F.; Mcmillan, D. Analysis of Offshore Wind Turbine Operation & Maintenance Using a Novel Time Domain Meteo-Ocean Modeling Approach. Turbo Expo Power Land Sea Air 2012, 6, 847–857. [Google Scholar] [CrossRef] [Green Version]
- Dostal, L.; Grossert, H.; Duecker, D.A.; Grube, M.; Kreuter, D.C.; Sandmann, K.; Zillmann, B.; Seifried, R. Predictability of Vibration Loads From Experimental Data by Means of Reduced Vehicle Models and Machine Learning. IEEE Access 2020, 8, 177180–177194. [Google Scholar] [CrossRef]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. An Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2002; Volume 39. [Google Scholar] [CrossRef] [Green Version]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning. arXiv 2021, arXiv:2106.11342. [Google Scholar]
- Olah, C. Understanding LSTM Networks. 2015. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 15 April 2022).
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 18 April 2022).
- Bhattacharyya, A. On a Measure of Divergence between Two Multinomial Populations. Sankhyā Indian J. Stat. 1946, 7, 401–406. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Marden, J.I. Positions and QQ Plots. Stat. Sci. 2004, 19, 606–614. [Google Scholar] [CrossRef]
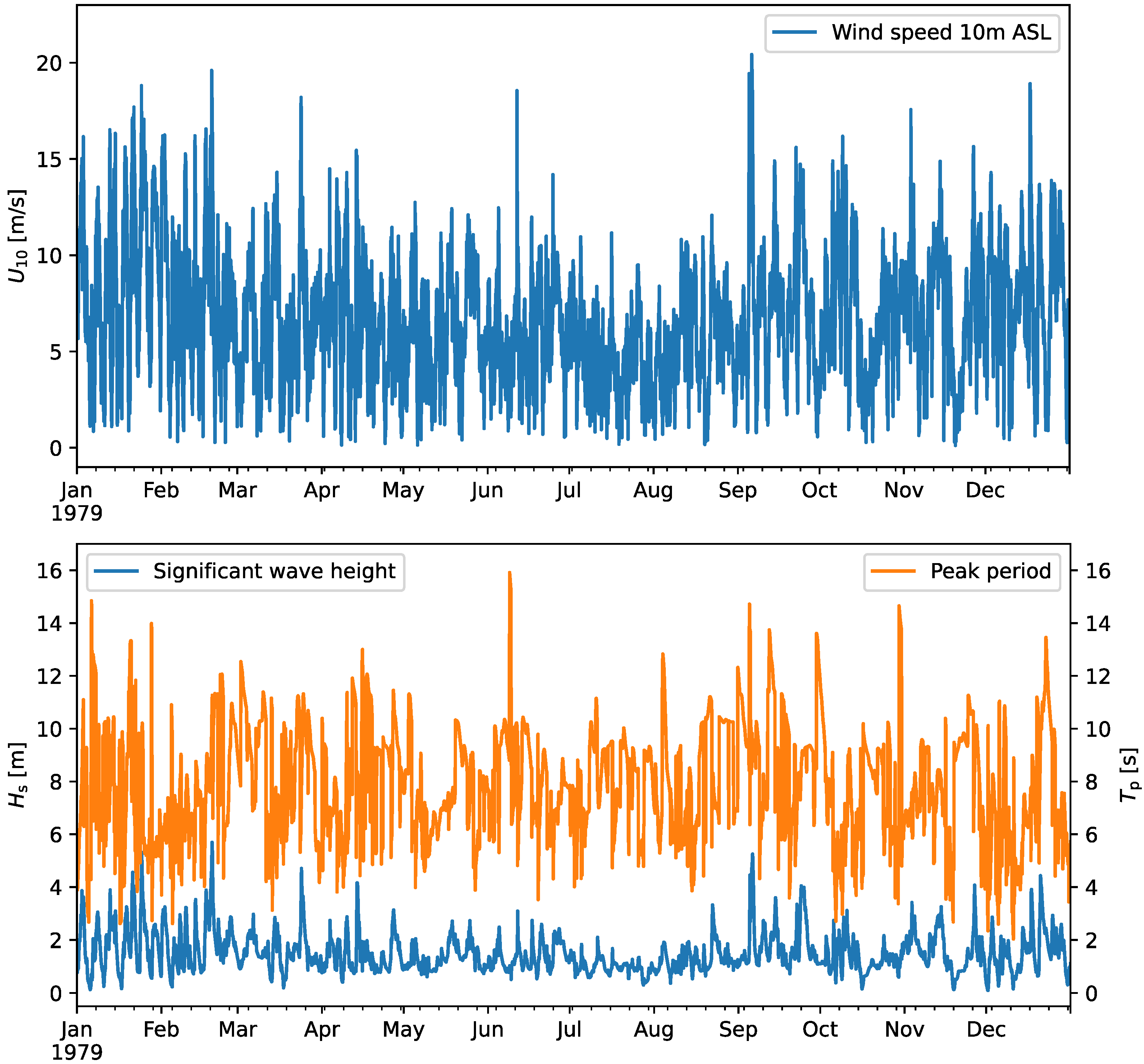


| Parameter | Value |
|---|---|
| Mean annual significant wave height | 1.520 m |
| Mean annual wind speed at 10 m ASL | 6.837 m/s |
| Mean annual peak wave period | 7.701 s |
| Hs | U10 | Tp | |
|---|---|---|---|
| Min value | −1.2892 | −1.7000 | −1.6515 |
| Number of states | 15 | 20 | 15 |
| Max value | 2.5363 | 2.0940 | 2.2084 |
| Order p | AIC | BIC | HQ |
|---|---|---|---|
| 1 | −73,961 | −73,792 | −73,909 |
| 2 | −159,656 | −159,403 | −159,579 |
| 3 | −170,549 | −170,211 | −170,446 |
| 4 | −172,847 | −172,425 | −172,719 |
| 5 | −173,016 | −172,509 | −172,861 |
| 6 | −172,881 | −172,290 | −172,701 |
| 7 | −173,919 | −173,243 | −173,713 |
| 8 | −174,156 | −173,396 | −173,924 |
| 9 | −174,171 | −173,326 | −173,913 |
| 10 | −174,185 | −173,257 | −173,902 |
| 11 | −174,212 | −173,199 | −173,903 |
| Parameter | Value |
|---|---|
| Order | 8 |
| Input neurons | 3 |
| Neurons in LSTM layer | 100 |
| Output neurons | 3 |
| Optimiser | Adam |
| Loss function | MSE |
| Epochs | 5 |
| Batch size | 500 |
| VAR Model | LSTM | MC(1) | MC(2) | Original | ||
|---|---|---|---|---|---|---|
| Hs | mean | −0.0151 | 2.8167 | −0.0287 | −0.0484 | −0.0022 |
| std | 1.0073 | 2.4503 | 0.9036 | 0.8670 | 0.9948 | |
| min | −4.3077 | −2.6322 | −1.2892 | −1.2892 | −2.2746 | |
| 25% | −0.6968 | 0.4199 | −0.6867 | −0.6854 | −0.6652 | |
| 50% | −0.0139 | 3.3725 | −0.2328 | −0.2417 | −0.2199 | |
| 75% | 0.6671 | 4.8972 | 0.4139 | 0.4037 | 0.4186 | |
| max | 3.9227 | 8.3683 | 2.5363 | 2.5361 | 13.9059 | |
| U10 | mean | −0.0020 | 0.8251 | −0.0132 | −0.0239 | −0.0006 |
| std | 1.0101 | 1.1068 | 0.9470 | 0.9285 | 0.9980 | |
| min | −4.5885 | −4.0388 | −1.7000 | −1.7000 | −2.6080 | |
| 25% | −0.6838 | 0.0601 | −0.7223 | −0.7270 | −0.7209 | |
| 50% | 0.0003 | 0.8593 | −0.0763 | −0.0781 | −0.0656 | |
| 75% | 0.6786 | 1.5875 | 0.6315 | 0.6213 | 0.6369 | |
| max | 4.4298 | 5.8560 | 2.0940 | 2.0940 | 8.7361 | |
| Tp | mean | 0.0018 | 1.9856 | −0.0054 | −0.0158 | −0.0009 |
| std | 0.9976 | 1.9515 | 0.9566 | 0.9287 | 0.9978 | |
| min | −4.5479 | −5.4943 | −1.6515 | −1.6514 | −3.1213 | |
| 25% | −0.6751 | 0.1651 | −0.7291 | −0.7356 | −0.7221 | |
| 50% | −0.0038 | 2.4620 | −0.1392 | −0.1299 | −0.1337 | |
| 75% | 0.6734 | 3.5614 | 0.6626 | 0.6380 | 0.6506 | |
| max | 4.6768 | 9.2085 | 2.2083 | 2.2084 | 5.4062 |
| EMD of the Values | EMD of the Increments | ||
|---|---|---|---|
| VAR model | 0.3031 | 0.4160 | |
| HS | LSTM | 1.0487 | 0.4219 |
| MC(1) | 0.0797 | 0.5396 | |
| MC(2) | 0.0726 | 0.5363 | |
| VAR model | 0.0402 | 0.2877 | |
| U10 | LSTM | 0.1580 | 0.1089 |
| MC(1) | 0.0577 | 0.1237 | |
| MC(2) | 0.0612 | 0.1276 | |
| Tp | VAR model | 0.2255 | 1.2661 |
| LSTM | 0.6922 | 0.8886 | |
| MC(1) | 0.2250 | 0.8730 | |
| MC(2) | 0.2377 | 0.8728 |
| BC | HI | |||
|---|---|---|---|---|
| VAR model | 0.1141 | ∞ | 1.2496 | 0.0594 |
| LSTM | 0.1918 | ∞ | 1.1545 | 0.1034 |
| MC(1) | 0.4082 | ∞ | 0.8840 | 0.2305 |
| MC(2) | 0.4163 | ∞ | 0.8735 | 0.2359 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eberle, S.; Cevasco, D.; Schwarzkopf, M.-A.; Hollm, M.; Seifried, R. Multivariate Simulation of Offshore Weather Time Series: A Comparison between Markov Chain, Autoregressive, and Long Short-Term Memory Models. Wind 2022, 2, 394-414. https://doi.org/10.3390/wind2020021
Eberle S, Cevasco D, Schwarzkopf M-A, Hollm M, Seifried R. Multivariate Simulation of Offshore Weather Time Series: A Comparison between Markov Chain, Autoregressive, and Long Short-Term Memory Models. Wind. 2022; 2(2):394-414. https://doi.org/10.3390/wind2020021
Chicago/Turabian StyleEberle, Sebastian, Debora Cevasco, Marie-Antoinette Schwarzkopf, Marten Hollm, and Robert Seifried. 2022. "Multivariate Simulation of Offshore Weather Time Series: A Comparison between Markov Chain, Autoregressive, and Long Short-Term Memory Models" Wind 2, no. 2: 394-414. https://doi.org/10.3390/wind2020021
APA StyleEberle, S., Cevasco, D., Schwarzkopf, M.-A., Hollm, M., & Seifried, R. (2022). Multivariate Simulation of Offshore Weather Time Series: A Comparison between Markov Chain, Autoregressive, and Long Short-Term Memory Models. Wind, 2(2), 394-414. https://doi.org/10.3390/wind2020021






