Subseasonal-to-Seasonal Forecasting for Wind Turbine Maintenance Scheduling
Abstract
:1. Introduction
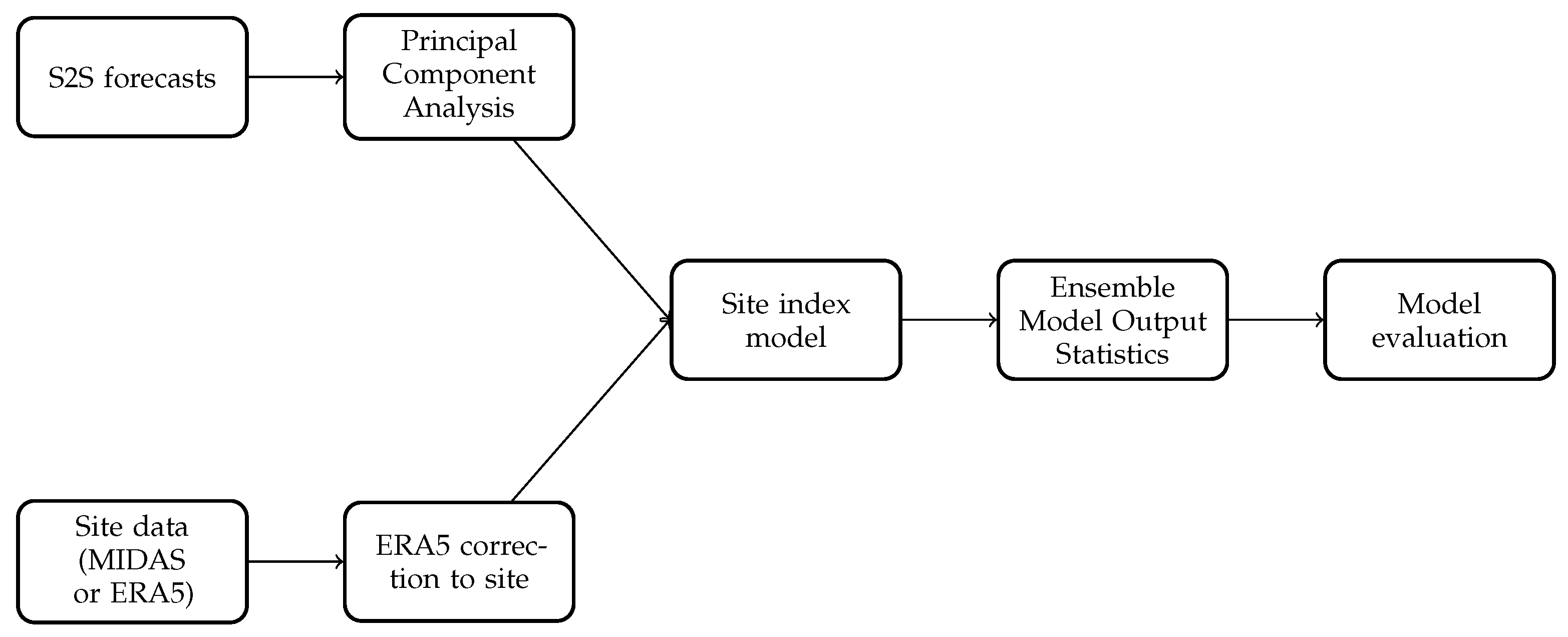
2. Materials and Methods
2.1. Data
2.2. Site Wind Speed Data
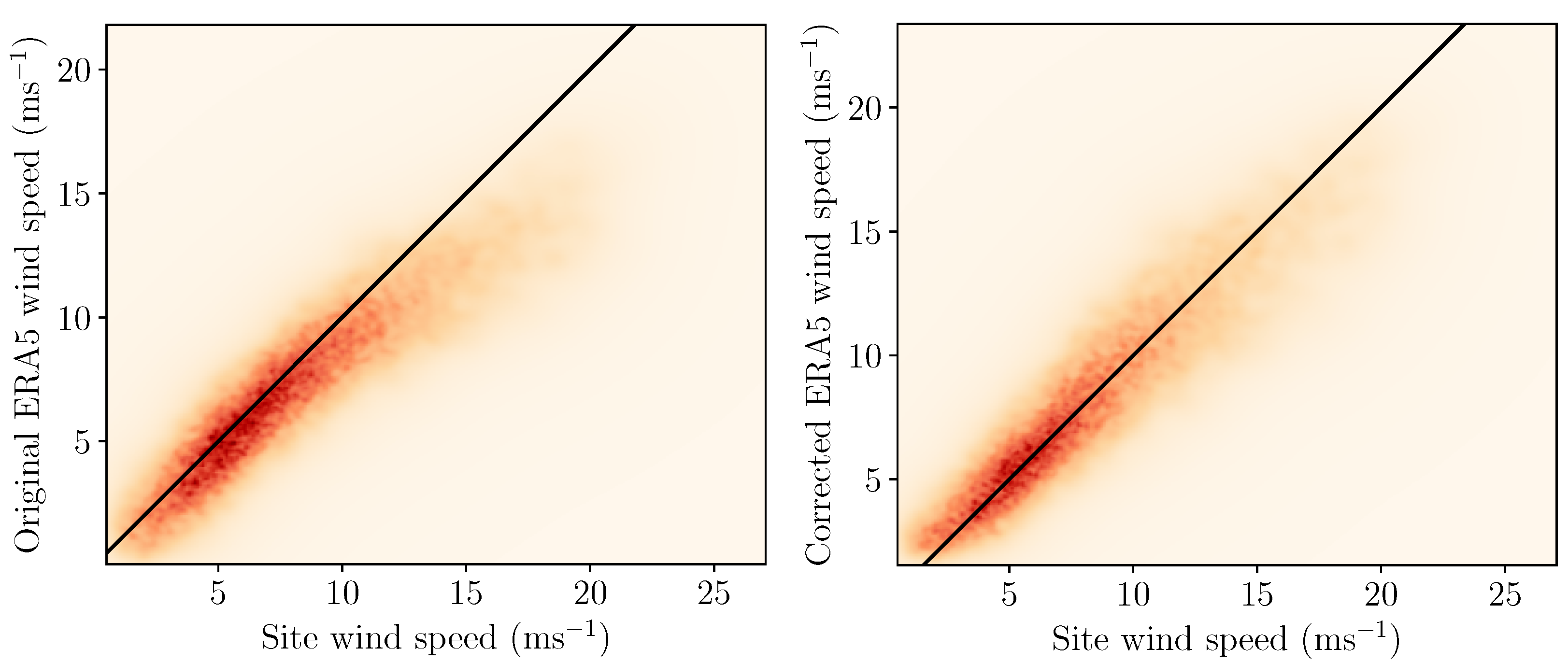
2.3. Initial Transformations and Corrections
2.4. Site-Specific Index Models
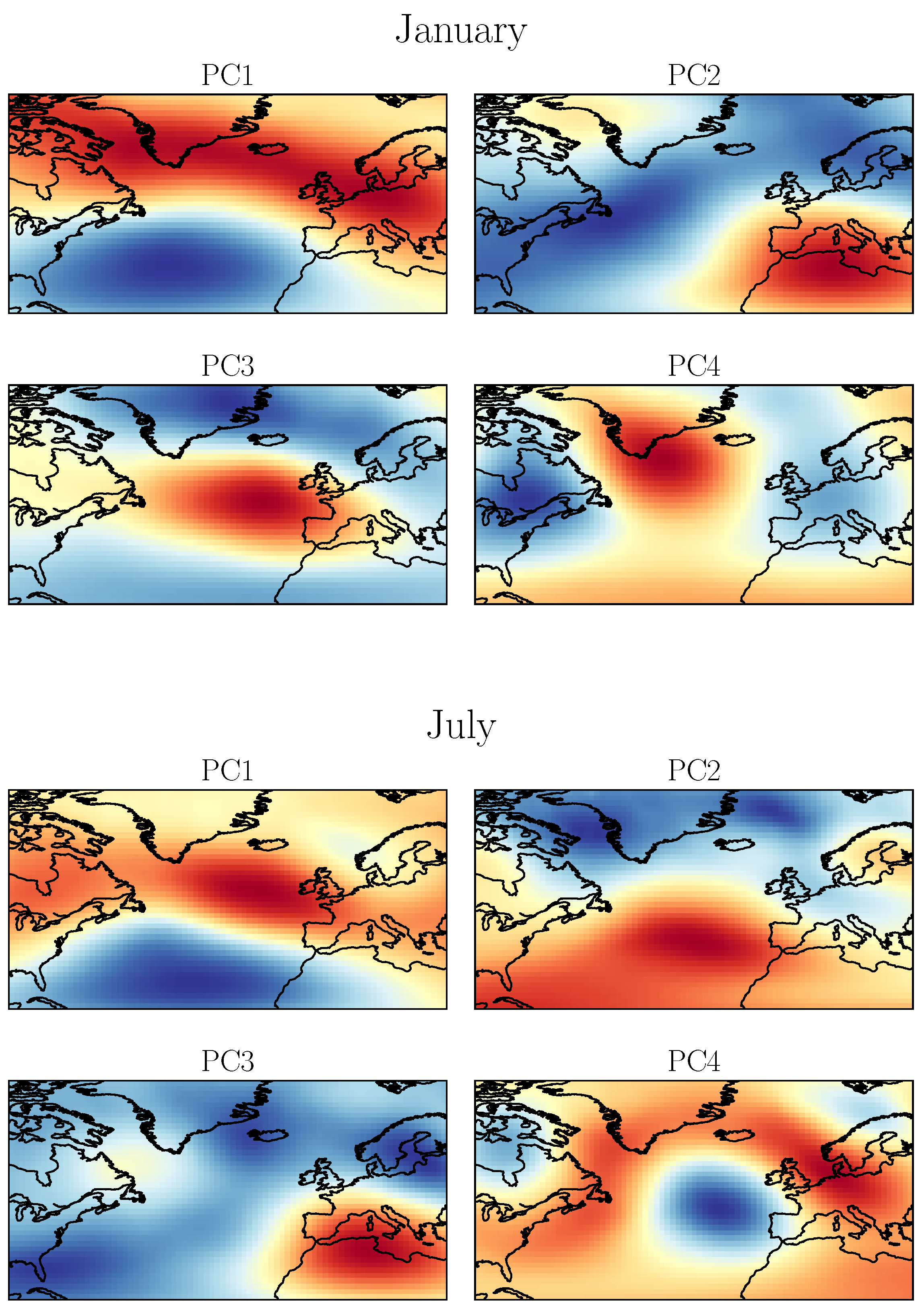
2.4.1. Mean Wind Speed Index
2.4.2. Variability Index
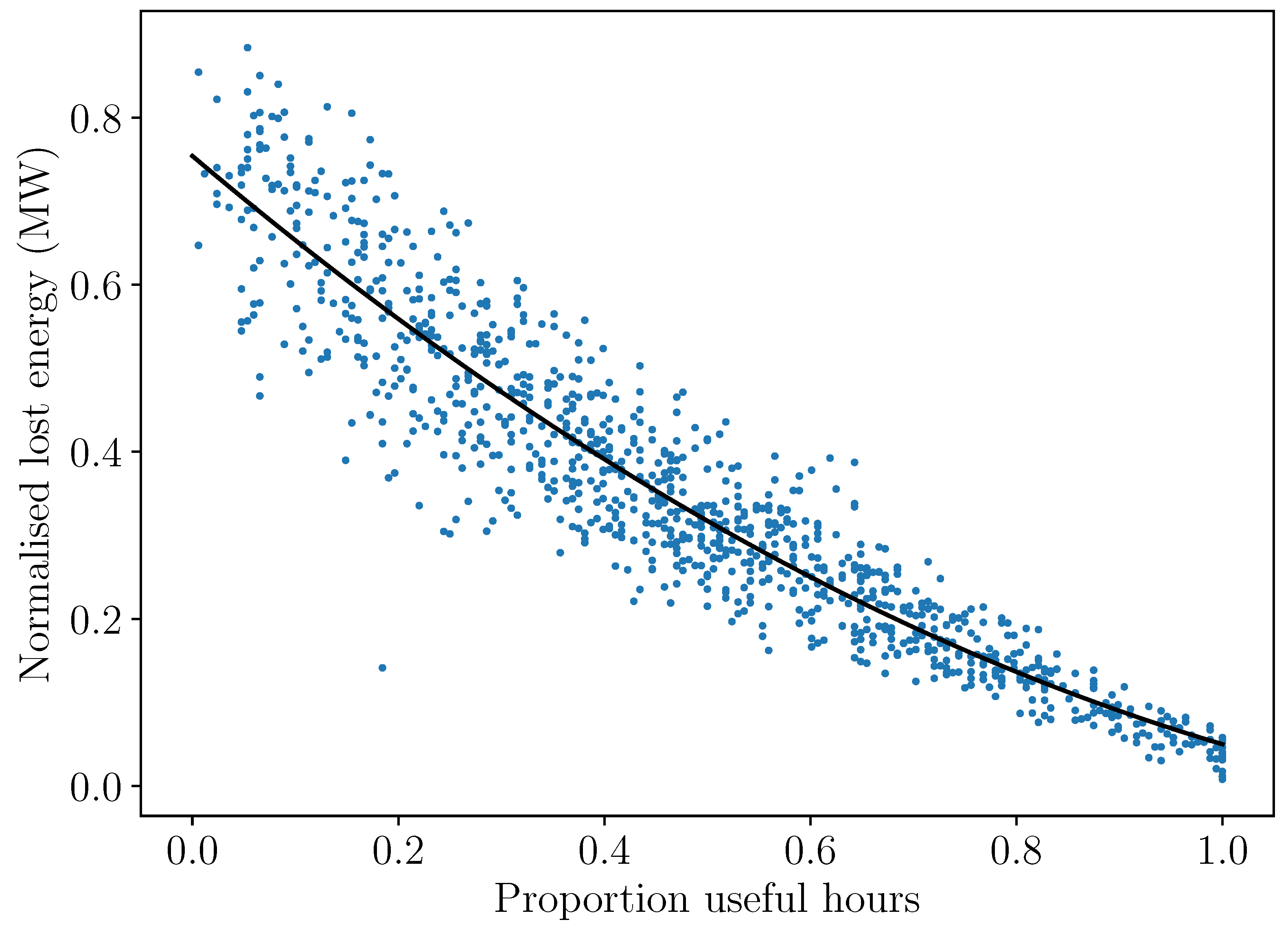
2.4.3. Weather Window Indices
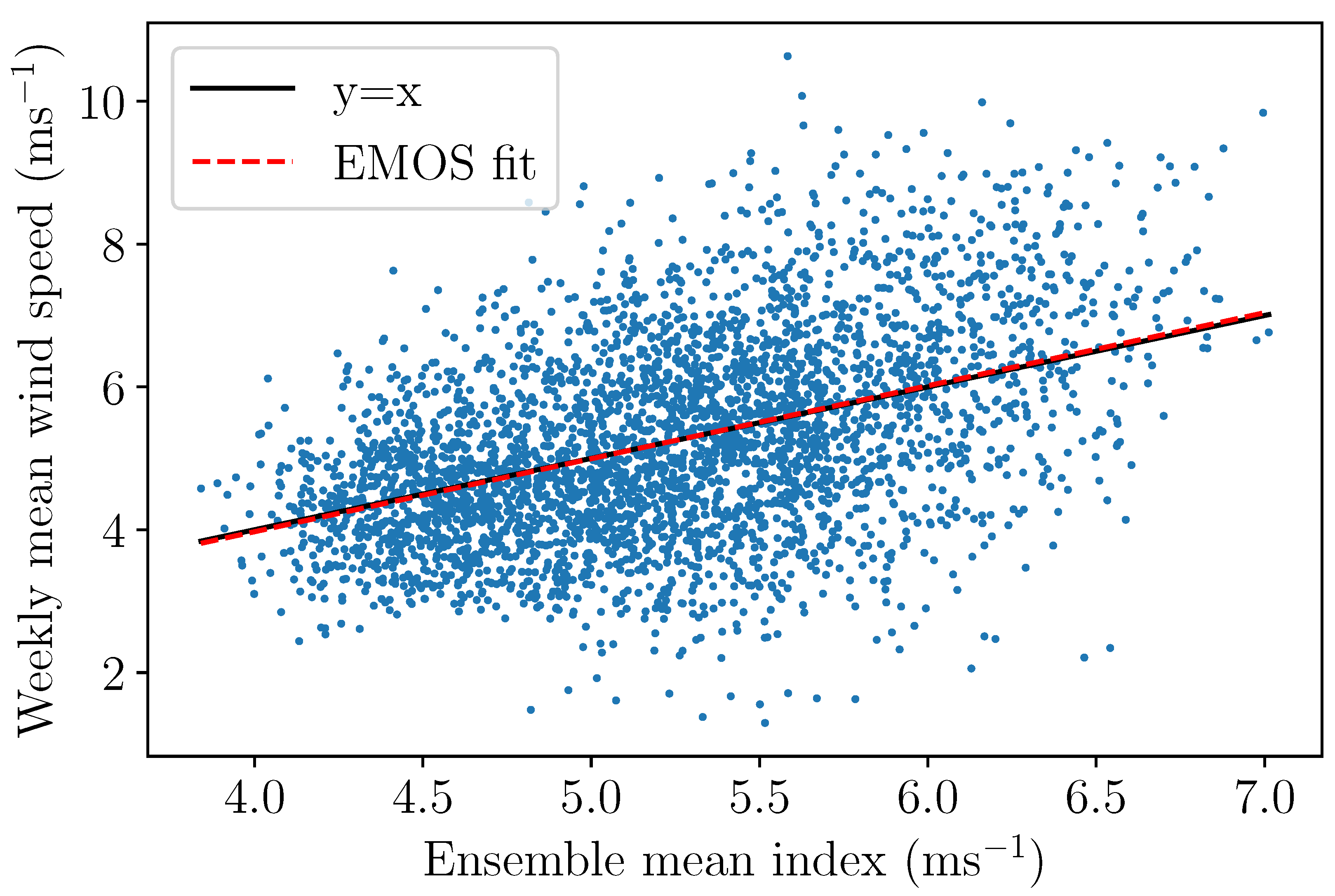
2.5. Ensemble Model Output Statistics
2.6. Benchmark Climatology
3. Results
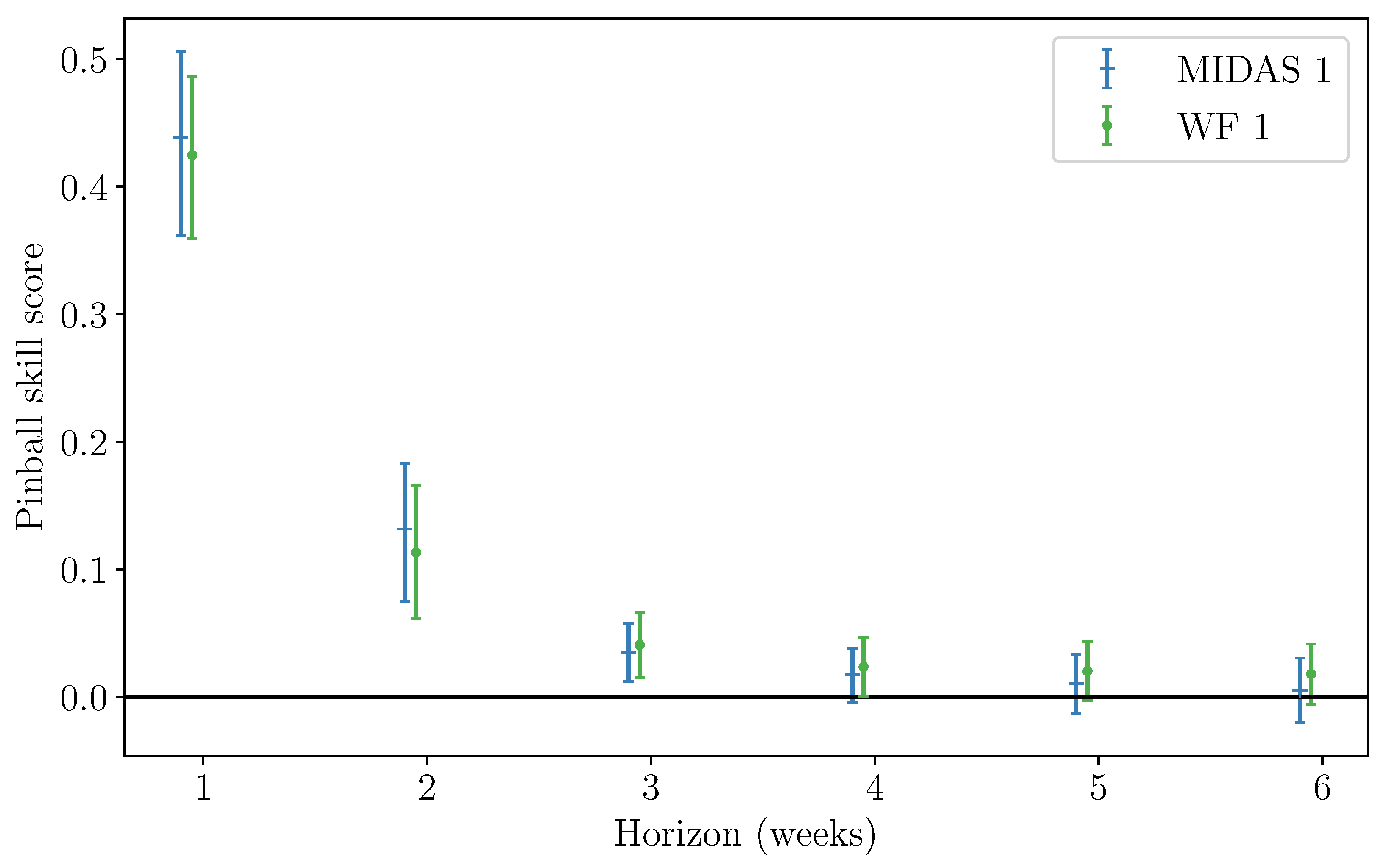
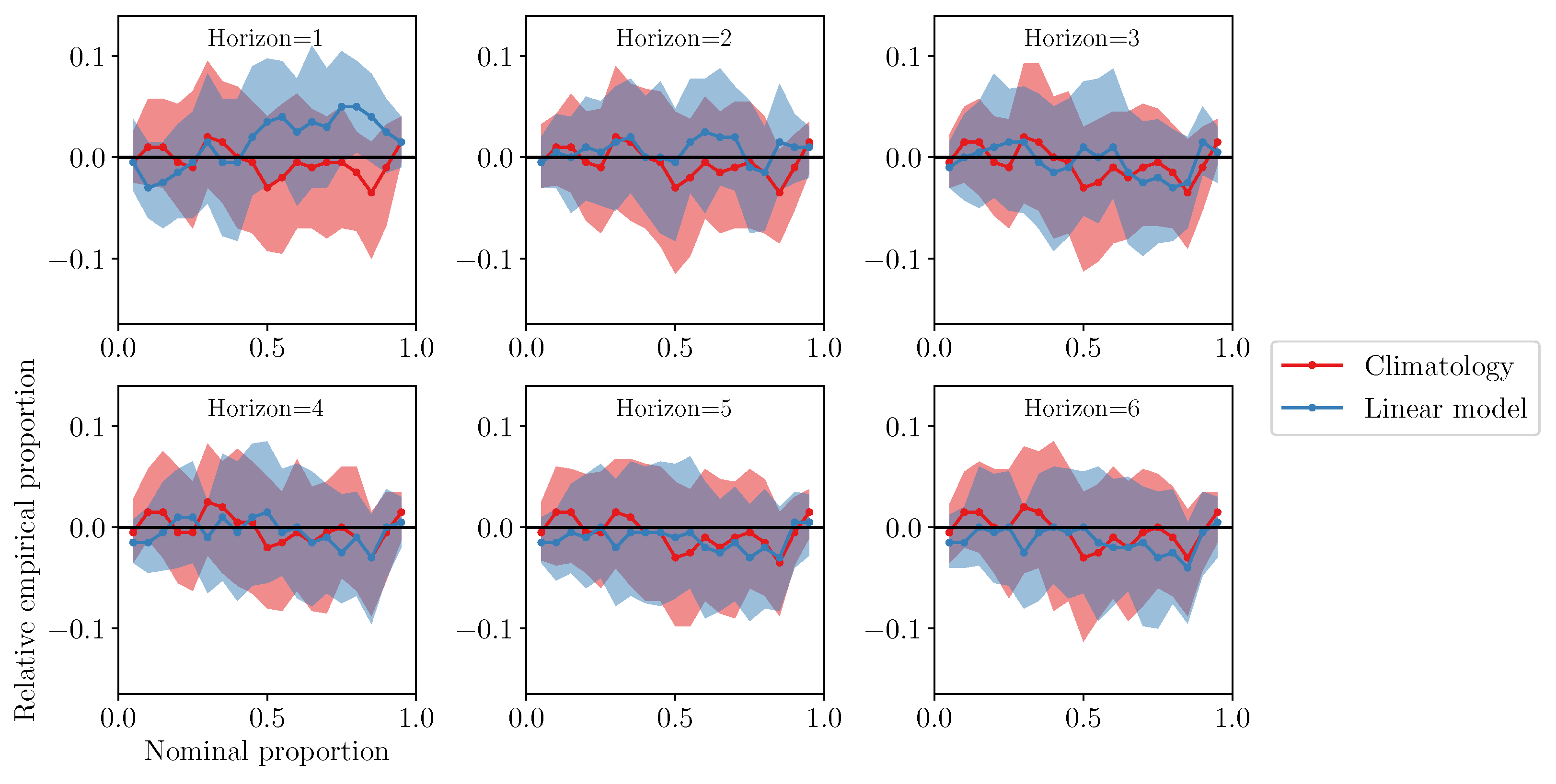
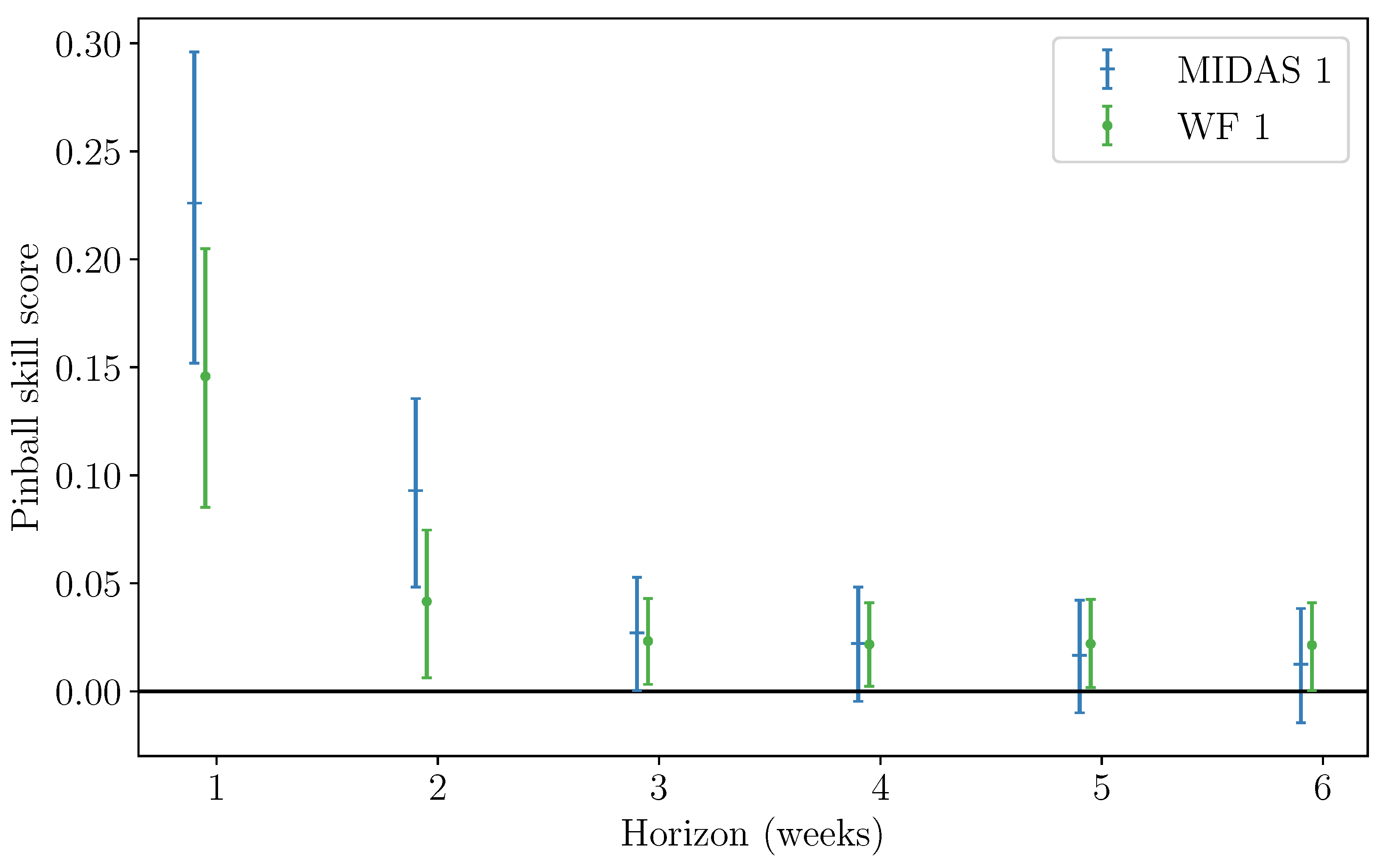
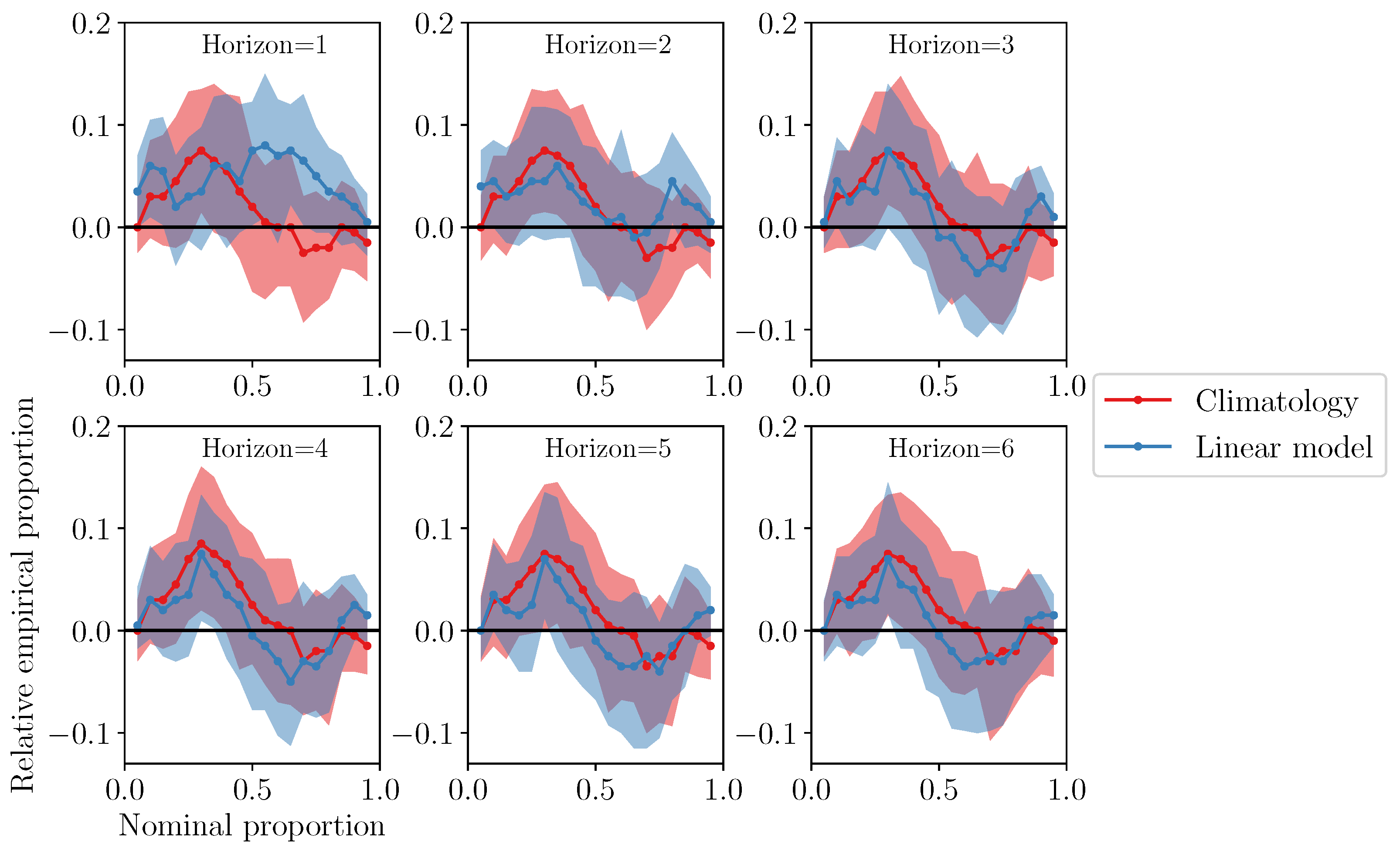
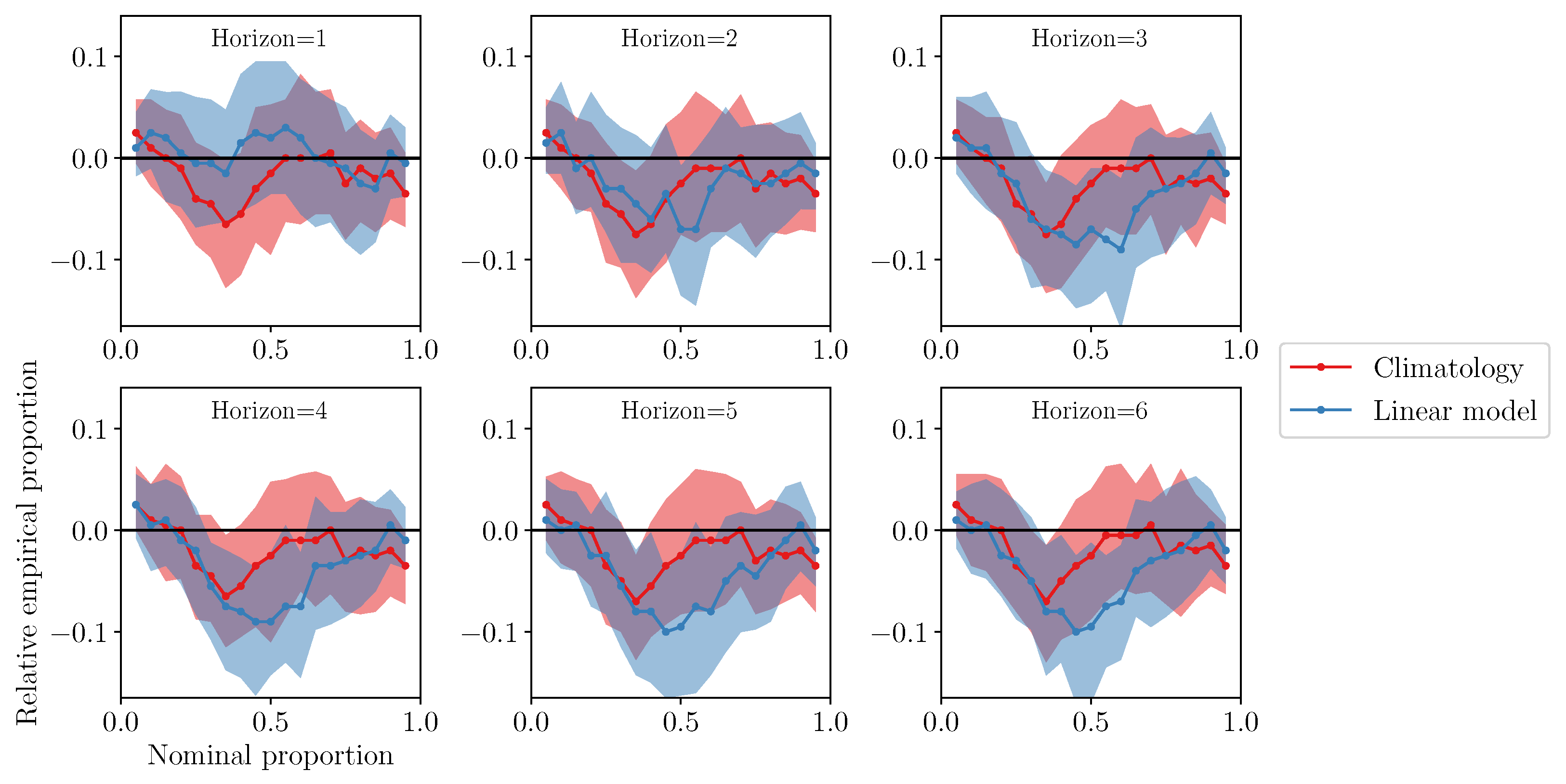
3.1. Mean Wind Speed Forecasts Trained on MIDAS Data
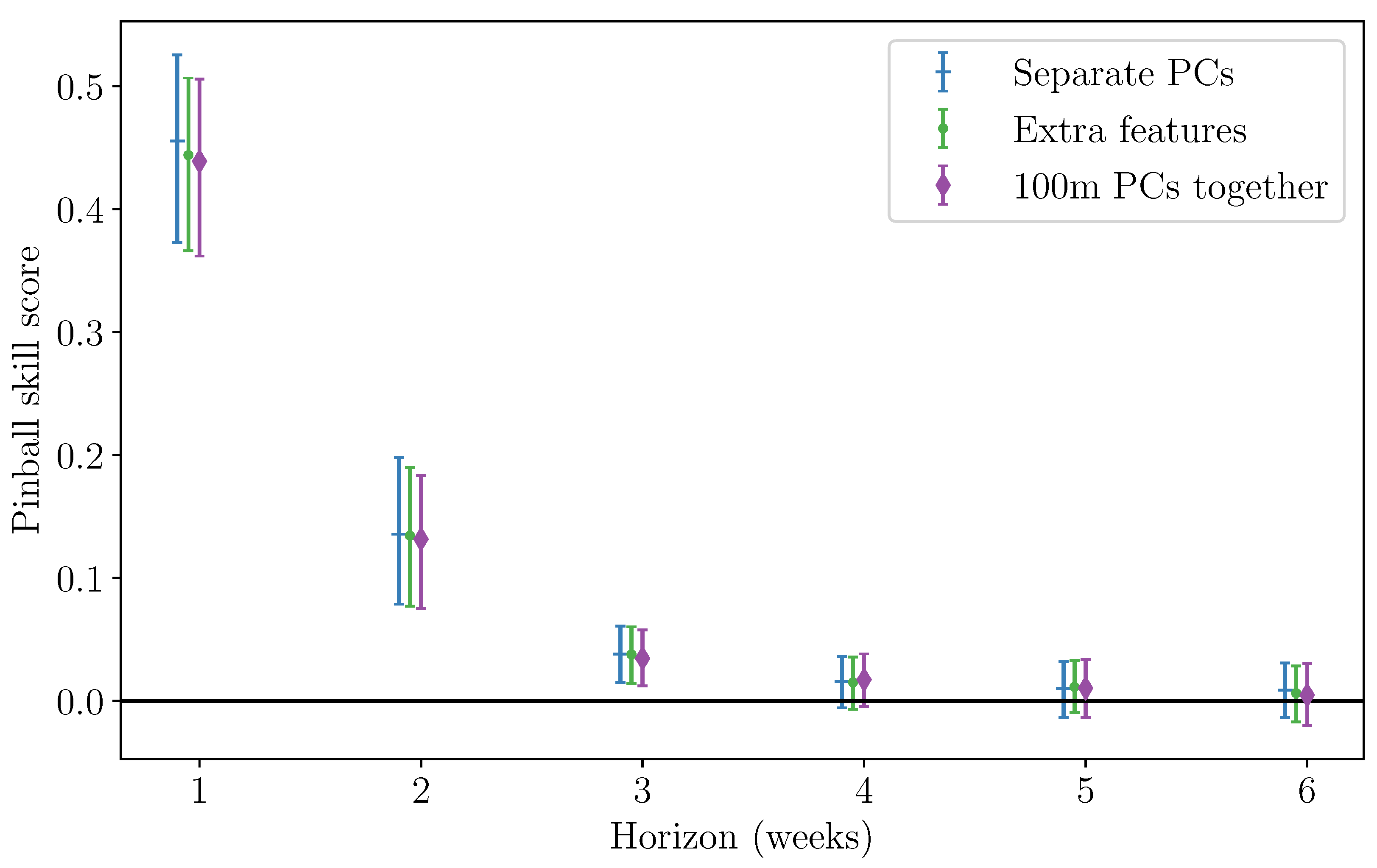
3.2. Mean Wind Speed Forecasts Trained on ERA5 Data
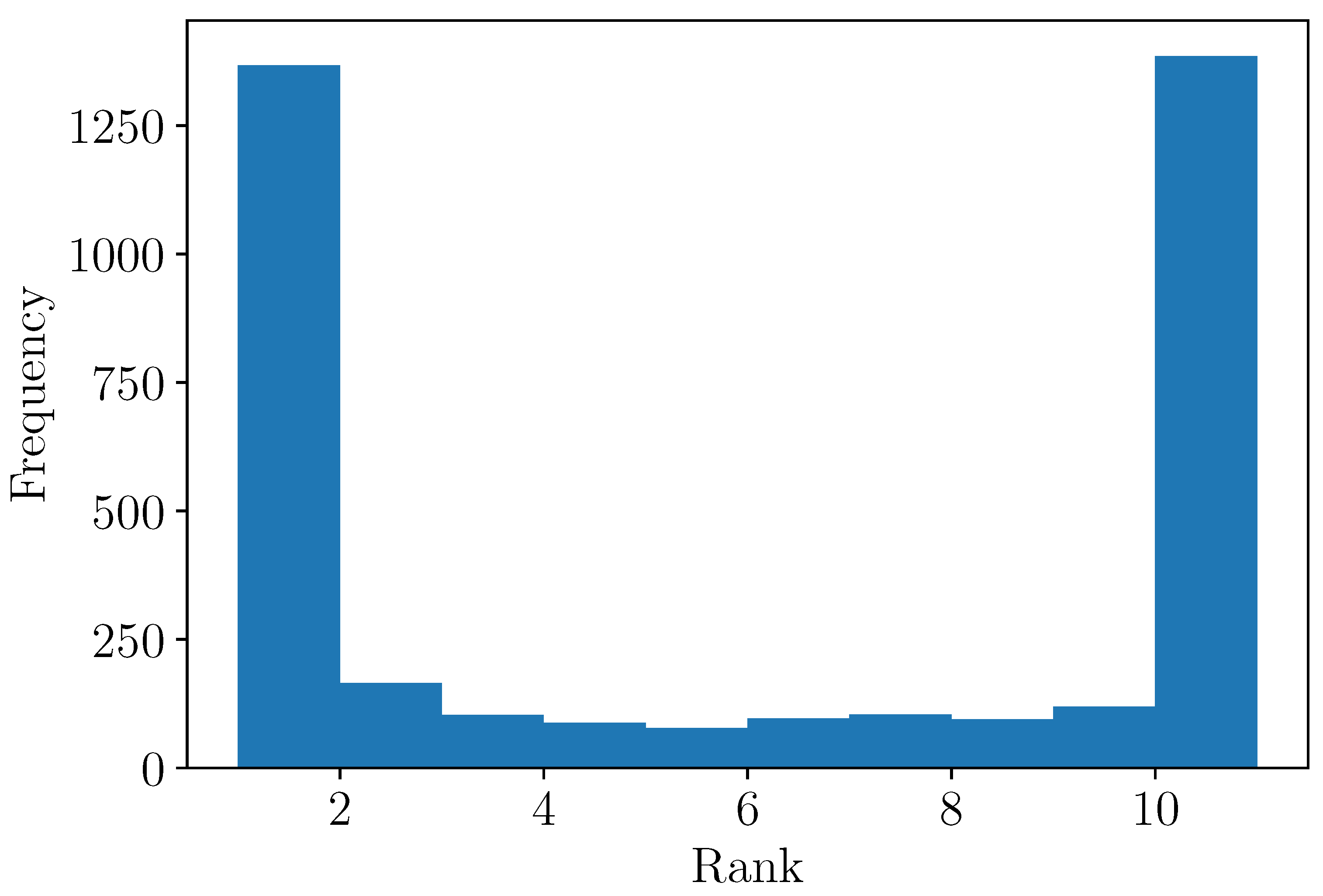
3.3. Variability Indices
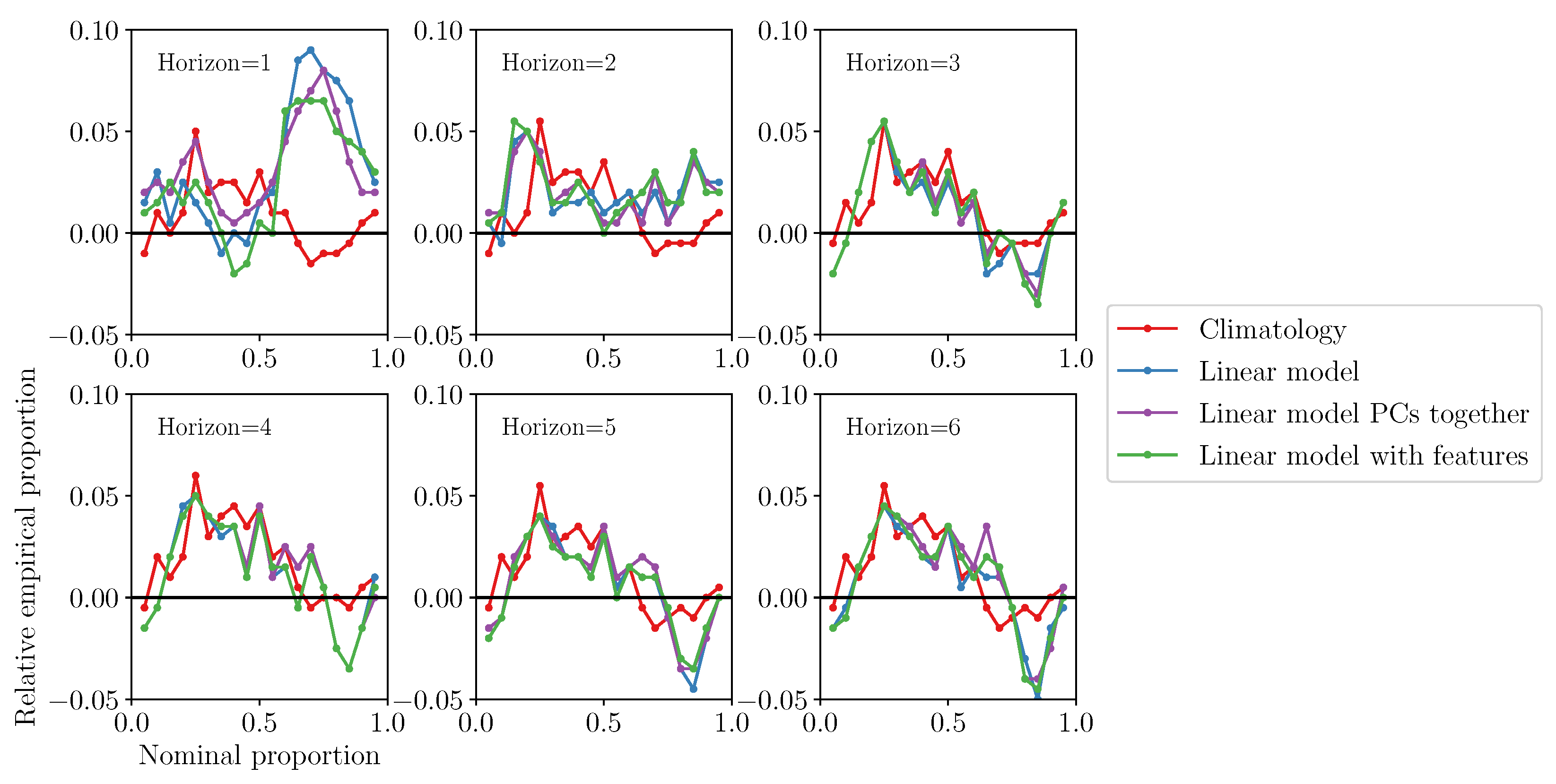
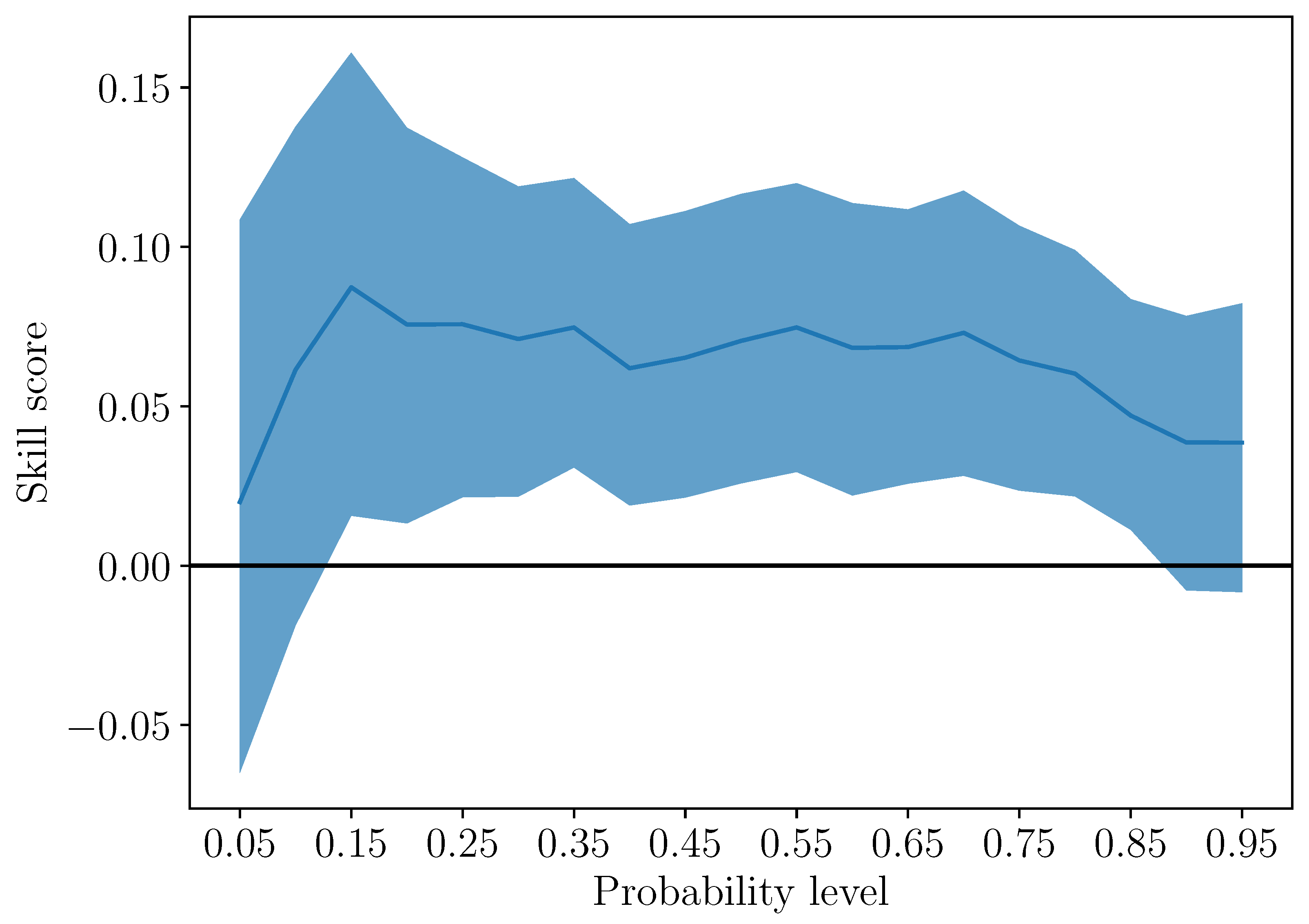
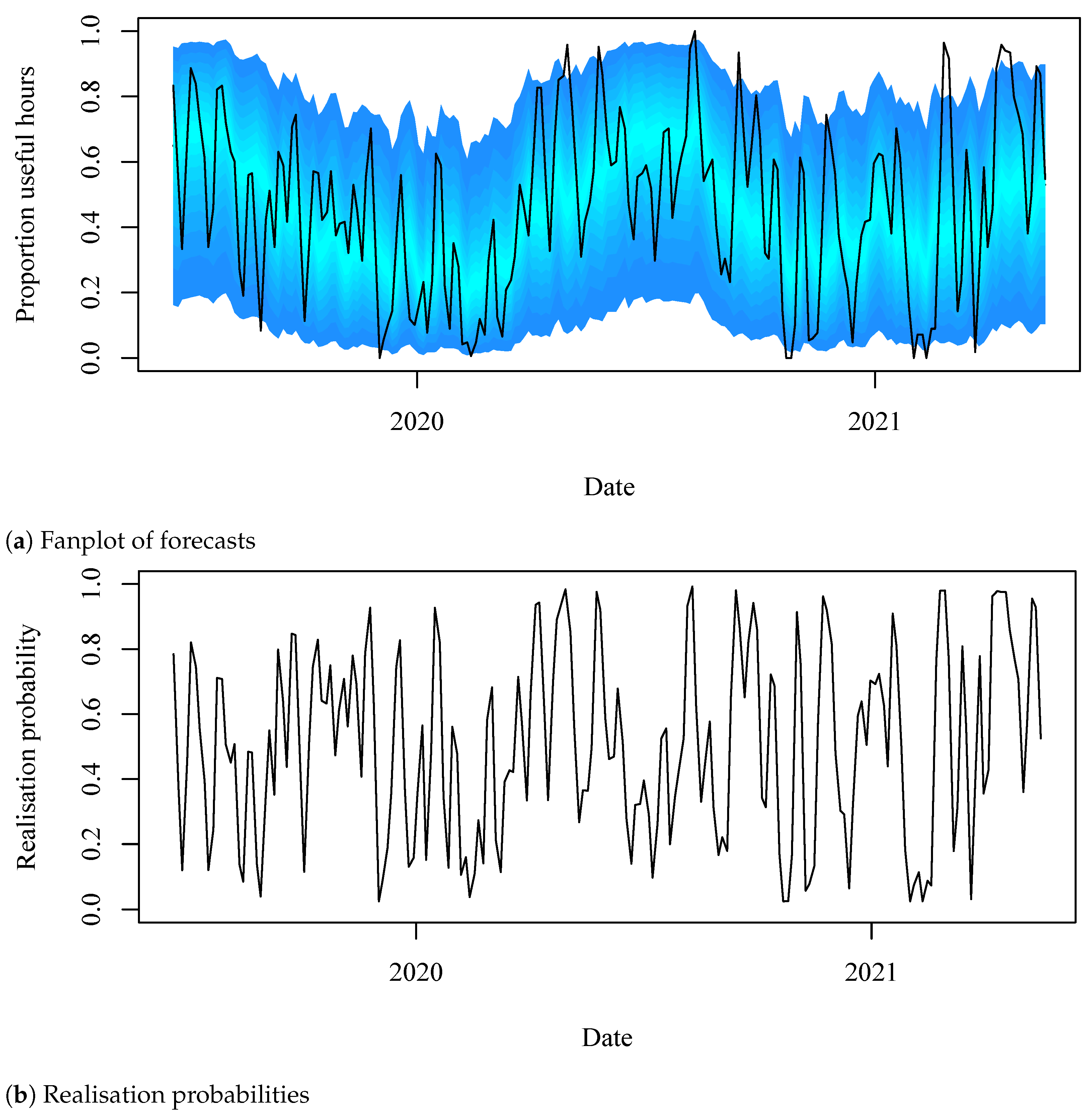
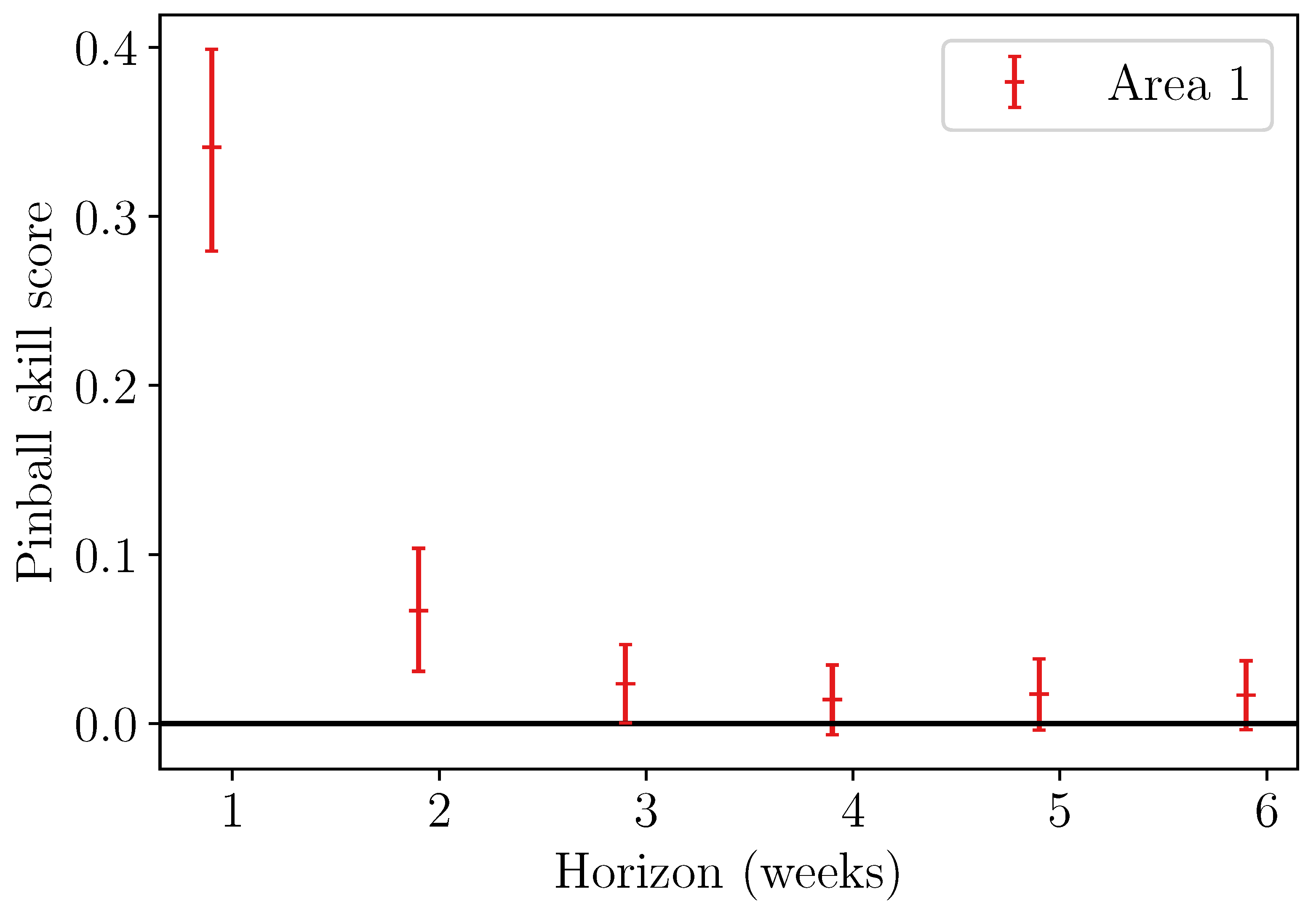
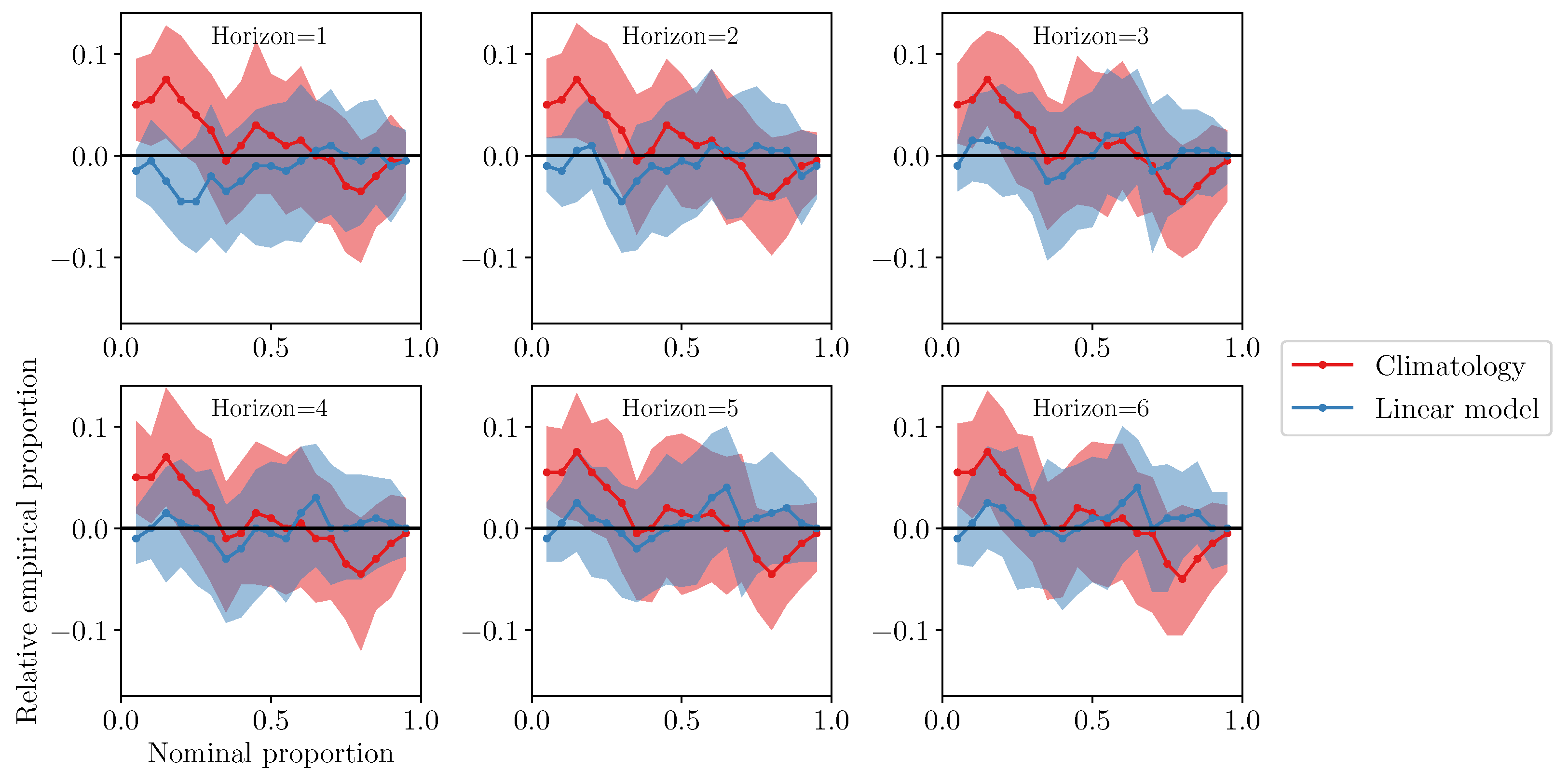
3.4. Weather Window Indices and Economic Value of Forecasts
4. Conclusions
- A comparison between forecasts generated with a complete measured time series and those using reanalysis data corrected with a limited history of site data. This bridges the gap between common methods for desk-based studies and those necessary to apply models to real-world sites.
- Determination of the skill of S2S forecasts across three different metrics that are relevant for maintenance planning.
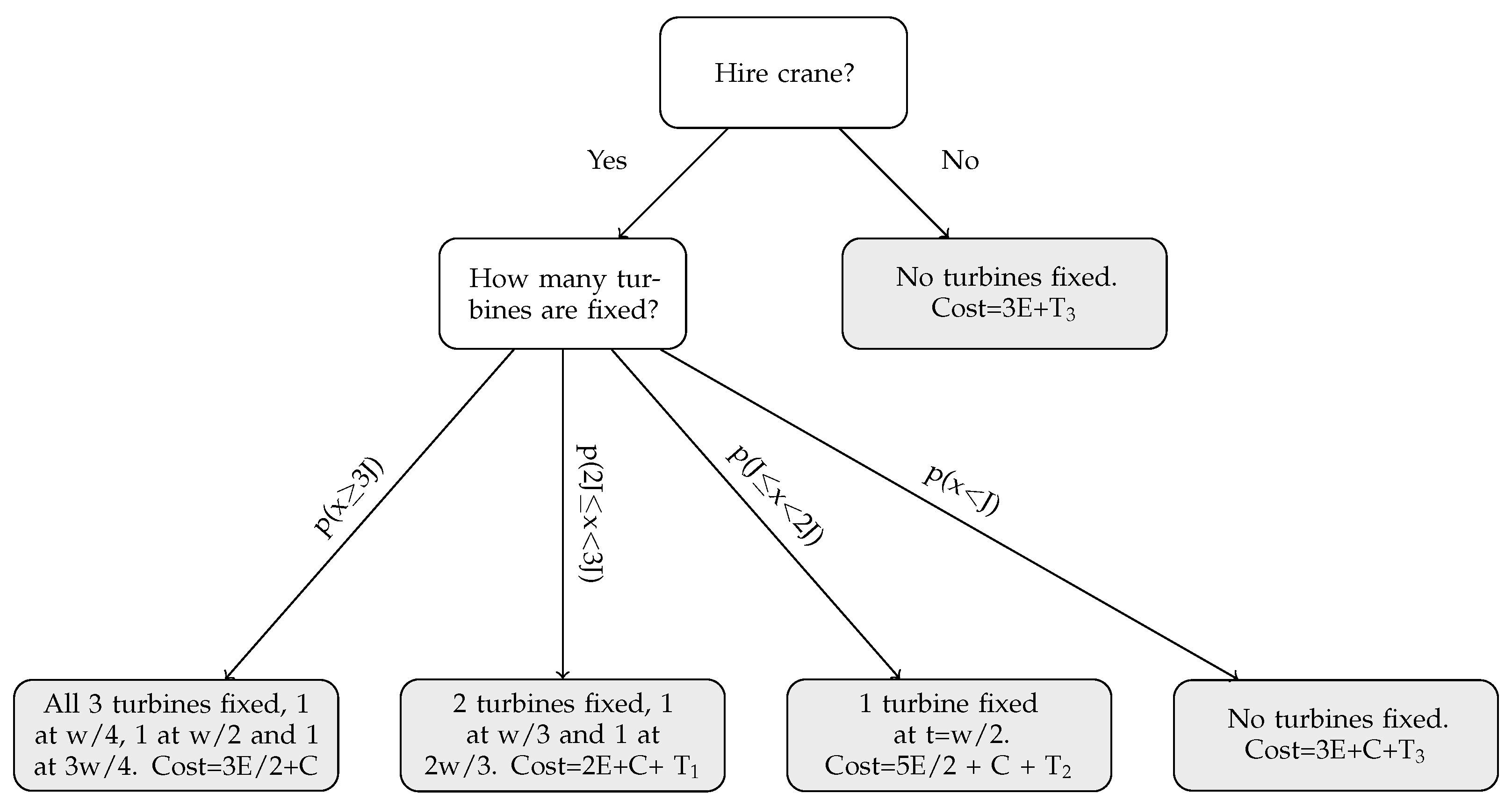
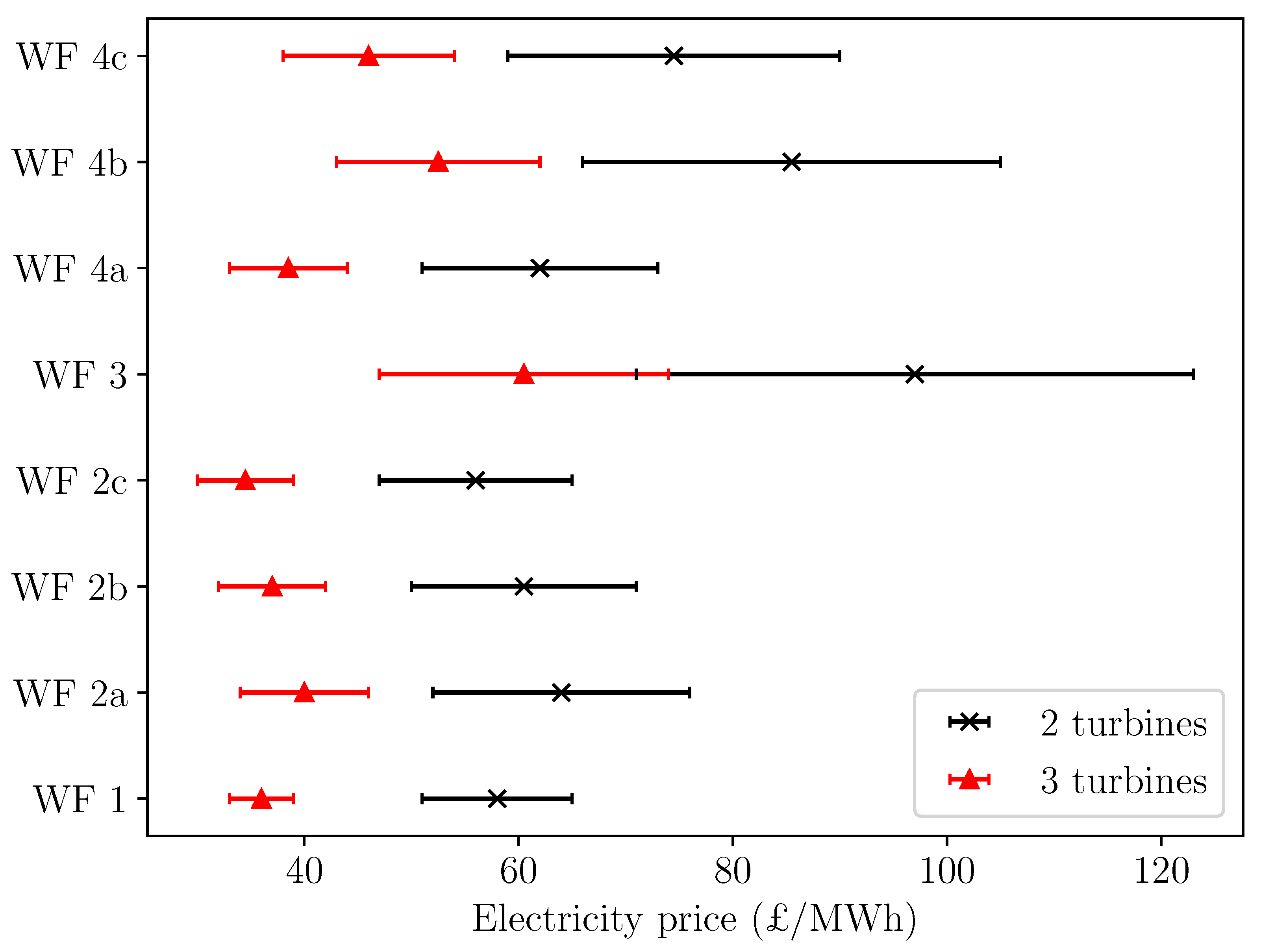
- Implementation of a cost-loss model and investigation of the sensitivity of hiring decisions to electricity prices.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EA | East Atlantic |
| EAWR | East Atlantic Western Russia |
| ECMWF | European Centre for Medium-range Weather Forecasts |
| EMOS | Ensemble Model Output Statistics |
| GAM(LSS) | Generalised Additive Model (for Location, Scale and Shape) |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| MIDAS | Met Office Integrated Data Archive System |
| MJO | Madden–Julian Oscillation |
| NAO | North Atlantic Oscillation |
| NWP | Numerical Weather Prediction |
| PCA | Principal Component Analysis |
| S2S | Subseasonal-to-Seasonal |
| S2S4E | Subseasonal-to-Seasonal Forecasting for Energy |
| SCA | Scandinavian Pattern |
References
- Soret, A.; Torralba, V.; Cortesi, N.; Christel, I.; Palma, L.; Manrique-Suñén, A.; Lledó, L.; González-Reviriego, N.; Doblas-Reyes, F.J. Sub-Seasonal to Seasonal Climate Predictions for Wind Energy Forecasting. J. Phys. Conf. Ser. 2019, 1222, 012009. [Google Scholar] [CrossRef]
- Lledó, L.; Torralba, V.; Soret, A.; Ramon, J.; Doblas-Reyes, F. Seasonal Forecasts of Wind Power Generation. Renew. Energy 2019, 143, 91–100. [Google Scholar] [CrossRef]
- White, C.J.; Domeisen, D.I.V.; Acharya, N.; Adefisan, E.A.; Anderson, M.L.; Aura, S.; Balogun, A.A.; Bertram, D.; Bluhm, S.; Brayshaw, D.J.; et al. Advances in the Application and Utility of Subseasonal-to-Seasonal Predictions. Bull. Am. Meteorol. Soc. 2021; Early online release. [Google Scholar] [CrossRef]
- White, C.J.; Carlsen, H.; Robertson, A.W.; Klein, R.J.T.; Lazo, J.K.; Kumar, A.; Vitart, F.; Coughlan de Perez, E.; Ray, A.J.; Murray, V.; et al. Potential Applications of Subseasonal-to-Seasonal (S2S) Predictions. Meteorol. Appl. 2017, 24, 315–325. [Google Scholar] [CrossRef]
- World Meteorological Organisation. Subseasonal-to-Seasonal Prediction Project. Available online: http://s2sprediction.net (accessed on 11 August 2021).
- Soret, A. Subseasonal-to-Seasonal Forecasting for Energy. Available online: http://s2s4e.eu (accessed on 11 August 2021).
- Orlov, A.; Sillmann, J.; Vigo, I. Better Seasonal Forecasts for the Renewable Energy Industry. Nat. Energy 2020, 5, 108–110. [Google Scholar] [CrossRef]
- Lledó, L.; Doblas-Reyes, F.J. Predicting Daily Mean Wind Speed in Europe Weeks Ahead from MJO Status. Mon. Weather Rev. 2020, 148, 3413–3426. [Google Scholar] [CrossRef]
- Lledó, L.; Cionni, I.; Torralba, V.; Bretonnière, P.A.; Samsó, M. Seasonal Prediction of Euro-Atlantic Teleconnections from Multiple Systems. Environ. Res. Lett. 2020, 15, 074009. [Google Scholar] [CrossRef]
- Alonzo, B.; Tankov, P.; Drobinski, P.; Plougonven, R. Probabilistic Wind Forecasting up to Three Months Ahead Using Ensemble Predictions for Geopotential Height. Int. J. Forecast. 2020, 36, 515–530. [Google Scholar] [CrossRef]
- Bloomfield, H.C.; Brayshaw, D.J.; Charlton-Perez, A.J. Characterizing the Winter Meteorological Drivers of the European Electricity System Using Targeted Circulation Types. Meteorol. Appl. 2020, 27, e1858. [Google Scholar] [CrossRef]
- Cortesi, N.; Torralba, V.; González-Reviriego, N.; Soret, A.; Doblas-Reyes, F.J. Characterization of European Wind Speed Variability Using Weather Regimes. Clim. Dyn. 2019, 53, 4961–4976. [Google Scholar] [CrossRef] [Green Version]
- Bloomfield, H.C.; Brayshaw, D.J.; Gonzalez, P.L.M.; Charlton-Perez, A. Sub-Seasonal Forecasts of Demand, Wind Power and Solar Power Generation for 28 European Countries. Earth Syst. Sci. Data 2021, 13, 2259–2274. [Google Scholar] [CrossRef]
- van der Wiel, K.; Bloomfield, H.C.; Lee, R.W.; Stoop, L.P.; Blackport, R.; Screen, J.A.; Selten, F.M. The Influence of Weather Regimes on European Renewable Energy Production and Demand. Environ. Res. Lett. 2019, 14, 094010. [Google Scholar] [CrossRef]
- Dalgic, Y.; Lazakis, I.; Dinwoodie, I.; McMillan, D.; Revie, M. Advanced Logistics Planning for Offshore Wind Farm Operation and Maintenance Activities. Ocean. Eng. 2015, 101, 211–226. [Google Scholar] [CrossRef] [Green Version]
- Lazakis, I.; Khan, S. An Optimization Framework for Daily Route Planning and Scheduling of Maintenance Vessel Activities in Offshore Wind Farms. Ocean. Eng. 2021, 225, 108752. [Google Scholar] [CrossRef]
- Shafiee, M. Maintenance Logistics Organization for Offshore Wind Energy: Current Progress and Future Perspectives. Renew. Energy 2015, 77, 182–193. [Google Scholar] [CrossRef]
- Taboada, J.V.; Diaz-Casas, V.; Yu, X. Reliability and Maintenance Management Analysis on Offshore Wind Turbines (OWTs). Energies 2021, 14, 7662. [Google Scholar] [CrossRef]
- Irawan, C.A.; Ouelhadj, D.; Jones, D.; Stålhane, M.; Sperstad, I.B. Optimisation of Maintenance Routing and Scheduling for Offshore Wind Farms. Eur. J. Oper. Res. 2017, 256, 76–89. [Google Scholar] [CrossRef] [Green Version]
- Barlow, E.; Tezcaner Öztürk, D.; Revie, M.; Boulougouris, E.; Day, A.H.; Akartunalı, K. Exploring the Impact of Innovative Developments to the Installation Process for an Offshore Wind Farm. Ocean. Eng. 2015, 109, 623–634. [Google Scholar] [CrossRef] [Green Version]
- Ji, G.; Wu, W.; Zhang, B. Robust Generation Maintenance Scheduling Considering Wind Power and Forced Outages. IET Renew. Power Gener. 2016, 10, 634–641. [Google Scholar] [CrossRef]
- Yu, Q.; Patriksson, M.; Sagitov, S. Optimal Scheduling of the next Preventive Maintenance Activity for a Wind Farm. arXiv 2020, arXiv:2001.03889. [Google Scholar] [CrossRef]
- Barlow, E.; Bedford, T.; Revie, M.; Tan, J.; Walls, L. A Performance-Centred Approach to Optimising Maintenance of Complex Systems. Eur. J. Oper. Res. 2021, 292, 579–595. [Google Scholar] [CrossRef]
- Pelajo, J.C.; Brandão, L.E.; Gomes, L.L.; Klotzle, M.C. Wind Farm Generation Forecast and Optimal Maintenance Schedule Model. Wind Energy 2019, 22, 1872–1890. [Google Scholar] [CrossRef]
- Browell, J.; Dinwoodie, I.; McMillan, D. Forecasting for Day-Ahead Offshore Maintenance Scheduling under Uncertainty. In Risk, Reliability and Safety: Innovating Theory and Practice; Walls, L., Revie, M., Bedford, T., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 1137–1144. [Google Scholar] [CrossRef] [Green Version]
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M.; et al. The Subseasonal to Seasonal (S2S) Prediction Project Database. Bull. Am. Meteorol. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- Wiser, R.; Bolinger, M.; Hoen, B.; Millstein, D.; Rand, J.; Barbose, G.; Darghouth, N.; Gorman, W.; Jeong, S.; Mills, A.; et al. Land-Based Wind Market Report: 2021 Edition; Technical Report; US Department for Energy: Washington, DC, USA, 2021.
- Met Office. Met Office Integrated Data Archive System (MIDAS) Land and Marine Surface Stations Data (1853–Current). 2012. Available online: http://catalogue.ceda.ac.uk/uuid/220a65615218d5c9cc9e4785a3234bd0 (accessed on 11 August 2021).
- Ramon, J.; Lledó, L.; Torralba, V.; Soret, A.; Doblas-Reyes, F.J. What Global Reanalysis Best Represents Near-surface Winds? Q. J. R. Meteorol. Soc. 2019, 145, 3236–3251. [Google Scholar] [CrossRef] [Green Version]
- Schuhen, N.; Thorarinsdottir, T.L.; Gneiting, T. Ensemble Model Output Statistics for Wind Vectors. Mon. Weather Rev. 2012, 140, 3204–3219. [Google Scholar] [CrossRef] [Green Version]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized Additive Models for Location, Scale and Shape. Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef] [Green Version]
- Scheuerer, M. Probabilistic Quantitative Precipitation Forecasting Using Ensemble Model Output Statistics: Probabilistic Precipitation Forecasting Using EMOS. Q. J. R. Meteorol. Soc. 2014, 140, 1086–1096. [Google Scholar] [CrossRef] [Green Version]


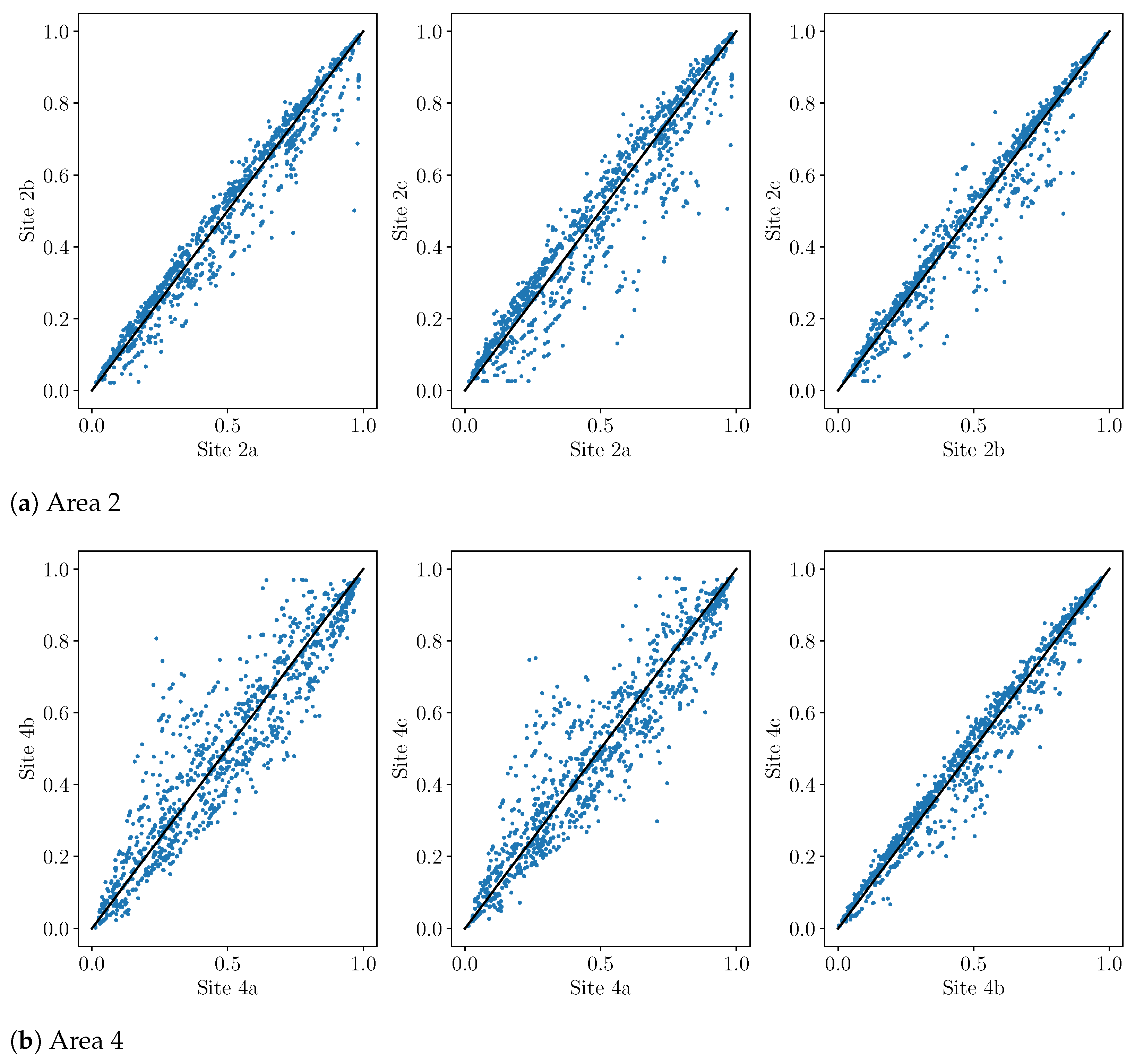

| Variable (s) | PCs Kept | Features | Index Models | ||
|---|---|---|---|---|---|
| Mean ws | Variability | Weather Window | |||
| weekly mean | √ | √ | √ | ||
| 500 hPa gph | 20 | weekly sd | √ | ||
| weekly min, max | √ | ||||
| weekly mean | √ | √ | √ | ||
| 10 m ws | 40 | weekly sd | √ | ||
| weekly min, max | √ | ||||
| weekly mean | √ | √ | √ | ||
| 100 m variables * | 20 | weekly sd | √ | ||
| weekly min, max | √ | ||||
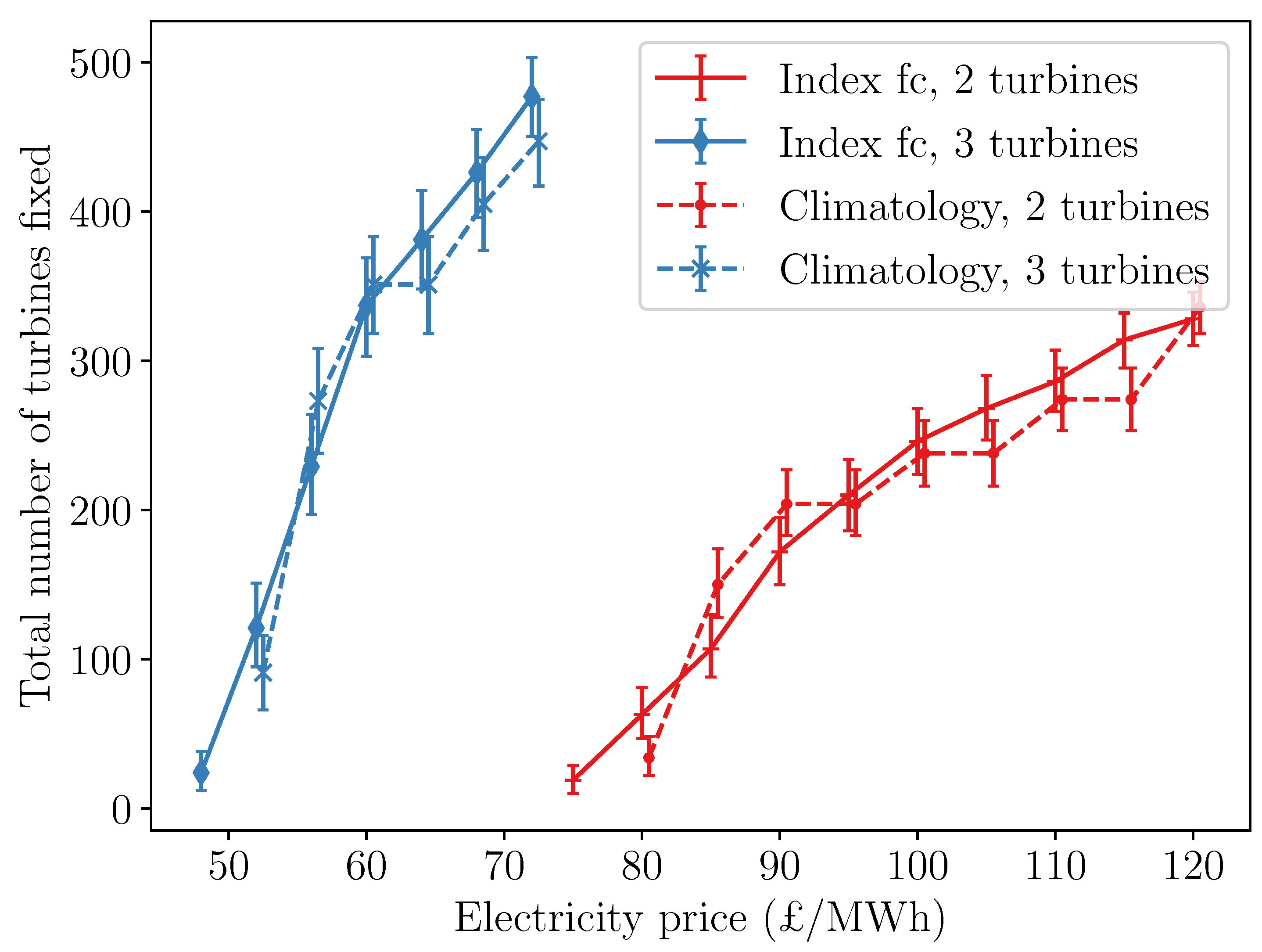
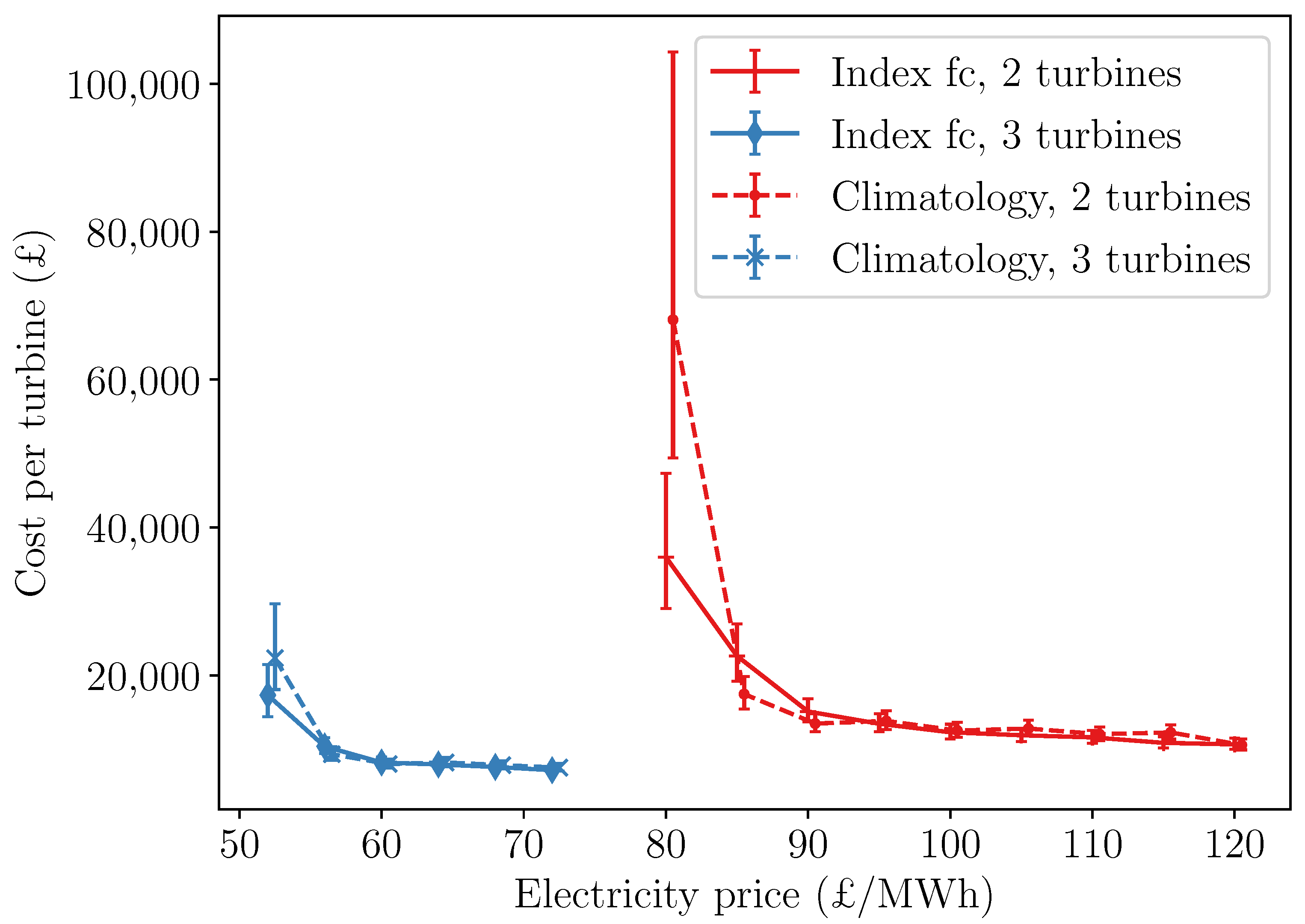
| N Turbines Down | Electricity Price £/MWh | N Fixed (Index Model) | £/Turbine (Index Model) | N Fixed (Climatology) | £/Turbine (Climatlogy) |
|---|---|---|---|---|---|
| 2 | 75 | 19 | 110,900 | 0 | - |
| 2 | 80 | 63 | 35,980 | 34 | 68,090 |
| 2 | 85 | 107 | 22,610 | 150 | 17,470 |
| 2 | 90 | 172 | 15,100 | 204 | 13,480 |
| 2 | 95 | 210 | 13,450 | 204 | 13,830 |
| 2 | 100 | 246 | 12,300 | 238 | 12,530 |
| 2 | 105 | 268 | 11,890 | 238 | 12,800 |
| 2 | 110 | 286 | 11,600 | 274 | 12,050 |
| 2 | 115 | 314 | 10,860 | 274 | 12,270 |
| 2 | 120 | 328 | 10,660 | 336 | 10,580 |
| 3 | 48 | 24 | 73,300 | 0 | - |
| 3 | 52 | 121 | 17,320 | 91 | 22,340 |
| 3 | 56 | 229 | 10,380 | 273 | 9330 |
| 3 | 60 | 337 | 8220 | 351 | 8000 |
| 3 | 64 | 381 | 7940 | 351 | 8200 |
| 3 | 68 | 426 | 7608 | 405 | 7850 |
| 3 | 72 | 477 | 7170 | 447 | 7520 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tawn, R.; Browell, J.; McMillan, D. Subseasonal-to-Seasonal Forecasting for Wind Turbine Maintenance Scheduling. Wind 2022, 2, 260-287. https://doi.org/10.3390/wind2020015
Tawn R, Browell J, McMillan D. Subseasonal-to-Seasonal Forecasting for Wind Turbine Maintenance Scheduling. Wind. 2022; 2(2):260-287. https://doi.org/10.3390/wind2020015
Chicago/Turabian StyleTawn, Rosemary, Jethro Browell, and David McMillan. 2022. "Subseasonal-to-Seasonal Forecasting for Wind Turbine Maintenance Scheduling" Wind 2, no. 2: 260-287. https://doi.org/10.3390/wind2020015
APA StyleTawn, R., Browell, J., & McMillan, D. (2022). Subseasonal-to-Seasonal Forecasting for Wind Turbine Maintenance Scheduling. Wind, 2(2), 260-287. https://doi.org/10.3390/wind2020015






