1. Introduction
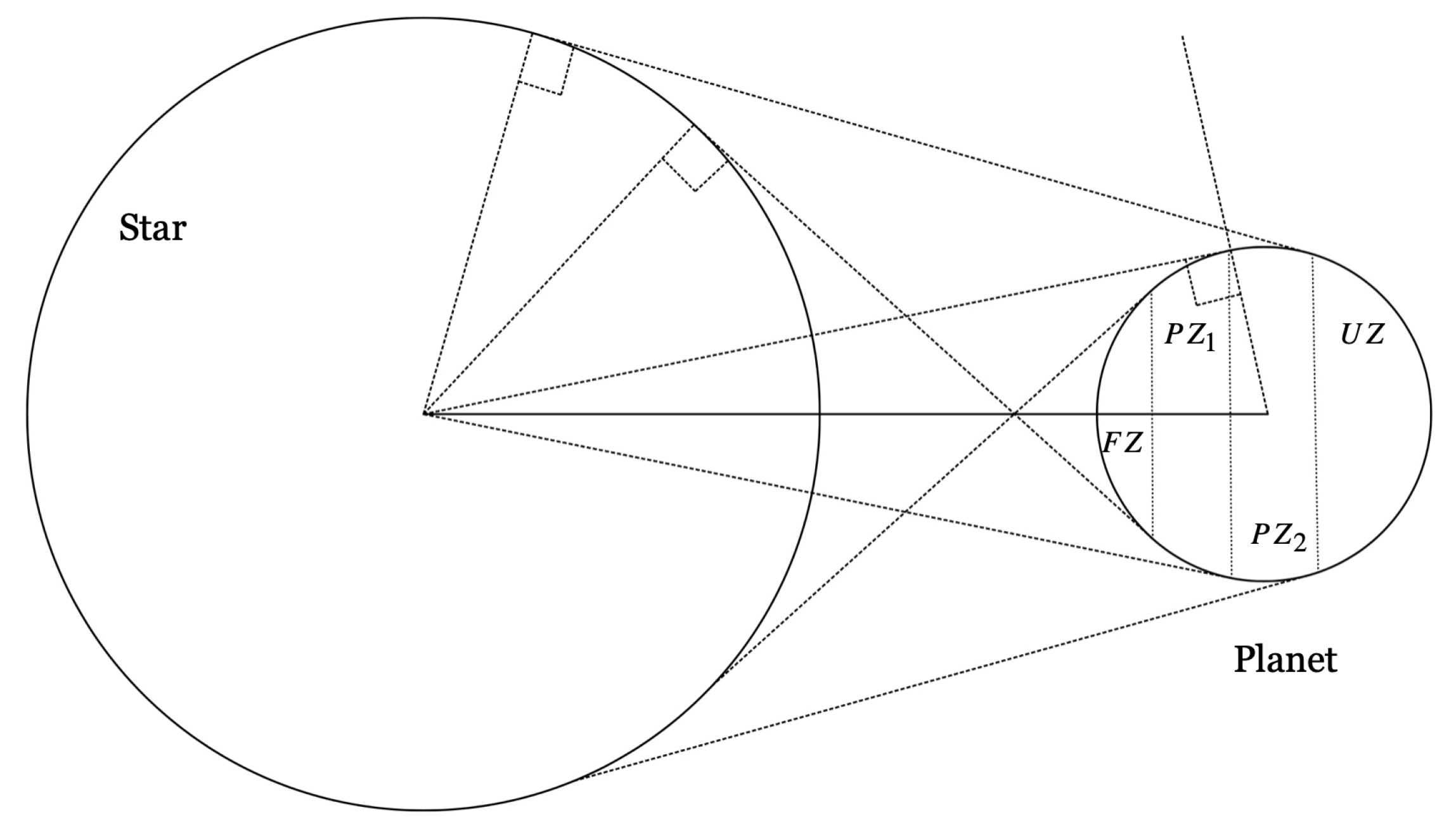
Typically, the illumination of exoplanets is determined under the assumption that the incident stellar radiation reaches the exoplanet as plane parallel rays. In this situation, half of the planet is fully illuminated and the other half is dark. For extremely close-in exoplanets for which the star-planet separation is on the order of only a few stellar radii, it is particularly important to take into account the finite angular size of the host star. Doing so reveals that two additional zones are necessary to describe the illumination of the exoplanet. Previous work has shown that the planet will have four distinct illumination zones: the fully-illuminated zone, the first penumbral zone, the second penumbral zone, and the un-illuminated (or night) zone [
1] (
Figure 1).
The fully-illuminated zone (FZ) is the region on the planet in which the entire apparent disk of the star is visible in the sky. However, due to the close-in geometry, the surface area of the visible star is less than one-half of the total area. The first penumbral zone () is the region on the planet in which a portion of the star (less than one-half of the potentially visible area) is occluded by the horizon; that is, the star is on the verge of setting. The second penumbral zone () is the region on the planet in which more than one-half of the potentially visible area of the star is occluded by the horizon and the un-illuminated zone (UZ) is the region on the planet from which the star cannot be seen.
The result is that the rather abrupt terminator between the day-side and night-side of a distant planet is, in the case of a close-in planet, spread out into the two penumbral zones, which impinge on both the fully illuminated and the un-illuminated zones. So while a smaller surface area of the close-in planet is fully-illuminated, more of the planet’s surface receives light because the un-illuminated zone is also smaller. For example, in the case of the close-in orbiting hot Jupiter, Kepler-91b, about 30% of the surface is in full daylight, 40% of the surface is in partial penumbral light, and 30% of the surface is in full darkness, so that approximately 70% of the planet is receiving some light at any point in time [
2]. These differences in illumination are expected to impact the planet’s climate.
The main goal of this paper is to construct analytic expressions for the flux incident on an exoplanet to be implemented in EXONEST, a Bayesian machine learning application developed for exoplanet characterization [
2,
3].
2. Methods
In this section we build analytic expressions for the light received by a point on the exoplanet taking into account the finite angular size of the host star.
2.1. Instellation Setup
Suppose that the star emits
P photons per unit time. Integrating the photons over the blackbody spectrum will give the amount of emitted energy, and therefore this
P is related to the power emitted by the star. If each area element of the star,
, emits
photons per unit time, the total number of photons emitted by the star in unit time,
P, is given by:
If
p is the number of photons emitted by an area element in a unit time, then
and
Let the radius of the star be
. Assuming the star to be a sphere, we can write
in terms of the surface area element as
Integrating over the whole star yields
which allows us to write
Some of these photons will hit the planet.
Next, let us consider photons emitted from the area element on the stellar surface at point
A, and determine how many of these photons will be incident at a point
B on the planet. Let
denote the number of photons emitted by
A and arriving at
B in a unit time. Then, from
Figure 2:
Substituting
and
using Equations (
2)–(
6) gives:
2.2. Coordinate Systems
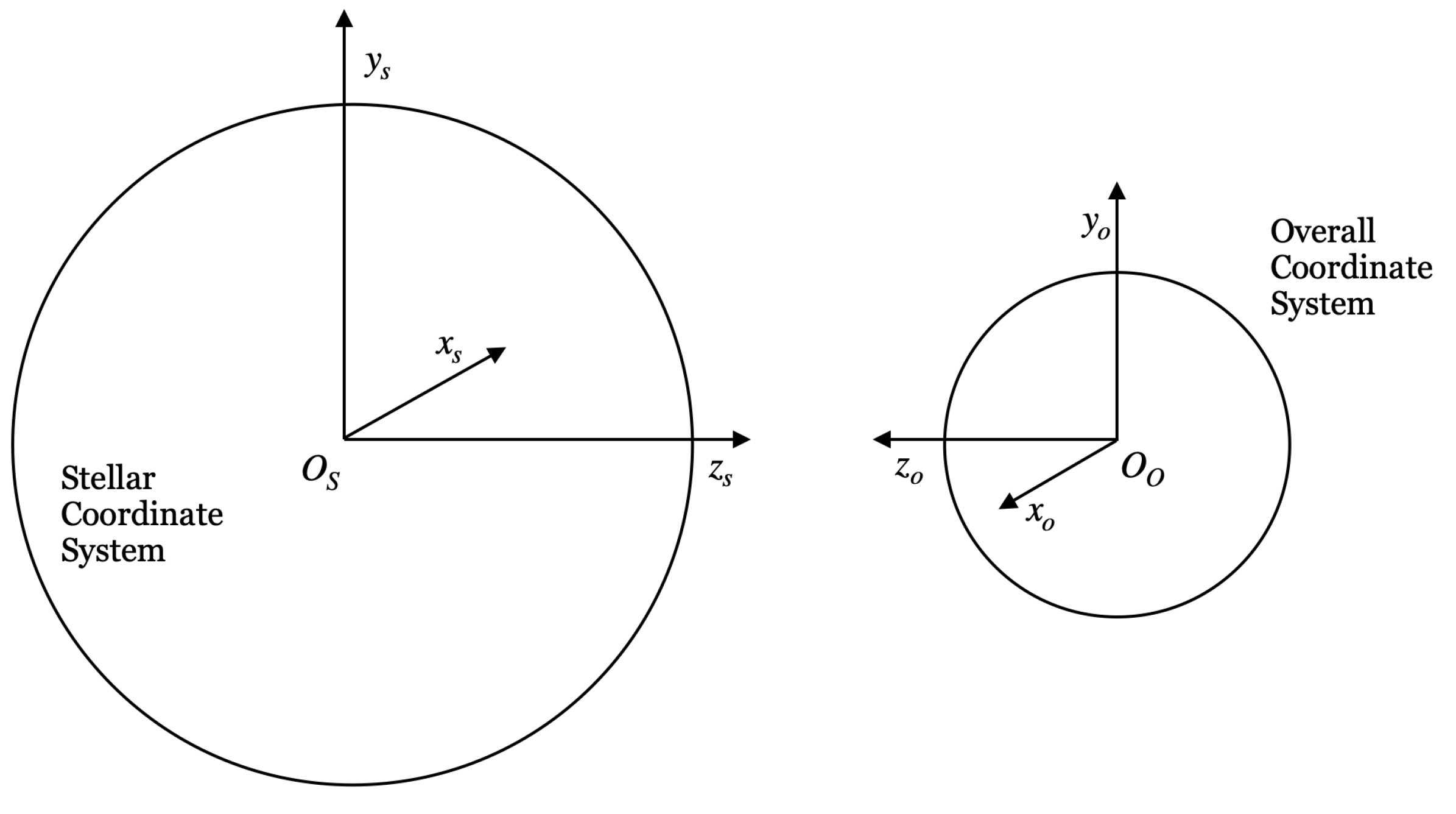
When we have a star–planet dynamical system, it is convenient to introduce three coordinate systems: stellar, planetocentric, and overall. For the scope of this paper, it suffices to use just two, stellar and overall, by choosing the origin of the overall coordinate system at the center of the exoplanet such that it would coincide with the planetocentric coordinate system (
Figure 3). Furthermore, the axial symmetry of stellar illumination about the axis joining the centers of the planet and the star can be exploited by orienting the z-axis of the overall coordinate system in this direction. With this coordinate system, the problem simplifies to having to determine the illumination along one semicircular arc.
The stellar and overall Cartesian coordinate systems are related to one another as follows:
and
Now that we have chosen appropriate coordinate systems, next let us derive the vectors required for the illumination in (
8).
2.3. The Vector
The vector
is given by
where in the overall frame
and
is the position vector of the point
B in the overall frame:
The sum then gives
which has a magnitude of
We can now verify that if the point
B is located at
, then
as expected.
2.4. The Vector
Let us consider the triangle
in
Figure 2.
The vector
in the stellar coordinate system is given by
Constructing the vector
in the overall coordinate system requires some care. We can use the fact that
where by the relation in Equation (
10),
and
such that
which simplifies to
The squared-magnitude of
is
The distance
is then found by taking the square root of the result above.
We can check this result by looking at points
and
for which
such that
as expected.
2.5. The Unit Vectors
Now let us obtain the relevant unit vectors,
and
, in the overall coordinate system. Note that
is the unit vector in the
direction and therefore
Noting that
, by Equation (
23) we have
Similarly noting that
is the unit vector in the
direction and using Equation (
13) gives
With an understanding of how to construct the relevant vectors and express them in the overall coordinate system, we can now write out the necessary integrals to obtain the total instellation.
2.6. Total Instellation
To compute the total instellation, we must integrate over the visible surface of the star, which is described by the spherical coordinates
and
. The total instellation at a point
B on the planet is given by integrating over all possible points,
A, on the star that is visible to point
B on the planet:
where
,
,
and
are the limits of integration that depend on the zone in which point
B is located.
Upon substitution of
, its magnitude and the unit vectors
and
, into the total instellation in (
31), it simplifies to 5 distinct double integrals with respect to
and
, which must be integrated over the limits of each zone to obtain an analytic model.
3. Discussion
In this section, we discuss the applications and implications of improved instellation models to illustrate the benefits of having accurate models for stellar illumination in order to determine the habitability of close-in exoplanets.
3.1. Bayesian Exoplanet Characterization and Model Testing
The EXONEST software suite performs Bayesian model-based exoplanet characterization using photometric and radial velocity data [
2,
3,
4,
5]. EXONEST relies on predictive photometric models that generate a predicted stellar light curve based on a set of hypothesized model parameters. Bayesian probability theory [
6,
7,
8,
9] uses this predicted stellar light curve to compute the posterior probability that the set of hypothetical model parameters could have been responsible for the recorded light curve. This allows detailed astrophysical models to be evaluated by the data analysis algorithm, as well as statistical testing among competing models [
3,
8,
10,
11]. EXONEST allows the user to employ one of several variants of the Nested Sampling Algorithm, such as Nested Sampling [
8,
12], MultiNest [
13,
14], and the state-of-the-art Nested Sampling with Galilean Monte Carlo [
15,
16,
17]. These Nested Sampling algorithms provide estimates of the model parameter values as well as the Bayesian evidence, which allows for statistical model testing. Using evidence-based Bayesian techniques [
10], exoplanetary models can be ranked based on the Bayesian evidence providing the capability for scientific hypothesis testing. One can test various photometric effects and compute the evidence to determine the probability that these effects are present in any given system. Relying on data from the NASA Exoplanet Archive, we can utilize EXONEST and its ability to perform Bayesian model testing to evaluate the efficacy of our improved instellation models by computing the Bayesian evidence of the parallel-ray approximation models versus our proposed models.
In any problem involving model parameter estimation, there are legitimate concerns about potential degeneracies among the model parameters, especially as the number of parameters increases. Degeneracies can be expected when more than one parameter affects the predicted light curve in a similar way. In reality, this is a warning that additional, different data are needed to effectively estimate the model parameters. Examining the cross-correlations between the parameter estimates is a very effective way to identify degeneracies. Model testing, as described above, can be used to detect degeneracies as well, since a degenerate set of model parameters will not significantly increase the likelihood function, but it will significantly decrease the prior probability, resulting in lower evidence.
3.2. Implications for Potentially Habitable M-Dwarf Worlds
The exoplanet TRAPPIST-1d
,
, which closely orbits its host M-dwarf star in the habitable zone (HZ), has a penumbral zone that covers about 2.5% of its surface or 8.25 million km
2. While this is a small percentage of the surface of the planet, this is greater than the area of Central and South America combined, which contains several important biogeographical regions on Earth. (e.g., [
18,
19,
20,
21]). Our estimates reveal that planets orbiting M-dwarf stars on the inner edge of the HZ will have penumbral zones ranging in area from around 1 to 3% of the surface area of the planet. While this may seem like a small value, it may have its greatest climatological impact at the poles of low obliquity worlds where the ice–albedo feedback manifests itself consistently and tends to drive mean surface temperatures lower, which can affect the fractional habitability metrics like that proposed in [
22]. A detailed understanding of the incident stellar radiation in these penumbral regions is expected to have significant relevance to understanding habitability on these worlds.
3.3. Climate Modeling of Close-In Orbiting Planets
As mentioned before, corrections are required to the illumination models used in planetary General Circulation Models (GCM) in order to properly model the climate of a close-in exoplanet. The analytical expressions for the incident stellar flux can be applied to the illumination model in the ROCKE-3D GCM [
23]. Not only have such corrections never been applied in a GCM, but their effects have never been quantified. For example, differences in illumination at the poles of zero obliquity worlds due to these corrected illumination models could have large effects on ice coverage at the poles. Recent work [
24] has shown that polar supercontinents and ocean circulation can affect global mean surface temperatures by several degrees because of the extent of polar ice and the resulting ice-albedo feedback. We expect corrected illumination models to have similar effects. Using the modified ROCKE-3D code for close-in planets, we could study the climates of potentially habitable planets. Critically, we can make one-to-one comparisons of GCM results between penumbral and parallel ray (the current default) illuminations and derive statistical measures of difference (e.g., systematic latitudinal—and global—surface temperature differences, ice-cover, precipitation patterns). We could look at a variety of topographies, land/sea masks, and surface water content used in previous ROCKE-3D publications such as Proxima Centauri b [
25], Future Earth [
24], and ancient Venus [
26].
4. Conclusions
Developing accurate analytical stellar instellation models for close-in orbiting exoplanets will increase both the accuracy and precision of inferred model parameter estimates obtained from data, thereby improving exoplanet characterization and potentially the detection of habitable exoplanets. This is a multidisciplinary project, founded on astrophysics with machine learning. Studying the implications of these improved illumination models in the context of exoplanetary climate modeling will provide a better understanding of the climates and atmospheric physics of close-in orbiting exoplanets.
Author Contributions
The authors contributed equally to the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
We wish to thank Jennifer L. Carter, Michael J. Way, Oleg Lunin and Jonathan Petruccelli for helpful advice as well as the organizers, Udo von Toussaint, Roland Preuss, Svenja Eichler and Anja Bauer for their generous hospitality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carter, J.L. Estimation of Planetary Photometric Emissions for Extremely Close-in Exoplanets; University at Albany: Albany, NY, USA, 2018. [Google Scholar]
- Knuth, K.H.; Placek, B.; Angerhausen, D.; Carter, J.L.; D’Angelo, B.; Gai, A.D.; Carado, B. Exonest: The bayesian exoplanetary explorer. Entropy 2017, 19, 559. [Google Scholar] [CrossRef]
- Placek, B.; Knuth, K.H.; Angerhausen, D. EXONEST: Bayesian model selection applied to the detection and characterization of exoplanets via photometric variations. Astrophys. J. 2014, 795, 112. [Google Scholar] [CrossRef]
- Placek, B. Bayesian Detection and Characterization of Extra-Solar Planets via Photometric Variations; University at Albany: Albany, NY, USA, 2014. [Google Scholar]
- Placek, B.; Knuth, K.H.; Angerhausen, D.; Jenkins, J.M. Characterization of Kepler-91b and the investigation of a potential Trojan companion using EXONEST. Astrophys. J. 2015, 814, 147. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gregory, P. Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica® Support; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sivia, D.; Skilling, J. Data Analysis: A Bayesian Tutorial; OUP Oxford: Oxford, UK, 2006. [Google Scholar]
- Knuth, K.H.; Skilling, J. Foundations of inference. Axioms 2012, 1, 38–73. [Google Scholar] [CrossRef]
- Knuth, K.H.; Habeck, M.; Malakar, N.K.; Mubeen, A.M.; Placek, B. Bayesian evidence and model selection. Digit. Signal Process. 2015, 47, 50–67. [Google Scholar] [CrossRef]
- Gai, A.D.; Knuth, K.H. Bayesian model testing of ellipsoidal variations on stars due to hot Jupiters. Astrophys. J. 2018, 853, 49. [Google Scholar] [CrossRef]
- Skilling, J. Nested sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar]
- Feroz, F.; Hobson, M.P. Multimodal nested sampling: An efficient and robust alternative to Markov Chain Monte Carlo methods for astronomical data analyses. Mon. Not. R. Astron. Soc. 2008, 384, 449–463. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.; Bridges, M. MultiNest: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef]
- Skilling, J. Bayesian computation in big spaces-nested sampling and Galilean Monte Carlo. AIP Conf. Proc. 2012, 1443, 145–156. [Google Scholar]
- Feroz, F.; Skilling, J. Exploring multi-modal distributions with nested sampling. AIP Conf. Proc. 2013, 1553, 106–113. [Google Scholar]
- Skilling, J. Galilean and Hamiltonian Monte Carlo. Multidiscip. Digit. Publ. Inst. Proc. 2019, 33, 19. [Google Scholar]
- Dickinson, R.E.; Kennedy, P. Impacts on regional climate of Amazon deforestation. Geophys. Res. Lett. 1992, 19, 1947–1950. [Google Scholar] [CrossRef]
- Yang, Y.; Saatchi, S.S.; Xu, L.; Yu, Y.; Choi, S.; Phillips, N.; Kennedy, R.; Keller, M.; Knyazikhin, Y.; Myneni, R.B. Post-drought decline of the Amazon carbon sink. Nat. Commun. 2018, 9, 3172. [Google Scholar] [CrossRef] [PubMed]
- Molina, R.; Salazar, J.; Martínez, J.; Villegas, J.; Arias, P. Exponential growth of precipitation along a “forest-fed moisture convey or belt” above the Amazon. J. Geophys. Res. Atmos 2019, 124, 2589–2599. [Google Scholar] [CrossRef]
- Pereira, J.C. Reducing catastrophic climate risk by revolutionizing the Amazon: Novel pathways for Brazilian diplomacy. In Climate Change and Global Development: Market, Global Players and Empirical Evidence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 189–218. [Google Scholar]
- Spiegel, D.S.; Menou, K.; Scharf, C.A. Habitable climates. Astrophys. J. 2008, 681, 1609. [Google Scholar] [CrossRef]
- Way, M.J.; Aleinov, I.; Amundsen, D.S.; Chandler, M.; Clune, T.; Del Genio, A.D.; Fujii, Y.; Kelley, M.; Kiang, N.Y.; Sohl, L.; et al. Resolving orbital and climate keys of Earth and extraterrestrial environments with dynamics (ROCKE-3D) 1.0: A general circulation model for simulating the climates of rocky planets. Astrophys. J. Suppl. Ser. 2017, 231, 12. [Google Scholar] [CrossRef]
- Way, M.J.; Davies, H.S.; Duarte, J.C.; Green, J. The climates of Earth’s next supercontinent: Effects of tectonics, rotation rate, and insolation. Geochem. Geophys. Geosyst. 2021, 22, e2021GC009983. [Google Scholar] [CrossRef]
- Del Genio, A.D.; Way, M.J.; Amundsen, D.S.; Aleinov, I.; Kelley, M.; Kiang, N.Y.; Clune, T.L. Habitable climate scenarios for Proxima Centauri b with a dynamic ocean. Astrobiology 2019, 19, 99–125. [Google Scholar] [CrossRef] [PubMed]
- Way, M.J.; Del Genio, A.D. Venusian habitable climate scenarios: Modeling Venus through time and applications to slowly rotating Venus-like exoplanets. J. Geophys. Res. Planets 2020, 125, e2019JE006276. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).