Magnetohydrodynamic Equilibrium Reconstruction with Consistent Uncertainties †
Abstract
:1. Introduction
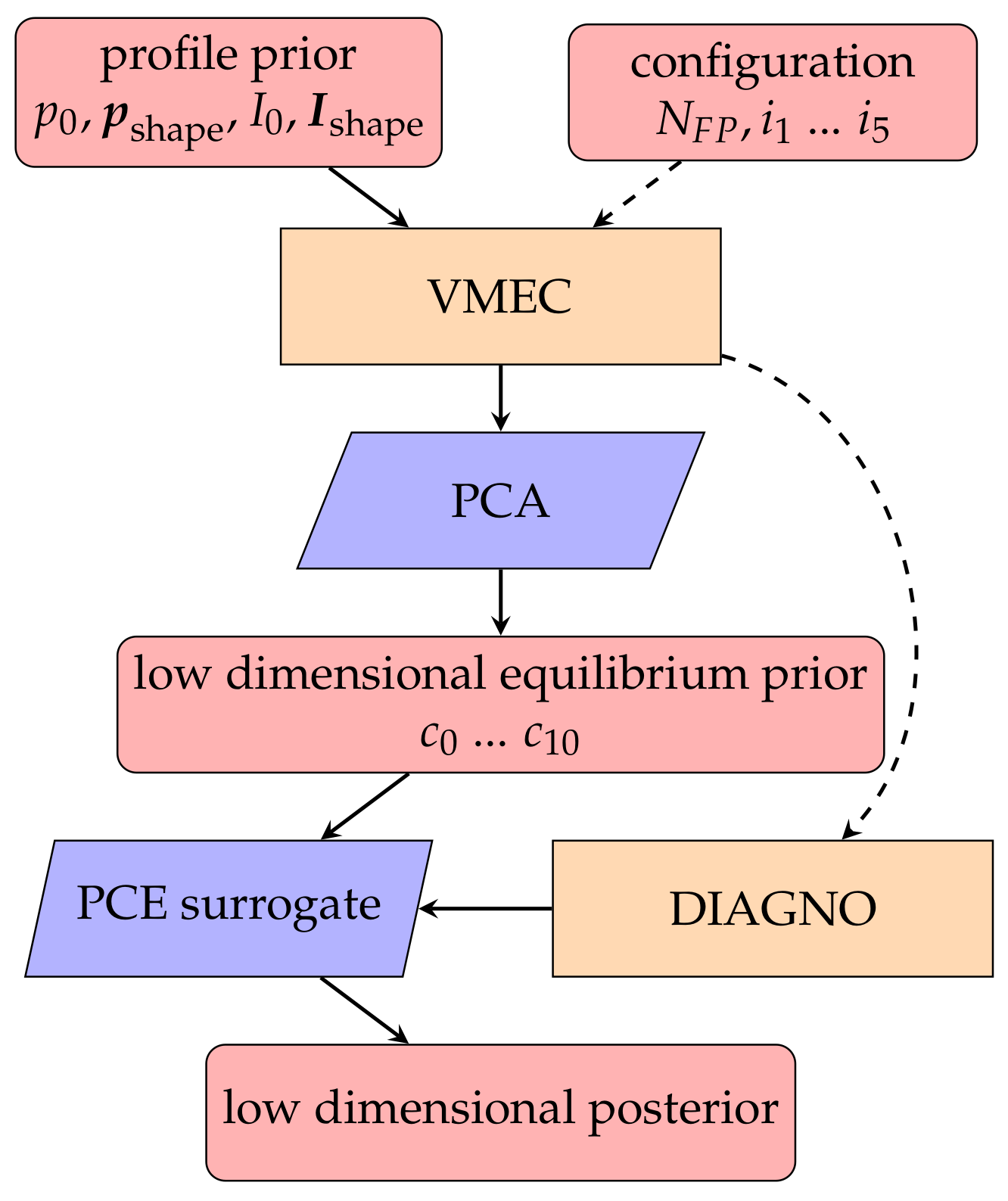
2. Methods
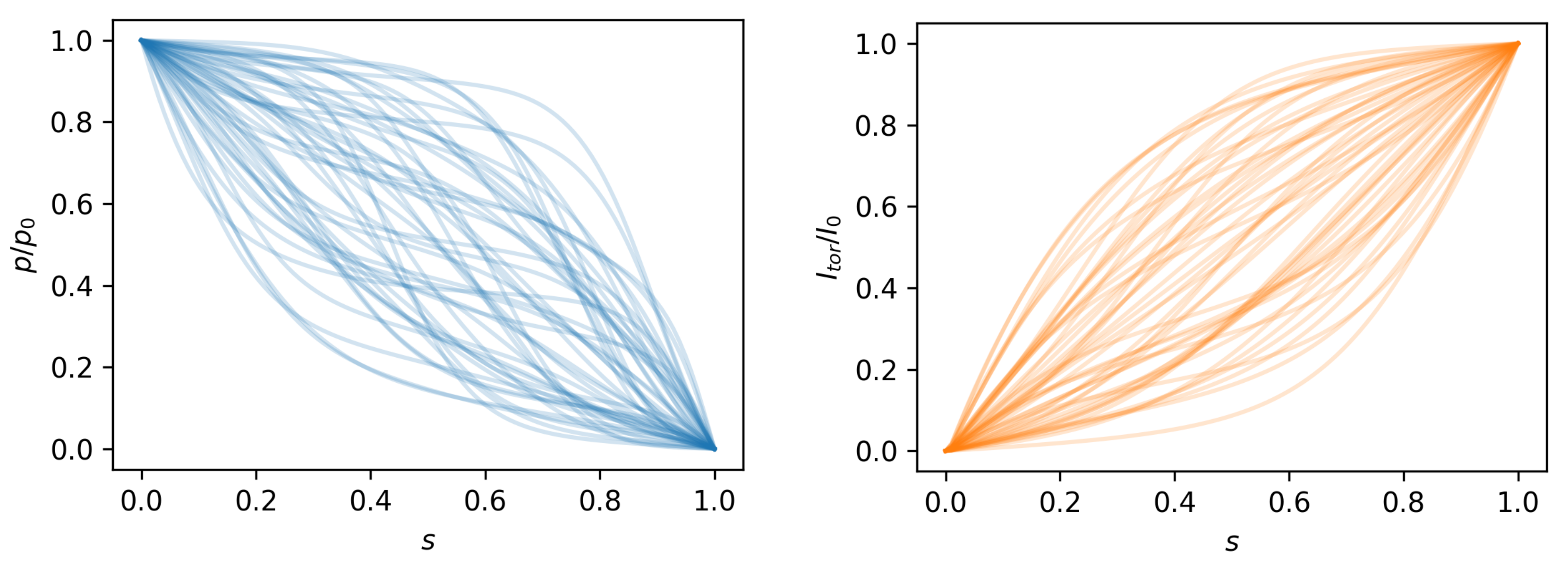
2.1. Prior Distribution of Current and Pressure Profiles
2.2. VMEC
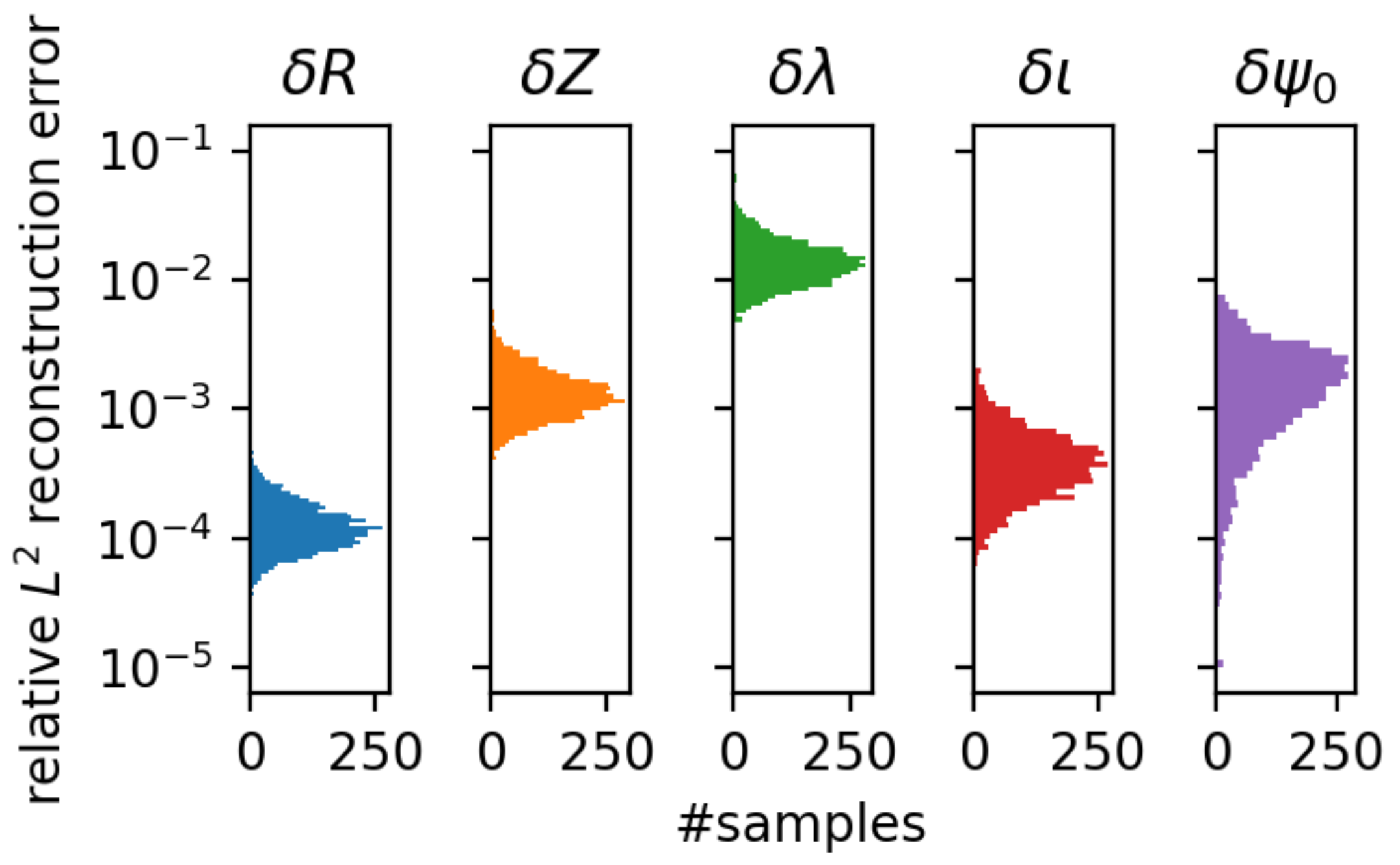
2.3. Dimensionality Reduction
2.4. Synthetic Diagnostics Surrogate Model
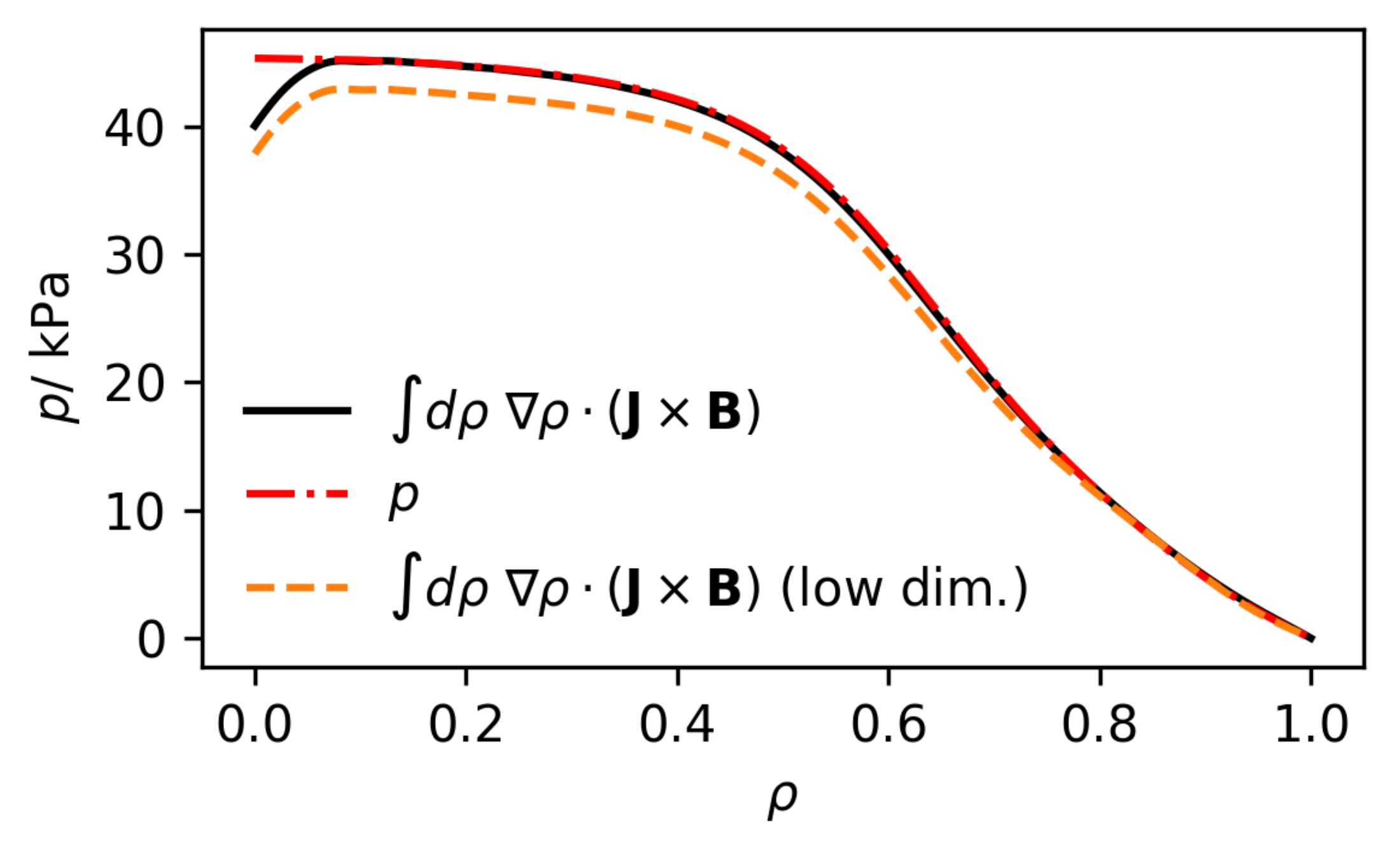
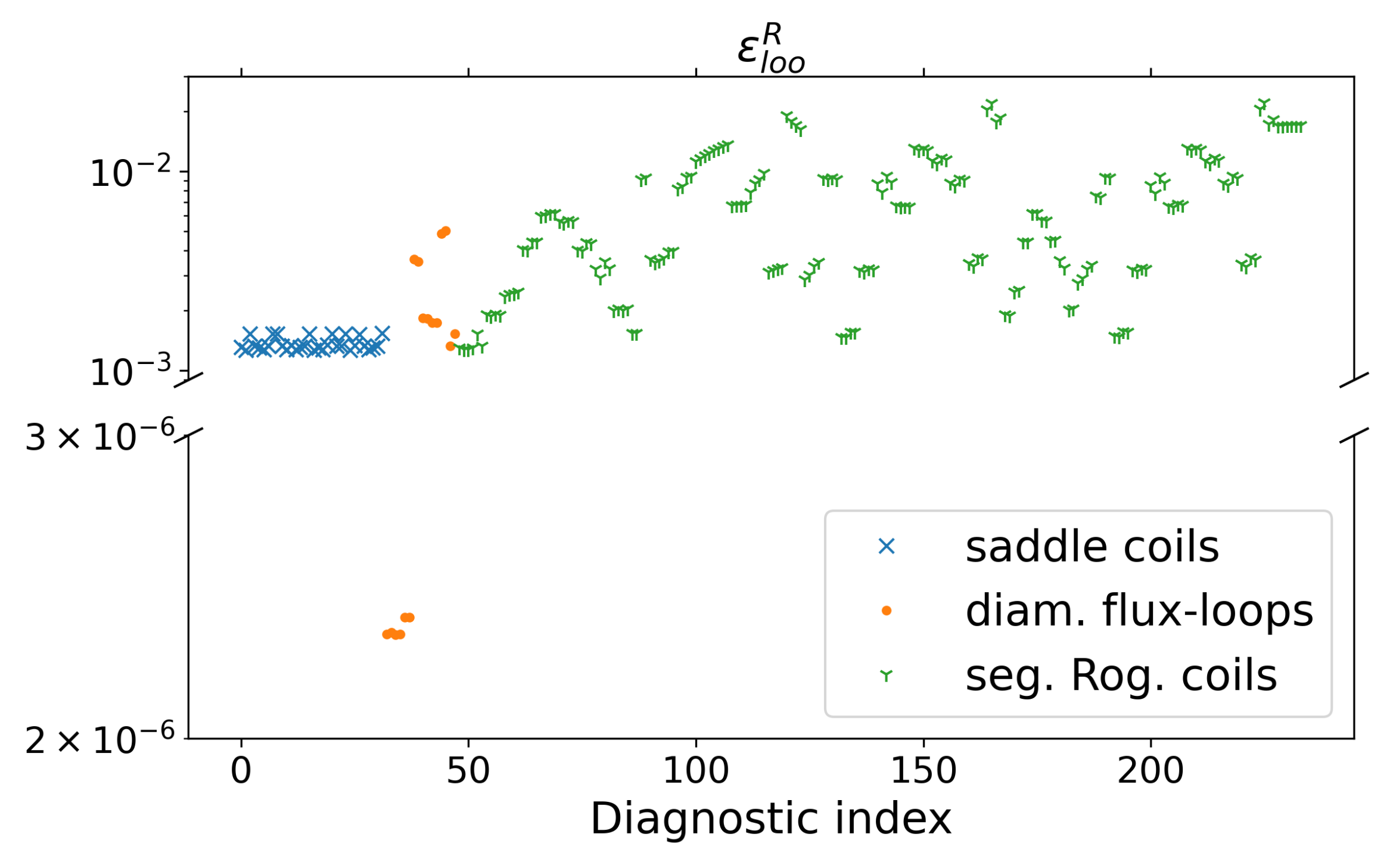
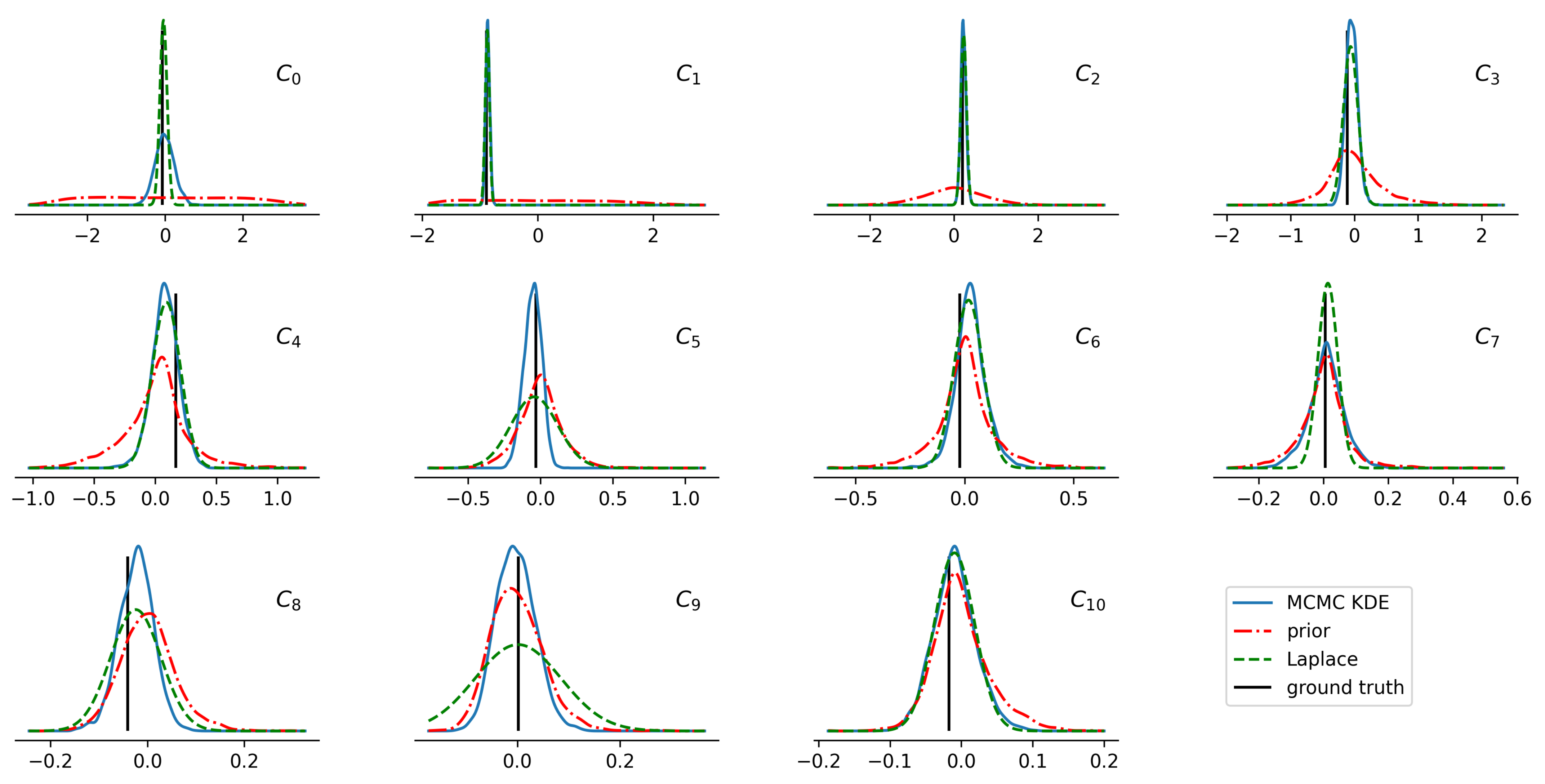
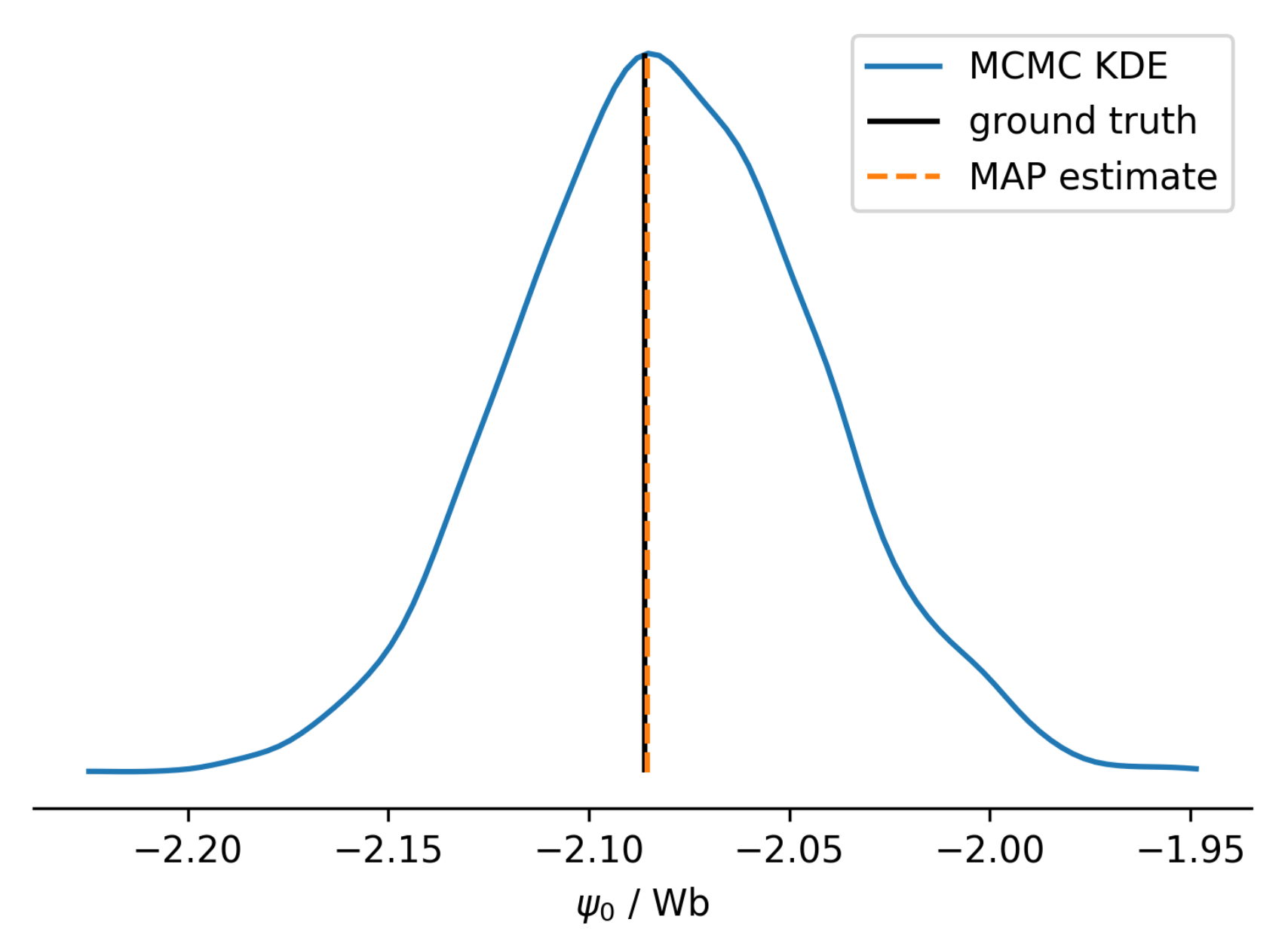
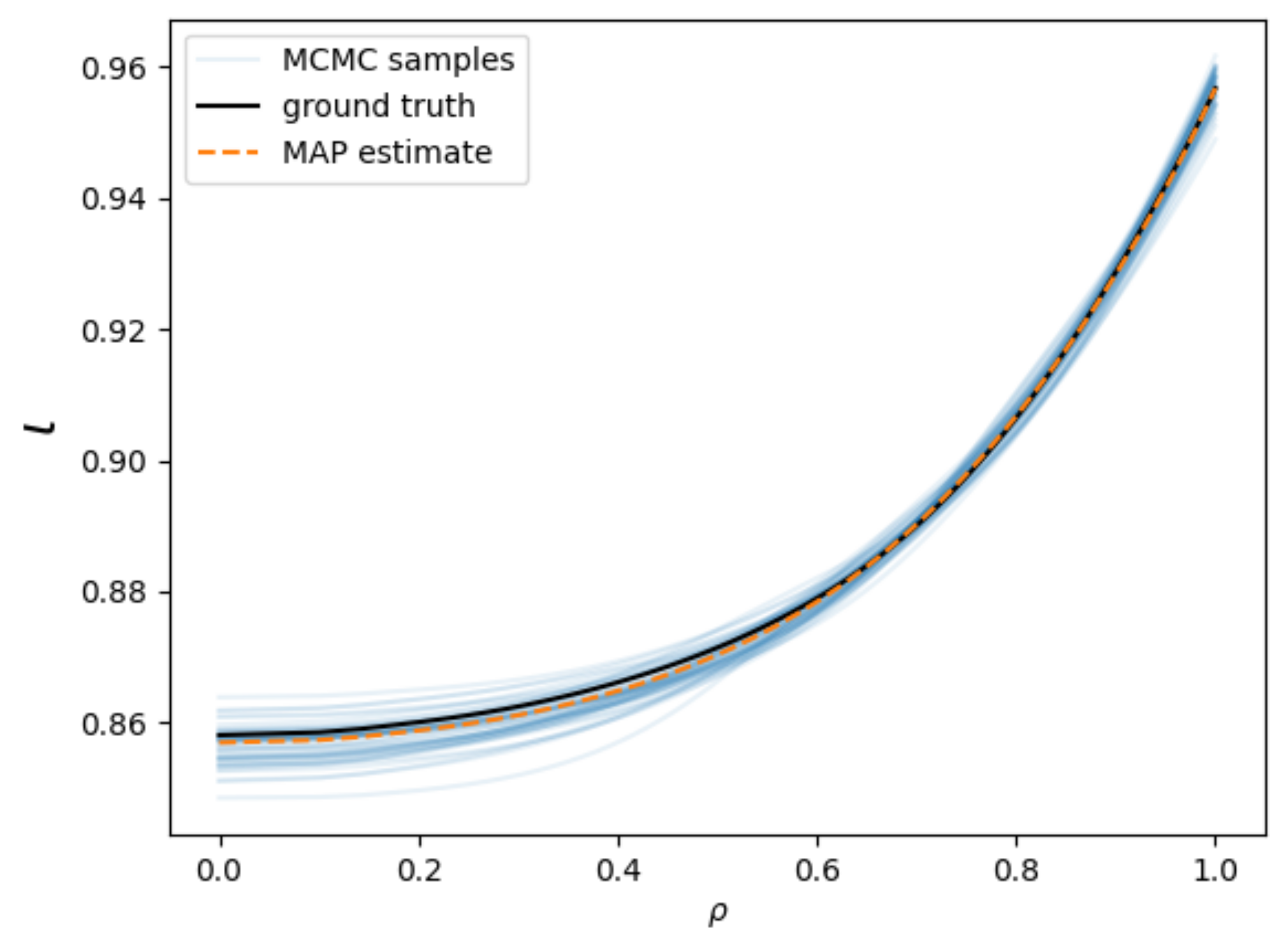
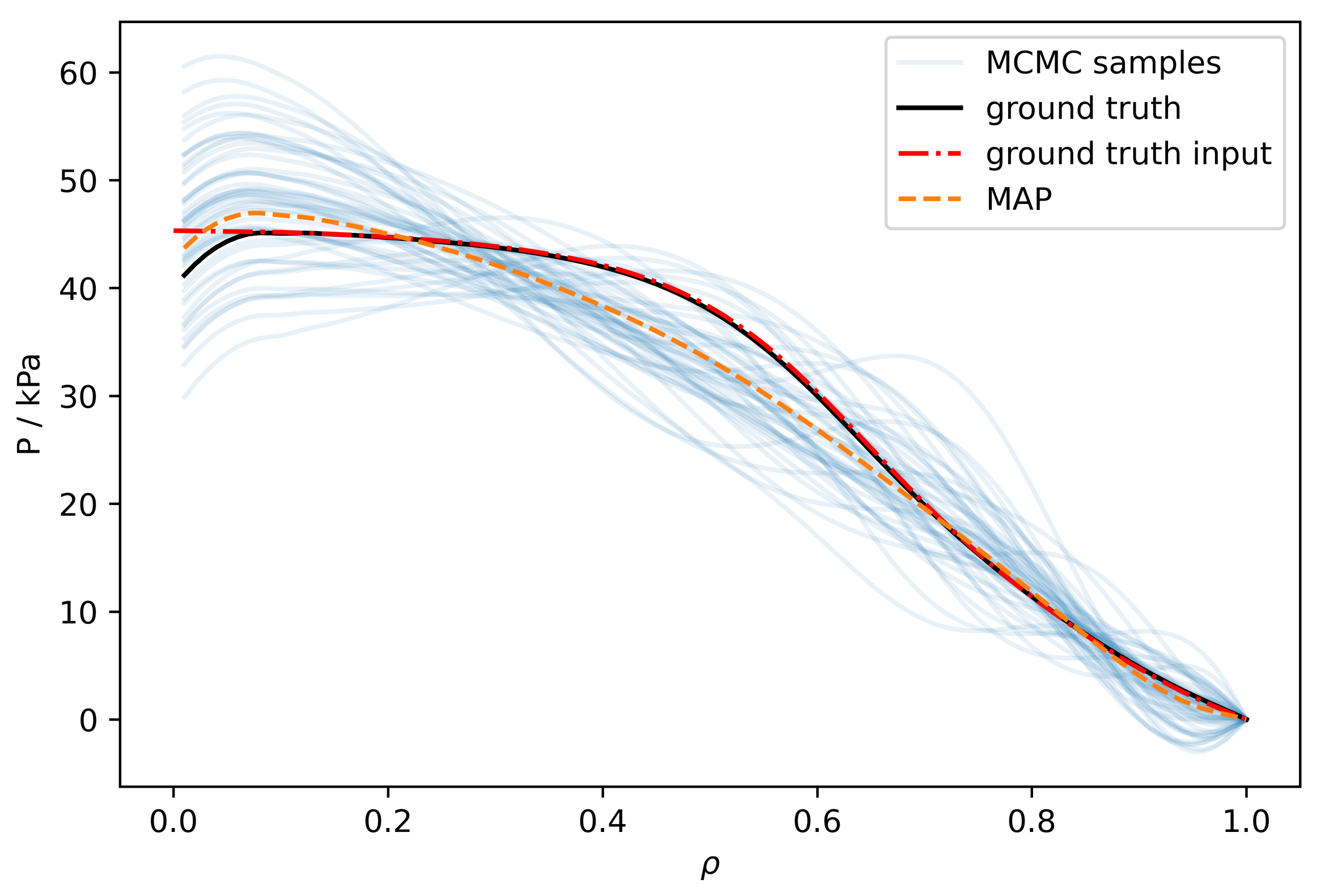
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freidberg, J.P. Ideal MHD; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- D’haeseleer, W.D.; Hitchon, W.N.G.; Callen, J.D.; Shohet, J.L. Flux Coordinates and Magnetic Field Structure; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar] [CrossRef]
- Lazerson, S.; The DIII-D Team. Three-Dimensional Equilibrium Reconstruction on the DIII-D Device. Nucl. Fusion 2015, 55, 023009. [Google Scholar] [CrossRef]
- Fischer, R.; Fuchs, C.J.; Kurzan, B.; Suttrop, W.; Wolfrum, E.; ASDEX Upgrade Team. Integrated Data Analysis of Profile Diagnostics at ASDEX Upgrade. Fusion Sci. Technol. 2010, 58, 675–684. [Google Scholar] [CrossRef]
- Fischer, R.; Giannone, L.; Illerhaus, J.; McCarthy, P.J.; McDermott, R.M.; ASDEX Upgrade Team. Estimation and Uncertainties of Profiles and Equilibria for Fusion Modeling Codes. Fusion Sci. Technol. 2020, 76, 879–893. [Google Scholar] [CrossRef]
- Andreeva, T.; Alonso, J.; Bozhenkov, S.; Brandt, C.; Endler, M.; Fuchert, G.; Geiger, J.; Grahl, M.; Klinger, T.; Krychowiak, M.; et al. Equilibrium Evaluation for Wendelstein 7-X Experiment Programs in the First Divertor Phase. Fusion Eng. Des. 2019, 146, 299–302. [Google Scholar] [CrossRef]
- Sanders, M.; Ida, K.; Yoshinuma, M.; Suzuki, C.; Yoshimura, Y.; Seki, R.; Emoto, M.; Yoshida, M.; Kobayashi, T. Analysis of the Motional Stark Effect (MSE) Diagnostic to Measure the Rotational Transform and Current Profile in the Large Helical Device. Rev. Sci. Instrum. 2021, 92, 053503. [Google Scholar] [CrossRef] [PubMed]
- Cianciosa, M.R.; Hanson, J.D.; Maurer, D.A. Uncertainty Analysis in 3D Equilibrium Reconstruction. Fusion Sci. Technol. 2018, 74, 1–12. [Google Scholar] [CrossRef]
- Seal, S.K.; Cianciosa, M.R.; Hirshman, S.P.; Wingen, A.; Wilcox, R.S.; Unterberg, E.A. Parallel Reconstruction of Three Dimensional Magnetohydrodynamic Equilibria in Plasma Confinement Devices. In Proceedings of the 2017 46th International Conference on Parallel Processing (ICPP), Bristol, UK, 14–17 August 2017; pp. 282–291. [Google Scholar] [CrossRef]
- Merlo, A.; Böckenhoff, D.; Schilling, J.; Höfel, Z.; Kwak, S.; Svensson, J.; Pavone, A.; Lazerson, S.A.; Pedersen, T.S. Proof of Concept of a Fast Surrogate Model of the VMEC Code via Neural Networks in Wendelstein 7-X Scenarios. Nucl. Fusion 2021, 61, 096039. [Google Scholar] [CrossRef]
- Köberl, R.; von Toussaint, U.; Bungartz, H.J.; Schilling, J.; Albert, C.G.; W7-X Team. Uncertainty Quantification in Three-Dimensional Magnetohydrodynamic Equilibrium Reconstruction via Surrogate-Assisted Bayesian Inference. Contrib. Plasma Phys. 2023, 63, e202200173. [Google Scholar] [CrossRef]
- Svensson, J.; Werner, A. Large Scale Bayesian Data Analysis for Nuclear Fusion Experiments. In Proceedings of the 2007 IEEE International Symposium on Intelligent Signal Processing, Alcala de Henares, Spain, 3–5 October 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Hirshman, S.P. Steepest-Descent Moment Method for Three-Dimensional Magnetohydrodynamic Equilibria. Phys. Fluids 1983, 26, 3553. [Google Scholar] [CrossRef]
- Lazerson, S.; Sakakibara, S.; Suzuki, Y. A Magnetic Diagnostic Code for 3D Fusion Equilibria. Plasma Phys. Control. Fusion 2013, 55, 025014. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Pavone, A.; Svensson, J.; Langenberg, A.; Höfel, U.; Kwak, S.; Pablant, N.; Wolf, R.C. Neural Network Approximation of Bayesian Models for the Inference of Ion and Electron Temperature Profiles at W7-X. Plasma Phys. Control. Fusion 2019, 61, 075012. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Endler, M.; Brucker, B.; Bykov, V.; Cardella, A.; Carls, A.; Dobmeier, F.; Dudek, A.; Fellinger, J.; Geiger, J.; Grosser, K.; et al. Engineering Design for the Magnetic Diagnostics of Wendelstein 7-X. Fusion Eng. Des. 2015, 100, 468–494. [Google Scholar] [CrossRef]
- Feinberg, J.; Langtangen, H.P. Chaospy: An Open Source Tool for Designing Methods of Uncertainty Quantification. J. Comput. Sci. 2015, 11, 46–57. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive Sparse Polynomial Chaos Expansion Based on Least Angle Regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Lüthen, N.; Marelli, S.; Sudret, B. Sparse Polynomial Chaos Expansions: Literature Survey and Benchmark. SIAM/ASA J. Uncertain. Quantif. 2021, 9, 593–649. [Google Scholar] [CrossRef]
- Schobi, R.; Sudret, B.; Wiart, J. Polynomial-Chaos-Based Kriging. Int. J. Uncertain. Quantif. 2015, 5, 171–193. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. arXiv 2011, arXiv:1111.4246. [Google Scholar] [CrossRef]

| Symbol | Distribution | Description |
|---|---|---|
| Uniform in | Total toroidal magnetic flux | |
| Uniform in | Pressure at the magnetic axis | |
| Pressure profile shape factors reduced to 6 principal components | ||
| Uniform in | Total toroidal current | |
| Current profile shape factors reduced to 3 principal components |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Köberl, R.; Babin, R.; Albert, C.G. Magnetohydrodynamic Equilibrium Reconstruction with Consistent Uncertainties. Phys. Sci. Forum 2023, 9, 6. https://doi.org/10.3390/psf2023009006
Köberl R, Babin R, Albert CG. Magnetohydrodynamic Equilibrium Reconstruction with Consistent Uncertainties. Physical Sciences Forum. 2023; 9(1):6. https://doi.org/10.3390/psf2023009006
Chicago/Turabian StyleKöberl, Robert, Robert Babin, and Christopher G. Albert. 2023. "Magnetohydrodynamic Equilibrium Reconstruction with Consistent Uncertainties" Physical Sciences Forum 9, no. 1: 6. https://doi.org/10.3390/psf2023009006
APA StyleKöberl, R., Babin, R., & Albert, C. G. (2023). Magnetohydrodynamic Equilibrium Reconstruction with Consistent Uncertainties. Physical Sciences Forum, 9(1), 6. https://doi.org/10.3390/psf2023009006






