Abstract
Current global analyses of 3 oscillation data point towards non-maximal , but the maximal value of is still allowed at 3 confidence level. It is expected that DUNE will establish the non-maximal value of at high confidence level if in nature. In this work, we present, in detail, the sensitivity of DUNE to establish the deviation from maximal . We find that a 3 (5) determination of non-maximal is possible in DUNE with an exposure of 336 kt·MW·years, if the true value of or for any value of true and true choice of normal mass ordering. We also discuss the extent of individual contributions from appearance and disappearance channels and the impacts of systematic uncertainties and total exposure, while addressing the discovery of non-maximal of in DUNE.
1. Introduction
Present 3 global oscillation data favor normal mass ordering (NMO) at 2.5 and provide hints for lower octant of atmospheric mixing angle () and leptonic CP violation at around 90% confidence level [1]. In this work, we explore the capabilities of the upcoming high-precision long-baseline experiment DUNE [2] to establish the non-maximal using an on-axis, wide-band neutrino beam with most of its flux peaking around 2.5 GeV. DUNE is enriched with substantial Earth’s matter effect, having a baseline of 1285 km with a line-averaged constant Earth matter density () of 2.848 g/cm. To simulate our results, we make use of the publicly available GLoBES software [3]. For generating our prospective data, we use the following benchmark values of oscillation parameters from Ref. [1]: , assuming NMO.
2. Results and Discussions
To estimate the median sensitivities in the frequentist approach, we use the Poissonian [4]. For estimating the sensitivity towards establishing deviation from non-maximal in DUNE, we define the following:
where is the set of oscillation parameters over which we marginalize within their current 3 allowed ranges (as mentioned in Ref. [1]). Here, are the respective systematic pulls on signal and background. In Figure 1, we show the sensitivity of DUNE in establishing deviation from non-maximal using an exposure of 336 kt·MW·years. Figure 1 depicts that, for the present best-fit values of oscillation parameters (assuming NMO), DUNE can establish deviation from non-maximal at 4.2 C.L., assuming a total run-time of 7 years, equally divided in both neutrino and antineutrino modes. Furthermore, we observe that a 3 (5) determination of non-maximal is possible in DUNE if the true value of or , irrespective of any value of true . The narrow width of the red-colored band in Figure 1 shows that this sensitivity hardly depends on the choice of true . This is because the contribution from the disappearance channel dominates while establishing deviation from maximal (see Figure 2), and this channel is almost independent of [5].
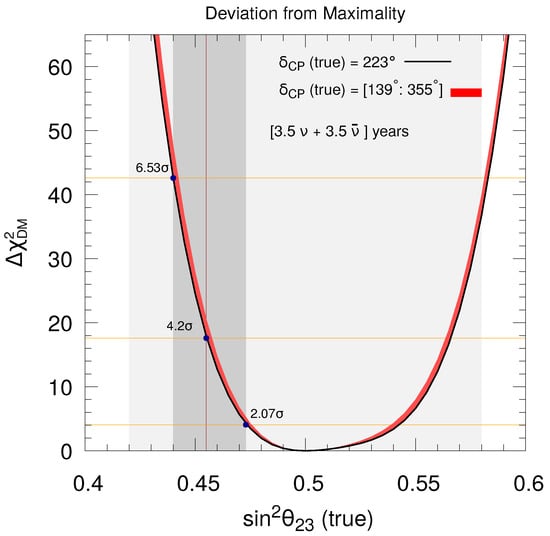
Figure 1.
The black curve depicts the potential of DUNE to establish the deviation from maximal as a function of true , assuming true NMO and (true) = 223, considering 336 kt·MW·years of exposure. The red band portrays the same for any true choice of in its current 3 range. In the fit, we marginalize over the current 3 range of eV and , keeping all other oscillation parameters fixed at their benchmark values, as mentioned before. The dark- and light-shaded gray areas show the currently allowed and ranges, respectively, in , as obtained in the global fit study [1]. The present best-fit value of is shown by a vertical brown line. The horizontal orange lines show the sensitivities for the current best-fit and 1 upper and lower bounds of . This figure is taken from Ref. [6].
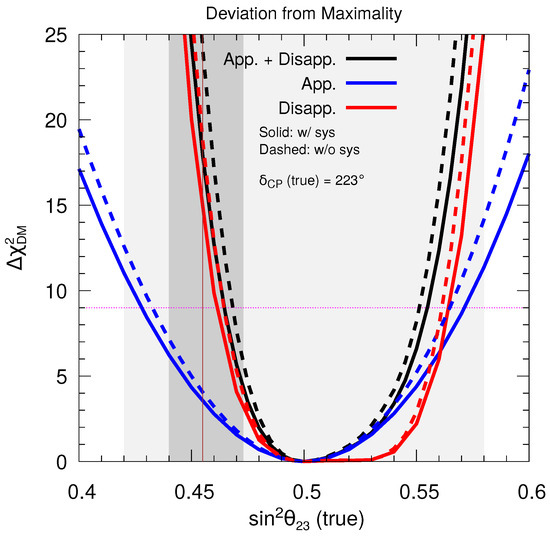
Figure 2.
Potential of DUNE to establish deviation from non-maximal as a function of true , assuming true NMO and (true) = 223 with 336 kt·MW·years of exposure. The red-, blue-, and black-colored curves represent the potential of disappearance channel, appearance channel, and their combinations, respectively. The solid (dashed) lines depict the results with (without) systematic uncertainties. In the fit, we marginalize over the current 3 range of and . The present best-fit value of is shown by a vertical brown line. The horizontal pink dotted line depicts the performance of DUNE at 3 C.L. This figure is taken from Ref. [6].
Figure 2 portrays the individual contributions from appearance (blue curves), disappearance (red curves), and their combination (black curve) as a function of true in establishing non-maximal . Note that, when lies in higher octant but remains close to maximal mixing, the appearance channel provides better sensitivity than the disappearance channel in excluding maximal mixing solution. However, for , the disappearance channel dominates, causing a sharp rise in total . Throughout the lower octant, the disappearance channel contributes the most towards the sensitivity. The solid and dashed curves depict the sensitivities with and without systematic uncertainties, suggesting that both the channels are affected due to the systematic errors in DUNE. In Table 1, we quantify the sensitivity towards non-maximal considering five different sets of normalization uncertainties on appearance and disappearance events, keeping the systematic errors in various backgrounds fixed at their nominal values. We observe that the sensitivity from the disappearance channel is deteriorated more than the appearance channel when we transition from a scenario with no systematic uncertainties to their nominal values . Nevertheless, if we increase the uncertainties further, then the deterioration in the sensitivity is quite substantial in the appearance channel, while the disappearance channel is hardly affected. Since, in this study, disappearance is the primary contributing channel, we expect, therefore, that the performance of DUNE in establishing non-maximal will remain mostly unaffected if the systematic uncertainties are enhanced in DUNE.

Table 1.
for various choices of normalization uncertainties on appearance and disappearance events: [(2%, 5%), (0%, 0%), (5%, 5%), (5%, 10%), and (10%, 10%)], where (2%, 5%) is the nominal choice [2]. Results are shown for (true) = 0.455 (current best-fit) and (true) = 0.473 (current upper bound), assuming true NMO and (true) = 223 with 336 kt·MW·years of exposure. This table is from Ref. [6].
In Figure 3, we depict the true values of that DUNE can distinguish from as a function of total exposure. With the proposed setup, we expect a significant improvement in the discovery of a non-maximal when exposure increases from 50 kt·MW·years to 100 kt·MW·years. Further, increasing the total exposure to its benchmark value of 336 kt·MW·years shows only marginal improvement. Any further increase in the statistics, does not result in much improvement in the sensitivity.
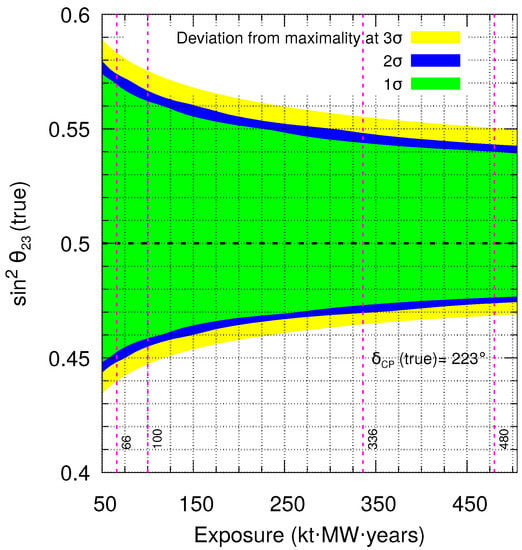
Figure 3.
Sensitivity towards deviation from maximal as a function of total exposure, equally divided into neutrino and antineutrino modes. Results are shown at (yellow curves), (blue curves), and (green curves) C.L., assuming true NMO and (true) = 223. In the fit, we marginalize over and in their 3 allowed ranges. This figure is taken from Ref. [6].
3. Conclusions
We explore, in detail, the performance of DUNE in establishing deviation from non-maximal , which plays a crucial role in constructing neutrino mass models, addressing the issue of leptonic CP violation, and performing precision measurement of other oscillation parameters. In light of the global fit of the current oscillation data assuming NMO, we find that DUNE can exclude at 4.2 with 336 kt·MW·years of exposure. This sensitivity can further deteriorate to 2 or enhance to 6.5, depending upon the true value of in its current 1 upper (0.47) and lower (0.44) bounds, respectively. We further observe that the disappearance channel plays a significant role and the impact of systematic uncertainties is minimal in this study.
Author Contributions
All authors have equally contributed in this project starting from the conceptualization till submission for publishing. All authors have read and agreed to the published version of the manuscript.
Funding
S.K.A. is supported by the Young Scientist Project [INSA/SP/YSP/144/2017/1578] from the Indian National Science Academy (INSA). S.K.A. acknowledges the financial support from the Swarnajayanti Fellowship Research Grant (No. DST/SJF/PSA-05/2019-20) provided by the Department of Science and Technology (DST), Govt. of India and the Research Grant (File no. SB/SJF/2020-21/21) from the Science and Engineering Research Board (SERB) under the Swarnajayanti Fellowship by the DST, Govt. of India. M.S. acknowledges financial support from the DST, Govt. of India (DST/INSPIRE Fellowship/2018/IF180059).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data was generated using GLoBES software. We use the latest ancillary files for DUNE provided by the collaboration.
Acknowledgments
S.K.A acknowledges the financial support from the DAE, DST, Swarnajyanti Fellowship from the DST-SERB, Government of India, INSA, and USIEF. M.S. acknowledges financial support from the DST, Govt. of India (DST/INSPIRE Fellowship/2018/IF180059). The numerical simulations were carried out using the “SAMKHYA: High-Performance Computing Facility” at the Institute of Physics, Bhubaneswar, India.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Capozzi, F.; Valentino, E.D.; Lisi, E.; Maronne, A.; Melchiorri, A.; Palazzo, A. Unfinished fabric of the three neutrino paradigm. Phys. Rev. D 2021, 104, 083031. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, J.; Ahmed, T.; Alion, S.; Alonso Monsalve, C.; et al. Experiment Simulation Configurations Approximating DUNE TDR. arXiv 2021, arXiv:2103.04797. [Google Scholar]
- Huber, P.; Kopp, J.; Linder, M.; Rolinec, M.; Winter, W. New features in the simulation of neutrino oscillation experiments with GLoBES 3.0: General Long Baseline Experimental Simulator. Comput. Phys. Commun. 2007, 177, 432–438. [Google Scholar] [CrossRef]
- Baker, S.; Cousins, R.D. Clarification of the use of chi square and likelihood functions in fits to histograms. Nucl. Instrum. Meth. 1984, 221, 437–442. [Google Scholar] [CrossRef]
- Agarwalla, S.K.; Das, S.; Giarnetti, A.; Meloni, D.; Singh, M. Enhancing Sensitivity to Leptonic CP Violation using Complementarity among DUNE, T2HK, and T2HKK. arXiv 2022, arXiv:2211.10620. [Google Scholar]
- Agarwalla, S.K.; Kundu, R.; Prakash, S.; Singh, M. A close look on 2–3 mixing angle with DUNE in light of current neutrino oscillation data. JHEP 2022, 206, 1–41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).