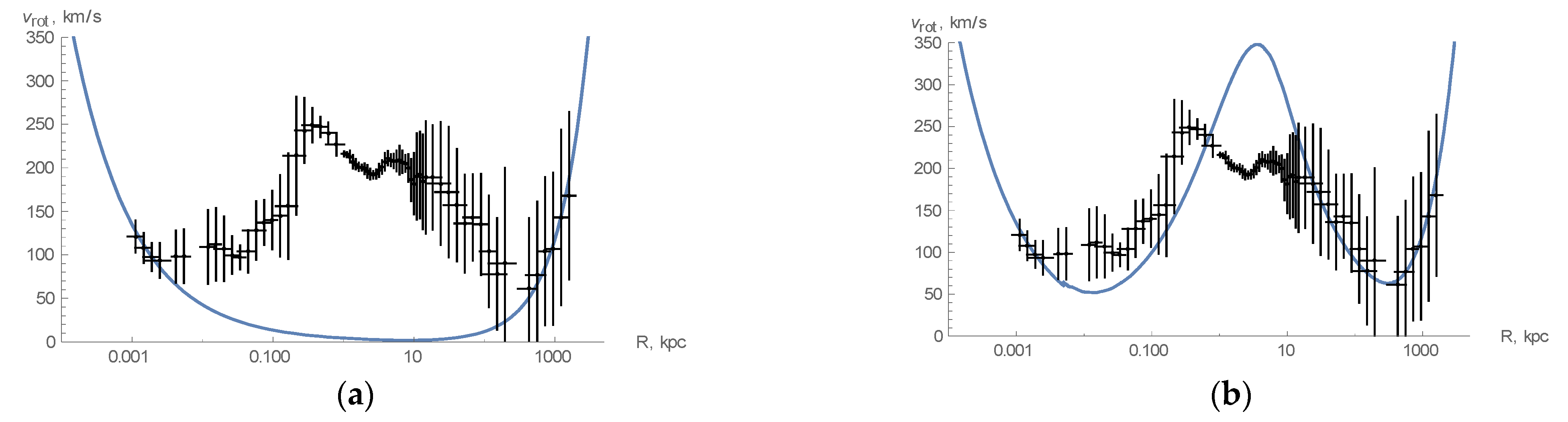
Dark Matter in the Milky Way as the F-Type of Vacuum Polarization †
Abstract
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the Massive Black Hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1975; Volume 2. [Google Scholar]
- Sofue, Y. Rotation Curve and Mass Distribution in the Galactic—From Black Hole to Entire Galaxy. Publ. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
- Milgrom, M. MOND vs. dark matter in light of historical parallels. Stud. Hist. Philos. Sci. Part B 2020, 71, 170–195. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Vacuum Polarization Instead of “Dark Matter” in a Galaxy. Universe 2022, 8, 456. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Aether as an Inevitable Consequence of Quantum Gravity. Universe 2022, 8, 626. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Eicheons instead of Black holes. Phys. Scr. 2020, 95, 085009. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherkas, S.L.; Kalashnikov, V.L. Dark Matter in the Milky Way as the F-Type of Vacuum Polarization. Phys. Sci. Forum 2023, 7, 8. https://doi.org/10.3390/ECU2023-14025
Cherkas SL, Kalashnikov VL. Dark Matter in the Milky Way as the F-Type of Vacuum Polarization. Physical Sciences Forum. 2023; 7(1):8. https://doi.org/10.3390/ECU2023-14025
Chicago/Turabian StyleCherkas, Sergey L., and Vladimir L. Kalashnikov. 2023. "Dark Matter in the Milky Way as the F-Type of Vacuum Polarization" Physical Sciences Forum 7, no. 1: 8. https://doi.org/10.3390/ECU2023-14025
APA StyleCherkas, S. L., & Kalashnikov, V. L. (2023). Dark Matter in the Milky Way as the F-Type of Vacuum Polarization. Physical Sciences Forum, 7(1), 8. https://doi.org/10.3390/ECU2023-14025