Gravitational, Electromagnetic and Quantum Interaction: From String to Cloud Theory ^†

Abstract

The recent Planck Legacy 2018 release verified the presence of an enhanced lensing amplitude in the power spectra of the cosmic microwave background with a confidence level of over 99%, which implies that the early Universe had a positive curvature. In this study, the curvature of the early Universe is regarded as the curvature of 4D conformal bulk while celestial objects that induce a localized curvature in the bulk are considered as 4D relativistic cloud-worlds. Likewise, quantum fields are considered as 4D relativistic quantum clouds that are affected by the curvature of the bulk as a manifestation of gravity. This approach could eliminate the singularities and satisfy the conditions of a conformal invariance theory.

1. Introduction

The Planck Legacy 2018 release preferred the presence of a primordial background curvature [1], which poses a challenge when trying to reconcile it with spatial flatness using baryon acoustic oscillation data, due to a 2.5 to 3σ tension in the curvature parameter between the two sets of data [2]. The feasible evolution of the primordial background curvature over the conformal time into the present Universe spatial flatness highlights the insufficiency of background-independent theories, which do not account for the evolution in background curvature and treat celestial objects in the early Universe similarly to those in the present Universe. This shortcoming can be the reason for the dark matter problem.

This study aims to obtain interaction field equations that consider the background curvature and its impact on both celestial and quantum objects/fields.

2. Interaction Field Equations

To consider the bulk’s curvature, a modulus indicating its resistance or field strength ${\mathcal{F}}_{\lambda \rho }$ using the Lagrangian formalism of the bulk’s vacuum energy density is defined as

$$E_D=\frac{T_{\mu \nu }-T{g}_{\mu \nu }/2}{R_{\mu \nu }/\mathcal{R}}=\frac{{-\mathcal{F}}_{\lambda \rho }{\mathcal{F}}^{\lambda \rho }}{4{\mu }_0}$$

(1)

By incorporating the bulk influence, the Einstein–Hilbert action is extended to

$$S=E_D{\int }_C^{}\left[\frac{R}{\mathcal{R}}+\frac{L}{\mathcal{L}}\right]{\sqrt{-g}d}^4\rho$$

(2)

where $R$ is the induced curvature by a celestial object (cloud-word) and $\mathcal{R}$ is the curvature of the background (bulk) while $L$ and $\mathcal{L}$ are their Lagrangian densities respectively.

Because of the bulk’s constant modulus [3] and by considering its expansion, a dual action concerning energy conservation on global and local scales can be presented as

$$S={\int }_B^{}\left[\frac{-{\mathcal{F}}_{\lambda \rho }{\tilde{g}}^{\lambda \gamma }{\mathcal{F}}_{\gamma \alpha }{\tilde{g}}^{\rho \alpha }}{4{\mu }_0}\right]\sqrt{-\tilde{g}}{\int }_C^{}\left[\frac{R_{\mu \nu }{g}^{\mu \nu }}{{\mathcal{R}}_{\mu \nu }{\tilde{g}}^{\mu \nu }}+\frac{L_{\mu \nu }{g}^{\mu \nu }}{{\mathcal{L}}_{\mu \nu }{\tilde{g}}^{\mu \nu }}\right]\sqrt{-g}{d}^4\rho d^4\sigma$$

(3)

where $g_{\mu \nu }$ is the metric of the 4D relativistic cloud-word while ${\tilde{g}}_{\mu \nu }$ is the metric of the 4D conformal bulk. The dual action should hold for any variation, which yields

$$\delta S={\int }_B^{}\left[\begin{array}{c}\frac{{-\mathcal{F}}_{\lambda \rho }{\mathcal{F}}_{\gamma }^{\rho }\delta {\tilde{g}}^{\lambda \gamma }-{\tilde{g}}^{\lambda \gamma }\delta {\mathcal{F}}_{\lambda \rho }{\mathcal{F}}_{\gamma }^{\rho }}{2{\mu }_0}\\ \\ +{\mathcal{F}}_{\lambda \rho }{\tilde{g}}^{\lambda \gamma }{\mathcal{F}}_{\gamma \alpha }{\tilde{g}}^{\rho \alpha }\frac{{\tilde{g}}_{\mu \nu }\delta {\tilde{g}}^{\mu \nu }}{8{\mu }_0}\end{array}\right]\sqrt{-\tilde{g}}{\int }_C^{}\left[\begin{array}{c}\frac{R_{\mu \nu }{\delta g}^{\mu \nu }+g^{\mu \nu }\delta R_{\mu \nu }}{\mathcal{R}}-\frac{{\mathcal{R}}_{\mu \nu }{\delta \tilde{g}}^{\mu \nu }+{\tilde{g}}^{\mu \nu }\delta {\mathcal{R}}_{\mu \nu }}{{\mathcal{R}}^2}R-\frac{g_{\mu \nu }R\delta g^{\mu \nu }}{2\mathcal{R}}\\ \\ +\frac{L_{\mu \nu }{\delta g}^{\mu \nu }+g^{\mu \nu }\delta L_{\mu \nu }}{\mathcal{L}}-\frac{{\mathcal{L}}_{\mu \nu }{\delta \tilde{g}}^{\mu \nu }+{\tilde{g}}^{\mu \nu }\delta {\mathcal{L}}_{\mu \nu }}{{\mathcal{L}}^2}L-\frac{g_{\mu \nu }L\delta g^{\mu \nu }}{2\mathcal{L}}\end{array}\right]\sqrt{-g}{d}^4\rho d^4\sigma$$

(4)

where $\delta \sqrt{-g}=-\sqrt{-g}{g}_{\mu \nu }\delta g^{\mu \nu }/2$ [4]. By transforming the boundary terms [3], a boundary action, $S_{boundary}$, is obtained as follows

$$S_{boundary}={\int }_{\partial B}^{}\left[\frac{f_{\lambda }}{2{\mu }_0}\right]\sqrt{\left|\tilde{p}\right|}{\int }_{\partial C}^{}ϵ\left(\left[\frac{K}{\mathcal{R}}+\frac{l}{\mathcal{L}}\right]\sqrt{\left|q\right|}-\left[\frac{R\mathcal{K}}{{\mathcal{R}}^2}+\frac{L\ell }{{\mathcal{L}}^2}\right]\sqrt{\left|p\right|}\right)d^3\varrho d^3\varsigma$$

(5)

where $K$ and $\mathcal{K}$ are the traces of extrinsic curvatures of the cloud-world and bulk; $l$ and $\ell$ are the extrinsic traces of the Lagrangian densities on their boundaries, respectively, and $f_{\lambda }$ is the Lorentz force density. The derivation of the whole action in Ref. [3] gives

$$\frac{R_{\mu \nu }}{\mathcal{R}}-\frac{1}{2}\frac{R}{\mathcal{R}}{g}_{\mu \nu }-\frac{R{\mathcal{R}}_{\mu \nu }}{{\mathcal{R}}^2}+\frac{R\left({\mathcal{K}}_{\mu \nu }-\frac{1}{2}\mathcal{K}{\widehat{p}}_{\mu \nu }\right)-\mathcal{R}\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)}{{\mathcal{R}}^2}=\frac{{\widehat{T}}_{\mu \nu }}{{\mathcal{T}}_{\mu \nu }}$$

(6)

As visualized in the next Section, these interaction field equations can be interpreted as expressing the interaction and flow of a cloud-world through the bulk. The equations reveal that the cloud-world’s induced curvature over the bulk’s conformal curvature is equal to the ratio of the cloud-world’s energy density and flux to the bulk’s vacuum energy density and flux through the expanding/contracting Universe. By transforming the bulk’s curvature terms [3], the interaction field equations reduce to

$$R_{\mu \nu }-\frac{1}{2}R{\widehat{g}}_{\mu \nu }-\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)=\frac{8\pi G_{\mathcal{R}}}{c^4}{\widehat{T}}_{\mu \nu }$$

(7)

where ${\widehat{g}}_{\mu \nu }=g_{\mu \nu }+2{\mathcal{R}}_{\mu \nu }/\mathcal{R}-2{\stackrel{=}{g}}_{\mu \nu }$, or can be expressed as ${\widehat{g}}_{\mu \nu }=g_{\mu \nu }+2{\tilde{g}}_{\mu \nu }-2{\stackrel{=}{g}}_{\mu \nu }$ because ${\mathcal{R}}_{\mu \nu }/\mathcal{R}={\mathcal{R}}_{\mu \nu }/{\mathcal{R}}_{\mu \nu }{\tilde{g}}^{\mu \nu }={\tilde{g}}_{\mu \nu }$, is the conformally transformed metric, which includes contributions from the cloud-world and bulk metrics. $K_{\mu \nu }$ belongs to the boundary term and $G_{\mathcal{R}}$ is an effective Newtonian gravitational parameter that relies on the curvature of the background while ${\widehat{T}}_{\mu \nu }$ is an extended conformal stress-energy tensor which also includes the electromagnetic energy flux from the boundary over the conformal time.

Regarding the wave-particle duality and analogous to the constant bulk modulus, the bulk curvature can be considered constant concerning quantum fields. Accordingly, the action can be further extended to include quantum fields as follows

$$S={\int }_B^{}\left[\frac{-{\mathcal{F}}_{\lambda \rho }{\tilde{g}}^{\lambda \gamma }{\mathcal{F}}_{\gamma \alpha }{\tilde{g}}^{\rho \alpha }}{4{\mu }_0}\right]\sqrt{-\tilde{g}}{\int }_C^{}\left[\frac{R_{\mu \nu }{g}^{\mu \nu }}{{\mathcal{R}}_{\mu \nu }{\tilde{g}}^{\mu \nu }}\right]\sqrt{-g}{\int }_Q^{}\left[\frac{p_{\mu }{p}_v{q}^{\mu \nu }}{{\pi }_{\mu }{\pi }_v{g}^{\mu \nu }}+\frac{L_{\alpha \beta }{q}^{\alpha \lambda }{L}_{\lambda \gamma }{q}^{\beta \gamma }}{2{\chi }_0{\mathcal{L}}_{\mu \nu }{g}^{\mu \nu }}\right]\sqrt{-q}{{\vartheta }^{2}d}^{12}\sigma$$

(8)

where $p_{\mu }{p}^v$ are the four-momentum of two entangled quantum fields, $L_{\alpha \beta }{L}^{\alpha \beta }/2{\chi }_0$ are their Lagrangian densities and ${\vartheta }^2$ is a dimension-hierarchy factor while ${\pi }_{\mu }{\pi }^v$ are the four-momentum of vacuum energy density. The derivation in Ref. [3] yields

$$p_{\mu }-\frac{1}{2}{p}^{\nu }\left(q_{\mu \nu }+2{\tilde{q}}_{\mu \nu }\right)-\left(J^{\mu }{A}_{\mu }-\frac{1}{2}{J}^{\mu }{A}^{\nu }{\zeta }_{\mu \nu }\right)+\frac{p^{\nu }}{{\pi }^{\nu }}\left({{\mathcal{J}}^{\mu }\mathcal{A}}_{\mu }-\frac{1}{2}{\mathcal{J}}^{\mu }{\mathcal{A}}^{\nu }{\varsigma }_{\mu \nu }\right)=\frac{\hslash G_{\mathcal{R}}}{2c^2{g}_R}{\mathcal{T}}_{\mu }$$

(9)

where $g_R$ is the gravitational field strength exerted by the parent cloud-world.

In addition, the field equations in terms of operators with implicit bulk boundary term are

$${\widehat{p}}_{\mu }-\frac{1}{2}{\widehat{p}}^{\nu }{\xi }_{\mu \nu }-\left(J^{\mu }{A}_{\mu }-\frac{1}{2}{J}^{\mu }{A}^{\nu }{\zeta }_{\mu \nu }\right)=\frac{\hslash G_{\mathcal{R}}}{{2c}^2{g}_R}{\hat{\mathcal{T}}}_{\mu }$$

(10)

where ${\xi }_{\mu \nu }$ and ${\zeta }_{\mu \nu }$ are the conformally transformed metric of the quantum cloud and the induced metric on its boundary respectively, $J^{\mu }{A}_{\mu }$ is the boundary interaction of the quantum cloud with the electromagnetic field and ${\mathcal{T}}_{\mu }$ is the energy density and flux of the quantum cloud of a deformed configuration shown in Figure 1.

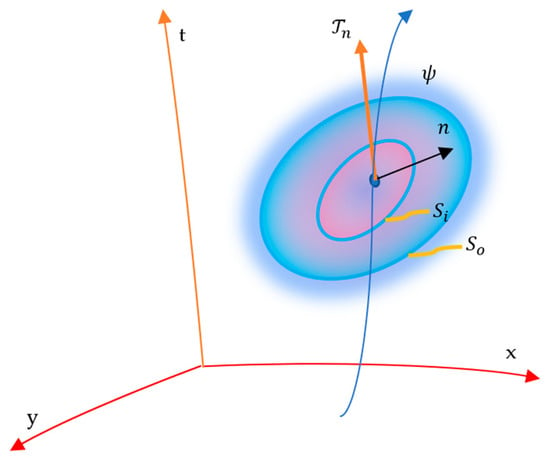
Figure 1. The deformed configuration of the quantum field of metric $q_{\mu \nu }$ along its travel and spin according to its wavefunction $\psi$ throughout the curved background of metric ${\tilde{q}}_{\mu \nu }$. $S_i$ is the inner surface of the quantum cloud that separates its continuum into two portions and encloses an arbitrary inner volume while $S_o$ is the outer surface of the quantum cloud’s boundary.

Applying the momentum ${\widehat{p}}_{\mu }$ and stress-energy (gravitational) ${\widehat{\mathcal{T}}}_{\mu }$ operators gives

$$i\hslash {\gamma }^{\mu }{\partial }_{\mu }\psi -\frac{1}{2}i\hslash {\gamma }^{\mu }{\partial }^{\nu }{\xi }_{\mu \nu }\psi -{\left(J^{\mu }{A}_{\mu }-\frac{1}{2}{J}^{\mu }{A}^{\nu }{\zeta }_{\mu \nu }\right)\psi }^{}=\frac{1}{2}\frac{\hslash }{x^{\mu }}R{\partial }_R\psi$$

(11)

where ${\gamma }^{\mu }$ are the Dirac matrices. On the other hand, by using the explicit boundary term of the bulk in Equation (9), the quantized interaction field equations are

$$i\hslash {\gamma }^{\mu }{\partial }_{\mu }\psi -\frac{1}{2}i\hslash {\gamma }^{\mu }{\partial }^{\nu }\left(q_{\mu \nu }+{\tilde{q}}_{\mu \nu }\right)\psi -{\left(J^{\mu }{A}_{\mu }-\frac{1}{2}{J}^{\mu }{A}^{\nu }{\zeta }_{\mu \nu }\right)\psi }^{}+\left({{\mathcal{J}}^{\mu }\mathcal{A}}_{\mu }-\frac{1}{2}{\mathcal{J}}^{\mu }{\mathcal{A}}^{\nu }{\varsigma }_{\mu \nu }\right)i\hslash \frac{{\gamma }^{\mu }{\partial }^{\nu }\psi }{{\pi }^{\nu }}=\frac{1}{2}\frac{\hslash }{x^{\mu }}R{\partial }_R\psi$$

(12)

where ${{\mathcal{J}}^{\mu }\mathcal{A}}_{\mu }$ denotes the bulk boundary term that looks to resemble the Higgs mechanism while the spin-spin correlation ${\gamma }^{\mu }{\partial }^{\nu }\psi /{\pi }^{\nu }$ of the conventional and vacuum energy fields seems to control the mechanism depending on the spin of the fields. These quantized field equations reduce to quantum electrodynamics for undeformed configuration of the quantum field in a flat spacetime background [3].

3. Evolution of the 4D Relativistic Cloud-Worlds over the 4D Conformal Bulk

A case study is considered to explore how galaxies form and evolve in a curved 4D conformal bulk. The semiclassical approach to calculating black hole entropy shows that the boundary term has the whole gravitational contribution. This concept can be used to arrange the interaction field equations in Equation (6) with multiplying them by the bulk curvature, $\mathcal{R}$, as follows

$$R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }-\frac{R}{\mathcal{R}}{\mathcal{R}}_{\mu \nu }=\frac{8\pi G_{\mathcal{R}}}{c^4}{\widehat{T}}_{\mu \nu }-\frac{R\left({\mathcal{K}}_{\mu \nu }-\frac{1}{2}\mathcal{K}{\widehat{p}}_{\mu \nu }\right)-\mathcal{R}\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)}{{\mathcal{R}}^2}=0$$

(13)

where the boundary term could weigh the stress-energy term.

From Equation (13), the field equations yield

$$R_{\mu \nu }=\frac{1}{2}R{g}_{\mu \nu }+\frac{R}{\mathcal{R}}{\mathcal{R}}_{\mu \nu }=\frac{1}{2}R\left(g_{\mu \nu }+2{\tilde{g}}_{\mu \nu }\right)=\frac{1}{2}R{g}_{\mu \nu }\left(1+2{\Omega }^2\right)=0.$$

(14)

The derived conformally transformed metric, ${\widehat{g}}_{\mu \nu }=g_{\mu \nu }\left(1+2{\Omega }^2\right)$, in Ref [5] is

$$d{s}^2=\left(1-\frac{r_s}{r}-\frac{{\tilde{r}}_p}{\tilde{r}}\right)\left(-c^{2}d{t}^2+S^2\left(\frac{d{r}^2}{1+\frac{{r_s}^2}{r^2}-2\frac{r_s}{r}}+\frac{r^{2}d{\theta }^2+r^2{sin}^2\theta d{\varphi }^2}{1-\frac{r_s}{r}-\frac{{\tilde{r}}_p}{\tilde{r}}}\right)\right).$$

(15)

This metric reduces to the Schwarzschild metric in a flat background ($\tilde{r}\to \infty )$, where ${\tilde{r}}_p$ is the gravitational radius of the early Universe. Figure 2 shows a visualization of the evolution of this metric in a curved evolving background.

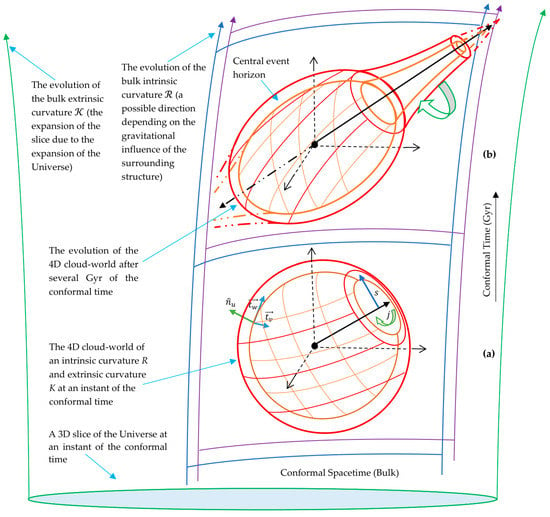
Figure 2. The evolution of the 4D relativistic cloud-world as it flows and spins through the curved 4D conformal bulk.

4. Conclusions

This study presented interaction field equations in terms of brane-world modified gravity and the perspective of geometrization of quantum mechanics. Celestial objects and quantum fields are regarded as 4D relativistic clouds where gravity is expressed as the curvature of the 4D conformal bulk. The interaction field equations reduce to standard said theories in a flat background and they could eliminate the singularities and satisfy a conformal invariance theory. Appendix A includes a further extended action for the non-abelian group. Future works could include testing the predictions of the interaction field equations such as that the Newtonian gravitational ‘constant’ is not constant but rather a parameter that depends on the background curvature where the position of the Moon could change the background curvature.