Development of a Mathematical Model Based on an Artificial Neural Network (ANN) to Predict Nickel Uptake Data by a Natural Zeolite †
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
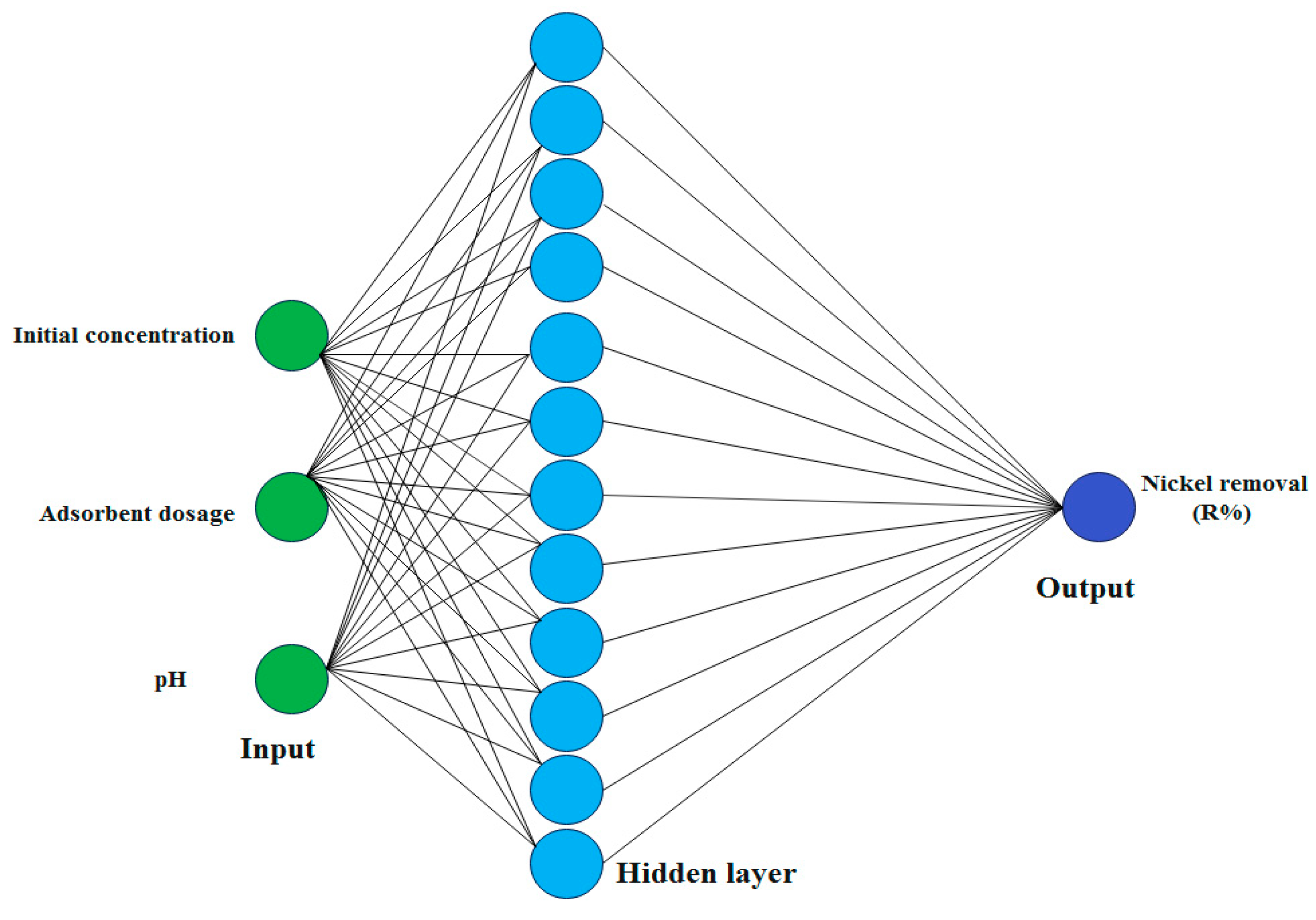
2.2. ANN Model
2.3. ANN Optimization
3. Results
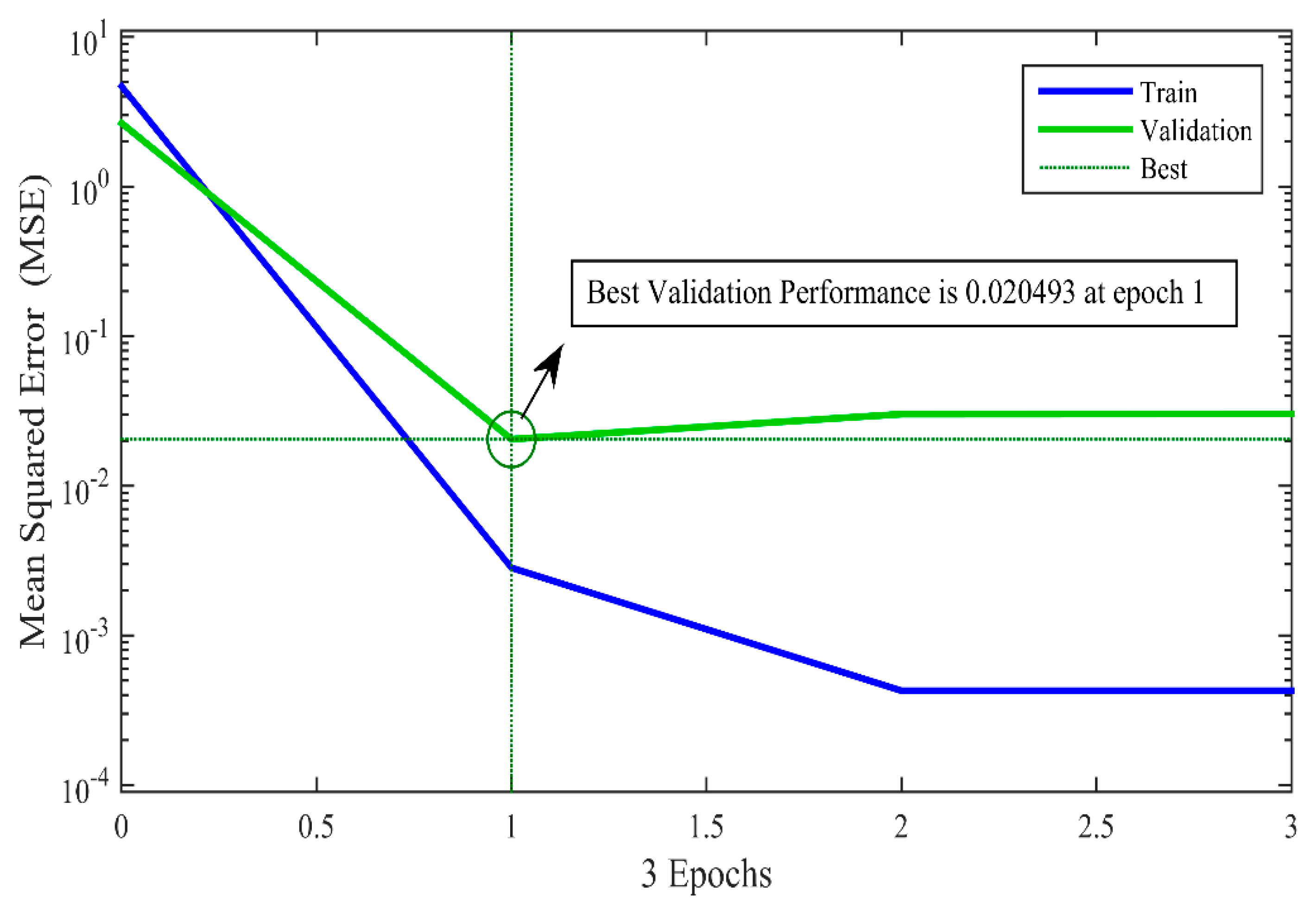
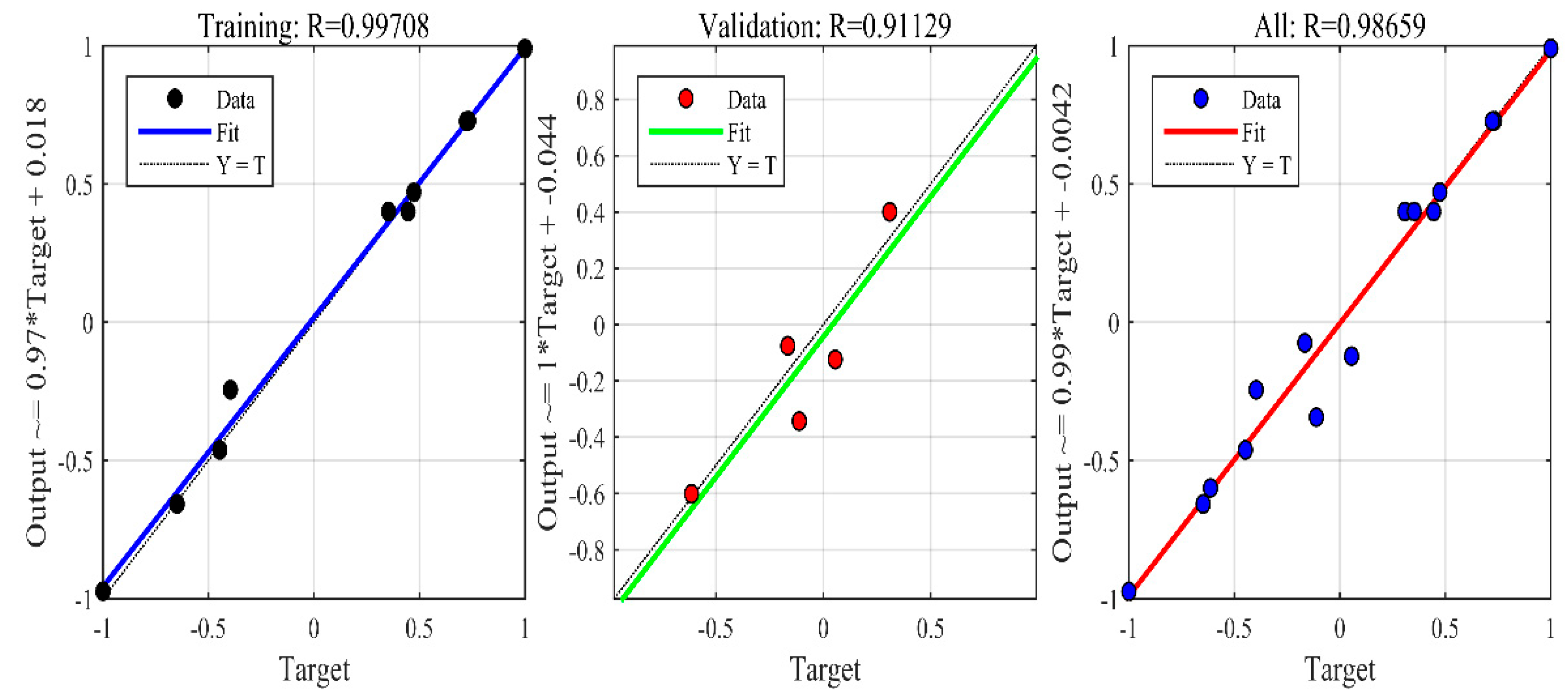
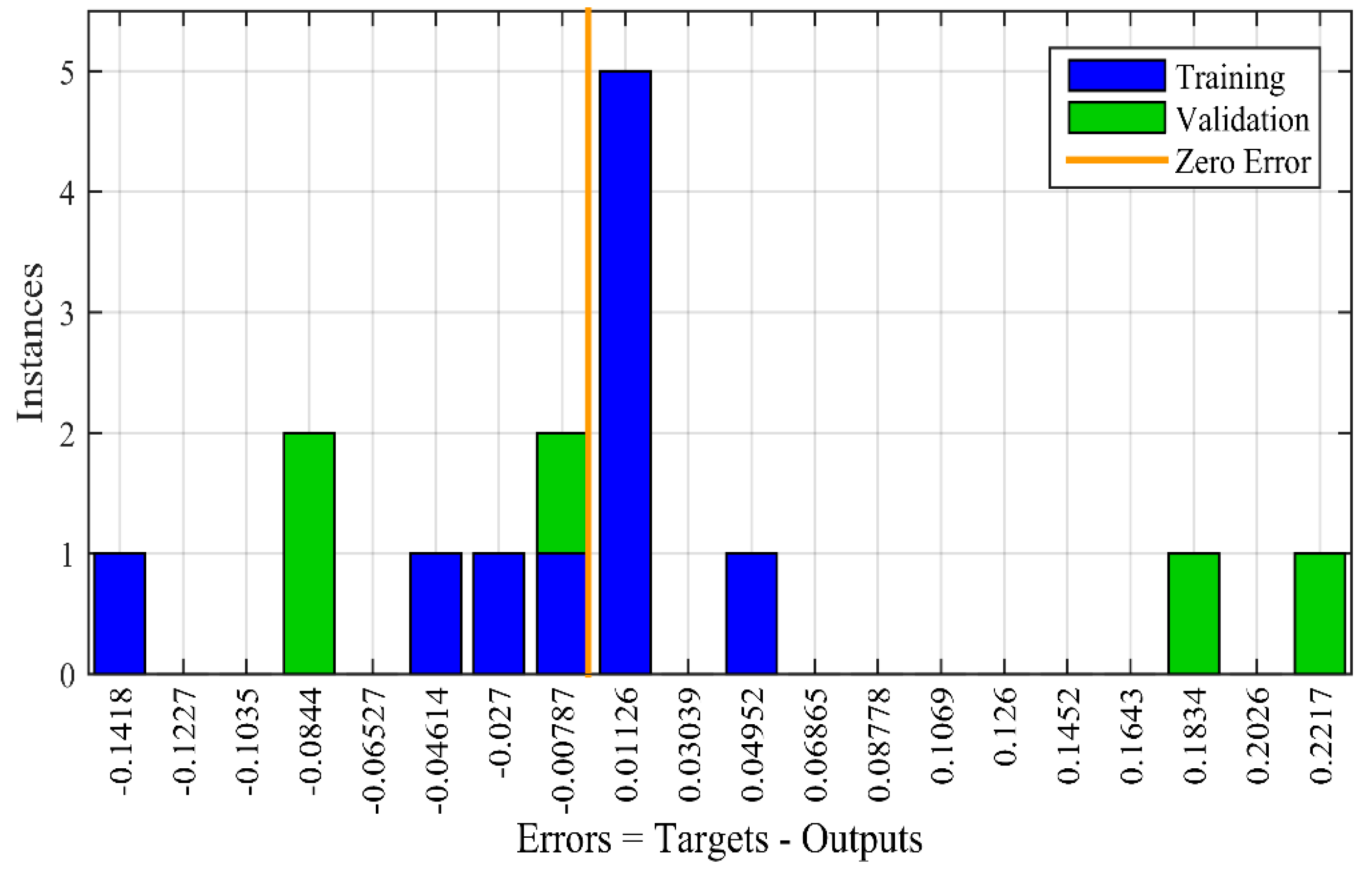
3.1. ANN Performance
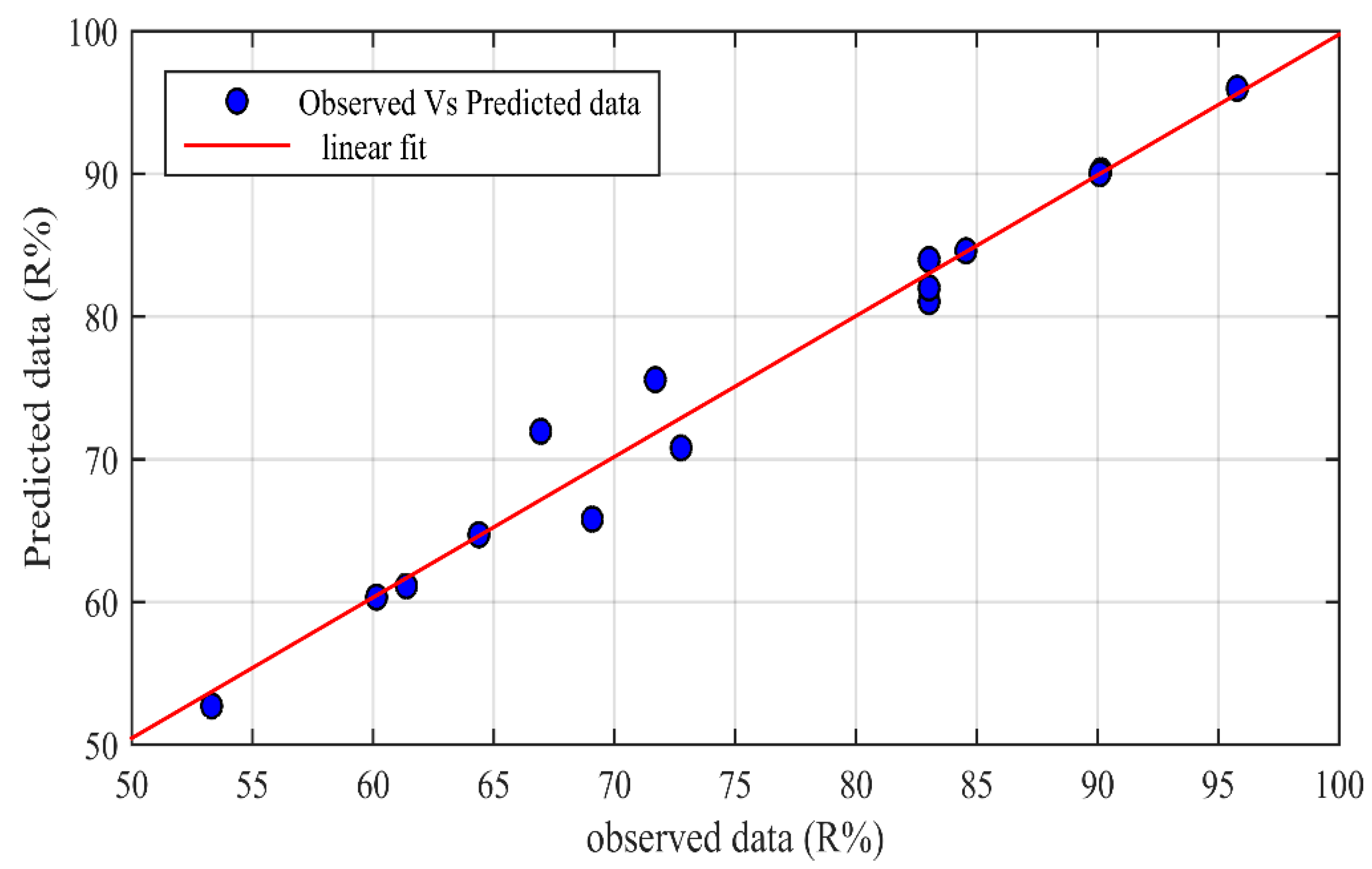
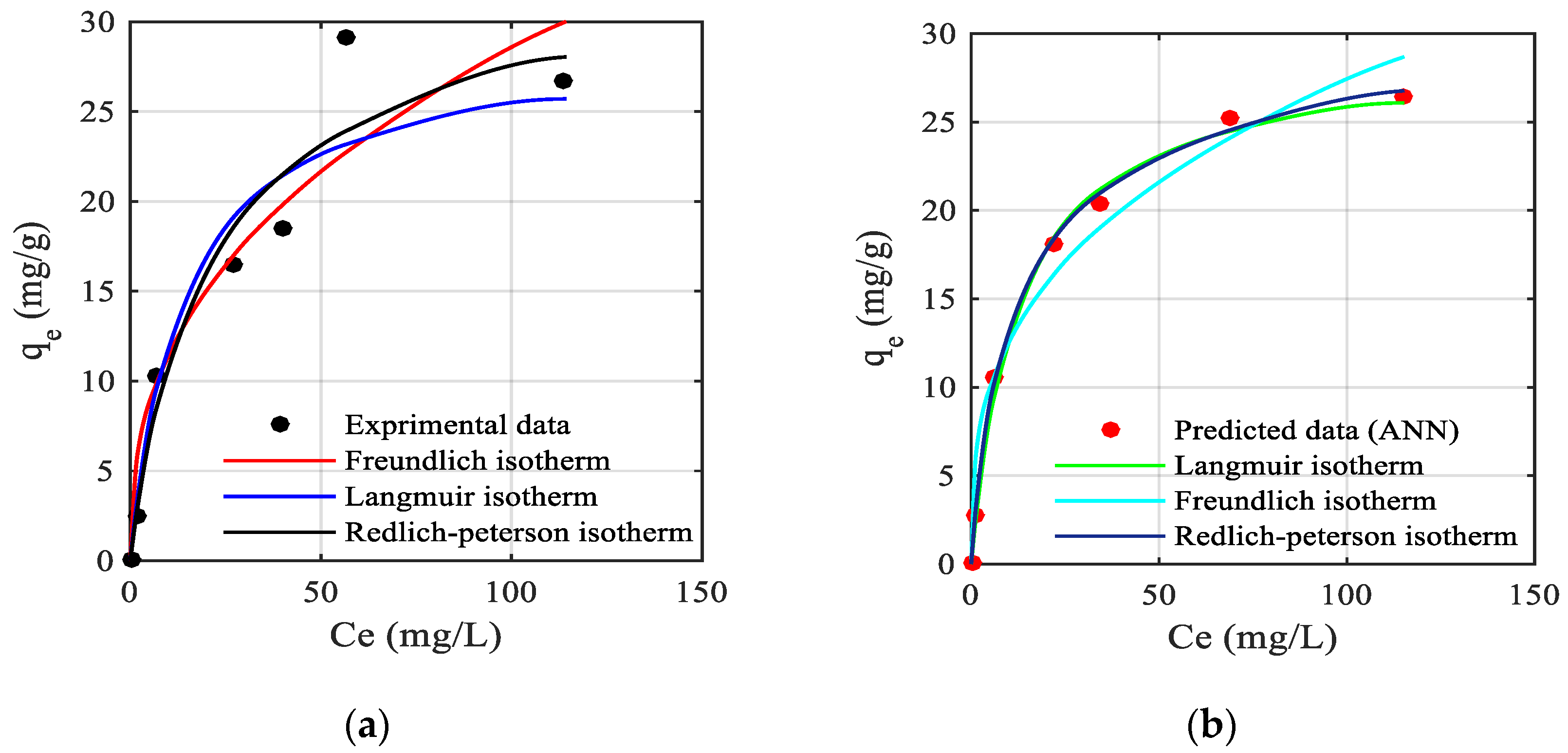
3.2. Mathematical Model Development
4. Discussion
4.1. ANN Validation
4.2. Isotherm Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, W.; Zheng, Y. Removal of lead, copper, nickel, cobalt, and zinc from water by a cancrinite-type zeolite synthesized from fly ash. Chem. Eng. J. 2009, 145, 483–488. [Google Scholar] [CrossRef]
- Wang, S.; Peng, Y. Natural zeolites as effective adsorbents in water and wastewater treatment. Chem. Eng. J. 2010, 156, 11–24. [Google Scholar] [CrossRef]
- Pauletto, P.; Dotto, G.; Salau, N. Diffusion mechanisms and effect of adsorbent geometry on heavy metal adsorption. Chem. Eng. Res. Des. 2020, 157, 182–194. [Google Scholar] [CrossRef]
- Mehdi, B.; Belkacemi, H.; Brahmi-Ingrachen, D.; Braham, L.; Muhr, L. Study of nickel adsorption on NaCl-modified natural zeolite using response surface methodology and kinetics modeling. Groundw. Sustain. Dev. 2022, 17, 100757. [Google Scholar] [CrossRef]
- Ahmad, R.; Mirza, A. Adsorptive removal of heavy metals and anionic dye from aqueous solution using novel Xanthan gum-Glutathione/ Zeolite bionanocomposite. Groundw. Sustain. Dev. 2018, 7, 305–312. [Google Scholar] [CrossRef]
- Saravanan, A.; Sundararaman, T.; Jeevanantham, S.; Karishma, S.; Kumar, P.; Yaashikaa, P. Effective adsorption of Cu(II) ions on sustainable adsorbent derived from mixed biomass (Aspergillus campestris and agro waste): Optimization, isotherm and kinetics study. Groundw. Sustain. Dev. 2020, 11, 100460. [Google Scholar] [CrossRef]
- Neag, E.; Török, A.; Tanaselia, C.; Aschilean, I.; Senila, M. Kinetics and equilibrium studies for the removal of Mn and Fe from binary metal solution systems using a Romanian thermally activated natural zeolite. Water 2020, 12, 1614. [Google Scholar] [CrossRef]
- Narayana, P.; Maurya, A.; Wang, X.; Harsha, M.; Srikanth, O.; Alnuaim, A.; Hatamleh, W.; Hatamleh, A.; Cho, K.; Paturi, U.; et al. Artificial neural networks modeling for lead removal from aqueous solutions using iron oxide nanocomposites from bio-waste mass. Environ. Res. 2021, 199, 111370. [Google Scholar] [CrossRef] [PubMed]
- Souza, P.; Dotto, G.; Salau, N. Artificial neural network (ANN) and adaptive neuro-fuzzy interference system (ANFIS) modelling for nickel adsorption onto agro-wastes and commercial activated carbon. J. Environ. Chem. Eng. 2018, 6, 7152–7160. [Google Scholar] [CrossRef]
- Lawal, A.; Idris, M. An artificial neural network-based mathematical model for the prediction of blast-induced ground vibrations. Int. J. Environ. Stud. 2020, 773, 18–334. [Google Scholar] [CrossRef]
- Ke, B.; Nguyen, H.; Bui, X.; Bui, H.; Nguyen-Thoi, T. Prediction of the sorption efficiency of heavy metal onto biochar using a robust combination of fuzzy C-means clustering and back-propagation neural network. J. Environ. Manage. 2021, 293, 112808. [Google Scholar] [CrossRef] [PubMed]
- Khandanlou, R.; Masoumi, H.F.; Ahmad, M.; Shameli, K.; Basri, M.; Kalantari, K. Enhancement of heavy metals sorption via nanocomposites of rice straw and Fe3O4 nanoparticles using artificial neural network (ANN). Ecol. Eng. 2016, 91, 249–256. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. Projecting the sorption capacity of heavy metal ions onto microplastics in global aquatic environments using artificial neural networks. J. Hazard. Mater. 2021, 402, 123709. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, S. Artificial Neural Network approach for modeling of Ni (II) adsorption from aqueous solution by peanut schell. Ecol. Chem. Eng. S 2018, 25, 581–604. [Google Scholar] [CrossRef]

| Input Data | Range | Output | ||
|---|---|---|---|---|
| Min | Max | Mean | Nickel removal (R %) | |
| Initial concentration (mg/L) | 10 | 150 | 80 | |
| Adsorbent dosage (mg/g) | 0.1 | 0.5 | 0.3 | |
| pH | 3 | 6 | 4.5 | |
| n 1 | Weights | Biases | ||||
|---|---|---|---|---|---|---|
| Ic 2 | Ad 3 | pH | R (%) | bnk | b0 | |
| n = 1 | 2.53 | 1.63 | 0.87 | 0.09 | −3.26 | −0.18 |
| n = 2 | 2.40 | 1.44 | −1.56 | −0.05 | −2.61 | |
| n = 3 | 1.73 | 1.06 | −2.48 | −0.79 | −2.03 | |
| n = 4 | 2.59 | 1.10 | −1.49 | 0.47 | −1.52 | |
| n = 5 | −0.17 | −2.19 | −2.29 | 0.65 | 0.89 | |
| n = 6 | 2.16 | −0.13 | 2.36 | −0.38 | −0.28 | |
| n = 7 | −0.89 | 2.17 | 2.41 | 0.72 | −0.33 | |
| n = 8 | −1.52 | −1.39 | −2.43 | −0.17 | −0.94 | |
| n = 9 | −0.01 | −3.05 | 0.98 | −0.50 | −1.43 | |
| n = 10 | −2.21 | −1.02 | −2.10 | 0.20 | −2.00 | |
| n = 11 | 2.51 | 2.01 | −0.56 | −0.78 | 2.54 | |
| n = 12 | −2.56 | −1.85 | 0.23 | −0.33 | −3.23 | |
| Isotherm Model | Isotherm Parameters | R2 | adjR2 | RMSE | ARE | ||
|---|---|---|---|---|---|---|---|
| Langmuir isotherm | Qm | K1 | 0.993 | 0.991 | 0.85 | 0.54 | |
| 28.92 (mg/g) | 0.08 (L/mg) | ||||||
| Freundlich isotherm | Kf | nf | 0.94 | 0.92 | 2.47 | 0.81 | |
| 5.74 | 2.95 | ||||||
| Redlich–Peterson isotherm | arp | krp | β | 0.996 | 0.993 | 0.74 | 0.50 |
| 0.15 | 3.05 | 0.91 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdi, B.; Brahmi-Ingrachen, D.; Belkacemi, H.; Muhr, L. Development of a Mathematical Model Based on an Artificial Neural Network (ANN) to Predict Nickel Uptake Data by a Natural Zeolite. Phys. Sci. Forum 2023, 6, 4. https://doi.org/10.3390/psf2023006004
Mehdi B, Brahmi-Ingrachen D, Belkacemi H, Muhr L. Development of a Mathematical Model Based on an Artificial Neural Network (ANN) to Predict Nickel Uptake Data by a Natural Zeolite. Physical Sciences Forum. 2023; 6(1):4. https://doi.org/10.3390/psf2023006004
Chicago/Turabian StyleMehdi, Boukhari, Daouia Brahmi-Ingrachen, Hayet Belkacemi, and Laurence Muhr. 2023. "Development of a Mathematical Model Based on an Artificial Neural Network (ANN) to Predict Nickel Uptake Data by a Natural Zeolite" Physical Sciences Forum 6, no. 1: 4. https://doi.org/10.3390/psf2023006004
APA StyleMehdi, B., Brahmi-Ingrachen, D., Belkacemi, H., & Muhr, L. (2023). Development of a Mathematical Model Based on an Artificial Neural Network (ANN) to Predict Nickel Uptake Data by a Natural Zeolite. Physical Sciences Forum, 6(1), 4. https://doi.org/10.3390/psf2023006004







