Abstract
This work deals with the deconfinement phase transition from a hadronic gas (HG) phase consisting of massive pions, to a quark–gluon plasma (QGP) phase consisting of gluons, massless up and down quarks and massive strange quarks, in addition to their antiquarks. Based on the Bag and coexistence models, we study the variations of pressure characterizing both HG and QGP phases. For the latter, we calculate the partition function of the color-singlet QGP within the projection method using a density of states containing the volume term only. We investigate the phase diagram of the strongly interacting matter, in the µ–T plane, in several cases: in the HG phase, we consider massless pions then we account for their masses, and in the QGP phase, first we take it consisting of two massless u and d quarks, then we consider additional massive strange quarks.
1. Introduction
Quantum chromodynamics (QCD) is the basic theory that describes the strong interactions between quarks and gluons in the hadrons [1]. QCD predicts the asymptotic freedom of short-range quarks (distances < 1 fm) inside the hadrons, in addition to the confinement property, which means that under ordinary conditions, quarks and gluons are confined to the hadrons. However, at high temperatures and/or density, hadronic matter undergoes a phase transition: quarks and gluons become deconfined, i.e., free [2], in a new phase called the quark–gluon plasma (QGP).The existence of this phase of matter was proposed in the mid-seventies, just ten years after the birth of the quark model of hadrons [3,4].
To illustrate the phase transition from the hadronic gas (HG) phase to the QGP phase, we will investigate the phase diagram of the strongly interacting matter, in the µ–T plane, based on the Gibbs criterion setting the mechanical equilibrium between the two phases at the transition, with massless and massive particles in the two phases.
2. Phase Diagram in the µ–T Plane
According to the Gibbs criterion, the HG and the QGP phases are in equilibrium when their pressures P, temperature T and chemical potential μ are equal, which reads:
Thus, we have to calculate the pressure of both phases, using the thermodynamic relation:
from the individual partition functions and of the two phases.
For the HG phase, we consider an ideal gas of pions (π+, π− and πo), which are the lightest bosons, and the obtained partition function reads:
where is the momentum, the pion degeneracy factor, the pion mass and .
The QGP being considered asan ideal gas of gluons, quarks and their antiquarks, and assuming non-interaction between its constituents, we can write ZQGP as:
where: , accounts for the real vacuum pressure B exerted on the perturbative vacuum, B being the bag constant. The calculation of and gives:
Setting the condition , with B1/4 = 200 MeV, we obtain the phase diagram in the plane shown in Figure 1, characterized by a critical line separating the HG and the QGP phases and giving at each point the transition parameters , in all the studied cases of massless and massive particles. When , the HG is favored, and when , the QGP is favored. There are two extreme cases: the first at μ = 0, obtainable in URHIC, and the second at T = 0, which could be reached in the core of certain neutron stars. It can also be noted by comparing the red dashed curve (with massless pions in the HG phase) and the solid blue curve (with massive pions), in Figure 1b, that there is a slight difference in at µ = 0, meaning that the pion mass has to be considered for accurate investigation of the transition temperature, while the small mass of u and d quarks can simply be neglected. Moreover, by examining the dashed-dotted magenta line, obtained by considering massive s quarks additionally to massless u and d quarks in the QGP phase, a clear mismatch appears compared to the two other curves, showing that the number of flavors considerably affects the transition parameters, and particularly the Tc value at µ = 0.
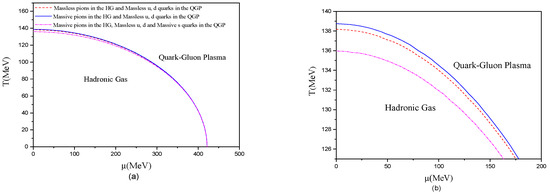
Figure 1.
(a) Phase diagram in the μ–T plane, with B1/4 = 200 MeV, for the three cases: (red dashed line) massless pions in the HG phase with massless u and d quarks in the QGP phase, (blue solid line) massive pions in the HG phase, with massless u and d quarks in the QGP phase, (magenta dashed-dotted line) massive pions in the HG and massive strange quarks additionally to massless u and d quarks in the QGP phase. (b) Magnification of the phase diagram in the region of high temperatures and low and intermediate chemical potentials for the same cases as in (a).
3. Phase Transition to a Color-Singlet QGP
To implement the color-singletness constraint into the quantum statistical description of the QGP, we use the group theoretical projection formulated by Turko and Redlich [5]. The projected partition function of a QGP on the color-singlet SU(3) representation, in a volume V, at temperature T and chemical potential reads:
, and result for massless u and d quarks, massive s quarks and massless gluons, respectively,
In the following, we study the variations of the pressures PHG and PQGP with temperatures T, at , for B1/4 =200 MeV, in different cases of massless and massive particles in both HG and QGP phases. Figure 2 shows the curve of the HG pressure, for massless pions (red dotted line) and massive pions (blue dotted line) as well as that of the QGP for massless u and d quarks only (dashed lines), then when adding the massive s quarks (solid lines), for a small and a large volume in both of the last cases.
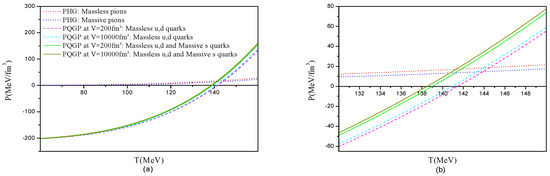
Figure 2.
(a) Variations of the pressure of the HG and a color-singlet QGP with temperature at μ = 0, for B1/4 =200 MeV, for massless and massive particles in both phases. (b) Magnification of the pressure curves at left (in (a)) in the region of high temperatures.
In Figure 2, we studied the effect of the particle masses for small and large volume of the QGP system on the deconfinement phase transition temperature at μ = 0, when considering the color-singletness requirement for the QGP phase, by the extraction of the value of from the intersection point of the curves . The obtained values of in the different studied cases are shown in Table 1, and we can easily see that as the volume increases, decreases until the volume reaches 10,000 fm3, where begins to stabilize. We can also notice that (massless particles) > (massive particles).

Table 1.
The critical temperature TC for different volumes, within a color-singlet QGP.
4. Conclusions
This work shows the influence of the mass of particles in both HG and QGP phases on the phase diagram in the μ–T plane, as we found that the (small) mass of the up and down quarks does not affect the study, while accounting for the mass of pions does affect the critical parameters and especially the critical temperatures at small µ. Moreover, considering massive strange quarks additionally to u and d quarks has a clear effect on the phase diagram. The same influence is also investigated when the color-singletness condition is considered for the QGP phase for different volumes of the system.
Author Contributions
Conceptualization, H.S. and A.A.E.D.; methodology, H.S. and A.A.E.D.; software, H.S.; validation, H.S. and A.A.E.D.; formal analysis, H.S.; investigation, H.S.; resources, H.S. and A.A.E.D.; data curation, H.S.; writing—original draft preparation, H.S.; writing—review and editing, A.A.E.D.; visualization, H.S.; supervision, A.A.E.D.; project administration, A.A.E.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is supported by the Algerian Ministry of Higher Education and Scientific Research.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akram, F. Basics of Quantum Chromodynamics. In Proceedings of the 5th School on LHC Physics, Islamabad, Pakistan, 15–26 August 2016; NCP: Islamabad, Pakistan, 2016. [Google Scholar]
- Ramadas, S. QGP in Quark Stars. Ph.D. Thesis, University of Calicut, Kerala, India, 2014. [Google Scholar]
- Pasechnik, R.; Šumbera, M. Phenomenological Review on Quark-Gluon Plasma: Concepts vs. Observations. Universe 2017, 3, 7. [Google Scholar] [CrossRef]
- Apolinário, L.; Milhano, J.G.; Salamand, G.P.; Salgado, C.A. Probing the Time Structure of the Quark-Gluon Plasma with Top Quarks. Phys. Rev. Lett. 2018, 120, 232301. [Google Scholar] [CrossRef] [PubMed]
- Redlich, K.; Turko, L. Quantum gases with internal symmetry. Phys. Lett. B 1981, 104, 153. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).