Nested Sampling of Materials’ Potential Energy Surfaces: Case Study of Zirconium †
Abstract
:1. Introduction
2. Nested Sampling Algorithm
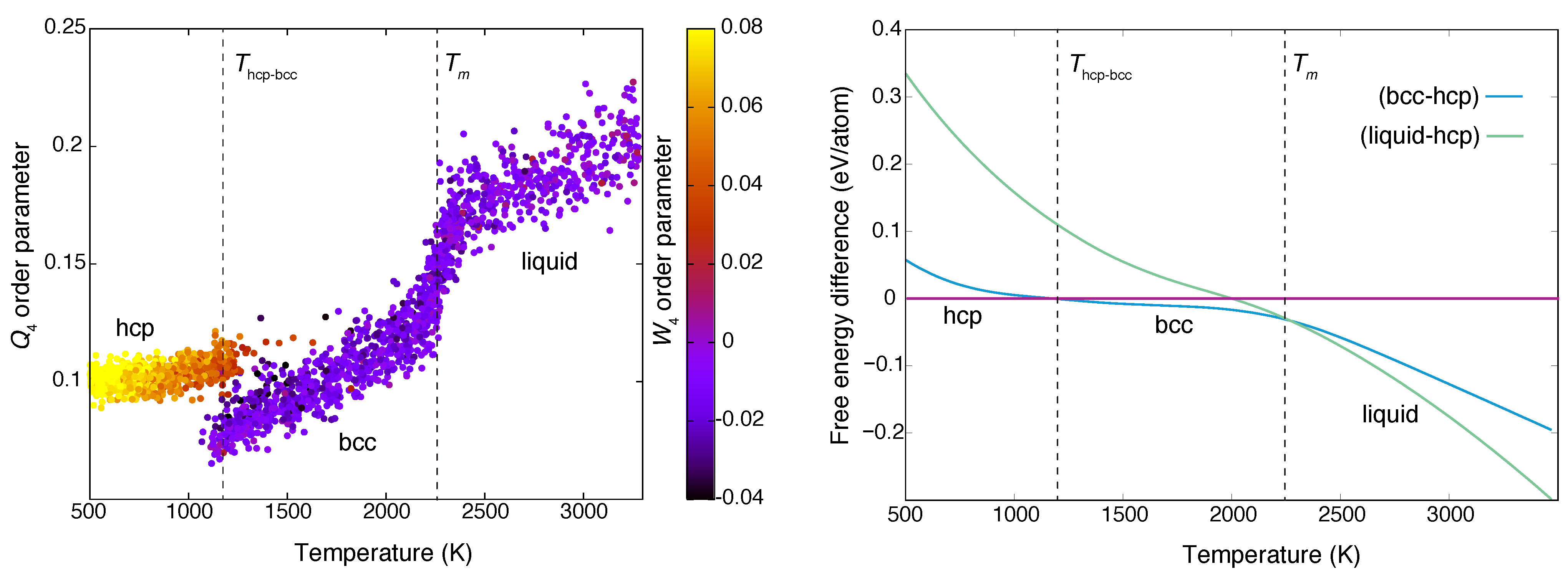
3. Calculating the Phase Diagram: Zirconium
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pickard, C.J.; Needs, R.J. High-Pressure Phases of Silane. Phys. Rev. Lett. 2006, 97, 045504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karabin, M.; Stuart, S.J. Simulated annealing with adaptive cooling rates. J. Chem. Phys. 2020, 153, 114103. [Google Scholar] [CrossRef] [PubMed]
- Rowe, P.; Deringer, V.L.; Gasparotto, P.; Csányi, G.; Michaelides, A. An accurate and transferable machine learning potential for carbon. J. Chem. Phys. 2020, 153, 034702. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Wales, D.J.; Miller, M.A. Thermodynamics and the Global Optimization of Lennard-Jones Clusters. J. Chem. Phys. 1998, 109, 8143–8153. [Google Scholar] [CrossRef] [Green Version]
- Finkler, J.A.; Goedecker, S. Funnel hopping Monte Carlo: An efficient method to overcome broken ergodicity. J. Chem. Phys. 2020, 152, 164106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirkpatrick, S.; Gelatt Jr, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Aqvist, J. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. 1990, 94, 8021–8024. [Google Scholar] [CrossRef]
- Panagiotopoulos, A. Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble. Mol. Phys. 1987, 61, 813–826. [Google Scholar] [CrossRef]
- Piaggi, P.M.; Parrinello, M. Calculation of phase diagrams in the multithermal-multibaric ensemble. J. Chem. Phys. 2019, 150, 244119. [Google Scholar] [CrossRef] [Green Version]
- Skilling, J. Bayesian inference and maximum entropy methods in science and engineering. AIP Conf. Proc. 2004, 735, 395. [Google Scholar]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 735, 833–859. [Google Scholar] [CrossRef]
- Ashton, G.; Bernstein, N.; Buchner, J.; Chen, X.; Csányi, G.; Feroz, F.; Fowlie, A.; Griffiths, M.; Habeck, M.; Handley, W.; et al. Nested Sampling for physical scientists. Nat. Rev. Methods Primer 2022, 2, 39. [Google Scholar] [CrossRef]
- Pártay, L.B.; Bartók, A.P.; Csányi, G. Efficient Sampling of Atomic Configurational Spaces. J. Phys. Chem B 2010, 114, 10502–10512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baldock, R.J.N.; Bernstein, N.; Salerno, K.M.; Pártay, L.B.; Csányi, G. Constant-pressure nested sampling with atomistic dynamics. Phys. Rev. E 2017, 96, 43311–43324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skilling, J. Bayesian computation in big spaces-nested sampling and Galilean Monte Carlo. AIP Conf. Proc. 2012, 1443, 145–156. [Google Scholar]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef] [Green Version]
- Dorrell, J.; Pártay, L.B. Thermodynamics and the potential energy landscape: Case study of small water clusters. Phys. Chem. Chem. Phys. 2019, 21, 7305–7312. [Google Scholar] [CrossRef]
- Dorrell, J.; Pártay, L.B. Pressure–Temperature Phase Diagram of Lithium, Predicted by Embedded Atom Model Potentials. J. Phys. Chem. B 2020, 124, 6015–6023. [Google Scholar] [CrossRef]
- Baldock, R.J.N.; Pártay, L.B.; Bartók, A.P.; Payne, M.C.; Csányi, G. Determining the pressure-temperature phase diagrams of materials. Phys. Rev. B 2016, 93, 174108. [Google Scholar] [CrossRef] [Green Version]
- Pártay, L.B. On the performance of interatomic potential models of iron: Comparison of the phase diagrams. Comput. Mater. Sci 2018, 149, 153–157. [Google Scholar] [CrossRef] [Green Version]
- Gola, A.; Pastewka, L. Embedded atom method potential for studying mechanical properties of binary Cu–Au alloys. Model. Simul. Mater. Sci. Eng 2018, 26, 055006. [Google Scholar] [CrossRef]
- Rosenbrock, C.W.; Gubaev, K.; Shapeev, A.V.; Pártay, L.B.; Bernstein, N.; Csànyi, G.; Hart, G.L.W. Machine-learned interatomic potentials for alloys and alloy phase diagrams. npj Comput. Mater. 2021, 7, 24. [Google Scholar] [CrossRef]
- Bartók, A.P.; Hantal, G.; Pártay, L.B. Insight into Liquid Polymorphism from the Complex Phase Behavior of a Simple Model. Phys. Rev. Lett. 2021, 127, 015701. [Google Scholar] [CrossRef] [PubMed]
- Pártay, L.B.; Ortner, C.; Bartók, A.P.; Pickard, C.J.; Csányi, G. Polytypism in the ground state structure of the Lennard-Jonesium. Phys. Chem. Chem. Phys. 2017, 19, 19369–19376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pártay, L.B.; Csányi, G.; Bernstein, N. Nested sampling for materials. Eur. Phys. J. B 2021, 94, 159. [Google Scholar] [CrossRef]
- Bernstein, N.; Baldock, R.J.N.; Pártay, L.B.; Kermode, J.R.; Daff, T.D.; Bartók, A.P.; Csányi, G. Pymatnest. 2016. Available online: https://github.com/libAtoms/pymatnest (accessed on 20 February 2022).
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhao, Y.; Pantea, C.; Qian, J.; Daemen, L.L.; Rigg, P.A.; Hixson, R.S.; Greeff, C.W.; Gray, G.T.; Yang, Y.; et al. Experimental constraints on the phase diagram of elemental zirconium. J. Phys. Chem. Solids 2005, 66, 1213–1219. [Google Scholar] [CrossRef]
- Pigott, J.S.; Velisavljevic, N.; Moss, E.K.; Draganic, N.; Jacobsen, M.K.; Meng, Y.; Hrubiak, R.; Sturtevant, B.T. Experimental melting curve of zirconium metal to 37 GPa. J. Phys. Condens. Matter 2020, 32, 355402. [Google Scholar] [CrossRef]
- Hao, Y.J.; Zhang, L.; Chen, X.R.; Cai, L.C.; Wu, Q.; Alfè, D. Ab initio calculations of the thermodynamics and phase diagram of zirconium. Phys. Rev. B 2008, 78, 134101. [Google Scholar] [CrossRef] [Green Version]
- Ackland, G.J.; Wooding, S.J.; Bacon, D.J. Defect, surface and displacement-threshold properties of alpha-zirconium simulated with a many-body potential. Philos. Mag. A 1995, 71, 553–565. [Google Scholar] [CrossRef]
- Mendelev, M.; Ackland, G. Development of an interatomic potential for the simulation of phase transformations in zirconium. Philos. Mag. Lett. 2007, 87, 349–359. [Google Scholar] [CrossRef]
- Skilling, J. Galilean and Hamiltonian Monte Carlo. Proceedings 2019, 33, 19. [Google Scholar] [CrossRef]
- Betancourt, M. Nested Sampling with Constrained Hamiltonian Monte Carlo. AIP Conf. Proc. 2011, 1305, 165. [Google Scholar]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond orientational ordel in liquids and glasses. Phys. Rev. B 1983, 28, 784. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchant, G.A.; Pártay , L.B. Nested Sampling of Materials’ Potential Energy Surfaces: Case Study of Zirconium. Phys. Sci. Forum 2022, 5, 5. https://doi.org/10.3390/psf2022005005
Marchant GA, Pártay LB. Nested Sampling of Materials’ Potential Energy Surfaces: Case Study of Zirconium. Physical Sciences Forum. 2022; 5(1):5. https://doi.org/10.3390/psf2022005005
Chicago/Turabian StyleMarchant, George A., and Livia B. Pártay . 2022. "Nested Sampling of Materials’ Potential Energy Surfaces: Case Study of Zirconium" Physical Sciences Forum 5, no. 1: 5. https://doi.org/10.3390/psf2022005005
APA StyleMarchant, G. A., & Pártay , L. B. (2022). Nested Sampling of Materials’ Potential Energy Surfaces: Case Study of Zirconium. Physical Sciences Forum, 5(1), 5. https://doi.org/10.3390/psf2022005005





