Comparing the Zeta Distributions with the Pareto Distributions from the Viewpoint of Information Theory and Information Geometry: Discrete versus Continuous Exponential Families of Power Laws †
Abstract
1. Introduction
2. Amari’s -Divergences and Sharma–Mittal Divergences
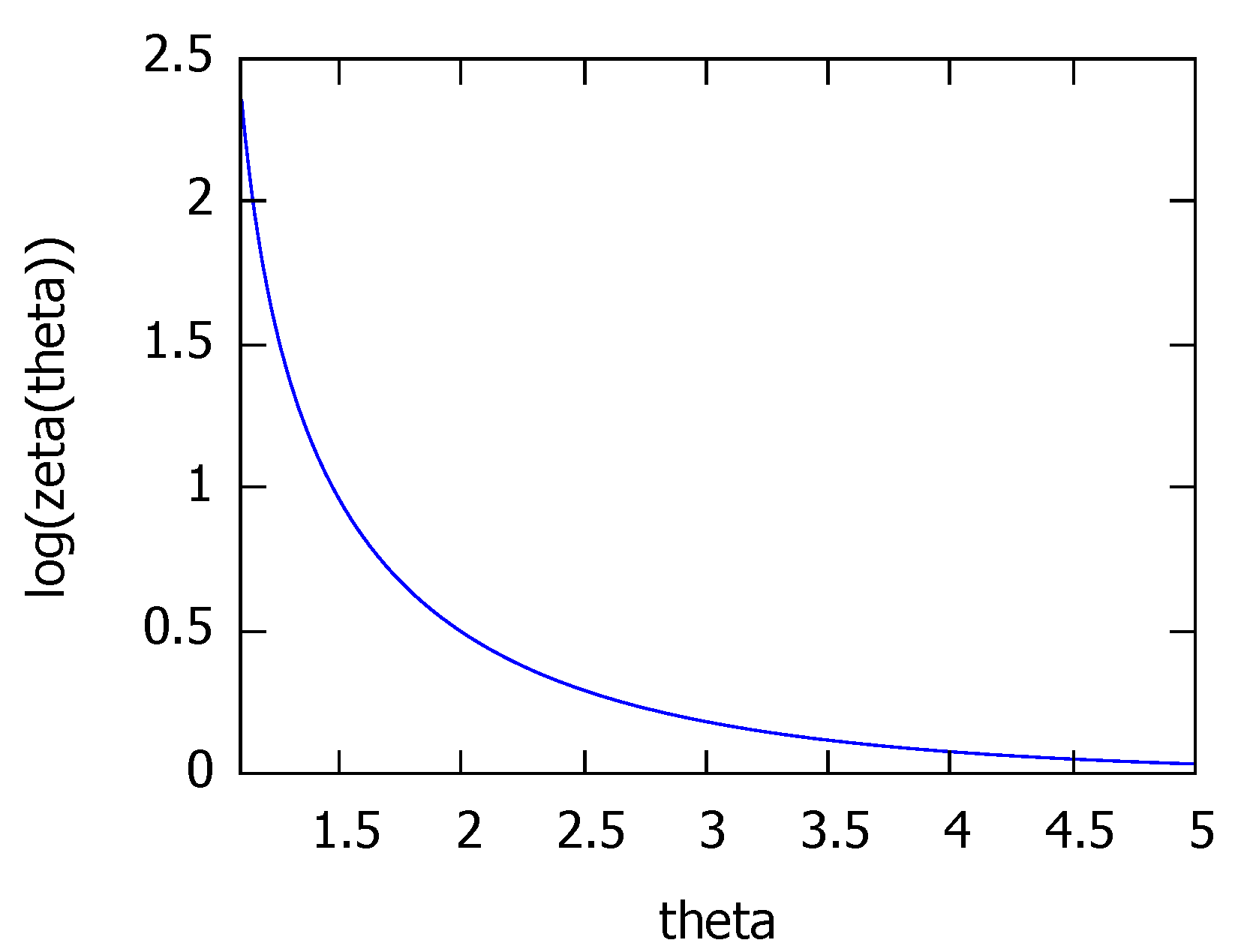
3. The Kullback–Leibler Divergence between Two Zeta Distributions
4. Comparison of the Zeta Family with a Pareto Subfamily
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kotz, S.; Balakrishnan, N.; Read, C.; Vidakovic, B. Encyclopedia of Statistical Sciences; Wiley: Hoboken, NJ, USA, 2005; Volume 15. [Google Scholar]
- Goldstein, M.L.; Morris, S.A.; Yen, G.G. Problems with fitting to the power-law distribution. Eur. Phys. J. Condens. Matter Complex Syst. 2004, 41, 255–258. [Google Scholar] [CrossRef]
- Titchmarsh, E.C.; Heath-Brown, D.R.; Titchmarsh, E.C.T. The Theory of the Riemann Zeta-Function; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121. [Google Scholar] [CrossRef] [PubMed]
- Iwaniec, H. Lectures on the Riemann Zeta Function; American Mathematical Society: Providence, RI, USA, 2014; Volume 62. [Google Scholar]
- Nielsen, F. A note on some information-theoretic divergences between Zeta distributions. arXiv 2021, arXiv:2104.10548. [Google Scholar]
- Barndorff-Nielsen, O. Information and Exponential Families in Statistical Theory; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Apéry, R. Irrationalité de ζ(2) et ζ(3). Astérisque 1979, 61, 1. [Google Scholar]
- Rivoal, T. La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs. C. R. de l’Académie des Sci.-Ser. I-Math. 2000, 331, 267–270. [Google Scholar] [CrossRef]
- Fischler, S.; Sprang, J.; Zudilin, W. Many odd zeta values are irrational. Compos. Math. 2019, 155, 938–952. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science; Addison-Wesley Professional: Boston, MA, USA, 1994. [Google Scholar]
- Hiary, G.A. Fast methods to compute the Riemann zeta function. Ann. Math. 2011, 174, 891–946. [Google Scholar] [CrossRef][Green Version]
- Johansson, F. Rigorous high-precision computation of the Hurwitz zeta function and its derivatives. Numer. Algorithms 2015, 69, 253–270. [Google Scholar] [CrossRef]
- Yildirim, C.Y. A Note on ζ′′(s) and ζ′′′(s). Proc. Am. Math. Soc. 1996, 124, 2311–2314. [Google Scholar] [CrossRef][Green Version]
- Powers, D.M. Applications and explanations of Zipf’s law. In New Methods in Language Processing and Computational Natural Language Learning; ACL anthology: Cambridge, MA, USA, 1998. [Google Scholar]
- Mandelbrot, B. Information Theory and Psycholinguistics: A Theory of Word Frequencies, Readings in Mathematical Social Sciences; MIT Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Lovričević, N.; Pečarić, D.; Pečarić, J. Zipf–Mandelbrot law, f-divergences and the Jensen-type interpolating inequalities. J. Inequalities Appl. 2018, 2018, 36. [Google Scholar] [CrossRef]
- Naldi, M. Approximation of the truncated Zeta distribution and Zipf’s law. arXiv 2015, arXiv:1511.01480. [Google Scholar]
- Hu, C.Y.; Iksanov, A.M.; Lin, G.D.; Zakusylo, O.K. The Hurwitz zeta distribution. Aust. N. Z. J. Stat. 2006, 48, 1–6. [Google Scholar] [CrossRef]
- Deluca, A.; Corral, Á. Fitting and goodness-of-fit test of non-truncated and truncated power-law distributions. Acta Geophys. 2013, 61, 1351–1394. [Google Scholar] [CrossRef]
- Nielsen, F. Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences. Entropy 2022, 24, 421. [Google Scholar] [CrossRef] [PubMed]
- Saito, S.; Tanaka, T. A note on infinite divisibility of zeta distributions. Appl. Math. Sci. 2012, 6, 1455–1461. [Google Scholar]
- Wang, T.; Zhang, W.; Maunder, R.G.; Hanzo, L. Near-capacity joint source and channel coding of symbol values from an infinite source set using Elias gamma error correction codes. IEEE Trans. Commun. 2013, 62, 280–292. [Google Scholar] [CrossRef][Green Version]
- Oosawa, T.; Matsuda, T. SQL injection attack detection method using the approximation function of zeta distribution. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014; pp. 819–824. [Google Scholar]
- Doray, L.G.; Luong, A. Quadratic distance estimators for the zeta family. Insur. Math. Econ. 1995, 16, 255–260. [Google Scholar] [CrossRef]
- Jung, H.; Phoa, F.K.H. A Mixture Model of Truncated Zeta Distributions with Applications to Scientific Collaboration Networks. Entropy 2021, 23, 502. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S.i. Families of alpha-beta-and gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Nielsen, F. An information-geometric characterization of Chernoff information. IEEE Signal Process. Lett. 2013, 20, 269–272. [Google Scholar] [CrossRef]
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci 1975, 10, 28–40. [Google Scholar]
- Nielsen, F.; Nock, R. A closed-form expression for the Sharma–Mittal entropy of exponential families. J. Phys. Math. Theor. 2011, 45, 032003. [Google Scholar] [CrossRef]
- Azoury, K.S.; Warmuth, M.K. Relative loss bounds for on-line density estimation with the exponential family of distributions. Mach. Learn. 2001, 43, 211–246. [Google Scholar] [CrossRef]
- Nielsen, F. On geodesic triangles with right angles in a dually flat space. In Progress in Information Geometry; Springer: Berlin/Heidelberg, Germany, 2021; pp. 153–190. [Google Scholar]
- Nielsen, F.; Nock, R. Entropies and cross-entropies of exponential families. In Proceedings of the 2010 IEEE International Conference on Image Processing, Washington, DC, USA, 11–12 November 2010; pp. 3621–3624. [Google Scholar]
- Walther, A. Anschauliches zur Riemannschen zetafunktion. Acta Math. 1926, 48, 393–400. [Google Scholar] [CrossRef]
- Kawalec, A. The inverse Riemann zeta function. arXiv 2021, arXiv:2106.06915. [Google Scholar]
- Weisstein, E.W. CRC Concise Encyclopedia of Mathematics; CRC press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Stopple, J. Notes on log(ζ(s))′′. Rocky Mt. J. Math. 2016, 46, 1701–1715. [Google Scholar]
- Agostini, D.; Améndola, C. Discrete Gaussian distributions via theta functions. SIAM J. Appl. Algebra Geom. 2019, 3, 1–30. [Google Scholar] [CrossRef]
- Nielsen, F. The Kullback–Leibler Divergence Between Lattice Gaussian Distributions. J. Indian Inst. Sci. 2022, 1–12. [Google Scholar] [CrossRef]
- Deconinck, B.; Heil, M.; Bobenko, A.; Van Hoeij, M.; Schmies, M. Computing Riemann theta functions. Math. Comput. 2004, 73, 1417–1442. [Google Scholar] [CrossRef]
| Zeta Distribution | Pareto Distribution | |
|---|---|---|
| Univariate Uni-Order Exponential Family | ||
| Discrete EF | Continuous EF | |
| PMF/PDF | ||
| Support | ||
| Natural parameter | s | s |
| Cumulant | ||
| Sufficient statistic | ||
| Moment parameter | ||
| Conjugate | ||
| Maximum likelihood estimator | ||
| Fisher information | ||
| Entropy | ||
| Bhattacharyya coefficient | ||
| Kullback-Leibler divergence | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F. Comparing the Zeta Distributions with the Pareto Distributions from the Viewpoint of Information Theory and Information Geometry: Discrete versus Continuous Exponential Families of Power Laws. Phys. Sci. Forum 2022, 5, 2. https://doi.org/10.3390/psf2022005002
Nielsen F. Comparing the Zeta Distributions with the Pareto Distributions from the Viewpoint of Information Theory and Information Geometry: Discrete versus Continuous Exponential Families of Power Laws. Physical Sciences Forum. 2022; 5(1):2. https://doi.org/10.3390/psf2022005002
Chicago/Turabian StyleNielsen, Frank. 2022. "Comparing the Zeta Distributions with the Pareto Distributions from the Viewpoint of Information Theory and Information Geometry: Discrete versus Continuous Exponential Families of Power Laws" Physical Sciences Forum 5, no. 1: 2. https://doi.org/10.3390/psf2022005002
APA StyleNielsen, F. (2022). Comparing the Zeta Distributions with the Pareto Distributions from the Viewpoint of Information Theory and Information Geometry: Discrete versus Continuous Exponential Families of Power Laws. Physical Sciences Forum, 5(1), 2. https://doi.org/10.3390/psf2022005002






