Full-Field Experimental Study and Numerical Modeling of Soft Polyurethane Foam Subjected to Cyclic Loading †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Specimens
2.2. Cyclic Compression Test
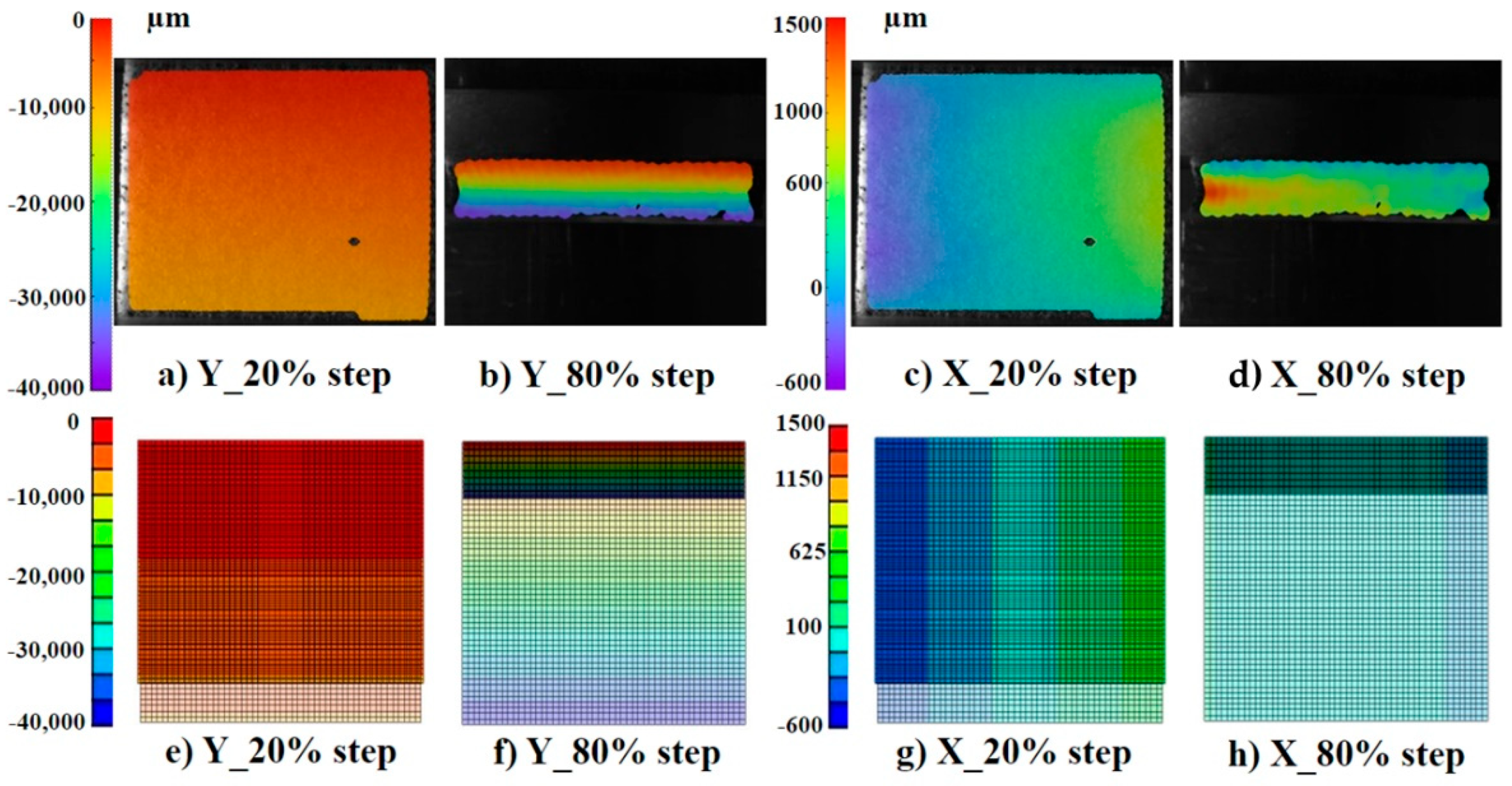
2.3. DIC Set-Up and Measurements
2.4. Numerical Modelling
3. Results
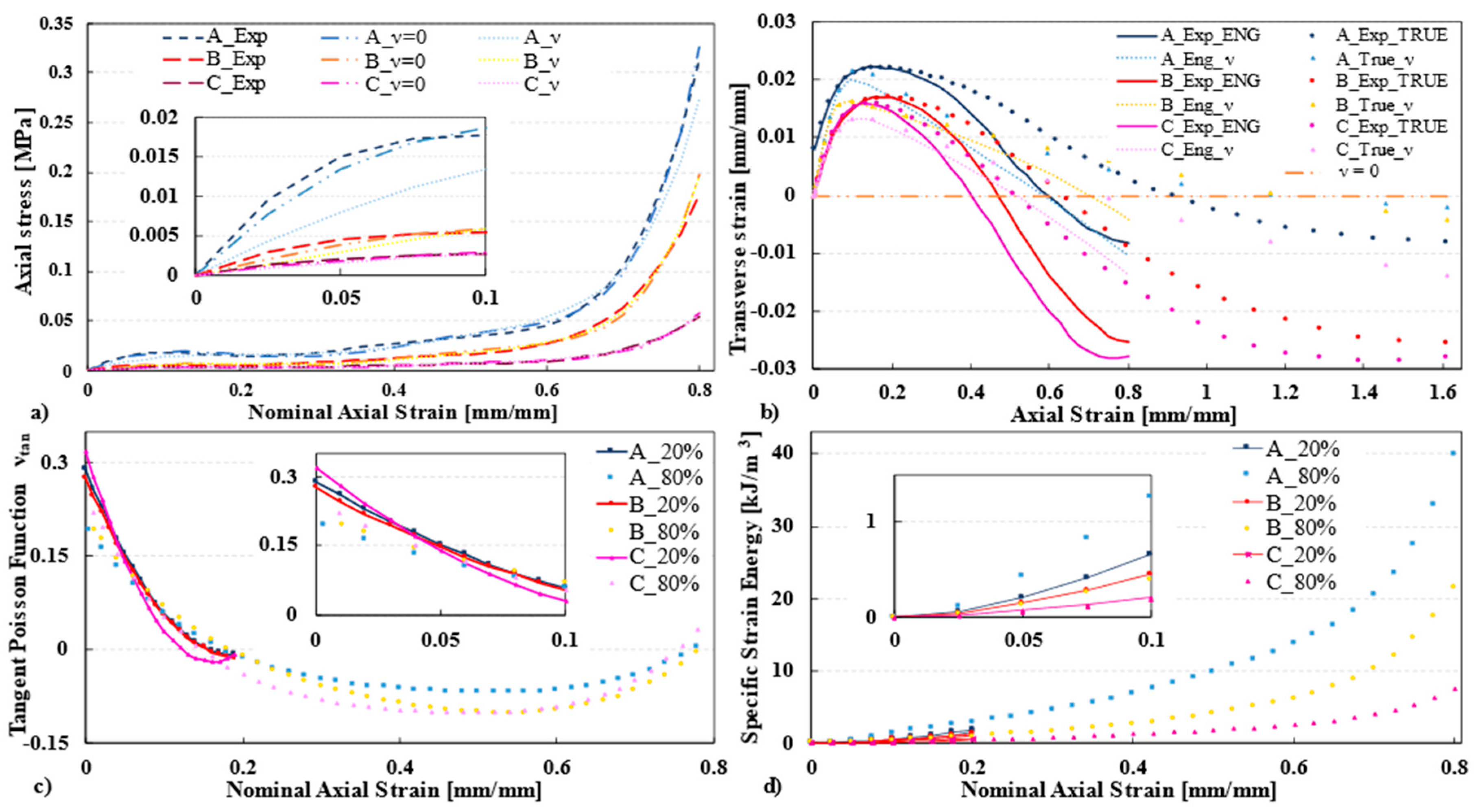
3.1. Natural Pattern Preliminary Evaluation and Measurements
3.2. Cyclic Compression Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Marsavina, L.; Constantinescu, D.; Linul, E.; Voiconi, T.; Apostol, D.; Sadowski, T. Damage identification and influence on mechanical properties of closed cell rigid foams. In Proceedings of the 13th International Conference on Fracture (ICF 2013), Beijing, China, 16–21 June 2013; Volume 4. [Google Scholar]
- Koohbor, B.; Mallon, S.; Kidane, A.; Lu, W.-Y. The deformation and failure response of closed-cell PMDI foams subjected to dynamic impact loading. Polym. Test. 2015, 44, 112–124. [Google Scholar] [CrossRef]
- Duncan, O.; Clegg, F.; Essa, A.; Bell, A.M.T.; Foster, L.; Allen, T.; Alderson, A. Effects of heat exposure and volumetric compression on Poisson’s ratios, young’s moduli, and polymeric composition during thermo-mechanical conversion of auxetic open cell polyurethane foam. Phys. Status Solidi 2018, 256, 1800393. [Google Scholar] [CrossRef]
- Guo, B.; Pierron, F.; Rotinat, R. Identification of low density polyurethane foam properties by DIC and the virtual fields method. In Proceedings of the International Conference on Experimental Mechanics 2008, Nanjing, China, 8–11 November 2008; p. 737554. [Google Scholar] [CrossRef]
- Casavola, C.; Del Core, L.; Moramarco, V.; Pappalettera, G.; Patronelli, M. Experimental and numerical analysis of the Poisson’s ratio on soft polyurethane foams under tensile and cyclic compression load. Mech. Adv. Mater. Struct. 2021; in press. [Google Scholar] [CrossRef]
- Casavola, C.; Del Core, L.; Moramarco, V.; Pappalettera, G.; Patronelli, M. Full-field mechanical characterization of polyurethane foams under large deformations by digital image correlation. Mech. Adv. Mater. Struct. 2021. [Google Scholar] [CrossRef]
- UNI EN ISO 3386-2:1997/Amd.1:2010; Flexible cellular polymeric materials-Determination of stress-strain Characteristics in compression. ISO: Geneva, Switzerland, 2010.
- Barile, C.; Casavola, C.; Pappalettera, G. Digital image correlation comparison of damaged and undamaged aeronautical cfrps during compression tests. Materials 2019, 12, 249. [Google Scholar] [CrossRef]
- Pan, B.; Dafang, W.; Yong, X. Incremental calculation for large deformation measurement using reliability-guided digital image correlation. Opt. Lasers Eng. 2012, 50, 586–592. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Widdle, R.; Bajaj, A.; Davies, P. Measurement of the Poisson’s ratio of flexible polyurethane foam and its influence on a uniaxial compression model. Int. J. Eng. Sci. 2008, 46, 31–49. [Google Scholar] [CrossRef]
- Smith, C.W.; Wootton, R.J.; Evans, K.E. Interpretation of experimental data for Poisson’s ratio of highly nonlinear materials. Exp. Mech. 1999, 39, 356–362. [Google Scholar] [CrossRef]
- Koumlis, S.; Lamberson, L. Strain rate dependent compressive response of open cell polyurethane foam. Exp. Mech. 2019, 59, 1087–1103. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual; Version 6.9; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2009. [Google Scholar]
- Ogden, R.W. Large deformation isotropic elasticity: On the correlation of theory and experiment for compressible rubberlike solids. Proc. R. Soc. Lond. A 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Belda, R.; Megías, R.; Feito, N.; Vercher-Martínez, A.; Giner, E. Some practical considerations for compression failure characterization of open-cell polyurethane foams using digital image correlation. Sensors 2020, 20, 4141. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.-Y.; Li, R.-L.; Zhao, H.-W.; Cheng, T.-H.; Cui, G.-J.; Tan, Q.-C.; Meng, G.-W. Quality assessment of speckle patterns for digital image correlation by Shannon entropy. Optik 2015, 126, 4206–4211. [Google Scholar] [CrossRef]
- Jones, E.M.C.; Iadicola, M.A. A Good Practices Guide for Digital Image Correlation; International Digital Image Correlation Society: Portland, OR, USA, 2018. [Google Scholar]


| Designation | Type A | Type B | Type C |
|---|---|---|---|
| Foam type | Flexible polyurethane foam | ||
| Cells type | open | ||
| Density [kg/m3] | 76 ÷ 94 | 60 ÷ 65 | 43 ÷ 49 |
| Cell size [mm] | 0.145 ± 0.018 | 0.210 ± 0.076 | 0.315 ± 0.064 |
| Cell wall size [mm] | 0.044 ± 0.008 | 0.043 ± 0.006 | 0.041 ± 0.011 |
| Void ratio % | 35 ± 0.024 | 53 ± 0.113 | 53 ± 0.113 |
| Type A | Type B | Type C | Generic | |
|---|---|---|---|---|
| SE | 7.07 | 7.21 | 7.18 | 6.22 |
| B/W ratio | 58.6% | 59.8% | 63.6% | 19.1% |
| Specimen | σpl 20% [kPa] | E5% 20% [kPa] | Epl 20% [kPa] | σpl 80% [kPa] | E5% 80% [kPa] | Epl 80% [kPa] |
|---|---|---|---|---|---|---|
| Type A | 10.3 | 159.5 | 23.7 | 7 | 110.7 | 24.1 |
| Type B | 7.2 | 125.7 | 14.3 | 4.4 | 87 | 16.4 |
| Type C | 3.4 | 73.7 | 6 | 2.3 | 38.7 | 5.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casavola, C.; Del Core, L.; Moramarco, V.; Pappalettera, G.; Patronelli, M. Full-Field Experimental Study and Numerical Modeling of Soft Polyurethane Foam Subjected to Cyclic Loading. Phys. Sci. Forum 2022, 4, 20. https://doi.org/10.3390/psf2022004020
Casavola C, Del Core L, Moramarco V, Pappalettera G, Patronelli M. Full-Field Experimental Study and Numerical Modeling of Soft Polyurethane Foam Subjected to Cyclic Loading. Physical Sciences Forum. 2022; 4(1):20. https://doi.org/10.3390/psf2022004020
Chicago/Turabian StyleCasavola, Caterina, Lucia Del Core, Vincenzo Moramarco, Giovanni Pappalettera, and Marika Patronelli. 2022. "Full-Field Experimental Study and Numerical Modeling of Soft Polyurethane Foam Subjected to Cyclic Loading" Physical Sciences Forum 4, no. 1: 20. https://doi.org/10.3390/psf2022004020
APA StyleCasavola, C., Del Core, L., Moramarco, V., Pappalettera, G., & Patronelli, M. (2022). Full-Field Experimental Study and Numerical Modeling of Soft Polyurethane Foam Subjected to Cyclic Loading. Physical Sciences Forum, 4(1), 20. https://doi.org/10.3390/psf2022004020







