Abstract
An experimental and numerical study on three flat specimen geometries for characterization of the dynamic shear behavior of metals with the use of the compression Split Hopkinson Pressure Bar (SHPB) technique is presented in the paper. The aim of the work is to determine for which specimen shape the most equilibrium state of stress is achieved, and the stress state in the shear zone is closest to simple shear during dynamic deformation. The high strain rate tests were performed on a Ti-6Al-4V titanium alloy, which was deformed with shear strain rate from 9200 to 12,700 s−1. The obtained results indicate that the specimen geometry marked as D2S (double-shear version 2 specimen) with double shear zones guarantees high quality of the obtained experimental data.
1. Introduction
Shear stress states dominate in many technical applications. Some examples of these are sheet metal forming, high-speed machining, and ballistic impact. These processes are often associated with very high strain rates, which can even reach the level of 107 s−1 [1]. In order to understand better material behavior at such complex and extreme loading condition, or to properly select material for a given application, or to conduct correct numerical simulations, it is necessary to determine the shear stress–strain response in a wide range of strain rates. Over the past decades, several techniques have been developed to study the dynamic shear behavior of engineering materials; however, the split-Hopkinson pressure bar is the most widely used experiment [2]. The specific nature of SHPB tests, however, imposes limitations that result from the selection of the appropriate specimen geometry and the method of fixing the specimen. Many different design solutions of the SHPB system and various specimen geometries have been proposed for dynamic simple shear testing. A detailed review on the SHPB experiments includes the torsion specimens, hat shape specimens, double shear specimens, or shear-compression specimens as presented in [1,2,3]. However, despite the large variety of shear sample geometries, new solutions are still proposed to improve the accuracy of material data describing dynamic shear behavior. In general, two groups of shear specimens are distinguished, i.e., specimens intended for metallographic tests of the shear zone and specimens with well-defined dimensions of the shear zone [4]. The specimen used in this study belongs to the second group, and the shape and dimensions of the specimen used are the result of experience gained during tests with the use of different shear specimen geometries found in the literature.
In the present work, three specimen geometries are considered, which slightly differ from the shape of the shear specimens presented in the literature, and which are adapted to making them from metal sheet. The goal is to figure out for which specimen shape, the desired equilibrium stress state within specimen is achieved, and the stress state in the shear zone is closest to simple shear during the SHPB tests.
The paper is organized as follows: Section 2 is devoted to the description of the considered specimen geometries, specimens’ preparation, and the SHPB system used in the work. The results of the performed dynamic tests and consideration on equilibrium stress state and obtained shear stress–strain curves for the Ti-6Al-4V alloy are presented in Section 3, whereas the numerical study on the stress state evolution in the shear zone during dynamic deformation is described in Section 4. The main conclusions of the present work are summarized in Section 5.
2. Methodology
2.1. Specimen Geometries and Specimen Preparation
The experimental and numerical investigations presented in the work was performed with the use of three planar (flat) specimens with single or double shear zones, the dimensions of which are well-defined by the following parameters: width w, height h, and thickness t (Figure 1).
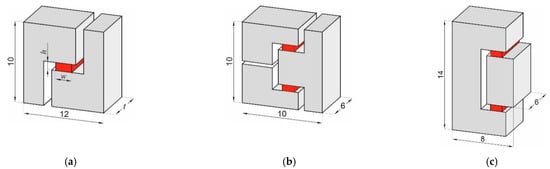
Figure 1.
Considered geometries of flat samples for simple shear tests: (a) SSS specimen; (b) DSS specimen; (c) D2S specimen.
The thickness of shear zone corresponds to the thickness of the sheet from which the specimens were cut away. The nominal dimensions of the shear zones of the specimens used in the tests are 1.5 × 0.7 × 6 mm, respectively. All specimens were made of the commercial Ti-6Al-4V alloy with the use of the wire electro discharge machining technology (WEDM). Particular attention was paid to the geometric correctness of the shear zone. For this purpose, a series of technological tests were carried out, as a result of which the WEDM cutting process parameters were selected, guaranteeing high cutting quality. Shear samples were made using a brass wire with a diameter of 0.15 mm. Figure 2 shows the general view of the specimen and the shear zone during the dimensional inspection performed with the vision measuring machine Baty Venture XT (Bowers Group, Burgess Hill, UK). The dimensional measurements confirmed the high accuracy of the specimens, i.e., the shear zones have well-defined dimensions and a regular cuboid-like shape. To reduce the stress concentration at the corners of the shear zone, the undercuts were rounded with a radius of 0.15 mm.

Figure 2.
Quality of sample cutting using the WEDM technology: (a) General view of SSS specimen; (b) dimensional control of shear zone of SS specimen; (c) dimensional control of shear zones of D2S specimen.
2.2. Experimental Procedure of Shear Testing
The high strain-rate shear tests were carried out with the use of the SHPB setup, the design solution of which is based on a typical design of the compression SHPB test (Figure 3a). The SHPB stand consists of striker bar, input, and output bars, between which shear specimen is placed (Figure 3b). All bars of the SHPB device are made of maraging steel (heat-treated MS350 grade: yield strength—2300 MPa; elastic wave speed—4960 m/s) with dimension of 12 mm. The lengths of striker bar and input bar, as well as output bar were 250 and 1200 mm, respectively.

Figure 3.
Scheme of the SHSB setup used in investigations (a); view of the D2S specimen placed between the SHPB bars (b).
The striker bar is driven by a compressed air system with a barrel length of 1200 mm and inner diameter of 12.1 mm. The impact striker bar velocities applied during the experiments were in the range of 12.2 to 12.6 m/s that ensures strain rates of 9200 to 12,700 s−1, depending on the geometry of the specimen used.
Dynamic shear curves were plotted using well-known formulas presented in the literature [5], according to the classical Kolsky theory [6,7] based on the use of the one-wave analysis method, which assume stress equilibrium for specimen under given testing conditions. The shear strain and the shear strain rate in the specimens were calculated based on the reflected wave profile (ɛr), whereas the shear stress in the specimen was determined from transmitted wave profile (ɛt). Wave signals were measured by pairs of strain gages (gauge length—1.5 mm; resistance—350 Ohm) glued at the half-length of the input and output bars (Figure 3). The signals from the strain gauges were conditioned by data-acquisition system including a Wheatstone bridge, an amplifier allowing a high cut-off frequency of 1 MHz and a digital oscilloscope.
Moreover, the SHPB stand is equipped with an optoelectronic measuring system for the impact velocity of the striker bar and a high-speed Phantom v1612 camera (Vision Research, Inc., Wayne, NJ, USA) for recording the process of dynamic shear deformation. The parameters of optical recording with the above-mentioned camera were as follows: optical resolution of the observation field—256 × 256 or 256 × 304 pixels; time interval—7.69 or 8.67 μs (frame rate—130,000 or 115,000 fps) for the SSS and D2S specimens, respectively. The exposure time of optical recording was the same in all experiments and was 2.5 μs. Based on high-speed camera records, values of shear strain at fracture were determined by measuring the shear angle of shear zones just before the occurrence of fracture, i.e., damages are initiated (Figure 4). The value of the maximum shear strain was then calculated based on the arithmetic average of measurements of the shear angles.

Figure 4.
Scheme of maximum shear angles measurement; (a) SSS specimen; (b) D2S specimen (θ1, θ2, θ3, θ4—max. shear angles).
To minimize the wave dispersion and to facilitate stress equilibrium, the pulse shapers, also called “wave shapers” were used [8]. The shapers had a shape of a disc made of soft materials and they were placed on the impact end of the input bar. Trials were made to find the appropriate size of the pulse shaper. It was found that for a given SHPB test condition, the copper pulse shaper with a diameter of 3 mm and the thickness of 0.2 mm guarantees damping high frequency oscillations.
3. Experimental Results
The history of the shearing process for all considered specimen geometries in the SHPB test conditions is shown in Figure 5. It is observed that during deformation, shear zones hardly do not rotate around the axis perpendicular to the direction of the load force. An exception is the SSS specimen (Figure 5a), in which a slight bending of the “support elements” adjacent to the shear zone was found. This deflection in turn causes the shear zone to turn slightly by an angle of less than 0.5°. The bending of the support elements was also observed in the specimens with the double shear zone. However, for these specimen geometries, the bending effect seems to be slightly smaller for the DSS geometry or not noticeable as in the D2S specimen (Figure 5c).


Figure 5.
The deformation process of the tested shear specimens captured by high-speed camera: (a) SSS specimen; (b) DSS specimen; (c) D2S specimen (arrows indicate where the cracks appear).
The data presented in Table 1 indicate that the specimen bending effect has some impact on values of shear strain at fracture. The highest shear strain at fracture (0.43) was found out for the D2S specimen, whereas the smallest one (0.35) for DSS specimen. It is believed that the observed differences in the values of shear strain result not only from the bending effect of the support elements, but also from the accuracy and repeatability of the shear zone cutting (e.g., rounding accuracy).

Table 1.
Values of shear strain at fracture depending on the specimen geometry.
In turn, Figure 6 shows the results of the equilibrium stress analysis in shear zones for the tested geometries of specimen. Representative curves of τin and τout describing stress changes acting on the end faces of the specimen are shown in Figure 6b–d, which were calculated based on the strain wave signals, an examples of which is shown in Figure 6a. It is seen from Figure 6 that equilibrium stress state in specimens with the SSS or DSS geometry is not satisfactory, i.e., the τin and τout curves do not match well and are distorted by oscillations. It is especially visible in the case of the geometry of the SSS sample. In contrast, the curves shown in Figure 6d prove that the specimen with the D2S geometry best meets the methodological requirement of the SHPB technique, because the stress state in this specimen, except for slight deviations, is almost in equilibrium for the entire duration of the load.
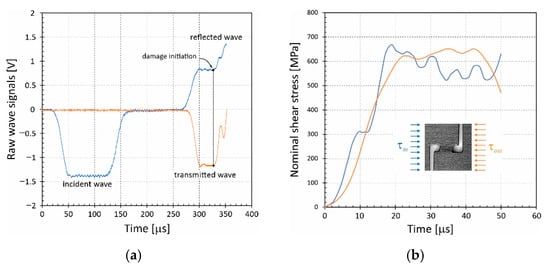
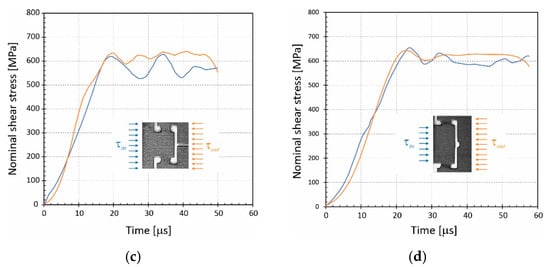
Figure 6.
(a) Typical raw wave signals of D2S specimen recorded by the SHPB technique, equilibrium stress state at specimens: (b) SSS; (c) DSS; (d) D2S.
To check the influence of specimen geometry on profile of shear stress–strain curve, three tests were performed under the same conditions. The resulting nominal τ—γ curves are shown in Figure 7. It is generally observed that the three curves obtained from the given specimen geometry match each other well. Apart from the SSS specimen (Figure 7a), for which the largest discrepancies in the curve profiles were noted, the other specimen geometries, as well as the SHPB device used guarantee good repeatability and reliability. Furthermore, shear curves profiles obtained from SSS and DSS specimens are distorted by irregular deviations, which in the case of the DSS specimen (Figure 7b) take the form of damped oscillations. At the present stage of research, it is difficult to assess whether these oscillations are the result of bending support elements of the specimen and/or the Pochhammer–Chree dispersion effect. On the other hand, the shear curves of the D2S specimens shown in Figure 7c are characterized by smooth profiles, devoid of clear oscillations.
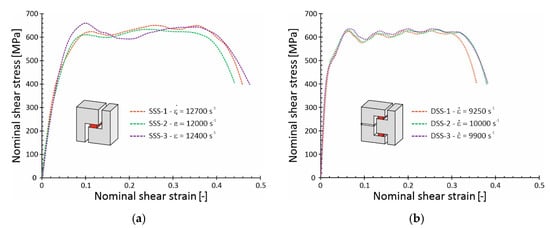
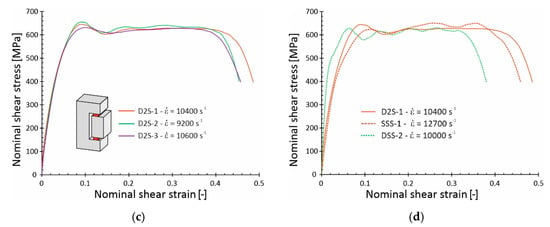
Figure 7.
Nominal shear stress–strain curves for the Ti-6Al-4V alloy obtained from various specimen geometries: (a) SSS specimen; (b) DSS specimen; (c) D2S specimen; (d) curves comparison.
At this point it should be noted that the slope of the shear curves corresponding to the range of elastic deformations differ slightly depending on the geometry of the sample (Figure 7d). It is well-known that the slope of the shear curve for the elastic strain range depends primarily on the shear modulus (Kirchhoff’s modulus—G), but for the SHPB experiments it is also a function of many other factors, such as the stiffness of the specimen. Figure 7d shows that the SSS and D2S specimens are characterized by the similar stiffness, while the DSS specimen seems more stiff (greater slope angle with respect to the abscissa).
Based on the obtained shear stress–strain curves for the Ti-6Al-4V alloy, the averaged level of plastic stress is almost the same for all tested specimen geometries, i.e., 630 MPa under nominal shear strain rates ranging from 9200 to 12,700 s−1. The obtained shear stress value corresponds well with the data presented in the literature [2,9].
4. Numerical Modelling and Discussion
Based on the experimental results, which revealed that the shear specimen with D2S geometry allows to obtain high-quality data, it was decided that numerical analyses of the shear stress state in the shear zone would be performed only for the D2S specimen.
4.1. Model Description
Numerical simulations of dynamic shear tests have been performed using software Ansys Workbench/Explicit. A 3D full size finite element (FE) model consisting of the bars system, i.e., striker, input, output bars, and the D2S specimen was developed (Figure 8). The mesh details of the FE model are also shown in Figure 8. The discretization of the geometry of the bar system and the specimen was carried out with the use of first-order tetrahedral elements of the Solid 185 type. In the case of the D2S specimen, mesh elements have different dimensions depending on where they are positioned. The minimum element size is 0.1 mm in the specimen shear zone. The numbers of elements are 7780 and 227,304 for the SHPB bars and the D2S specimen, respectively. The material parameters used in the FE model are shown in Table 2. The SHPB bars are defined as elastic. For the D2S specimen material, the constitutive Johnson–Cook (J-C) model was used. Values of material parameters of the J-C model were taken from the literature [10]. The single failure criterion was implemented to predict the failure onset occurred at the high strain rate experiments. Based on the results of dynamic tests, the maximum shear strain of 0.4 was assumed. Validity of developed numerical model was verified by comparison of experimental and numerical stress wave signals. The stress wave profiles were found to be similar, except that the experimental wave stress profiles have more irregular oscillations.
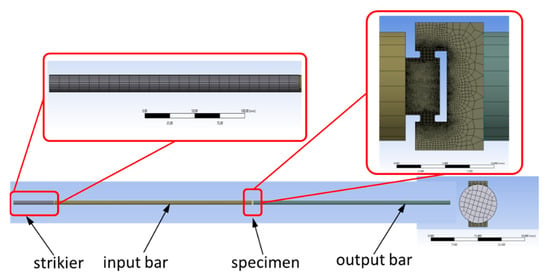
Figure 8.
Finite element model of The SHPB system with the D2S specimen.

Table 2.
Material parameters used in numerical modelling.
4.2. Stress State in Specimen Shear Zone
To assess a simple shear stress state in the specimen shear zone throughout the deformation process, stress triaxiality η and Lode angle parameter θ were calculated. For pure shear, these parameters take the value 0. The evolution of stress state represented by η and θ for the entire specimen shear zone as a function of nominal shear strain is shown in Figure 9.
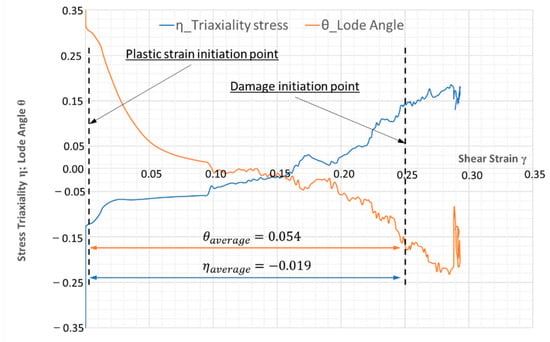
Figure 9.
Evolution of average stress triaxiality η, Lode angle parameter θ of the whole shear zone as a function of nominal shear strain.
The value of η increases continuously from −0.121 to 0.141, indicating that the stress state changes from shear-compression to shear-tension.
The average value of η calculated for shear strain range shown in Figure 9 is −0.019. On the other hand, changes in the value of θ have an opposite trend, i.e., it drops sharply from 0.303 to almost 0 at strain γ = 0.1, then deviates around 0, and next becomes negative and declines to −0.163 at damage initiation point. The mean value of θ is 0.054. Thus, the analysis of the stress state in the specimen shear zone proves that the specimen shear zone is dominated by simple shear, because values of η and θ are very close to zero.
5. Conclusions
The tested specimen geometries are designed to be simple and are easy to manufacture by conventional WDEM technology. Lack of any clamping specimen system does not induce waves disturbance and allows to obtain good accuracy of the calculated load and deformation. However, among all the tested specimens, the D2S specimen guarantees the best quality of obtained experimental data, i.e., smooth profile of reflected and transmitted waves and a good force equilibrium state. Moreover, the results of numerical analysis indicate that in the shear zone of the D2S specimen during dynamic deformation, a simple shear stress state dominates, i.e., the values of the stress triaxiality η and the Lode angle parameter θ fluctuates around zero.
Author Contributions
Conceptualization, J.J., K.C. and M.G.; methodology, J.J. and M.G.; formal analysis, J.J.; investigation, J.J., K.C., M.G. and Ł.K.; resources, K.C. and Ł.K.; data curation, J.J. and Ł.K.; writing—original draft preparation, J.J. and M.G.; writing—review and editing, K.C. and M.G.; visualization, J.J. and M.G.; supervision, J.J.; project administration, J.J.; funding acquisition, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was co-financed by Military University of Technology in Warsaw under research project UGB-774/2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest and the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Yan, N.; Li, Z.; Xu, Y.; Meyers, M.A. Shear localization in metallic materials at high strain rates. Prog. Mater. Sci. 2021, 119, 100755. [Google Scholar] [CrossRef]
- Verleysen, P. Shear Testing Using the Kolsky-Hopkinson Bar Machine. In Kolsky-Hopkinson Bar Machine: Selected Topics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 75–120. [Google Scholar]
- Meyer, L.W.; Halle, T. Shear strength and shear failure, overview of testing and behavior of ductile metals. Mech. Time-Depend Mater. 2011, 15, 327–340. [Google Scholar] [CrossRef]
- Jia, B.; Rusinek, A.; Pesci, R.; Bernier, R.; Bahi, S.; Wood, P. A novel technique for dynamic shear testing of bulk metals with application to 304 austenitic stainless steel. Int. J. Solids Struct. 2020, 204–205, 153–171. [Google Scholar] [CrossRef]
- Jia, B.; Rusinek, A.; Pesci, R.; Bernier, R.; Bahi, S.; Wood, P. Simple shear behavior and constitutive modeling of 304 stainless steel over a wide range of strain rates and temperatures. Int. J. Impact Eng. 2021, 154, 103896. [Google Scholar] [CrossRef]
- Kolsky, H. Propagation of stress waves in viscoelastic solids. Appl. Mech. Rev. 1958, 11, 465–468. [Google Scholar] [CrossRef] [Green Version]
- Kolsky, H. Stress waves in solids. J. Sound Vib. 1964, 1, 88–110. [Google Scholar] [CrossRef]
- Panowicz, R.; Janiszewski, J.; Kochanowski, K. The non-axisymmetric pulse shaper position influence on SHPB experiment data. J. Theor. App. Mech. 2018, 56, 873–886. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y. A Novel Approach to Testing the Dynamic Shear Response of Ti-6Al-4V. Acta Mech. Solida Sin. 2012, 25, 299–311. [Google Scholar] [CrossRef]
- Meyer, H.W.; Kleponis, D.S. Modeling the high strain rate behavior of titanium undergoing ballistic impact and penetration. Int. J. Impact Eng. 2001, 26, 509–521. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).