Abstract
The merger of a binary neutron star (BNS) system can lead to different final states depending on the total mass of the binary system and the equation of state (EOS). One of the possible outcomes of the merger is a long-lived (lifetime > 10 ms), compact and differentially rotating remnant. The Komatsu, Eriguchi and Hachisu (1989) differential rotation law (KEH) has been used almost exclusively in the literature to describe such configurations, despite the tension with corresponding rotational profiles reported from numerical simulations. New rotation laws suggested by Uryu et al. (2017) aspire to ease this tension and provide more realistic choices to describe the rotational profiles of BNS merger remnants. We recently started constructing equilibrium models with one of the new rotation laws proposed and comparing their physical properties to the KEH rotation law counterpart models. In addition, building on earlier work, the accuracy of the IWM-CFC conformal flatness approximation with the new differential rotation law was confirmed.
1. Introduction
Differential rotation in relativistic stars has drawn a steady research interest because it is relevant in phenomena such as binary neutron star (BNS) mergers that can provide information through gravitational and electromagnetic waves observations for the behaviour of matter at high densities, i.e., the equation of state (EOS). More specifically, if the total mass M of the BNS is greater than the maximum mass of a cold, uniformly rotating neutron star, , then the compact remnant that is formed during the merger can survive for several tens of milliseconds (ms) supported by differential rotation and thermal pressure. Oscillations of the post-merger remnant could lead to tight constraints for the EOS in the case of detection of one (or more) of three observable frequencies (, , ) [1,2,3,4].
While numerical simulations are used primarily to study BNS mergers, their high computational cost calls for complementary approaches, such as equilibrium modeling in order to allow for faster and wider parameter space exploration. In the equilibrium framework, several aspects of the merger remnant are neglected in order to obtain idealized models of its structure. Enriching these initial idealized models by adding gradually, selected realistic components of the binary coalescence problem ensures that this method can still provide useful insights.
Concerning the differential rotation aspect of the BNS merger problem, the simple solution that was adopted for years in the relevant literature was the rotation law
by [5] (hereafter KEH), where A is a positive constant that determines the length scale over which the angular velocity varies within the star, is the angular velocity at the rotation axis and denotes the gravitationally redshifted angular momentum per unit rest mass and enthalpy. Limiting cases of the rotation law (1) are the uniform rotation case for and the j-constant law for (where is the specific angular momentum).
More realistic rotation laws have been proposed [6] that better describe a remnant’s rotational profile as reported from simulations (e.g., see [7] for a recent study). In our recent work [8], we investigated one of the new rotation laws, compared physical properties of constructed models with the “classic” KEH law to the new law and verified its suitability to describe BNS merger remnants.
2. Methods
Within the framework of full general relativity (GR), in [8], we construct stationary and axisymmetric stellar configurations in equilibrium as described by the line element:
with , , , and being metric functions that depend only on the coordinates r and . Matter is described as a perfect fluid, assuming a polytropic EOS:
where p is the pressure, is the rest mass density, K is the polytropic constant and N is the polytropic index (see [9] for details). We chose and , which is a common choice in the literature for testing numerical codes. We note that a polytropic model is calculated with and then rescaled to (or any other choice of K) by multiplying with appropriate factors [10].
In order to create our equilibrium models, we used an extended version [11,12] of the public domain rns code [13,14]. The code is based on the KEH scheme [5] and includes modifications by [10]. We expanded the code in order to implement the four-parameter rotation law introduced in [6]
(hereafter Uryu+ law). The parameter p controls the growth of the rotation curve near the rotation axis, and parameter q controls the asymptotic behavior of . Setting recovers the Keplerian rotation law in the Newtonian limit. In Figure 1, we present an example of the angular velocity profile in the equatorial plane for the Uryu+ rotation law (4).
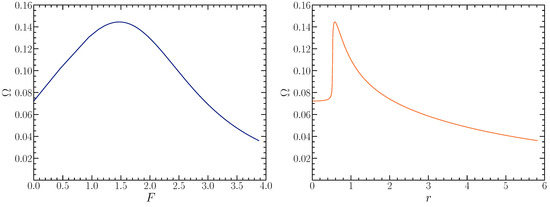
Figure 1.
Angular velocity profiles in the equatorial plane for model C6 (axis ratio = 0.43), constructed with the Uryu+ rotation law with (see Section 3 for details). (Left) plotted versus the gravitationally redshifted angular momentum per unit rest mass and enthalpy F. (Right) plotted versus the coordinate radius r. Figure from [8].
We choose the values , for which the integral in the hydrostationary equilibrium expression has an analytic solution. The parameters A and B are determined by solving for them in each iteration, via fixing the ratios of the maximum angular velocity over the angular velocity at the center of the configuration, , and of the angular velocity at the equator over the angular velocity at the center, , to certain selected values [6,15].
As reference values for the ratios , we adopt the choice as in [6]. However, differences in rotational profiles seen in numerical simulations of post-merger remnants, when different EOS and total masses are used [7,16], provides motivation to examine two values for the first parameter and two values for the second parameter , leading to four distinct pairs of .
3. Results
For comparison with previous work [11,17] employing the KEH differential rotation law, in [8], we constructed three sequences of equilibrium models using the new differential rotation law (4):
- Sequence A is a constant rest mass sequence with .
- Sequence B is a constant central energy density sequence with .
- Sequence C is a constant central energy density sequence with .
Throughout the text, we employ dimensionless units for all physical quantities by setting (see also [10]). We note that the maximum mass nonrotating model for our chosen EOS has a central energy density with a gravitational mass of and a rest mass of . Figure 2 acts as an illustrated definition of equilibrium sequences A, B and C.
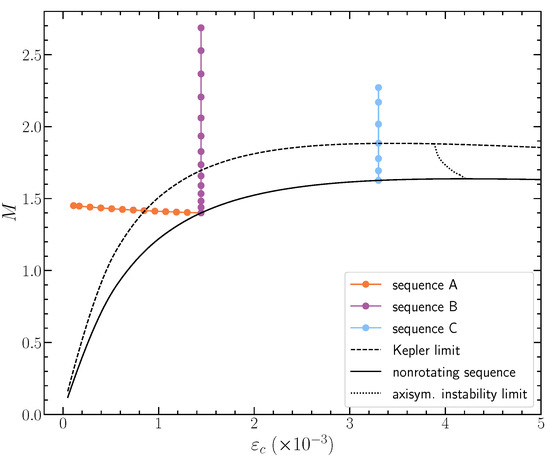
Figure 2.
Gravitational mass M versus the central energy density for the definition of sequences A, B and C. For reference, the nonrotating (TOV) sequence (solid line), the mass-shedding (Kepler) limit for uniform rotation (dashed line) and the axisymmetric instability limit for uniform rotation (dotted line) are shown. Figure from [8].
We performed a comparison between the new Uryu+ rotation law and the KEH law and verified a close agreement for the masses of the corresponding configurations. The left panel of Figure 3 shows a difference at the level for low density and rapidly rotating models, which became much smaller as the compactness increased for sequences B and C (right panel). There was a slightly larger influence of the rotation law choice on the radius, as smaller radii were found for the Uryu+ models. This was attributed to a weaker centrifugal force in the Uryu+ models, since the angular velocities at the equator were also found to be smaller. We note that results shown in Figure 3 were obtained with the reference values .
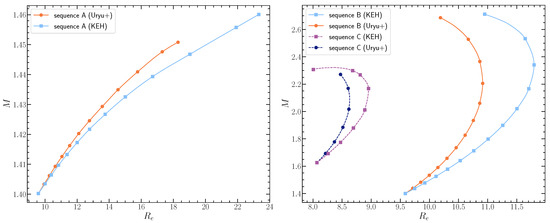
Figure 3.
Comparison of the gravitational mass M versus the circumferential radius for the equilibrium models of sequences A (Left), B and C (Right), constructed with the Uryu+ and the KEH differential rotation laws. The values were used for the Uryu+ law calculations. Figure from [8].
In order to highlight the distinction between quasi-toroidal and quasi-spheroidal morphologies, we explore additional values of parameters for a representative model with (Figure 4). From the four pairs of values considered, only the pair led to a quasi-toroidal configuration. This is consistent with the corresponding profile having the highest degree of differential rotation (right panel of Figure 4). Similar results were obtained with corresponding models with from sequences A and C.
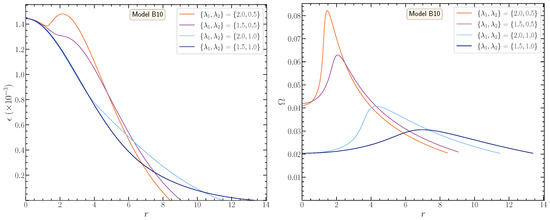
Figure 4.
Effect of the different options for parameters for model B10 (). (Left) energy density profile versus the coordinate radius r in the equatorial plane. (Right) angular velocity profile in the equatorial plane. Figure from [8].
We go on to construct full sequence C variations (i.e., of constant central energy density ) with the Uryu+ rotation law but different values. The curves in Figure 5 summarize the four equilibrium variation sequences (extra equilibrium solutions were calculated for Figure 5, in order to produce smoother curves).
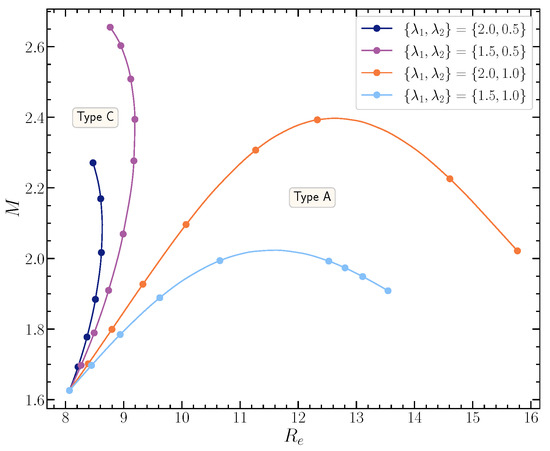
Figure 5.
Gravitational mass M versus the circumferential radius for the variations of sequence C, constructed with the Uryu+ differential rotation law and employing different values. Equilibrium models with and are type C solutions, while models with and are type A solutions [18]. Figure from [8].
A mass-shedding limit was found for the cases and at axis ratio values of 0.38602 and 0.46693, respectively. This classifies these sequences as type A solutions according to [18]. For the cases and , no mass-shedding limit was found. For the terminal models of the latter sequences, i.e., the highest mass models of the corresponding curves in Figure 5, the maximum density was located off-center, and a quasi-toroidal morphology was established. The above characteristics classify these sequences as type C solutions according to [18].
As a worst case scenario, in [8], we also performed a comparison between full GR and the IWM-CFC conformal flatness approximation [19,20] for a representative model of our most compact sequence C with for the highest degree of differential rotation considered here, i.e., . Figure 6 shows the energy density and angular velocity profiles of the specific model for the GR and IWM-CFC case.
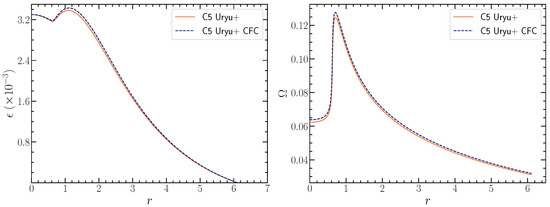
Figure 6.
Comparison between full GR and the IWM-CFC approximation for model C5 () calculated for the Uryu+ rotation law with . (Left) energy density profile in the equatorial lane versus the coordinate radius r. (Right) angular velocity profile in the equatorial plane versus the coordinate radius r. Figure from [8].
We found that the IWM-CFC approximation remained acceptably accurate for models with an axis ratio , which can be considered as merger-mimicking candidates. The relative errors for local quantities (such as the radius and the angular velocity) were up to ∼ and ∼ for the masses and the ratio of the rotational kinetic energy over the absolute value of the gravitational binding energy. This is consistent with the corresponding errors reported in [17] for the same sequence calculated with the KEH rotation law with (Figure 7).
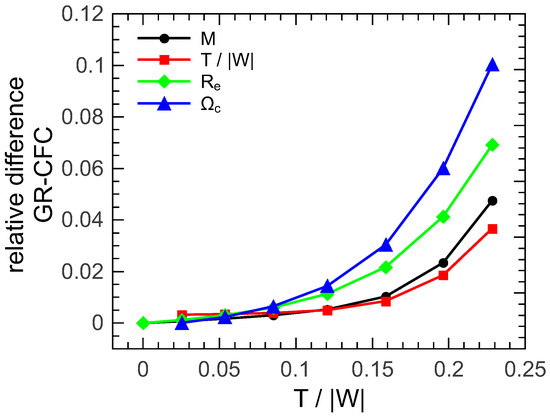
Figure 7.
Absolute values of the relative difference between full GR and IWM-CFC approximation for the gravitational mass M, the ratio of rotational to gravitational binding energy , the equatorial circumferential radius and the angular velocity at the center of the configuration for sequence C calculated with the KEH rotation law. Values at correspond to an axis ratio . Figure from [17].
4. Discussion
In [8], we found that the versatility of the new Uryu+ rotation law allowed for the construction of equilibrium solutions with a rotational profile much closer to the one observed for merger remnants in numerical simulations, while at the same time dwelling in the realm of type A solutions [18] (i.e., quasi-spherical). This is an important development toward constructing more realistic equilibrium models that can mimic the properties of merger remnants. Having more realistic models available will allow further insights about stellar stability and the threshold for prompt collapse to emerge in future studies. A necessary first step to that direction is to expand this study for realistic and hot EOS.
Recently, new multivariate empirical relations were reported (Figure 8) for the post-merger frequencies (the dominant oscillation frequency stemming from excitation of the fundamental quadrupolar mode), (stemming from a spiral deformation, the pattern of which rotates slower with respect to the double-core structure in the center of the remnant) and (stemming from a non-linear coupling of the mode to the fundamental quasi-radial mode) [21]. Another interesting follow-up would be to study these oscillations and empirical relations using configurations constructed with the new Uryu+ law via time evolution or perturbation methods.
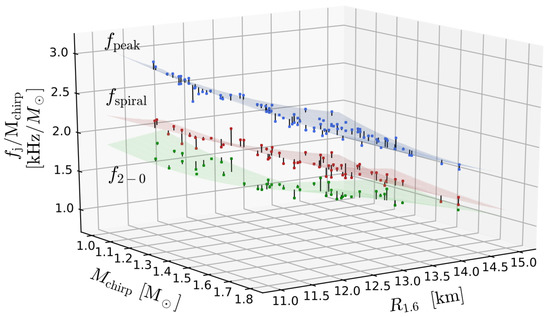
Figure 8.
Surfaces corresponding to empirical relations for the three different post-merger frequencies , and , as a function of the chirp mass and the equatorial circumferential radius of a nonrotating model with gravitational mass . Figure from [21].
Funding
PI gratefully acknowledges support by a Virgo-EGO Scientific Forum (VESF) PhD fellowship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the present article.
Acknowledgments
We would like to thank Gabriele Bozzola and Wolfgang Kastaun for useful discussions. In addition, we thank Giovanni Camelio, Tim Dietrich, Stephan Rosswog and Bryn Haskell for advanced sharing of a manuscript on a related topic and for comments on our manuscript. The authors gratefully acknowledge the Italian Istituto Nazionale di Fisica Nucleare (INFN), the French Centre National de la Recherche Scientifique (CNRS) and the Netherlands Organization for Scientific Research for the construction and operation of the Virgo detector and the creation and support of the EGO consortium.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KEH | Komatsu, Eriguchi and Hachisu |
| EOS | equation of state |
| BNS | binary neutron star |
| IWM | Isenberg, Wilson, Mathews |
| CFC | conformal flatness condition |
| GR | general relativity |
References
- Stergioulas, N.; Bauswein, A.; Zagkouris, K.; Janka, H.T. Gravitational waves and non-axisymmetric oscillation modes in mergers of compact object binaries. Mon. Not. R. Astron. Soc. 2011, 418, 427–436. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Unified picture of the post-merger dynamics and gravitational wave emission in neutron star mergers. Phys. Rev. D 2015, 91, 124056. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N.; Janka, H.T. Exploring properties of high-density matter through remnants of neutron-star mergers. Eur. Phys. J. A 2016, 52, 56. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Spectral classification of gravitational-wave emission and equation of state constraints in binary neutron star mergers. J. Phys. G Nucl. Part. Phys. 2019, 46, 113002. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I - Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Baiotti, L.; Galeazzi, F.; Taniguchi, K.; Yoshida, S. Modeling differential rotations of compact stars in equilibriums. Phys. Rev. D 2017, 96, 103011. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Font, J.A.; Löffler, F.; Pasquali, M.; Stergioulas, N. Numerical-relativity simulations of long-lived remnants of binary neutron star mergers. Phys. Rev. D 2020, 101, 064052. [Google Scholar] [CrossRef]
- Iosif, P.; Stergioulas, N. Equilibrium sequences of differentially rotating stars with post-merger-like rotational profiles. arXiv 2020, arXiv:gr-qc/2011.10612. [Google Scholar]
- Friedman, J.L.; Stergioulas, N. Rotating Relativistic Stars; Cambridge Monographs on Mathematical Physics, Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Spin-up of a Rapidly Rotating Star by Angular Momentum Loss: Effects of General Relativity. Astrophys. J. 1992, 398, 203. [Google Scholar] [CrossRef]
- Stergioulas, N.; Apostolatos, T.A.; Font, J.A. Non-linear pulsations in differentially rotating neutron stars: Mass-shedding-induced damping and splitting of the fundamental mode. Mon. Not. R. Astron. Soc. 2004, 352, 1089–1101. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Semi-analytic derivation of the threshold mass for prompt collapse in binary neutron-star mergers. Mon. Not. R. Astron. Soc. 2017, 471, 4956–4965. [Google Scholar] [CrossRef]
- Stergioulas, N.; Friedman, J.L. Comparing Models of Rapidly Rotating Relativistic Stars Constructed by Two Numerical Methods. Astrophys. J. 1995, 444, 306. [Google Scholar] [CrossRef]
- Stergioulas, N. RNS Public Domain Code. Available online: http://www.gravity.phys.uwm.edu/rns (accessed on 1st April 2020).
- Zhou, E.; Tsokaros, A.; Uryū, K.; Xu, R.; Shibata, M. Differentially rotating strange star in general relativity. Phys. Rev. D 2019, 100, 043015. [Google Scholar] [CrossRef]
- Hanauske, M.; Takami, K.; Bovard, L.; Rezzolla, L.; Font, J.A.; Galeazzi, F.; Stöcker, H. Rotational properties of hypermassive neutron stars from binary mergers. Phys. Rev. D 2017, 96, 043004. [Google Scholar] [CrossRef]
- Iosif, P.; Stergioulas, N. On the accuracy of the IWM–CFC approximation in differentially rotating relativistic stars. Gen. Relativ. Gravit. 2014, 46, 1800. [Google Scholar] [CrossRef][Green Version]
- Ansorg, M.; Gondek-Rosińska, D.; Villain, L. On the solution space of differentially rotating neutron stars in general relativity. Mon. Not. R. Astron. Soc. 2009, 396, 2359–2366. [Google Scholar] [CrossRef]
- Isenberg, J.A. Waveless Approximation Theories of Gravity. Int. J. Mod. Phys. D 2008, 17, 265–273. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J.; Marronetti, P. Relativistic numerical model for close neutron-star binaries. Phys. Rev. D 1996, 54, 1317–1331. [Google Scholar] [CrossRef] [PubMed]
- Vretinaris, S.; Stergioulas, N.; Bauswein, A. Empirical relations for gravitational-wave asteroseismology of binary neutron star mergers. Phys. Rev. D 2020, 101, 084039. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).