On Spacetime Duality and Bounce Cosmology of a Dual Universe ^†

Abstract

The recent Planck Legacy 2018 release confirmed the existence of an enhanced lensing amplitude in the cosmic microwave background (CMB) power spectra. Notably, this amplitude is higher than that estimated by the lambda cold dark matter model, which prefers a positively curved early Universe with a confidence level greater than 99%. In this study, the pre-existing curvature is incorporated to extend the field equations where the space-time worldlines are utilised to model the evolution of the Universe with reference to the scale factor of the early Universe and its radius of curvature upon the emission of the CMB. The worldlines reveal both positive and negative solutions, implying that matter and antimatter of early Universe plasma evolved in opposite directions as distinct Universe sides during a first decelerating phase. The worldlines then indicate a second accelerated phase in reverse directions, whereby both sides free-fall towards each other under gravitational acceleration. The simulation of the predicted conformal curvature evolution demonstrates the fast orbital speed of the outer stars owing to external fields exerted on galaxies as they travel through conformally curved space-time. Finally, the worldlines predict an eventual time-reversal phase comprising rapid spatial contraction that culminates in a Big Crunch, signalling a cyclic Universe. These findings reveal that the early Universe’s plasma could be separated and evolved into distinct sides of the Universe that collectively and geometrically inducing its evolution, physically explaining the effects attributed to dark energy and dark matter.

1. Introduction

Bounce cosmology provides an alternative perception of the Universe, in which our Universe expanded from a hot and very dense state of a previously collapsed Universe [1]. The idea was first proposed in the 1930s; since then, many bouncing models have been introduced with the aim of providing a systematic description of the beginning and the evolution of the Universe [2].

This cosmology is free from the singularity problem and offers a clearer view of the early Universe [2]. However, the null-energy condition is generally violated by the conjectured bounce of re-expansion in several modified gravity theories [3,4]. Alternatively, the bounce realization could be sought through other scenarios, such as the phenomenon of plasma drift in the presence of electromagnetic fields [5,6]. In this sense, matter and antimatter of the early Universe’s plasma could have been separated upon the emission of the CMB and consequently evolved in opposite directions due to their opposite spin and charge. Additionally, in realizing the singularity-free paradigm, a minimum radius of the Universe can be sought by considering the boundary contribution and the pre-existing curvature of the early Universe’s plasma based on the recent Planck release, which preferred a positively curved early Universe with a confidence level higher than 99% [7,8].

In this study, a closed early Universe model is considered, where the evolution of the Universe is modelled by using quantized space-time worldlines. This paper is organised as follows. Section 2 presents the extended field equations by considering the background curvature. Section 3 and Section 4 discuss the derivations of the quantized worldlines and the evolution of the Universe, while Section 5 illustrates spiral galaxy rotation under external fields. Section 6 discusses the early Universe boundary contribution and the minimum Universe radius. Finally, Section 7 concludes this work and suggests future works.

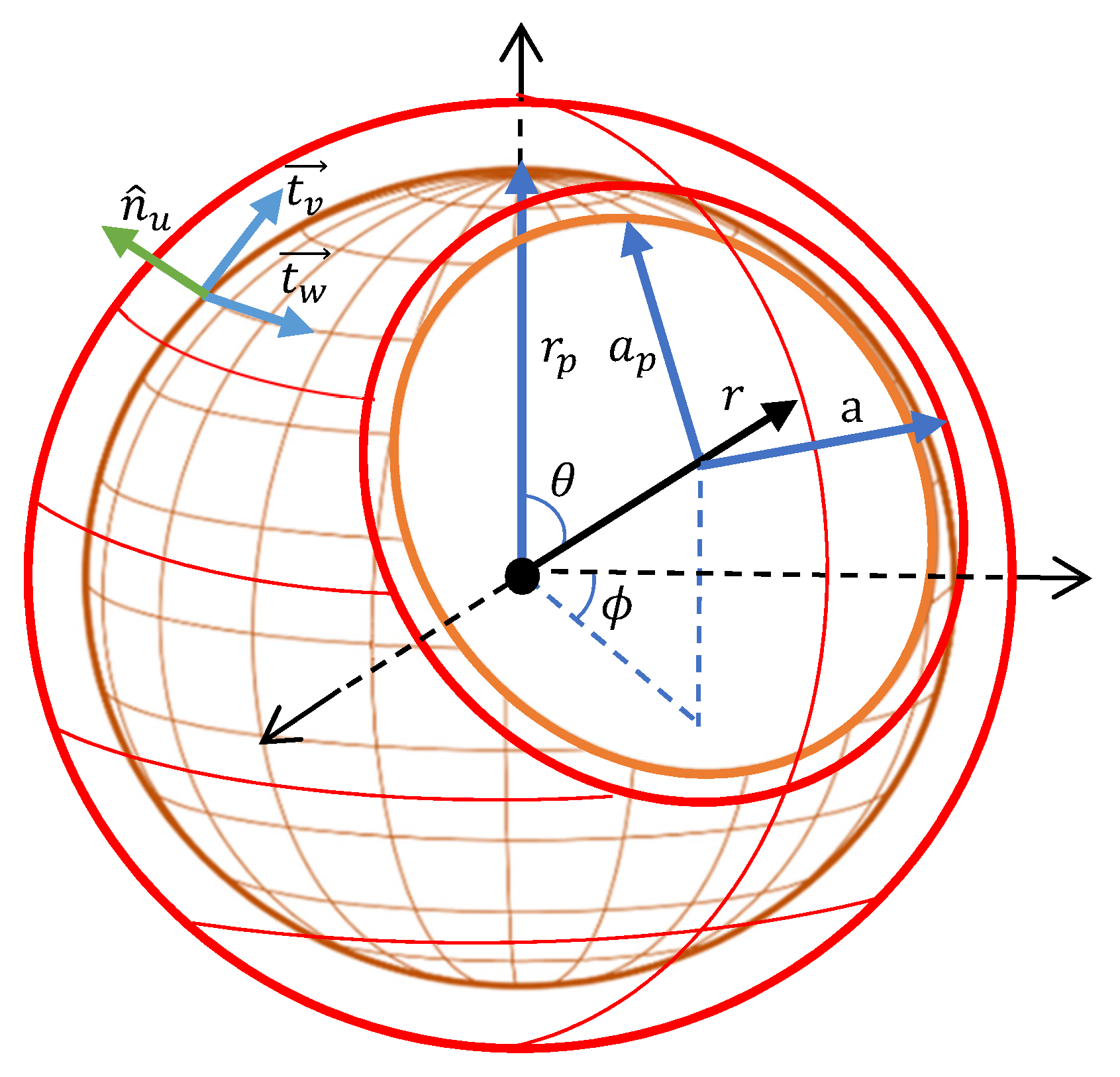
2. Extended Field Equations for a Conformally Curved Universe

To consider the pre-existing/background curvature and its evolution over cosmic time, a modulus of space-time continuum deformation/curvature $E_D$ is introduced based on the theory of elasticity [9]. By using the Einstein field equations, $E_D$ = (stress/strain) is

$$E_D=\frac{T_{\mu }^v-T{\delta }_{\mu }^v/2}{R_{\mu }^v/ℛ}$$

(1)

where the stress is signified by the stress-energy tensor $T_{\nu }^{\mu }$ of trace $T$, while the strain is signified by the Ricci curvature tensor $R_{\nu }^{\mu }$ as the change in the curvature divided by the pre-existing curvature $ℛ$, while ${\delta }_u^v$ is the Kronecker delta [10]. By complying with the energy conservation law, the Einstein–Hilbert action can be extended to

$$S={\displaystyle \int }\left[\frac{E_D}{2}\frac{R}{ℛ}+ℒ\right]\sqrt{-g}{d}^{4}x$$

(2)

where $R$ and $ℛ$ are the Ricci and the pre-existing scalar curvature respectively, $ℒ$ is the Lagrangian density and $g$ is the determinant of the metric tensor $g_{uv}$. According to Equation (1), $E_D=ℛc^4/8\pi G_t$ is in terms of the energy density and is proportional to the fourth power of the speed of light $c$, which can be in accordance with quantum field theory frequency cut-off predictions of the vacuum energy density [11]. Space-time can be regarded as a continuum with a dual quantum nature, that it curves as waves according to general relativity while fluxing as quantum energy particles; the latter can be justified because of the energy flux from the early Universe plasma into space at the speed of light creating a ‘space-time continuum’ or ‘vacuum energy’. This could be corroborated by light polarization from the CMB [12]. The derivations of the extended action in [13] give

$$\frac{R_{\mu \nu }}{ℛ}-\frac{1}{2}\frac{R}{ℛ}{g}_{\mu \nu }-\frac{R}{{ℛ}^2}{ℛ}_{\mu \nu }+\frac{R\left({\mathcal{K}}_{\mu \nu }-\frac{1}{2}\mathcal{K}{\widehat{p}}_{\mu \nu }\right)-ℛ\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)}{{ℛ}^2}=\frac{T_{\mu \nu }}{E_D}$$

(3)

Equation (3) can be interpreted as indicating that the induced curvature over the pre-existing curvature equals the ratio of the imposed energy density and its flux to the vacuum energy density and its flux through the expanding/contracting Universe. The relativistic term comprising $R_{\mu \nu }$ can be interpreted as signifying a local relativistic 4D Cloud-world of a celestial object of extrinsic boundary $K_{\mu \nu }$ that is embedded and travelling/spinning through a global 4D conformal space-time as the independent background represented by the term ${ℛ}_{\mu \nu }$ with extrinsic boundary ${\mathcal{K}}_{\mu \nu }$ (this interpretation is visualized in Section 5). The extended equations can be simplified by substituting Equation (1) to Equation (3) as

$$R_{\mu \nu }-\frac{1}{2}R{\widehat{g}}_{\mu \nu }+\frac{R\left({\mathcal{K}}_{\mu \nu }-\frac{1}{2}\mathcal{K}{\widehat{p}}_{\mu \nu }\right)-ℛ\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)}{ℛ}=\frac{8\pi G_t}{c^4}{T}_{\mu \nu }$$

(4)

where ${\widehat{g}}_{\mu \nu }=g_{\mu \nu }+2{\overline{g}}_{\mu \nu }$ denotes the conformal transformation of the metric tensor because Einstein spaces are a subclass of the conformal space [14]. The evolution in $G_t$ can accommodate the pre-existing curvature evolution over cosmic time against constant $G$ for a special flat space-time case, where this evolution is preferred to reduce the conflict of matter power spectrum amplitude with Planck datasets [15,16,17]. The new boundary term is only significant at high-energy limits, such as within black holes [18] and the early Universe and it could remove the singularities from the theory.

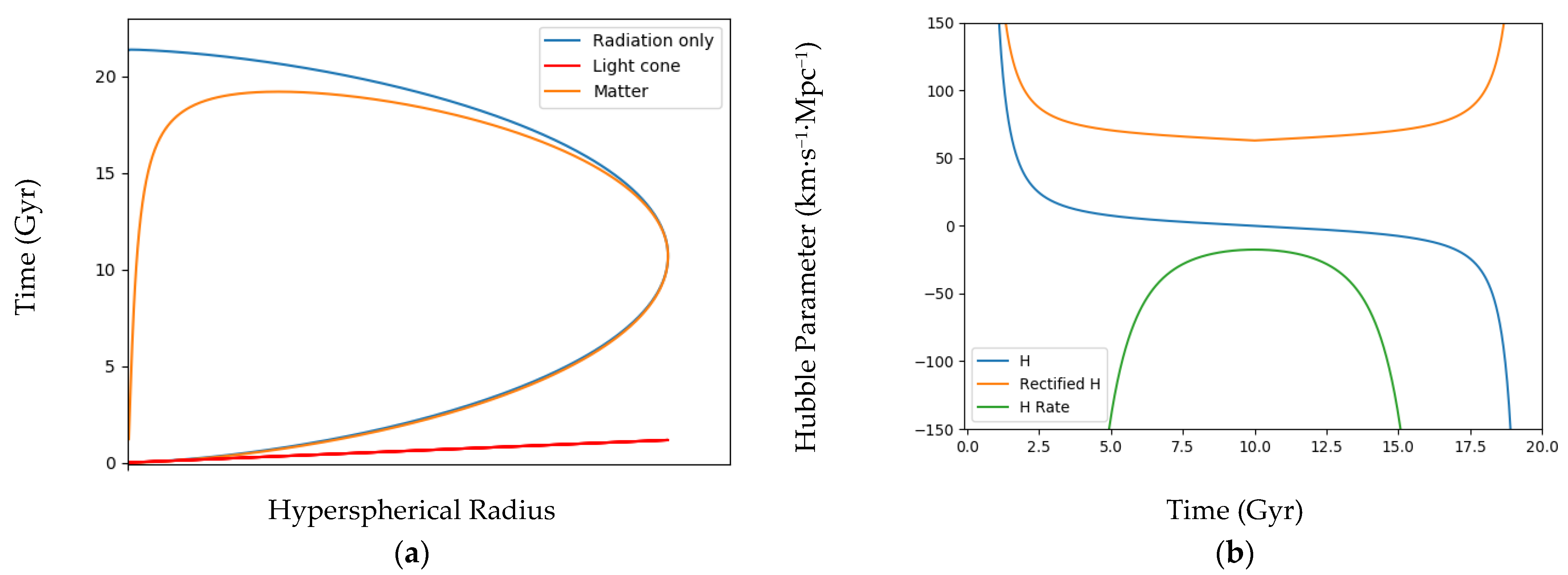
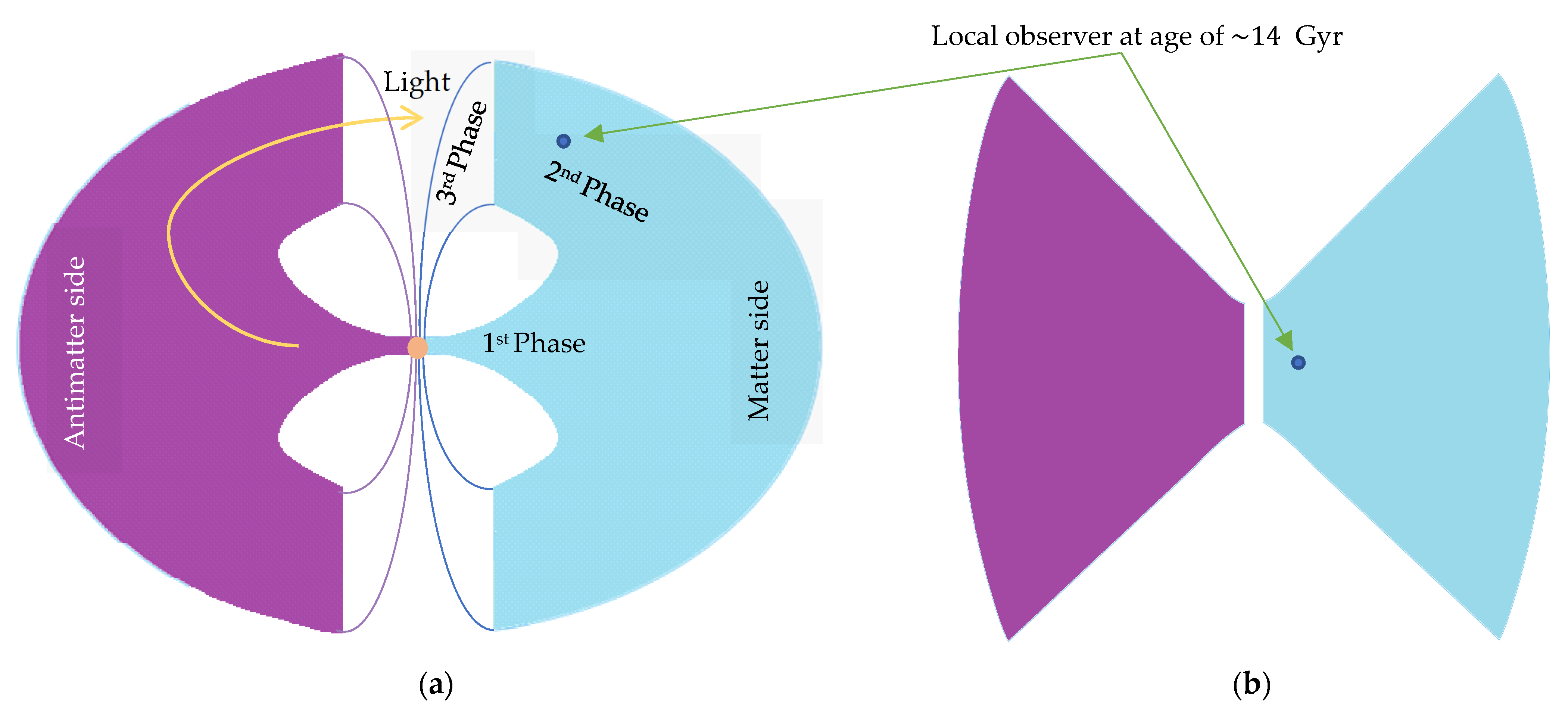
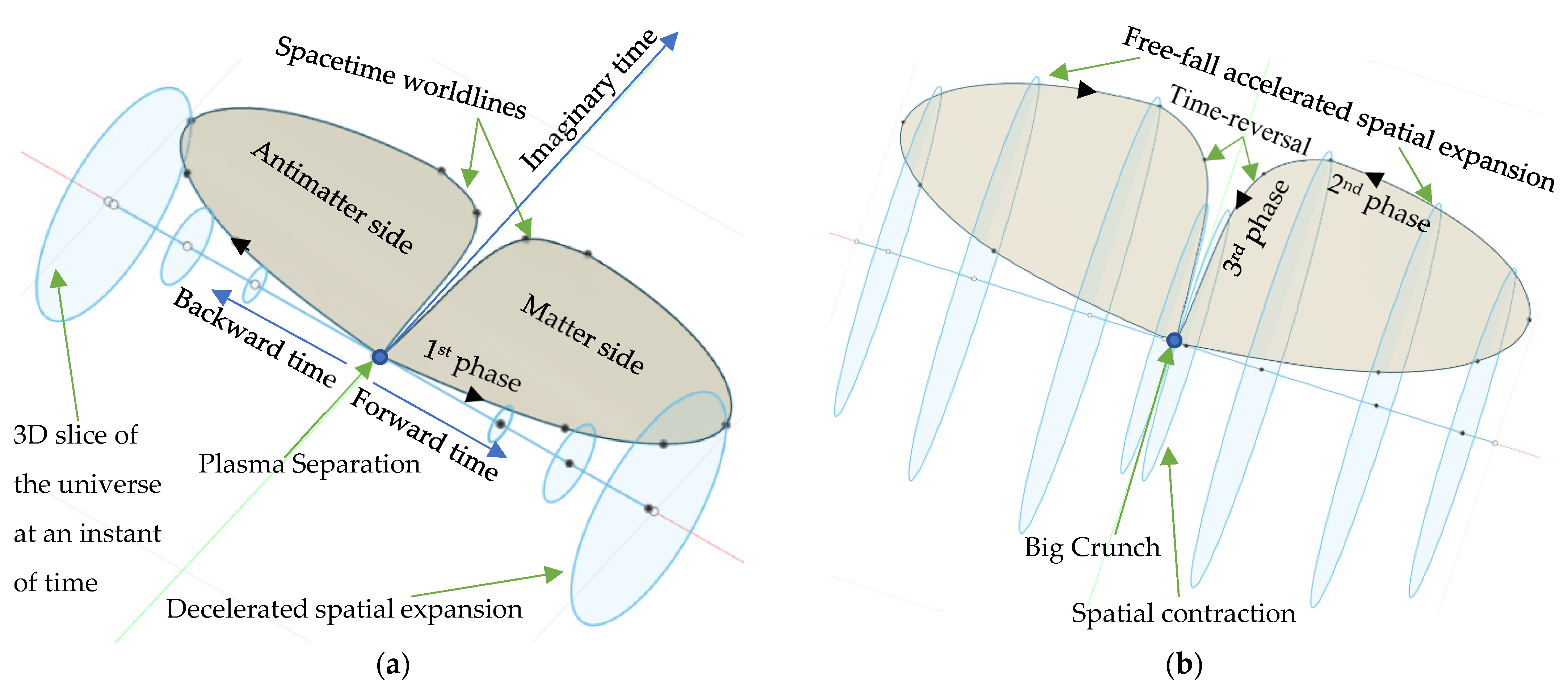
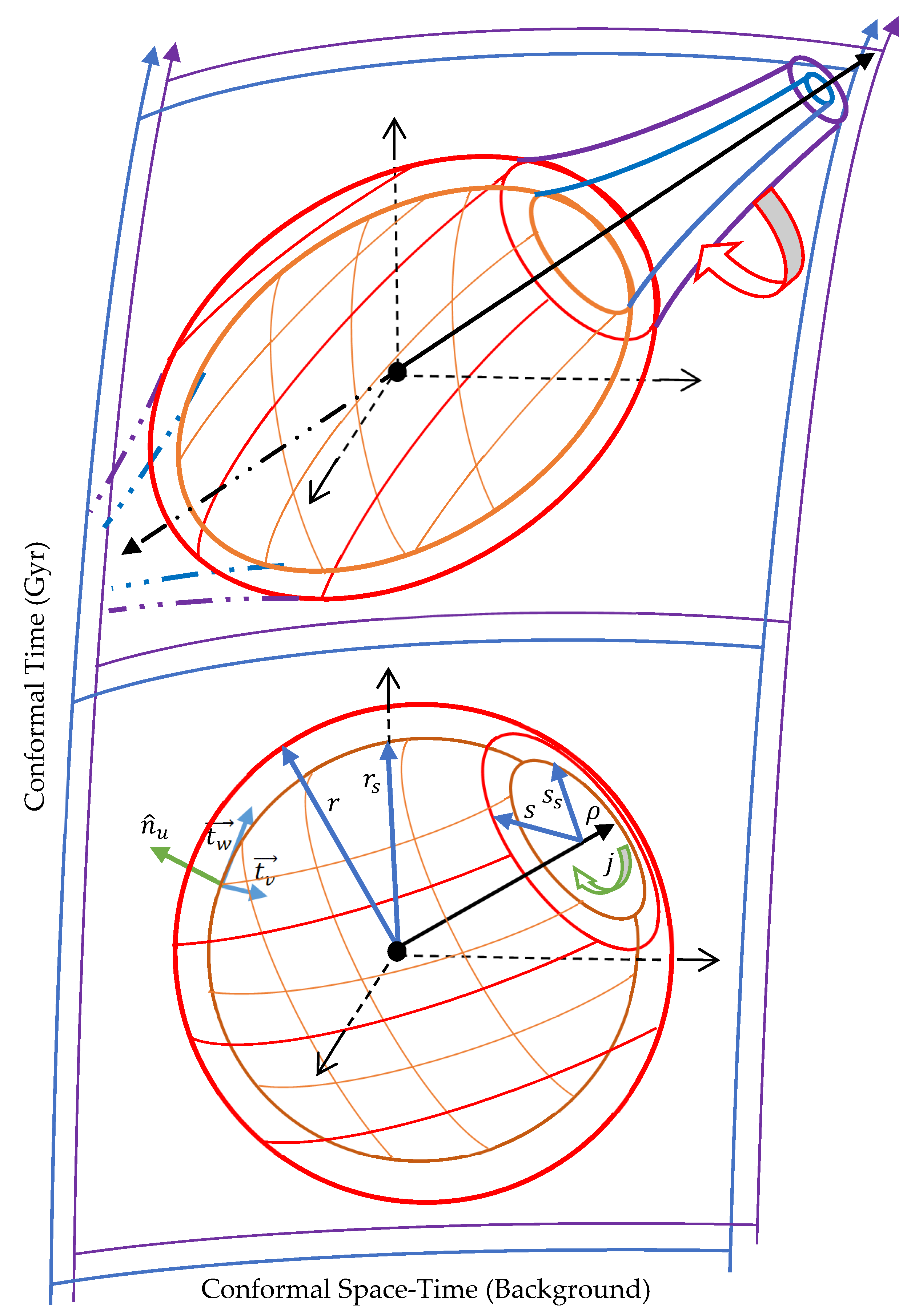
3. Bounce from a Closed Early Universe

The Friedmann–Lemaîtree–Robertson–Walker (FLRW) metric is the standard cosmological metric model, which assumes an isotropic and homogenous Universe [19,20], where the isotropy and homogeneity of the early Universe’s plasma based on the CMB are consistent with this model. The Planck release preferred a closed and positively curved early Universe. Accordingly, the plasma reference radius of curvature $r_P$ upon the emission of the CMB and the corresponding early Universe scale factor $a_P$ at reference time $t_p$ are incorporated to reference the FLRW metric model, as shown in Figure 1.

The referenced metric tensor is

$$\left[g_{\mu \nu }\left(\mathrm{x}\right)\right]=\mathrm{diag}\left(-c^2,\frac{a^2\left(t\right)}{a_p{}^2}/\left(1-\frac{r^2}{r_p{}^2}\right),\frac{a^2\left(t\right)}{a_p{}^2}{r}^2,\frac{a^2\left(t\right)}{a_p{}^2}{r}^2{\sin }^2\theta \right),$$

(5)

where $a\left(t\right)/a_p$ is a new dimensionless scale factor; $r,\varphi$ and $\theta$ are the comoving coordinates. No conformal transformation is included in this metric; therefore, its outcomes are comparable with the literature. The Ricci curvature tensor $R_{uv}$ is solved using Christoffel symbols for $g_{uv}$ in Equation (5) as follows:

$$\begin{gathered} R_{tt}=-3\frac{\ddot{a}}{a},\hspace{1em}\hspace{1em}{R}_{rr}=\frac{1}{c^2}\left(\frac{a\ddot{a}}{a_p{}^2}+\frac{2{\dot{a}}^2}{a_p{}^2}+\frac{2c^2}{r_p{}^2}\right)/\left(1-\frac{r^2}{r_p{}^2}\right), \\ {R}_{\theta \theta }=\frac{r^2}{c^2}\left(\frac{a\ddot{a}}{a_p{}^2}+\frac{2{\dot{a}}^2}{a_p{}^2}+\frac{2c^2}{r_p{}^2}\right),\hspace{1em}\hspace{1em}{R}_{\varphi \varphi }=\frac{r^2{\sin }^2\theta }{c^2}\left(\frac{a\ddot{a}}{a_p{}^2}+\frac{2{\dot{a}}^2}{a_p{}^2}+\frac{2c^2}{r_p{}^2}\right). \end{gathered}$$

(6)

The Ricci scalar curvature is

$$R=R_{\mu \nu }{g}^{\mu \nu }=-\frac{6}{c^2}\left(\frac{\ddot{a}}{a}+\frac{{\dot{a}}^2}{a^2}+\frac{c^2{a}_p{}^2}{a^2{r}_p{}^2}\right).$$

(7)

where $\ddot{a}$ and $\dot{a}$ are cosmic time derivatives of $a$. By using Equations (5)–(7), which account for the plasma parameters, and considering a perfect fluid given by $T_{\mu \nu }=\left(\rho +\frac{P}{c^2}\right)u_{\mu }{u}_{\nu }+P{g}_{\mu \nu }$ [10] when solving the field equations, this results in the referenced Friedmann equations:

$$H^2\equiv \frac{{\dot{a}}^2}{a^2}=\frac{8\pi G_t\rho }{3}-\frac{c^2{a}_p{}^2}{a^2{r}_p{}^2},$$

(8)

$$\dot{H}\equiv \frac{\ddot{a}}{a}=-\frac{4\pi G_t}{3}\left(\rho +3\frac{P}{c^2}\right).$$

(9)

where $H$, $P$, and $\rho$ are the Hubble parameter, pressure, and density respectively. By utilizing cosmic imaginary time, $\tau =it$, the referenced Friedman equations are solved at the reference imaginary time, ${\tau }_p$, by rewriting Equation (8) in terms of the conformal time in its parametric form $d\eta =-i\frac{a_p}{a}d\tau$ (where ${\dot{a}}^{}=i\frac{da}{d\tau }$); thus, $d\eta =\frac{a_p}{a\dot{a}}d\tau$ as follows:

$${{\displaystyle \int }}_0^{\eta }d\eta ={{\displaystyle \int }}_0^{2\pi }{a}_p{\left(\frac{8\pi G_p{\rho }_p{a}_p{}^3}{3}a-\frac{c^2{a}_p{}^2}{r_p{}^2}{a}^2\right)}^{-1/2}da$$

(10)

where $\rho =\frac{{\rho }_p{a}_p{}^3}{a^3}$ [21]. By integrating, the evolution of the spatial scale factor is

$$a\left(\eta \right)/a_p=\frac{G_p{M}_p}{c^2{r}_p}\left(1-\cos \frac{c}{r_p}\eta \right)$$

(11)

where $M_p=\frac{4}{3}\pi {\rho }_p{r}_p{}^3$ is the early Universe plasma mass. Additionally, the evolution of the imaginary cosmic time $\tau \left(\eta \right)$ can be obtained by integrating the length of the spatial factor contour over the expansion speed $H_{\eta }$ while initiating at the reference imaginary time ${\tau }_p$ with the corresponding spatial scale factor $a_p$. Thus, by rewriting Equation (9) in terms of the Hubble parameter by its definition at ${\tau }_p$ as $d\tau =i\frac{da\left(\eta \right)}{H{a}_p}$, gives

$${{\displaystyle \int }}_{{\tau }_P}^{\tau }d\tau =i{{\displaystyle \int }}_0^{\eta }\frac{E}{6H_{\eta }{E}_D}\left(1-\cos \frac{c}{r_p}\eta \right)d\eta$$

(12)

where the constant in Equation (11) is rewritten in terms of the modulus $E_D$ representing the vacuum energy density and the Universe energy density 𝐸 by using Equation (1). By performing the integration, the imaginary time evolution is

$$\tau \left(\eta \right)=i\frac{E}{6H_{\eta }{E}_D}\left(\eta -\sin \frac{c}{r_0}\eta \right)+{\tau }_p$$

(13)

According to the law of energy conservation, the covariant divergence of the stress-energy tensor vanishes, ${\Delta }_v{T}^{uv}=0$; this yields $\frac{\dot{a}}{\mathrm{a}}{T}_u^u+3\frac{\dot{a}}{\mathrm{a}}\rho -i\frac{\partial \rho }{\partial \tau }=0$, $3\left(\rho +\frac{P}{c^2}\right)\frac{\dot{a}}{\mathrm{a}}-i\frac{\partial \rho }{\partial \tau }=0$. By combining these outcomes, integrating, and substituting the spatial scale factor rate in Equation (11) to their outcome, the Universe density evolution over the conformal time is

$${\rho }_{\eta }=D_p{\left(1-\cos \frac{c}{r_p}\eta \right)}^{-3}$$

(14)

where $D_P$ is a constant. By substituting Equation (14) in Equation (9) and initiating the integration at ${\tau }_p$, thus, $\dot{H}=\frac{\ddot{a}}{a_p}$, which gives

$${{\displaystyle \int }}_{H_p}^H\dot{H}={{\displaystyle \int }}_0^{\eta }-\frac{4\pi G_p{D}_p}{3a_p}{\left(1-\cos \frac{c}{r_p}\eta \right)}^{-3}d\eta$$

(15)

By integration, the Hubble parameter evolution is

$$H_{\eta }=H_a\left(\frac{1}{5}{\cot }^5\frac{c}{2r_p}\eta +\frac{2}{3}{\cot }^3\frac{c}{2r_p}\eta +\cot \frac{c}{2r_p}\eta \right)+H_p$$

(16)

where $H_a$ and $H_p$ are constants. The spacetime worldline wavefunction ${\psi }_L\left(\eta \right)$ with respect to its reference value ${\psi }_p$ at ${\tau }_p$ is obtained using Equations (11) and (13)–(16) as a possible third quantization as:

$$\begin{array}{ll}\hfill {\psi }_L\left(\eta \right)/{\psi }_p& =\mp \frac{E}{6E_D}({\left(1-\cos \frac{c}{r_p}\eta \right)}^2\\ & +\frac{c^2}{H_{\eta }{}^2{a}_p{}^2}{{\left(\eta -\sin \frac{c}{r_p}\eta \right)}^2)}^{1/2}{e}^{i{\cot }^{-1}\frac{H_{\eta }{a}_p\left(1-\cos \frac{c}{r_p}\eta \right)}{c\left(\eta -\sin \frac{c}{r_p}\eta \right)}}\end{array}$$

(17)

where the wavefunction amplitude $E/6E_D=M_p\hslash /M_{pl}^2{r}_{p}c$ denotes a dimensionless energy parameter as the ratio of the Universe energy density $E$ to the vacuum energy density $E_D$.

4. Evolution of Universe Worldlines

The positive and negative solutions of the wavefunction in Equation (17) imply that matter and antimatter in the plasma evolved in opposite directions. The phenomenon of plasma drift is caused by the presence of electromagnetic fields [5,6], which drives matter and antimatter in opposite directions, as they have opposite electrical charges. A chosen mean evolution value of the Hubble parameter of $~70$ km∙s⁻¹∙Mpc⁻¹ and a phase transition of expansion at the Universe’s age of $~10$ Gyr were applied to tune the integration constants of the derived model, where the predicted energy density parameter is $~1.16$.

The cosmic evolution of matter/antimatter according to the wavefunction is predicted to experience three distinct phases (Figure 2a, orange curve) while radiation-only worldlines, which propagate faster than matter/antimatter, are predicted to pass to the other side as shown in Figure 2a, blue curve. Due to symmetry, only the positive solution is shown in Figure 2a. Additionally, the predicted Hubble parameter $H$ (speed of the spatial expansion) and its rate $\dot{H}$ (the acceleration of the spatial expansion), along with a rectified Hubble parameter reflecting the reverse expansion direction during the second phase, are shown in Figure 2b.

These findings in Figure 2 can be interpreted as follows. First, the matter and antimatter sides expanded in opposite directions away from the early Universe plasma, possibly due to the phenomenon of plasma drift, where they would be blue- and red-shifted, which in corresponding with the CMB axis. During the first phase (i.e., the first $~$10 Gyr), the expansion rate as shown in Figure 2b, blue curve, started with a hyperbolic expansion rate at the nascent stage upon the emission of CMB, where the expansion rate was at its highest value. Then, the rate decreased, which could be due to gravity between both sides, until it reached its minimal value at the phase transition.

However, at the second phase, the worldlines reversed their directions, with both sides of the matter and antimatter entering a state of free-fall towards each other under the gravitational acceleration perhaps causing the current accelerated expansion, where the vacuum energy could not be responsible for this acceleration [22]. The Hubble parameter started to increase in the second phase. According to the mechanics, the minus sign of the Hubble parameter (the speed of expansion) in the second phase indicates an opposite expansion direction. In addition, the opposite signs of the acceleration (green curve) and the expansion speed in the first phase indicate a slowing down, while the matching signs in the second phase indicate the expansion speed is increasing. Interestingly, the worldlines predict a third phase of spatial contraction that appears after $~18$ Gyr, where the Universe experiences a contraction, which could be due to the future high concentration of matter/antimatter at both sides, leading to the Big Crunch.

Congruence worldlines were simulated according to the model in Equation (17), where they produced a flat end or flat space-time at the second phase of reverse directions, as shown in Figure 3a, which presents a schematic of the 2D spatial and 1D temporal dimensions. The predicted radiation-only worldlines passing from one side to another could explain why the CMB light can be observed even though matter moves much more slowly than light. Additionally, Figure 3b shows an approximate apparent topology due to gravitational lensing effects, which is possibly in accordance with the large-angle correlations of the CMB and the SLOAN Digital Sky Survey data.

A schematic showing the 3D spatial and 1D temporal dimensions of the evolution of both sides is shown in Figure 4, where antimatter travels backwards in time. During the second phase, both sides move closer to each other; this could explain the current increase in the average temperature of the Universe [23], in contrast to the early state of cooling down from the hot plasma.

Due to the anisotropy in the expansion of the early Universe hypersphere into two sides, the expansion in time and hence the time dimension could be analysed and mathematically considered as two dimensions, the imaginary (future-past) and the real (forward-backwards) time components, where antimatter travels backwards in the real component.

5. Spiral Galaxy Formation and Rotation under External Fields

The derived wavefunction in Equation (17) predicted that the pre-existing/conformal curvature evolved over cosmic time, with the highest degree of curvature occurring at the phase transition (See Figure 2a and Figure 3a). Since gravitational forces were stronger when the Universe radius was smaller at the first phase according to Equation (1), a galaxy could form without the need for the dark matter where simulations showed galaxy formation using modified Newtonian dynamics [24]. The wavefunction showed the early Universe expanded hyperbolically at nascent stages; thus, a large gas cloud that was collapsing while travelling through the curved background would gain high spinning speed. The high-spinning speed can transform its hyperspherical core (Figure 5a) into a dual vortex that can be considered as a tower of almost hypercylinders (Figure 5b). Accordingly, the gravitational contributions come mainly from the extrinsic curvature terms, while the intrinsic curvature terms vanish as hypercylinders have no intrinsic curvature [25]; therefore, the extended field equations in Equation (4) reduced to $R_{\mu \nu }=R{\widehat{g}}_{\mu \nu }/2\cong 0$. For an ideal case $R_{\mu \nu }=0$, which gives Schwarzschild metric as $d{s}^2=\left(1-r_s/r\right)c^{2}d{t}^2-s_s{}^2/s^2\left(d{r}^2/\left(1-r_s/r\right)+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\varphi }^2\right)$, where $r_s$ is the Schwarzschild radius and $s_s{}^2/s^2$ is a dimensionless scale factor that is incorporated to account for the conformal shrinking. This is because when by comparing the conformal transformation of the time coordinate as ${\widehat{g}}_{tt}=g_{tt}+2{\overline{g}}_{tt}=\left(1-\left(r_s/r\right)\right)c^{2}d{t}^2$, which shows the conformal transformation function is ${\mathsf{\Omega }}^2=-r_s/2r$, revealing a spatial shrinking through the conformal time agreeing with the vortex model, i.e., forming a dual vortex perpendicular on the galaxy plane in opposite directions, as shown in Figure 5b. Orbiting a vortex could explain the observations of the G2 cloud where it just faced drag forces [26].

The 4D cloud (the gas cloud forming a galaxy) has 4D spin and 4D flow with respect to the 4D independent background/conformal space-time, as shown in Figure 5.

To evaluate the influence of the spinning momentum and the curvature of the background on the core of the galaxy and the surrounding gas clouds (the spiral arms), a fluid simulation has been performed based on Newtonian dynamics using the Fluid Pressure and Flow software [27]. In this simulation, the fluid was deemed to represent the space-time continuum throughout incrementally flattening curvature paths representing the conformal curvature evolution. Using these conditions, a fluid model was used to analyze the external momenta exerted on objects flowing throughout the incrementally flattening curvatures, as shown in Figure 6a. The momenta yielded by the fluid simulation were used to inform a simulation of a spiral galaxy as a forced vortex (under external fields), as shown in Figure 6b.

The simulation in Figure 6b shows that the tangential speeds of the outer parts of the spiral galaxy are rotating faster in comparison with the rotational speeds of the inner parts. Additionally, galaxies of the same mass in the present Universe should be rotating faster than they were in the past because of the increase in the external fields due to the highest spatial curvature at the phase transition; these findings are consistent with the baryonic Tully-Fisher relation [28]. Based on the simulation results, it can be concluded that the space-time conformal curvature is responsible for the high speed of outer stars, explaining the effects attributed to dark matter. This is in contrast with the dark matter hypothesis as particles which is being challenged by the detection of external fields [17].

6. Early Universe Boundary Contribution

The gravitational contributions of the early Universe plasma boundary can be obtained for high energy limits by using the boundary term in the extended field equations. At the reference imaginary time ${\tau }_p$, there is no conformal transformation. Therefore, the global ${\mathcal{K}}_{\mu \nu }$ and local $K_{\mu \nu }$ boundaries are the same; thus, $\frac{R-ℛ}{ℛ}\left(K_{\mu \nu }-\frac{1}{2}K{\widehat{q}}_{\mu \nu }\right)=\frac{8\pi G_t}{c^4}{T}_{\mu \nu }$. The induced metric tensor $q_{\mu \nu }$ on the early Universe plasma hypersphere is given in Equation (18), where $R$ is the extrinsic radius of curvature [25]:

$$\left[q_{\mu \nu }\left(\mathrm{x}\right)\right]=\mathrm{diag}\left(-c^2,\frac{a^2\left(t\right)}{a_p{}^2}{R}^2,\frac{a^2\left(t\right)}{a_p{}^2}{R}^2{\sin }^2\theta \right),$$

(18)

The extrinsic curvature tensor is solved by utilizing the formula $K_{uv}=-\overrightarrow{t_v}.{\nabla }_u{\widehat{n}}_u$. Due to the smoothness of the hypersphere, the covariant derivative reduces to the partial derivative as $K_{uv}=-\overrightarrow{t_v}\partial {\widehat{n}}_u/\partial \overrightarrow{t^u}$ [25]. The extrinsic curvature tensor at ${\tau }_p$ is

$$\left[K_{\mu \nu }\left(\mathrm{x}\right)\right]=\mathrm{diag}\left(0,-\frac{a^2\left(t\right)}{a_p{}^2}R,-\frac{a^2\left(t\right)}{a_p{}^2}R{\sin }^2\theta \right)$$

(19)

The trace of the extrinsic curvature is $K=K_{\mu \nu }{q}^{\mu \nu }=2/R$. The pre-existing/intrinsic curvature of early Universe plasma boundary at ${\tau }_p$ is ${ℛ}_p=1/r_p{}^2$ [25]. On the other hand, the Ricci scalar curvature $R_p$ at ${\tau }_p$ can be written in terms of the kinetic and potential energy densities whereby substituting Friedmann equations in Equations (8) and (9) into the Ricci scalar curvature in Equation (7) gives

$$R_p=\frac{6G_p}{c^2}\left(\frac{4\pi P_p}{c^2}-\frac{4\pi {\rho }_p}{3}\right)$$

(20)

By solving the boundary term for a perfect fluid given by $T_{\mu \nu }=\left(\rho +\frac{P}{c^2}\right)u_{\mu }{u}_{\nu }+P{g}_{\mu \nu }$ [10], and then substituting Equations (18)–(20) into the boundary term, this produces:

$$\frac{\frac{6G_p}{c^2}\left(\frac{4\pi P_p}{c^2}-\frac{4\pi {\rho }_p}{3}\right)-\frac{1}{r_p{}^2}}{1/r_p{}^2}\left(\frac{-c^2}{r_p{}^2}\right)=8\pi G_p{\rho }_p$$

(21)

By multiplying both sides by the early Universe plasma volume $V_p$ yields

$$r_p=\frac{4G_p{P}_p{V}_p}{c^4}=\sqrt[3]{\frac{E_p}{2\pi E_D}}$$

(22)

where $E_p$ is the early Universe plasma energy. The reference radius of curvature $r_p>0$ because any reduction in the volume causes an increase in the pressure, which can realise a singularity-free paradigm.

7. Conclusions and Future Works

In this study, a closed early Universe model was considered by utilizing the referenced FLRW metric model. The evolution of the Universe from early plasma was modelled by utilizing quantized space-time worldlines. The worldlines revealed two opposite solutions, implying that the early Universe plasma separated into two sides: matter and antimatter.

The derived model predicted that a nascent hyperbolic expansion was followed by a phase of decelerating spatial expansion during the first ~10 Gyr, followed by a second phase of accelerating expansion. Both sides of the Universe expanded away from the early plasma during the first phase. Then, during the second phase, they reversed their directions and fell towards each other. It is conceivable that the matter and antimatter are free-falling towards each other, causing the current accelerating expansion of the Universe. This could explain the effects attributed to dark energy, as well as the observed dark flow.

Further, the simulated space-time worldlines during the decelerating phase were found to be flattened during the accelerating phase due to the reverse direction of the continuum worldlines, explaining the current space flatness. Regarding the fast orbital speed of the outer stars, the simulation could provide a physical explanation by which the conformal curvature evolution over the cosmic time exerts external fields on galaxies. Thus, the geometrical space-time curvature could be causing them to increase in speed, rather than the existence of dark matter.

The model predicted a final phase of time-reversal of spatial contraction, leading to a Big Crunch, signifying a cyclic Universe. The derived smallest possible reference radius of the early plasma due to its boundary gravitational contributions can reveal the early Universe expansion upon emission of the CMB might mark the beginning of the Universe from a previously collapsed one. Finally, this theoretical work will be tested against observational data in future works. See supplementary materials with more relevant information.