Reconstruction of Models with Variable Cosmological Parameter in f(R,T) Theory †
Abstract
:1. Introduction
2. Basic Equations
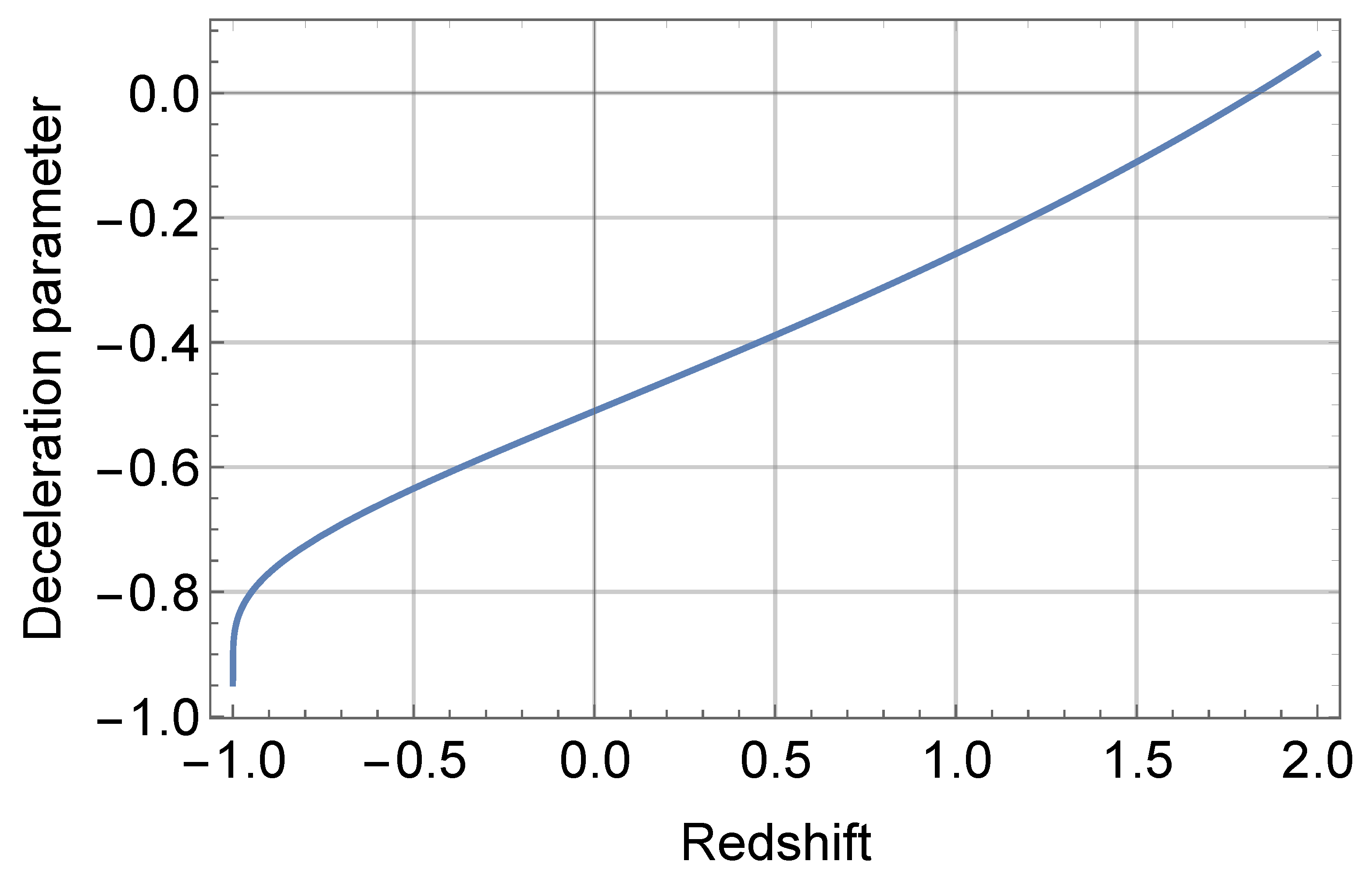
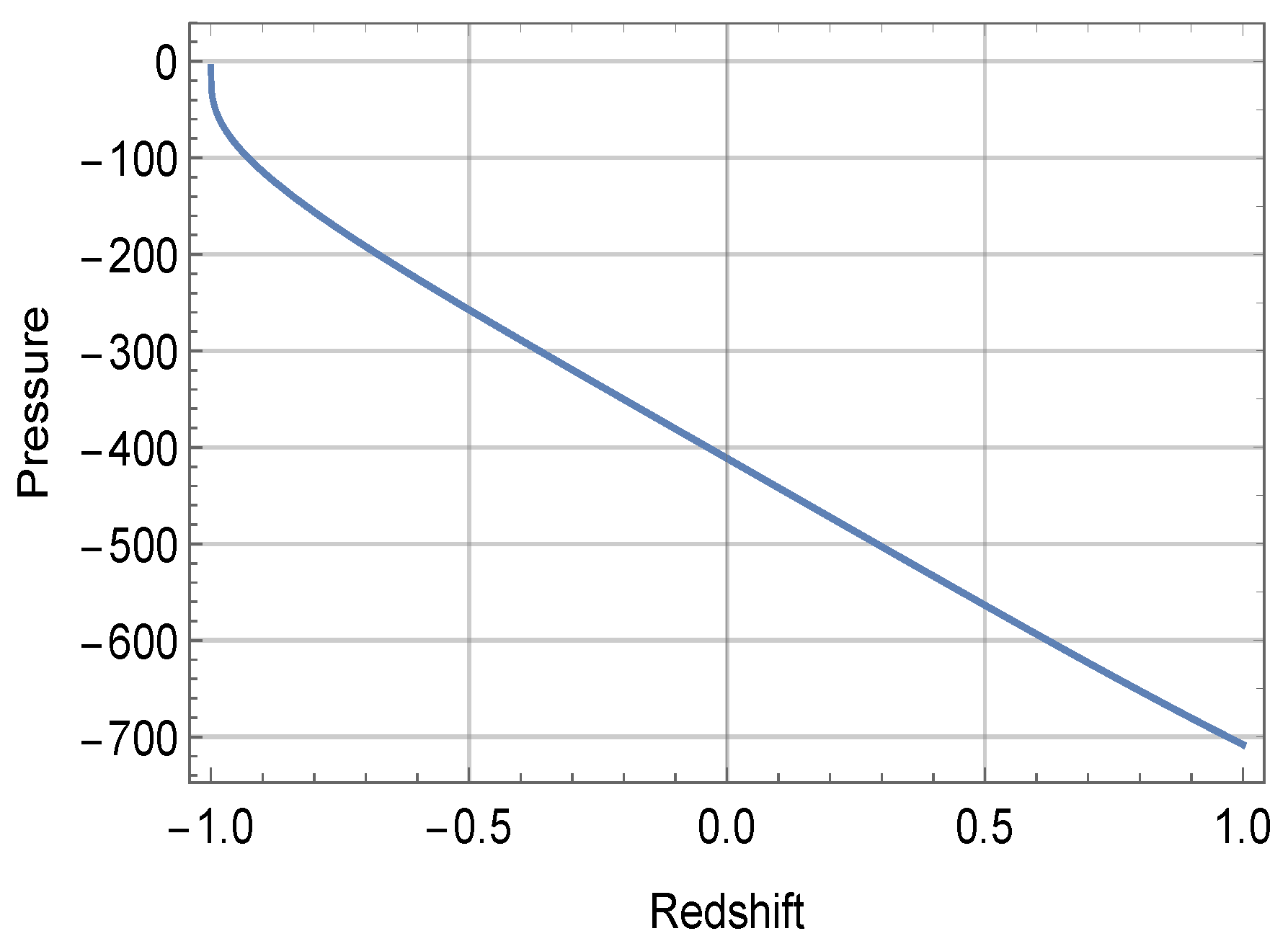
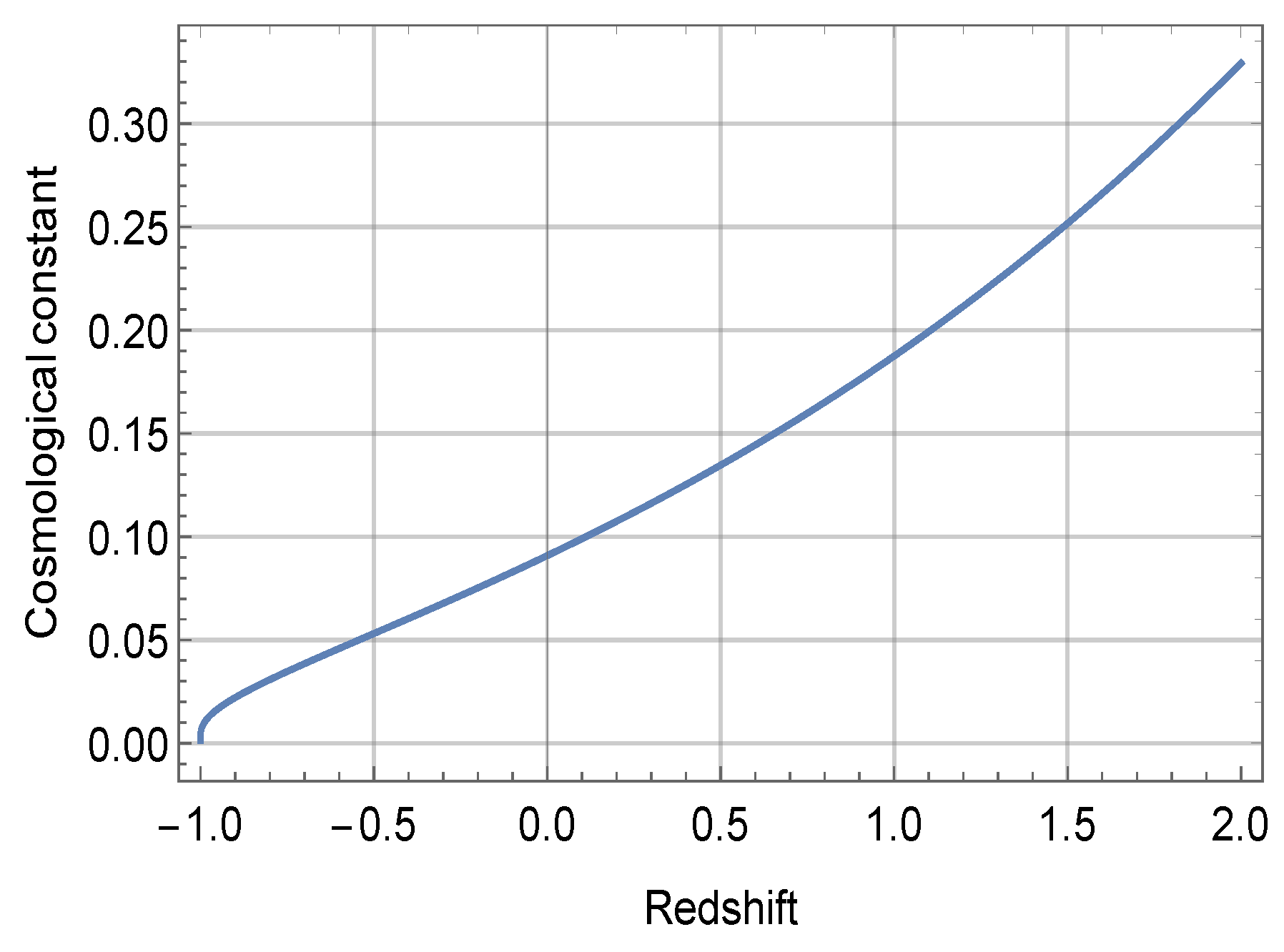
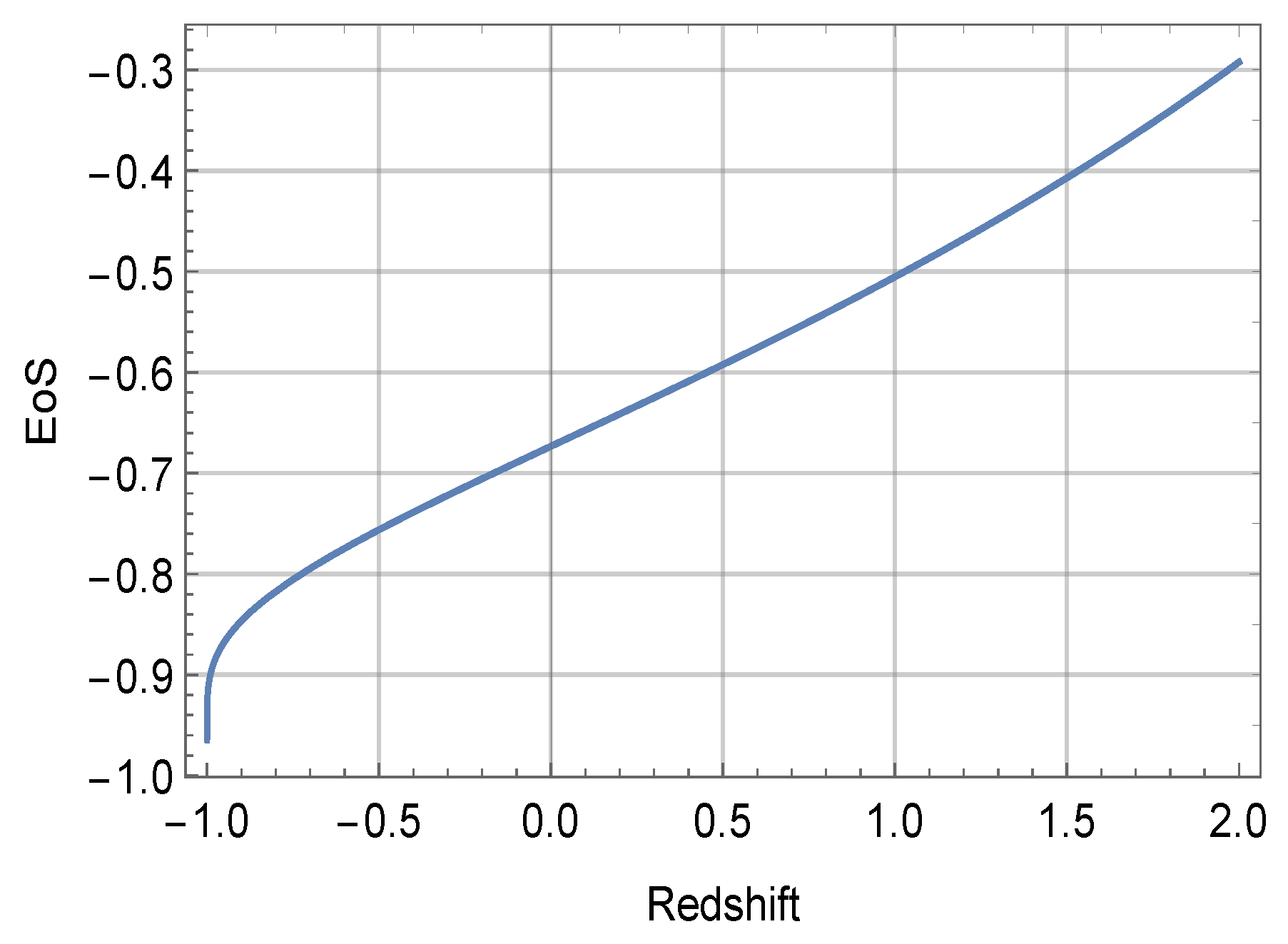
3. Solution to Field Equations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Percival, W.J.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; Collins, C.; Couch, W.; Dalton, G.; et al. The 2dF Galaxy Redshift Survey: The power spectrum and the matter content of the universe. Mon. Not. R. Astron. Soc. 2001, 327, 1297–1306. [Google Scholar] [CrossRef]
- Suwa, M.; Kobayashi, K.; Oshima, H. The Interacting Generalized Ricci Dark Energy Model in Non-Flat Universe. J. Cosmol. Astropart. Phys. 2010, 1002, 008. [Google Scholar] [CrossRef] [Green Version]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Jimenez, J.B.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Phys. Dark Univ. 2016, 12, 56–99. [Google Scholar] [CrossRef] [Green Version]
- Durrer, R.; Maartens, R. Dark Energy and Dark Gravity. Gen. Relativ. Grav. 2008, 40, 301–328. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Lobo, F.S.N.; Nokiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Beesham, A. Anisotropic model with decaying cosmological term. Astrophys. Space Sci. 2018, 363, 234. [Google Scholar] [CrossRef]
- Pasqua, A.; Chattopadhyay, S.; Khomenko, I. A reconstruction of modified holographic Ricci dark energy in f(R,T) gravity. Can. J. Phys. 2013, 91, 632–638. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.K.; Singh, R.; Shukla, B.K. A Cosmological Model with Variable Deceleration Parameter. Afr. Rev. Phys. 2015, 10, 48. [Google Scholar] [CrossRef]
- Jusus, J.F. Gaussian process estimation of transition redshift. J. Cosmol. Astropart. Phys. 2020, 4, 053. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, R.K.; Beesham, A.; Shukla, B.K. Reconstruction of Models with Variable Cosmological Parameter in f(R,T) Theory . Phys. Sci. Forum 2021, 2, 59. https://doi.org/10.3390/ECU2021-09372
Tiwari RK, Beesham A, Shukla BK. Reconstruction of Models with Variable Cosmological Parameter in f(R,T) Theory . Physical Sciences Forum. 2021; 2(1):59. https://doi.org/10.3390/ECU2021-09372
Chicago/Turabian StyleTiwari, Rishi Kumar, Aroonkumar Beesham, and Bhupendra Kumar Shukla. 2021. "Reconstruction of Models with Variable Cosmological Parameter in f(R,T) Theory " Physical Sciences Forum 2, no. 1: 59. https://doi.org/10.3390/ECU2021-09372
APA StyleTiwari, R. K., Beesham, A., & Shukla, B. K. (2021). Reconstruction of Models with Variable Cosmological Parameter in f(R,T) Theory . Physical Sciences Forum, 2(1), 59. https://doi.org/10.3390/ECU2021-09372





